光学第二章习题
《应用光学》第2章课后答案全文

12. 由两个透镜组成的一个倒像系统,设第一组透镜的焦距 为f1′,第二组透镜的焦距为f2′,物平面位于第一组透镜 的物方焦面上,求该倒像系统的垂轴放大率。
解:
1
1
1
1
F2
1
1
第一组透镜
第二组透镜
1
第二组透镜
13. 由两个同心的反射球面(二球面球心重合)构成的光学系 统,按照光线反射的顺序第一个反射球面是凹的,第二个 反射球面是凸的,要求系统的像方焦点恰好位于第一个反 射球面的顶点,求两个球面的半径r1,r2和二者之间的间隔 d之间的关系。
B′
面,如图示.
l ′ = 2f′
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l = −f′
B
……
F
F′
A
H H′
像平面在像 空间无限远 处.
l′=∞
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l f' 2
B′
r1 无穷远物点
r2
r1/2
最终像点
11 2
l2 l2 r2
l2
l2
2 r2
(l2l2 )
14. 假定显微镜物镜由相隔20mm的两个薄透镜组构成,物平 面和像平面之间的距离为180mm,放大率β=-10×,要求近 轴光线通过二透镜组时的偏角Δu1和Δu2相等,求二透镜 组的焦距。
y n1u1 u1 10
l = −f′
B
……
F′
F
H H′
A
像平面在像 空间无限远 处.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
应用光学习题(第二章)

个面对不晕像点。
n2 n2 n 1 l2 r2 r2 n2 n n2 n2 l2 r2 n 1r2 n2
1 n n 1 n 1 r1 - r2 r1 r2 n n n 由于 d始终都是大于零的,所 以r1 r2 (由于 r1 0,r2 0,且 r1 r2,该透镜为负弯月型透 镜)
1 n2
S1
S1与S2重合,所以 r2 l2 l2
d l1 l2
n
r1
C1 l2 l2 l1 r2 l1
C2
n1 n1 1 n 而 l1 r1 r1 n1 n 1 n d r1 r2 n
b. 同心球面透镜 物像点重合且位于两个 球面的共同曲率中心 C1,C 2点上Leabharlann 所以编号出处
2_004
P193_7
什么是不晕透镜?当透 镜成无球差点实像点时 ,应采用 什么样的结构形式 ?
答: ( 1)所谓不晕透镜,是轴 上物点单色光成像时, 不产生球差的透镜
(2) 由于不晕条件,物象点 在透镜的同一侧,所以 不晕透镜 分为两种情况:一种是 实物成虚像,而另一种 是虚物成实像。 该题中得到实像点时, 采用的就是虚物成实像 的形式(会聚光入射) r1 0,r2 0 a. 正弯月单透镜 r1 r2 r1 r2,所以第一个面对球心 C 1点在 C2点的左边
,S2,S 同心球面透镜构成不晕 透镜C ( ,S1,S1 2 C1 2)
n1 1
1 n2
C1 C2
n
r1 l1 l1 r2 l2 l2
,S2与S2重合 S1,S1 d r1 r2
编号
出处
2_005
课后习题试题

物理光学作业习题第一章光波的基本性质(1)作业习题1、试说明下列各组光波表达式所代表的偏振态。
⑴Ex=Eo sin(ωt-kz),Ey=Eo cos(ωt-kz)⑵Ex=Eo cos(ωt-kz),Ey=Eo cos(ωt-kz+π)4⑶Ex=Eo sin(ωt-kz),Ey=-Eo sin(ωt-kz)2、试证明:频率相同,振幅不同的右旋与左旋圆偏振光能合成一椭圆偏振光。
3、把一根截面是矩形的玻璃棒(折射率为1.5)弯成马蹄形,如图所示。
矩形宽为d,弯曲部分是一个圆,内半径是R。
光线从一个端面正入射。
欲使光线从另一端面全部出射,R/d应等于多少?4、若入射光线是线偏振光,入射角为︒45,其振动面与入射面间的夹角为︒45。
试证:这时空气和玻璃的分界面上,反射光仍然是线偏振光,并求其振动面和入射面间的夹角α以及振r动面的旋转方向。
5、欲使线偏振光的激光束通过红宝石棒时,在棒的端面上没有反射损失,则棒端面对棒轴倾角α应取何值?光束入射角φ1等于多少?入射光的振动方向如何?已知红宝石的折射率为n=1.76。
光束在棒内沿棒轴方向传播。
6、 试证明琼斯矢量⎥⎦⎤⎢⎣⎡∆i Be A 表示的椭圆偏振光,其主轴与X 轴夹角为21tan —1⎪⎭⎫ ⎝⎛-∆22cos 2B A AB (2)讨论习题1、 如图用棱镜是光束方向改变,要求光束垂直于棱镜表面射出,入射光是平行于纸面振动的H e —N e 激光(波长λ=3628Å)。
问,入射角φi 等于多少时,透射光为最强?并由此计算此棱镜底角α应磨成多少??已知棱镜材料的折射率n=1.52。
若入射光是垂直纸面振动的H e —N e 激光束,则能否满足反射损失小于1%的要求?2、 下图是激光技术中用以选择输出波长的方法之一。
它是利用在入射面内振动的光,在布鲁斯特角入射时反射光强为零,以及布鲁斯特角的值与波长有关的这些事实,使一定波长的光能以最低损耗通过三棱镜而在腔内产生振荡,其余波长的光则因损耗大而被抑制不能振荡,从而达到选择输出波长的目的。
光学第二章习题解答

∆y = y2 − y1 ≈ 2 f ′
λ
b
− f′
λ
b
= f′
λ
b
∆y ⋅ b 0.02 × 0.885 ɺ λ= = = 5900 A f′ 300
(2)波长为 波长为0.1nm的x射线时,相邻最小值间的距离为 射线时, 波长为 的 射线时
′λ 300 × 0.1×10−9 f ∆y = = 0.02 b −6 −4 = 1.5 × 10 m = 1.5 × 10 cm
主焦点
还有次焦点: 还有次焦点:± f ′ /3,
± f ′ /5, ± f ′ / 7⋯
故:光强极大值出现在轴上 1/3m,1/5m,1/7m……1/(2k+1)m等处 , , 等处
2.6 波长为 的点光源波带片成一个像点,该波带 波长为λ的点光源波带片成一个像点 的点光源波带片成一个像点, 个透明奇数半波带(1, , )。另外 有100个透明奇数半波带 ,3,5 ……199)。另外 个透明奇数半波带 )。 100个不透明偶数半波带。比较用波带片换上同样焦 个不透明偶数半波带。 个不透明偶数半波带 距和口径的透镜时像点的强度比I: 距和口径的透镜时像点的强度比 :I0 解:(1) 只有 ) 只有100个透明奇数半波带透过 个透明奇数半波带透过
∵
θ3 < θ 2
∴
二级和三级光谱部分重叠 二级和三级光谱部分重叠
2.14 用波长为 用波长为589nm的单色光照射一衍射光栅, 的单色光照射一衍射光栅 的单色光照射一衍射光栅, 其光谱的中央最大值和第二十级主最大值之间的衍 射角为15 10′。试求该光栅1cm内的缝数是多少? 15° cm内的缝数是多少 射角为15°10′。试求该光栅 cm内的缝数是多少? 解: 由光栅方程 d sin θ = jλ
工程光学习题参考答案第二章理想光学系统
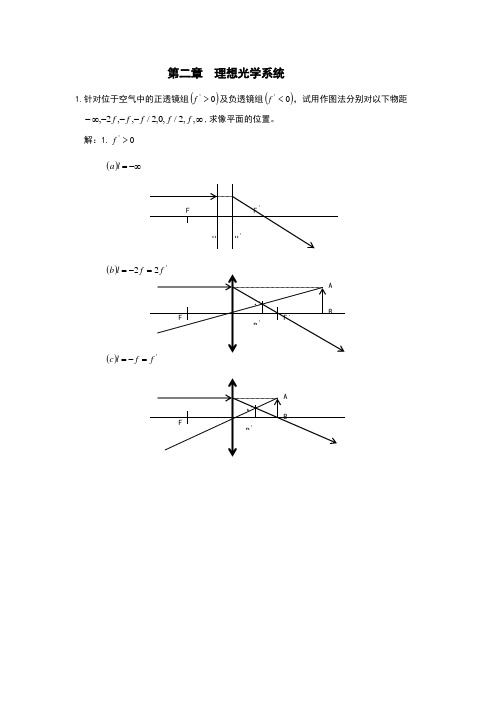
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ,试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解:1.0'>f ()-∞=l a()'2f l b -=()f f l c =-=()/f l d -=()0=l e()/f l f =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’=75mm,被摄景物位于(以F 点为坐标原点)=x ,2,4,6,8,10,m m m m m -----∝-处,试求照相底片应分别放在离物镜的像方焦面多远的地方。
解: (1)x= -∝ ,xx ′=ff ′ 得到:x ′=0 (2)x ′= (3)x ′= (4)x ′= (5)x ′=(6)x ′=3.设一系统位于空气中,垂轴放大率*-=10β,由物面到像面的距离(共轭距离)为7200mm , 物镜两焦点间距离为1140mm 。
求该物镜焦距,并绘出基点位置图。
解:∵ 系统位于空气中,f f -='10''-===ll y y β 由已知条件:1140)('=+-+x f f7200)('=+-+x l l解得:mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上,当透镜向物体移近18mm 时,物体将被放大*-4,试求透镜的焦距,并用图解法校核之。
解:方法一:31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二: 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三: 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像,放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动,放大率为原先的3/4倍,求两块透镜的焦距为多少 解:⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向物体移近100mm , 则所得像与物同大小,求该正透镜组的焦距。
光学课件全部习题

解:三列平面波的复振幅分别为
选z=0平面
~ E1 = A1e i ( − k sin θx + k cosθz ) = A1e − ik sin θx ~ ikz E2 = A2 e = 2 A1
~ E3 = A3e i ( k sin θx + k cosθz ) = A1e ik sin θx
~ ~* ~ ~ ~ ~* ~* ~* I = EE = ( E1 + E2 + E3 )( E1 + E2 + E3 )
wwwwenku1comview9c970f097eb60a1分布a2sinkz221有三列在xz平面内传播的同频率单色平面波其振幅分别为a1a2a3传播方向如图求xy平面上的光强分布可设三列波在坐标原点初相均为0
第二章部分典型习题答案
2h1 +
λ1
2
= m1λ1
2h1 +
λ2
2
= m2 λ2
2h2 + 2h2 +
λ1
2
kλ1 = (k + 1)λ2
= (m1 + k )λ1 = (m2 + k + 1)λ2
980λ1 = 981λ2
λ2
2
λ1 = 589.6nm λ1 = 589nm
第四章部分典型习题答案
4.10 单色平面波垂直照射图示的衍射屏,图中标出的是该处到轴上场点 的光程,屏中心到场点的光程为ro,阴影区为不透光区.试用矢量图解 法求场点的光强与波自由传播时该场点的光强的比值.
2
2
I = 5I F
r0 + λ r0 + λ / 4
1 A= 2 AF 4
工程光学第二版习题答案(李湘宁_贾志宏)

丝,问其通过球面的共轭像在何处?当入射高度
h=10mm,实际光线的像方截距为多少?与高斯像面的距离
为多少?
解:
8、一球面镜半径 r=-100mm, 求 = 0 , -0.1 , -0.2 , -1 ,1 , 5, 10,∝时的物距像距。
第 4 页 共 29 页
解:( 1)
东北石油大学测控 09 级工程光学期末复习资料
解:
100mm,则所得像与物
6.希望得到一个对无限远成像的长焦距物镜,焦距 系统最后一面到像平面的距离 (工作距) 为 并画出光路图。
解:
=1200mm,由物镜顶点到像面的距离 L=700 mm,由 ,按最简单结构的薄透镜系统考虑, 求系统结构,
7.一短焦距物镜,已知其焦距为 系统结构。
35 mm,筒长 L=65 mm,工作距 , 按最简单结构的薄透镜系统考虑,求
3.一光学系统由一透镜和平面镜组成,如图
3-29 所示,平面镜 MM与透镜光轴垂直交于 D 点,透镜前方
离平面镜 600 mm有一物体 AB,经透镜和平面镜后,所成虚像
至平面镜的距离为 150 mm,且像高为
物高的一半,试分析透镜焦距的正负,确定透镜的位置和焦距,并画出光路图。
解:平面镜成 β =1 的像,且分别在镜子两侧,物像虚实相反 级工程光学期末复习资料
第六章习题
1.如果一个光学系统的初级子午彗差等于焦宽(),则
应等于多少?
解:
2.如果一个光学系统的初级球差等于焦深
(),则
应为多少? 解:
3. 设计一双胶合消色差望远物镜,
和火石玻璃 F2(
,
面的曲率半径。
解:
,采用冕牌玻璃 K9 (
解:设一个气泡在中心处,另一个在第二面和中心之间。
《光学教程》(姚启钧)第二章 光的衍射

3. 惠更斯-菲涅耳原理(1818)
菲涅耳对惠更斯原理的改进: 给不同次波赋予相应的相位和振幅,并将次波的干涉 叠加性引入惠更斯原理,得到衍射的定量表达式。
波面S上每个面元dS都是次波源,次波在p点引起振动的振幅与面积dS成正 比,与距离r成反比,且与倾角有关。
A(Q) K ( ) dE( P) dS r
相应的振动相位依次为:
a1 a2 a3 a4 ...... ak ak 1
f1,f1+,f1+2, f1+3,…f1+(k-1),f1+k。
对于轴上光源点 S 和轴上场点 P ,设圆孔恰好分 为 k 个半波带,则有
~ i 1 E1 a1e ~ i 1 E2 a2e ~ i 1 2 E3 a3e
次波中心Q 的光振幅 Q点在p 点引起的 光波振幅 倾斜因子 次波中心附 近的小面元
d · r S Q S(波面)
次波中心 设初相为零
n
dE(p) · p
观 察 点
倾斜因子K()的特点
A(Q) K ( ) dE( p) C dS cos(kr t ) r
0, K K max K ( ) , K 0 2
2
1mm 1000 mm 1000 mm 4 6 1000 mm 1000 mm 500 10 mm
2
半径为0.5mm的圆屏挡住的波带数为:
j
'
0.5mm 1000mm 1000mm 1 1000mm 1000mm 500 106 mm
又:
( h r0 , R)
2 2
R rk (r0 h)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题一、选择题:2008.在菲涅耳圆屏衍射的几何阴影中心处( B )(A)永远是个亮点,其强度只与入射光强有关。
(B)永远是个亮点,其强度随着圆屏的大小而变。
(C)有时是亮点,有时是暗点。
2014.一波长为500nm的单色平行光,垂直射到0.02cm宽的狭缝上,在夫琅禾费衍射花样中心两旁第二条暗纹之间的距离为3mm,则所用透镜的焦距为( D )(A)60mm (B)60cm (C)30mm (D)30cm2026.一个衍射光栅宽为3cm,以波长为600nm的光照射,第二级主极大出现于衍射角为300处。
则光栅的总刻度线数为A(A)1.25*104 (B)2.5*104 (C)6.25*103 (D)9.48*1032028.X 射线投射在间距为d的平行点阵面的晶体中,试问发生布拉格晶体衍射的最大波长为多少?D(A)d/4 (B)d/2 (C)d (D)2d2128. 菲涅尔圆孔衍射实验表明,几何光学是波动光学在一定条件下的近似,如果从圆孔露出来的波面对所考察的点作出的的半波带的数目为K,这种条件下可表达成:( D )(A)衍射波级数K~0;(B)衍射波级数K=1;(C)衍射波级数K〉1;(D)衍射波级数K〉〉1。
2129. 用半波带法研究菲涅尔圆孔的衍射的结果说明,圆孔轴线上的P点的明暗决定于:(C )(A)圆孔的大小;(B)圆孔到P点的距离;(C)半波带数目的奇偶;(D)圆孔半径与波长的比值。
2130 用半波带法研究菲涅尔圆孔衍射时,圆孔线上P点的明暗决定于:(D )(A)圆孔的直径;(B)光源到圆孔的距离;(C)圆孔到P的距离;(D)圆孔中心和边缘光线到P点的光程差。
2131 一波带片主焦点的光强约为入射光强的400倍,则波带片的开带数为:( A )(A)10;(B)20;(C)40;(D)100。
2132 在夫琅和费单缝衍射中,当入射光的波长变大时,中央零级条纹:(B )(A)宽度变小;(B)宽度变大;(C)宽度不变;(D)颜色变红。
2135 从光栅衍射光谱中你看出哪种可见光衍射比较显著?(A )(A)红光;(B)黄光;(C)绿光;(D)紫光。
2136 在光栅衍射实验中,为了得到较多的谱线,应该:( B )(A)适当减小光栅常数d;(B)适当增加光栅常数d;(C)适当减少缝数N;(D)适当增加缝数N。
2137 在光栅衍射实验中,若只增加光栅的缝数N,将会改变衍射图中的:(C )(A)干涉主最大的位置;(B)单缝衍射中亮纹内的谱线数;(C)光谱线的亮度和宽度;(D)光谱线的亮度和位置。
2138 若白光照射到衍射光栅上,在某一级光谱中,偏离中心最远的光的颜色是:( A )(A)红;(B)黄;(C)蓝;(D)紫。
2139 为了增加光栅衍射的分辨本领,可以:( C )(A)减小缝的宽度;(B)减小光栅常数;(C)增加缝数;(D)增加光的波长。
3140 NaCl晶体的晶格常数为0.28nm,用波长为1.40?的伦琴射线照射晶面,转动晶体出现第二级衍射条纹的偏向角φ为:( D )(A)30度;(B)40度;(C)50度;(D)60度。
2141 NaCl晶体的晶格常数为0.28nm,用x射线照射晶面,第二级光谱的掠射角为1度,则x射线的波长为:( A )(A)0.049?;(B)0.025?; (C) 2.8?;(D)1.4?。
二、填空题:1002.衍射可分为菲涅耳衍射和夫琅禾费衍射两大类。
1014.光的衍射条件是障碍物的限度和波长可比拟。
1133. 光波的波长为λ的单色光,通过线度为l的障碍物时,只有当_________________才能观察到明显的衍射现象。
1134. 惠更斯-菲涅尔原理是在惠更斯原理基础上,进一步考虑了_次波的干涉,补充和发展了惠更斯原理二建立起来的。
1135. 在菲涅尔圆孔衍射中,单色点光源距圆孔为R,光波波长为λ,半径为ρ的圆孔露出的波面对在轴线上的距圆孔无限远处可作的半波带数为1136. 在菲涅尔圆孔衍射中,圆孔半径为6 mm,波长为600nm的平行单色光垂直通过圆孔,在圆孔的轴线上距圆孔6 m处可作___10_____个半波带。
1137. 在菲涅尔圆孔衍射中,入射光的强度为I0,在轴线上P点的光程差为λ/2时,P点的光强与入射光强的比为1138. 在菲涅尔圆孔衍射中,入射光的振幅为A,在轴线上P点恰好作出一个半波带,该点的光强为2a1139. 在夫琅禾费单缝衍射中,缝宽为a,在衍射角为方向θ,狭缝边缘与中心光线的光程差为.。
1140. 在夫琅禾费单缝衍射中,缝宽为a,波长为λ,在衍射角为方向θ,狭缝两边缘光波的位相差为。
1141. 在夫琅禾费单缝衍射中,缝宽为a,波长为λ,在观察屏上出现暗纹的条件,有衍射角θ可表示为.(k=1,2,3等)。
1142. 夫琅禾费双缝衍射是与单缝衍射和双缝衍射的总效果,其光强表达式中, (sinu/u)^2 _是单缝衍射因子,(cos&/2)^2是双缝干涉因子。
1143. 光栅衍射是夫琅禾费单缝衍射和多缝干涉的总效果,单缝衍射因子是(sinu/u)^2 _,多缝干涉因子是(cos&/2)^21144. 光栅衍射实验中,光栅常数为a+b,缝数为N,两相邻主最大之间有N-1个最小,两相邻次最小中有N-2 个最大1145. 在光栅衍射实验中,光栅常数为d,能观察到衍射条纹的最大波长为。
d1146. 光栅衍射的第三级缺级,则光栅常数与缝宽之比为3;还有第6,9,12……级主级大缺级。
1147. 光栅常数为2.5×10-4 cm的光栅,它的第一级和第四级谱线的分辨本领分别为12000和48000。
1148. 波长为λ的平行单色光垂直这是到半径为a的圆孔上所产生的衍射,中心亮斑称爱里斑,它的角半径为1149. 强激光从激光器孔径为d的输出窗射向月球,得到直径为D的光斑。
如果激光器的孔径是2d,则月球上的光斑直径是D/2。
1150. 直径为2 mm的氦氖激光束(λ=633 nm),西欧那个地面射向月球,已知月球到地面的建立为3.76×105 km,则在月球上得到的光斑直径为2.90*105m。
三、简答题:3026.什么是光的衍射?.答:光绕过障碍物偏离直线传播而进入几何阴影,并在屏幕上出现光强分布不均匀的现象3027.明显产生衍射现象的条件是什么?答:障碍物的线度和光的波长可以比拟。
3028.惠更斯-菲涅耳原理是怎样表述的?8.答:障碍物的线度和光的波长可以比拟3029.衍答:障碍物的线度和光的波长可以比拟。
:衍射分菲涅耳衍射和夫琅禾费衍射两大类。
3030.什么叫半波带?答:由任何相邻两带的对应部分所发出的次波到达P点时的光程差都为半个波长(即相位相反)而分成的环形带。
3031.为什么圆屏几何影子的中心永远有光?答:由于圆屏衍射。
3032.夫琅禾费单缝衍射有哪些明显特征?答:中央有一条特别明亮的亮条纹,两侧排列着一些强度较小的亮条纹,相邻的亮条纹之间有一条暗条纹;两侧的亮条纹是等宽的,而中央亮条纹的宽度为其他亮条纹的两倍3033.什么是艾里斑?答:在夫琅禾费圆孔衍射图样的中央,光强占总光强的84%的亮斑。
3034.艾里斑的半角宽度为多少?答:艾里斑的半角宽度为:3035.艾里斑的线半径怎样计算?答:艾里斑的线半径为:3036.干涉和衍射有什么关系?3037.光栅的光谱线在什么情况下缺级?在什么情况下重叠?计算题:答:当 d 是 b 的倍数时,光栅的光谱线发生缺级。
光栅的光谱线发生重叠的条件是:。
四、4003.波长为546.1 nm 的平行光垂直地射在1 mm 宽的缝上,若将焦距为100 cm 的透镜紧贴于缝的后面,并使光聚焦到屏上,试问衍射图样的中央到⑴ 第一最大值;⑵第一最小值;⑶ 第三最小值的距离分别为多少?.解:4005.请按以下要求设计一块光栅:① 使波长600 nm 的第二级谱线的衍射角小于30°,并能分辨其0.02 nm 的波长差;② 色散尽可能大;③ 第三级谱线缺级。
则该光栅的缝数、光栅常量、缝宽和总宽度分别是多少?用这块光栅总共能看到600 nm 的几条谱线?解:4013.钠光通过宽为0.2mm的狭缝后,投射到与缝相距300cm的照相版上,所得的第二最小距离为0.885cm,则钠光的波长为多少?若改用波长为0.1nm的X射线作此实验,则版上的这两个最小值之间的距离是多少?解:(1)强度为最小值的点满足:第二最小的距离为:(2)4018.一平面透射光栅的光栅常数d=1.5mm,宽度D=3cm,一束准单色光以300角射到光栅上,已知光栅后透镜只能接受衍射角小于600角的衍射光,在透镜后焦面上接受衍射光谱。
试求:(1).在第一级光谱中能否分辨波长为500nm和500.01nm的两条相邻谱线?(2).最多能收到第几级光谱?能分辨的最小波长间隔是多少?.解:(1)光栅的分辨本领入射光中所含双线的波长差为0.01nm<0.025nm,故第一级光谱不能分辨该双线。
(2)平行光斜入射时,对于与入射线在法线同侧的衍射线所满足的光栅方程为将==300,=600代入上式,得最大光谱级次为故最多能观察到第4级光谱,在第4级能分辨的最小波长间距为继续阅读。
