matlab第三章习题解答

合集下载

matlab课后习题及答案

第一章 5题已知a=4.96，b=8.11，计算)ln(b a eba +-的值。

解：clear clc a=4.96; b=8.11;exp(a-b)/log(a+b) ans =0.0167 6题已知三角形的三边a=9.6,b=13.7, c=19.4,求三角形的面积。

提示：利用海伦公式area =))()((c s b s a s s ---计算，其中S=(A+B+C)/2. 解：clear clc a=9.6; b=13.7; c=19.4; s=(a+b+c)/2area=sqrt(s*(s-a)*(s-b)*(s-c)) s =21.3500 第二章 8题已知S=1+2+2^2+2^3+……+2^63,求S 的值解：clear clc S=0;for i=0:1:63 S=S+2^i; end S S =1.8447e+019 9题分别用for 和while 循环结构编写程序，计算∑=-1001n 1n 2）（的值。

解：clear clc s=0;for n=1:100 s=s+(2*n-1); end s s =10000 clear clc n=1; s=0;while n<=100 s=s+(2*n-1); n=n+1; end s s =10000 第三章 2题在同一坐标下绘制函数x ,,2x-,2x xsin(x)在()∏∈,0x 的曲线。

解：clear clcx=0:0.2:pi; y1=x; y2=x.^2; y3=-(x.^2); y4=x.*sin(x);plot(x,y1,'-' ,x,y2,'-' ,x,y3,'-' ,x,y4,'-')0.511.522.53-10-8-6-4-202468109题用不同的线型和颜色在同一坐标内绘制曲线y1=2ex5.0 、y2=sin(2∏x )的图形。

MATLAB基础及其应用教程-周开利-邓春晖课后答案,第三章

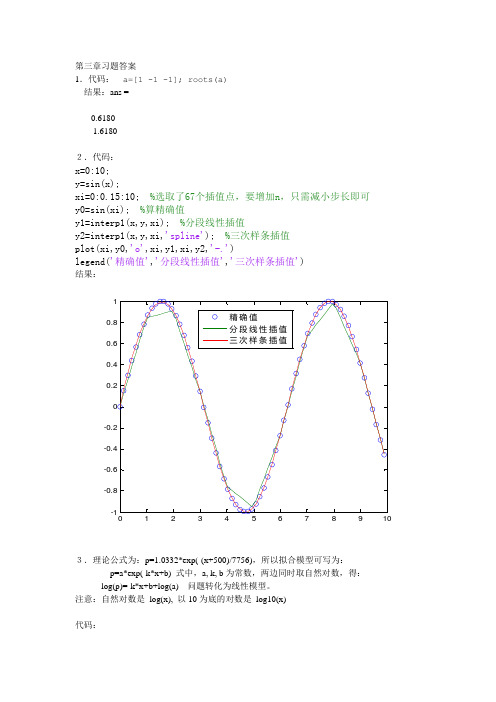
第三章习题答案1．代码：a=[1 -1 -1]; roots(a)结果：ans =-0.61801.6180２．代码：x=0:10;y=sin(x);xi=0:0.15:10; %选取了67个插值点，要增加n，只需减小步长即可y0=sin(xi); %算精确值y1=interp1(x,y,xi); %分段线性插值y2=interp1(x,y,xi,'spline'); %三次样条插值plot(xi,y0,'o',xi,y1,xi,y2,'-.')legend('精确值','分段线性插值','三次样条插值')结果：３．理论公式为：p=1.0332*exp(-(x+500)/7756)，所以拟合模型可写为：p=a*exp(-k*x+b) 式中，a, k, b为常数，两边同时取自然对数，得：log(p)=-k*x+b+log(a)问题转化为线性模型。

注意：自然对数是log(x), 以10为底的对数是log10(x)代码：clear;x=[0 300 600 1000 1500 2000];p=[0.9689 0.9322 0.8969 0.8519 0.7989 0.7491];lnp=log(p); %转化为 p 的自然对数值,模型转化为线性模型pk=polyfit(x,lnp,1); % 线性拟合,得到模型的斜率pk(1)和常数pk(2) 模型为: p=exp(pk(1)*x)*exp(pk(2))xi=0:50:2000;p0=1.0332*exp(-(xi+500)/7756); %理论值p1=exp(pk(1)*xi+pk(2)); %拟合模型值p2=interp1(x,p,xi,'spline'); %三次样条插值plot(x,p,'p',xi,p0,xi,p1,'--',xi,p2,'-.');legend('测量值','理论值','拟合值','三次样条值');format long % 数据显示格式为15位有效数字x2=0:200:2000 % 取10个点，比较差异pp1=1.0332*exp(-(x2+500)/7756) %理论值pp2=exp(pk(1)*x2+pk(2)) % 拟合值pp3=interp1(x,p,x2,'spline') % 样条插值err1=sum(abs(pp2-pp1).^2) % 拟合值的误差绝对值总和err2=sum(abs(pp3-pp1).^2) % 样条值的误差绝对值总和结果：0200400600800100012001400160018002000从图像上，都符合得很好，但很难看出差异。

matlab课后习题答案第三章

第3章数值数组及其运算习题3及解答1 要求在闭区间]2,0[ 上产生具有10个等距采样点的一维数组。

试用两种不同的指令实现。

〖目的〗●数值计算中产生自变量采样点的两个常用指令的异同。

〖解答〗%方法一t1=linspace(0,2*pi,10)%方法二t2=0:2*pi/9:2*pi %要注意采样间距的选择，如这里的2*pi/9.t1 =Columns 1 through 70 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 Columns 8 through 104.88695.58516.2832t2 =Columns 1 through 70 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 Columns 8 through 104.88695.58516.28322 由指令rng('default'),A=rand(3,5)生成二维数组A，试求该数组中所有大于0.5的元素的位置，分别求出它们的“全下标”和“单下标”。

〖目的〗●数组下标的不同描述：全下标和单下标。

●sub2ind, int2str, disp的使用。

●随机发生器的状态控制：保证随机数的可复现性。

〖解答〗rng('default')A=rand(3,5)[ri,cj]=find(A>0.5);id=sub2ind(size(A),ri,cj);ri=ri';cj=cj';disp(' ')disp('大于0.5的元素的全下标')disp(['行号 ',int2str(ri)])disp(['列号 ',int2str(cj)])disp(' ')disp('大于0.5的元素的单下标')disp(id')A =0.8147 0.9134 0.2785 0.9649 0.95720.9058 0.6324 0.5469 0.1576 0.48540.1270 0.0975 0.9575 0.9706 0.8003大于0.5的元素的全下标行号 1 2 1 2 2 3 1 3 1 3列号 1 1 2 2 3 3 4 4 5 5大于0.5的元素的单下标1 2 4 5 8 9 10 12 13 153 采用默认全局随机流，写出产生长度为1000的“等概率双位（即取-1，+1）取值的随机码”程序指令，并给出 -1码的数目。

(完整版)第3章MATLAB矩阵处理_习题答案

3
B．y=cond(A) D．y=norm(A)
1．建立 3 阶幺矩阵的命令是
。ones(3)
2．设 A 为 2×3 矩阵，则用 zeros(size(A))建立的矩阵是
行
列的
矩阵。2，3，零
3．将 3 阶魔方矩阵主对角线元素加 10，命令是
。10*eye(3)+magic(3)
4．
可以用来描述矩阵的性能，它越接近于
D．B=diag(tril(A))
7．在 MATLAB 中定义 A=randn(5,4,3,2)，则下列关于 A 的操作中正确的是（
）。D
A．y=eig(A)
B．y=reshape(A,[4 3 6 7])
C．y=cond(A)
D．y=sin(A)
8．在命令行窗口中分别输入下列命令，对应输出结果正确的是（
7 8 9
10 11 12
，
B
10
7
4
1
11 8 5 2
12
3
9
，
C
6
6
9
3
12
2 5 8 11
1
4
7
10
第 1 题: (1)
a=1:12;
A=reshape(a,3,4)
(2)
B=rot90(A)
(3)
C=rot90(A,-1) 3．用矩阵求逆法求线性方程组的解。
4
x1
3x1
2x2 x3 x2 2x3
）。 C
A．命令 x=[-2:2]'，结果 x=[-2 -1 0 1 2]
B．命令 x=zeros(1,2);x>0，结果 ans=1
C．命令 y=diag(eye(3),1)&#,2)，结果 ans=[-5.0501 1.2311]

matlab第三章课后部分答案

matlab第三章课后部分答案习题三3-2 从键盘输入一个三位整数，将它反向输出。

如输入639，输出为936程序如下：m=input('请输入一个三位整数：');m1=fix(m/100);%求m的百位整数m2=rem(fix(m/10),10);%求m的十位数字m3=rem(m,10);%求m的个位数字m=m3*100+m2*10+m1%反向输出m3-3 输入一个百分制成绩，要求输出成绩等级A,B,C,D,E。

其中90~100分为A，80~89分为B，70~79分为C，60~69分为D，60分以下为E。

要求：（1）分别用if语句和switch语句实现。

（2）输入百分制成绩后要判断该成绩的合理性，对不合理的成绩应输出出错信息。

程序如下：（1）if语句c=input('请输入成绩：');if c>=90&c<=100disp('A 成绩合理');elseif c>=80&c<=89disp('B 成绩合理');elseif c>=70&c<=79disp('C 成绩合理');elseif c>=60&c<=69disp('D 成绩合理');elseif c<60disp('E 成绩合理');elsedisp('成绩错误');end（2）switch语句c=input('请输入成绩：');switch fix(c)case num2cell(90:100)disp('A 成绩合理');case num2cell(80:89)disp('B 成绩合理');case num2cell(70:79)disp('C 成绩合理');case num2cell(60:69)disp('D 成绩合理');case num2cell(0:59)disp('E 成绩合理');otherwisedisp('成绩错误');end3-4 建立5*6矩阵，要求输出矩阵第N行元素。

matlab第二版课后习题答案

matlab第二版课后习题答案
《MATLAB第二版课后习题答案》
MATLAB是一种强大的数学软件，被广泛应用于工程、科学和金融等领域。

《MATLAB第二版》是一本经典的教材，为了帮助学生更好地掌握MATLAB的使用，书中提供了大量的课后习题。

下面我们将为大家总结一些MATLAB第二版课后习题的答案，希望能对大家的学习有所帮助。

1. 第一章课后习题答案
第一章主要介绍了MATLAB的基本操作，包括变量的定义、矩阵的运算、函数的使用等。

在课后习题中，有一道题目是要求计算一个矩阵的逆矩阵。

答案是使用MATLAB中的inv函数，将原矩阵作为参数传入即可得到逆矩阵。

2. 第二章课后习题答案
第二章介绍了MATLAB中的绘图功能，包括二维和三维图形的绘制。

有一道课后习题是要求绘制一个正弦曲线和余弦曲线，并在同一张图上显示。

答案是使用MATLAB中的plot函数，分别绘制正弦曲线和余弦曲线，并使用legend函数添加图例。

3. 第三章课后习题答案
第三章介绍了MATLAB中的控制流程，包括if语句、for循环和while循环等。

有一道课后习题是要求编写一个程序，计算1到100之间所有偶数的和。

答案是使用for循环遍历1到100之间的所有数，判断是否为偶数并累加。

通过以上几个例子，我们可以看到MATLAB第二版课后习题的答案涵盖了各种基本和高级的操作，对于学习MATLAB是非常有帮助的。

希望大家在学习MATLAB的过程中能够多加练习，掌握更多的技巧和方法。

matlab第三章课后题

(1).> a={1,2,3,4}a =[1] [2] [3] [4]结论这个是一种单元结构(2).卷积简单定义：卷积是分析数学中一种重要的运算。

设:f(x),g(x)是R1上的两个可积函数，作积分：可以证明，关于几乎所有的实数x，上述积分是存在的。

这样，随着x的不同取值，这个积分就定义了一个新函数h(x)，称为函数f与g的卷积，记为h(x)=(f*g)(x)。

容易验证，(f * g)(x) = (g * f)(x)，并且(f * g)(x)仍为可积函数。

这就是说，把卷积代替乘法，L1（R1）空间是一个代数，甚至是巴拿赫代数。

卷积与傅里叶变换有着密切的关系。

利用一点性质，即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换，能使傅里叶分析中许多问题的处理得到简化。

由卷积得到的函数f*g一般要比f和g都光滑。

特别当g为具有紧致集的光滑函数，f 为局部可积时，它们的卷积f * g也是光滑函数。

利用这一性质，对于任意的可积函数f，都可以简单地构造出一列逼近于f的光滑函数列fs，这种方法称为函数的光滑化或正则化。

卷积的概念还可以推广到数列、测度以及广义函数上去。

(3).% polynomial operationp1=[1 2 1]; %¶¨Òå¶àÏîÊ½p2=[1 1];length_of_p1=length(p1);length_of_p2=length(p2);if (length_of_p1==length_of_p2 ) % ÅÐ¶ÏÁ½¸ö¶àÏîÊ½ÊÇ·ñ³¤¶ÈÏàµÈp1_plus_p2=p1+p2; % ¶àÏîÊ½Ïà¼Óp1_minus_p2=p1-p2; % ¶àÏîÊ½Ïà¼õelseif length_of_p1<length_of_p2temp_p1=[zeros(length_of_p2-length_of_p1)p1];p1_plus_p2=temp_p1+p2;p1_minus_p2=temp_p1-p2;elsetemp_p2=[zeros(length_of_p1-length_of_p2)p2];p1_plus_p2=p1+temp_p2;p1_minus_p2=p1-temp_p2;endp1_multiply_p2=conv(p1,p2);p1_divide_p2=deconv(p1,p2);p1=poly2sym(p1)p2=poly2sym(p2)p1_plus_p2=poly2sym(p1_plus_p2)p1_minus_p2=poly2sym(p1_minus_p2)p1_multiply_p2=poly2sym(p1_multiply_p2)p1_divide_p2=poly2sym(p1_divide_p2)>>duoxiangship1 =x^2 + 2*x + 1p2 =x + 1p1_plus_p2 =x^2 + 3*x + 2p1_minus_p2 =x^2 + xp1_multiply_p2 =x^3 + 3*x^2 + 3*x + 1p1_divide_p2 =x + 1总结总是出错，也不知道错那啦，他说不符合matlab的语法我在书上照着模样敲得也错，没办法！解决了这个毛病原来一点点空格还会影响！真心对她弗拉！。

matlab程序设计第三章课后习题答案资料

m a t l a b程序设计第三章课后习题答案1. p138 第6题在同一坐标轴中绘制下列两条曲线并标注两曲线交叉点。

>> t=0:0.01:pi;>> x1=t;>> y1=2*x1-0.5;>> x2=sin(3*t).*cos(t);>> y2=sin(3*t).*sin(t);>> plot(x1,y1,'r-',x2,y2,'g-')>> axis([-1,2,-1.5,1])>> hold on>> s=solve('y=2*x-0.5','x=sin(3*t)*cos(t)','y=sin(3*t)*sin(t)');>> plot(double(s.x),double(s.y),'*');截图：p366 第4题绘制极坐标曲线，并分析对曲线形状的影响。

function [ output_args ] = Untitled2( input_args )%UNTITLED2 Summary of this function goes here% Detailed explanation goes heretheta=0:0.01:2*pi;a=input('请输入a的值：');b=input('请输入b的值：');n=input('请输入n的值：');rho=a*sin(b+n*theta);polar(theta,rho,'k');end下面以a=1，b=1，n=1的极坐标图形为基础来分析a、b、n的影响。

对a的值进行改变：对比发现a只影响半径值的整倍变化对b的值进行改变：对比发现b的值使这个圆转换了一定的角度对n的值进行改变：对比发现当n>=2时有如下规律1、当n为整数时，图形变为2n个花瓣状的图形2、当n为奇数时，图形变为n个花瓣状的图形分别让n为2、3、4、5同时改变b和n的值，对比发现图形变为2n个花瓣状，并且还旋转了一定角度1 绘制sin(x)曲线，通过句柄修改曲线的颜色，要求：a）生成曲线的同时，获取句柄，再修改颜色；>> x=0:pi/50:2*pi;>> y=sin(x);>> h=plot(x,y)h =174.0101>> set(h,'color','r');截图如下：b）先生成曲线，然后再获取句柄，再完成颜色修改。

matlab答案第三章

第三章1.写出完成下列操作的命令。

（1）建立3阶单位矩阵A 。

（2）建立5x6随机矩阵A ，其元素为[100，200]范围内的随机整数。

（3）产生均值为1，方差为0.2的500个正态分布的随机数。

（4）产生和A 同样大小的幺矩阵。

（5）将矩阵A 对角线的元素加30。

答：(1)A=eye(3)(2) A=100+100*rand(5,6)(3)A=1+sqrt(0.2)*randn(10,50) (4)B=ones(size(A)) (5)A+30*eye(size(A))2.建立一个方阵A ，求A 的逆矩阵和A的行列式的值，并验证A 与A -1是互逆的。

答：B=inv(A) ;A 的逆矩阵 C=det(A) ;A 的行列式的值 D=A*B E=B*AD=E=同阶单位矩阵因此A 与A -1是互逆的。

3.求下面线性方程组的解。

⎪⎩⎪⎨⎧=+=+-=-+8312102322421321321x x x x x x x x 答：A=[4 2 -1;3 -1 2;12 3 0]; b=[2;10;8]; x=inv(A)*b x =-6.0000 26.6667 27.33334.求下列矩阵的秩、迹、条件数。

（1）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=901511250324153211A （2） ⎥⎦⎤⎢⎣⎡-=2149.824343.0B 答： (1)rank(A) ；秩 ans =4cond(A) ；条件数 ans =11.1739trace(A) ；迹 ans =16 （2）略5.求矩阵A 的特征值和相应的特征向量。

⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=225.05.025.0115.011A 答：A=[1 1 0.5;1 1 0.25;0.5 0.25 2] A =1.0000 1.0000 0.5000 1.0000 1.0000 0.2500 0.5000 0.25002.0000 [V,D]=eig(A) V =0.7212 0.4443 0.5315 -0.6863 0.5621 0.4615 -0.0937 -0.6976 0.7103 D =-0.0166 0 0 0 1.4801 0 0 0 2.5365。

Matlab第三章习题答案

Matlab第三章习题答案第三章3.5计算多项式乘法()()222254x x x x ++++>> a=[1 2 2];>> b=[1 5 4];>> c=conv(a,b)c =1 7 16 18 8poly2sym(c)ans =x^4 + 7*x^3 + 16*x^2 + 18*x + 83.6计算多项式的除法()()3231368/4x x x x ++++ >> a=[3 13 6 8];>> b=[1 4];>> [q r]=deconv(a,b)q =3 1 2r =0 0 0 0>> poly2sym(q)ans =3*x^2 + x + 23.8求多项式4324121459x x x x --++的微分和积分（1）微分：>> a=[4 -12 -14 5 9];>> b=polyder(a)b =16 -36 -28 5>> poly2sym(b)ans =16*x^3 - 36*x^2 - 28*x + 5（2）积分：polyint(a)ans =0.8000 -3.0000 -4.6667 2.5000 9.00000 >> poly2sym(ans)ans =(4*x^5)/5 - 3*x^4 - (14*x^3)/3 + (5*x^2)/2 + 9*x3.9求代数⽅程32349x x x +-+=0的解。

>> [x]=solve('x^3+3*x^2-4*x+9')x =- 7/(3*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 -1/108*108^(1/2)*4703^(1/2))^(1/3) - 17/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 - (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 - 1 7/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 + (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 – 1 3.10求线性⽅程组223430x xy y x x ?++=??-+=??的解 eqn1='x^2+x*y+y=3';>> eqn2='x^2-4*x+3=0';[x,y]=solve(eqn1,eqn2)x =13y =1-3/23.11求微分⽅程64dy y x dx=+的通解。

MATLAB教程2012a第3章习题解答张志涌

第3章数值阵列及其运算习题3及解答1 在MATLAB 中，先运行指令A=magic(3), B=[1,2,1;3,4,3;5,6,7]生成阵列33⨯A ，33⨯B ，然后根据运行结果回答以下问题：〖目的〗● 体验矩阵乘法次序不可交换；● 体验矩阵左除、右除的不同；● 体验数组乘法次序可交换；● 体验数组左除、右除的相同性；● 体验矩阵乘法与数组乘法的根本性差别● 体验矩阵求逆的两种方法；● 体验数组“逆”概念〖解答〗A=magic(3), B=[1,2,1;3,4,3;5,6,7]%创建阵列A =8 1 63 5 74 9 2B =1 2 13 4 35 6 7（1）C1amb=A*B%相乘矩阵的次序不可交换C1bma=B*AC1amb =41 56 5353 68 6741 56 45C1bma =18 20 2248 50 5286 98 86（2）C2adb=A\B %矩阵左除和右除根本不同C2bda=B/AC2adb =0.0333 0.1000 0.16110.5333 0.6000 0.74440.0333 0.1000 -0.1722C2bda =0.0056 0.0889 0.17220.1389 0.2222 0.30560.2333 0.7333 0.2333（3）C3amb=A.*B %数组乘法不分左、右乘，因为是“元素对元素的运算”C3bma=B.*AC3amb =8 2 69 20 2120 54 14C3bma =8 2 69 20 2120 54 14（4）C4adb=A.\B %数组除法不分左、右除，因为是“元素对元素的运算”C4bda=B./AC4adb =0.1250 2.0000 0.16671.0000 0.8000 0.42861.2500 0.6667 3.5000C4bda =0.1250 2.0000 0.16671.0000 0.8000 0.42861.2500 0.6667 3.5000（5）C5ada=A\A %相当于inv(A)*A，所以得到“单位阵”C5adda=A.\A %相当于“数组逆”乘数组，得到“单位数组”C5ada =1 0 00 1 00 0 1C5adda =1 1 11 1 11 1 1（6）C6ade=A\eye(3) %矩阵求逆的代数方程法C6inv=inv(A) %直接利用求逆指令。

MATLAB课后习题集附标准答案

第2章 MATLAB概论1、与其他计算机语言相比较，MATLAB语言突出的特点是什么？答：起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富，可扩展性强.2、MATLAB系统由那些部分组成？答：开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB时，在选择组件窗口中哪些部分必须勾选，没有勾选的部分以后如何补安装？答：在安装MATLAB时，安装内容由选择组件窗口中各复选框是否被勾选来决定，可以根据自己的需要选择安装内容，但基本平台（即MATLAB选项）必须安装.第一次安装没有选择的内容在补安装时只需按照安装的过程进行，只是在选择组件时只勾选要补装的组件或工具箱即可.矚慫润厲钐瘗睞枥庑赖。

4、MATLAB操作桌面有几个窗口？如何使某个窗口脱离桌面成为独立窗口？又如何将脱离出去的窗口重新放置到桌面上？聞創沟燴鐺險爱氇谴净。

答：在MATLAB操作桌面上有五个窗口，在每个窗口的右下角有两个小按钮，一个是关闭窗口的Close 按钮，一个是可以使窗口称为独立的Undock按钮，点击Undock按钮就可以使该窗口脱离桌面称为独立窗口，在独立窗口的view菜单中选择Dock，菜单项就可以将独立的窗口重新防止的桌面上.残骛楼諍锩瀨濟溆塹籟。

5、如何启动M文件编辑/调试器？答：在操作桌面上选择“建立新文件”或“打开文件”操作时，M文件编辑/调试器将被启动.在命令窗口中键入edit命令时也可以启动M文件编辑/调试器.酽锕极額閉镇桧猪訣锥。

6、存储在工作空间中的数组能编辑吗？如何操作？答：存储在工作空间的数组可以通过数组编辑器进行编辑：在工作空间浏览器中双击要编辑的数组名打开数组编辑器，再选中要修改的数据单元，输入修改内容即可.彈贸摄尔霁毙攬砖卤庑。

7、命令历史窗口除了可以观察前面键入的命令外，还有什么用途？答：命令历史窗口除了用于查询以前键入的命令外，还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中.謀荞抟箧飆鐸怼类蒋薔。

MATLAB第三章和第四章作业

习题三1.选择题(1)已知a=4，b='4'，下面说法错误的为C 。

A. 变量a比b占用的存储空间大B. 变量a和b可以进行加、减、乘、除运算C. 变量a和b的数据类型相同D. 变量b可以用eval命令执行(2)已知s='显示"hello"'，则s的元素个数是B 。

A. 12B. 9C. 7D. 18(3)运行命令>>a=sym('pi','d')则对于变量a的描述D是正确的。

A. a是符号变量B. a显示为10位的数值C. a显示为32位的数值D. a不存在(4)对于符号表达式g=sym('sin(a*z)+cos(w*v)')，如果运行命令diff(g)，则求导自变量是D。

A. aB. zC. wD. v(5)运行命令>>a=double(sym('sin(pi/2)'))，则变量a是 C。

A. 符号变量B. 字符串'1'C. double型的数值1D. 出错(6)运行命令>>y=dsolve('x*D2y-3*Dy=x^2','t')求解微分方程，则D。

A. Dy是指dy/dxB. 得出的y是通解有一个常数符C1C. D2y是指d2y/dxD. 得出的y是通解有两个常数符C1和C2(7)有一个2行2列的元胞数组c，则c(2)是指C 。

A. 第1行第2列的元素内容B. 第2行第1列的元素内容C. 第1行第2列的元素D. 第2行第1列的元素(8)对于一个2行2列的元胞数组c，如果要删除第二列的元素，应该使用的命令是B 。

A.c{:,2}=[]B.c(:,2)=[]C.A、B两种方式均可D.A、B两种方式均不可(9)有一个3行10列的构架数组student，每个构架有name（姓名）、scores两个字段，其中scores是以1×5数组表示的五门课的成绩，那么要查看第4个学生的第2门课成绩，采用的命令中达不到要求的是。

（完整版）matlab经典习题及解答

（完整版）matlab经典习题及解答第1章 MATLAB 概论1.1 与其他计算机语⾔相⽐较，MATLAB 语⾔突出的特点是什么？MATLAB 具有功能强⼤、使⽤⽅便、输⼊简捷、库函数丰富、开放性强等特点。

1.2 MATLAB 系统由那些部分组成？MATLAB 系统主要由开发环境、MATLAB 数学函数库、MATLAB 语⾔、图形功能和应⽤程序接⼝五个部分组成。

1.4 MATLAB 操作桌⾯有⼏个窗⼝？如何使某个窗⼝脱离桌⾯成为独⽴窗⼝？⼜如何将脱离出去的窗⼝重新放置到桌⾯上？在MATLAB 操作桌⾯上有五个窗⼝，在每个窗⼝的右上⾓有两个⼩按钮，⼀个是关闭窗⼝的Close 按钮，⼀个是可以使窗⼝成为独⽴窗⼝的Undock 按钮，点击Undock 按钮就可以使该窗⼝脱离桌⾯成为独⽴窗⼝，在独⽴窗⼝的view 菜单中选择Dock ……菜单项就可以将独⽴的窗⼝重新防⽌的桌⾯上。

1.5 如何启动M ⽂件编辑/调试器？在操作桌⾯上选择“建⽴新⽂件”或“打开⽂件”操作时，M ⽂件编辑/调试器将被启动。

在命令窗⼝中键⼊edit 命令时也可以启动M ⽂件编辑/调试器。

1.6 存储在⼯作空间中的数组能编辑吗？如何操作？存储在⼯作空间的数组可以通过数组编辑器进⾏编辑：在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器，再选中要修改的数据单元，输⼊修改内容即可。

1.7 命令历史窗⼝除了可以观察前⾯键⼊的命令外，还有什么⽤途？命令历史窗⼝除了⽤于查询以前键⼊的命令外，还可以直接执⾏命令历史窗⼝中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M ⽂件中。

1.8 如何设置当前⽬录和搜索路径，在当前⽬录上的⽂件和在搜索路径上的⽂件有什么区别？当前⽬录可以在当前⽬录浏览器窗⼝左上⽅的输⼊栏中设置，搜索路径可以通过选择操作桌⾯的file 菜单中的Set Path 菜单项来完成。

在没有特别说明的情况下，只有当前⽬录和搜索路径上的函数和⽂件能够被MATLAB 运⾏和调⽤，如果在当前⽬录上有与搜索路径上相同⽂件名的⽂件时则优先执⾏当前⽬录上的⽂件，如果没有特别说明，数据⽂件将存储在当前⽬录上。

MATLAB课后习题集附标准答案

第2章MATLAB概论1、与其他计算机语言相比较，MA TLAB 语言突出的特点是什么？答：起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富，可扩展性强.2、MA TLAB 系统由那些部分组成？答：开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB 时，在选择组件窗口中哪些部分必须勾选，没有勾选的部分以后如何补安装？答：在安装MATLAB时，安装内容由选择组件窗口中各复选框是否被勾选来决定，可以根据自己的需要选择安装内容，但基本平台（即MATLAB选项）必须安装. 第一次安装没有选择的内容在补安装时只需按照安装的过程进行，只是在选择组件时只勾选要补装的组件或工具箱即可. 矚慫润厲钐瘗睞枥庑赖。

4、MATLAB 操作桌面有几个窗口？如何使某个窗口脱离桌面成为独立窗口？又如何将脱离出去的窗口重新放置到桌面上？聞創沟燴鐺險爱氇谴净。

答：在MATLAB 操作桌面上有五个窗口，在每个窗口的右下角有两个小按钮，一个是关闭窗口的Close 按钮，一个是可以使窗口称为独立的Undock 按钮，点击Undock 按钮就可以使该窗口脱离桌面称为独立窗口，在独立窗口的view 菜单中选择Dock，菜单项就可以将独立的窗口重新防止的桌面上.残骛楼諍锩瀨濟溆塹籟。

5、如何启动M 文件编辑/调试器？答：在操作桌面上选择“建立新文件”或“打开文件”操作时，M 文件编辑/调试器将被启动.在命令窗口中键入edit 命令时也可以启动M 文件编辑/调试器.酽锕极額閉镇桧猪訣锥。

MATLAB习题参考答案（胡良剑

第一章 MATLAB 入门4、求近似解解：>> x=-2:0.05:2;y=x.^4-2.^x两个近似解：y1=f(-0.85)= -0.0328; y2=f(1.250)= 0.0630第二章 MATLAB 编程与作图1、设x 是数组，求均值和方差解：函数文件如下：function [xx,s]=func1(x)n=length(x);xx=sum(x)/n;s=sqrt((sum(x.^2)-n*xx^2)/(n-1));命令窗口：>> x=[1 2 3 4 5];[xx,s]=func1(x)2、求满足的最小m 值 100)1ln(0>+∑=m n n s=0;n=0;while(s<=100)s=s+log(1+n);n=n+1;endn,s3、用循环语句形成Fibonacci 数列,....4,3,,12121=+===−−k F F F F F k k k 。

并验证极限2511+→−k k F F （提示：计算至两边误差小于精度1e-8为止）解：求Fibonacci 数列的函数文件：function f=fun(n)if n<=2f=1;elsef=fun(n-1)+fun(n-2);end验证极限的函数文件：function [k,a]=funTest(e)a=abs(1-(1+sqrt(5))/2);k=2;while(a>e)k=k+1;a=abs(fun(k)/fun(k-1)-(1+sqrt(5))/2);end命令行：>> [k,a]=funTest(10^-8)k =21a =9.7719e-009或者M 文件如下：clear; F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1; F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1);enda,x,k4、分别用for 和while 循环结构编写程序，求出∑==610123i i K ，并考虑一种避免循环语句的程序设计，比较各种算法的运行时间。

matlab程序设计第三章课后习题答案

1. p138 第6题在同一坐标轴中绘制以下两条曲线并标注两曲线交叉点。

>> t=0:0.01:pi;>> x1=t;>> y1=2*x1-0.5;>> x2=sin(3*t).*cos(t);>> y2=sin(3*t).*sin(t);>> plot(x1,y1,'r-',x2,y2,'g-')>> axis([-1,2,-1.5,1])>> hold on>> s=solve('y=2*x-0.5','x=sin(3*t)*cos(t)','y=sin(3*t)*sin(t)'); >> plot(double(s.x),double(s.y),'*');截图：p366 第4题绘制极坐标曲线，并分析对曲线形状的影响。

对a的值进行改变：比照发现a只影响半径值的整倍变化对b的值进行改变：比照发现b的值使这个圆转换了一定的角度对n的值进行改变：比照发现当n>=2时有如下规律1、当n为整数时，图形变为2n个花瓣状的图形2、当n为奇数时，图形变为n个花瓣状的图形分别让n为2、3、4、5同时改变b和n的值，比照发现图形变为2n个花瓣状，并且还旋转了一定角度1 绘制sin(x)曲线，通过句柄修改曲线的颜色，要求：a）生成曲线的同时，获取句柄，再修改颜色；>> x=0:pi/50:2*pi;>> y=sin(x);>> h=plot(x,y)h =>> set(h,'color','r');截图如下：b〕先生成曲线，然后再获取句柄，再完成颜色修改。

matlab第三章习题解答

matlab课后习题及答案

MATLAB基础及其应用教程-周开利-邓春晖课后答案,第三章

matlab课后习题答案第三章

(完整版)第3章MATLAB矩阵处理_习题答案

matlab第三章课后部分答案

matlab第二版课后习题答案

matlab第三章课后题

matlab程序设计第三章课后习题答案资料

matlab答案第三章

Matlab第三章习题答案

MATLAB教程2012a第3章习题解答 张志涌

MATLAB课后习题集附标准答案

MATLAB第三章和第四章作业

（完整版）matlab经典习题及解答

MATLAB课后习题集附标准答案

MATLAB习题参考答案（胡良剑

matlab程序设计第三章课后习题答案

MATLAB教程2012a第3章习题解答张志涌