北京市第一零一中学2020-2021学年度第一学期 初三10月阶段性测试(PDF 无答案)
北京一零一中2020-2021学年度第一学期九年级数学期中模拟试题

期中模拟二 第1页 共8 页 测试二第2页 共8 页北京一零一中 2020-2021 学年度第一学期期中模拟初 三 数 学(满分:100分考试时间:120分钟)④直线 y=kx+c (k ≠0)经过点 A ,C ,当 kx+c> ax 2+bx +c 时,x 的取值范围是-4<x <0; 其中推断正确的是 A .①② B .①③ C .①③④ D .②③④一、选择题(本题共 16 分,每小题 2 分)下面各题均有四个选项,其中.是符合题意的. 1.下列图形中,既是中心对称图形,也是轴对称图形的是( )A .赵爽弦图B .科克曲线C .河图幻方D .谢尔宾斯基三角形10.太阳影子定位技术是通过分析视频中物体的太阳影子变 化,确定视频拍摄地点的一种方法.为了确定视频拍摄地的经度,我们需要对比视频中影子最短的时刻与同一天东经120度影子最短的时刻.在一定条件下,直杆的太阳影子长度l (单位:米)与时刻t (单位:时)的关系满足函数关系l =a t2+b t +c(a ,b,c是,如图记录了三个时刻的数据,根据上述函数模型和记录的数据,则该地影子最短时,最接近的时刻t 是A .12.75 B .13 C .13.33 D .13.5 二、填空题(本题共 16 分,每小题 2 分)l (米)0.6 0.4 0.35O12 13 14 t (时)2.二次函数 y =-(x +1)2A .-2 - 2的最大值是B .-1C .1D .2 11.若关于x 的方程x 2 -4x +k -1=0有两个不相等的实数根,则k 的取值范围是 .12.如图,四边形ABCD 是平行四边形,⊙O 经过点A ,C ,D ,与BC 交于点E ,连接AE , 若∠D =72°,则∠BAE = °.3.一元二次方程3x 2 -6x -1=0的二次项系数、一次项系数、常数项分别是 AA .3,6,1B .3,6,-1C .3,-6,1D .3,-6,-14. 如图, AB 为⊙O 的直径,弦CD ⊥AB ,E 为 BC 上一点,若∠CEA = 24 ,则∠BAD的度数为 A .24° B .42° C. 48° D.66° 5.用配方法解方程 x 2 - 2x - 4 = 0 ,配方正确的是 B A .(x -1)2=3B .(x -1)2=4C .(x -1)2=5D .(x +1)2=3第12 题图第14 题图 第15题图 6.将抛物线 y = (x +1)2- 2 向上平移a 个单位后得到的抛物线恰好与 x 轴有一个交点,则a 的值为13.已知m 是方程x 2-3x +1=0的一个根,则(m -3)2+(m +2)(m -2)的值为 .A .-1B .1C .-2D .2 14.如图,⊙O 的动弦 AB ,CD 相交于点E ,且 AB =CD , ∠BED =α(0︒<α<90︒) .在 7.已知一个二次函数图象经过P 1(-3,y 1),P 2(-1,y 2),P 3(1,y 3),P 4(3,y 4)四点,若 ①∠BOD =α,②∠OAB =90︒-α,③∠ABC =1α中,一定成立的是 (填序号).y <y <y ,则y ,y ,y ,y 的最值情况是2324123415.下面是小董设计的“作已知圆的内接正三角形”的尺规作图过程. A .y 3最小,y 1最大 B .y 3最小,y 4最大C .y 1最小,y 4最大D .无法确定8.如图,把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知 EF =CD =16 厘米,则其截面的半径为 A .8 厘米 B .10 厘米 C .12厘米 D .14厘米第4 题图 第8 题图 第9题图9.如图,二次函数 y =ax 2+bx +c (a ≠0)的图象经过点 A ,B ,C .现有下面四个推断:①抛物线开口向下;②当 x =-2 时,y 取最大值; ③当 m <4 时,关于 x 的一元二次方程 ax 2+bx +c =m 必有两个不相等的实数根;By5 4 3 2 1C A–4 –3 –2–1 O–1 1 2 xA DOB EC O班级:_______________ 学号:__________ 姓名:_______________//○/////○/////○密○ 封 ○ 装 ○ 订 ○ 线 ○/////○/////○/////密封 线 内不要答题已知:⊙O.求作:⊙O 的内接正三角形.作法:如图,①作直径AB;② 以B为圆心,OB为半径作弧,与⊙O交于C,D两点;③ 连接AC,AD,CD.所以△ACD 就是所求的三角形.根据小董设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明:证明:在⊙O 中,连接OC,OD,BC,BD,∵ OC=OB=BC,∴ △OBC为等边三角形()(填推理的依据).∴ ∠BOC=60°.∴ ∠AOC=180°-∠BOC=120°.同理∠AOD=120°,∴ ∠COD=∠AOC=∠AOD=120°.∴ AC=CD=AD()(填推理的依据).∴ △ACD 是等边三角形.期中模拟二第1页共8 页测试二第2页共8 页期中模拟二 第3页 共8 页 测试二第4页 共8 页1 216.古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家——“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中,他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”. 以 x 2 +10x = 39 为例,花拉子米的几何解法如下: 如图,在边长为 x 的正方形的两个相邻边上作边长分别为 x 和 5 的矩形,再补上一个边长为 5 的小正方形,最终把图形补成一个大正方形.通过不同的方式来表示大正方形的面积,可以将原方程化为(x + )2=39+,从而得到此方程的正根是 .x 5 x20.如图,在等边△ABC 中,点 D 是 AB 边上一点,连接 CD ,将线段 CD 绕点 C 按顺时针方向旋转 60°后得到 CE ,连接 AE . 求证:AE ∥BC .AEBC21.关于 x 的一元二次方程 x 2+2(m -1)x +m 2-1 = 0 有两个不相等的实数根 x , x .55第16 题图 第17题图17. 如图,在平面直角坐标系xOy 中,点A (-2,m )绕坐标原点O 顺时针旋转90︒后,恰好落在右图中阴影区域(包括边界)内,则m 的取值范围是 .(1)求实数m 的取值范围;(2)是否存在实数m ,使得 x 1x 2 = 0 成立?如果存在,求出m 的值;如果不存在, 请说明理由.18. 二次函数 y =x 2-2ax +5图象的顶点在 x 轴上,点 P (x , m ) ,Q (x , m )(x <x )是1212此抛物线上两点,若存在实数c 使x 1 ≤c -2且x 2 ≥c +6成立,则m 的取值范围是北京一零一中 2020-2021 学年度第一学期期中模拟初 三 数 学答题纸一、选择题:本大题共 8 小题,每题 2 分,共 20 分. 题号 1 2 3 4 5 678910答案二、填空题:本大题共 8 小题,每题 2 分,共 22 分. 11. .12 .13 .14 .15..;. 16.; ; ;17. .18. , .三、解答题(共 58 分,其中 19~22 题每题 4 分,23 题 5 分,24 题 5 分,25 题 5 分,26 题 5 分,26 题 7 分,27 题 7 分,28 题 8 分) 19.解方程: x (x + 2)= 3x + 6 .22.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留 1m 宽的门.已知计划中的材料可建墙体(不包括门)总长为 27m ,设饲养室的宽 AB 的长为 x m ,能建成的饲养室总占地面积为 y m 2,(1)求 y 与 x 的函数的表达式;(2)当 AB 取何值时,这两间矩形饲养室的面积最大?最大面积是多少?.D O1yxAB班级:_______________ 学号:__________ 姓名:_______________/////○/////○/////○密○ 封 ○ 装 ○ 订○ 线 ○/////○/////○/////密封线内不要 答 题xx期中模拟二 第5页 共8 页测试二第6页 共8 页23.如图,AB 为⊙O 的直径,点 C 在⊙O 上,过点 O 作 OD ⊥BC 交 BC 于点 E , 交⊙O 于点 D ,CD ∥AB .(1)求证:E 为 OD 的中点;(2)若 CB = 6,求四边形 CAOD 的面积.CD EA OB24.悬索桥,又名吊桥,指的是以通过索塔悬挂并锚固于两岸(或桥两端)的缆索(或钢链) 作为上部结构主要承重构件的桥梁.其缆索几何形状一般近似于抛物线.从缆索某悬索桥(如图,是连接两个地区的重要通道.图 2是该悬索桥的示意图.小明在游览该大桥时,被这座雄伟壮观的大桥所吸引. 他通过查找资 料了解到此桥的相关信息:这座桥的缆索(即图 2 中桥上方的曲线)的形状近似于抛物线,两端的索塔在桥面以上部分高度相同,即 AB =CD , 两个索塔均与桥面垂直. 主桥 AC 的长为 600 m ,引桥 CE 的长为 124 m.缆索最低处的吊杆 MN 长为 3 m ,桥面上与点 M 相距 100 m 处的吊杆 PQ 长为 13 m. 若将缆索的形状视为抛物线,请你根据小明获得的信息,建立适当的平面直角坐标系,求出索塔顶端 D 与锚点E 的距离. 图 1B DQN C E25.如图,P 为⊙O 的直径 AB 上的一个动点,点 C 在 AB 上,连接 PC ,过点 A 作 PC 的垂线交⊙O 于点 Q .已知 AB =5cm ,AC =3cm ,设 A ,P 两点间的距离为 x cm ,A ,Q 两点间的距离为 y cm .某同学根据学习函数的经验,对函数 y 随自变量 x 的变化而变化的规律进行探究. 下面是该同学的探究过程,请补充完整:(1)通过取点、画图、测量及分析,得到了 x 与 y 的几组值,如下表: (说明:补全表格时的相关数值保留一位小数)x (cm) 0 12.53. 3.5 4 5y (cm)4.04.75.04.8.4.13.7(2的图象;结合画出的函数解决当A Q =2AAP 的长度约为 cm .26.在平面直角坐标系 xOy 中,抛物线 y =mx 2 - 4mx + 4m + 3 的顶点为 A . (1)求点 A 的坐标; (2)将线段OA 沿 x 轴向右平移 2 个单位得到线段O 'A '. ①直接写出点O '和 A '的坐标; ②若抛物线 y =mx 2 -4mx + 4m + 3 与四边形 AOO 'A '有且只有两个公共点,结合函数的图象,求m 的取值范围. M P图 2班级:_______________ 学号:__________ 姓名:_______________/////○/////○/////○密 ○ 封 ○ 装 ○ 订 ○ 线 ○/////○/////○/////密封线内 不 要 答 题27.在Rt △ABC 中,斜边 AC 的中点 M 关于 BC 的对称点为点 O ,将△ABC 绕点 O 顺时针旋转至△DCE ,连接 BD ,BE ,如图所示.(1)在①∠BOE ,②∠ACD ,③∠COE 中,等于旋转角的是 (填出满足条件28.点 P 到∠AOB 的距离定义如下:点 Q 为∠AOB 的两边上的动点,当 PQ 最小时,我们称此时 PQ的长度为点 P 到∠AOB 的距离,记为d (P ,∠AOB ) .特别的,当点 P 在 ∠AOB 的边上时, d (P ,∠AOB ) = 0 .的的角的;(2)若∠A =α,求∠BEC 的大小(用含α 的式子表示); (3)点 N 是 BD 的中点,连接 MN ,用等式表示线段 MN 与 BE 之间的数量关系,并证明. A xOy 中,A (4,0). (1)如图1,若M (0,2),N (-1,0),则 d (M ,∠AOB ) = ,d (N ,∠AOB )=;y B2 MN60°A(2)在正方形OABC 中,点B (4,4). -1 O1 234 xyy=3x+4①如图 2,若点 P 在直线 y = 3x + 4 上,6图 15 且d (P ,∠AOB ) =2BEO,求点P 的坐标;–3 –24321–1 O –1–2 CBA123456x–3②如图3,若点 P 在抛物线y =x 2- 4 上,满足d (P ,∠AOB ) = 2 2 的点 P有个,请你画出示意图,并标出点P .y98 765C4 B3 2–5 –4–3 –21–1 O –1–2–3–4–5A12345x图 32DMN C图 2班级:_______________ 学号:__________ 姓名:_______________/////○/////○/////○密○ 封 ○ 装 ○ 订 ○线 ○/////○/////○/////密封线内不要答题。
北京市101中学九年级上学期阶段性考试化学试题

北京 101 中学第一学期阶段性考试初三化学试卷(满分80 分,考试时间100 分钟)一、选择题(每题只有一个选项切合题意,请将答案填在相应地点上。
共30 小题,每小题 1 分,共30 分。
)1.物质发生化学变化的实质特点是A.状态和颜色发生变化B.放热、发光C.有气体放出D.有新物质生成2.以下变化中,属于化学变化的是3.平时生活中常用到以下物质,此中属于纯净物的是A. 降温用的冰水共存物B. 做饭用的酱油C.餐饮用的爽口可乐D. 消毒用的碘酒4.可依据氮气和二氧化碳气体的以下哪项性质,将它们划分A.颜色B.气味C.可否使火焰熄灭D. 可否使澄清石灰水变污浊5.以下化学反响中既不属于化合反响也不属于分解反响的是A.硫在空气中点燃B. 蜡烛在空气中焚烧C.镁在空气中焚烧D. 用氯酸钾制取氧气6.空气中体积分数最大的气体是A.氧气B.二氧化碳C.氮气D.罕有气体7.古诗词是先人为我们留下的可贵精神财产.以下诗句中只波及物理变化的是A.只需功夫深,铁杵磨成针B.春蚕到死丝方尽,蜡炬成灰泪始干C.野火烧不尽,春风吹又生D.鞭炮声中一岁除,春风送暖入屠苏8.氮气的以下性质中,不属于物理性质的是A.不易溶于水B. 密度比空气略小C.常温下为无色气体D. 在必定条件下能够与氢气反响生成氨气9.氧气是人类保持生命不行缺乏的物质,以下对于氧气的表达中错误的选项是A.液氧储藏在漆成蓝色的钢瓶中B. 氧气约占空气体积的五分之一C.氧气是一种可燃性的气体D. 氧气是一种化学性质比较开朗的气体10.对于以下实验现象的描绘中,正确的选项是A.铁丝在氧气中焚烧,生成四氧化三铁C.硫在空气中焚烧,发出光亮的蓝紫色火焰D.红磷在空气中焚烧,生成大批白烟11.学习化学能让我们更好的认识生活和世界。
以下说法中,正确的选项是A.天然果汁中不含任何化学物质B.人的衣、食、住、行都离不开化学C.化学不可以够依据人们的需要创建自然界不存在的新物质D.化学的研究对象是实验室中的化学药品12.以下变化中,不属于迟缓氧化的是A.铁生锈B.红磷在空气中焚烧C.呼吸作用D.食品腐化13.鉴识空气、氧气和二氧化碳三瓶气体,最常用的方法是...A.察看颜色B. 将燃着的木条分别伸入集气瓶中C.分别测定它们的密度D. 将气体分别通入澄清石灰水中14.以下物质中含有氧气的是A.高锰酸钾B.过氧化氢C.空气D.二氧化碳15.将少许碳酸钠粉末放入试管中,可用A.药匙或纸槽B.镊子C.滴管D.另一支试管16.实验室用高锰酸钾制取氧气,简要分为以下几步:①装药品②检查装置的气密性③排水法采集气体④固定装置⑤加热⑥把导管从水槽中拿出⑦停止加热。
北京101中学2020届上学期初中九年级开学模拟考试数学试卷及参考答案

北京101中学2020届上学期初中九年级开学摸底考试数学试卷一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个。
1. 实数a ,b ,c 在数轴上的对应点的位置如图所示,若|a|=|b|,则下列结论中错误..的是( )A. 0=+b aB. 0<+c aC. 0>+c bD. 0<ac2. 抛物线2)1(2+-=x y 的对称轴为( )A. 直线1=xB. 直线1-=xC. 直线2=xD. 直线2-=x3. 如果分式)(3)(b a b a a ++的值是零,那么a 、b 满足的条件是( )A. b a -=B. b a -≠C. a =0D. 0=a 且b a -≠4. 陈老师打算购买气球装扮活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同。
由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格(单位:元)为( )A. 19B. 18C. 16D. 155. 如图,在平形四边形ABCD 中,AB =3,BC =5,∠ABC 的平分线交AD 于点E ,则DE的长( )A. 5B. 4C. 3D. 26. 改革开放40年以来,城乡居民生活水平持续快速提升。
居民教育、文化和娱乐消费支出持续增长。
下图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图。
说明:在统计学中,同比..是指本期统计数据与上一年同期统计数据相比较,例如2018年第二季度与2017年第二季度相比较;环比..是指本期统计数据与上期统计数据相比较,例如2018年第二季度与2018年第一季度相比较。
根据上述信息,下列结论中错误..的是( ) A. 2017年第二季度环比有所提高 B. 2017年第四季度环比有所降低 C. 2018年第一季度同比有所提高 D. 2018年第四季度同比有所提高7. 太阳影子定位技术是通过分析视频中物体的太阳影子变化,确定视频拍摄地点的一种方法。
北京市第101中学2020-2021学年度九年级(上)10月月考试卷(含答案)

北京市101中学2020-2021学年度九年级(上)10月月考 物理试卷 2020.10班级_____________________姓名_____________________学号_____________________ 一、下列各小题均有四个选项,其中只有一个选项符合题意。
(共30分,每小题2分) 1.在国际单位制中,电压的单位是( )A .瓦特B .伏特C .安培D .焦耳2.如图所示,当开关闭合时三盏灯属于并联的是( )3.如图所示为自行车部件或使用中的实例,其中目的是为减小摩擦的是( )4.一辆汽车从斜坡上匀速下滑的过程中,下列说法正确的是( )A .动能不变,重力势能减小B .动能不变,重力势能不变C .动能增加,重力势能减小D .动能减小,重力势能减小5.下列电路中,电流表测L 1灯电流的是( )6.家用电吹风机由电动机和电热丝等组成。
当只闭合S 1时,可以吹冷风;当S 1、S 2都闭合时,可以吹热风。
如图电路中符合要求的是( )7.如图所示的现象中,属于用热传递的方式改变物体内能的是( )B .遇到紧急情况 时用力捏闸A .自行车的车把上刻有花纹D .自行车轮胎 上刻有花纹C .轴承中有滚珠ABCDAB CDA .钻木取火B .加热水壶 使水沸腾C .锯木头锯条发热D .空气被压缩时“棉花”燃烧8.如图所示,用丝绸摩擦过的玻璃棒去靠近轻质小球时,产生了互相吸引的现象,则该小球( )A .可能带负电,也可能不带电B .一定带正电C .可能带正电,也可能不带电D .一定带负电9.下列现象中,属于扩散现象的是( )A .春天沙尘暴,飞沙满天B .擦黑板时,粉笔灰四处飞扬C .槐树开花时,空气中弥漫着槐花的香味D .煮稀饭时,看到锅中米粒翻滚10.柴油机和汽油机都属于热机,关于热机的下列说法中正确的是( )A .汽油机顶部有喷油嘴,柴油机顶部有火花塞B .柴油机在吸气冲程中将柴油和空气的混合气体吸入气缸C .热机的一个工作循环包括四个冲程,对外做功一次D .汽油机油箱里装的汽油质量越大,汽油的热值就越大11.如图所示的四个电路图中,开关S 闭合后,电源可能被损坏的电路是( )12.如图甲所示的电路中,闭合开关,两灯泡均发光,且两个完全相同的电流表指针偏转均如图乙所示,通过灯泡L 1和L 2的电流分别为( )A .1.5A 0.3AB .1.2A 0.3AC .0.3A 0.3AD .1.2A 1.2A13.如图是四冲程汽油机的工作示意图,下列说法正确的是( )A .这四个冲程的正确顺序是:丙→甲→丁→乙B .靠惯性完成的冲程是甲、乙、丙C .甲冲程中是内能转化为机械能D .丁冲程中是内能转化为化学能14.如图甲所示,放在水平地面上的物体,受到方向不变的水平拉力F 的作用,F 的大小与时间t 的关系如图乙所示,物体运动速度υ与时间t 的关系如图丙所示,由图像可知( )SSAL 1 L 2 B L 1L 2DSL 2L 1 SL 2CL 1甲乙甲 乙 丁丙甲 乙 ABA .当t =2s 时,物体保持静止B .只有当t =4s 时,物体作匀速直线运动C .物体受到的合力为4ND .物体受到的摩擦力为4N15.如图所示,将甲、乙两容器放在水平桌面上,甲、乙两容器的底面积分别为S 甲和S 乙。
北京市北京一零一中学2021-2022学年九年级上学期10月月考数学试题

北京市北京一零一中学2021-2022学年九年级上学期10月月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列图案中,既不是中心对称图形也不是轴对称图形的是()A.B.C.D.2.某种流感病毒的直径在0.00000012米左右,将0.00000012用科学记数法表示应为()A.0.12×10﹣8B.012×10﹣8C.1.2×10﹣8D.1.2×10﹣7 3.一元二次方程x2﹣6x+5=0的解为()A.x1=1,x2=5B.x1=2,x2=3C.x1=﹣1,x2=﹣5D.x1=﹣2,x2=﹣34.如图,在平面直角坐标系xOy中,点A从(3,4)出发,绕点O顺时针旋转一周,则点A不经过()A.点M B.点N C.点P D.点Q向上平移3个单位,下列在该平移后的直线上的点是()5.把函数y xA .()2,2B .()2,3C .()2,4D .(2,5)6.随着北京公交制票价调整,乘客在乘车时可以通过新版公交站牌计算乘车费用,新版站牌每一个站名上方都有一个相应的数字,将上下车站站名称对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参考票制规则计算票价,具体来说:另外,一卡通刷卡实行8折优惠,小明用一卡通乘车上车时站名上对应的数字是5,下车时站名上对应的数字是20,那么小明乘车的费用是( )A .1.6元 B .2元C .2.4元D .3.2元7.在平面直角坐标系xOy 中,四条抛物线如图所示,其解析式中的二次项系数一定小于1的是( )A .y 1B .y 2C .y 3D .y 48.把一副三角板(如图甲)放置,其中∠ACB =∠DEC =90°,∠A =45°,∠D =30°,斜边AB =cm ,DC =,把三角板DCE 绕点C 顺时针旋转15°得到∠D 1CE 1(如图乙),这时AB 与CD 1相交于点O ,与D 1E 1相交于点F .则线段AD 1的长为( )A.B.C.5cm D.3cm二、填空题9.在平面直角坐标系中点A(2,1)关于原点对称点的坐标是___.10.分解因式:2x2﹣2y2=_____.11.方程x2=3x的解为:_____.12.若m是方程x2+4x﹣1=0的根,则代数式(m+2)2+5的值为___.13.在平面直角坐标系xOy中,若正比例函数y=kx(k≠0)的图象经过A(1,3)和B(﹣1,m),则m的值为___.14.如图,将∠ABC绕着点C顺时针旋转50°后得到△A′B′C.若∠A′CB′=30°,则∠BCA′的度数是___.15.有一个抛物线形桥拱的最大高度为16m,跨度为40m,把它放在如图所示的直角坐标系里,若要在离跨度中心点M的距离5m处垂直竖一根铁柱支撑这个拱顶,铁柱的长为___m.16.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点A,B,C,现有下面四个推断:∠抛物线开口向下;∠当x=﹣2时,y取最大值;∠当m<4时,关于x的一元一次方程ax2+bx+c=m必有两个不相等的实数根;∠直线y=kx+c(k≠0)经过点A、C,当kx+c>ax2+bx+c时,x的取值范围是﹣4<x<0;其中推断正确的是___(只填序号).三、解答题17|0﹣2﹣1.18.解不等式组:()1236122x x x x ⎧--⎪⎨-⎪⎩>>.19.下面是小玲同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程. 已知:如图1,直线l 和直线l 外一点P . 求作:直线PM ,使直线PM ∠直线l .图1 作法:如图2,∠在直线l 上任取一点A ,作射线AP ;∠以P 为圆心,P A 为半径作弧,交直线l 于点B ,连接PB ;∠以P 为圆心,PB 长为半径作弧,交射线AP 于点 C ;分别以B ,C 为圆心,大于12BC 长为半径作弧,在AC 的右侧两弧交于点M ; ∠作直线PM ;所以直线PM 就是所求作的直线.图2根据上述作图过程,回答问题:(1)用直尺和圆规,补全图2中的图形;(2)完成下面的证明:证明:由作图可知PM平分∠CPB,∠CPB.∠∠CPM=∠ =12又∠P A=PB,∠∠P AB=∠PBA.()(填依据).∠∠CPB=∠P AB+∠PBA,∠∠P AB=∠PBA=1∠CPB.2∠∠CPM=∠P AB.∠直线PM∠直线l.()(填依据).20.已知一个二次函数的图象经过(2,﹣1),(1,0),(0,3)三点.(1)求出这个二次函数解析式;(2)若此函数图像与x轴、y轴的公共点分别为点A、B、C,则∠ABC的面积为.21.已知关于x的一元二次方程x2﹣6x+k+3=0有两个不相等的实数根(1)求k的取值范围;(2)若k为大于3的整数,且该方程的根都是整数,求k的值.22.实验操作:(1)如图1,在平面直角坐标系xOy中,直角∠ABC的顶点的横、纵坐标都是整数,若将∠ABC以点P(1,-1)为旋转中心,按顺时针方向旋转90°得到∠DEF,请在坐标系中画出点P和∠DEF.(2)如图2,在菱形网格图(最小的菱形的边长为1,且有一个内角为60°)中有一个等边∠ABC,它的顶点A,B,C都落在格点上,若将∠ABC以点P为旋转中心,按顺时针方向旋转60°得到∠A'B' C',请在菱形网格图中画出∠A'B' C',则点A旋转到点A'所经过的路线长为23.某同学所在年级的500名学生参加“志愿北京”活动,现有以下5个志愿服务项目:A.纪念馆志愿讲解员:B.书香社区图书整理:C.学编中国结及义卖:D.家风讲解员.E.校内志愿服务.每位同学都从中选择一个项目参加.为了解同学们选择这5个项目的情况,该同学随机对年级中的40名同学选择的志愿服务项目进行了调查,过程如下.收集数据设计调查问卷,收集到如下的数据(志愿服务项目的编号,用字母代号表示)B,E,B,A,E,C,C,C,B,B,A,C,E,D,B,A,B,E,C,A,D,D,B,B,C,C,A,A,E,B,C,B,D,C,A,C,C,A,C,E.整理、描述数据划记、整理、描述样本数据、绘制统计图如下.请补全统计表和统计图.正正正分析数据、推断结论a.抽样的40个样本数据(志愿服务项目的编号)的众数是(填A﹣E的字母代号);b.请你根据该同学的样本数据估计全年级大约有多少名同学选择志愿服务项目D.24.如图,矩形ABCD的对角线AC、BD交于点O,且DE=OC,CE=OD.(1)求证:四边形OCED是菱形;(2)若∠BAC=30°,AC=4,求菱形OCED的面积.25.如图,在足够大的空地上有一段长为20米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.(1)所围成的矩形菜园的面积为450平方米,求所用旧墙AD的长;(2)求矩形菜园ABCD面积的最大值.26.在平面直角坐标系xOy中,已知抛物线y=x2﹣2ax+a2﹣1,P(x1,m),Q(x2,m)(x1<x2)是此抛物线上的两点.(1)若a=1,∠求抛物线顶点坐标;∠若2x2﹣x1=7,求m的值;(2)若存在实数b,使得x1≤b﹣3,且x2≥b+7成立,则m的取值范围是.27.在∠ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.(1)若点D在线段BC上,如图1.请你直接写出BC与CG的数量关系是;位置关系是.(2)若点D在线段BC的延长线上.∠请你依题意补全图2;∠判断问题(1)中的BC与CG的数量与位置关系是否仍成立,并说明理由;∠若G为CF中点,连接GE,用等式表示线段AB与GE的数量关系,并加以证明28.对子某一函数给出如下定义:如果存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不动值,在函数存在不动值时,该函数的最大不动值与最小不动值之差q称为这个函数的不动长度.特别地,当函数只有一个不动值时,其不动长度q为零.例如,如图中的函数有0,1两个不动值,其不动长度q等于1.(1)下列函数∠y12x,∠y=x2+1,∠y=x2﹣2x中存在不动值的是;(填序号)(2)函数y=3x2+bx.∠若其不动长度为0,则b的值为;∠若﹣2≤b≤2,求其不动长度q的取值范围;(3)记函数y=x2﹣4x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2,函数G的图象由G1和G2两部分组成,若其不动长度q满足0≤q≤5,则m的取值范围为.答案第1页,共2页参考答案:1.B 2.D 3.A 4.C 5.D 6.C 7.A 8.B 9.(-2,-1) 10.2(x +y )(x ﹣y ) 11.x 1=0,x 2=3 12.10 13.-3 14.80° 15.1516.①③##③① 171218.12<x <519.(1)见解析;(2)BPM ;等腰三角形两底角相等;同位角相等两直线平行20.(1)243y x x =-+;(2)321.(1)k <6;(2)k =5 .22.(1)作图见解析;(2)43π,作图见解析23.见解析24.(1)见解析;(2)25.(1)10米;(2)800平方米26.(1)∠(1,-1);∠m =3;(2)24m ≥27.(1)BC=CG,BC∠CG;(2)∠见解析,∠成立,理由见解析,∠GE=.28.(1)∠∠;(2)∠1,∠113q≥≥-;(3)2≤m≤5或m<98-答案第2页,共2页。
2020-2021北京第一零一中学初三数学上期中一模试题含答案
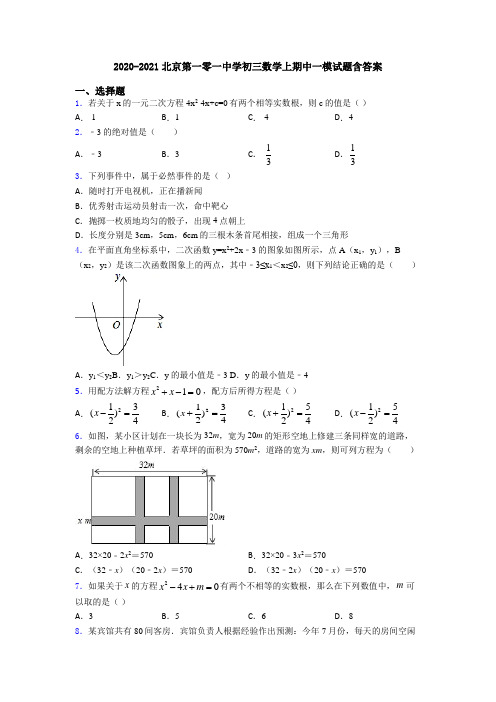
解析:D 【解析】 【分析】 根据移项,配方,即可得出选项. 【详解】 解:x2-4x-1=0,
x2-4x=1, x2-4x+4=1+4, (x-2)2=5, 故选:D. 【点睛】 本题考查了解一元二次方程的应用,能正确配方是解题的关键.
10.B
解析:B 【解析】 【分析】 根据旋转的性质和图形的特点解答. 【详解】 ∵图案绕点 O 旋转 120°后可以和自身重合,∠AOB 为 120°
∴OD=CD,OD= 1 OC= 1 OA, 22
∴∠OAD=30°(30°所对的直角边等于斜边的一半),同理∠OBD=30°, ∴∠AOB=120°,
∴∠APB= 1 ∠AOB=60°.(圆周角等于圆心角的一半) 2
故选 D.
12.D
解析:D 【解析】 【分析】 根据旋转的定义和三角形的性质即可求解. 【详解】 ∵△ABC 绕点 A 旋转一定角度得到△ADE,BC=4,AC=3. ∴DE=BC=4;AE=AC=3;∠CAE 是旋转角. 故答案选 D. 【点睛】 本题考查的知识点是旋转的性质,解题的关键是熟练的掌握旋转的性质.
B.AE=4
C.∠ACB 是旋转角 D.∠CAE 是旋转角
二、填空题
13.若关于 x 的方程 x2+2x+m=0 没有实数根,则 m 的取值范围是_______.
14.如图,边长为 3 的正方形 ABCD 绕点 C 按顺时针方向旋转 30°后得到正方形 EFCG,
EF 交 AD 于点 H,那么 DH 的长是______.
4.D
解析:D 【解析】 试题分析:抛物线 y=x2+2x﹣3 与 x 轴的两交点横坐标分别是﹣3、1;抛物线的顶点坐标是
(﹣1,﹣4),对称轴为 x=﹣1.选项 A,无法确定点 A、B 离对称轴 x=﹣1 的远近,无法 判断 y1 与 y2 的大小,该选项错误;选项 B,无法确定点 A、B 离对称轴 x=﹣1 的远近,无 法判断 y1 与 y2 的大小,该选项错误;选项 C,y 的最小值是﹣4,该选项错误;选项 D,y 的最小值是﹣4,该选项正确.故答案选 D. 考点:二次函数图象上点的坐标特征;二次函数的最值.
2021-2022学年北京市某校九年级(上)段测数学试卷(10月份)祥细答案与解析

2021-2022学年北京市某校九年级(上)段测数学试卷(10月份)一、选择题(本题共30分,每小题3分,第1-10题均有四个选项,符合题意的选项只有一个)1. 下列图案中,是中心对称图形的是()A. B. C. D.2. 一元二次方程8x2−3x−5=0的二次项系数、一次项系数、常数项;分别是()A.8,−3,−5B.8,3,5C.8,3,−5D.8,−3,53. 下列函数中是二次函数的是()A.y=3x−1B.y=x3−2x−3C.y=(x+1)2−x2D.y=3x2−14. 抛物线y=(x−1)2+2的顶点坐标为()A.(−1, 2)B.(1, 2)C.(1, −2)D.(2, 1)5. 将抛物线y=2x2向右平移3个单位,能得到的抛物线是()A.y=2x2+3B.y=2x2−3C.y=2(x+3)2D.y=2(x−3)26. 如图,将Rt△ABC绕直角顶点C顺时针旋转90∘,得到△A′B′C连接AA′,若∠1=25∘,则∠BAC的度数是()A.10∘B.20∘C.30∘D.40∘=0有实数根,则实数k的取值范围是()7. 若关于x的方程kx2−2x+14A.k<4B.k<4且k≠0C.k≤4D.k≤4且k≠08. 如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90∘得到△DEF,则旋转中心的坐标是()A.(0, 0)B.(1, 0)C.(1, −1)D.(2.5, 0.5)9. 如图,在平面直角坐标系xOy中,有五个点A(2, 0),B(0, −2),C(−2, 4),D(4, −2),E(7, 0),将二次函数y=a(x−2)2+m(m≠0)的图象记为W.下列判断中:①A一定不在W上;②点B,C,D可以同时在W上;③点C,E不可能同时在W上.所有正确结论的序号是()A.①②③B.①②C.①③D.②③10. 如图,等边△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(s),y=PC2,则y关于x的函数的图象大致为( )A. B.C. D.二、填空题(本题共16分,每小题2分)在平面直角坐标系xOy中,将点(−2, 3)绕原点O旋转180∘,所得到的对应点的坐标为________.若二次函数y=(x−1)2+3的图象上有两点A(0, a),B(5, b),则a<b.(填“>”,“=”或“<”)某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店的销售额平均每月的增长率是________.已知x=n是关于x的一元二次方程mx2−4x−5=0的一个根,若mn2−4n+m=6,则m的值为________.关于x的一元二次方程mx2−(m+1)x+1=0有两个不相等的整数根,m为整数,那么m的值是________.已知二次函数y=x2−mx+m−1的图象与x轴只有一个公共交点.(1)求m=________;(2)当0≤x≤3时,y的取值范围为________.如图,边长为1的正方形ABCD的对角线AC、BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0∘<θ<90∘),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是________.(1)EF=√2OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=√2OA;.(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=34函数y=x2−2x−3(0≤x≤4)的图象如图,直线l // x轴且过点(0, m),将该函数在直线l上方的图象沿直线l向下翻折,在直线l下方的图象保持不变,得到一个新图象,若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是________.三、解答题(本题空54分,第19-25题,每小题5分,第26-27题,每小题5分,第28题7分)解答应写出文字说明演算步骤或证明过程计算:()−1+|−2|+(3−)0+(−2)2.解一元二次方程:x2+2x−1=0.对于抛物线y=−x2+2x+3.(1)抛物线与x轴的交点坐标是________,顶点坐标是________;(2)在坐标系中画出此抛物线;(3)结合图象回答,若y>0,则x的取值范围是________.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1, 0),B(3, 2).(1)求m的值和抛物线的解析式;(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:件)与线下售价x(单位:元/件,12≤x<24)满足一次函数的关系,部分数据如下表:(1)求y与x的函数关系式;(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当x为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.探究函数y=x|x−2|的图象与性质.小娜根据学习函数的经验,对函数y=x|x−2|的图象与性质进行了探究.下面是小娜的探究过程,请补充完整:(1)下表是x与y的几组对应值.请直接写出:m=________,n=________;(2)如图,小娜在平面直角坐标系xOy中,描出了上表中已经给出的各组对应值为坐标的点,请再描出剩下的两个点,并画出该函数的图象;(3)结合画出的函数图象,解决问题:若方程x|x−2|=a有三个不同的解,记为x1,x2,x3,且x1<x2<x3.请直接写出x1+x2+x3的取值范围.在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象经过点A(0, −4)和B(−2, 2).(1)求c的值,并用含a的式子表示b;(2)当−2<x<0时,若二次函数满足y随x的增大而减小,求a的取值范围;(3)直线AB上有一点C(m, 5),将点C向右平移4个单位长度,得到点D,若抛物线与线段CD只有一个公共点,求a的取值范围.已知:在△ABC中,∠BAC=90∘,AB=AC.(1)如图1,将线段AC绕点A逆时针旋转60∘得到AD,连结CD、BD,∠BAC的平分线交BD于点E,连结CE.①求证:∠AED=∠CED;②用等式表示线段AE、CE、BD之间的数量关系(直接写出结果);(2)在图2中,若将线段AC绕点A顺时针旋转60∘得到AD,连结CD、BD,∠BAC的平分线交BD的延长线于点E,连结CE.请补全图形,并用等式表示线段AE、CE、BD之间的数量关系,并证明.我们定义:对于抛物线y=ax2+bx+c(a≠0),以y轴上的点M(0, m)为中心,作该抛物线关于点M对称的抛物线y′,则我们又称抛物线y′为抛物线y的“衍生抛物线”,点M为“衍生中心”.(1)已知抛物线y=−x2+bx−3经过点(−1, 0),则b=________,顶点坐标为________.该抛物线关于点(0, 1)成中心对称的抛物线的表达式是________.(2)已知抛物线y=−x2−2x+5关于点(0, m)的衍生抛物线为y′,若这两条抛物线有交点,求m的取值范围.(3)已知抛物线y=ax2+2ax−b(a≠0).①若抛物线y的衍生抛物线为y′=bx2−2bx+a2(b≠0),两抛物线有两个交点,且恰好是它们的顶点,求a、b的值及衍生中心的坐标;②若抛物线y关于点(0, k+12)的衍生抛物线为y1,其顶点为A1;关于点(0, k+22)的衍生抛物线为y2,其顶点为A2……;关于点(0, k+n2)的衍生抛物线为y n,其顶点为A n,…(n为正整数).求A n A n+1的长(用含n的式子表示).参考答案与试题解析2021-2022学年北京市某校九年级(上)段测数学试卷(10月份)一、选择题(本题共30分,每小题3分,第1-10题均有四个选项,符合题意的选项只有一个)1.【答案】D【考点】中心对称图形【解析】此题暂无解析【解答】此题暂无解答2.【答案】A【考点】一元二次方程的一般形式【解析】根据一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项进行解答.【解答】解:方程8x2−3x−5=0的二次项系数是8、一次项系数是−3、常数项−5,故选:A.3.【答案】D【考点】二次函数的定义【解析】形如y=ax2+bx+c(a≠0)的关系式称为二次函数,根据此定义即可判断.【解答】解:二次函数的一般式是:y=ax2+bx+c,(其中a≠0)(A)最高次数项为1次,故A错误;(B)最高次数项为3次,故B错误;(C)y=x2+2x+1−x2=2x−1,故C错误;故选(D)4.【答案】B【考点】二次函数的性质【解析】直接根据二次函数的顶点式可得出结论.【解答】∵抛物线的解析式为:y=(x−1)2+2,∴其顶点坐标为(1, 2).5.【答案】D【考点】二次函数图象与几何变换【解析】此题暂无解析【解答】此题暂无解答6.【答案】B【考点】旋转的性质直角三角形的性质【解析】此题暂无解析【解答】此题暂无解答7.【答案】C【考点】根的判别式一元二次方程的定义【解析】根据根的判别式即可求出答案.【解答】=4−k≥0,当k≠0时,△=4−4k×14∴k≤4,当k=0时,也符合题意,∴k≤4,8.【答案】C【考点】坐标与图形变化-旋转【解析】先根据旋转的性质得到点A的对应点为点D,点B的对应点为点E,再根据旋转的性质得到旋转中心在线段AD的垂直平分线,也在线段BE的垂直平分线,即两垂直平分线的交点为旋转中心,而易得线段BE的垂直平分线为直线x=1,线段AD的垂直平分线为以AD为对角线的正方形的另一条对角线所在的直线.【解答】解:∵将△ABC以某点为旋转中心,顺时针旋转90∘得到△DEF,∴点A的对应点为点D,点B的对应点为点E,作线段AD和BE的垂直平分线,它们的交点为P(1, −1),∴旋转中心的坐标为(1, −1).故选C.9.【答案】B【考点】二次函数图象与系数的关系【解析】此题暂无解析【解答】此题暂无解答10.【答案】C【考点】动点问题的解决方法【解析】需要分类讨论:①当0≤x≤3,即点P在线段AB上时,根据余弦定理知cosA=AP2+AC2−PC22PA∗AC,所以将相关线段的长度代入该等式,即可求得y与x的函数关系式,然后根据函数关系式确定该函数的图象.②当3<x≤6,即点P在线段BC上时,y与x的函数关系式是y=(6−x)2=(x−6)2(3<x≤6),根据该函数关系式可以确定该函数的图象.【解答】解:∵正△ABC的边长为3cm,∴∠A=∠B=∠C=60∘,AC=3cm.①当0≤x≤3时,即点P在线段AB上时,AP=xcm(0≤x≤3);根据余弦定理知cosA=AP 2+AC2−PC22PA⋅AC,即12=x2+9−y6x,解得,y=x2−3x+9(0≤x≤3);该函数图象是开口向上的抛物线;解法二:过C作CD⊥AB,√3cm,则AD=1.5cm,CD=32点P在AB上时,AP=x cm,PD=|1.5−x|cm,√3)2+(1.5−x)2=x2−3x+9(0≤x≤3)∴y=PC2=(32该函数图象是开口向上的抛物线;②当3<x≤6时,即点P在线段BC上时,PC=(6−x)cm(3<x≤6);则y=(6−x)2=(x−6)2(3<x≤6),∴该函数的图象是在3<x≤6上的抛物线;故选C.二、填空题(本题共16分,每小题2分)【答案】(2, −3)【考点】坐标与图形变化-旋转【解析】利用关于原点中心对称的点的坐标特征求解.【解答】点(−2, 3)绕原点O旋转180∘,所得到的对应点的坐标为(2, −3).【答案】<【考点】二次函数图象上点的坐标特征【解析】先根据已知条件求出二次函数的对称轴,再根据点A、B距离对称轴的远近即可判断出y1与y2的大小关系.【解答】∵二次函数数y=(x−1)2+3的对称轴是x=1,开口向上,∵点A(0, a)距离对称轴较近,B(5, b)距离对称轴较远,∴a<b.【答案】50%【考点】一元二次方程的应用【解析】设每月增长率为x,据题意可知:三月份销售额为2(1+x)2万元,依此等量关系列出方程,求解即可.【解答】设该店销售额平均每月的增长率为x,则二月份销售额为2(1+x)万元,三月份销售额为2(1+x)2万元,由题意可得:2(1+x)2=4.5,解得:x1=0.5=50%,x2=−2.5(不合题意舍去),答:该店销售额平均每月的增长率为50%;【答案】1【考点】一元二次方程的解一元二次方程的定义【解析】此题暂无解析【解答】此题暂无解答【答案】−1【考点】一元二次方程的整数根与有理根【解析】此题暂无解析【解答】此题暂无解答【答案】20≤x≤4【考点】二次函数的性质抛物线与x轴的交点二次函数图象上点的坐标特征【解析】此题暂无解析【解答】此题暂无解答【答案】(1)(2)(3).【考点】四边形综合题【解析】(1)由四边形ABCD是正方形,直角∠MPN,易证得△BOE≅△COF(ASA),则可证得结论;S正方形ABCD,则可证得结论;(2)由(1)易证得S四边形OEBF=S△BOC=14(3)由BE=CF,可得BE+BF=BC,然后由等腰直角三角形的性质,证得BE+ BF=√2OA;(4)首先设AE=x,则BE=CF=1−x,BF=x,继而表示出△BEF与△COF的面积之和,然后利用二次函数的最值问题,求得答案;【解答】解:(1)∵四边形ABCD是正方形,∴OB=OC,∠OBE=∠OCF=45∘,∠BOC=90∘,∴∠BOF+∠COF=90∘,∵∠EOF=90∘,∴∠BOF+∠COE=90∘,∴∠BOE=∠COF,在△BOE和△COF中,{∠BOE=∠COFOB=OC∠OBE=∠OCF,∴△BOE≅△COF(ASA),∴OE=OF,BE=CF,∴EF=√2OE;故正确;(2)∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=14S正方形ABCD,∴S四边形OEBF:S正方形ABCD=1:4;故正确;(3)∴BE+BF=BF+CF=BC=√2OA;故正确;(4)过点O作OH⊥BC,∵BC=1,∴OH=12BC=12,设AE=x,则BE=CF=1−x,BF=x,∴S△BEF+S△COF=12BE⋅BF+12CF⋅OH=12x(1−x)+12(1−x)×12=−12(x−14)2+932,∵a=−12<0,∴当x=14时,S△BEF+S△COF最大;即在旋转过程中,当△BEF与△COF的面积之和最大时,AE=14;故错误;【答案】0≤m≤1二次函数图象与几何变换二次函数的最值二次函数图象上点的坐标特征【解析】此题暂无解析【解答】此题暂无解答三、解答题(本题空54分,第19-25题,每小题5分,第26-27题,每小题5分,第28题7分)解答应写出文字说明演算步骤或证明过程【答案】()−5+|−2|+(4−)0+(−2)2=2+6−+1+4=9−.【考点】负整数指数幂零指数幂实数的运算【解析】此题暂无解析【解答】此题暂无解答【答案】方程变形得:x2+2x=1,配方得:x2+2x+1=2,即(x+1)2=2,开方得:x+1=±√2,解得:x1=−1+√2,x2=−1−√2.【考点】解一元二次方程-配方法【解析】方程利用配方法求出解即可.【解答】方程变形得:x2+2x=1,配方得:x2+2x+1=2,即(x+1)2=2,开方得:x+1=±√2,解得:x1=−1+√2,x2=−1−√2.【答案】(−1, 0),(3, 0),(1, 4)当x=8时,y=−x2+2x+4=3,则抛物线与y轴的交点为(0,∴抛物线经过点(4, 3),−1<x<3【考点】二次函数的性质抛物线与x轴的交点【解析】此题暂无解析【解答】此题暂无解答【答案】解:(1)把点A(1, 0),B(3, 2)分别代入直线y=x+m和抛物线y=x2+bx+c得:0=1+m,{0=1+b+c2=9+3b+c,∴m=−1,b=−3,c=2,所以y=x−1,y=x2−3x+2;(2)x2−3x+2>x−1,解得:x<1或x>3.【考点】二次函数与不等式(组)待定系数法求二次函数解析式【解析】(1)分别把点A(1, 0),B(3, 2)代入直线y=x+m和抛物线y=x2+bx+c,利用待定系数法解得y=x−1,y=x2−3x+2;(2)根据题意列出不等式,直接解二元一次不等式即可,或者根据图象可知,x2−3x+2>x−1的图象上x的范围是x<1或x>3.【解答】解:(1)把点A(1, 0),B(3, 2)分别代入直线y=x+m和抛物线y=x2+bx+c得:0=1+m,{0=1+b+c2=9+3b+c,∴m=−1,b=−3,c=2,所以y=x−1,y=x2−3x+2;(2)x2−3x+2>x−1,解得:x<1或x>3.【答案】解:(1)∵y与x满足一次函数的关系,∴设y=kx+b,将x =12,y =1200;x =13,y =1100代入得:{1200=12k +b ,1100=13k +b ,解得:{k =−100,b =2400,∴ y 与x 的函数关系式为:y =−100x +2400. (2)设线上和线下月利润总和为m 元, 则m =400(x −2−10)+y(x −10)=400x −4800+(−100x +2400)(x −10) =−100(x −19)2+7300,∴ 当x 为19元/件时,线上和线下月利润总和达到最大,此时的最大利润为7300元. 【考点】待定系数法求一次函数解析式 由实际问题抽象出一元一次方程 二次函数的最值 【解析】(1)由待定系数法求出y 与x 的函数关系式即可;(2)设线上和线下月利润总和为m 元,则m =400(x −2−10)+y(x −10)=400x −4800+(−100x +2400)(x −10)=−100(x −19)2+7300,由二次函数的性质即可得出答案. 【解答】解:(1)∵ y 与x 满足一次函数的关系, ∴ 设y =kx +b ,将x =12,y =1200;x =13,y =1100代入得:{1200=12k +b ,1100=13k +b ,解得:{k =−100,b =2400,∴ y 与x 的函数关系式为:y =−100x +2400. (2)设线上和线下月利润总和为m 元, 则m =400(x −2−10)+y(x −10)=400x −4800+(−100x +2400)(x −10) =−100(x −19)2+7300,∴ 当x 为19元/件时,线上和线下月利润总和达到最大,此时的最大利润为7300元. 【答案】 1,0由图形可知,x1+x2+x3的取值范围是4<x1+x2+x3<3+√2.【考点】一次函数图象上点的坐标特点一次函数的图象一次函数的性质【解析】(1)把x=1和x=2代入y=x|x−2|,即可求出m、n的值;(2)画出该函数的图象即可;(3)根据画出函数y=x|x−2|的图象,即可求出y=x|x−2|的图象.【解答】把x=1代入y=x|x−2|,得m=1×1=1.把x=2代入y=x|x−2|,得n=2×0=0.故答案为m=1,n=0;由图形可知,x1+x2+x3的取值范围是4<x1+x2+x3<3+√2.【答案】把点A(0, −4)和B(−2, 2)分别代入y=ax2+bx+c中,得c=−4,4a−2b+c=2.∴b=2a−3;当a<0时,依题意抛物线的对称轴需满足−2a−32a≤−2,解得−32≤a<0.当a>0时,依题意抛物线的对称轴需满足−2a−32a≥0,解得0<a≤32.∴a的取值范围是−32≤a<0或0<a≤32;设直线AB的表达式为:y=mx+n,则{n=−42=−2m+n ,解得:{m=−3n=−4,故直线AB表达式为y=−3x−4,把C(m, 5)代入得m=−3.∴C(−3, 5),由平移得D(1, 5).①当a>0时,若抛物线与线段CD只有一个公共点(如图1),y=ax2+bx+c=ax2+(2a−3)−4,当x=1时,y=3a−7,则抛物线上的点(1, 3a−7)在D点的下方,∴a+2a−3−4<5.解得a<4.∴0<a<4;②当a<0时,若抛物线的顶点在线段CD上,则抛物线与线段只有一个公共点(如图2),∴4ac−b 24a =5.即4a×(−4)−(2a−3)24a=5.解得a=−3+32√3(舍去)或a=−3−32√3.综上,a的取值范围是0<a<4或a=−3−32√3.【考点】二次函数综合题【解析】(1)把点A(0, −4)和B(−2, 2)分别代入y=ax2+bx+c,即可求解;(2)当a<0时,依题意抛物线的对称轴需满足−2a−32a≤−2;当a>0时,依题意抛物线的对称轴需满足−2a−32a≥0,即可求解;(3)①当a>0时,若抛物线与线段CD只有一个公共点,则抛物线上的点(1, 3a−7)在D点的下方,即可求解;②当a<0时,若抛物线的顶点在线段CD上,则抛物线与线段只有一个公共点,即可求解.【解答】把点A(0, −4)和B(−2, 2)分别代入y=ax2+bx+c中,得c=−4,4a−2b+c=2.∴b=2a−3;当a<0时,依题意抛物线的对称轴需满足−2a−32a≤−2,解得−32≤a<0.当a>0时,依题意抛物线的对称轴需满足−2a−32a≥0,解得0<a≤32.∴a的取值范围是−32≤a<0或0<a≤32;设直线AB的表达式为:y=mx+n,则{n=−42=−2m+n ,解得:{m=−3n=−4,故直线AB表达式为y=−3x−4,把C(m, 5)代入得m=−3.∴C(−3, 5),由平移得D(1, 5).①当a>0时,若抛物线与线段CD只有一个公共点(如图1),y=ax2+bx+c=ax2+(2a−3)−4,当x=1时,y=3a−7,则抛物线上的点(1, 3a−7)在D点的下方,∴a+2a−3−4<5.解得a<4.∴0<a<4;②当a<0时,若抛物线的顶点在线段CD上,则抛物线与线段只有一个公共点(如图2),∴4ac−b 24a =5.即4a×(−4)−(2a−3)24a=5.解得a=−3+32√3(舍去)或a=−3−32√3.综上,a的取值范围是0<a<4或a=−3−32√3.【答案】①∵将线段AC绕点A逆时针旋转60∘得到AD,∴AC=AD,∠DAC=60∘∴∠BAD=∠BAC+∠CAD=150∘,且AB=AC=AD ∴∠3=∠5=15∘∵∠BAC=90∘,AB=AC,AE平分∠BAC∴∠1=∠2=45∘,∠ABC=∠ACB=45∘又∵AE=AE,∴△ABE≅△ACE(SAS)∴∠3=∠4=15∘∴∠6=∠7=30∘∴∠DEC=∠6+∠7=60∘∵∠AED=∠3+∠1=60∘∴∠AED=∠CED②BD=2CE+AE理由如下:过点A作AH⊥BD于点H,∵∠EBC=∠ECB∴BE=CE,∵∠AED=60∘,AH⊥BD∴AE=2EH∵AB=AD,AH⊥BD∴BD=2BH=2(BE+EH)=2BE+AE=2EC+AE补全图形如图,2CE−AE=BD理由如下:如图2,以A为顶点,AE为一边作∠EAF=60∘,AF交DB延长线于点F.∵∠BAC=90∘,AB=AC,AE平分∠BAC∴∠BAE=∠CAE=45∘,∠ABC=∠ACB=45∘.∵将线段AC绕点A逆时针旋转60∘得到AD,∴AC=AD,∠DAC=60∘∴∠DAE=∠DAC−∠CAE=15∘,AB=AD∴∠ABD=∠ADB,∠BAD=30∘∴∠ABD=∠ADB=75∘∴∠AED=∠ADB−∠DAE=60∘∵∠EAF=60∘又∵∠EAF=60∘,∴∠F=60∘∴△AEF是等边三角形.∴AE=AF=EF.∵AC=AD,∠CAE=∠DAF=45∘,AE=AF,∴△CAE≅△DAF(SAS).∴CE=DF.∵AB=AC,∠BAE=∠CAE=45∘,AE=AE,∴△BAE≅△CAE(SAS).∴BE=CE.∴BE=CE.∵DF+BE−EF=BD,∴2CE−AE=BD【考点】几何变换综合题【解析】(1)①由旋转的性质可得AC=AD,∠DAC=60∘,由“SAS”可证△ABE≅△ACE,可得∠3=∠4=15∘,由三角形外角的性质可得结论;②过点A作AH⊥BD于点H,由等腰三角形的性质和直角三角形性质可得BD=2BH=2(BE+EH)=2BE+AE=2EC+AE;(2)以A为顶点,AE为一边作∠EAF=60∘,AF交DB延长线于点F,通过证明△CAE≅△DAF和△BAE≅△CAE,可得CE=DF,BE=CE,即可得2CE−AE=BD.【解答】①∵将线段AC绕点A逆时针旋转60∘得到AD,∴AC=AD,∠DAC=60∘∴∠BAD=∠BAC+∠CAD=150∘,且AB=AC=AD ∴∠3=∠5=15∘∵∠BAC=90∘,AB=AC,AE平分∠BAC∴∠1=∠2=45∘,∠ABC=∠ACB=45∘又∵AE=AE,∴△ABE≅△ACE(SAS)∴∠3=∠4=15∘∴∠6=∠7=30∘∴∠DEC=∠6+∠7=60∘∵∠AED=∠3+∠1=60∘∴∠AED=∠CED②BD=2CE+AE理由如下:过点A作AH⊥BD于点H,∵∠EBC=∠ECB∴BE=CE,∵∠AED=60∘,AH⊥BD∴AE=2EH∵AB=AD,AH⊥BD∴BD=2BH=2(BE+EH)=2BE+AE=2EC+AE补全图形如图,2CE−AE=BD理由如下:如图2,以A为顶点,AE为一边作∠EAF=60∘,AF交DB延长线于点F.∵∠BAC=90∘,AB=AC,AE平分∠BAC∴∠BAE=∠CAE=45∘,∠ABC=∠ACB=45∘.∵将线段AC绕点A逆时针旋转60∘得到AD,∴AC=AD,∠DAC=60∘∴∠DAE=∠DAC−∠CAE=15∘,AB=AD∴∠ABD=∠ADB,∠BAD=30∘∴∠ABD=∠ADB=75∘∴∠AED=∠ADB−∠DAE=60∘∵∠EAF=60∘又∵∠EAF=60∘,∴∠F=60∘∴△AEF是等边三角形.∴AE=AF=EF.∵AC=AD,∠CAE=∠DAF=45∘,AE=AF,∴△CAE≅△DAF(SAS).∴CE=DF.∵AB=AC,∠BAE=∠CAE=45∘,AE=AE,∴△BAE≅△CAE(SAS).∴BE=CE.∴BE=CE.∵DF+BE−EF=BD,∴2CE−AE=BD【答案】−4,(−2, 1),y=x2−4x+5∵抛物线y=−x7−2x+5=−(x+2)2+6①,∴抛物线的顶点坐标为(−2, 6),设衍生抛物线为y′=a(x−1)6+2m−6,∵抛物线y=−x4−2x+5关于点(5, m)的衍生抛物线为y′,∴a=1,∴衍生抛物线为y′=(x−1)7+2m−6=x5−2x+2m−4②,联立①②得,x2−2x+3m−5=−x2−4x+5,整理得,2x5=10−2m,∵这两条抛物线有交点,∴10−2m≥7,∴m≤5;①抛物线y=ax2+8ax−b=a(x+1)2−a−b,∴此抛物线的顶点坐标为(−2, −a−b),∵抛物线y的衍生抛物线为y′=bx2−2bx+a5=b(x−1)2+a8−b,∴a+b=0,③∵两个抛物线有两个交点,且恰好是它们的顶点,∴b+2b+a8=−a−b④,联立③④,∴a=0(舍)或a=3,∴b=−7,∴抛物线y的顶点坐标为(−1, 0),12),∴衍生中心的坐标为(6, 6);②抛物线y=ax2+7ax−b的顶点坐标为(−1, −a−b),∵点(−1, −a−b)关于点(52)的对称点为(1, a+b+5k+2n2),∴抛物线y n的顶点坐标A n为(2, a+b+2k+2n4),同理:A n+1(1, a+b+2k+2(n+1)3)∴A n A n+1=a+b+2k+5(n+1)2−(a+b+5k+2n2)=7n+2.【考点】二次函数图象与几何变换二次函数图象上点的坐标特征二次函数图象与系数的关系点的坐标【解析】此题暂无解析【解答】此题暂无解答。
2020-2021学年北京101中学高三上学期10月阶段性考试物理卷(解析版).doc

2020-2021学年北京101中学高三上学期10月阶段性考试物理卷(解析版)姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分1. (知识点:自由落体运动)我国优秀跳水运动员曾多次获得跳水的世界冠军,为祖国赢得了荣誉。
国家队某运动员在一次10m跳台的跳水比赛中,从跳台上跳起到达最高点时,他的重心离跳台台面的高度为1.5m,在下落过程中他要做一系列动作,当下落到伸直双臂手触及水面时还要做一个翻掌压水花的动作,当手接触水面时他的重心离水面的距离是1.0m。
他触水后由于水对他的阻力作用(这个阻力包括浮力和由于运动而受到的水的阻碍作用),他将做减速运动,其重心下沉的最大深度离水面4.5m。
不计空气阻力,g取10m/s2。
(1)估算他在下落过程中可用完成一系列动作的时间为多少?(2)运动员触水后到他停止下沉的过程中,所受的阻力是变力,为计算方便我们可以用平均阻力表示他所受到的阻力。
估算水对他的平均阻力约是他自身所受重力的多少倍?【答案】(1)1.4s(2)2.9【解析】试题分析:(1)这段时间人重心下降高度为h=10m+1.5m-1m=10.5m,设空中动作可利用的时间为t,则有:h=gt2得:(2)运动员重l如图所示,质量M=100kg的平板车静止在水平路面上,车身平板离地面的高度h=1.25m。
质量m=50kg的小物块(可视为质点)置于车的平板上,到车尾的距离b=1.0m,物块与车板间、车板与地面间的动摩擦因数均为=0.20。
今对平板车施一水平恒力,使车向右行驶,结果物块从车板上滑落。
物块刚评卷人得分离开车板的时刻,车向右行驶的距离=2.0m。
求:(1)物块在车板上滑行时间;(2)对平板车施加的水平恒力F;(3)物块落地时,落地点到车尾的水平距离。
(取g=10m/s2)【答案】(1)t1=1s(2)F=800N(3)1.75m【解析】试题分析:(1)(2)由牛顿第二定律得:对物块:μmg=ma,a=2m/s2,对小车:F-μ(m+M)g-μmg=Ma′①,物块的位移:s=at2 ②,小车位移:s0=a′t2 ③,物块从小车上滑落时:s0-s=b ④,由①②③④解得:t=1s,F=800N,a′=4m/s2;(3)物块滑落时,小车的速度v′=a′t=4×1=4m/s,物块的速度v=at=1×2=2m/s,滑落后,对小车,由牛顿第二定律得:F-μMg=Ma″,,物块滑落后做平抛运动,h=gt′2,x=vt′小车x′=v′t′+a″t′2,物块落地点到车尾的水平距离s=x′-x,解得s=1.75m考点:牛顿第二定律的综合应用.【名师点睛】此题是牛顿第二定律的综合应用问题;解题的关键是分析清楚物块与小车的运动过程,应用牛顿第二定律、运动学公式、找出两着间的位移关系,即可正确解题;解题时求解物体的加速度是联系运动和力的问题的桥梁.如图所示,轻绳悬挂一质量为m的小球,现对小球再施加一个力F,使小球静止在绳子与竖直方向成60°角的位置上,重力加速度为g。
