多边形及其内角和同步练习含答案
人教版 七年级数学下册 (7.3多边形及其内角和) 课时同步优化训练习题(含答案)

7.3 多边形及其内角和5分钟训练(预习类训练,可用于课前)1.三角形的内角和等于_____________度,外角和等于_____________度.解析:三角形的内角和等于180°,外角和等于360°.答案:180 3602.n 边形的内角和等于_____________度,外角和等于_____________度.解析:n 边形的内角和等于(n-2)180°,外角和等于360°.答案:(n-2)180 3603.如果一个多边形的内角和为1 440°,那么这个多边形是( )A.6边形B.8边形C.10边形D.12边形解析:设这个多边形为n 边形,由n 边形的内角和定理得(n-2)180°=1 440°,解得n=10. 答案:C4.过多边形一个顶点可引5条对角线,那么这个多边形是______________边形.( )A.5B.7C.8D.10解析:过n 边形的一个顶点可作(n-3)条对角线,则n-3=5,∴n=8.答案:C10分钟训练(强化类训练,可用于课中)1.若一个多边形的边数减少1,则它的内角和( )A.不变B.增加180°C.减少180°D.无法确定解析:因为(n-2)180°-(n-1-2)180°=180°,所以应选C.答案:C2.若正n 边形的一个外角为60°,则n 为( )A.4B.5C.6D.9解析:n 边形的外角和为360°,由于正n 边形的一个外角为60°,所以n=360°÷60°=6.答案:C3.凸n 边形的n 个内角与某一个外角的和为1 350°,则n 等于( )A.6B.7C.8D.9解析:设该外角为α,则(1 350°-α)应是180°的整数倍,所以1 350°÷180°的整数部分即n 边形的边数. 答案:D4.过n 边形一个顶点可作_______________条对角线,过n 个顶点可作_______________条对角线. 解析:由图形规律可得,过n 边形的一个顶点可作(n-3)条对角线,则过n 个顶点可作(n-3)·n÷2,即21n (n-3)条.答案:n-3 21n(n-3) 5.已知多边形的每一个内角都是150°,求它的边数和内角和.解:设这个多边形为n 边形,则(n-2)180°=n·150°,所以n=12.所以(12-2)×180°=1 800°.答:它的边数为12,内角和为1 800°.6.一个多边形除去一个内角外,其余各角之和为2 750°,求这个多边形的边数及去掉的角的度数. 解析:由于多边形的内角和是180°的整数倍,所以去掉的这个角与2 750°÷180的余数的和应是180°. 设去掉的这个角为α,又有2 750°÷180的余数为50°,所以可得α+50°=180°.所以α=130°.∴该多边形的边数为(2 750°+130°)÷180°+2=18.所以这个多边形的边数为18,去掉的角度为130°.30分钟训练(巩固类训练,可用于课后)1.一个多边形的内角与外角的总和为2 160°,则此多边形是_____________边形.( )A.五B.六C.十D.十二解析:设这个多边形为n 边形,则(n-2)180°+360°=2 160°,解得n=12.答案:D2.若多边形的边数由n (n 为正整数)减少到3,则其外角和的度数( )A.不变B.增加C.减少D.无法确定解析:由多边形的外角和等于360°,故应选A. 答案:A3.若一个多边形的每个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数为( )A.9B.8C.7D.6解析:先求出多边形的边数n ,则从这个多边形的一个顶点出发的对角线的条数为(n-3)条.答案:D4.(2010四川广安模拟,22)已知一个多边形的内角和等于外角和的2倍,则这个多边形的边数是_________________.解析:设多边形的边数为n ,则(n-2)180°=2×360°,解得n=6.答案:65.多边形的每个内角都等于它的相邻外角的6倍,则多边形是_______________边形.解析:设多边形的边数为n ,则多边形的每个外角为7180︒,则7180︒n=360°,解得n=14. 答案:十四6.某多边形所有内角的和与某一个外角的差是1 710°,那么这个多边形是_____________边形,这个外角的度数为__________________.解析:设这个多边形的边数为n ,则n 是满足(n-2)×180°>1 710°的最小整数,所以n=12.所以这个外角的度数为(12-2)·180°-1 710°=90°.答案:12 90°7.已知一个多边形的每一个内角都是钝角,则这样的多边形至少是几边形?解:设这样的多边形至少是n 边形,因为每个内角都是钝角,则每个外角都是锐角,由此可得90°·n >360°,∴n >4.∴n=5.答:这样的多边形至少是五边形.8.一块多边形的纸片,减去一个角后(没有过顶点)得到的多边形的内角和为1 620°,求原来的纸片为几边形?分析:减去一个角后比原来的多边形多了一条边.解:设新多边形的边数为n ,则(n-2)180°= 1 620°,解得n=11,所以原来的纸片为十边形.9.小明想:2008年奥运会在北京召开,设计一个内角和为2 008°的多边形图案多有意义,试问小明的想法能实现吗?并说明理由解:小明的想法不能实现.因为多边形的内角和是180°的整数倍,而2 008°不能被180°整除,所以多边形的内角和不能是2 008°,所以小明的想法不能实现.10.如图7-3-1所示,求∠A+∠B+∠C+∠D+∠E+∠F 的值.图7-3-1解:如图,连结AD.∵∠1+∠2+∠AOD=180°,∠E+∠F+∠EOF=180°,又∵∠AOD=∠EOF ,∴∠1+∠2=∠E+∠F.∴∠BAF+∠B+∠C+∠CDE+E+∠F=∠BAF+∠1+∠B+∠C+∠CDE+∠2=∠BAD+∠B+∠C+∠CDA=360°.11.已知一个多边形的对角线条数是边数的3倍,求它的内角和.解:设这个多边形的边数为n ,n 边形的对角线为21n(n-3)条,根据题意列方程,得21n(n-3)=3n, 即n(n-3)=6n.∵n≠0,两边都除以n ,得n-3=6,∴n=9.从而它的内角和为(n-2)·180°=(9-2)×180°=1 260°.答:这个多边形的内角和为1 260°.。
八年级数学人教版上册同步练习11.3多边形及其内角和(含答案解析)
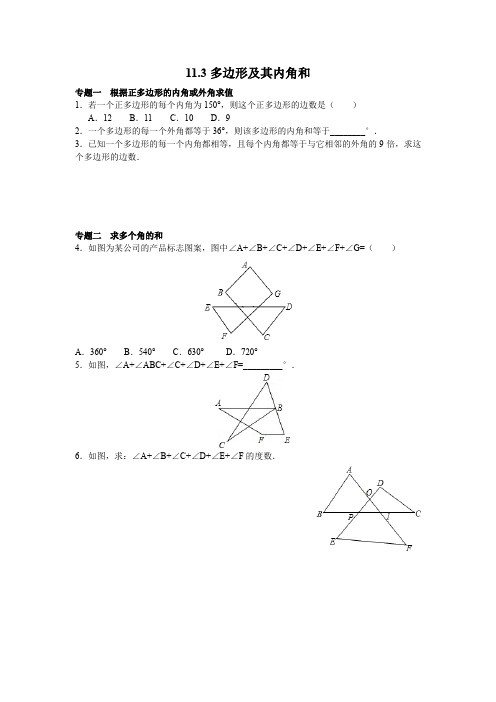
11.3多边形及其内角和专题一根据正多边形的内角或外角求值1.若一个正多边形的每个内角为150°,则这个正多边形的边数是()A.12 B.11 C.10 D.92.一个多边形的每一个外角都等于36°,则该多边形的内角和等于________°.3.已知一个多边形的每一个内角都相等,且每个内角都等于与它相邻的外角的9倍,求这个多边形的边数.专题二求多个角的和4.如图为某公司的产品标志图案,图中∠A+∠B+∠C+∠D+∠E+∠F+∠G=()A.360°B.540°C.630°D.720°5.如图,∠A+∠ABC+∠C+∠D+∠E+∠F=_________°.6.如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数.状元笔记【知识要点】1.多边形及相关概念多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.2.多边形的内角和与外角和内角和:n边形的内角和等于(n-2)·180°.外角和:多边形的外角和等于360°.【温馨提示】1.从n边形的一个顶点出发,可以做(n-3)条对角线,它们将n边形分为(n-2)个三角形.对角线的条数与分成的三角形的个数不要弄错.2.多边形的外角和等于360°,而不是180°.【方法技巧】1.连接多边形的对角线,将多边形转化为多个三角形,将多边形问题转化为三角形问题来解决.2.多边形的内角和随边数的变化而变化,但外角和不变,都等于360°,可利用多边形的外角和不变求多边形的边数等.参考答案:1.A 解析:∵每个内角为150°,∴每个外角等于30°.∵多边形的外角和是360°,360°÷30°=12,∴这个正多边形的边数为12.故选A.2.1440 解析:∵多边形的边数为360°÷36°=10,多边形的内角为180°-36°=144°,∴多边形的内角和等于144°×10=1440°.3.解:设多边形的边数为n,根据题意,得(n-2)·180°=9×360°,解得n=20.所以这个多边形的边数为20.4.B 解析:∵∠1=∠C+∠D,∠2=∠E+∠F,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=∠A+∠B+∠1+∠2+∠G=540°.故选B.5.360°解析:在四边形BEFG中,∵∠EBG=∠C+∠D,∠BGF=∠A+∠ABC,∴∠A+∠ABC+∠C+∠D+∠E+∠F=∠EBG+∠BGF+∠E+∠F=360°.6.解:∵∠POA是△OEF的外角,∴∠POA=∠E+∠F.同理:∠BPO=∠D+∠C.∵∠A+∠B+∠BPO+∠POA=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.。
人教版八年级数学上册同步练习11.3多边形及其内角和(含答案解析)
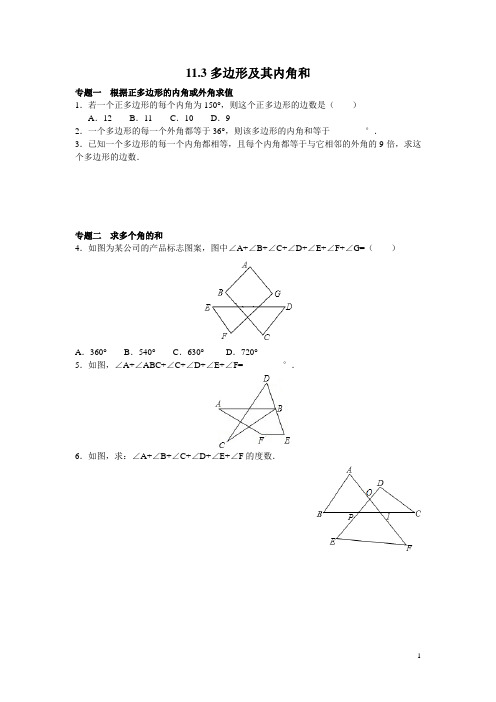
11.3多边形及其内角和专题一根据正多边形的内角或外角求值1.若一个正多边形的每个内角为150°,则这个正多边形的边数是()A.12 B.11 C.10 D.92.一个多边形的每一个外角都等于36°,则该多边形的内角和等于________°.3.已知一个多边形的每一个内角都相等,且每个内角都等于与它相邻的外角的9倍,求这个多边形的边数.专题二求多个角的和4.如图为某公司的产品标志图案,图中∠A+∠B+∠C+∠D+∠E+∠F+∠G=()A.360°B.540°C.630°D.720°5.如图,∠A+∠ABC+∠C+∠D+∠E+∠F=_________°.6.如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数.状元笔记【知识要点】1.多边形及相关概念多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.2.多边形的内角和与外角和内角和:n边形的内角和等于(n-2)·180°.外角和:多边形的外角和等于360°.【温馨提示】1.从n边形的一个顶点出发,可以做(n-3)条对角线,它们将n边形分为(n-2)个三角形.对角线的条数与分成的三角形的个数不要弄错.2.多边形的外角和等于360°,而不是180°.【方法技巧】1.连接多边形的对角线,将多边形转化为多个三角形,将多边形问题转化为三角形问题来解决.2.多边形的内角和随边数的变化而变化,但外角和不变,都等于360°,可利用多边形的外角和不变求多边形的边数等.参考答案:1.A 解析:∵每个内角为150°,∴每个外角等于30°.∵多边形的外角和是360°,360°÷30°=12,∴这个正多边形的边数为12.故选A.2.1440 解析:∵多边形的边数为360°÷36°=10,多边形的内角为180°-36°=144°,∴多边形的内角和等于144°×10=1440°.3.解:设多边形的边数为n,根据题意,得(n-2)·180°=9×360°,解得n=20.所以这个多边形的边数为20.4.B 解析:∵∠1=∠C+∠D,∠2=∠E+∠F,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=∠A+∠B+∠1+∠2+∠G=540°.故选B.5.360°解析:在四边形BEFG中,∵∠EBG=∠C+∠D,∠BGF=∠A+∠ABC,∴∠A+∠ABC+∠C+∠D+∠E+∠F=∠EBG+∠BGF+∠E+∠F=360°.6.解:∵∠POA是△OEF的外角,∴∠POA=∠E+∠F.同理:∠BPO=∠D+∠C.∵∠A+∠B+∠BPO+∠POA=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.。
人教版八年级数学上册同步练习11.3多边形及其内角和(含答案解析)
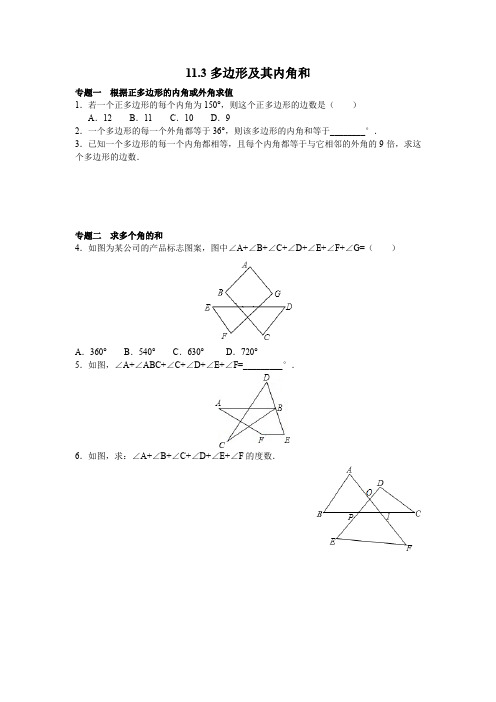
11.3多边形及其内角和专题一根据正多边形的内角或外角求值1.若一个正多边形的每个内角为150°,则这个正多边形的边数是()A.12 B.11 C.10 D.92.一个多边形的每一个外角都等于36°,则该多边形的内角和等于________°.3.已知一个多边形的每一个内角都相等,且每个内角都等于与它相邻的外角的9倍,求这个多边形的边数.专题二求多个角的和4.如图为某公司的产品标志图案,图中∠A+∠B+∠C+∠D+∠E+∠F+∠G=()A.360°B.540°C.630°D.720°5.如图,∠A+∠ABC+∠C+∠D+∠E+∠F=_________°.6.如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数.状元笔记【知识要点】1.多边形及相关概念多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.2.多边形的内角和与外角和内角和:n边形的内角和等于(n-2)·180°.外角和:多边形的外角和等于360°.【温馨提示】1.从n边形的一个顶点出发,可以做(n-3)条对角线,它们将n边形分为(n-2)个三角形.对角线的条数与分成的三角形的个数不要弄错.2.多边形的外角和等于360°,而不是180°.【方法技巧】1.连接多边形的对角线,将多边形转化为多个三角形,将多边形问题转化为三角形问题来解决.2.多边形的内角和随边数的变化而变化,但外角和不变,都等于360°,可利用多边形的外角和不变求多边形的边数等.参考答案:1.A 解析:∵每个内角为150°,∴每个外角等于30°.∵多边形的外角和是360°,360°÷30°=12,∴这个正多边形的边数为12.故选A.2.1440 解析:∵多边形的边数为360°÷36°=10,多边形的内角为180°-36°=144°,∴多边形的内角和等于144°×10=1440°.3.解:设多边形的边数为n,根据题意,得(n-2)·180°=9×360°,解得n=20.所以这个多边形的边数为20.4.B 解析:∵∠1=∠C+∠D,∠2=∠E+∠F,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=∠A+∠B+∠1+∠2+∠G=540°.故选B.5.360°解析:在四边形BEFG中,∵∠EBG=∠C+∠D,∠BGF=∠A+∠ABC,∴∠A+∠ABC+∠C+∠D+∠E+∠F=∠EBG+∠BGF+∠E+∠F=360°.6.解:∵∠POA是△OEF的外角,∴∠POA=∠E+∠F.同理:∠BPO=∠D+∠C.∵∠A+∠B+∠BPO+∠POA=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.。
8年级数学人教版上册同步练习11.3多边形及其内角和(含答案解析)

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!11.3多边形及其内角和专题一根据正多边形的内角或外角求值1.若一个正多边形的每个内角为150°,则这个正多边形的边数是( )A.12 B.11 C.10 D.92.一个多边形的每一个外角都等于36°,则该多边形的内角和等于________°.3.已知一个多边形的每一个内角都相等,且每个内角都等于与它相邻的外角的9倍,求这个多边形的边数.专题二求多个角的和4.如图为某公司的产品标志图案,图中∠A+∠B+∠C+∠D+∠E+∠F+∠G=( )A.360° B.540° C.630° D.720°5.如图,∠A+∠ABC+∠C+∠D+∠E+∠F=_________°.6.如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数.状元笔记【知识要点】1.多边形及相关概念多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.2.多边形的内角和与外角和内角和:n边形的内角和等于(n-2)·180°.外角和:多边形的外角和等于360°.【温馨提示】1.从n边形的一个顶点出发,可以做(n-3)条对角线,它们将n边形分为(n-2)个三角形.对角线的条数与分成的三角形的个数不要弄错.2.多边形的外角和等于360°,而不是180°.【方法技巧】1.连接多边形的对角线,将多边形转化为多个三角形,将多边形问题转化为三角形问题来解决.2.多边形的内角和随边数的变化而变化,但外角和不变,都等于360°,可利用多边形的外角和不变求多边形的边数等.参考答案:1.A解析:∵每个内角为150°,∴每个外角等于30°.∵多边形的外角和是360°,360°÷30°=12,∴这个正多边形的边数为12.故选A.2.1440解析:∵多边形的边数为360°÷36°=10,多边形的内角为180°-36°=144°,∴多边形的内角和等于144°×10=1440°.3.解:设多边形的边数为n,根据题意,得(n-2)·180°=9×360°,解得n=20.所以这个多边形的边数为20.4.B 解析:∵∠1=∠C+∠D,∠2=∠E+∠F,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=∠A+∠B+∠1+∠2+∠G=540°.故选B.5.360° 解析:在四边形BEFG中,∵∠EBG=∠C+∠D,∠BGF=∠A+∠ABC,∴∠A+∠ABC+∠C+∠D+∠E+∠F=∠EBG+∠BGF+∠E+∠F=360°.6.解:∵∠POA是△OEF的外角,∴∠POA=∠E+∠F.同理:∠BPO=∠D+∠C.∵∠A+∠B+∠BPO+∠POA=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.。
多边形及其内角和练习题(含答案)

多边形及其内角和练习题(含答案)1.如果四边形ABCD中∠A+∠C+∠D=280°,那么∠B的角度是多少?选项:A.80° B.90° C.170° D.20°2.如果一个多边形的内角和为1080°,那么这个多边形有多少条边?选项:A.9 B.8 C.7 D.63.内角和等于外角和的两倍的多边形是什么形状?选项:A.五边形B.六边形C.七边形D.八边形4.六边形的内角和是多少度?5.正十边形的每个内角的度数是多少?每个外角的度数是多少?6.图中有多少种不同的四边形?7.四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?为什么?8.求下列图形中x的值:9.在四边形ABCD中,已知∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC。
BE与DF有什么位置关系?为什么?10.有10个城市进行篮球比赛,每个城市派出3个代表队参加比赛,规定同一城市间的代表队不进行比赛,其他代表队都要比赛一场。
按照这个规定,所有代表队需要打多少场比赛?11.在一个五边形的每个顶点处以1为半径画圆,求圆与五边形重合的面积。
12.(1) 已知一个多边形的内角和为540°,那么这个多边形是什么形状?选项:A.三角形 B.四边形 C.五边形 D.六边形 (2) 五边形的内角和是多少度?13.一个多边形的每个顶点处取一个外角,这些外角中最多有几个钝角?选项:A.1个 B.2个 C.3个 D.4个14.(1) 四边形有几条对角线?五边形有几条对角线?六边形有几条对角线?猜想并探索:n边形有几条对角线?(2) 一个n边形的边数增加1,对角线增加多少条?15.如果一个多边形的边数增加1,那么这个多边形的内角和会增加多少度?如果将n边形的边数增加1倍,那么它的内角和会增加多少度?16.壁虎想捕捉一只害虫,它在油罐下底边A处,害虫在油罐上边缘B处。
人教版八年级上册 11.3 多边形及其内角和 同步练习(含答案)
多边形及其内角和同步练习一.选择题1.正多边形的每个内角为135度,则多边形为()A.4B.6C.8D.102.若一个多边形减去一个角后,内角和为720°,则原多边形不可能是几边形()A.四边形B.五边形C.六边形D.七边形3.一个四边形的四个内角度数之比为1:2:4:5,则这个四边形中,最小的内角为()A.30°B.40°C.50°D.60°4.一个正多边形的每个内角的度数都等于相邻外角的2倍,则该正多边形的边数是()A.3B.4C.6D.125.如图,已知一个五边形ABCDE纸片,一条直线将该纸片分割成两个多边形.若这两个多边形内角和分别为m和n,则m+n不可能是()A.540°B.720°C.900°D.1080°6.如图,在五边形ABCDE中,AE∥BC,延长DE至点F,连接BE,若∥A=∥C,∥1=∥3,∥AEF=2∥2,则下列结论正确的是()∥∥1=∥2 ∥AB∥CD ∥∥AED=∥A ∥CD∥DEA.1个B.2个D.4个7.如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α (0°<α<90°),若DE∥B′C′,则∥α为()A.36°B.54°C.60°D.72°8.如图,在四边形ABCD中,∥DAB的角平分线与∥ABC的外角平分线相交于点P,且∥D+∥C=210°,则∥P=()A.10°B.15°C.30°D.40°9.设BF交AC于点P,AE交DF于点Q.若∥APB=126°,∥AQF=100°,则∥A-∥F=()A.60°B.46°C.26°D.45°10.如图,已知四边形ABCD中,∥C=90°,若沿图中虚线剪去∥C,则∥1+∥2等于()B.135°C.270°D.315°11.如图,在六边形ABCDEF中,若∥A+∥B+∥C+∥D=500°,∥DEF与∥AFE的平分线交于点G,则∥G等于()A.55°B.65°C.70°D.80°12.如图,A,B,C,D,E,F是平面上的6个点,则∥A+∥B+∥C+∥D+∥E+∥F的度数是()A.180°B.360°C.540°D.720°二.填空题13.八边形的内角和为;一个多边形的每个内角都是120°,则它是边形.14.一个多边形,除了一个内角外,其余各角的和为2750°,则内角和是.15.如图,已知在四边形ABCD中,∥A+∥C=135°,∥ADE=125°,则∥B= .16.如图所示,若∥DBE=78°,则∥A+∥C+∥D+∥E= °.17.如图所示,∥A+∥B+∥C+∥D+∥E+∥F+∥G+∥H= °.三.解答题18.(1)已知一个正多边形的每个内角比它的每个外角的4倍多30°,求这个多边形的边数;(2)一个多边形的外角和是内角和的七分之二,求这个多边形的边数.19.如图,在四边形ABCD中,BD∥CD,EF∥CD,且∥1=∥2.(1)求证:AD∥BC;(2)若BD平分∥ABC,∥A=130°,求∥C的度数.20.如图,四边形ABCD中,∥BAD=106°,∥BCD=64°,点M,N分别在AB,BC上,将∥BMN沿MN翻折得∥FMN,若MF∥AD,FN∥DC.求(1)∥F的度数;(2)∥D的度数.21.将纸片∥ABC沿DE折叠使点A落在点A'处【感知】如图∥,点A落在四边形BCDE的边BE上,则∥A与∥1之间的数量关系是;【探究】如图∥,若点A落在四边形BCDE的内部,则∥A与∥1+∥2之间存在怎样的数量关系?并说明理由.【拓展】如图∥,点A落在四边形BCDE的外部,若∥1=80°,∥2=24°,则∥A的大小为.22.已知,在四边形ABCD中,∥A+∥C=160°,BE,DF分别为四边形ABCD的外角∥CBN,∥MDC的平分线.(1)如图1,若BE∥DF,求∥C的度数;(2)如图2,若BE,DF交于点G,且BE∥AD,DF∥AB,求∥C的度数.参考答案1-5:CAACD 6-10:CBBBC 11-12:CB13、1080°;六14、2880°15、170°16、10217、72018、:(1)设这个多边形的每个内角是x°,每个外角是y°,则得到一个方程组得而任何多边形的外角和是360°,则多边形内角和中的外角的个数是360÷30=12,则这个多边形的边数是12边形;(2)设这个多边形的边数为n,依题意得:(n-2)180°=360°,解得n=9,答:这个多边形的边数为9.19、:(1)证明:∵BD⊥CD,EF⊥CD(已知),∴BD∥EF(垂直于同一直线的两条直线平行),∴∠2=∠3(两直线平行,同位角相等).∵∠1=∠2,∴∠1=∠3(等量代换).∴AD∥BC(内错角相等,两直线平行).(2)∵AD∥BC(已知),∴∠ABC+∠A=180°(两直线平行,同旁内角互补).∵∠A=130°(已知),∴∠ABC=50°.∵DB平分∠ABC(已知),∴∠3=25°.∴∠C=90°-∠3=65°.20、:(1)∵MF∥AD,FN∥DC,∠BAD=106°,∠BCD=64°,∴∠BMF=106°,∠FNB=64°,∵将△BMN沿MN翻折,得△FMN,∴∠FMN=∠BMN=53°,∠FNM=∠MNB=32°,∴∠F=∠B=180°-53°-32°=95°;(2)∠F=∠B=95°,∠D=360°-106°-64°-95°=95°.21、:(1)如图,∠1=2∠A.理由如下:由折叠知识可得:∠EA′D=∠A;∵∠1=∠A+∠EA′D,∴∠1=2∠A.(2)如图②,2∠A=∠1+∠2.理由如下:∵∠1+∠A′DA+∠2+∠A′EA=360°,∠A+∠A′+∠A′DA+∠A′EA=360°,∴∠A′+∠A=∠1+∠2,由折叠知识可得:∠A=∠A′,∴2∠A=∠1+∠2.(3)如图③,∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,∴∠1=∠A+∠A′+∠2=2∠A+∠2,∴2∠A=∠1-∠2=56°,解得∠A=28°.故答案为:∠1=2∠A;28°.22、:(1)过点C作CH∥DF,∵BE∥DF,∴BE∥DF∥CH,∴∠FDC=∠DCH,∠BCH=∠EBC,∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC,∵BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线,∴∠FDC=∠CDM,∠EBC=∠CBN,∵∠A+∠BCD=160°,∴∠ADC+∠ABC=360°160°=200°,∴∠MDC+∠CBN=160°,∴∠FDC+∠CBE=80°,∴∠DCB=80°;(2)连接GC并延长,同理得∠MDC+∠CBN=160°,∠MDF+∠NBG=80°,∵BE∥AD,DF∥AB,∴∠A=∠MDF=∠DGB=∠NBG=40°,∵∠A+∠BCD=160°,∴∠BCD=160°-40°=120°.。
多边形及其内角和练习题含答案
9-2多边形的内角和及外角和练习一一.填空题1.若一凸多边形的内角和等于它的外角和,则它的边数是______ •2.五边形的内角和等于______ •3.十边形的对角线有_________ 条.4・正十五边形的每一个内角等于_______ . 5.内角和是1620°的多边形的边数是_・6.用正n边形拼地板,则n的值可能是______ ・二、选择题7.一个多边形的内角和是720°,则这个多边形是()A.四边形B.五边形C.六边形D.七边形8•—个多边形的内角和比它的外角和的3倍少180。
,这个多边形的边数是() A.5 B.6 C.7 9.若正n 边形的一个外() A.4 B.5 C.6 10.下列角度中,不能成为多边形内角和的是(A. 600°B. 720°C. 900°D.8角为60 °,则n 的值是D.8)D. 1080°11.若一个多边形的内角和及外角和之和是1800。
,则此多边形是()A.八边形B.十边形C・十二边形 D.十四边形12.用下列两种正多边形能拼地板的是()A.正三角形和正八边形B.正方形和正八边形C.正六边形和正八边形D.正十边形和正八边形三、解答题13.一个多边形的每一个外角都等于45。
,求这个多边形的内角和.14.己知一个多边形的内角和是1440。
,求这个多边形的对角线的条数.15•—个多边形,除一个内角外,其余各内角之和等于1000°,求这个内角及多边形的边数・11・3多边形及其内角和16•—个多边形中,每个内角都相等,并且每个外角等于它的相邻内角的2/3,求这个多边形的边数及内角和.17.如图,一个六边形的木个内角都是120° , AB二1, BC=CD=3, DE=2,求该六边形的周长.19.若两个多边形的边数之比是1:2,内角和度数之比为1:3,求这两个多边形的边数.20.如果多边形恰有四个内角是钝角,那么多边形的边数共有几种可能?其中最多是几边形?最少是几边形?21.下列地板是由正方形、正六边形、正十二边形拼成的,试说明由这三种正多边形能拼地板的理由・22•已知四边形ABCD 中,ZA:ZB=7:5, ZA-ZC=ZB, ZC=ZD-40° , 求各内角的度数.23.一个多边形除了一个内角等于a,其余角的和等于2750°,求这个多边形的边数及a •21.下列地板是由正方形、正六边形、正十二边形拼成的,试说明由这三种正多边形能拼地板的理由.22•已知四边形ABCD中,ZA: ZB=7:5, ZA-ZC=ZB, ZC=ZD-40°求各内角的度数.23. 一个多边形除了一个内角等于a ,其余角的和等于2750°,求这个多边形的边数及a.24.一个广场地面的一部分如图所示,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖拼成,从里往外共12层(不包括中央的正六边形地砖),每一层的外界都围成一个多边形•若中央正六边形地砖的边长是0. 5米,则第12层的外边界所围成的多边形的周长是多少1.四边形ABCD中,如果ZA+ZC+ZD=280° ,则ZB的度数是()A. 80°B. 90°C. 170°D. 20°2.一个多边形的内角和等于1080° ,这个多边形的边数是()A. 9B. 8C. 7D. 63.内角和等于外角和2倍的多边形是()A.五边形B.六边形C.七边形D.八边形4.六边形的内角和等于 _______ .5.正十边形的每一个内角的度数等于_______ ,每一个外角的度数等于 ________ .6.如图,你能数出多少个不同的四边形?7.四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是宜角吗?&求下列图形中x的值:综合创新作业9.(综合题)已知:如图,在四边形ABCD中,ZA=ZC=90° , BE平分ZABC, DF平分Z ADC. BE及DF有怎样的位置关系?为什么?多边形及其内角和练习题(含答案)10.(应用题)有10个城市进行篮球比赛,每个城市均派3个代表队参加比赛,规定同一城市间代表队不进行比赛,其他代表队都要比赛一场,问按此规定,所有代表队要打多少场比赛?11.(创新题)如图,以五边形的每个顶点为圆心,以1为半径画圆,求圆及五边形重合的面积.12.(1)(2005年,南通)己知一个多边形的内角和为540。
数学人教版八年级上册多边形及其内角和同步练习(配套练习附答案)
∴∠BAG+∠AGD=90°,
则AG⊥DE.
点睛:此题考查了平行线的性质,以及外角性质,熟练掌握平行线的性质是解本题的关键.
18.如图,小东在足球场的中间位置,从A点出发,每走6m向左转60°,已知AB=BC=6m.
(1)小东是否能走回A点,若能回到A点,则需走几m,走过的路径是一个什么图形?为什么?(路径A到B到C到…)
详解:(1)由平移的性质得:△ABC≌△DEF,
∴AB=DE,AB∥DE,
∴四边形ABED为平行四边形,
∴AD∥BF,∠ADG=∠ABC,
∴∠ADG=∠DEF,
∴∠ABC=∠DEF=∠ADG,
∵∠AGE为△ADG的外角,
∴∠AGE=∠DAG+∠ADG=∠GAD+∠ABC;
(2)AG⊥DE,理由为:
由平移的性质得到∠EDF=∠BAC,
A. 200米B. 180米C. 160米D. 140米
【答案】B
【解析】
【分析】
多边形的外角和为360°每一个外角都为20°,依此可求边数,再求多边形的周长.
【详解】∵多边形的外角和为360°,而每一个外角为20°,
∴多边形的边数为360°÷20°=18,
∴小华一共走了:18×10=180米.
故选B.
∴∠AEF+∠CFE=540°-∠A-∠B-∠C=540°-90°-90°-90°=270°.
故选B.
点睛:本题考查了四边形的性质及多边形的内角和定理.解决本题亦可通过外角关系.
6.如图所示,小华从A点出发,沿直线前进10米后左转 ,再沿直线前进10米,又向左转 , ,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
八年级数学同步练习-多边形及其内角和
11.3多边形及其内角和1、若一个凸多边形的内角和为720°,则这个多边形的边数为().A. 4B. 5C. 6D. 72、若多边形的边数由3增加到n(n为大于3的整数),则其外角和的度数().A. 增加B. 减少C. 不变D. 不能确定3、如果一个多边形的内角和等于它的外角和的2倍,则这个多边形是().A. 三角形B. 四边形C. 五边形D. 六边形4、正十边形的每一个内角的度数为().A. 120°B. 135°C. 140°D. 144°5、一个多边形的每一个外角都是45°,则这个多边形的边数为().A. 6B. 7C. 8D. 96、如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前12米,又向左转36°⋯照这样走下去,他第一次回到出发地A点时,一共走了米.7、若一个正多边形的内角和为720°,则这个正多边形的每一个内角是().A. 60°B. 90°C. 108°D. 120°8、如果过一个多边形的一个顶点的对角线有6条,则该多边形是().A. 九边形B. 八边形C. 七边形D. 六边形9、从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是().A. n个B. (n−1)个C. (n−2)个D. (n−3)个10、下面的平面图形中,不能镶嵌平面的图形是().A. 正三角形B. 正六边形C. 正四边形D. 正五边形11、如图,将一个长方形剪去一个角,则剩下的多边形为().A. 五边形B. 四边形或五边形C. 三角形或五边形D. 三角形或四边形或五边形12、一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为().A. 5B. 5或6C. 5或7D. 5或6或713、如图,∠1是五边形ABCDE的一个外角,若∠1=65°,则∠A+∠B+∠C+∠D=°.14、如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是.15、若正多边形的内角和是1080°,则该正多边形的边数是.16、一个多边形的每一个外角都等于40°,则它的边数为.17、如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是().A. 8B. 9C. 10D. 1118、某多边形的内角和加上其外角和等于1080°,则此多边形的边数是().A. 4B. 5C. 6D. 719、一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为().A. 8B. 9C. 10D. 1220、如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,⋅⋅⋅,照这样走下去,他第一次回到出发地A点时,一共走的路程是().A. 140米B. 150米C. 160米D. 240米21、经过多边形一个顶点的所有对角线把多边形分成10个三角形,多边形的边数是().A. 8条B. 9条C. 12条D. 11条22、如果一个多边形的每个外角是40°,那么从这个多边形的一个顶点出发,可以引出条对角线.23、如果限于用一种正多边形镶嵌,下列正多边形不能镶嵌成一个平面图形的是().A. 正三角形B. 正方形C. 正五边形D. 正六边形24、如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是.25、一个多边形截去一个角后,形成另一个多边形的内角和为2520°,则原多边形的边数是().A. 17B. 16C. 15D. 16或15或1726、如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P=().A. 50°B. 55°C. 60°D. 65°27、如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=°.28、如图,∠A+∠B+∠C+∠D+∠E+∠F=°.1 、【答案】 C;【解析】设这个多边形的边数为n,则(n−2)×180°=720°,解得n=6,故这个多边形为六边形.故选C.2 、【答案】 C;【解析】因为多边形外角和固定为360°,所以外角和的度数是不变的.故选:C.3 、【答案】 D;【解析】设多边形为n边形,由题意,得(n−2)⋅180=360×2,解得n=6.故选D.4 、【答案】 D;【解析】方法一 : ∵一个十边形的每个外角都相等,∴十边形的一个外角为360÷10=36°.∴每个内角的度数为180°−36°=144°;故选:D.方法二 : 由多边形的内角和公式可知,正十边形的内角和为180°×(10−2)=1440°.所以每个内角的度数为1440°÷10=144°.故选D.5 、【答案】 C;【解析】由多边形外角和为360°,=8,则边数:360°45°所以多边形为8边形.故选C.6 、【答案】120;【解析】由题意得:360°÷36°=10,则他第一次回到出发地A点时,一共走了12×10=120(米).7 、【答案】 D;【解析】(n−2)×180°=720°,∴n−2=4,∴n=6.则这个正多边形的每一个内角为720°÷6=120°.故选:D.8 、【答案】 A;【解析】∵过一个多边形的一个顶点的对角线有6条,∴多边形的边数为6+3=9,∴这个多边形是九边形.9 、【答案】 C;【解析】从n边形的一个顶点作对角线,把这个n边形分成(n−2)个三角形.10 、【答案】 D;【解析】 A选项 : 正三角形的一个内角度数为180°−360°÷3=60°,是360°的约数,能镶嵌平面,不符合题意,故A错误;B选项: 正六边形的一个内角度数为180°−360°÷6=120°,是360°的约数,能镶嵌平面,不符合题意,故B错误;C选项 : 正四边形的一个内角度数为180°−360°÷4=90°,是360°的约数,能镶嵌平面,不符合题意,故C错误;D选项 : 正五边形的一个内角度数为180°−360°÷5=108°,不是360°的约数,不能镶嵌平面,符合题意,故D正确;11 、【答案】 D;【解析】沿对角线剪则剩下三角形.剪痕过一个顶点,并与一面相交得四边形.剪痕与相邻的两边相交,得五边形.12 、【答案】 D;【解析】如图:剪切的三种情况:①不经过顶点剪,则比原来边数多1,②只过一个顶点剪,则和原来边数相等,③按照顶点连线剪,则比原来的边数少1,设内角和为720°的多边形的边数是n,则(n−2)⋅180°=720°,解得:n=6,则原多边形的边数为5或6或7,故选:D.13 、【答案】425;【解析】∠A+∠B+∠C+∠D+∠AED=180°×(5−2)=540°,∵∠1+∠AED=180°,∠1=65°,∴∠AED=180°−65°=115°,∴∠A+∠B+∠C+∠D=540°−∠AED=540°−115°=425°.14 、【答案】100°;【解析】如图:∵五边形ABCDE的外角和是360°,∴∠5=360°−70°×4=80°,∴∠AED=180°−80°=100°.15 、【答案】8;【解析】根据n边形的内角和公式,得:(n−2)⋅180=1080,解得n=8.∴这个多边形的边数是8.故答案为:8.16 、【答案】9;【解析】解法一:360°÷40°=9.多边形外角和是360°,边数=外角数=内角数.解法二:∵外角都是40°,∴内角都是140°,设它为n边形则度数总和为140n°,又∵n边形的度数和是(n−2)×180°,所以140n=(n−2)×180,解得n=9.17 、【答案】 A;【解析】设该多边形边数为n,则内角和为180°(n−2),外角和为360°,∴180°⋅(n−2)=3×360°,解得n=8,故选A.18 、【答案】 C;【解析】多边形外角和为360°,则此多边形内角和为720°,+2=6.∴边数为=720°180°19 、【答案】 C;【解析】由外角与它相邻的内角是邻补角可得:x+4x=180°,一个外角度数x=36°,∴正多边形的边数为360°÷36°=10.20 、【答案】 B;【解析】∵多边形的外角和为360°,而每一个外角为24°,∴多边形的边数为360°÷24°=15,∴小华一共走了:15×10=150米.故选:B.21 、【答案】 C;【解析】从n边形的一个顶点出发可引出(n−3)条对角线,可组成(n−2)个三角形,即可得n−2=10,解得n=12.故选C.22 、【答案】6;【解析】多边形的边数:360°÷40°=9,从一个顶点出发可以引对角线的条数:9−3=6(条).23 、【答案】 C;【解析】 A选项 : 正三角形每个内角是60°,能整除360°,能镶嵌.B选项 : 正方形每个内角是180°−360°÷4=90°,能整除360°,能镶嵌.C选项 : 正五边形每个内角为180°−360°÷5=108°,不能整除360°,不能镶嵌.D选项 : 正六边形每个内角为180°−360°÷6=120°,能整除360°,能镶嵌.24 、【答案】540°或360°或180°;【解析】n边形的内角和是(n−2)⋅180°,所得新的多边形的边数增加1,则新的多边形的内角和是(4+1−2)×180°=540°,所得新的多边形的边数不变,则新的多边形的内角和是(4−2)×180°=360°,所得新的多边形的边数减少1,则新的多边形的内角和是(4−1−2)×180°=180°,因而所成的新多边形的内角和是540°或360°或180°.25 、【答案】 D;【解析】一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或者减少了一条,根据(n−2)×180°=2520°,解得n=16.∴多边形的边数为15,16或17.故选D.26 、【答案】 C;【解析】方法一 : ∵在五边形ABCDE中,∠A+∠B+∠E=300°,∴∠EDC+∠BCD=240°,又∵DP、CP分别平分∠EDC、∠BCD,∴∠PDC+∠PCD=120°,∴△CDP中,∠P=180°−(∠PDC+∠PCD)=180°−120°=60°.方法二 : 五边形的内角和为(5−2)×180°=540°∵∠A+∠B+∠E=300°,∴∠EDC+∠BCD=240°.∵DP、CP分别平分∠EDC,∠BCD,∴∠PDC=12∠EDC,∠PCD=12∠BCD,∴∠PDC+∠PCD=12(∠EDC+∠BCD)=12×240°=120°∴∠P=60°.故选C.27 、【答案】360;【解析】∠1+∠2+∠3+∠4+∠5=(180°−∠BAE)+(180°−∠ABC)+(180°−∠BCD)+(180°−∠CDE)+(180°−∠DEA)=180°×5−(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)=900°−(5−2)×180°=900°−540°=360°.故答案为:360°.28 、【答案】360;【解析】如下图所示∵∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,∴∠AHG+∠DNG+∠EGN=∠A+∠B+∠C+∠D+∠E+∠F,又∵∠AHG、∠DNG、∠EGN是△GHN的三个不同的外角,∴∠AHG+∠DNG+∠EGN=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.故答案为:360.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多边形及其内角和
基础过关作业
1.四边形ABCD中,如果∠A+∠C+∠D=280°,则∠B的度数是()
A.80° B.90° C.170° D.20°
2.一个多边形的内角和等于1080°,这个多边形的边数是()
A.9 B.8 C.7 D.6
3.内角和等于外角和2倍的多边形是()
A.五边形 B.六边形 C.七边形 D.八边形
4.六边形的内角和等于_______度.
5.正十边形的每一个内角的度数等于______,每一个外角的度数等于_______.
6.如图,你能数出多少个不同的四边形?
7.四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?•为什么?8.求下列图形中x的值:
综合创新作业
9.(综合题)已知:如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,•DF平分∠ADC.BE 与DF有怎样的位置关系?为什么?
10.(应用题)有10个城市进行篮球比赛,每个城市均派3个代表队参加比赛,规定同一城市间代表队不进行比赛,其他代表队都要比赛一场,问按此规定,•所有代表队要打多少场比赛?
11.(创新题)如图,以五边形的每个顶点为圆心,以1为半径画圆,求圆与五边形重合的面积.
12.(1)(2005年,南通)已知一个多边形的内角和为540°,则这个多边形为()
A.三角形 B.四边形 C.五边形 D.六边形
(2)(2005年,福建泉州)五边形的内角和等于_______度.
13.(易错题)一个多边形的每一个顶点处取一个外角,这些外角中最多有钝角(• )
A.1个 B.2个 C.3个 D.4个
培优作业
14.(探究题)
(1)四边形有几条对角线?
五边形有几条对角线?
六边形有几条对角线?
……
猜想并探索:
n边形有几条对角线?
(2)一个n边形的边数增加1,对角线增加多少条?
15.(开放题)如果一个多边形的边数增加1,•那么这个多边形的内角和增加多少度?若将n边形的边数增加1倍,则它的内角和增加多少度?
数学世界
攻其不备
壁虎在一座油罐的下底边沿A 处.它发现在自己的正上方──油罐上边缘的B•处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突然袭击如图7-3-5.结果,•壁虎的偷袭得到成功,获得了一顿美餐.
请问:壁虎沿着螺旋线爬行是最短的路程吗(线段AB 除外)?
答案:
1.A 点拨:∠B=360°-(∠A+∠C+∠D )=360°-280°=80°.故选A .
2.B 点拨:设这个多边形的边数为n ,则(n-2)·180=1080.解得n=8.故选B .
3.B 点拨:设这个多边形的边数为n ,根据题意,得(n-2)·180=2×360.解得n=6.故选B . 4.720
5.144°;36°
点拨:正十边形每一个内角的度数为:(102)18010
-⨯︒
=144°,
每一个外角的度数为:180°-144°=36°.
6.有27个不同的四边形.
7.解:四边形的四个内角不可以都是锐角,不可以都是钝角,可以都是直角.
因为四边形的内角和为360°,如果四个内角都是锐角或都是钝角,• 则内角和小于360°或大于360°,与四边形的内角和为360°矛盾.• 所以四个内角不可以都是锐角或都是钝角.
若四个内角都是直角,则四个内角的和等于360°,与内角和定理相符, 所以四个内角可以都是直角. 8.解:(1)90+70+150+x=360. 解得x=50.
(2)90+73+82+(180-x )=360. 解得x=65.
(3)x+(x+30)+60+x+(x-10)=(5-2)×180. 解得x=115. 9.解:BE ∥DF .
理由:∵∠A=∠C=90°, ∴∠A+∠C=180°.
∴∠ABC+∠ADC=360°-180°=180°.
∵∠ABE=1
2
∠ABC,∠ADF=
1
2
∠ADC,
∴∠ABE+∠ADF=1
2
(∠ABC+∠ADC)=
1
2
×180°=90°.
又∵∠ABE+∠AEB=90°,
∴∠AEB=∠ADF,
∴BE∥DF(同位角相等,两直线平行).
10.解:1
2
n(n-3)=
1
2
×10×(10-3)=
1
2
×10×7=35(场).
答:按此规定,所有代表队要打35场比赛.
点拨:问题类似于求多边形对角线的个数.
11.解:(5-2)×180°÷360°×12=1.5.
点拨:不能直接求出扇形的度数,用整体法圆与五边形重合部分的角度和正好是五边形的内角和.
12.(1)C 点拨:设这个多边形的边数为n,
依题意,得(n-2)×180°=540°,解得n=5,故选C.
(2)540 点拨:(n-2)×180°=(5-3)×180°=540°.
13.C
14.解:(1)四边形有2条对角线;
五边形有5条对角线;
六边形有9条对角线;
……
n边形有
(3)
2
n n-
条对角线.
(2)当n边形的边数增加1时,对角线增加(n-1)条.
点拨:从n边形的一个顶点出发,向其他顶点共可引(n-3)条对角线,n个顶点共可引
n(n-3)条,但这些对角线每一条都重复了一次,故n边形的对角线条数为
(3)
2
n n-
.
15.180°,n·180°.
数学世界答案:
是最短的路程.可用纸板做一个模型,沿AB剪开便可看出结论.。
