平面系统平衡习题课
理论力学2.2、平面任意力系的合成与平衡

m F1 OA F2 OB F1 ( OA OB ) F1 AB
3
力 线 作用在刚体上的力可以离开其作用线而平 平 行移动到刚体上任意位置处,但必须对刚体 移 附加一个力偶,附加力偶的力偶矩等于原力 定 对平移后所得新力作用点的力矩。 理
求细绳的拉力和A、B两处的支持力。
解、研究对象:AB,受力 如图所示,则有:
Fix Fiy mD
0 0
(Fi )
0
FB FD G FA c
FA
os
sin 0
FB
BD
G
AB 2
0 sin
FA
AD
0
FA 115.5(N) FB 72.2(N ) FD 129.9(N) 12
例2.2-6、匀质细杆AB长度为L,重量为mg,静 止在半径为r的光滑半圆槽内(图2.2-17),
L=3r;求AB杆与水平线之间的夹角
解、研究对象:AB杆,受力如 图所示,则有:
Fix 0 Fiy 0 mO (Fi ) 0
FB FB
cos(2 ) FD sin sin(2 ) FD cos
d mO 2402 3.39(m) FR 709 .5
xE
d
sin
3.39 sin 70.8
3.59(m)
y yE tan 70.8 (x xE ) y 2.87x 10.31 0
10
课堂练习题(图示):
考研专业课复习 东南大学结构力学习题集及答案
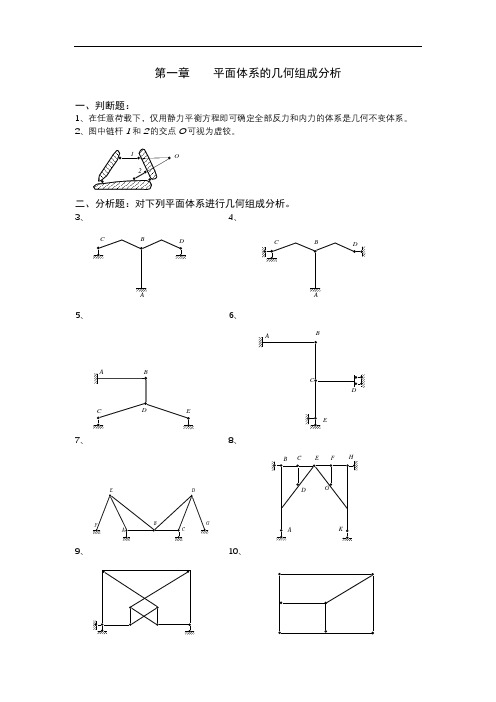
第一章 平面体系的几何组成分析一、判断题:1、在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
2、图中链杆1和2的交点O 可视为虚铰。
O二、分析题:对下列平面体系进行几何组成分析。
3、 4、ACDBACDB5、 6、A CD BEABCDE7、 8、ABCD GE FA BCDEFGHK9、 10、11、 12、1234513、 14、15、 16、17、 18、19、 20、1245321、 22、123456781234523、 24、12345625、 26、27、 28、29、 30、31、 32、33、BA CFDE三、在下列体系中添加支承链杆,使之成为无多余约束的几何不变体系。
34、35、第二章 静定结构内力计算一、判断题:1、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图(a)所示结构||M C =0。
aa(a)BCa aAϕ2a2(b)5、图(b)所示结构支座A 转动ϕ角,M AB = 0, R C = 0。
6、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图(c)所示静定结构,在竖向荷载作用下,AB 是基本部分,BC 是附属部分。
ABC(c)8、图(d)所示结构B 支座反力等于P /2()↑。
(d)9、图(e)所示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB(e)10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
11、图(f)所示桁架有9根零杆。
(f)a a a a(g)12、图(g)所示桁架有:N1=N2=N3= 0。
13、图(h)所示桁架DE杆的内力为零。
a a(h)(i)14、图(i)所示对称桁架在对称荷载作用下,其零杆共有三根。
15、图(j)所示桁架共有三根零杆。
平面一般力系习题

单体
[例] 图示力系,已知:P1=100N, P2=50N, P3=200N,图中距离
单位cm。
求:1、力系主矢及对A、B、C
三点之矩? 2、力系简化最后结果。
y
P1
A
P2
R
4
B
6 3C
解: 1、建立坐标系
P3 x
2、X=∑Fx=P3 =200N
Y=∑Fy=P1+ P2 =100+50 =150N
Q2
q
l 4
联立求解:可得
mA= 30 kN·m NA= -12.5 kN
求图示机构平衡时,力偶m, F2K 0 N
B
C
B
SBC
SB C C
2m 2m
m
F
m
A
D
列平衡方程求解:
A RAX R AY
D
RD
m AF0: SBC 4F 20 SBC240210KN
m0:
SB C 4m0 m 1 4 0 4 K 0 .m N
P2
R
P1
B
4
A 6 3C
P3
m A30 N0 cm
P2
P1
B
4
R
m B20 N0 cm
A 6 3C
P3
P2
P1
B
4
R
m C10N 5 c0mA 6 3 C
P3
3、简化最终结果 选简化中心:A点 主矢Fra bibliotekR 2N 50
方向: =36.9°
y
P2
P1
mA
B
A
R R C
P3 x
n
mO(R)mO(Fi)
平面一般力系的平衡方程

-
-
-专业资料-
-
-
-
课时
教 学 容、方 法、步 骤
附
分配
记
(2)空载时 W=0,Q=Qmax,机架可能绕 A 点左翻,在临界平衡状态, B 处悬空,NB=0,受力图如图 3-10c 所示。则
故 平衡锤的范围应满足不等式
例 4-5 一简易起重机如图 4-11 所示。横梁 AB 的 A 端为固定铰支座,B 端用 拉杆 BC 与立柱相连。已知梁的重力 G1=4kN,载荷 G2=12kN,横梁长 L=6m, α=30°,求当载荷距 A 端距离 x=4m 时,拉杆 BC 的受力和铰支座 A 的约束 反力。
其中 A、B、C 三点不能在一条直线上。
20 二. 平面平行力系的平衡方程
-
-
-专业资料-
-
-
-
课时
教 学 容、方 法、步 骤
附
分配
记
在基本式中,坐标轴是任选的。现取 y 轴平行各力,则平面平行力系中 各力在 x 轴上的投影均为零,即∑Fx ≡0。于是平面平行力系只有两独立的平 衡方程,即
∑Fy=0 ∑MO(F)=0
和投影轴,合理的选用方程组的形式,尽量避免联立解方程组
的麻烦。另外,平面平行力系是平面任意力系的一种特殊情形。
复习思考题、 作业题
1、思考平面汇交力系的平衡方程中,可否取两个力矩方程,或 一个力矩方程和一个投影方程?这时,其矩心和投影轴的选 择有什么限制?
2、课本习题 4-7、4-6。
-
-
-专、方 法、步 骤
附
分配
记
40
§4.3 平面任意力系的平衡方程
一. 平面一般力系的平衡方程
1. 基本形式
理论力学02习题课

M F d 1 2 F d 2ABC 2
平面内两个力偶,如果力偶矩相等,则两个力偶等效
8
主要内容和方法
平面力偶系的合成和平衡条件
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系
平面力偶系合成结果还是一个力偶,其力偶矩为各力偶矩的 代数和。
M FR d F1d F2 d M1 M 2
例题7:在刚体的A、B、C、D四点作用 有四个大小相等的力,此四力沿四个边 恰好组成封闭的力多边形,如图所示.此 刚体是否平衡?选择其中一对平行力, 同时改变方向,此刚体是否平衡? 答:图示情况下刚体不平衡,依然存在顺时针方向力矩,选择其 中一对平行力,同时改变方向,此时刚体平衡。
14
典型题目
例题8:在下面各图中,力或力偶对点A的矩都相等,它们引起的支座 约束力是否相同?
解:
F 0 F F 0 M 0 F l M 0
x A B A B
M M FA ; FB l l
23
作业题
2-12已知梁上作用有力偶,重量不计,在下面三种情况下,计算 之作的约束力
解:
F 0 F cos F cos 0 M 0 F l cos M 0
Fx 0 F FA
2 5 0 FA F 2 5
Fy 0 FD FA
19
1 1 0 FD F 2 5
支座A点的约束力与假设的方向相反
作业题
2-6如图所示,输电线重量沿AB均匀分布,求电线中点和两 端拉力 f 1m, AB 40m, P 400 N
0 M 2 F cos r2 0 M1 r cos r2 M 1 2 cos r1 r1
理论力学平面力系的简化和平衡

原力偶系的合力偶矩
n
M Mi i 1
只受平面力偶系作用的刚体平衡充要条件:
n
M Mi 0 i 1
对BC物块对B点取矩,以逆时针为正列方程应为:
M 2 M B (FC ) M FCY a FCx b M FC (b a) cos45 0
[例] 在一钻床上水平放置工件,在工件上同时钻四个等直径 的孔,每个钻头的力偶矩为 m1m2 m3 m4 15Nm 求工件的总切削力偶矩和A 、B端水平反力?
两轴不平行即 条件:x 轴不 AB
可,矩心任意
连线
mA (Fi ) 0 mB (Fi ) 0 mC (Fi ) 0
③三矩式 条件:A,B,C不在
同一直线上
上式有三个独立方程,只能求出三个未知数。
4. 平面一般力系的简化结果分析
简化结果: 主矢R ,主矩 MO ,下面分别讨论。 ① R =0, MO =0,则力系平衡,下节专门讨论。 ② R =0,MO≠0 即简化结果为一合力偶, MO=M 此时刚
解除约束,可把支反
力直接画在整体结构
的原图上)
解除约束
由
mA (Fi
)
0
P2a N B
3a0,
N B
2P 3
X 0 XA 0
Y 0 YB NB P0,
YA
P 3
2.5物体系统的平衡、静定与超静定问题
1、物体系统的平衡问题 物体系统(物系):由若干个物体通过约束所组成的系统叫∼。 [例]
外力:外界物体作用于系统上的力叫外力。 内力:系统内部各物体之间的相互作用力叫内力。
N2个物体受平面汇交力系(或平面平行力系)
X 0 Y 0
2*n2个独立平衡方程
N3个物体受平 X 0 面任意力系 Y 0
平面力系平衡问题课堂练习题
例2-19 已知: PE 10kN, PG 7kN, 各杆长度均为1m;
求: 1,2,3杆受力.
解: 取整体,求支座约束力.
Fx 0
FAx 0
M B 0 2PE PG 3FAy 0
Fy 0 FAy FBy PE PG 0
FAy 9kN
FBy 8kN
38
用截面法,取桁架左边部分.
2m
2m
解方程可得 F4 10kN
节点C在y方向的平衡方程可用来校核
C
F1
F4
F’3
当计算出杆的受力的代数值为正时,表明 该杆受力的方向符合假设的方向,即该杆受拉。 反之,当计算出该杆受力的代数值为负时,表 明该杆受压。
34
平面桁架如图所示。设两主动力大小F =10 kN , 作用在节点A和节点B上,a =1.5 m,h =3 m。求1, 2,3和4各杆受的内力。
19
例2- 已知:P , a ,各杆重不计; 24求:B 铰处约束力.
解:取整体,画受力图
MC 0 FBy 2a 0
FBy 0
取DEF杆,画受力图
M D 0 FE sin 45 a F 2a 0
Fx 0 FE cos 45 FD' x 0 ME 0 FDy 'a F 2a 0
取AB杆(不含销钉B),画受力图.
Fx 0
FAx
1 2
q
3a
FABx
0
FAx qa
Fy 0 FAy FABy 0
MA 0
FAy P qa
1 M A 2 q 3a a FABx 3a FABy a 0
M A (P qa)a
26
组合梁AC和CE用铰链C相连,A端为固定端,E端为活动 铰链支座。受力如图所示。已知: l =8 m,F=5 kN,均布载 荷集度q=2.5 kN/m,力偶矩的大小M= 5 kN•m,试求固端A, 铰链C和支座E的约束力。
平面任意力系平衡方程的基本形式例题分析
《工程力学》课程习题-例题分析学习项目二(平面任意力系的合成与平衡)平面任意力系平衡方程的基本形式1、起重设备重G1=10kN,可绕铅直轴AB转动;起重机的挂钩上挂一重为G2=40k N的重物,如图所示。
起重机的重心C到转动轴的距离为,其它尺寸如图所示。
求在止推轴承A和轴承B处的反作用力。
解:以起重机为研究对象,它所受的主动力有G1和G2。
由于对称性,约束反力和主动力都在同一平面内。
止推轴承A处有两个约束反力F Ax、F Ay,轴承B处只有一个与转轴垂直的约束反力F B,约束反力方向如图所示。
上述力形成平面一般力系,取坐标系如图所示,列平衡方程,即∑F x=0 F Ax+F B =0∑F y=0 F Ay-G1-G2=0∑M A(F i)=0 -F B×5-G1×-G2×=0联立以上方程,得F Ay=G1+G2=50 kNF B =--=-31kNF Ax =-F B =31kNF B 为负值,说明其方向与假设的方向相反,即应指向左。
2、防洪用弧形闸门有对称的两个支架和铰链支座。
已知闸门重G =1100kN ,静水总压力2P 2G B V A (F i )=0 B V ×2G×=0得 V B = kN 取x 、y 轴方向如图b ,列投影方程由∑F x =0 05531sin 25531sin 21='︒-'︒+-G V R P B得 R 1=由∑F y =0 05531c 25531cos 2='︒-'︒+os G V R B得R2=反力的方向如图b所示。
七年级数学《平面直角坐标系-习题课》教学设计
《平面直角坐标系习题课》教学设计1. 教材内容义务教育课程标准实验教科书(人教版)《数学》八年级上册第6章第一小节平面直角坐标系。
2.知识背景分析从《课程标准》看,本章隶属于“空间与图形”领域, 本章共3小节,主要内容包括平面直角坐标系的有关概念、点与坐标(坐标为整数)的对应关系、用作标表示地理位置和用坐标表示平移等。
教科书首先从生活实际中常见的表示位置的方法(如用“几排几号”表示电影院中的座位,用“几行几列”表示教室中学生的座位等)出发,引出有序数对的概念,指出利用有序数对可以确定物体的位置,由此联想到是否可以用有序数对表示平面内点的位置的问题,结合数轴上确定点的位置的方法,引出平面直角坐标系,学习平面直角坐标系的有关概念(如横轴、纵轴、原点、坐标、象限等),建立点与坐标(坐标为整数)的对应关系。
本节课是在教学了第一小节平面直角坐标系3课时之后的一节习题课。
旨在使学生进一步感受有序数对在确定点的位置中的作用,理解点与坐标的对应关系;在给定的平面直角坐标系中,能熟练的根据点的坐标(坐标为整数)描出点的位置,能由点的位置熟练地写出点的坐标(坐标为整数)。
学生对这部分知识做以全面、系统的梳理,增强解决实际问题的能力,提高学生学习的兴趣性和积极性,为后续学习奠定基础。
3.学情背景分析教学对象是七年级学生。
在学习本章之前,学生已经学习了有理数及其数轴的相关知识,已经明确了任何有理数都可以用数轴上的点来表示的这一关系,且能够熟练地在数轴上表示一个有理数,能够根据数轴上点的位置确定一个有理数的大小。
在进行本节的习题课之前,学生已经了解了有序数对的概念,并初步学会了利用有序数对确定物体的位置,并用有序数对表示平面内点的位置,结合数轴上确定点的位置的方法,还学习了平面直角坐标系的有关概念(如横轴、纵轴、原点、坐标、象限等),建立点与坐标(坐标为整数)的对应关系。
但对知识之间的逻辑关系缺乏深层理解和整体认识,加之思维以经验性为主,抽象概括、归纳总结等理性思维能力还需要进一步锤炼。
平面一般力系习题
YA
NB
X 0 XA 0
ND
mA 0 Y 0
N B 3 N D 12 P 10 Q 6 0
N B 100(kN) YA N B N D Q P 0 YA 48.33(kN)
XA 0 YA 48.33(kN)
N B 100(kN) N D 8.33(kN)
求图示伸出梁得支座反力。
SBC 4 m 0
m 10 4 40KN.m
例题分析
[例] 已知各杆均铰接,B端插入地
内,P=1000N,AE=BE=CE=DE=1m,杆重不计。 求AC 杆内力?B
点得反力?
解:① 选整体研究
② 受力如图 ③ 选坐标、取矩点、Bxy,B点
④ 列方程为:
X 0 X B 0; Y 0 YB P 0; YB P mB 0 M B P DE 0
物体系得平衡问题
例 组合梁AC 与CE 用铰链C 相连,A端为固定端,E 端 为活动铰链支座。受力如图所示。已知: l =8 m,P=5 kN,均布载荷集度q=2、5 kN/m,力偶矩得大小m=
5kN·m,试求固端A、铰链C 与支座E 得反力。
P
q
m
E AHB C D
l/8 l/8 l/4 l/4 l/4
mC mC (Fi ) P1 9 P2 3 100 9 50 3 1050N cm
P2
R
P1
B
4
A 6 3C
P3
mA 300N cm
P2
P1
B
4
R
mB 200N cm
A 6 3C
P3
P2
P1
B
4
R
mC 1050N cm A 6 3 C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平衡方程要点:各类力系独立平衡方程数
63 3
3 3
221
可用于判断问题是否可解
物体系统平衡问题求解
(1)审题,确定已知量和未知量,取适当的分离体,画出分离体的受力图
(2)根据分离体受力特点,选适当坐标系(使一个坐标轴与某一未知力的作用线垂直)、列平衡方程(尽量使一个方
程只含一个未知量),力矩方程的矩心取在未知力作用线
相交处
(3)对物体系平衡问题(若整体平衡,则局部必平衡),要想求得全部约束力,必须从中间铰处拆开,从受力最简单的构件开始分析求解(二力杆,三力汇交)
(4)注意杆件之间的相互作用力协调,一旦作用力方向设定,则其反作用力方向必须画成与作用力反向,不能再任意假设(5)列平衡方程求解,结果为正,说明假设方向与实际方向一致,为负,假设方向与实际方向相反
F A
F B
∑F=0判断固定铰支座A、
取矩心避免三个未知力的求解
∑M G=0, -F Dx∙L2+F T·0.5L2=0
F Dx=3KN
综之D处的约束力为
F Dx=3KN F Dy=16.5KN
[思考] 求A、B处的约束力?
本题启示
(1)充分利用二力杆件、三力汇交平衡的性质:解题突破口(2)拆开中间铰:深入分析的关键
(3)选取关键对象,恰当选取矩心!
M A F
F B
Ay
(有铰拆铰,本题只有一个铰)
=0F Cx=6KN
[杆CDB]
∑M B=0,
M+F1cos60 0· 2L+2qL· L-F Cy· 2L -F Cx· 2L-F1sin60 0· L=0
F Cy=3.8KN F Ay=3.8KN
综之,A处的约束反力为
F Ax=2KN F Ay=3.8KN
M A=-24kN·m(顺时针方向)本题启示:整体分析,见铰拆铰
M B F By F Bx F Ay F Ax
[绳CD]0:0
y
D C F
F F =−=∑[左边系统]
0:00
:0
()0:0
x B x
y
B y
D
B
B
D
F F F F
F
M
M F L M ⎧==⎪⎪=−=⎨⎪=−−=⎪⎩
∑∑∑F 02kN
16kN m
B x B y B F F M =⎧=•⇒⎪
⎨⎪
=⎩
例4-25:如图所示结构,C 、D 、E 处为中间铰约束,各构件自重不计。
已知L =2m ,F 1=F 2=200kN 。
试求固定铰支座A 、B 处和中间铰支座C
的约束反力。
解:[整体]
分析受力状态图:A 点和B 点
200kN 5000
:()0kN 30::k )00(N
A x
B x
B
A y
A F M M
F
F F
⎧=⎪⎪====⎨⎪=⎪⎩
∑∑∑F F 整体后,见铰拆铰!
[杆件HCDA]:选取恰当矩心!
1()0:2240
D
Cx Ax M
F F F =−−=∑F 600kN
C x F =[杆件CEB]:选取恰当矩心!
()0:
2220
E
B Cx Cy M F F F =−−=∑F 100kN
C y
F
=−注意:求C 铰的约束反力,D 和E 可以取为矩心!
C
F
E
D
C
A
F′
C
F
A
D
C
F
A
F′
DE
F
CA
F
DE
F
ED
E
C
B
F
B
F′
C
F′
ED
F′
CA
E
D
C
F
G
T F
O
A
B
O
A
M A B
C
F A
A
M D E
D F C
课堂练习A
O
M
G
A
B
G
A
B
C
D E
2
B
B BD
F DB
F Cy
F BD
′B ′
F 2
G A
F C
A
B
Cx
F Cy
F G
E
C
B
A
G
A
B
F BD
′By
′F B
2
G
2
G E
C
B
A
G。
