专题07二次函数与幂函数-2019年高三数学(理)二轮复习题Word版含解析
高考数学复习、高中数学 幂函数与二次函数附答案解析

m+3 则对称轴 x= ≤2,解得 m≤1;
2 则对称轴 x= ≥4,解得 m≥5.
2
故所求 m 的取值范围是(-∞,1]∪[5,+∞).
1 16.解:(1)由 f(x)为幂函数知-2m2+m+2=1,得 m=1 或 m=- .当 m=1 时,f(x)=x2,
能力提升题组 (建议用时:20 分钟) 13. 若函数 f(x)=x2+ax+b 在区间[0,1]上的最大值是 M,最小值是 m,则 M-m( )
A.与 a 有关,且与 b 有关
B.与 a 有关,但与 b 无关
C.与 a 无关,且与 b 无关
D.与 a 无关,但与 b 有关
14.已知函数 f(x)=x2+2mx+2m+3(m∈R),若关于 x 的方程 f(x)=0 有实数根,且两根分别 为 x1,x2,则(x1+x2)·x1x2 的最大值为________.
15.已知函数 f(x)=ax2-2ax+2+b(a>0)在区间[2,3]上的值域为 (1) 求 a,b 的值; (2) 若关于 x 的函数 g(x)=f(x)-(m+1)x 在[2,4]上为单调函数,求 m 的取值范围.
16.已知幂函数 f(x)=(-2m2+m+2)xm+1 为偶函数. (1)求 f(x)的解析式; (2)若函数 h(x)=f(x)+ax+3-a≥0 在区间[-2,2]上恒成立,求实数 a 的取值范围.
C.若任意实数 a,b,使得 f(a)≥g (b)+n 成立,则 n≤-2
D.若存在实数 a,b,使得 f(a)=g(b)成立,则 2- 2≤b≤2+ 2
三、填空题
1
9.已知函数 f(x)=x2,且 f(2x-1)<f(3x),则 x 的取值范围是________.
高考数学一轮复习专题2.7二次函数及幂函数练习(含解析)

第七讲二次函数与幂函数1.幂函数(1)幂函数的定义一般地,形如y=xα的函数称为幂函数,其中x是自变量,α是常数.(2)常见的五种幂函数的图象和性质比较R R R{x|x≥0}{x|x≠0}(1)二次函数解析式的三种形式:一般式:f(x)=ax2+bx+c(a≠0).顶点式:f(x)=a(x-m)2+n(a≠0),顶点坐标为(m,n).零点式:f(x)=a(x-x1)(x-x2)(a≠0),x1,x2为f(x)的零点.(2)二次函数图像R R考向一 幂函数概念及性质【例1】已知幂函数223(22)n nf x n n x -=+-(n ∈Z)的图象关于y 轴对称,且在(0,+∞)上是减函数,则n 的值为________. 【答案】 1【解析】由于f (x )为幂函数,所以n 2+2n -2=1,解得n =1或n =-3,经检验只有n =1符合题意. 【举一反三】1.已知函数f (f )=(f 2−f −1)f f 2+2f −3是幂函数,且其图象与两坐标轴都没有交点,则实数f =() A .−1 B .2 C .3 D .2或−1【答案】A【解析】∵函数f (f )=(f 2−f −1)f f2+2f −3是幂函数,∴f 2−f −1=1,解得:f =2或f =−1,f =2时,f (f )=f ,其图象与两坐标轴有交点不合题意,f =−1时,f (f )=1f 4,其图象与两坐标轴都没有交点,符合题意,故f =−1,故选:A .2.已知函数f(f)=(3f2−2f)f f是幂函数,若f(x)为增函数,则m等于()A.−13B.−1C.1 D.−13或1【答案】C【解析】函数f(x)=(3m2-2m)x m是幂函数,则3m2-2m=1,解得m=1或m=-13,又f(x)为增函数,则m=1满足条件,即m的值为1.故选:C.3.已知幂函数f(f)=f f的图像过点(2,√2),则下列说法正确的是()A.f(f)是奇函数,且在(0,+∞)上单调递增B.f(f)是偶函数,且在(0,+∞)上单调递减C.f(f)既不是奇函数也不是偶函数,且在(0,+∞)上单调递增D.f(f)既不是奇函数也不是偶函数,且在(0,+∞)上单调递减【答案】C【解析】∵幂函数y=xα的图象过点(2,√2),∴√2=2α,解得α=12,故f(x)=√f,故f(x)既不是奇函数也不是偶函数,且在(0,+∞)上是增函数,故选:C.4.设α∈{−1,1,12,3},则使函数y=f f的定义域为R且为奇函数的所有α的值为()A.−1,1,3 B.12,1 C.−1,3 D.1,3【答案】D【解析】当α=﹣1时,函数的定义域为{x|x≠0},不满足定义域为R;当α=1时,函数y=f f的定义域为R且为奇函数,满足要求;当α=12函数的定义域为{x|x≥0},不满足定义域为R;当α=3时,函数y=f f的定义域为R且为奇函数,满足要求;故选:D.考向二图像问题【例2】(1)当f∈{−1,12,1,3}时,幂函数f=f f的图象不可能经过的象限是A.第二象限 B.第三象限 C.第三、四象限 D.第二、四象限(2)在同一直角坐标系中,函数f(x)=f f(x≥0),g(x)=fff f x的图象可能是()A. B.C. D.【答案】(1)D (2)D【解析】(1)因为f=f−1经过第一、三象限;f=f12经过第一象限;f=f1经过第一、三象限;f=f3经过第一、三象限;所以不可能经过的象限是第二、四象限,选D.(2)∵实数a>0且a≠1,∴函数f(x)=x a(x>0)是上增函数,故排除A;∴当a>1时,在同一直角坐标系中,函数f(x)=x a(x>0)是下凹增函数,g(x)=log a x的是增函数,观察四个选项,没有符合条件选项;当0<a<1时,∴在同一直角坐标系中,函数f(x)=x a(x>0)是增函数,g(x)=log a x是减函数,由此排除B和C,符合条件的选项只有D.故选:D.【举一反三】1.如图表示的是四个幂函数在同一坐标系中第一象限内的图象,则幂函数f=f 12的图象可能是()A.① B.② C.③ D.④【答案】D【解析】幂函数y=f12为增函数,且增加的速度比价缓慢,只有④符合.故选:D.2.下图给出四个幂函数的图象,则图象与函数的大致对应是()①②③④A.①f=f 13,②f=f2,③f=f12,④f=f−1B.①f=f3,②f=f2,③f=f 12,④f=f−1C.①f=f2,②f=f3y=x3,③f=f−1,④f=f 1 2D.①f=f 13,②f=f12,③f=f2,④f=f−1【答案】B【解析】②的图象关于y轴对称,②应为偶函数,故排除选项C,D,①由图象知,在第一象限内,图象下凸,递增的较快,所以幂函数的指数大于1,故排除A故选:B.3.在同一直角坐标系中,函数f(f)=f f(f≥0),f(f)=log f f(f>0,且f≠1)的图象可能是().A. B. C. D.【答案】D【解析】对于A项,对数函数过(1,0)点,但是幂函数不过(0,1)点,所以A项不满足要求;对于B项,幂函数f>1,对数函数0<f<1,所以B项不满足要求;对于C项,幂函数要求0<f<1,而对数函数要求,f>1,所以C项不满足要求;对于D项,幂函数与对数函数都要求0<f<1,所以D项满足要求;故选D.4.如图是幂函数y=x m和y=x n在第一象限内的图象,则( )A.-1<n<0,0<m<1 B.n<-1,0<m<1 C.-1<n<0,m>1 D.n<-1,m>1【答案】B【解析】由题图知,f=f f在[0,+∞)上是增函数,f=f f在(0,+∞)上为减函数,∴f>0,f<0,又当f>1时,f=f f的图象在f=f的下方,f=f f的图象在f=f−1的下方,∴f<1,f<−1,从而0<f <1,f <−1,故选B.考向三 比较大小【例3】设f =(35)25,f=(25)35,f=(25)25,则f ,f ,f 的大小关系是A .f >f >fB .f >f >fC .f >f >fD .f >f >f【答案】A【解析】对于函数f =(25)f ,在(0,+∞)上是减函数,∵35>25,∴(25)35<(25)25,即f <f ;对于函数f =f 25,在(0,+∞)上是增函数,∵35>25,∴(35)25>(25)25,即f >f .从而f <f <f .故A 正确. 【举一反三】1.已知点(f ,9)在幂函数f (f )=(f −2)f f 的图象上,设f =f (f − 13),f =f (ln 13),f =f (√22) 则f ,f ,f 的大小关系为( )A .f <f <fB .f <f <fC .f <f <fD .f <f <f【答案】A【解析】由f (f )=(f −2)f f 为幂函数得f −2=1,f =3, 因为点(3,9)在幂函数f (f )上,所以3f =9,f =2,即f (f )=f 2, 因为f =f (f − 13)=f (3− 13),f =f (ln 13)=f (ff3),又3− 13<√22<1<ff3,所以f <f <f ,选A.2.设f =20.3,f =30.2,f =70.1,则f 、f 、f 的大小关系为( ) A .f <f <f B .f <f <f C .f <f <f D .f <f <f【答案】B【解析】由题意得:f =20.3=√2310=√810,f =30.2=√3210=√910,f =70.1=√710f =√f 10在(0,+∞)上是增函数且9>8>7∴f >f >f 本题正确选项:f3..已知f =(√2)125,f =925,f =4log 4f 2,则下列结论成立的是( ) A .f <f <f B .f <f <f C .f <f <f D .f <f <f 【答案】A【解析】f =265=6415,f =345=8115,∵64<81,∴6415<8115,即f <f ,f =e 2>4>3>345=f ,故f <f <f ,选A .考向四 二次函数解析式【例4】 (1)已知二次函数f (x )=x 2-bx +c 满足f (0)=3,对∀x ∈R ,都有f (1+x )=f (1-x )成立,则f (x )的解析式为________________.(2)已知二次函数f (x )与x 轴的两个交点坐标为(0,0)和(-2,0)且有最小值-1,则f (x )=________. (3)已知二次函数f (x )=ax 2+bx +1(a ,b ∈R ,a ≠0),x ∈R ,若函数f (x )的最小值为f (-1)=0,则f (x )=________.【答案】(1)f (x )=x 2-2x +3 (2)x 2+2x (3)x 2+2x +1【解析】(1)由f (0)=3,得c =3,又f (1+x )=f (1-x ),∴函数f (x )的图象关于直线x =1对称,∴b2=1,∴b =2,∴f (x )=x 2-2x +3.(2)设函数的解析式为f (x )=ax (x +2)(a ≠0),所以f (x )=ax 2+2ax ,由4a ×0-4a24a=-1,得a =1,所以f (x )=x 2+2x .(3)设函数f (x )的解析式为f (x )=a (x +1)2=ax 2+2ax +a (a ≠0),又f (x )=ax 2+bx +1,所以a =1, 故f (x )=x 2+2x +1. 【举一反三】1.已知二次函数f (x )的图象经过点(4,3),它在x 轴上截得的线段长为2,并且对任意x ∈R ,都有f (2-x )=f (2+x ),则f (x )=________. 【答案】 x 2-4x +3【解析】因为f (2-x )=f (2+x )对任意x ∈R 恒成立,所以f (x )图象的对称轴为直线x =2.又因为f (x )的图象被x 轴截得的线段长为2,所以f (x )=0的两根为1和3.设f (x )的解析式为f (x )=a (x -1)(x -3)(a ≠0),又f (x )的图象过点(4,3),所以3a =3,即a =1,所以f (x )的解析式为f (x )=(x -1)(x -3),即f (x )=x 2-4x +3.2.已知二次函数f (x )满足f (2)=-1,f (-1)=-1,且f (x )的最大值是8,试确定此二次函数的解析式.【套路总结】1. 求二次函数解析式的方法【答案】f (x )=-4x 2+4x +7.【解析】设f (x )=ax 2+bx +c (a ≠0). 由题意得⎩⎪⎨⎪⎧4a +2b +c =-1,a -b +c =-1,4ac -b 24a =8,解得⎩⎪⎨⎪⎧a =-4,b =4,c =7.∴所求二次函数的解析式为f (x )=-4x 2+4x +7.3.已知二次函数f (x )的图象经过点(4,3),它在x 轴上截得的线段长为2,并且对任意x ∈R ,都有f (2-x )=f (2+x ),求f (x )的解析式. 【答案】f (x )=x 2-4x +3.【解析】∵f (2-x )=f (2+x )对x ∈R 恒成立,∴f (x )的对称轴为x =2. 又∵f (x )图象被x 轴截得的线段长为2,∴f (x )=0的两根为1和3. 设f (x )的解析式为f (x )=a (x -1)(x -3)(a ≠0).又∵f (x )的图象过点(4,3),∴3a =3,a =1.∴所求f (x )的解析式为f (x )=(x -1)(x -3),即f (x )=x 2-4x +3.4.已知二次函数f (x )=x 2+2bx +c (b ,c ∈R).(1)若f (x )≤0的解集为{x |-1≤x ≤1},求实数b ,c 的值;(2)若f (x )满足f (1)=0,且关于x 的方程f (x )+x +b =0的两个实数根分别在区间(-3,-2),(0,1)内,求实数b 的取值范围.【答案】⎝ ⎛⎭⎪⎫15,57【解析】(1)设x 1,x 2是方程f (x )=0的两个根.由根与系数的关系得⎩⎪⎨⎪⎧x 1+x 2=-2b ,x 1x 2=c ,即⎩⎪⎨⎪⎧-2b =0,c =-1.所以b =0,c =-1.(2)由题,知f (1)=1+2b +c =0,所以c =-1-2b .记g (x )=f (x )+x +b =x 2+(2b +1)x +b +c =x 2+(2b +1)x -b -1,则⎩⎪⎨⎪⎧g (-3)=5-7b >0,g (-2)=1-5b <0,g (0)=-1-b <0,g (1)=b +1>0⇒15<b <57,即实数b 的取值范围为⎝ ⎛⎭⎪⎫15,57. 考向五 二次函数的性质【例5】(1)设二次函数f (x )=ax 2-2ax +c 在区间[0,1]上单调递减,且f (m )≤f (0),则实数m 的取值范围是________.(2) 函数f (x )=ax 2+(a -3)x +1在区间[-1,+∞)上是递减的,则实数a 的取值范围是________ (3) 已知函数f (x )=ax 2+2ax +1在区间[-1,2]上有最大值4,求实数a 的值. 【答案】(1)[0,2] (2)[-3,0] (3)38或-3【解析】(1)二次函数f (x )=ax 2-2ax +c 在区间[0,1]上单调递减,则a ≠0, 又由--2a 2a=1得图象的对称轴是直线x =1,所以a >0.所以函数的图象开口向上,且在[1,2]上单调递增,f (0)=f (2),则当f (m )≤f (0)时,有0≤m ≤2. (2)当a =0时,f (x )=-3x +1在[-1,+∞)上单调递减,满足题意.当a ≠0时,f (x )的对称轴为x =3-a2a ,由f (x )在[-1,+∞)上单调递减,知⎩⎪⎨⎪⎧a <0,3-a2a≤-1,解得-3≤a <0.综上,a 的取值范围为[-3,0]. (3)f (x )=a (x +1)2+1-a .(1)当a =0时,函数f (x )在区间[-1,2]上的值为常数1,不符合题意,舍去;(2)当a >0时,函数f (x )在区间[-1,2]上是增函数,最大值为f (2)=8a +1=4,解得a =38;(3)当a <0时,函数f (x )在区间[-1,2]上是减函数,最大值为f (-1)=1-a =4,解得a =-3. 综上可知,a 的值为38或-3.【举一反三】1.已知函数f (x )=-x 2+2ax +1-a ,x ∈[0,1]有最大值2,则a =________. 【答案】 2或-1【解析】函数f (x )=-x 2+2ax +1-a =-(x -a )2+a 2-a +1,其图象的对称轴方程为x =a .当a <0时,f (x )max =f (0)=1-a ,所以1-a =2,所以a =-1;当0≤a ≤1时,f (x )max =f (a )=a 2-a +1,所以a 2-a +1=2,所以a 2-a -1=0,所以a =1±52(舍去);当a >1时,f (x )max =f (1)=a ,所以a =2.综上可知,a =-1或a =2.2.已知函数f (x )=x 2-(a -1)x +5在区间⎝ ⎛⎭⎪⎫12,1上为增函数,那么f (2)的取值范围是______.【答案】 [7,+∞)【解析】 函数f (x )=x 2-(a -1)x +5在区间⎝ ⎛⎭⎪⎫12,1上为增函数,由于其图象(抛物线)开口向上,所以其对称轴x =a -12或与直线x =12重合或位于直线x =12的左侧,即应有a -12≤12,解得a ≤2,所以f (2)=4-(a -1)×2+5≥7,即f (2)≥7.3.若函数φ(x )=x 2+m |x -1|在[0,+∞)上单调递增,则实数m 的取值范围是__________. 【答案】 [-2,0]【解析】当0≤x <1时,φ(x )=x 2-mx +m ,此时φ(x )单调递增,则m2≤0,即m ≤0;当x ≥1时,φ(x )=x 2+mx -m ,此时φ(x )单调递增,则-m2≤1,即m ≥-2.综上,实数m 的取值范围是[-2,0].考向六 二次函数恒成立【例6】 (1)已知二次函数f (x )满足f (x +1)-f (x )=2x ,且f (0)=1,若不等式f (x )>2x +m 在区间[-1,1]上恒成立,则实数m 的取值范围为____________.((2)函数f (x )=a 2x+3a x-2(a >1),若在区间[-1,1]上f (x )≤8恒成立,则a 的最大值为________.【答案】(1) (-∞,-1) (2)2【解析】(1)设f (x )=ax 2+bx +c (a ≠0),由f (0)=1,得c =1,又f (x +1)-f (x )=2x ,得2ax +a +b =2x ,所以a =1,b =-1,所以f (x )=x 2-x +1.f (x )>2x +m 在区间[-1,1]上恒成立,即x 2-3x +1-m >0在[-1,1]上恒成立,令g (x )=x 2-3x +1-m =⎝ ⎛⎭⎪⎫x -322-54-m ,x ∈[-1,1],g (x )在[-1,1]上单调递减,所以g (x )min =g (1)=1-3+1-m >0,所以m <-1.(2) 令a x =t ,因为a >1,x ∈[-1,1],所以1a≤t ≤a ,原函数化为g (t )=t 2+3t -2,t ∈⎣⎢⎡⎦⎥⎤1a ,a ,显然g (t )在⎣⎢⎡⎦⎥⎤1a ,a 上单调递增,所以f (x )≤8恒成立,即g (t )max =g (a )≤8恒成立,所以有a 2+3a -2≤8,解得-5≤a ≤2,又a >1,所以1<a ≤2,所以a 的最大值为2.1.已知函数f (x )=ax 2+bx +1(a ,b ∈R),x ∈R.(1)若函数f (x )的最小值为f (-1)=0,求f (x )的解析式,并写出单调区间; (2)在(1)的条件下,f (x )>x +k 在区间[-3,-1]上恒成立,试求k 的范围. 【答案】【解析】(1)由题意得f (-1)=a -b +1=0,a ≠0,且-b2a =-1,∴a =1,b =2.∴f (x )=x 2+2x +1,单调减区间为(-∞,-1],单调增区间为[-1,+∞).(2)解法一:f (x )>x +k 在区间[-3,-1]上恒成立,转化为x 2+x +1>k 在区间[-3,-1]上恒成立. 设g (x )=x 2+x +1,x ∈[-3,-1],则g (x )在[-3,-1]上递减.∴g (x )min =g (-1)=1. ∴k <1,即k 的取值范围为(-∞,1).解法二:f (x )>x +k 在区间[-3,-1]上恒成立,转化为x 2+x +1-k >0在区间[-3,-1]上恒成立,设g (x )=x 2+x +1-k ,则g (x )在[-3,-1]上单调递减,∴g (-1)>0,得k <1.2.设函数f (x )=ax 2-2x +2,对于满足1<x <4的一切x 值都有f (x )>0,则实数a 的取值范围为________.【答案】 ⎝ ⎛⎭⎪⎫12,+∞【解析】由题意得a >2x -2x 2对1<x <4恒成立,又2x -2x 2=-2⎝ ⎛⎭⎪⎫1x -122+12,14<1x <1,∴⎝ ⎛⎭⎪⎫2x -2x 2max =12,∴a >12.3.已知函数f (x )=x 2+mx -1,若对于任意x ∈[m ,m +1],都有f (x )<0成立,则实数m 的取值范围是____________. 【答案】 ⎝ ⎛⎭⎪⎫-22,0 【解析】 因为函数图象开口向上,所以根据题意只需满足⎩⎪⎨⎪⎧f (m )=m 2+m 2-1<0,f (m +1)=(m +1)2+m (m +1)-1<0,解得-22<m <0. 考向七 二次函数根的分布【例7】一元二次方程02)12(2=-+-+a x a x 的一根比1大,另一根比-1小,则实数a 的取值范围是.【答案】203a <<【解析】记2()(21)2f x x a x a =+-+-,由已知得,(1)0,(1)0,f f <⎧⎨-<⎩解得203a <<.【举一反三】1.已知关于x 的方程11()()2042x x a -+=在区间[]1,0-上有实数根,则实数a 的取值范围是. 【答案】[]1,0-【解析】当0a =时,方程为1()202x -+=,解得1x =-,符合;当0a ≠时,记2()2f m am m =-+,其中1()2x m =.当[1,0]x ∈-时,1()[1,2]2x m =∈,所以题目条件等价于函数2()2f m am m =-+在区间[1,2]内有零点. 当0a >时有函数对称轴102x a =>,若180a ∆=-=,即18a =,此时21()28f m m m =-+的零点为4m =,不符合.因为(2)40f a =>,180a ∆=->,即18a <,所以可知对称轴142x a=>,画图可知此时()f m 在区间[1,2]内无零点. 当0a <时有函数对称轴102x a=<,此时180a ∆=->恒成立.因为(2)40f a =<,所以有(1)10f a =+≥,解得1a ≥-.所以此时10a -≤<.综上可得,10a -≤≤.2.若方程210x mx -+=的两实根分别为,αβ,且012αβ<<<<,则m 的取值范围是. 【答案】5(2,)2【解析】因为关于x 的方程012=+-mx x 的两个根为,αβ,且012αβ<<<<则满足(1)020(2)0520<-<⎧⎧∴⎨⎨>->⎩⎩f m f m ,这样可以解得m 的范围5(2,)2. 3.已知二次函数()2f x x bx c =++的两个零点分别在区间()2,1--和()1,0-内,则()3f 的取值范围是 ( )A .()12,20B .()12,18C .()18,20D .()8,18 【答案】A【解析】由题意得()()()20420{10{1000f b c f b c f c ->-+>-<⇒-+<>>,可行域如图三角形内部(不包括三角形边界,其中三角形三顶点为()()()2,0,1,0,3,2A B C ):,而()393f b c =++,所以直线()393f b c =++过C 取最大值20,过B 点取最小值12,()3f 的取值范围是()12,20,选A .4.已知函数()42f x xx x =-+,存在3210x x x >>≥,使得()()()123f x f x f x ==,则()123x x f x ⋅⋅的取值范围是__________. 【答案】()64,81【解析】根据题意,()222,442{ 6,4x x x f x x x x x x x -≥=-+=-+<,由图象可知,126,x x +=()()()1231116x x f x x x f x ∴⋅⋅=⋅-⋅()()2111166x x x x =⋅-⋅-+=()22116x x -+=()22139x ⎡⎤--+⎣⎦,()()21123,398,9x x <<∴--+∈,()()12364,81x x f x ∴⋅⋅∈,故答案为()64,81.1.已知函数f(f)=(f−1)2f f2−4f+2是在(0,+∞)上单调递增的幂函数,则f=( ) A.0或4 B.0或2 C.0 D.2【答案】C【解析】∵f(x)是幂函数,∴(m﹣1)2=1,得m=0,或m=2,∵f(x)在(0,+∞)上单调递增,∴m2﹣4m+2>0,则当m=0时,2>0成立,当m=2时,4﹣8+2=﹣2,不成立,故选C.2.已知幂函数f(x)=x a(a是常数),则()A.f(x)的定义域为R B.f(x)在(0,+∞)上单调递增C.f(x)的图象一定经过点(1,1)D.f(x)的图象有可能经过点(1,−1)【答案】C【解析】(1)对于A,幂函数f(x)=x a的定义域与a有关,不一定为R,A错误;(2)对于B,a>0时,幂函数f(x)=x a在(0,+∞)上单调递增,a<0时,幂函数f(x)=x a在(0,+∞)上单调递减,B错误;(3)对于C,幂函数f(x)=x a的图象过定点(1,1),C正确;(4)对于D,幂函数f(x)=x a的图象一定不过第四象限,D错误.故选:C.3.如图所示的曲线是幂函数f=f f在第一象限的图象,已知f∈{−4,−14,14,4},相应曲线f1,f2,f3,f4对应的f值依次为()A.−4,−14,14,4 B.4,14,−14,−4 C.−14,−4,4,14D.4,14,−4,−14【答案】B【解析】结合幂函数的单调性及图象,易知曲线f1,f2,f3,f4对应的f值依次为4,14,−14,−4.故选B.4.函数f=2|f|−f2(f∈f)的图象为( )A .B .C .D .【答案】A【解析】由于函数y=2|x|﹣x 2(x ∈R )是偶函数,图象关于y 轴对称,故排除B 、D . 再由x=0时,函数值y=1,可得图象过点(0,1),故排除C ,从而得到应选A ,故选:A .5.已知函数g (x )=log a (x ﹣3)+2(a >0,a ≠1)的图象经过定点M ,若幂函数f (x )=x α的图象过点M ,则α的值等于( )A .﹣1B .12 C .2 D .3 【答案】B【解析】∵y=log a (x ﹣3)+2(a >0,a ≠1)的图象过定点M ,∴M (4,2),∵点M (4,2)也在幂函数f (x )=x α的图象上,∴f (4)=4α=2,解得α=12,故选:B . 6.已知幂函数y =x n 在第一象限内的图象如图所示,则曲线C 1、C 2、C 3、C 4的n 值可能依次为A .–2,–12,12,2B .2,12,–12,–2C .–12,–2,2,12D .2,12,–2,–12 【答案】B【解析】由图象可知:C 1的指数n>1,C 2的指数0<n<1,C 3,C 4的指数小于0,且C 3的指数大于C 4的指数.据此可得,只有B 选项符合题意.故选B .7.幂函数y =x n是奇函数,但图象不与坐标轴相交,则n 的值可以是 A .3 B .1 C .0 D .–1 【答案】D【解析】根据幂函数的性质判断出幂函数f =f f 是奇函数时,指数f 为奇数;幂函数f =f f 的图象与两坐标轴不相交时,幂函数的指数f 小于0,对照选项,只有D 正确.故选D . 8.在函数f =1f 2,f =2f 2,f =f 2+f ,f =3f 中,幂函数的个数为A .0B .1C .2D .3 【答案】B【解析】显然,根据幂函数定义可知,只有f =1f 2=f −2是幂函数,故选B .9.已知函数f =f f ,f =f f ,f =f f 的图象如图所示,则f ,f ,f 的大小关系为( )A .f <f <fB .f <f <fC .f <f <fD .f <f <f 【答案】A【解析】由图像可知,f >1,f =12,0<f <12,得f >f >f ,故答案为:A. 10.当f ∈{−1,12,3}时,幂函数f =f f 的图象不可能经过的象限是 A .第二象限 B .第三象限C .第四象限 D .第二、四象限 【答案】D【解析】f =f −1的图象经过第一、三象限,f =f 12的图象经过第一象限,f =f 的图象经过第一、三象限,f =f 3的图象经过第一、三象限.故选D .11.已知正实数f ,f ,f 满足log f 2=2,log 3f =13,f 6=172,则f ,f ,f 的大小关系是( ) A .f <f <f B .f <f <f C .f <f <f D .f <f <f【答案】B【解析】由题得f 2=2,∴f 6=8,f =313,∴f 6=32=9, 因为8<172<9,a,b,c 都是正数,所以f <f <f .故选:B12.已知幂函数f (x )=x a的图象经过点(2,√2),则函数f (x )为( ) A .奇函数且在(0,+∞)上单调递增 B .偶函数且在(0,+∞)上单调递减 C .非奇非偶函数且在(0,+∞)上单调递增D .非奇非偶函数且在(0,+∞)上单调递减【答案】C,【解析】∵幂函数f(x)=x a的图象经过点(2,√2),∴2a=√2,解得a=12∴函数f(x)=f12,∴函数f(x)是非奇非偶函数且在(0,+∞)上单调递增.故选:C.13.已知函数f=f f2−5f+4(m∈Z)为偶函数且在区间(0,+∞)上单调递减,则m=()A.2或3 B.3 C.2 D.1【答案】A【解析】幂函数f=f f2−5f+4为偶函数,且在(0,+∞)递减,∴f2−5f+4<0,且f2−5f+4是偶数,由f2−5f+4<0得1<f<4,又由题设f是整数,故f的值可能为2或3,验证知f=2或者3时,都能保证f2−5f+4是偶数,故f=2或者3即所求.故选:A14.已知函数f(f)为偶函数,当f>0时,f(f)=f2−3f,则()A.f(tan70∘)>f(1.4)>f(−1.5)B.f(tan70∘)>f(−1.5)>f(1.4)C.f(1.4)>f(tan70∘)>f(−1.5)D.f(−1.5)>f(1.4)>f(tan70∘)【答案】A【解析】当f>0时,f(f)=(f−1.5)2−1.52,tan70∘−1.5>tan60∘−1.5≈0.232,又函数f(f)为偶函数,所以f(−1.5)=f(1.5),1.5−1.4=0.1,根据二次函数的对称性以及单调性,所以f(tan70∘)>f(1.4)>f(−1.5).故选A15.已知函数f(f)=f2+ff+1在区间(−∞,−1]上是减函数,在区间[1,+∞)上是增函数,则实数f的取值范围是( )A.[−2,2]B.(−∞,−2]C.[2,+∞)D.R【答案】A【解析】由题意,函数f(f)=f2+ff+1表示开口向上,且对称轴的方程为f=−f2,要使得函数f(f)在区间(−∞,−1]上是减函数,在区间[1,+∞)上是增函数,≤1,解得−2≤f≤2,故选A.则−1≤−f216.幂函数f(f)=(f2−2f+1)f2f−1在(0,+∞)上为增函数,则实数f的值为____________.【答案】2【解析】由函数f(f)=(f2−2f+1)f2f−1是幂函数,则f2−2f+1=1,解得f=0或f=2;当f=0时,f(f)=f−1,在(0,+∞)上为减函数,不合题意;当f=2时,f(f)=f3,在(0,+∞)上为增函数,满足题意.故答案为:2.17. 已知函数f (f )=(f 2−f −1)f f 是幂函数,且f (f )在(0,+∞)上单调递增,则实数f =________. 【答案】2【解析】∵幂函数f (x )=(m 2﹣m ﹣1)x m在区间(0,+∞)上单调递增,∴{f 2−f −1=1f>0,解得m =2或-1(舍).故答案为:2.18.已知幂函数f (f )=(f 2−2f −7)f f −1在(0,+∞)上是减函数,则实数f 的值为__________. 【答案】-2【解析】因为函数f (f )=(f 2−2f −7)f f −1是幂函数,所以f 2−2f −7=1,即(f +2)(f −4)=0, 解得f =−2或f =4,当f =−2时,f (f )=f −3,满足在(0,+∞)上是减函数,当f =4时,f (f )=f 3,在(0,+∞)上是增函数,所以f =−2,故答案是:−2. 19.若f (f )=(f −1)2f f 是幂函数且在(0,+∞)单调递增,则实数f =_______. 【答案】2【解析】f (f )=(f −1)2f f 为幂函数,所以(f −1)2=1,解得f =0或2. 当f =0时,f (f )=f 0=1,在(0,+∞)不单调递增,舍去; 当f =2时,f (f )=f 2,在(0,+∞)单调递增成立.故答案为:f =2. 20.已知幂函数f (x )=(m 3–m +1)x12(1−8f −f 2)的图象与x 轴和y 轴都无交点.(1)求f (x )的解析式;(2)解不等式f (x +1)>f (x –2). 【答案】(1)f (x )=x –4;(2){x |x <12,x ≠0}.【解析】(1)因为f (x )是幂函数,所以m 3–m+1=1,解得m ∈{0,±1},又f (x )的图象与x 轴和y 轴都无交点,经检验,只有当m=1时符合题意,所以m=1,此时f (x )=x –4; (2)f (x )=x –4是偶函数且在(0,+∞)递减,所以要使f (x+1)>f (x –2)成立,只需|x+1|<|x –2|,解得x<12, 又f (x )的定义域为{x|x ≠0},所以不等式的解集为{x|x<12,x ≠0}. 21.已知幂函数y =f (x )=f −2f2−f +3,其中m ∈[–2,2],m ∈Z ,①定区间(0,+∞)的增函数;②对任意的x ∈R ,都有f (–x )+f (x )=0;求同时满足①、②两个条件的幂函数f (x )的解析式,并求x ∈[0,3]时,f (x )的值域.【答案】f (f )=f 3;[0,27]. 【解析】∵幂函数y =f (x )=f −2f2−f +3在区间(0,+∞)为增函数,∴–2m 2–m +3>0,即2m 2+m –3<0,解得m ∈(−32,1), 又∵m ∈Z ,∴m =–1或m =0,当m =–1时,y =f (x )=x 2为偶函数,不满足f (–x )+f (x )=0; 当m =0时,y =f (x )=x 3为奇函数,满足f (–x )+f (x )=0. ∴同时满足①、②两个条件的幂函数f (x )=x 3,当x ∈[0,3]时,f (x )∈[0,27],即函数f (x )的值域为[0,27]. 22.已知函数f (f )=(f 2−2f −2)log f f 是对数函数.(1)若函数f (f )=log f (f +1)+log f (3−f ),讨论函数f (f )的单调性;(2)在(1)的条件下,若f ∈[13,2],不等式f (f )−f +3≤0的解集非空,求实数f 的取值范围. 【答案】(1)见解析;(2)[4,+∞).【解析】(1)由题意可知{f 2−2f −2=1f >0且f ≠1,解得f =3(负值舍去),所以f (f )=log 3f .因为f (f )=log f (f +1)+log f (3−f ),所以{f +1>03−f >0 ,即{f >−1f <3,即−1<f <3,故f (f )的定义域为{f |−1<f <3}.由于f (f )=log 3(f +1)+log 3(3−f )=log 3(−f 2+2f +3), 令f (f )=−f 2+2f +3(−1<f <3),则由对称轴f =1可知,f (f )在(−1,1)上单调递增,在(1,3)上单调递减; 因为f =log 3f 在(0,+∞)上单调递增,所以函数f (f )的单调递增区间为(−1,1),单调递减区间为(1,3).(2)因为不等式f (f )−f +3≤0的解集非空,所以f −3≥f (f )min ,f ∈[13,2], 由(1)知,当f ∈[13,2]时,函数f (f )的单调递增区间为[13,1],单调递减区间为(1,2], 因为f (13)=log 3329,f (2)=1,所以f (f )min =1,所以f −3≥1,即f ≥4,故实数f 的取值范围为[4,+∞). 23.设二次函数f (f )=f 2+ff +f ,f ,f ∈f .(1)若f (f )满足:对任意的f ∈f ,均有f (−f )≠−f (f ),求f 的取值范围; (2)若f (f )在(0,1)上与f 轴有两个不同的交点,求f 2+(1+f )f 的取值范围.【答案】(1) (0,+∞) (2) (0,116)【解析】(1)∵f (−f )+f (f )=(−f )2+f (−f )+f +f 2+ff +f =2(f 2+f )≠0恒成立, 所以,方程f 2+f =0无实数解所以,f 取值范围为(0,+∞)(2)设f (f )=0的两根为f 1,f 2,且0<f 1<f 2<1,则f (f )=(f −f 1)(f −f 2), 所以f 2+(1+f )f =f (1+f +f )=f (0)f (1)=(0−f 1)(0−f 2)(1−f 1)(1−f 2)=f 1f 2(1−f 1)(1−f 2)=(−f 12+f 1)(−f 22+f 2)=[−(f 1−12)2+14][−(f 2−12)2+14]≤116.又因为f 1,f 2不能同时取到12,所以f 2+(1+f )f 取值范围为(0,116). 24. 已知函数f (f )=f 2−2(f −1)f +4. (Ⅰ)若f (f )为偶函数,求f (f )在[−1,2]上的值域;(Ⅱ)若f (f )在区间(−∞,2]上是减函数,求f (f )在[1,f ]上的最大值. 【答案】(Ⅰ)[4,8];(Ⅱ)7-2f【解析】(Ⅰ)因为函数f (f )为偶函数,故f (−f )=f (f ),得f =1.f (f )=f 2+4,因为−1≤f ≤2,所以4≤f (f )≤8,故值域为:[4,8].(Ⅱ)若f (f )在区间(−∞,2]上是减函数,则函数对称轴f =f −1≥2,f ≥3因为1<f −1<f ,所以f ∈[1,f −1]时,函数f (f )递减,[f −1,f ]时,函数f (f )递增,故当f ∈[1,f ]时,f (f )max {f (1),f (f )} ,∴f (1)=7−2f ,f (f )=−f 2+2f +4,f (1)−f (f )=(7−2f )−(−f 2+2f +4)=f 2−4f +3=(f −2)2−1由于f ≥3∴f (1)≥f (f ) ,故f (f )在[1,f ]上的最大值为7-2f .25.已知函数f (x )=x 2+(2a -1)x -3.(1)当a =2,x ∈[-2,3]时,求函数f (x )的值域; (2)若函数f (x )在[-1,3]上的最大值为1,求实数a 的值. 【答案】(1)⎣⎢⎡⎦⎥⎤-214,15. (2)a =-13或-1【解析】(1)当a =2时,f (x )=x 2+3x -3,x ∈[-2,3],函数图象的对称轴为x =-32∈[-2,3],∴f (x )min =f ⎝ ⎛⎭⎪⎫-32=94-92-3=-214,f (x )max =f (3)=15,∴f (x )的值域为⎣⎢⎡⎦⎥⎤-214,15. (2)函数图象的对称轴为直线x =-2a -12.①当-2a -12≤1,即a ≥-12时,f (x )max =f (3)=6a +3,∴6a +3=1,即a =-13,满足题意; ②当-2a -12>1,即a <-12时,f (x )max =f (-1)=-2a -1,∴-2a -1=1,即a =-1,满足题意. 综上可知,a =-13或-1. 26.设函数f (x )=x 2-2x +2,x ∈[t ,t +1],t ∈R ,求函数f (x )的最小值.【答案】见解析【解析】 f (x )=x 2-2x +2=(x -1)2+1,x ∈[t ,t +1],t ∈R ,函数图象的对称轴为x =1. 当t +1≤1,即t ≤0时,函数图象如图(1)所示,函数f (x )在区间[t ,t +1]上为减函数,所以最小值为f (t +1)=t 2+1;当t <1<t +1,即0<t <1时,函数图象如图(2)所示,在对称轴x =1处取得最小值,最小值为f (1)=1;当t ≥1时,函数图象如图(3)所示,函数f (x )在区间[t ,t +1]上为增函数,所以最小值为f (t )=t 2-2t +2. 综上可知,f (x )min =⎩⎪⎨⎪⎧ t 2+1,t ≤0,1,0<t <1,t 2-2t +2,t ≥1.。
专题07 二次函数与幂函数 高考复习资料(解析版)

a x= .
2
a ①当 ≥1,即 a≥2 时,f(x)在[0,1]上单调递增,
2
∴f(x)max=f(1)=-4-a2. 令-4-a2=-5,得 a=±1(舍去).
a a ②当 0< <1,即 0<a<2 时,f(x)max=f 2 =-4a. 2
5 令-4a=-5,得 a= .
4
a ③当 ≤0,即 a≤0 时,f(x)在[0,1]上单调递减,
【答案】(1)-1 或 2 (2)[0,2] 【解析】 (1)函数 f(x)=-x2+2ax+1-a=-(x-a)2+a2-a+1,对称轴方程为 x=a.
当 a<0 时,f(x)max=f(0)=1-a, 所以 1-a=2,所以 a=-1. 当 0≤a≤1 时,f(x)max=a2-a+1, 所以 a2-a+1=2,所以 a2-a-1=0,
B.幂函数的图象都经过点(0,0),(1,1) C.若幂函数 y=xα是奇函数,则 y=xα是增函数
D.幂函数的图象不可能出现在第四象限
【答案】D 【解析】 A 中,点(0,1)不在直线上,A 错;B 中,y=xα,当α<0 时,图象不过原点,B 错;C 中,当 α<0 时,y=xα在(-∞,0),(0,+∞)上为减函数,C 错.幂函数图象一定过第一象限,一定不过第四象
2021 高考领跑一轮复习资料·数学篇
专题 07 二次函数与幂函数
一、【知识精讲】 1.幂函数 (1)幂函数的定义 一般地,形如 y=xα的函数称为幂函数,其中 x 是自变量,α为常数. (2)常见的 5 种幂函数的图象
(3)幂函数的性质
①幂函数在(0,+∞)上都有定义;
②当α>0 时,幂函数的图象都过点(1,1)和(0,0),且在(0,+∞)上单调递增;
2019年高考数学理课时作业7二次函数与幂函数 含解析

课时作业(七)第7讲二次函数与幂函数基础热身1.[2018·运城夏县中学月考]已知幂函数f(x)=k·xα的图像过点,,则k+α=()A. B.1C. D.22.函数y=x2+bx+c(x∈[0,+∞))是单调函数的充要条件是()A.b≥0B.b≤0C.b>0D.b<03.[2018·南阳一中月考]若函数f(x)=ax2+bx+c对于一切实数x都有f(2+x)=f(2-x),则下列关系可能成立的为()A.f(2)<f(1)<f(4)B.f(1)<f(2)<f(4)C.f(2)<f(4)<f(1)D.f(4)<f(2)<f(1)4.函数y=|x(n∈N,n>2)的图像只可能是()图K7-15.函数f(x)=ln(x2-3x-4)的单调递增区间是.能力提升6.已知函数f(x)=的定义域是R,则实数a的取值范围是()A.(0,2)B.(0,2]C.[-2,2]D.(-2,2]7.已知二次函数f(x)的图像与x轴交于(-2,0),(4,0)两点,且过点1,-,则函数的解析式为()A.f(x)=x2-x-4B.f(x)=x2-x-2C.f(x)=x2-x-4D.f(x)=x2-x-28.[2017·日照二模]函数f(x)=(x-2)(ax+b)为偶函数,且在(0,+∞)上单调递增,则f(2-x)>0的解集为()A.{x|-2<x<2}B.{x|x>2或x<-2}C.{x|0<x<4}D.{x|x>4或x<0}9.已知函数f(x)=-x2+2ax+1-a,x∈[0,1]有最大值2,则a=()A.2B.0C.0或-1D.2或-110.[2017·岳阳一中月考]若对任意x∈R,函数f(x)=2mx2-2(4-m)x+1与g(x)=mx的值至少有一个为正数,则实数m的取值范围为()A.(0,4]B.(0,8)C.(2,5)D.(-∞,0)11.[2018·岳阳质检]已知幂函数y=f(x)的图像过点,,则log2f(2)的值为.12.[2018·南阳一中月考]已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是.13.(15分)已知函数f(x)=x2+(2a-1)x-3.(1)当a=2,x∈[-2,3]时,求函数f(x)的值域;(2)若函数f(x)在[-1,3]上的最大值为1,求实数a的值.14.(15分)若二次函数f(x)=ax2+bx+c(a≠0)满足f(x+1)-f(x)=2x,且f(0)=1.(1)求f(x)的解析式;(2)若在区间[-1,1]上,不等式f(x)>2x+m恒成立,求实数m的取值范围.难点突破15.(5分)[2017·温州二模]已知函数f(x)=a-x2(1≤x≤2)与g(x)=x+2的图像上存在关于x 轴对称的点,则实数a的取值范围是()A.[-2,0]B.-C.[2,4]D.-16.(5分)[2017·吉林实验中学二模]若f(x)=2x2+(x-2a)|x-a|在[-2,1]上不是单调函数,则实数a的取值范围是.课时作业(七)1.C[解析]∵函数f(x)=k·xα是幂函数,∴k=1.∵幂函数f(x)=xα的图像过点,,∴=,得α=,则k+α=1+=.故选C.2.A[解析]∵函数y=x2+bx+c(x∈[0,+∞))是单调函数,∴图像的对称轴x=-在区间[0,+∞)的左边,即-≤0,得b≥0.3.A[解析]因为函数f(x)=ax2+bx+c对任意实数x都有f(2+x)=f(2-x)成立,所以该函数图像关于直线x=2对称,当a<0时f(2)最大,四个选项均不满足,当a>0时f(2)最小,由2-1<4-2,得f(1)<f(4),故选A.4.C[解析]显然y=|x(n∈N,n>2)是偶函数,故可排除A和B,又n∈N,n>2,所以应选择C.5.(4,+∞)[解析]由题意可知x2-3x-4>0,得x<-1或x>4,结合图像易知该函数的单调递增区间为(4,+∞).6.C[解析]由题知,对于任意实数x,x2+ax+1≥0恒成立,故只要Δ=a2-4≤0,即-2≤a≤2即可,故实数a的取值范围是[-2,2].7.A[解析]设函数的解析式为f(x)=a(x+2)(x-4),又其图像过点1,-,所以-=a(1+2)×(1-4),得a=,所以所求函数解析式为f(x)=(x+2)(x-4),即f(x)=x2-x-4.8.D[解析]函数f(x)=ax2+(b-2a)x-2b为偶函数,则b-2a=0,故f(x)=ax2-4a=a(x-2)(x+2),因为函数f(x)在(0,+∞)上单调递增,所以a>0.根据二次函数的性质可知,不等式f(2-x)>0的解集为{x|2-x>2或2-x<-2}={x|x<0或x>4},故选D.9.D[解析]函数f(x)=-x2+2ax+1-a=-(x-a)2+a2-a+1,其图像的对称轴方程为x=a.当a<0时,f(x)max=f(0)=1-a,所以1-a=2,所以a=-1;当0≤a≤1时,f(x)max=f(a)=a2-a+1,所以a2-a+1=2,所以a2-a-1=0,所以a=(舍去);当a>1时,f(x)max=f(1)=a,所以a=2.综上可知,a=-1或a=2. 10.B[解析]当m=0时,f(x)=-8x+1>0不恒成立,g(x)=0,此时不符合条件;当m<0时,g(x)=mx在x>0时恒为负,而f(x)=2mx2-2 (4-m)x+1的图像开口向下,所以对任意x>0显然不恒为正值;当m>0 时,g(x)=mx在x>0时恒为正,所以只需f(x)=2mx2-2(4-m)x+1在x≤0时恒为正即可,若-=≥0,即0<m≤4,此时结论显然成立,若-=<0,即m>4,此时只要Δ=4(4-m)2-8m<0 即可,得4<m<8.综上可知m的取值范围为0<m<8,选B.11.[解析]设幂函数f(x)=x a,把,代入函数方程f(x)=x a,得=,解得a=,则f(x)=,∴f(2)=,∴log2f(2)=log2=.12.-[解析]因为函数图像开口向上,所以据题意只需满足-解得-<m<0.13.解:(1)当a=2时,f(x)=x2+3x-3,x∈[-2,3],函数图像的对称轴为x=-∈[-2,3],∴f(x)min=f-=--3=-,f(x)max=f(3)=15,∴值域为-,15.(2)函数图像的对称轴为直线x=--.①当--≤1,即a≥-时,f(x)max=f(3)=6a+3,∴6a+3=1,即a=-,满足题意;②当-->1,即a<-时,f(x)max=f(-1)=-2a-1,∴-2a-1=1,即a=-1,满足题意.综上可知a=-或-1.14.解:(1)由f(0)=1,得c=1,所以f(x)=ax2+bx+1.又f(x+1)-f(x)=2x,所以a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,即2ax+a+b=2x,所以所以因此,所求解析式为f(x)=x2-x+1.(2)f(x)>2x+m等价于x2-x+1>2x+m,即x2-3x+1-m>0,要使此不等式在区间[-1,1]上恒成立,只需使函数g(x)=x2-3x+1-m在区间[-1,1]上的最小值大于0即可.因为g(x)=x2-3x+1-m在区间[-1,1]上单调递减,所以g(x)min=g(1)=-m-1,由-m-1>0,得m<-1.因此满足条件的实数m的取值范围是(-∞,-1).15.A[解析]若函数f(x)=a-x2(1≤x≤2)与g(x)=x+2的图像上存在关于x轴对称的点,则方程a-x2=-(x+2),即a=x2-x-2在区间[1,2]上有解.令h(x)=x2-x-2,1≤x≤2,由于h(x)=x2-x-2的图像是开口朝上且以直线x=为对称轴的抛物线,故当x=1时,h(x)取得最小值-2,当x=2时,h(x)取得最大值0,故a∈[-2,0].16.-[解析]f(x)=2x2+(x-2a)|x-a|可化为f(x)=--若a>0,函数y=3x2-3ax+2a2(x≥a)单调递增,此时函数y=x2+3ax-2a2(x<a)的图像的对称轴为直线x=-,结合图像可知要使函数f(x)在[-2,1]上不单调,则-2<-<1,得0<a<;若a=0,函数f(x)=在[-2,1]上不单调,符合题意;若a<0,函数y=x2+3ax-2a2(x<a)单调递减,函数y=3x2-3ax+2a2(x≥a)的图像的对称轴为直线x=,结合图像可知,若函数f(x)在[-2,1]上不单调,则-2<<1,得-4<a<0.综合以上可知-4<a<.。
2019年高考数学(理)一轮复习精品资料专题07二次函数与幂函数(押题专练)含解析

2019年高考数学(理)一轮复习精品资料1.若幂函数的图象过点⎝ ⎛⎭⎪⎫2,14,则它的单调递增区间是( ) A .(0,+∞) B .[0,+∞) C .(-∞,+∞) D .(-∞,0)答案 D解析 设y =x a ,则14=2a ,∴a =-2,∴y =x -2其单调递增区间为(-∞,0).故选D.2.如果函数f (x )=x 2+bx +c 对任意的实数x ,都有f (1+x )=f (-x ),那么( ) A .f (0)<f (2)<f (-2) B .f (0)<f (-2)<f (2) C .f (2)<f (0)<f (-2) D .f (-2)<f (0)<f (2)答案 A3.若不等式(a -2)x 2+2(a -2)x -4<0对一切x ∈R 恒成立,则a 的取值范围是( ) A .(-∞,2] B .[-2,2] C .(-2,2] D .(-∞,-2)答案 C解析 当a -2=0即a =2时,不等式为-4<0,恒成立.当a -2≠0时,⎩⎪⎨⎪⎧a -2<0,Δ<0,解得-2<a <2,所以a的取值范围是-2<a ≤2.故选C.4.已知幂函数f (x )=x α,当x >1时,恒有f (x )<x ,则α的取值范围是( ) A .(0,1) B .(-∞,1) C .(0,+∞) D .(-∞,0)答案 B解析 当x >1时,恒有f (x )<x ,即当x >1时,函数f (x )=x α的图象在y =x 的图象的下方,作出幂函数f (x )=x α在第一象限的图象,由图象可知α<1时满足题意.故选B.5.已知函数f (x )=-x 2+4x ,x ∈[m,5]的值域是[-5,4],则实数m 的取值范围是( ) A .(-∞,-1) B .(-1,2] C .[-1,2] D .[2,5)答案 C解析 二次函数f (x )=-x 2+4x 的图象是开口向下的抛物线,最大值为4,且在x =2时取得,而当x =5或-1时,f (x )=-5,结合图象可知m 的取值范围是[-1,2]. 6.设函数f (x )=x 2+x +a (a >0),已知f (m )<0,则( ) A .f (m +1)≥0 B .f (m +1)≤0 C .f (m +1)>0 D .f (m +1)<0答案 C解析 ∵f (x )的对称轴为x =-12,f (0)=a >0,∴f (x )的大致图象如图所示.由f (m )<0,f (-1)=f (0)=a >0,得-1<m <0,∴m +1>0,又∵x >-12时,f (x )单调递增,∴f (m +1)>f (0)>0.7.已知a ,b ,c ∈R ,函数f (x )=ax 2+bx +c .若f (0)=f (4)>f (1),则( ) A .a >0,4a +b =0 B .a <0,4a +b =0 C .a >0,2a +b =0 D .a <0,2a +b =0答案 A解析 由f (0)=f (4),得f (x )=ax 2+bx +c 的对称轴为x =-b2a=2,所以4a +b =0,又f (0)> f (1),所以f (x )先减后增,所以a >0.选A.8.如图是二次函数y =ax 2+bx +c 图象的一部分,图象过点A (-3,0),对称轴为x =-1.给出下面四个结论:①b 2>4ac ;②2a -b =1;③a -b +c =0;④5a <b .其中正确的是( ) A .②④ B .①④ C .②③ D .①③答案 B9.已知幂函数y =f (x )的图像经过点⎝ ⎛⎭⎪⎫4,12,则f (2)=( ) A.14 B .4 C.22D. 2解析 设f (x )=x α,因为图像过点⎝ ⎛⎭⎪⎫4,12,代入解析式得:α=-12,∴f (2)=2-12=22.答案 C10.若函数f (x )是幂函数,且满足ff =3,则f (12)的值为( )A .-3B .-13C .3D.13解析 设f (x )=x α,则由ff=3,得4α2α=3.∴2α=3,∴f (12)=(12)α=12α=13.答案 D11.已知函数f (x )=e x -1,g (x )=-x 2+4x -3,若有f (a )=g (b ),则b 的取值范围为 ( ). A .[2-2,2+2] B .(2-2,2+2) C .[1,3]D .(1,3)解析 f (a )=g (b )⇔e a-1=-b 2+4b -3⇔e a=-b 2+4b -2成立,故-b 2+4b -2>0,解得2-2<b <2+ 2. 答案 B12.已知函数f (x )=⎩⎪⎨⎪⎧2x ,x >0,x +1,x ≤0,若f (a )+f (1)=0,则实数a 的值等于( ).A .-3B .-1C .1D .3解析 f (a )+f (1)=0⇔f (a )+2=0⇔⎩⎪⎨⎪⎧a >0,2a +2=0或⎩⎪⎨⎪⎧a ≤0,a +1+2=0,解得a =-3. 答案 A13 .函数f (x )=ax 2+bx +c (a ≠0)的图象关于直线x =-b2a对称.据此可推测,对任意的非零实数a ,b ,c ,m ,n ,p ,关于x 的方程m [f (x )]2+nf (x )+p =0的解集都不可能是( ).A .{1,2}B .{1,4}C .{1,2,3,4}D .{1,4,16,64}解析 设关于f (x )的方程m [f (x )]2+nf (x )+p =0有两根,即f (x )=t 1或f (x )=t 2.而f (x )=ax 2+bx +c 的图象关于x =-b 2a 对称,因而f (x )=t 1或f (x )=t 2的两根也关于x =-b2a 对称.而选项D 中4+162≠1+642.答案 D14.二次函数f (x )=ax 2+bx +c ,a 为正整数,c ≥1,a +b +c ≥1,方程ax 2+bx +c =0有两个小于1的不等正根,则a 的最小值是( ).A .3B .4C .5D .615.对于函数y =x 2,y =x 12有下列说法:①两个函数都是幂函数;②两个函数在第一象限内都单调递增;③它们的图像关于直线y =x 对称;④两个函数都是偶函数;⑤两个函数都经过点(0,0)、(1,1);⑥两个函数的图像都是抛物线型. 其中正确的有________.解析 从两个函数的定义域、奇偶性、单调性等性质去进行比较. 答案 ①②⑤⑥16.若二次函数f (x )=ax 2-4x +c 的值域为[0,+∞),则a ,c 满足的条件是________.解析 由已知得⎩⎪⎨⎪⎧a >0,4ac -164a=0⇒⎩⎪⎨⎪⎧a >0,ac -4=0.答案 a >0,ac =417.方程x 2-mx +1=0的两根为α、β,且α>0,1<β<2,则实数m 的取值范围是________.18.已知f (x )=m (x -2m )(x +m +3),g (x )=2x-2.若同时满足条件: ①∀x ∈R ,f (x )<0或g (x )<0; ②∃x ∈(-∞,-4),f (x )g (x )<0, 则m 的取值范围是________.解析 当x <1时,g (x )<0,当x >1时,g (x )>0,当x =1时,g (x )=0, m =0不符合要求;当m >0时,根据函数f (x )和函数g (x )的单调性,一定存在区间[a ,+∞)使f (x )≥0且g (x )≥0,故m >0时不符合第①条的要求;当m <0时,如图所示,如果符合①的要求,则函数f (x )的两个零点都得小于1,如果符合第②条要求,则函数f (x )至少有一个零点小于-4,问题等价于函数f (x )有两个不相等的零点,其中较大的零点小于1,较小的零点小于-4,函数f (x )的两个零点是2m ,-(m +3),故m 满足⎩⎪⎨⎪⎧m <0,2m <-m +,2m <-4,-m +或⎩⎪⎨⎪⎧m <0,-m +m ,2m <1,-m +-4,解第一个不等式组得-4<m <-2,第二个不等式组无解,故所求m 的取值范围是(-4,-2).答案 (-4,-2)19.已知函数f (x )=⎩⎨⎧x 12,0≤x ≤c ,x 2+x ,-2≤x <0,其中c >0.那么f (x )的零点是________;若f (x )的值域是⎣⎢⎡⎦⎥⎤-14,2,则c 的取值范围是________. 答案 -1和0 (0,4]20.已知f (x )=-4x 2+4ax -4a -a 2在[0,1]内的最大值为-5,求a 的值. 解 f (x )=-4⎝ ⎛⎭⎪⎫x -a 22-4a ,对称轴为x =a2,①当a2≥1,即a ≥2时,f (x )在[0,1]上递增,∴f (x )max =f (1)=-4-a 2, 令-4-a 2=-5,得a =±1(舍去).②当0<a2<1,即0<a <2时,f (x )max =f ⎝ ⎛⎭⎪⎫a 2=-4a ,令-4a =-5,得a =54.③当a2≤0,即a ≤0时,f (x )在[0,1]上递减,∴f (x )max =f (0)=-4a -a 2,令-4a -a 2=-5, 得a =-5或a =1(舍去).综上所述,a =54或-5.21.已知函数f (x )是定义在R 上的偶函数,且当x ≤0时,f (x )=x 2+2x .现已画出函数f (x )在y 轴左侧的图象,如图所示,请根据图象:(1)写出函数f (x )(x ∈R )的增区间; (2)写出函数f (x )(x ∈R )的解析式;(3)若函数g (x )=f (x )-2ax +2(x ∈[1,2]),求函数g (x )的最小值. 解 (1)f (x )在区间(-1,0),(1,+∞)上单调递增.(2)设x >0,则-x <0,函数f (x )是定义在R 上的偶函数,且当x ≤0时,f (x )=x 2+2x , 所以f (x )=f (-x )=(-x )2+2×(-x )=x 2-2x (x >0),所以f (x )=⎩⎪⎨⎪⎧x 2-2xx ,x 2+2x x(3)g (x )=x 2-2x -2ax +2,对称轴方程为x =a +1, 当a +1≤1,即a ≤0时,g (1)=1-2a 为最小值;当1<a +1≤2,即0<a ≤1时,g (a +1)=-a 2-2a +1为最小值; 当a +1>2,即a >1时,g (2)=2-4a 为最小值. 综上可得g (x )min =⎩⎪⎨⎪⎧1-2a ,a ≤0,-a 2-2a +1,0<a ≤1,2-4a ,a >1.22.设f (x )是定义在R 上以2为最小正周期的周期函数.当-1≤x <1时,y =f (x )的表达式是幂函数,且经过点⎝ ⎛⎭⎪⎫12,18.求函数在[2k -1,2k +1)(k ∈Z )上的表达式.解 设在[-1,1)上,f (x )=x n,由点⎝ ⎛⎭⎪⎫12,18在函数图象上,求得n =3.令x ∈[2k -1,2k +1),则x -2k ∈[-1,1), ∴f (x -2k )=(x -2k )3.又f (x )周期为2,∴f (x )=f (x -2k )=(x -2k )3.即f (x )=(x -2k )3(k ∈Z ).23.设函数f (x )=ax 2-2x +2,对于满足1<x <4的一切x 值都有f (x )>0,求实数a 的取值范围.。
专题05 二次函数与幂函数-2019年高考数学(理)考点分析与突破性讲练

一、考纲要求:1. (1)了解幂函数的概念;(2)结合函数y =x ,y =x 2,y =x 3,y =,y =1x的图象,了解它们的变化情况.2.理解二次函数的图象和性质,能用二次函数、方程、不等式之间的关系解决简单问题. 二、概念掌握及解题上的注意点:1.幂函数的形式是y =x α(α∈R ),其中只有一个参数α,因此只需一个条件即可确定其解析式. 2.若幂函数y =xαα∈R 是偶函数,则α必为偶数.当α是分数时,一般先将其化为根式,再判断.3.若幂函数y =x α在,+上单调递增,则α>0,若在,+上单调递减,则α<0.4.用待定系数法求二次函数的解析式,关键是灵活选取二次函数解析式的形式,选法如下:5.二次函数的最值问题的类型及求解方法1)类型:①对称轴、区间都是给定的;②对称轴动、区间固定;③对称轴定、区间变动. )求解方法:抓住“三点一轴”进行数形结合,三点是指区间两个端点和中点,一轴指的是对称轴,具体方法是利用配方法、函数的单调性及分类讨论的思想求解. 6.二次函数中恒成立问题的求解思路由不等式恒成立求参数的取值范围,常用分离参数法,转化为求函数最值问题,其依据是a ≥f (x) ⇔a ,a ≤f (x)⇔a二、高考考题题例分析:例1(2016·全国卷Ⅲ)已知a =243,b =323,c =2513,则( ) A .b <a <c B .a <b <c C .b <c <aD .c <a <bA 解析: a =243=423,b =323,c =2513=523.∵y =x 23在第一象限内为增函数,又5>4>3, ∴c >a >b .]例2.【2015高考浙江,理18】已知函数2()(,)f x x ax b a b R =++∈,记(,)M a b 是|()|f x 在区间[1,1]-上的最大值.(1) 证明:当||2a ≥时,(,)2M a b ≥;(2)当a ,b 满足(,)2M a b ≤,求||||a b +的最大值. 【答案】(1)详见解析;(2)3.详细解析:(1)由22()()24a a f x x b =++-,得对称轴为直线2a x =-,由||2a ≥,得||12a-≥,故()f x 在[1,1]-上单调,∴(,)max{|(1)|,|(1)|}M a b f f =-,当2a ≥时,由 (1)(1)24f f a --=≥,得max{(1),(1)}2f f -≥,即(,)2M a b ≥,当2a ≤-时,由 (1)(1)24f f a --=-≥,得max{(1),(1)}2f f --≥,即(,)2M a b ≥,综上,当||2a ≥时, (,)2M a b ≥;(2)由(,)2M a b ≤得|1||(1)|2a b f ++=≤,|1||(1)|2a b f -+=-≤,故||3a b +≤,||3a b -≤,由||,0||||||,0a b ab a b a b ab +≥⎧+=⎨-<⎩,得||||3a b +≤,当2a =,1b =-时,||||3a b +=,且2|21|x x +-在[1,1]-上的最大值为2,即(2,1)2M -=,∴||||a b +的最大值为3..【考点定位】1.二次函数的性质;2.分类讨论的数学思想. 逻辑推理能力与运算求解能力,在复习时应予以关注。
高考数学总复习(基础知识+高频考点+解题训练)二次函数与幂函数
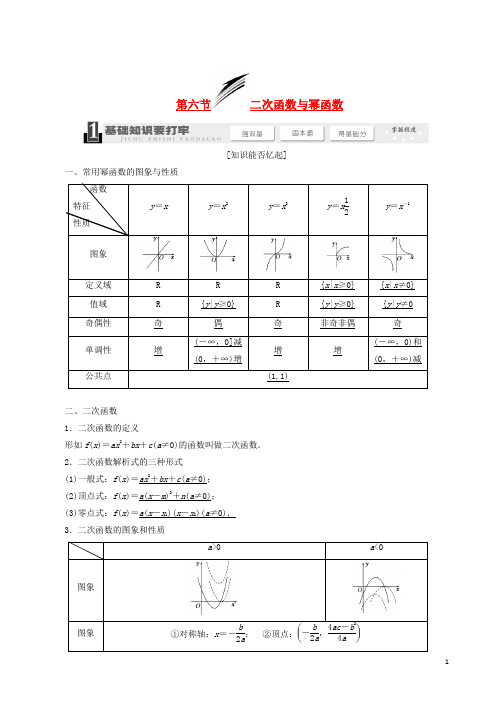
第六节二次函数与幂函数[知识能否忆起]一、常用幂函数的图象与性质函数特征性质y=x y=x2y=x3y=x12y=x-1图象定义域R R R{x|x≥0}{x|x≠0}值域R{y|y≥0}R{y|y≥0}{y|y≠0奇偶性奇偶奇非奇非偶奇单调性增(-∞,0]减(0,+∞)增增增(-∞,0)和(0,+∞)减公共点(1,1)二、二次函数1.二次函数的定义形如f(x)=ax2+bx+c(a≠0)的函数叫做二次函数.2.二次函数解析式的三种形式(1)一般式:f(x)=ax2+bx+c(a≠0);(2)顶点式:f(x)=a(x-m)2+n(a≠0);(3)零点式:f(x)=a(x-x1)(x-x2)(a≠0).3.二次函数的图象和性质a>0a<0图象图象①对称轴:x=-b2a ;②顶点:⎝⎛⎭⎪⎫-b2a,4ac-b24a[小题能否全取]1.若f (x )既是幂函数又是二次函数,则f (x )可以是( ) A .f (x )=x 2-1 B .f (x )=5x 2C .f (x )=-x 2D .f (x )=x 2解析:选D 形如f (x )=x α的函数是幂函数,其中α是常数.2.(教材习题改编)设α∈⎩⎨⎧⎭⎬⎫-1,1,12,3,则使函数y =x α的定义域为R 且为奇函数的所有α值为( )A .1,3B .-1,1C .-1,3D .-1,1,3解析:选A 在函数y =x -1,y =x ,y =x 12,y =x 3中,只有函数y =x 和y =x 3的定义域是R ,且是奇函数,故α=1,3.3.(教材习题改编)已知函数f (x )=ax 2+x +5的图象在x 轴上方,则a 的取值范围是( ) A.⎝ ⎛⎭⎪⎫0,120B.⎝⎛⎭⎪⎫-∞,-120 C.⎝⎛⎭⎪⎫120,+∞D.⎝ ⎛⎭⎪⎫-120,0解析:选C 由题意知⎩⎪⎨⎪⎧ a >0,Δ<0,即⎩⎪⎨⎪⎧a >0,1-20a <0得a >120.4.(教材习题改编)已知点M ⎝⎛⎭⎪⎫33,3在幂函数f (x )的图象上,则f (x )的表达式为________. 解析:设幂函数的解析式为y =x α,则3=⎝ ⎛⎭⎪⎫33α,得α=-2.故y =x -2. 答案:y =x -25.如果函数f (x )=x 2+(a +2)x +b (x ∈[a ,b ])的图象关于直线x =1对称,则函数f (x )的最小值为________.解析:由题意知⎩⎪⎨⎪⎧-a +22=1,a +b =2,得⎩⎪⎨⎪⎧a =-4,b =6.则f (x )=x 2-2x +6=(x -1)2+5≥5. 答案:51.幂函数图象的特点(1)幂函数的图象一定会经过第一象限,一定不会经过第四象限,是否经过第二、三象限,要看函数的奇偶性;(2)幂函数的图象最多只能经过两个象限内;(3)如果幂函数的图象与坐标轴相交,则交点一定是原点. 2.与二次函数有关的不等式恒成立问题(1)ax 2+bx +c >0,a ≠0恒成立的充要条件是⎩⎪⎨⎪⎧a >0,b 2-4ac <0.(2)ax 2+bx +c <0,a ≠0恒成立的充要条件是⎩⎪⎨⎪⎧a <0,b 2-4ac <0.[注意] 当题目条件中未说明a ≠0时,就要讨论a =0和a ≠0两种情况.幂函数的图象与性质典题导入[例1] 已知幂函数f (x )=(m 2-m -1)x-5m -3在(0,+∞)上是增函数,则m =________. [自主解答] ∵函数f (x )=(m 2-m -1)x -5m -3是幂函数,∴m 2-m -1=1,解得m =2或m =-1. 当m =2时,-5m -3=-13,函数y =x-13在(0,+∞)上是减函数;当m =-1时,-5m -3=2,函数y =x 2在(0,+∞)上是增函数. ∴m =-1. [答案] -1由题悟法1.幂函数y =x α的图象与性质由于α的值不同而比较复杂,一般从两个方面考查:(1)α的正负:α>0时,图象过原点和(1,1),在第一象限的图象上升;α<0时,图象不过原点,在第一象限的图象下降.(2)曲线在第一象限的凹凸性:α>1时,曲线下凸; 0<α<1时,曲线上凸;α<0时,曲线下凸.2.在比较幂值的大小时,必须结合幂值的特点,选择适当的函数.借助其单调性进行比较,准确掌握各个幂函数的图象和性质是解题的关键.以题试法1.(1)如图给出4个幂函数大致的图象,则图象与函数对应正确的是( )A .①y =x 13,②y =x 2,③y =x 12,④y =x -1B .①y =x 3,②y =x 2,③y =x 12,④y =x -1C .①y =x 2,②y =x 3,③y =x 12,④y =x -1D .①y =x 13,②y =x 12,③y =x 2,④y =x -1解析:选B 由图①知,该图象对应的函数为奇函数且定义域为R ,当x >0时,图象是向下凸的,结合选项知选B.(2)(2013·淄博模拟)若a <0,则下列不等式成立的是( )A .2a >⎝ ⎛⎭⎪⎫12a >(0.2)aB .(0.2)a >⎝ ⎛⎭⎪⎫12a>2aC.⎝ ⎛⎭⎪⎫12a >(0.2)a>2aD .2a >(0.2)a>⎝ ⎛⎭⎪⎫12a 解析:选B 若a <0,则幂函数y =x a 在(0,+∞)上是减函数,所以(0.2)a >⎝ ⎛⎭⎪⎫12a >0.所以(0.2)a >⎝ ⎛⎭⎪⎫12a>2a .求二次函数的解析式典题导入[例2] 已知二次函数f (x )有两个零点0和-2,且它有最小值-1. (1)求f (x )解析式;(2)若g (x )与f (x )图象关于原点对称,求g (x )解析式.[自主解答] (1)由于f (x )有两个零点0和-2, 所以可设f (x )=ax (x +2)(a ≠0), 这时f (x )=ax (x +2)=a (x +1)2-a , 由于f (x )有最小值-1,所以必有⎩⎪⎨⎪⎧a >0,-a =-1,解得a =1.因此f (x )的解析式是f (x )=x (x +2)=x 2+2x .(2)设点P (x ,y )是函数g (x )图象上任一点,它关于原点对称的点P ′(-x ,-y )必在f (x )图象上, 所以-y =(-x )2+2(-x ), 即-y =x 2-2x ,y =-x 2+2x ,故g (x )=-x 2+2x .由题悟法求二次函数的解析式常用待定系数法.合理选择解析式的形式,并根据已知条件正确地列出含有待定系数的等式,把问题转化为方程(组)求解是解决此类问题的基本方法.以题试法2.设f (x )是定义在R 上的偶函数,当0≤x ≤2时,y =x ,当x >2时,y =f (x )的图象是顶点为P (3,4),且过点A (2,2)的抛物线的一部分.(1)求函数f (x )在(-∞,-2)上的解析式;(2)在下面的直角坐标系中直接画出函数f (x )的草图; (3)写出函数f (x )的值域.解:(1)设顶点为P (3,4)且过点A (2,2)的抛物线的方程为y =a (x -3)2+4,将(2,2)代入可得a =-2, 则y =-2(x -3)2+4,即x >2时,f (x )=-2x 2+12x -14. 当x <-2时,即-x >2.又f (x )为偶函数,f (x )=f (-x )=-2×(-x )2-12x -14, 即f (x )=-2x 2-12x -14.所以函数f (x )在(-∞,-2)上的解析式为f (x )=-2x 2-12x -14.(2)函数f (x )的图象如图,(3)由图象可知,函数f (x )的值域为(-∞,4].二次函数的图象与性质典题导入[例3] 已知函数f (x )=x 2+2ax +3,x ∈[-4,6]. (1)当a =-2时,求f (x )的最值;(2)求实数a 的取值范围,使y =f (x )在区间[-4,6]上是单调函数.[自主解答] (1)当a =-2时,f (x )=x 2-4x +3=(x -2)2-1,由于x ∈[-4,6]. 所以f (x )在[-4,2]上单调递减,在[2,6]上单调递增,故f (x )的最小值是f (2)=-1,又f (-4)=35,f (6)=15,故f (x )的最大值是35.(2)由于函数f (x )的图象开口向上,对称轴是x =-a ,所以要使f (x )在[-4,6]上是单调函数,应有-a ≤-4或-a ≥6,即a ≤-6或a ≥4.故a 的取值范围为(-∞,-6]∪[4,+∞).本例条件不变,求当a =1时,f (|x |)的单调区间. 解:当a =1时,f (x )=x 2+2x +3,则f (|x |)=x 2+2|x |+3,此时定义域为x ∈[-6,6],且f (x )=⎩⎪⎨⎪⎧x 2+2x +3,x ∈0,6],x 2-2x +3,x ∈[-6,0],故f (|x |)的单调递增区间是(0,6], 单调递减区间是[-6,0].由题悟法解决二次函数图象与性质问题时要注意:(1)抛物线的开口,对称轴位置,定义区间三者相互制约,常见的题型中这三者有两定一不定,要注意分类讨论.(2)要注意数形结合思想的应用,尤其是给定区间上二次函数最值问题的求法.以题试法3.(2012·泰安调研)已知函数f (x )=-x 2+2ax +1-a 在x ∈[0,1]时有最大值2,则a 的值为________.解析:f (x )=-(x -a )2+a 2-a +1, 当a >1时,y max =a ;当0≤a ≤1时,y max =a 2-a +1; 当a <0时,y max =1-a .根据已知条件⎩⎪⎨⎪⎧a >1,a =2或⎩⎪⎨⎪⎧0≤a ≤1,a 2-a +1=2或⎩⎪⎨⎪⎧a <0,1-a =2,解得a =2或a =-1. 答案:2或-1二次函数的综合问题典题导入[例4] (2012·衡水月考)已知函数f (x )=x 2,g (x )=x -1. (1)若存在x ∈R 使f (x )<b ·g (x ),求实数b 的取值范围;(2)设F (x )=f (x )-mg (x )+1-m -m 2,且|F (x )|在[0,1]上单调递增,求实数m 的取值范围. [自主解答] (1)∃x ∈R ,f (x )<bg (x )⇒∃x ∈R ,x 2-bx +b <0⇒(-b )2-4b >0⇒b <0或b >4.故b 的取值范围为(-∞,0)∪(4,+∞). (2)F (x )=x 2-mx +1-m 2,Δ=m 2-4(1-m 2)=5m 2-4.①当Δ≤0,即-255≤m ≤255时,则必需⎩⎪⎨⎪⎧m2≤0,-255≤m ≤255⇒-255≤m ≤0.②当Δ>0,即m <-255或m >255时,设方程F (x )=0的根为x 1,x 2(x 1<x 2).若m2≥1,则x 1≤0,即⎩⎪⎨⎪⎧ m 2≥1,F 0=1-m 2≤0⇒m ≥2;若m2≤0,则x 2≤0, 即⎩⎪⎨⎪⎧m 2≤0,F 0=1-m 2≥0⇒-1≤m ≤-255.综上所述,m 的取值范围为[-1,0]∪[2,+∞).由题悟法二次函数与二次方程、二次不等式统称“三个二次”,它们之间有着密切的联系,而二次函数又是“三个二次”的核心,通过二次函数的图象贯穿为一体.因此,有关“三个二次”的问题,数形结合,密切联系图象是探求解题思路的有效方法.以题试法4.若二次函数f (x )=ax 2+bx +c (a ≠0)满足f (x +1)-f (x )=2x ,且f (0)=1. (1)求f (x )的解析式;(2)若在区间[-1,1]上,不等式f (x )>2x +m 恒成立,求实数m 的取值范围. 解:(1)由f (0)=1,得c =1.即f (x )=ax 2+bx +1. 又f (x +1)-f (x )=2x ,则a (x +1)2+b (x +1)+1-(ax 2+bx +1)=2x , 即2ax +a +b =2x ,所以⎩⎪⎨⎪⎧2a =2,a +b =0,解得⎩⎪⎨⎪⎧a =1,b =-1.因此,f (x )=x 2-x +1.(2)f (x )>2x +m 等价于x 2-x +1>2x +m ,即x 2-3x +1-m >0,要使此不等式在[-1,1]上恒成立,只需使函数g (x )=x 2-3x +1-m 在[-1,1]上的最小值大于0即可.∵g (x )=x 2-3x +1-m 在[-1,1]上单调递减, ∴g (x )min =g (1)=-m -1, 由-m -1>0得,m <-1.因此满足条件的实数m 的取值范围是(-∞,-1).1.已知幂函数f (x )=x α的部分对应值如下表:x 1 12 f (x )122则不等式f (|x |)≤2的解集是( ) A .{x |0<x ≤2} B .{x |0≤x ≤4} C .{x |-2≤x ≤2}D .{x |-4≤x ≤4}解析:选D 由f ⎝ ⎛⎭⎪⎫12=22⇒α=12,即f (x )=x 12,故f (|x |)≤2⇒|x |12≤2⇒|x |≤4,故其解集为{x |-4≤x ≤4}.2.已知函数y =ax 2+bx +c ,如果a >b >c 且a +b +c =0,则它的图象可能是( )解析:选D ∵a >b >c ,且a +b +c =0, ∴a >0,c <0.∴图象开口向上与y 轴交于负半轴.3.已知f (x )=x 12,若0<a <b <1,则下列各式中正确的是( )A .f (a )<f (b )<f ⎝ ⎛⎭⎪⎫1a <f ⎝ ⎛⎭⎪⎫1bB .f ⎝ ⎛⎭⎪⎫1a <f ⎝ ⎛⎭⎪⎫1b<f (b )<f (a )C .f (a )<f (b )<f ⎝ ⎛⎭⎪⎫1b <f ⎝ ⎛⎭⎪⎫1aD .f ⎝ ⎛⎭⎪⎫1a <f (a )<f ⎝ ⎛⎭⎪⎫1b <f (b ) 解析:选C 因为函数f (x )=x 12在(0,+∞)上是增函数,又0<a <b <1b <1a ,故f (a )<f (b )<f ⎝ ⎛⎭⎪⎫1b <f ⎝ ⎛⎭⎪⎫1a .4.已知f (x )=x 2+bx +c 且f (-1)=f (3),则( )A .f (-3)<c <f ⎝ ⎛⎭⎪⎫52B .f ⎝ ⎛⎭⎪⎫52<c <f (-3)C .f ⎝ ⎛⎭⎪⎫52<f (-3)<cD .c <f ⎝ ⎛⎭⎪⎫52<f (-3) 解析:选D 由已知可得二次函数图象关于直线x =1对称,则f (-3)=f (5),c =f (0)=f (2),二次函数在区间(1,+∞)上单调递增,故有f (-3)=f (5)>f ⎝ ⎛⎭⎪⎫52>f (2)=f (0)=c . 5.设二次函数f (x )=ax 2-2ax +c 在区间[0,1]上单调递减,且f (m )≤f (0),则实数m 的取值范围是( )A .(-∞,0]B .[2,+∞)C .(-∞,0]∪[2,+∞)D .[0,2]解析:选D 二次函数f (x )=ax 2-2ax +c 在区间[0,1]上单调递减,则a ≠0,f ′(x )=2a (x -1)≤0,x ∈[0,1],所以a >0,即函数图象的开口向上,对称轴是直线x =1. 所以f (0)=f (2),则当f (m )≤f (0)时,有0≤m ≤2.6.若方程x 2-2mx +4=0的两根满足一根大于1,一根小于1,则m 的取值范围是( ) A.⎝⎛⎭⎪⎫-∞,-52B.⎝ ⎛⎭⎪⎫52,+∞C .(-∞,-2)∪(2,+∞)D.⎝ ⎛⎭⎪⎫-52,+∞ 解析:选B 设f (x )=x 2-2mx +4,则题设条件等价于f (1)<0,即1-2m +4<0,解得m >52.7.对于函数y =x 2,y =x 12有下列说法:①两个函数都是幂函数;②两个函数在第一象限内都单调递增; ③它们的图象关于直线y =x 对称; ④两个函数都是偶函数;⑤两个函数都经过点(0,0)、(1,1); ⑥两个函数的图象都是抛物线型. 其中正确的有________.解析:从两个函数的定义域、奇偶性、单调性等性质去进行比较. 答案:①②⑤⑥8.(2012·北京西城二模)已知函数f (x )=x 2+bx +1是R 上的偶函数,则实数b =________,不等式f (x -1)<x 的解集为________.解析:因为f (x )=x 2+bx +1是R 上的偶函数,所以b =0,则f (x )=x 2+1,解不等式(x -1)2+1<x ,即x 2-3x +2<0得1<x <2.答案:0 {x |1<x <2}9.若x ≥0,y ≥0,且x +2y =1,那么2x +3y 2的最小值为________. 解析:由x ≥0,y ≥0,x =1-2y ≥0知0≤y ≤12,令t =2x +3y 2=3y 2-4y +2,则t =3⎝ ⎛⎭⎪⎫y -232+23.在⎣⎢⎡⎦⎥⎤0,12上递减,当y =12时,t 取到最小值,t min =34. 答案:3410.如果幂函数f (x )=x -12p 2+p +32(p ∈Z)是偶函数,且在(0,+∞)上是增函数.求p 的值,并写出相应的函数f (x )的解析式.解:∵f (x )在(0,+∞)上是增函数, ∴-12p 2+p +32>0,即p 2-2p -3<0.∴-1<p <3.又∵f (x )是偶函数且p ∈Z , ∴p =1,故f (x )=x 2.11.已知二次函数f (x )的图象过点A (-1,0)、B (3,0)、C (1,-8). (1)求f (x )的解析式;(2)求f (x )在x ∈[0,3]上的最值; (3)求不等式f (x )≥0的解集.解:(1)由题意可设f (x )=a (x +1)(x -3), 将C (1,-8)代入得-8=a (1+1)(1-3),得a =2. 即f (x )=2(x +1)(x -3)=2x 2-4x -6. (2)f (x )=2(x -1)2-8,当x ∈[0,3]时,由二次函数图象知,f (x )min =f (1)=-8,f (x )max =f (3)=0.(3)f (x )≥0的解集为{x |x ≤-1,或x ≥3}.12.已知函数f (x )=ax 2-2ax +2+b (a ≠0),若f (x )在区间[2,3]上有最大值5,最小值2. (1)求a ,b 的值;(2)若b <1,g (x )=f (x )-m ·x 在[2,4]上单调,求m 的取值范围. 解:(1)f (x )=a (x -1)2+2+b -a . 当a >0时,f (x )在[2,3]上为增函数, 故⎩⎪⎨⎪⎧f 3=5,f2=2,⇒⎩⎪⎨⎪⎧9a -6a +2+b =5,4a -4a +2+b =2,⇒⎩⎪⎨⎪⎧a =1,b =0.当a <0时,f (x )在[2,3]上为减函数,故⎩⎪⎨⎪⎧f 3=2,f 2=5,⇒⎩⎪⎨⎪⎧9a -6a +2+b =2,4a -4a +2+b =5,⇒⎩⎪⎨⎪⎧a =-1,b =3.(2)∵b <1,∴a =1,b =0,即f (x )=x 2-2x +2.g (x )=x 2-2x +2-mx =x 2-(2+m )x +2,∵g (x )在[2,4]上单调, ∴2+m 2≤2或m +22≥4.∴m ≤2或m ≥6.1.已知y =f (x )是偶函数,当x >0时,f (x )=(x -1)2,若当x ∈⎣⎢⎡⎦⎥⎤-2,-12时,n ≤f (x )≤m 恒成立,则m -n 的最小值为( )A.13 B.12 C.34D .1解析:选D 当x <0时,-x >0,f (x )=f (-x )=(x +1)2, ∵x ∈⎣⎢⎡⎦⎥⎤-2,-12, ∴f (x )min =f (-1)=0,f (x )max =f (-2)=1, ∴m ≥1,n ≤0,m -n ≥1.2.(2012·青岛质检)设f (x )与g (x )是定义在同一区间[a ,b ]上的两个函数,若函数y =f (x )-g (x )在x ∈[a ,b ]上有两个不同的零点,则称f (x )和g (x )在[a ,b ]上是“关联函数”,区间[a ,b ]称为“关联区间”.若f (x )=x 2-3x +4与g (x )=2x +m 在[0,3]上是“关联函数”,则m 的取值范围为________.解析:由题意知,y =f (x )-g (x )=x 2-5x +4-m 在[0,3]上有两个不同的零点.在同一坐标系下作出函数y =m 与y =x 2-5x +4(x ∈[0,3])的图象如图所示,结合图象可知,当x ∈[2,3]时,y =x 2-5x +4∈⎣⎢⎡⎦⎥⎤-94,-2,故当m ∈⎝ ⎛⎦⎥⎤-94,-2时,函数y =m 与y =x 2-5x +4(x ∈[0,3])的图象有两个交点.答案:⎝ ⎛⎦⎥⎤-94,-23.(2013·滨州模拟)已知函数f (x )=ax 2+bx +c (a >0,b ∈R ,c ∈R).(1)若函数f (x )的最小值是f (-1)=0,且c =1,F (x )=⎩⎪⎨⎪⎧f x ,x >0,-f x ,x <0,求F (2)+F (-2)的值;(2)若a =1,c =0,且|f (x )|≤1在区间(0,1]上恒成立,试求b 的取值范围. 解:(1)由已知得c =1,a -b +c =0,-b2a=-1,解得a =1,b =2.则f (x )=(x +1)2.则F (x )=⎩⎪⎨⎪⎧x +12,x >0,-x +12,x <0.故F (2)+F (-2)=(2+1)2+[-(-2+1)2]=8.(2)由题意得f (x )=x 2+bx ,原命题等价于-1≤x 2+bx ≤1在(0,1]上恒成立,即b ≤1x -x 且b ≥-1x-x 在(0,1]上恒成立.又当x ∈(0,1]时,1x -x 的最小值为0,-1x-x 的最大值为-2,故-2≤b ≤0.1.比较下列各组中数值的大小. (1)30.8,30.7;(2)0.213,0.233;(3)4.125,3.8-25,(-1.4)35;(4)0.20.5,0.40.3.解:(1)函数y =3x 是增函数,故30.8>30.7. (2)y =x 3是增函数,故0.213<0.233.(3)4.125>1,0<3.8-25<1,而(-1.4)35<0,故4.125>3.8-25>(-1.4)35.(4)先比较0.20.5与0.20.3,再比较0.20.3与0.40.3,y =0.2x 是减函数,故0.20.5<0.20.3;y =x 0.3在(0,+∞)上是增函数,故0.20.3<0.40.3.则0.20.5<0.40.3.2.设abc >0,二次函数f (x )=ax 2+bx +c 的图象可能是( )解析:选D 当-b2a <0时,ab >0,从而c >0,可排除A ,C ;当-b2a >0时,ab <0,从而c <0,可排除B ,选D.3.已知函数f (x )=ax 2-2x +1. (1)试讨论函数f (x )的单调性;(2)若13≤a ≤1,且f (x )在[1,3]上的最大值为M (a ),最小值为N (a ),令g (a )=M (a )-N (a ),求g (a )的表达式;(3)在(2)的条件下,求证:g (a )≥12.解:(1)当a =0时,函数f (x )=-2x +1在(-∞,+∞)上为减函数; 当a >0时,抛物线f (x )=ax 2-2x +1开口向上,对称轴为x =1a,故函数f (x )在⎝ ⎛⎦⎥⎤-∞,1a 上为减函数,在⎣⎢⎡⎭⎪⎫1a ,+∞上为增函数;当a <0时,抛物线f (x )=ax 2-2x +1开口向下,对称轴为x =1a,故函数f (x )在⎝ ⎛⎦⎥⎤-∞,1a 上为增函数,在⎣⎢⎡⎭⎪⎫1a ,+∞上为减函数.(2)∵f (x )=a ⎝ ⎛⎭⎪⎫x -1a 2+1-1a,由13≤a ≤1得1≤1a ≤3,∴N (a )=f ⎝ ⎛⎭⎪⎫1a =1-1a . 当1≤1a <2,即12<a ≤1时,M (a )=f (3)=9a -5,故g (a )=9a +1a-6;当2≤1a ≤3,即13≤a ≤12时,M (a )=f (1)=a -1,故g (a )=a +1a-2.∴g (a )=⎩⎪⎨⎪⎧a +1a -2,a ∈⎣⎢⎡⎦⎥⎤13,12,9a +1a -6,a ∈⎝ ⎛⎦⎥⎤12,1.(3)证明:当a ∈⎣⎢⎡⎦⎥⎤13,12时,g ′(a )=1-1a 2<0,∴函数g (a )在⎣⎢⎡⎦⎥⎤13,12上为减函数;当a ∈⎝ ⎛⎦⎥⎤12,1时,g ′(a )=9-1a 2>0, ∴函数g (a )在⎝ ⎛⎦⎥⎤12,1上为增函数,∴当a =12时,g (a )取最小值,g (a )min =g ⎝ ⎛⎭⎪⎫12=12.故g (a )≥12.。
高三一轮复习精题组二次函数与幂函数(有详细答案)
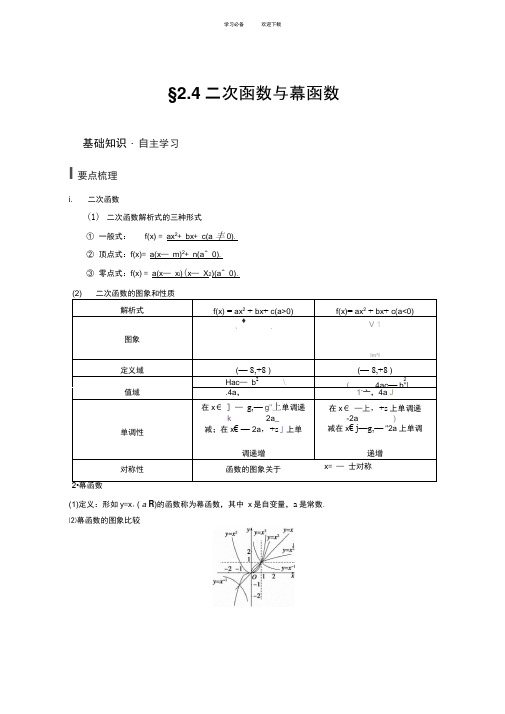
§2.4二次函数与幕函数基础知识・自主学习I要点梳理i. 二次函数(1)二次函数解析式的三种形式①一般式:f(x) = ax2+ bx+ c(a 丰 0).②顶点式:f(x)= a(x—m)2+ n(a^ 0).③零点式:f(x) = a(x—x i)(x—X2)(a^ 0).(2) 二次函数的图象和性质解析式f(x) = ax2+ bx+ c(a>0)f(x)= ax2+ bx+ c(a<0)♦V 1\ ;j图象Im^l定义域(— 8,+8 )(— 8,+8 )Hac—b2\2( 4ac—b"|值域.4a,1-亠,4a J在x€ ] —g,—g"上单调递在x€ —上,+s上单调递k 2a_-2a )单调性减;在x€ —2a,+s」上单减在x€ j—g,—"2a上单调调递增递增对称性函数的图象关于x= —士对称2•幕函数(1)定义:形如y=x:( a R)的函数称为幕函数,其中x是自变量,a是常数.⑵幕函数的图象比较I 夯基释疑1 •判断下面结论是否正确(请在括号中打或“X”2⑴二次函数y = ax + bx + c , x € [a , b]的最值一定是⑵二次函数y = ax 2 + bx + c , x € R ,不可能是偶函数. ⑶幕函数的图象都经过点(1,1)和点(0,0). ⑷当n>0时,幕函数y = x n 是定义域上的增函数.(5) 若函数 f(x)= (k 2— 1)x 2+ 2x — 3 在(一汽 2)上单调递增,则 k = ±22. (6)已知 f(x)= x —4x + 5, x € [0,3),则 f(x)max = f(0) = 5, f (X )min = f (3) = 22. (2013 重庆).3— a a + 6 (— 6< a < 3)的最大值为9 3/2C . 3 D~2答案 B _______________ ____________ 解析 因为' 3 — a a + 6 = 18— 3a — a 2=7-,所以当a = — 2时,打3—a a +6的值最大,最大值为 |3 .函数f(x)= (m — 1)x 2+ 2mx + 3为偶函数,则f(x)在区间(一5,— 3)上C .单调递减D •单调递增答案 D解析 由f(x)为偶函数可得 m = 0, ••• f(x) = — x 2 + 3, ••• f(x)在区间(一5,— 3)上单调递增. 4.已知函数 y = x 2— 2x + 3在闭区间[0, m ]上有最大值 3,最小值2,贝V m 的取值范围为)24ac — b4aA •先减后增B •先增后减答案[1,2]2解析y = x —2x+ 3的对称轴为x= 1.当m<1时,y= f(x)在[0, m]上为减函数.2…y max =f(0) = 3,ymin= f(m)= m—2m+ 3= 2・•m = 1,无解.当 1 w m W 2 时,y min = f(1) = 12—2X 1 + 3 = 2,y max= f(0) = 3.当m>2 时,y max = f(m) = m —2m+ 3= 3,•m = 0 或m= 2,无解.•1 w m w 2.5. 若幕函数y= (m2—3m+ 3)xm2—m —2的图象不经过原点,则实数m的值为__________ .答案1或2厂2m —3m+ 3=1解析由$ ,解得m= 1或2.m2—m—2w 0经检验m= 1或2都适合.题型一二次函数的图象和性质例 1 已知函数f(x) = x2+ 2ax + 3, x€ [—4,6].(1) 当a= —2时,求f(x)的最值;⑵求实数a的取值范围,使y= f(x)在区间[—4,6]上是单调函数;(3)当a= 1时,求f(|x|)的单调区间.思维启迪对于(1)和(2)可根据对称轴与区间的关系直接求解,对于(3),应先将函数化为分段函数,再求单调区间,注意函数定义域的限制作用.解(1)当a=— 2 时,f(x)= x2—4x+ 3= (x—2)2—1,由于x€ [—4,6],•f(x)在[—4,2]上单调递减,在[2,6]上单调递增,•f(x)的最小值是f(2) = —1,又f(—4)= 35, f(6) = 15,故f(x)的最大值是35.(2) 由于函数f(x)的图象开口向上,对称轴是x=—a,所以要使f(x)在[—4,6]上是单调函数, 应有一a w —4 或一a> 6,即a w —6 或a > 4.2(3) 当a= 1 时,f(x)= x + 2x+ 3,•f(|x|)= x2+ 2|x| + 3,此时定义域为x€ [—6,6],f x + 2x+ 3, x€ 0, 6]且f(x) = 2,X2- 2x+ 3, x€ [—6, 0]••• f(|x|)的单调递增区间是(0,6],单调递减区间是[一6,0].思维升华(1)二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动,不论哪种类型,解决的关键是考查对称轴与区间的关系,当含有参数时,要依据对称轴与区间的关系进行分类讨论;(2)二次函数的单调性问题则主要依据二次函数图象的对称轴进行分析讨论求解.跟踪训练1 (1)二次函数的图象过点(0,1),对称轴为x= 2,最小值为一1,则它的解析式是1 2答案y=5(x—2) —1⑵若函数f(x) = 2x2+ mx —1在区间[—1 ,+^ )上递增,则f( —1)的取值范围是_答案(一3—3]解析•••抛物线开口向上,对称轴为x=—m,•- m< —1, m>4.又f(—1) = 1 —m W—3, • f( —1)€ (—3,—3].题型二二次函数的应用例 2 已知函数f(x) = ax2+ bx + 1(a, b € R), x € R.(1) 若函数f(x)的最小值为f(—1) = 0,求f(x)的解析式,并写出单调区间;(2) 在(1)的条件下,f(x)>x+ k在区间[—3,—1]上恒成立,试求k的范围.思维启迪利用f(x)的最小值为f(—1) = 0可列两个方程求出a、b;恒成立问题可以通过求函数最值解决.解(1)由题意有f(—1)= a—b+ 1 = 0,口b且一2a=—1, •a= 1, b= 2.•f(x)= x2+ 2x+ 1,单调减区间为(一a,—1],单调增区间为[—1 ,+ ^).(2)f(x)>x+ k在区间[—3,—1]上恒成立,转化为x2+ x+ 1>k在区间[—3,—1]上恒成立.设g(x) = x2+ x+ 1, x€ [—3,—1],贝U g(x)在[—3,—1]上递减. …g(x)min = g( - 1)=•k<1,即k的取值范围为(一3,1).1解2m +1 > 0,得m》—^;思维升华有关二次函数的问题,数形结合,密切联系图象是探求解题思路的有效方法. 用函数思想研究方程、不等式(尤其是恒成立)问题是高考命题的热点.&【养;丨%:二已知函数f(x)= x1 2+ 2ax+ 2, x€ [ —5,5].(1) 当a=—1时,求函数f(x)的最大值和最小值;⑵求实数a的取值范围,使y= f(x)在区间[—5,5]上是单调函数.解(1)当a=— 1 时,f(x)= x2—2x+ 2= (x—1)2+ 1 , x€ [ —5,5],所以当x= 1时,f(x)取得最小值1;当x=—5时,f(x)取得最大值37.⑵函数f(x)= (x+ a)2+ 2 —a2的图象的对称轴为直线x=—a,因为y= f(x)在区间[—5,5]上是单调函数,所以一a< — 5 或一a> 5,即a< — 5 或 a > 5.故a的取值范围是(一5] U [5 ,+^).题型三幕函数的图象和性质例3 (1)已知幕函数f(x)= (n2+ 2n —2)xn2—3n(n € Z)的图象关于y轴对称,且在(0,+^ )上是减函数,则n的值为()A . —3B . 1C . 2D . 1 或21 1⑵若(2m+ 1)2 >(m2+ m—1) 2,则实数m的取值范围是()-亚-12C. (—1,2)D. ,2思维启迪(1)由幕函数的定义可得n2+ 2n —2= 1,再利用f(x)的单调性、对称性求n;⑵1构造函数y= x2,利用函数单调性求m范围.答案(1)B (2)D解析(1)由于f(x)为幕函数,所以n2+2n— 2 = 1,解得n= 1或n =—3,经检验只有n= 1适合题意,故选 B.1(2) 因为函数y= x2的定义域为[0,+^), 且在定义域内为增函数,2m+ 1 > 0,所以不等式等价于m2+ m —1 > 0,| 22m+ 1>m + m—1.2解m + m—1 > 0, mW —,5 — 12或m》躬—1综上一^< m<2.思维升华⑴幕函数解析式一定要设为y= x a(a为常数的形式);(2)可以借助幕函数的图象理解函数的对称性、单调性.乐金叮%:S 已知幕函数f(x)= x(m2+ m)—1(m€ N*)(1) 试确定该函数的定义域,并指明该函数在其定义域上的单调性;⑵若该函数还经过点(2, .2),试确定m的值,并求满足条件f(2 —a)>f(a—1)的实数a的取值范围.解(1)m2+ m= m(m+ 1), m€ N*,而m与m + 1中必有一个为偶数,••• m(m+ 1)为偶数.•••函数f(x) = x(m2+ m)—1(m€ N*)的定义域为[0,+ ),并且在定义域上为增函数.(2) •/ 函数f(x)经过点(2, ,2),1• 2 = 2(m2+ m)—1,即22= 2(m2+ m)—1.•m2+ m= 2.解得m= 1 或m=— 2.1_ * 石又T m€ N , •m= 1.「. f(x)= x2 .[2— a > 0,由f(2—a)>f(a—1)得| a—1》02—a>a—1.3 3解得1< a<夕•••a的取值范围为[1 ,刁.思想与方法系列2分类讨论思想在函数中的应用典例:(12分)已知函数f(x)= ax2—|x|+ 2a—1(a为实常数).(1)若a= 1,作出函数f(x)的图象;⑵设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式.思维启迪(1)因f(x)的表达式中含|x|,故应分类讨论,将原表达式化为分段函数的形式,然后作图.⑵因a€ R,而a的取值决定f(x)的表现形式,或为直线或为抛物线,若为抛物线又分为开口向上和向下两种情况,故应分类讨论解决.规范解答解(1)当 a = 1 时,2f(x)= x -凶 + 1广2x + x + 1, x<0 i 2.[3 分]x -x +1, x >0作图(如右图所示)[5分]⑵当 x € [1,2]时,f(x)= ax - x + 2a - 1.[6 分] 若a = 0,则f(x) = - x - 1在区间[1,2]上是减函数, g(a) = f(2) = - 3.[7 分] 若a 工0,则 f (x )=a [x -2a ― 4a -1,1f(x)图象的对称轴是直线 x =当a<0时,f(x)在区间[1,2]上是减函数,g(a) = f(2) = 6a - 3.1 1当0< <1,即a>;时,f(x)在区间[1,2]上是增函数,2a 2 g(a) = f(1) = 3a - 2. 1 1 1当 1 < < 2,即;w aw :时,2a 4 2 f 1、 1g (a )=f 旁=2a -扃―j 1 1当2a>2,即0<a<4时,f(x)在区间[1,2]上是减函数, g(a) = f(2) = 6a - 3.[11 分]1 a<43a - 2, a>2温馨提醒本题解法充分体现了分类讨论的数学思想方法,在二次函数最值问题的讨论中,一是要对二次项系数进行讨论, 二是要对对称轴进行讨论. 在分类讨论时要遵循分类 的原则:一是分类的标准要一致, 二是分类时要做到不重不漏, 三是能不分类的要尽量避 免分类,绝不无原则的分类讨论 •思想方法・感悟提高方法与技巧_ 1综上可得,g(a) = 2a -扃―1,1 1 1 w a w[12 分]1. 二次函数、二次方程、二次不等式间相互转化的一般规律:(1) 在研究一元二次方程根的分布问题时,常借助于二次函数的图象数形结合来解,一般 从:①开口方向;②对称轴位置;③判别式;④端点函数值符号四个方面分析.(2) 在研究一元二次不等式的有关问题时,一般需借助于二次函数的图象、性质求解. 2 •幕函数y = x a (a€ R )图象的特征o>0时,图象过原点和(1,1),在第一象限的图象上升; a <0时,图象不过原点,在第一象限的图象下降,反之也成立. 失误与防范1 •对于函数y = ax2 + bx + c ,要认为它是二次函数,就必须满足a 丰0,当题目条件中未说明0时,就要讨论 a = 0和0两种情况.2.幕函数的图象一定会出现在第一象限内, 一定不会出现在第四象限,至于是否出现在第二、三象限内,要看函数的奇偶性; 幕函数的图象最多只能同时出现在两个象限内; 如果幕函 数图象与坐标轴相交,则交点一定是原点练出高分A 组专项基础训练一、选择题 1.若f (x) = x 2— ax + 1有负值,则实数a 的取值范围是 A. a <— 2 C . a>2 或 a<— 2 答案 C解析 ■/ f(x)= x 2— ax + 1有负值, ••• △= a 2 — 4>0,贝U a>2 或 a< — 2.答案 C解析 若a>0,则一次函数y = ax + b 为增函数,二次函数 y = ax 2 + bx + c 的开口向上,故 可排除A ;若a<0,一次函数y = ax + b 为减函数,二次函数 y = ax 2 + bx + c 开口向下,故可排除 D ; 对于—2<a<2 1<a<32 .一次函数y =ax + b 与二次函数y = ax 2 + bx + c 在同一坐标系中的图象大致是()D选项B,看直线可知a>0, b>0,从而—f<0,而二次函数的对称轴在y轴的右侧,2a故应排除B,因此选C.3. 如果函数f(x)= x2+ bx+ c对任意的实数x,都有f(1 + x)= f(—x),那么()A . f(—2)<f(0)<f(2)B. f(0)< f( —2)<f(2)C. f(2)<f(0)<f( —2)D . f(0)<f(2)<f( —2)答案D解析由f(1 + x)= f( —x)知f(x)的图象关于x=舟对称,又抛物线开口向上,结合图象(图略)可知f(0)<f(2)<f( —2).4 .设二次函数f(x)= ax2—2ax+ c在区间[0,1]上单调递减,且f(m) < f(0),则实数m的取值范围是()A .(―汽0]B . [2 ,+^ )C.(―汽0] U [2 ,+ s) D . [0,2]答案 D解析二次函数f(x) = ax2—2ax+ c在区间[0,1]上单调递减,则a^ 0, f' (x) = 2a(x—1)<0, x€ [0,1],所以a>0,即函数图象的开口向上,对称轴是直线x= 1.所以f(0) = f(2),则当f(m)w f(0)时,有0< m W 2.15.已知f(x)= x2,若0<a<b<1,则下列各式中正确的是()1 1A. f(a)<f(b)<f(a)<f(b)B. f(a)<f(b)<f(b)<f(a)1 1C. f(a)<f(b)<f(b)<fq1 1D. f(a)<f(a)<f(b)<f(b)答案C1解析因为函数f(x) = x 2在(0, + s)上是增函数,1 1又0<a<b<;<-,故选 C.b a、填空题6 .若函数y= mx2+ x+ 5在[—2 ,+s )上是增函数,则m的取值范围是 ______________1答案0W m<-4解析m=0时,函数在给定区间上是增函数;1 m z 0时,函数是二次函数,对称轴为x=—2,1 1由题意知 m>0, • 0<mw :综上0w m W ;.4 47 .若方程x 2— 11x + 30 + a = 0的两根均大于5,则实数a 的取值范围是1答案 0<a W 14解析令 f(x)= x — 11x + 30 + a. 01i , • 0<a W 4.f 5 >0 41的图象经过第一、三象限;当a=㊁时,y = 乂“的图象经过第一象限. 三、解答题9 .已知二次函数f(x)的二次项系数为=0有两个相等的根,求 f(x)的单调区间. 解•/ f(x) + 2x>0 的解集为(1,3), 设 f(x) + 2x = a(x — 1)(x — 3),且 a<0,••• f(x)= a(x — 1)(x — 3) — 2x = ax 2 — (2 + 4a)x + 3a.① 由方程 f(x) + 6a = 0 得 ax 2— (2 + 4a)x + 9a = 0•②•••方程②有两个相等的根, •- △=[ — (2 + 4a)]2— 4a 9a = 0,1解得a = 1或a =—匚.由于a<0,舍去a = 1.51将a = — 1代入①式得5 1 26 3 1 2 6f(x)=—5x— 5x— 5=—尹+ 3)+5,•函数f(x)的单调增区间是(—8, — 3],单调减区间是[一 3, + m.10.已知函数f(x) = — x 2 + 2ax +1 — a 在x € [0,1]时有最大值2,求a 的值. 解函数 f(x)=— x 2+ 2ax +1 — a2 2=—(x — a) + a — a + 1, 对称轴方程为x = a.(1)当 a<0 时,f(x) max = f (0) = 1 一a,结合图象有 8 .当a€ 1 1 1匸 1 ? 2? 1 ,幕函数 y = x a 的图象不可能经过第象限.答案 二、四解析当%=— 1、1、3时,y = x a ,且不等式f(x)> — 2x 的解集为(1,3) •若方程f(x) + 6a--1 一a= 2, - - a = —1.2⑵当0W a W 1 时,f(x)max= a — a +1,2 9…a — a + 1 = 2, a — a — 1 = 0, •a=丄±先舍).⑶当 a>1 时,f(x)max = f ⑴=a , a = 2. 综上可知,a =— 1或a = 2.即 2— <2 ,a> — 3,二—3<a<0. 当 a > 0 时,_ a<1 , O w a<1.故—3<a<1. 2.已知函数 f(x)= ax 2 + bx + c ,且 a>b>c , a + b + c = 0,集合 A = {m|f(m)<0},则()A. ? m € A ,都有 f(m + 3)>0B. ? m € A ,都有 f(m + 3)<0C. ? m °€ A ,使得 f(m °+ 3) = 0D. ? m °€ A ,使得 f(m °+ 3)<0 答案 A解析 由 a>b>c , a + b + c = 0 可知 a>0, c<0, 且 f(1) = 0, f(0) = c<0,即1是方程ax 2 + bx + c = 0的一个根, 当 x>1 时,f(x)>0. 由 a>b ,得 1>a设方程ax 2 + bx + c = 0的另一个根为 治,b贝y X 1 + 1 = — b >— 1, 即卩 X 1>— 2,a 由 f(m)<0 可得—2<m<1, 所以 1<m + 3<4,由抛物线的图象可知,f(m + 3)>0,选A. 3.已知函数f(x) = x 2— 2ax + 2a + 4的定义域为 R ,值域为[1 ,),则a 的值域为 _________答案 —1或3解析 由于函数f(x)的值域为[1 , + s ),1 •设函数 f(x)=!(2X—W x , x >0,7, x<0,B 组专项能力提升若f(a)<1,则实数a 的取值范围是A.(―汽一3)C . (— 3,1) 答案 C解析当a<0时, (2)「7<1 ,B . (1 ,+^ )D . (— s,— 3) U (1 ,+^ )所以f(x)min = 1 且A<0. •• —v'5+ 1<a<.;;5+ 1.2 2又f(x) = (x—a) — a + 2a + 4,当x€ R 时,f(x)min = f(a) = —a?+ 2a+4 = 1,即 a —2a—3= 0,解得a= 3或a =— 1.4 .已知函数f(x)= 3ax + 2bx+ c, a + b+ c= 0,且f(0) f(1)>0. b(1)求证:一2<b< —1 ;a⑵若X1、X2是方程f(x) = 0的两个实根,求x1 —X2|的取值范围.(1)证明当a= 0 时,f(0) = c, f(1) = 2b+ c,又b+ c= 0, 则f(0) f(1) = c(2b+ c)=—c2<0 与已知矛盾,因而0,则f(0) f(1) = c(3a+ 2b+ c)=—(a + b)(2a+ b)>0 b b b即(匚 + 1)(匚 + 2)<0,从而-2<;<— 1.a a a(2)解X1、X2是方程f(x) = 0的两个实根,2b a+ b则X1 + X2=—3a, X1X2=—3a ,那么(X1 —X2) = (X1 + X2) —4X1X22b 2 a+ b 4=(—刃 + 4% 右=44, b丄3、2丄1=9(a+ 2)+ 3 二2<a<-1••• 3=(x1—X2)2<9,二jw |x1 —X2|<|,x/3 2(1)若函数f(x)的最小值是f(—1) = 0,且c= 1,F(x) =即|X1 —X2I的取值范围是[g, 3). 55 .已知函数f(x)= ax2+ bx+ c(a>0, b € R, c€ R).f(x , x>0,八‘求F(2) + F(—2)的值;、—f(x), x<0,⑵若a= 1, c= 0,且|f(x)|w 1在区间(0,1]上恒成立,试求b的取值范围.解(1)由已知c= 1, a—b+ c= 0,且一2^ =—1,解得a= 1, b= 2.••• f(x)= (x+ 1)2.1(x+ 1 2, X>0 ,•F(x) = 2I —(x+12, x<0.•F(2)+ F(—2) = (2 + 1)2+ [—(— 2 + 1)2]= 8.(2)f(x) = x2+ bx,原命题等价于—1w x2+ bx w 1在(0,1]上恒成立,1 1即b三-―x且b> —-― x在(0,1]上恒成立.1 1又-一x的最小值为0,—- —x的最大值为一2. x x ••• — 2< bw 0.故b的取值范围是[—2,0].X X。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题07 二次函数与幂函数
1.已知幂函数的图象过点,则()
A.B.3C.D.2
【答案】B
【解析】
由题意令f(x)=,图象过点得,解得a=
∴f(x)=∴f(9)=3.
故选:B.
2.已知幂函数在上单调递增,则实数m的值为()A.B.3C.或3D.1或
【答案】B
3.函数的值域为
A.B.C.D.
【答案】D
【解析】
设μ=﹣x2﹣6x﹣5(μ≥0),
则原函数可化为y=.
又∵μ=﹣x2﹣6x﹣5=﹣(x+3)2+4≤4,
∴0≤μ≤4,故∈[0,2],
∴y=的值域为[0,2].
故选:D.
4.在上随机取一个实数m,能使函数在R上有零点的概率为()
A.B.C.D.
【答案】B
5.已知函数(其中)的图象如图所示,则函数的图象大致是( )
A.B.
C.D.
【答案】B
6.函数的图象大致是()
A.B.
C.D.
【答案】C
【解析】
当时,,所以舍去A,D,
当时,,所以舍去B,
综上选C.
7.已知,则函数f(x)=(a2-2)x+b为增函数的概率是()
A.B.C.D.
【答案】B
从集合{-2,0,1,3,4}中任选一个数有5种选法,使函数f(x)=(a2-2)x+b为增函数的是a2-2>0解
得或者,所以满足此条件的a有-2,3,4共有3个,由古典概型公式得函数f(x)=(a2-2)
x+b为增函数的概率是;
故选:B.
8.函数与,这两个函数在区间上都是减函数,则实数()A.B.C.D.
【答案】D
9.若函数在区间[0,1]上的最大值是M,最小值是m,则的值()
A.与a有关,且与b有关B.与a有关,但与b无关
C.与a无关,且与b无关D.与a无关,但与b有关
【答案】B
【解析】
因为最值在中取,所以最值之差一定与无关,选B.
10.若函数有最小值,则实数的取值范围是( )
A.(0,1) B.C.D.
【答案】C
.当a>1且有最小值时,f(x)才有最小值.∴⇒1<a<.
11.设函数,则“”是“与”都恰有两个零点的().
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】C
12.二次函数,则实数a的取值范是____________.
【答案】[1,+∞)
13.已知函数,则该函数的最小值是________.
【答案】2
【解析】
设,则,此时,
当时,即,函数取得最小值,此时最小值为.
14.若幂函数的图象不过原点,则的值为___.
【答案】或
【解析】
由幂函数定义可得可求出或者,
当时,,
此时幂函数,图象不过原点,满足题意;
当时,,
此时幂函数,图象不过原点,满足题意.
15.若幂函数在上为增函数,则____________ .【答案】
【解析】
在上为增函数,
,解得,
,故答案为4.
16.若幂函数在上为增函数,则____________ .
【答案】。
