2019中考数学压轴题解析
最新2019中考数学压轴题精选资料讲解
2019中考数学压轴题1.(眉山)如图1，在平面直角坐标系中，抛物线y ＝﹣94x 2+bx+c 经过点A （﹣5，0）和点B （1，0）.（1）求抛物线的解析式及顶点D 的坐标；（2）点P 是抛物线上A 、D 之间的一点，过点P 作PE ⊥x 轴于点E ，PG ⊥y 轴，交抛物线于点G.过点G 作GF ⊥x 轴于点F.当矩形PEFG 的周长最大时，求点P 的横坐标；（3）如图2，连接AD 、BD ，点M 在线段AB 上（不与A 、B 重合），作∠DMN ＝∠DBA , MN 交线段AD 于点N ，是否存在这样点M ，使得△DMN 为等腰三角形？若存在，求出AN 的长；若不存在，请说明理由.O2.(甘肃)如图，已知二次函数y＝x2+bx+c的图象与x轴交于点A（1，0）、B（3，0），与y轴交于点C．（1）求二次函数的解析式；（2）若点P为抛物线上的一点，点F为对称轴上的一点，且以点A、B、P、F为顶点的四边形为平行四边形，求点P的坐标；（3）点E是二次函数第四象限图象上一点，过点E作x轴的垂线，交直线BC于点D，求四边形AEBD面积的最大值及此时点E的坐标．3.(广安)如图，抛物线与x轴交于A、B两点在B的左侧，与y轴交于点N，过A点的直线l：与y轴交于点C，与抛物线的另一个交点为D，已知，，P点为抛物线上一动点不与A、D重合．求抛物线和直线l的解析式；当点P在直线l上方的抛物线上时，过P点作轴交直线l于点E，作轴交直线l于点F，求的最大值；设M为直线l上的点，探究是否存在点M，使得以点N、C，M、P为顶点的四边形为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．4.(武威)如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，点P的横坐标为m．（1）求此抛物线的表达式；（2）过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由；（3）过点P作PN⊥BC，垂足为点N．请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？5.(无锡)已知二次函数42-+=bx ax y (a ＞0)的图像与x 轴交于A 、B 两点，（A 在B 左侧，且OA ＜OB ），与y 轴交于点C ．D 为顶点，直线AC 交对称轴于点E ，直线BE 交y 轴于点F ，AC ：CE ＝2：1．（1）求C 点坐标，并判断b 的正负性；（2）设这个二次函数的图像的对称轴与直线AC 交于点D ，已知DC ：CA ＝1：2，直线BD 与y 轴交于点E ，连接BC ．①若△BCE 的面积为8，求二次函数的解析式；②若△BCD 为锐角三角形，请直接写出OA 的取值范围．6.(菏泽)如图，抛物线与x轴交于A，B两点，与y轴交于点C（0，﹣2），点A的坐标是（2，0）P为抛物线上的一个动点，过点P作PD⊥x轴于点D，交直线BC于点E，抛物线的对称轴是直线x＝﹣1．（1）求抛物线的函数表达式；（2）若点P在第二象限内，且PE＝OD，求△PBE的面积．（3）在（2）的条件下，若M为直线BC上一点，在x轴的上方，是否存在点M，使△BDM 是以BD为腰的等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．7.(凉山州)如图，抛物线y＝ax2+bx+c的图象过点A（﹣1，0）、B（3，0）、C（0，3）．（1）求抛物线的解析式；（2）在抛物线的对称轴上是否存在一点P，使得△P AC的周长最小，若存在，请求出点P的坐标及△P AC的周长；若不存在，请说明理由；（3）在（2）的条件下，在x轴上方的抛物线上是否存在点M（不与C点重合），使得S＝S△P AC？若存在，请求出点M的坐标；若不存在，请说明理由．△P AMyA M OB xPCyA OB xC8. (河南)如图，抛物线y =ax2 +12x +c 交x 轴于A，B 两点，交y 轴于点C，直线y =-12x - 2经过点A，C．(1)求抛物线的解析式．(2)点P 是抛物线上一动点，过点P 作x 轴的垂线，交直线AC 于点M，设点P 的横坐标为m．①当△PCM 是直角三角形时，求点P 的坐标；②作点B 关于点C 的对称点B'，则平面内存在直线l，使点M，B，B'到该直线的距离都相等．当点P 在y 轴右侧的抛物线上，且与点B 不重合时，请直接写出直线l：y =kx +b 的解析式．（k，b 可用含m 的式子表示）9.(衡阳)如图，二次函数c bx x y ++=2的图象与x 轴交于点A （-1，0）和点B （3，0），与y 轴交于点N ，以AB 为边在x 轴上方作正方形ABCD ，点P 是x 轴上的一动点，连接CP ，过点P 作CP 的垂线与y 轴交于点E. （1）求该抛物线的函数关系表达式；（2）当P 点在线段OB （点P 不与O 、B 点重合）上运动至何处时，线段OE 的长有最大值？并求出这个最大值.（3）在第四象限的抛物线上任取一点M ，连接MN 、MB.请问：△MNB 的面积是否存在最大值？若存在，求此时点M 的坐标；若不存在，请说明理由.10.(青岛)已知：如图，在四边形ABCD中，AB∥CD，∠ACB＝90°，AB＝10cm，BC＝8cm，OD垂直平分A C．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，点Q 从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动，另一个点也停止运动．过点P作PE⊥AB，交BC于点E，过点Q作QF∥AC，分别交AD，OD于点F，G．连接OP，EG．设运动时间为t（s）（0＜t＜5），解答下列问题：（1）当t为何值时，点E在∠BAC的平分线上？（2）设四边形PEGO的面积为S（cm2），求S与t的函数关系式；（3）在运动过程中，是否存在某一时刻t，使四边形PEGO的面积最大？若存在，求出t的值；若不存在，请说明理由；（4）连接OE，OQ，在运动过程中，是否存在某一时刻t，使OE⊥OQ？若存在，求出t的值；若不存在，请说明理由．11.(怀化)如图，在直角坐标系中有Rt△AOB，O为坐标原点，OB＝1，tan∠ABO＝3，将此三角形绕原点O顺时针旋转90°，得到Rt△COD，二次函数y＝﹣x2+bx+c的图象刚好经过A，B，C三点．（1）求二次函数的解析式及顶点P的坐标；（2）过定点Q的直线l：y＝kx﹣k+3与二次函数图象相交于M，N两点．①若S△PMN＝2，求k的值；②证明：无论k为何值，△PMN恒为直角三角形；③当直线l绕着定点Q旋转时，△PMN外接圆圆心在一条抛物线上运动，直接写出该抛物线的表达式．12.(连云港)问题情境：如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段DN、MB、EC 之间的数量关系，并说明理由．问题探究：在“问题情境”的基础上．（1）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF的度数；（2）如图3，当垂足P在正方形ABCD的对角线BD上时，连接AN，将△APN沿着AN 翻折，点P落在点P'处，若正方形ABCD的边长为4，AD的中点为S，求P'S的最小值．问题拓展：如图4，在边长为4的正方形ABCD中，点M、N分别为边AB、CD上的点，将正方形ABCD沿着MN翻折，使得BC的对应边B'C'恰好经过点A，C'N交AD于点F．分别过点A、F作AG⊥MN，FH⊥MN，垂足分别为G、H．若AG＝，请直接写出FH的长．13.(泰州)已知一次函数y1＝kx+n（n＜0）和反比例函数y2＝（m＞0，x＞0）．（1）如图1，若n＝﹣2，且函数y1、y2的图象都经过点A（3，4）．①求m，k的值；②直接写出当y1＞y2时x的范围；（2）如图2，过点P（1，0）作y轴的平行线l与函数y2的图象相交于点B，与反比例函数y3＝（x＞0）的图象相交于点C．①若k＝2，直线l与函数y1的图象相交点D．当点B、C、D中的一点到另外两点的距离相等时，求m﹣n的值；②过点B作x轴的平行线与函数y1的图象相交与点E．当m﹣n的值取不大于1的任意实数时，点B、C间的距离与点B、E间的距离之和d始终是一个定值．求此时k的值及定值d．14.(无锡)如图1，在矩形ABCD中，BC＝3，动点P从B出发，以每秒1个单位的速度，沿射线BC方向移动，作△PAB关于直线PA的对称△PAB′，设点P的运动时间为t(s)．（1）若AB＝2，当点B′落在AC上时，显然△PAB′是直角三角形，求此时t的值；②是否存在异于图2的时刻，使得△PC B′是直角三角形？若存在，请直接写出所有符合题意的t的值？若不存在，请说明理由．（2）当P点不与C点重合时，若直线PB′与直线CD相交于点M，且当t＜3时存在某一时刻有结论∠PAM＝45°成立，试探究：对于t＞3的任意时刻，结论∠PAM＝45°是否总是成立？请说明理由．15.(宿迁)如图，抛物线y＝x2+bx+c交x轴于A、B两点，其中点A坐标为（1，0），与y轴交于点C（0，﹣3）．（1）求抛物线的函数表达式；（2）如图①，连接AC，点P在抛物线上，且满足∠PAB＝2∠ACO．求点P的坐标；（3）如图②，点Q为x轴下方抛物线上任意一点，点D是抛物线对称轴与x轴的交点，直线AQ、BQ分别交抛物线的对称轴于点M、N．请问DM+DN是否为定值？如果是，请求出这个定值；如果不是，请说明理由．16.(德州) 如图，抛物线y＝mx2﹣mx﹣4与x轴交于A（x1，0），B（x2，0）两点，与y轴交于点C，且x2﹣x1＝．（1）求抛物线的解析式；（2）若P（x1，y1），Q（x2，y2）是抛物线上的两点，当a≤x1≤a+2，x2≥时，均有y1≤y2，求a的取值范围；（3）抛物线上一点D（1，﹣5），直线BD与y轴交于点E，动点M在线段BD上，当∠BDC＝∠MCE时，求点M的坐标．17.(菏泽)如图，抛物线与x轴交于A，B两点，与y轴交于点C（0，﹣2），点A的坐标是（2，0），P为抛物线上的一个动点，过点P作PD⊥x轴于点D，交直线BC于点E，抛物线的对称轴是直线x＝﹣1．（1）求抛物线的函数表达式；（2）若点P在第二象限内，且PE＝OD，求△PBE的面积．（3）在（2）的条件下，若M为直线BC上一点，在x轴的上方，是否存在点M，使△BDM是以BD为腰的等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．18.(聊城) 如图，在平面直角坐标系中，抛物线y＝ax2+bx+c与x轴交于点A（﹣2，0），点B（4，0），与y轴交于点C（0，8），连接BC，又已知位于y轴右侧且垂直于x轴的动直线l，沿x轴正方向从O运动到B（不含O点和B点），且分别交抛物线、线段BC以及x 轴于点P，D，E．（1）求抛物线的表达式；（2）连接AC，AP，当直线l运动时，求使得△PEA和△AOC相似的点P的坐标；（3）作PF⊥BC，垂足为F，当直线l运动时，求Rt△PFD面积的最大值．19.(自贡) 如图，已知直线AB 与抛物线C ：2y ax 2x c =++ 相交于()A 1,0-和点()B 2,3两点.⑴.求抛物线C 的函数表达式；⑵.若点M 是位于直线AB 上方抛物线上的一动点，以MA MB 、为相邻两边作平行四边形MANB ,当平行四边形MANB 的面积最大时，求此时四边形MANB 的面积S 及点M的坐标；⑶.在抛物线C 的对称轴上是否存在定点F ,使抛物线C 上任意一点P 到点F 的距离等于到直线17y 4=的距离，若存在，求出定点F 的坐标；若不存在，请说明理由.20.(安徽)如图，Rt△ABC中，∠ACB＝90°，AC＝BC，P为△ABC内部一点，且∠APB＝∠BPC＝135°．（1）求证：△P AB∽△PBC；（2）求证：P A＝2PC；（3）若点P到三角形的边AB，BC，CA的距离分别为h1，h2，h3，求证h12＝h2•h3．21.(长沙)如图，抛物线y＝ax2+6ax（a为常数，a＞0）与x轴交于O，A两点，点B为抛物线的顶点，点D的坐标为（t，0）（﹣3＜t＜0），连接BD并延长与过O，A，B三点的⊙P 相交于点C．（1）求点A的坐标；（2）过点C作⊙P的切线CE交x轴于点E．①如图1，求证：CE＝DE；②如图2，连接AC，BE，BO，当a＝，∠CAE＝∠OBE时，求﹣的值．22.(株洲)已知二次函数y＝ax2+bx+c（a＞0）（1）若a＝1，b＝﹣2，c＝﹣1①求该二次函数图象的顶点坐标；②定义：对于二次函数y＝px2+qx+r（p≠0），满足方程y＝x的x的值叫做该二次函数的“不动点”．求证：二次函数y＝ax2+bx+c有两个不同的“不动点”．（2）设b＝c3，如图所示，在平面直角坐标系Oxy中，二次函数y＝ax2+bx+c的图象与x 轴分别相交于不同的两点A（x1，0），B（x2，0），其中x1＜0，x2＞0，与y轴相交于点C，连结BC，点D在y轴的正半轴上，且OC＝OD，又点E的坐标为（1，0），过点D 作垂直于y轴的直线与直线CE相交于点F，满足∠AFC＝∠ABC．F A的延长线与BC的延长线相交于点P，若＝，求二次函数的表达式．23.(苏州)如图①，抛物线y=-x2+（a+1）x-a与x轴交于A，B两点（点A位于点B的左侧），与y轴交于点C．已知△ABC的面积是6．（1）求a的值；（2）求△ABC外接圆圆心的坐标；（3）如图②，P是抛物线上一点，Q为射线CA上一点，且P、Q两点均在第三象限内，Q、A是位于直线BP同侧的不同两点，若点P到x轴的距离为d，△QPB的面积为2d，且∠PAQ=∠AQB，求点Q的坐标．24.(威海)（1）方法选择如图①，四边形ABCD是⊙O的内接四边形，连接AC，BD，AB＝BC＝AC．求证：BD＝AD+CD．小颖认为可用截长法证明：在DB上截取DM＝AD，连接AM…小军认为可用补短法证明：延长CD至点N，使得DN＝AD…请你选择一种方法证明．（2）类比探究【探究1】如图②，四边形ABCD是⊙O的内接四边形，连接AC，BD，BC是⊙O的直径，AB＝AC．试用等式表示线段AD，BD，CD之间的数量关系，井证明你的结论．【探究2】如图③，四边形ABCD是⊙O的内接四边形，连接AC，BD．若BC是⊙O的直径，∠ABC＝30°，则线段AD，BD，CD之间的等量关系式是．（3）拓展猜想如图④，四边形ABCD是⊙O的内接四边形，连接AC，BD．若BC是⊙O的直径，BC：AC：AB＝a：b：c，则线段AD，BD，CD之间的等量关系式是．25.(淄博)如图，顶点为M的抛物线y＝ax2+bx+3与x轴交于A（3，0），B（﹣1，0）两点，与y轴交于点C．（1）求这条抛物线对应的函数表达式；（2）问在y轴上是否存在一点P，使得△PAM为直角三角形？若存在，求出点P的坐标；若不存在，说明理由．（3）若在第一象限的抛物线下方有一动点D，满足DA＝OA，过D作DG⊥x轴于点G，设△ADG的内心为I，试求CI的最小值．1.26.(绵阳)如图，在以点O为中心的正方形ABCD中，AD=4，连接AC，动点E从点O出发沿O→C以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，△ADE 的外接圆交AB于点F，连接DF交AC于点G，连接EF，将△EFG沿EF翻折，得到△EFH．（1）求证：△DEF是等腰直角三角形；（2）当点H恰好落在线段BC上时，求EH的长；（3）设点E运动的时间为t秒，△EFG的面积为S，求S关于时间t的关系式．27.(遂宁)如图，顶点为P（3，3）的二次函数图象与x轴交于点A（6，0），点B在该图象上，OB交其对称轴l于点M，点M、N关于点P对称，连接BN、ON．（1）求该二次函数的关系式．（2）若点B在对称轴l右侧的二次函数图象上运动，请解答下列问题：①连接OP，当OP＝MN时，请判断△NOB的形状，并求出此时点B的坐标．②求证：∠BNM＝∠ONM．页）数学试题28.(东营) 已知抛物线 y = ax 2 + bx - 4经过点 A （2,0）、 B （-4,0），与 y 轴交于点C .（1）求这条抛物线的解析式；（2）如图 1，点 P 是第三象限内抛物线上的一个动点，当四边形 ABPC 的面积最大时， 求点 P 的坐标；（3）如图 2，线段 AC 的垂直平分线交 x 轴于点 E ，垂足为 D ，M 为抛物线的顶点，在直线 DE 上是否存在一点 G ，使△CMG 的周长最小？若存在，求出点 G 的坐标；若不存在，请说明理由.（第 28 题图 1）（第 28 题图 2）29.(广东)30.(宿迁) 如图，抛物线y=x2+bx+c交x轴于A、B两点，其中点A坐标为(1,0)，与y轴交于点C(0,-3).(1)求抛物钱的函数表达式；⑵如图①，连接AC，点P在抛物线上，且满足∠PAB=2∠AC0。
2019年全国各地中考真题压轴题精选：四边形综合(带答案解析)
四边形综合题一．选择题（共1小题）1．（2019•连云港）如图，利用一个直角墙角修建一个梯形储料场ABCD ，其中∠C ＝120°．若新建墙BC 与CD 总长为12m ，则该梯形储料场ABCD 的最大面积是（ ）A ．18m 2B ．18√3m 2C ．24√3m 2D ．45√32m 2 二．填空题（共2小题）2．（2019•日照）规定：在平面直角坐标系xOy 中，如果点P 的坐标为（a ，b ），那么向量OP→可以表示为：OP →=（a ，b ），如果OA →与OB →互相垂直，OA →=（x 1，y 1），OB →=（x 2，y 2），那么x 1x 2+y 1y 2＝0．若OM →与ON →互相垂直，OM →=（sin α，1），ON →=（2，−√3），则锐角∠α＝ ．3．（2019•上海）如图，在正六边形ABCDEF 中，设BA →=a →，BC →=b →，那么向量BF →用向量a →、b →表示为 ．三．解答题（共38小题）4．（2019•抚顺）如图，点E ，F 分别在正方形ABCD 的边CD ，BC 上，且DE ＝CF ，点P在射线BC 上（点P 不与点F 重合）．将线段EP 绕点E 顺时针旋转90°得到线段EG ，过点E 作GD 的垂线QH ，垂足为点H ，交射线BC 于点Q ．（1）如图1，若点E 是CD 的中点，点P 在线段BF 上，线段BP ，QC ，EC 的数量关系为 ．（2）如图2，若点E 不是CD 的中点，点P 在线段BF 上，判断（1）中的结论是否仍然成立．若成立，请写出证明过程；若不成立，请说明理由．（3）正方形ABCD的边长为6，AB＝3DE，QC＝1，请直接写出线段BP的长．5．（2019•盘锦）如图，四边形ABCD是菱形，∠BAD＝120°，点E在射线AC上（不包括点A和点C），过点E的直线GH交直线AD于点G，交直线BC于点H，且GH∥DC，点F在BC的延长线上，CF＝AG，连接ED，EF，DF．（1）如图1，当点E在线段AC上时，①判断△AEG的形状，并说明理由．②求证：△DEF是等边三角形．（2）如图2，当点E在AC的延长线上时，△DEF是等边三角形吗？如果是，请证明你的结论；如果不是，请说明理由．6．（2019•朝阳）如图，四边形ABCD是正方形，连接AC，将△ABC绕点A逆时针旋转α得△AEF，连接CF，O为CF的中点，连接OE，OD．（1）如图1，当α＝45°时，请直接写出OE与OD的关系（不用证明）．（2）如图2，当45°＜α＜90°时，（1）中的结论是否成立？请说明理由．（3）当α＝360°时，若AB＝4√2，请直接写出点O经过的路径长．7．（2019•鄂尔多斯）（1）【探究发现】如图1，∠EOF的顶点O在正方形ABCD两条对角线的交点处，∠EOF＝90°，将∠EOF 绕点O旋转，旋转过程中，∠EOF的两边分别与正方形ABCD的边BC和CD交于点E 和点F（点F与点C，D不重合）．则CE，CF，BC之间满足的数量关系是．（2）【类比应用】如图2，若将（1）中的“正方形ABCD”改为“∠BCD＝120°的菱形ABCD”，其他条件不变，当∠EOF＝60°时，上述结论是否仍然成立？若成立，请给出证明；若不成立，请猜想结论并说明理由．（3）【拓展延伸】如图3，∠BOD＝120°，OD=34，OB＝4，OA平分∠BOD，AB=√13，且OB＞2OA，点C是OB上一点，∠CAD＝60°，求OC的长．8．（2019•湘潭）如图一，在射线DE的一侧以AD为一条边作矩形ABCD，AD＝5√3，CD ＝5，点M是线段AC上一动点（不与点A重合），连结BM，过点M作BM的垂线交射线DE于点N，连接BN．（1）求∠CAD的大小；（2）问题探究：动点M在运动的过程中，①是否能使△AMN为等腰三角形，如果能，求出线段MC的长度；如果不能，请说明理由．②∠MBN的大小是否改变？若不改变，请求出∠MBN的大小；若改变，请说明理由．（3）问题解决：如图二，当动点M运动到AC的中点时，AM与BN的交点为F，MN的中点为H，求线段FH的长度．9．（2019•娄底）如图，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA（不包括端点）上运动，且满足AE＝CG，AH＝CF．（1）求证：△AEH≌△CGF；（2）试判断四边形EFGH的形状，并说明理由．（3）请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系，并说明理由．10．（2019•陕西）问题提出：（1）如图1，已知△ABC，试确定一点D，使得以A，B，C，D为顶点的四边形为平行四边形，请画出这个平行四边形；问题探究：（2）如图2，在矩形ABCD中，AB＝4，BC＝10，若要在该矩形中作出一个面积最大的△BPC，且使∠BPC＝90°，求满足条件的点P到点A的距离；问题解决：（3）如图3，有一座塔A，按规定，要以塔A为对称中心，建一个面积尽可能大的形状为平行四边形的景区BCDE．根据实际情况，要求顶点B是定点，点B到塔A的距离为50米，∠CBE＝120°，那么，是否可以建一个满足要求的面积最大的平行四边形景区BCDE？若可以，求出满足要求的平行四边形BCDE的最大面积；若不可以，请说明理由．（塔A的占地面积忽略不计）11．（2019•贵阳）（1）数学理解：如图①，△ABC是等腰直角三角形，过斜边AB的中点D 作正方形DECF，分别交BC，AC于点E，F，求AB，BE，AF之间的数量关系；（2）问题解决：如图②，在任意直角△ABC内，找一点D，过点D作正方形DECF，分别交BC，AC于点E，F，若AB＝BE+AF，求∠ADB的度数；（3）联系拓广：如图③，在（2）的条件下，分别延长ED，FD，交AB于点M，N，求MN，AM，BN的数量关系．12．（2019•通辽）如图，点P是正方形ABCD内的一点，连接CP，将线段CP绕点C顺时旋转90°，得到线段CQ，连接BP，DQ．（1）如图1，求证：△BCP≌△DCQ；（2）如图，延长BP交直线DQ于点E．①如图2，求证：BE⊥DQ；②如图3，若△BCP为等边三角形，判断△DEP的形状，并说明理由．13．（2019•吉林）如图，在矩形ABCD中，AD＝4cm，AB＝3cm，E为边BC上一点，BE ＝AB，连接AE．动点P、Q从点A同时出发，点P以√2cm/s的速度沿AE向终点E运动；点Q以2cm/s的速度沿折线AD﹣DC向终点C运动．设点Q运动的时间为x（s），在运动过程中，点P，点Q经过的路线与线段PQ围成的图形面积为y（cm2）．（1）AE＝cm，∠EAD＝°；（2）求y关于x的函数解析式，并写出自变量x的取值范围；（3）当PQ=54cm时，直接写出x的值．14．（2019•长春）如图，在Rt△ABC中，∠C＝90°，AC＝20，BC＝15．点P从点A出发，沿AC向终点C运动，同时点Q从点C出发，沿射线CB运动，它们的速度均为每秒5个单位长度，点P到达终点时，P、Q同时停止运动．当点P不与点A、C重合时，过点P作PN⊥AB于点N，连结PQ，以PN、PQ为邻边作▱PQMN．设▱PQMN与△ABC重叠部分图形的面积为S，点P的运动时间为t秒．（1）①AB的长为；②PN的长用含t的代数式表示为．（2）当▱PQMN为矩形时，求t的值；（3）当▱PQMN与△ABC重叠部分图形为四边形时，求S与t之间的函数关系式；（4）当过点P且平行于BC的直线经过▱PQMN一边中点时，直接写出t的值．15．（2019•吉林）性质探究如图①，在等腰三角形ABC中，∠ACB＝120°，则底边AB与腰AC的长度之比为．理解运用（1）若顶角为120°的等腰三角形的周长为8+4√3，则它的面积为；（2）如图②，在四边形EFGH中，EF＝EG＝EH．①求证：∠EFG+∠EHG＝∠FGH；②在边FG，GH上分别取中点M，N，连接MN．若∠FGH＝120°，EF＝10，直接写出线段MN的长．类比拓展顶角为2α的等腰三角形的底边与一腰的长度之比为（用含α的式子表示）．16．（2019•常州）【阅读】数学中，常对同一个量（图形的面积、点的个数、三角形的内角和等）用两种不同的方法计算，从而建立相等关系，我们把这一思想称为“算两次”．“算两次”也称做富比尼原理，是一种重要的数学思想．【理解】（1）如图1，两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成一个梯形．用两种不同的方法计算梯形的面积，并写出你发现的结论；（2）如图2，n行n列的棋子排成一个正方形，用两种不同的方法计算棋子的个数，可得等式：n2＝；【运用】（3）n边形有n个顶点，在它的内部再画m个点，以（m+n）个点为顶点，把n边形剪成若干个三角形，设最多可以剪得y个这样的三角形．当n＝3，m＝3时，如图3，最多可以剪得7个这样的三角形，所以y＝7．①当n＝4，m＝2时，如图4，y＝；当n＝5，m＝时，y＝9；②对于一般的情形，在n边形内画m个点，通过归纳猜想，可得y＝（用含m、n的代数式表示）．请对同一个量用算两次的方法说明你的猜想成立．17．（2019•鸡西）如图，在平面直角坐标系中，矩形ABCD的边AB在x轴上，AB、BC的长分别是一元二次方程x2﹣7x+12＝0的两个根（BC＞AB），OA＝2OB，边CD交y轴于点E，动点P以每秒1个单位长度的速度，从点E出发沿折线段ED﹣DA向点A运动，运动的时间为t（0≤t＜6）秒，设△BOP与矩形AOED重叠部分的面积为S．（1）求点D的坐标；（2）求S关于t的函数关系式，并写出自变量的取值范围；（3）在点P的运动过程中，是否存在点P，使△BEP为等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．18．（2019•舟山）小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．（1）温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，若BC＝a，AD＝h，求正方形PQMN的边长（用a，h表示）．（2）操作：如何画出这个正方形PQMN呢？如图2，小波画出了图1的△ABC，然后按数学家波利亚在《怎样解题》中的方法进行操作：先在AB上任取一点P'，画正方形P'Q'M'N'，使点Q'，M'在BC边上，点N'在△ABC 内，然后连结BN'，并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PQMN．（3）推理：证明图2中的四边形PQMN是正方形．（4）拓展：小波把图2中的线段BN称为“波利亚线”，在该线上截取NE＝NM，连结EQ，EM（如图3），当∠QEM＝90°时，求“波利亚线”BN的长（用a，h表示）．请帮助小波解决“温故”、“推理”、“拓展”中的问题．19．（2019•海南）如图，在边长为1的正方形ABCD中，E是边CD的中点，点P是边AD上一点（与点A 、D 不重合），射线PE 与BC 的延长线交于点Q ．（1）求证：△PDE ≌△QCE ；（2）过点E 作EF ∥BC 交PB 于点F ，连结AF ，当PB ＝PQ 时，①求证：四边形AFEP 是平行四边形；②请判断四边形AFEP 是否为菱形，并说明理由．20．（2019•益阳）如图，在平面直角坐标系xOy 中，矩形ABCD 的边AB ＝4，BC ＝6．若不改变矩形ABCD 的形状和大小，当矩形顶点A 在x 轴的正半轴上左右移动时，矩形的另一个顶点D 始终在y 轴的正半轴上随之上下移动．（1）当∠OAD ＝30°时，求点C 的坐标；（2）设AD 的中点为M ，连接OM 、MC ，当四边形OMCD 的面积为212时，求OA 的长；（3）当点A 移动到某一位置时，点C 到点O 的距离有最大值，请直接写出最大值，并求此时cos ∠OAD 的值．21．（2019•天水）如图1，对角线互相垂直的四边形叫做垂美四边形．（1）概念理解：如图2，在四边形ABCD 中，AB ＝AD ，CB ＝CD ，问四边形ABCD 是垂美四边形吗？请说明理由；（2）性质探究：如图1，四边形ABCD 的对角线AC 、BD 交于点O ，AC ⊥BD ．试证明：AB 2+CD 2＝AD 2+BC 2；（3）解决问题：如图3，分别以Rt △ACB 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ，连结CE 、BG 、GE ．已知AC ＝4，AB ＝5，求GE 的长．22．（2019•无锡）如图1，在矩形ABCD中，BC＝3，动点P从B出发，以每秒1个单位的速度，沿射线BC方向移动，作△P AB关于直线P A的对称△P AB′，设点P的运动时间为t（s）．（1）若AB＝2√3．①如图2，当点B′落在AC上时，显然△P AB′是直角三角形，求此时t的值；②是否存在异于图2的时刻，使得△PCB′是直角三角形？若存在，请直接写出所有符合题意的t的值？若不存在，请说明理由．（2）当P点不与C点重合时，若直线PB′与直线CD相交于点M，且当t＜3时存在某一时刻有结论∠P AM＝45°成立，试探究：对于t＞3的任意时刻，结论“∠P AM＝45°”是否总是成立？请说明理由．23．（2019•岳阳）操作体验：如图，在矩形ABCD中，点E、F分别在边AD、BC上，将矩形ABCD沿直线EF折叠，使点D恰好与点B重合，点C落在点C′处．点P为直线EF 上一动点（不与E、F重合），过点P分别作直线BE、BF的垂线，垂足分别为点M和N，以PM、PN为邻边构造平行四边形PMQN．（1）如图1，求证：BE＝BF；（2）特例感知：如图2，若DE＝5，CF＝2，当点P在线段EF上运动时，求平行四边形PMQN的周长；（3）类比探究：若DE＝a，CF＝b．①如图3，当点P在线段EF的延长线上运动时，试用含a、b的式子表示QM与QN之间的数量关系，并证明；②如图4，当点P在线段FE的延长线上运动时，请直接用含a、b的式子表示QM与QN之间的数量关系．（不要求写证明过程）24．（2019•盐城）如图①是一张矩形纸片，按以下步骤进行操作：（Ⅰ）将矩形纸片沿DF折叠，使点A落在CD边上点E处，如图②；（Ⅱ）在第一次折叠的基础上，过点C再次折叠，使得点B落在边CD上点B′处，如图③，两次折痕交于点O；（Ⅲ）展开纸片，分别连接OB、OE、OC、FD，如图④．【探究】（1）证明：△OBC≌△OED；（2）若AB＝8，设BC为x，OB2为y，求y关于x的关系式．25．（2019•苏州）已知矩形ABCD中，AB＝5cm，点P为对角线AC上的一点，且AP＝2√5cm．如图①，动点M从点A出发，在矩形边上沿着A→B→C的方向匀速运动（不包含点C）．设动点M的运动时间为t（s），△APM的面积为S（cm2），S与t的函数关系如图②所示．（1）直接写出动点M的运动速度为cm/s，BC的长度为cm；（2）如图③，动点M重新从点A出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点N从点D出发，在矩形边上沿着D→C→B的方向匀速运动，设动点N 的运动速度为v（cm/s）．已知两动点M，N经过时间x（s）在线段BC上相遇（不包含点C），动点M，N相遇后立即同时停止运动，记此时△APM与△DPN的面积分别为S1（cm2），S2（cm2）①求动点N运动速度v（cm/s）的取值范围；②试探究S1•S2是否存在最大值，若存在，求出S1•S2的最大值并确定运动时间x的值；若不存在，请说明理由．26．（2019•资阳）在矩形ABCD中，连结AC，点E从点B出发，以每秒1个单位的速度沿着B→A→C的路径运动，运动时间为t（秒）．过点E作EF⊥BC于点F，在矩形ABCD 的内部作正方形EFGH．（1）如图，当AB＝BC＝8时，①若点H在△ABC的内部，连结AH、CH，求证：AH＝CH；②当0＜t≤8时，设正方形EFGH与△ABC的重叠部分面积为S，求S与t的函数关系式；（2）当AB＝6，BC＝8时，若直线AH将矩形ABCD的面积分成1：3两部分，求t的值．27．（2019•宁波）定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．（1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD 上的点．求证：四边形ABEF是邻余四边形．（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB是邻余线，E，F在格点上．（3）如图3，在（1）的条件下，取EF中点M，连结DM并延长交AB于点Q，延长EF 交AC于点N．若N为AC的中点，DE＝2BE，QB＝3，求邻余线AB的长．28．（2019•衡阳）如图，在等边△ABC中，AB＝6cm，动点P从点A出发以1cm/s的速度沿AB匀速运动．动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动，当点P到达点B时，点P、Q同时停止运动．设运动时间为t（s）．过点P作PE⊥AC于E，连接PQ交AC边于D．以CQ、CE为边作平行四边形CQFE．（1）当t为何值时，△BPQ为直角三角形；（2）是否存在某一时刻t，使点F在∠ABC的平分线上？若存在，求出t的值，若不存在，请说明理由；（3）求DE的长；（4）取线段BC的中点M，连接PM，将△BPM沿直线PM翻折，得△B′PM，连接AB′，当t为何值时，AB'的值最小？并求出最小值．29．（2019•绵阳）如图，在以点O为中心的正方形ABCD中，AD＝4，连接AC，动点E从点O出发沿O→C以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，△ADE的外接圆交AB于点F，连接DF交AC于点G，连接EF，将△EFG沿EF翻折，得到△EFH．（1）求证：△DEF是等腰直角三角形；（2）当点H恰好落在线段BC上时，求EH的长；（3）设点E运动的时间为t秒，△EFG的面积为S，求S关于时间t的关系式．30．（2019•扬州）如图，四边形ABCD是矩形，AB＝20，BC＝10，以CD为一边向矩形外部作等腰直角△GDC，∠G＝90°．点M在线段AB上，且AM＝a，点P沿折线AD﹣DG运动，点Q沿折线BC﹣CG运动（与点G不重合），在运动过程中始终保持线段PQ ∥AB．设PQ与AB之间的距离为x．（1）若a＝12．①如图1，当点P在线段AD上时，若四边形AMQP的面积为48，则x的值为；②在运动过程中，求四边形AMQP的最大面积；（2）如图2，若点P在线段DG上时，要使四边形AMQP的面积始终不小于50，求a 的取值范围．31．（2019•泰州）如图，线段AB＝8，射线BG⊥AB，P为射线BG上一点，以AP为边作正方形APCD，且点C、D与点B在AP两侧，在线段DP上取一点E，使∠EAP＝∠BAP，直线CE与线段AB相交于点F（点F与点A、B不重合）．（1）求证：△AEP≌△CEP；（2）判断CF与AB的位置关系，并说明理由；（3）求△AEF的周长．32．（2019•嘉兴）小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．（1）温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，若BC＝6，AD＝4，求正方形PQMN的边长．（2）操作：能画出这类正方形吗？小波按数学家波利亚在《怎样解题》中的方法进行操作：如图2，任意画△ABC，在AB上任取一点P'，画正方形P'Q'M'N'，使Q'，M'在BC 边上，N'在△ABC内，连结BN'并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PPQMN．小波把线段BN称为“波利亚线”．（3）推理：证明图2中的四边形PQMN是正方形．（4）拓展：在（2）的条件下，在射线BN上截取NE＝NM，连结EQ，EM（如图3）．当tan∠NBM=34时，猜想∠QEM的度数，并尝试证明．请帮助小波解决“温故”、“推理”、“拓展”中的问题．33．（2019•台州）我们知道，各个角都相等，各条边都相等的多边形叫做正多边形．对一个各条边都相等的凸多边形（边数大于3），可以由若干条对角线相等判定它是正多边形．例如，各条边都相等的凸四边形，若两条对角线相等，则这个四边形是正方形．（1）已知凸五边形ABCDE的各条边都相等．①如图1，若AC＝AD＝BE＝BD＝CE，求证：五边形ABCDE是正五边形；②如图2，若AC＝BE＝CE，请判断五边形ABCDE是不是正五边形，并说明理由：（2）判断下列命题的真假．（在括号内填写“真”或“假”）如图3，已知凸六边形ABCDEF的各条边都相等．①若AC＝CE＝EA，则六边形ABCDEF是正六边形；（）②若AD＝BE＝CF，则六边形ABCDEF是正六边形．（）34．（2019•天津）在平面直角坐标系中，O为原点，点A（6，0），点B在y轴的正半轴上，∠ABO＝30°．矩形CODE的顶点D，E，C分别在OA，AB，OB上，OD＝2．（Ⅰ）如图①，求点E的坐标；（Ⅱ）将矩形CODE沿x轴向右平移，得到矩形C′O′D′E′，点C，O，D，E的对应点分别为C′，O′，D′，E′．设OO′＝t，矩形C′O′D′E′与△ABO重叠部分的面积为S．①如图②，当矩形C′O′D′E′与△ABO重叠部分为五边形时，C′E′，E′D′分别与AB相交于点M，F，试用含有t的式子表示S，并直接写出t的取值范围；②当√3≤S≤5√3时，求t的取值范围（直接写出结果即可）．35．（2019•青岛）已知：如图，在四边形ABCD中，AB∥CD，∠ACB＝90°，AB＝10cm，BC＝8cm，OD垂直平分A C．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动，另一个点也停止运动．过点P作PE⊥AB，交BC于点E，过点Q作QF∥AC，分别交AD，OD于点F，G．连接OP，EG．设运动时间为t（s）（0＜t＜5），解答下列问题：（1）当t为何值时，点E在∠BAC的平分线上？（2）设四边形PEGO的面积为S（cm2），求S与t的函数关系式；（3）在运动过程中，是否存在某一时刻t，使四边形PEGO的面积最大？若存在，求出t的值；若不存在，请说明理由；（4）连接OE，OQ，在运动过程中，是否存在某一时刻t，使OE⊥OQ？若存在，求出t的值；若不存在，请说明理由．36．（2019•白银）阅读下面的例题及点拨，并解决问题：例题：如图①，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC的外角∠ACH的平分线上一点，且AM＝MN．求证：∠AMN＝60°．点拨：如图②，作∠CBE＝60°，BE与NC的延长线相交于点E，得等边△BEC，连接EM．易证：△ABM≌△EBM（SAS），可得AM＝EM，∠1＝∠2；又AM＝MN，则EM ＝MN，可得∠3＝∠4；由∠3+∠1＝∠4+∠5＝60°，进一步可得∠1＝∠2＝∠5，又因为∠2+∠6＝120°，所以∠5+∠6＝120°，即：∠AMN＝60°．问题：如图③，在正方形A1B1C1D1中，M1是B1C1边上一点（不含端点B1，C1），N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，且A1M1＝M1N1．求证：∠A1M1N1＝90°．37．（2019•济宁）如图1，在矩形ABCD中，AB＝8，AD＝10，E是CD边上一点，连接AE，将矩形ABCD沿AE折叠，顶点D恰好落在BC边上点F处，延长AE交BC的延长线于点G．（1）求线段CE的长；（2）如图2，M，N分别是线段AG，DG上的动点（与端点不重合），且∠DMN＝∠DAM，设AM＝x，DN＝y．①写出y关于x的函数解析式，并求出y的最小值；②是否存在这样的点M，使△DMN是等腰三角形？若存在，请求出x的值；若不存在，请说明理由．38．（2019•连云港）问题情境：如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段DN、MB、EC之间的数量关系，并说明理由．问题探究：在“问题情境”的基础上．（1）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF的度数；（2）如图3，当垂足P在正方形ABCD的对角线BD上时，连接AN，将△APN沿着AN 翻折，点P落在点P'处，若正方形ABCD的边长为4，AD的中点为S，求P'S的最小值．问题拓展：如图4，在边长为4的正方形ABCD中，点M、N分别为边AB、CD上的点，将正方形ABCD沿着MN翻折，使得BC的对应边B'C'恰好经过点A，C'N交AD于点F．分别过点A、F作AG⊥MN，FH⊥MN，垂足分别为G、H．若AG=52，请直接写出FH的长．39．（2019•威海）如图，在正方形ABCD中，AB＝10cm，E为对角线BD上一动点，连接AE，CE，过E点作EF⊥AE，交直线BC于点F．E点从B点出发，沿着BD方向以每秒2cm的速度运动，当点E与点D重合时，运动停止．设△BEF的面积为ycm2，E点的运动时间为x秒．（1）求证：CE＝EF；（2）求y与x之间关系的函数表达式，并写出自变量x的取值范围；（3）求△BEF面积的最大值．40．（2019•达州）箭头四角形模型规律如图1，延长CO交AB于点D，则∠BOC＝∠1+∠B＝∠A+∠C+∠B．因为凹四边形ABOC形似箭头，其四角具有“∠BOC＝∠A+∠B+∠C”这个规律，所以我们把这个模型叫做“箭头四角形”．模型应用（1）直接应用：①如图2，∠A+∠B+∠C+∠D+∠E+∠F＝．②如图3，∠ABE、∠ACE的2等分线（即角平分线）BF、CF交于点F，已知∠BEC＝120°，∠BAC＝50°，则∠BFC＝．③如图4，BO i、CO i分别为∠ABO、∠ACO的2019等分线（i＝1，2，3， (2017)2018）．它们的交点从上到下依次为O1、O2、O3、…、O2018．已知∠BOC＝m°，∠BAC ＝n°，则∠BO1000C＝度．（2）拓展应用：如图5，在四边形ABCD中，BC＝CD，∠BCD＝2∠BAD．O是四边形ABCD内一点，且OA＝OB＝OD．求证：四边形OBCD是菱形．41．（2019•自贡）（1）如图1，E是正方形ABCD边AB上的一点，连接BD、DE，将∠BDE 绕点D逆时针旋转90°，旋转后角的两边分别与射线BC交于点F和点G．①线段DB和DG的数量关系是；②写出线段BE，BF和DB之间的数量关系．（2）当四边形ABCD为菱形，∠ADC＝60°，点E是菱形ABCD边AB所在直线上的一点，连接BD、DE，将∠BDE绕点D逆时针旋转120°，旋转后角的两边分别与射线BC 交于点F和点G．①如图2，点E在线段AB上时，请探究线段BE、BF和BD之间的数量关系，写出结论并给出证明；②如图3，点E在线段AB的延长线上时，DE交射线BC于点M，若BE＝1，AB＝2，直接写出线段GM的长度．四边形综合题参考答案与试题解析一．选择题（共1小题）1．【解答】解：如图，过点C作CE⊥AB于E，则四边形ADCE为矩形，CD＝AE＝x，∠DCE＝∠CEB＝90°，则∠BCE＝∠BCD﹣∠DCE＝30°，BC＝12﹣x，在Rt△CBE中，∵∠CEB＝90°，∴BE=12BC＝6−12x，∴AD＝CE=√3BE＝6√3−√32x，AB＝AE+BE＝x+6−12x=12x+6，∴梯形ABCD面积S=12（CD+AB）•CE=12（x+12x+6）•（6√3−√32x）=−3√38x2+3√3x+18√3=−3√38（x﹣4）2+24√3，∴当x＝4时，S最大＝24√3．即CD长为4m时，使梯形储料场ABCD的面积最大为24√3m2；故选：C．二．填空题（共2小题）2．【解答】解：依题意，得2sinα+1×（−√3）＝0，解得sinα=√3 2．∵α是锐角，∴α＝60°．故答案是：60°．3．【解答】解：连接CF．∵多边形ABCDEF 是正六边形，AB ∥CF ，CF ＝2BA ，∴CF →=2a →，∵BF →=BC →+CF →，∴BF →=2a →+b →，故答案为2a →+b →．三．解答题（共38小题）4．【解答】解：（1）BP +QC ＝EC ；理由如下：∵四边形ABCD 是正方形，∴BC ＝CD ，∠BCD ＝90°，由旋转的性质得：∠PEG ＝90°，EG ＝EP ，∴∠PEQ +∠GEH ＝90°，∵QH ⊥GD ，∴∠H ＝90°，∠G +∠GEH ＝90°，∴∠PEQ ＝∠G ，又∵∠EPQ +∠PEC ＝90°，∠PEC +∠GED ＝90°，∴∠EPQ ＝∠GED ， 在△PEQ 和△EGD 中，{∠EPQ =∠GEDEP =EG ∠PEQ =∠G，∴△PEQ ≌△EGD （ASA ），∴PQ ＝ED ，∴BP +QC ＝BC ﹣PQ ＝CD ﹣ED ＝EC ，即BP +QC ＝EC ；故答案为：BP +QC ＝EC ；（2）（1）中的结论仍然成立，理由如下：由题意得：∠PEG ＝90°，EG ＝EP ，∴∠PEQ +∠GEH ＝90°，∵QH ⊥GD ，∴∠H ＝90°，∠G +∠GEH ＝90°，∴∠PEQ ＝∠G ，∵四边形ABCD 是正方形，∴∠DCB ＝90°，BC ＝DC ，∴∠EPQ +∠PEC ＝90°，∵∠PEC +∠GED ＝90°，∴∠GED ＝∠EPQ ，在△PEQ 和△EGD 中，{∠EPQ =∠GEDEP =EG ∠PEQ =∠G，∴△PEQ ≌△EGD （ASA ），∴PQ ＝ED ，∴BP +QC ＝BC ﹣PQ ＝CD ﹣ED ＝EC ，即BP +QC ＝EC ；（3）分两种情况：①当点P 在线段BC 上时，点Q 在线段BC 上，由（2）可知：BP ＝EC ﹣QC ，∵AB ＝3DE ＝6，∴DE ＝2，EC ＝4，∴BP ＝4﹣1＝3；②当点P 在线段BC 上时，点Q 在线段BC 的延长线上，如图3所示：同（2）可得：△PEQ ≌△EGD （AAS ），∴PQ ＝DE ＝2，∵QC ＝1，∴PC ＝PQ ﹣QC ＝1，∴BP ＝BC ﹣PC ＝6﹣1＝5；综上所述，线段BP 的长为3或5．5．【解答】（1）①解：△AEG 是等边三角形；理由如下：∵四边形ABCD 是菱形，∠BAD ＝120°，∴AD ∥BC ，AB ＝BC ＝CD ＝AD ，AB ∥CD ，∠CAD =12∠BAD ＝60°，∴∠BAD +∠ADC ＝180°，∴∠ADC ＝60°，∵GH ∥DC ，∴∠AGE ＝∠ADC ＝60°，∴∠AGE ＝∠EAG ＝∠AEG ＝60°，∴△AEG 是等边三角形；②证明：∵△AEG 是等边三角形，∴AG ＝AE ，∵CF ＝AG ，∴AE ＝CF ，∵四边形ABCD 是菱形，∴∠BCD ＝∠BAD ＝120°，∴∠DCF ＝60°＝∠CAD ，在△AED 和△CFD 中，{AD =CD∠EAD =∠FCD AE =CF，∴△AED ≌△CFD （SAS ）∴DE ＝DF ，∠ADE ＝∠CDF ，∵∠ADC ＝∠ADE +∠CDE ＝60°，∴∠CDF +∠CDE ＝60°，即∠EDF ＝60°，∴△DEF 是等边三角形；（2）解：△DEF 是等边三角形；理由如下：同（1）①得：△AEG 是等边三角形，∴AG ＝AE ，∵CF ＝AG ，∴AE ＝CF ，∵四边形ABCD 是菱形，∴∠BCD ＝∠BAD ＝120°，∠CAD =12∠BAD ＝60°，∴∠FCD ＝60°＝∠CAD ，在△AED 和△CFD 中，{AD =CD∠EAD =∠FCD AE =CF，∴△AED ≌△CFD （SAS ），∴DE ＝DF ，∠ADE ＝∠CDF ，∵∠ADC ＝∠ADE ﹣∠CDE ＝60°，∴∠CDF ﹣∠CDE ＝60°，即∠EDF ＝60°，∴△DEF 是等边三角形．6．【解答】解：（1）OE ＝OD ，OE ⊥OD ；理由如下：由旋转的性质得：AF ＝AC ，∠AFE ＝∠ACB ，∵四边形ABCD 是正方形，∴∠ACB ＝∠ACD ＝∠F AC ＝45°，∴∠ACF ＝∠AFC =12（180°﹣45°）＝67.5°，∴∠DCF ═∠EFC ＝22.5°，∵∠FEC ＝90°，O 为CF 的中点，∴OE =12CF ＝OC ＝OF ，同理：OD =12CF ，∴OE ＝OD ＝OC ＝OF ，∴∠EOC ＝2∠EFO ＝45°，∠DOF ＝2∠DCO ＝45°，∴∠DOE ＝180°﹣45°﹣45°＝90°，∴OE ⊥OD ；（2）当45°＜α＜90°时，（1）中的结论成立，理由如下：延长EO 到点M ，使OM ＝EO ，连接DM 、CM 、DE ，如图2所示：∵O 为CF 的中点，∴OC ＝OF ，在△COM 和△FOE 中，{OM =EO∠COM =∠FOE OC =OF，∴△COM ≌△FOE （SAS ），∴∠MCF ＝∠EFC ，CM ＝EF ，∵四边形ABCD 是正方形，∴AB ＝BC ＝CD ，∠BAC ＝∠BCA ＝45°，∵△ABC 绕点A 逆时针旋转α得△AEF ，∴AB ＝AE ＝EF ＝CD ，AC ＝AF ，∴CD ＝CM ，∠ACF ＝∠AFC ，∵∠ACF ＝∠ACD +∠FCD ，∠AFC ＝∠AFE +∠CFE ，∠ACD ＝∠AFE ＝45°， ∴∠FCD ＝∠CFE ＝∠MCF ，∵∠EAC +∠DAE ＝45°，∠F AD +∠DAE ＝45°，∴∠EAC ＝∠F AD ，在△ACF 中，∵∠ACF +∠AFC +∠CAF ＝180°，∴∠DAE +2∠F AD +∠DCM +90°＝180°，∵∠F AD +∠DAE ＝45°，∴∠F AD +∠DCM ＝45°，∴∠DAE ＝∠DCM ，在△ADE 和△CDM 中，{AE =CM∠DAE =∠DCM AD =CD，∴△ADE ≌△CDM （SAS ），∴DE ＝DM ，∵OE ＝OM ，∴OE ⊥OD ，在△COM 和△COD 中，{CM =CD∠MCF =∠FCD OC =OC，∴△COM≌△COD（SAS），∴OM＝OD，∴OE＝OD，∴OE＝OD，OE⊥OD；（3）连接AO，如图3所示：∵AC＝AF，CO＝OF，∴AO⊥CF，∴∠AOC＝90°，∴点O在以AC为直径的圆上运动，∵α＝360°，∴点O经过的路径长等于以AC为直径的圆的周长，∵AC=√2AB=√2×4√2=8，∴点O经过的路径长为：πd＝8π．7．【解答】解：（1）如图1中，结论：CE+CF＝BC．理由如下：∵四边形ABCD是正方形，∴AC⊥BD，OB＝OC，∠OBE＝∠OCF＝45°，∵∠EOF＝∠BOC＝90°，∴∠BOE＝∠OCF，∴△BOE≌△COF（ASA），∴BE＝CF，∴CE+CF＝CE+BE＝BC．故答案为CE+CF＝BC．（2）如图2中，结论不成立．CE+CF=12BC．理由：连接EF，在CO上截取CJ＝CF，连接FJ．∵四边形ABCD是菱形，∠BCD＝120°，∴∠BCO＝∠OCF＝60°，∵∠EOF+∠ECF＝180°，∴O，E，C，F四点共圆，∴∠OFE＝∠OCE＝60°，∵∠EOF＝60°，∴△EOF是等边三角形，∴OF＝FE，∠OFE＝60°，∵CF＝CJ，∠FCJ＝60°，∴△CFJ是等边三角形，∴FC＝FJ，∠EFC＝∠OFE＝60°，∴∠OFJ＝∠CFE，∴△OFJ≌△EFC（SAS），∴OJ＝CE，∴CF+CE＝CJ+OJ＝OC=12BC，（3）如图3中，由OB＞2OA可知△BAO是钝角三角形，∠BAO＞90°，作AH⊥OB于H，设OH＝x．在Rt△ABH中，BH=√13−3x2，∵OB＝4，∴√13−3x2+x＝4，解得x=32或12，∴OH=12或32，∴OA＝2OH＝1或3（舍弃），∵∠COD+∠ACD＝180°，∴A，C，O，D四点共圆，∵OA平分∠COD，∴∠AOC＝∠AOD＝60°，∴∠ADC＝∠AOC＝60°，∵∠CAD＝60°，∴△ACD是等边三角形，由（2）可知：OC+OD＝OA，∴OC＝1−34=14．8．【解答】解：（1）如图一（1）中，∵四边形ABCD是矩形，∴∠ADC＝90°，∵tan∠DAC=DCAD=553=√33，∴∠DAC＝30°．（2）①如图一（1）中，当AN＝NM时，∵∠BAN＝∠BMN＝90°，BN＝BN，AN＝NM，∴Rt△BNA≌Rt△BNM（HL），∴BA＝BM，在Rt△ABC中，∵∠ACB＝∠DAC＝30°，AB＝CD＝5，∴AC＝2AB＝10，∵∠BAM＝60°，BA＝BM，∴△ABM是等边三角形，∴AM＝AB＝5，∴CM＝AC﹣AM＝5．如图一（2）中，当AN＝AM时，易证∠AMN＝∠ANM＝15°，∵∠BMN＝90°，∴∠CMB＝75°，∵∠MCB＝30°，∴∠CBM＝180°﹣75°﹣30°＝75°，∴∠CMB＝∠CBM，∴CM＝CB＝5√3，综上所述，满足条件的CM的值为5或5√3．②结论：∠MBN＝30°大小不变．理由：如图一（1）中，∵∠BAN+∠BMN＝180°，∴A，B，M，N四点共圆，∴∠MBN＝∠MAN＝30°．如图一（2）中，∵∠BMN＝∠BAN＝90°，∴A，N，B，M四点共圆，∴∠MBN+∠MAN＝180°，∵∠DAC+∠MAN＝180°，∴∠MBN＝∠DAC＝30°，综上所述，∠MBN＝30°．（3）如图二中，∵AM＝MC，∴BM＝AM＝CM，∴AC＝2AB，∴AB＝BM＝AM，∴△ABM是等边三角形，∴∠BAM＝∠BMA＝60°，∵∠BAN＝∠BMN＝90°，∴∠NAM＝∠NMA＝30°，∴NA＝NM，∵BA＝BM，∴BN垂直平分线段AM，∴FM=5 2，∴NM=FMcos30°=5√33，∵∠NFM＝90°，NH＝HM，∴FH=12MN=5√36．9．【解答】证明：（1）∵四边形ABCD是矩形，∴∠A＝∠C．∴在△AEH与△CGF中，{AE=CG ∠A=∠C AH=CF，∴△AEH≌△CGF（SAS）；（2）∵由（1）知，△AEH≌△CGF，则EH＝GF，同理证得△EBF≌△GDH，则EF＝GH，∴四边形EFGH是平行四边形；（3）四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度．理由如下：作G 关于BC的对称点G′，连接EG′，可得EG′的长度就是EF+FG的最小值．连接AC，∵CG′＝CG＝AE，AB∥CG′，∴四边形AEG′C为平行四边形，∴EG′＝AC．在△EFG′中，∵EF+FG′≥EG′＝AC，∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度．10．【解答】解：（1）如图记为点D所在的位置．（2）如图，∵AB＝4，BC＝10，∴取BC的中点O，则OB＞AB．∴以点O为圆心，OB长为半径作⊙O，⊙O一定于AD相交于P1，P2两点，。
2019年中考数学冲刺压轴题---由比例线段产生的函数关系问题(有解析)
2019年中考数学冲刺压轴题---由比例线段产生的函数关系问题（有解析）例1：在Rt △ABC 中，∠C ＝90°，AC ＝6，53sin =B ，⊙B 的半径长为1，⊙B 交边CB 于点P ，点O 是边AB 上的动点．（1）如图1，将⊙B 绕点P 旋转180°得到⊙M ，请判断⊙M 与直线AB 的位置关系；（2）如图2，在（1）的条件下，当△OMP 是等腰三角形时，求OA 的长；（3）如图3，点N 是边BC 上的动点，如果以NB 为半径的⊙N 和以OA 为半径的⊙O 外切，设NB ＝y ，OA ＝x ，求y 关于x 的函数关系式及定义域．图1 图2 图3思路点拨1．∠B 的三角比反复用到，注意对应关系，防止错乱．2．分三种情况探究等腰△OMP ，各种情况都有各自特殊的位置关系，用几何说理的方法比较简单．3．探求y 关于x 的函数关系式，作△OBN 的边OB 上的高，把△OBN 分割为两个具有公共直角边的直角三角形．满分解答（1） 在Rt △ABC 中，AC ＝6，53sin =B ， 所以AB ＝10，BC ＝8．过点M 作MD ⊥AB ，垂足为D ．在Rt △BMD 中，BM ＝2，3sin 5MD B BM ==，所以65MD =． 因此MD ＞MP ，⊙M 与直线AB 相离． 图4（2）①如图4，MO ≥MD ＞MP ，因此不存在MO ＝MP 的情况．②如图5，当PM ＝PO 时，又因为PB ＝PO ，因此△BOM 是直角三角形． 在Rt △BOM 中，BM ＝2，4cos 5BO B BM ==，所以85BO =．此时425OA =． ③如图6，当OM ＝OP 时，设底边MP 对应的高为OE ．在Rt △BOE 中，BE ＝32，4cos 5BE B BO ==，所以158BO =．此时658OA =． 图5 图6（3）如图7，过点N 作NF ⊥AB ，垂足为F ．联结ON ．当两圆外切时，半径和等于圆心距，所以ON ＝x ＋y ．在Rt △BNF 中，BN ＝y ，3sin 5B =，4cos 5B =，所以35NF y =，45BF y =． 在Rt △ONF 中，4105OF AB AO BF x y =--=--，由勾股定理得ON 2＝OF 2＋NF 2． 于是得到22243()(10)()55x y x y y +=--+．整理，得2505040x y x -=+．定义域为0＜x ＜5． 图7 图8考点伸展第（2）题也可以这样思考：如图8，在Rt △BMF 中，BM ＝2，65MF =，85BF =． 在Rt △OMF 中，OF ＝8421055x x --=-，所以222426()()55OM x =-+． 在Rt △BPQ 中，BP ＝1，35PQ =，45BQ =． 在Rt △OPQ 中，OF ＝4461055x x --=-，所以222463()()55OP x =-+． ①当MO ＝MP ＝1时，方程22426()()155x -+=没有实数根． ②当PO ＝PM ＝1时，解方程22463()()155x -+=，可得425x OA == ③当OM ＝OP 时，解方程22426()()55x -+22463()()55x =-+，可得658x OA ==． 例2：如图1，甲、乙两人分别从A 、B 两点同时出发，点O 为坐标原点．甲沿AO 方向、乙沿BO 方向均以每小时4千米的速度行走，t 小时后，甲到达M点，乙到达N 点．（1）请说明甲、乙两人到达点O 前，MN 与AB 不可能平行；（2）当t 为何值时，△OMN ∽△OBA ？（3）甲、乙两人之间的距离为MN 的长．设s ＝MN 2，求s 与t之间的函数关系式，并求甲、乙两人之间距离的最小值． 图1（1）当M 、N 都在O 右侧时，24122OM t t OA -==-，642163ON t t OB -==-， 所以OM ON OA OB≠．因此MN 与AB 不平行． （2）①如图2，当M 、N 都在O 右侧时，∠OMN ＞∠B ，不可能△OMN ∽△OBA ．②如图3，当M 在O 左侧、N 在O 右侧时，∠MON ＞∠BOA ，不可能△OMN ∽△OBA ．③如图4，当M 、N 都在O 左侧时，如果△OMN ∽△OBA ，那么ON OA OM OB=． 所以462426t t -=-．解得t ＝2． 图2 图3 图4（3）①如图2，24OM t =-，12OH t =-，3(12)MH t =-．②如图3，42OM t =-，21OH t =-，3(21)MH t =-．③如图4，42OM t =-，21OH t =-，3(21)MH t =-．综合①、②、③，s 222MN MH NH ==+所以当t ＝1时，甲、乙两人的最小距离为12千米．例3：在Rt △ABC 中，∠ACB ＝90°，BC ＝30，AB ＝50．点P 是AB 边上任意一点，直线PE ⊥AB ，与边AC 或BC 相交于E ．点M 在线段AP 上，点N 在线段BP 上，EM ＝EN ，12sin 13EMP ∠=． （1）如图1，当点E 与点C 重合时，求CM 的长；（2）如图2，当点E 在边AC 上时，点E 不与点A 、C 重合，设AP ＝x ，BN ＝y ，求y 关于x 的函数关系式，并写出函数的定义域；（3）若△AME ∽△ENB （△AME 的顶点A 、M 、E 分别与△ENB 的顶点E 、N 、B 对应），求AP 的长．图1 图2 备用图思路点拨1．本题不难找到解题思路，难在运算相当繁琐．反复解直角三角形，注意对应关系．2．备用图暗示了第（3）题要分类讨论，点E 在BC 上的图形画在备用图中．3．第（3）题当E 在BC 上时，重新设BP ＝m 可以使得运算简便一些．满分解答（1）在Rt △ABC 中，BC ＝30，AB ＝50，所以AC ＝40，3sin 5A ∠=，3tan 4A ∠=． 在Rt △ACP 中，3sin 40245CP AC A =⋅∠=⨯=． 在Rt △CMP 中，因为12sin 13CP CMP CM ∠==，所以131324261212CM CP ==⨯=． （2）在Rt △AEP 中，3tan 4EP AP A x =⋅∠=． 在Rt △E MP 中，因为12sin 13EP EMP EM ∠==，所以12tan 5EP EMP MP ∠==． 因此55351212416MP EP x x ==⨯=，13133131212416EM EP x x ==⨯=． 已知EM ＝EN ，PE ⊥AB ，所以MP ＝NP 516x =． 于是52150501616y BN AB AP NP x x x ==--=--=-． 定义域为0＜x ＜32．（3）①如图3，当E 在AC 上时，由AM EN ME NB =，得51316161321501616x x x x x -=-． 解得x ＝AP ＝22．②如图4，当E 在BC 上时，设BP ＝m ，那么AP ＝50－m ．在Rt △BEP 中，43EP m =． 在Rt △EMP 中，5545121239MP EP m m ==⨯=，131313412129EM EP m m ==⨯=．所以514505099AM AB BP MP m m m =--=--=-，54599BN BP NP m m m =-=-=． 这时由AM EN ME NB =，得1413509913499m m m m -=．解得m ＝BP ＝8．所以AP ＝50－m ＝42． 图3 图4 图5考点伸展如果第（3）题没有条件“△AME 的顶点A 、M 、E 分别与△ENB 的顶点E 、N 、B 对应”，那么还存在图5所示的一种情况，∠EAM ＝∠EBN ，此时PE 垂直平分AB ，AP ＝25．由面积产生的函数关系问题例1：如图1，抛物线213922y x x =--与x 轴交于A 、B 两点，与y 轴交于点C ，联结BC 、AC ．（1）求AB 和OC 的长；（2）点E 从点A 出发，沿x 轴向点B 运动（点E 与点A 、B 不重合），过点E 作BC 的平行线交AC 于点D ．设AE 的长为m ，△ADE 的面积为s ，求s 关于m 的函数关系式，并写出自变量m 的取值范围；（3）在（2）的条件下，联结CE ，求△CDE 面积的最大值；此时，求出以点E 为圆心，与BC 相切的圆的面积（结果保留π）．图1思路点拨1．△ADE 与△ACB 相似，面积比等于对应边的比的平方．2．△CDE 与△ADE 是同高三角形，面积比等于对应底边的比．满分解答（1）由21319(3)(6)222y x x x x =--=+-，得A (－3,0)、B (6,0)、C (0,－9)． 所以AB ＝9，OC ＝9．（2）如图2，因为DE //CB ，所以△ADE ∽△ACB ．所以2()ADE ACB S AE S AB ∆∆=． 而18122ACB S AB OC ∆=⋅=，AE ＝m ， 所以222811()()922ADE ACB AE m s S S m AB ∆∆==⨯=⨯=． m 的取值范围是0＜m ＜9． 图2 图3（3）如图2，因为DE //CB ，所以9CD BE m AD AE m-==． 因为△CDE 与△ADE 是同高三角形，所以9CDE ADE S CD m S AD m ∆∆-==．所以22291191981()222228CDE m S m m m m m ∆-=⨯=-+=--+． 当92m =时，△CDE 的面积最大，最大值为818． 此时E 是AB 的中点，92BE =． 如图3，作EH ⊥CB ，垂足为H ．在Rt △BOC 中，OB ＝6，OC ＝9，所以sinB ==在Rt △BEH 中，9sin 2EH BE B =⋅==． 当⊙E 与BC 相切时，r EH =．所以272952S r ππ==． 考点伸展在本题中，△CDE 与△BEC 能否相似？如图2，虽然∠CED ＝∠BCE ，但是∠B ＞∠BCA ≥∠ECD ，所以△CDE 与△BEC 不能相似．例2：如图1，图2，在△ABC 中，AB ＝13，BC ＝14，5cos 13ABC ∠=． 探究 如图1，AH ⊥BC 于点H ，则AH ＝_____，AC ＝______，△ABC 的面积S △ABC ＝________．拓展 如图2，点D 在AC 上（可与点A 、C 重合），分别过点A 、C 作直线BD 的垂线，垂足为E 、F ．设BD ＝x ，AE ＝m ，CF ＝n ．（当点D 与点A 重合时，我们认为S △ABD ＝0）（1）用含x ，m 或n 的代数式表示S △ABD 及S △CBD ；（2）求(m ＋n )与x 的函数关系式，并求(m ＋n )的最大值和最小值；（3）对给定的一个x 值，有时只能确定唯一的点D ，指出这样的x 的取值范围． 发现 请你确定一条直线，使得A 、B 、C 三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值．图1 图2 动感体验动点D 由A 向C 运动，观察(m ＋n )随x 变化的图象，可以体验到，D 到达G 之前，(m ＋n )的值越来越大；D 经过G 之后，(m ＋n )的值越来越小．观察圆与线段AC 的交点情况，可以体验到，当D 运动到G 时（如图3），或者点A 在圆的内部时（如图4），圆与线段AC 只有唯一的交点D ．图3 图4拓展 （1）S △ABD ＝12mx ，S △CBD ＝12nx ． （2）由S △ABC ＝S △ABD ＋S △CBD ，得118422mx nx +=．所以168m n x+=． 由于AC 边上的高565BG =，所以x 的取值范围是565≤x ≤14．所以(m ＋n )的最大值为15，最小值为12．（3）x 的取值范围是x ＝565或13＜x ≤14． 发现 A 、B 、C 三点到直线AC 的距离之和最小，最小值为565． 例3：如图1，在Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6，点P 在AB 上，AP ＝2．点E 、F 同时从点P 出发，分别沿P A 、PB 以每秒1个单位长度的速度向点A 、B 匀速运动，点E 到达点A 后立刻以原速度沿AB 向点B 运动，点F 运动到点B 时停止，点E 也随之停止．在点E 、F 运动过程中，以EF 为边作正方形EFGH ，使它与△ABC 在线段AB 的同侧．设E 、F 运动的时间为t 秒(t ＞0)，正方形EFGH 与△ABC 重叠部分的面积为S ．（1）当t ＝1时，正方形EFGH 的边长是________；当t ＝3时，正方形EFGH 的边长是________；（2）当1＜t ≤2时，求S 与t 的函数关系式；（3）直接答出：在整个运动过程中，当t 为何值时，S 最大？最大面积是多少？图1思路点拨 1．全程运动时间为8秒，最好的建议就是在每秒钟选择一个位置画8个图形，这叫做磨刀不误砍柴工．2．这道题目的运算太繁琐了，如果你的思路是对的，就坚定地、仔细地运算，否则放弃也是一种好的选择．满分解答（1）当t ＝1时，EF ＝2；当t ＝3时，EF ＝4．（2）①如图1，当6011t ＜≤时，2EF t =．所以24S t =． ②如图2，当66115t ＜≤时，2EF EH t ==，2AE t =-，33(2)44NE AE t ==-． 于是31132(2)442NH EH NE t t t =-=--=-， 所以22221132511343422422S t t t t ⎛⎫=--=-+- ⎪⎝⎭． ③如图3，当625t ＜≤时，4EF =，2AE t =-，2AF t =+． 所以2233388AFM AEN S S S AF AE t =-=-=△△． 图2 图3 图4（3）如图4，图5，图6，图7，重叠部分的最大面积是图6所示的六边形EFNDQN ，S 的最大值为110275，此时14625t =． 图5 图6 图7 考点伸展第（2）题中t 的临界时刻是这样求的：如图8，当H 落在AC 上时，2AE t =-，2EH EF t ==，由2324t t =-，得611t =．如图9，当G 落在AC 上时，2AF t =+，2GF EF t ==，由2324t t =+，得65t =． 图8 图9例4：如图1，在平面直角坐标系中，四边形OABC 是平行四边形．直线l 经过O 、C 两点，点A 的坐标为(8，0)，点B 的坐标为(11，4)，动点P 在线段OA 上从O 出发以每秒1个单位的速度向点A 运动，同时动点Q 从点A 出发以每秒2个单位的速度沿A→B→C 的方向向点C 运动，过点P 作PM 垂直于x 轴，与折线O —C —B 相交于点M ．当P 、Q 两点中有一点到达终点时，另一点也随之停止运动，设点P 、Q 运动的时间为t 秒（t ＞0），△MPQ 的面积为S ．（1）点C 的坐标为____________，直线l 的解析式为____________；（2）试求点Q 与点M 相遇前S 与t 的函数关系式，并写出相应的t 的取值范围．（3）试求题（2）中当t 为何值时，S 的值最大？最大值是多少？图1 思路点拨1．用含有t 的式子表示线段的长，是解题的关键．2．第（2）题求S 与t 的函数关系式，容易忽略M 在OC 上、Q 在BC 上的情况．3．第（2）题建立在第（2）题的基础上，应用性质判断图象的最高点，运算比较繁琐． 满分解答（1）点C 的坐标为(3，4)，直线l 的解析式为43y x =． （2）①当M 在OC 上，Q 在AB 上时，502t ＜≤． 在Rt △OPM 中，OP ＝t ，4tan 3OMP ∠=，所以43PM t =． 在Rt △AQE 中，AQ ＝2t ，3cos 5QAE ∠=，所以65AE t =． 于是618855PE t t t =+-=+．因此212162153S PE PM t t =⋅=+． ②当M 在OC 上，Q 在BC 上时，532t ＜≤． 因为25BQ t =-，所以11(25)163PF t t t =---=-． 因此2132223S PF PM t t =⋅=-+． ③当M 、Q 相遇时，根据P 、Q 的路程和2115t t +=+，解得163t =． 因此当M 、Q 都在BC 上，相遇前，1633t ＜≤，PM ＝4，162163MQ t t t =--=-． 所以16322S MQ PM t =⋅=-+． 图2 图3 图4（3）①当502t ＜≤时，222162160(20)153153S t t t =+=+-． 因为抛物线开口向上，在对称轴右侧，S 随t 的增大而增大，所以当52t=时，S最大，最大值为856．②当532t＜≤时，2232812822()339S t t t=-+=--+．因为抛物线开口向下，所以当83t=时，S最大，最大值为1289．③当1633t＜≤时，16322S MQ PM t=⋅=-+．因为S随t的增大而减小，所以当3t=时，S最大，最大值为14．综上所述，当83t=时，S最大，最大值为1289．考点伸展第（2）题中，M、Q从相遇到运动结束，S关于t的函数关系式是怎样的？此时161332t＜≤，216316MQ t t t=+-=-．因此16322S MQ PM t=⋅=-．图5例6：如图1，矩形ABCD中，AB＝6，BC＝23，点O是AB的中点，点P在AB的延长线上，且BP＝3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点出发，以每秒1个单位长度的速度沿射线P A匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线P A的同侧．设运动的时间为t秒（t≥0）．（1）当等边△EFG的边FG恰好经过点C时，求运动时间t的值；（2）在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请直接写出S与t之间的函数关系式和相应的自变量t的取值范围；（3）设EG与矩形ABCD的对角线AC的交点为H，是否存在这样的t，使△AOH是等腰三角形？若存在，求出对应的t的值；若不存在，请说明理由．图1思路点拨1．运动全程6秒钟，每秒钟选择一个点F画对应的等边三角形EFG，思路和思想以及分类的标准尽在图形中．2．用t表示OE、AE、EF、AH的长，都和点E折返前后相关，分两种情况．3．探求等腰三角形AOH，先按顶点分三种情况，再按点E折返前后分两种情况．4．本题运算量很大，多用到1∶2∶3，注意对应关系不要错乱．满分解答（1）在Rt△ABC中，233 tanBCBACAB∠===，所以∠BAC＝30°．如图2，当等边△EFG 的边FG 恰好经过点C 时，在Rt △BCF 中，∠BFC ＝60°，BC =所以BF ＝2．因此PF ＝3－2＝1，运动时间t ＝1． 图2（2）①如图3，当0≤t ＜1时，重叠部分为直角梯形BCNE ，S =+．②如图4，当1≤t ＜3时，重叠部分为五边形BQMNE ，2S =++③如图5，当3≤t ＜4时，重叠部分为梯形FMNE ，S =-+④如图6，当4≤t ＜6时，重叠部分为等边三角形EFG ，26)S t =-．图3 图4 图5（3）等腰△AOH 分三种情况：①AO ＝AH ，②OA ＝OH ，③HA ＝HO ．在△AOH 中，∠A ＝30°为定值，AO ＝3为定值，AH 是变化的．△AEH 的形状保持不变，AH ．当E 由O 向A 运动时，AE ＝3－t ；当E 经A 折返后，AE ＝t －3．图6 图7 图8①当AO ＝AH )3t -=，得3t =-（如图7）；3)3t -=，得3t =+8）．②当OA ＝OH 时，∠AOH ＝120°，点O 与点E 重合，t ＝0（如图9）．③当HA ＝HO 时，H 在AE 的垂直平分线上，AO AH ＝3AE ．解3(3)3t -=，得t ＝2（如图10）；解3(3)3t -=，得t ＝4（如图11）．图9 图10 图11考点伸展图3，图4中，点E 向A 运动，EF ＝6；图5，图6中，点E 折返，EF ＝12－2t ．。
2019年湖南省中考数学真题精选分类汇编：压轴题(含答案解析)
2019年湖南省各市中考数学真题精选汇编压轴题：1-16页2019年湖南省各市中考数学真题精选压轴题剖析：17-79页一．选择题（共10小题）1．（2019•长沙）如图，△ABC中，AB＝AC＝10，tan A＝2，BE⊥AC于点E，D是线段BE 上的一个动点，则CD+BD的最小值是（）A．2B．4C．5D．10 2．（2019•永州）若关于x的不等式组有解，则在其解集中，整数的个数不可能是（）A．1B．2C．3D．4 3．（2019•衡阳）如图，在直角三角形ABC中，∠C＝90°，AC＝BC，E是AB的中点，过点E作AC和BC的垂线，垂足分别为点D和点F，四边形CDEF沿着CA方向匀速运动，点C与点A重合时停止运动，设运动时间为t，运动过程中四边形CDEF与△ABC的重叠部分面积为S．则S关于t的函数图象大致为（）A．B．C．D．4．（2019•娄底）如图，在单位长度为1米的平面直角坐标系中，曲线是由半径为2米，圆心角为120°的多次复制并首尾连接而成．现有一点P从A（A为坐标原点）出发，以每秒π米的速度沿曲线向右运动，则在第2019秒时点P的纵坐标为（）A．﹣2B．﹣1C．0D．1 5．（2019•湘潭）现代互联网技术的广泛应用，催生了快递行业的高速发展．据调查，湘潭某家小型快递公司的分拣工小李和小江，在分拣同一类物件时，小李分拣120个物件所用的时间与小江分拣90个物件所用的时间相同，已知小李每小时比小江多分拣20个物件．若设小江每小时分拣x个物件，则可列方程为（）A．＝B．＝C．＝D．＝6．（2019•株洲）从﹣1，1，2，4四个数中任取两个不同的数（记作a k，b k）构成一个数组M K＝{a k，b k}（其中k＝1，2…S，且将{a k，b k}与{b k，a k}视为同一个数组），若满足：对于任意的M i＝{a i，b i}和M j＝{a j，b j}（i≠j，1≤i≤S，1≤j≤S）都有a i+b i≠a j+b j，则S的最大值（）A．10B．6C．5D．4 7．（2019•岳阳）对于一个函数，自变量x取a时，函数值y也等于a，我们称a为这个函数的不动点．如果二次函数y＝x2+2x+c有两个相异的不动点x1、x2，且x1＜1＜x2，则c 的取值范围是（）A．c＜﹣3B．c＜﹣2C．c＜D．c＜1 8．（2019•邵阳）某出租车起步价所包含的路程为0～2km，超过2km的部分按每千米另收费．津津乘坐这种出租车走了7km，付了16元；盼盼乘坐这种出租车走了13km，付了28元．设这种出租车的起步价为x元，超过2km后每千米收费y元，则下列方程正确的是（）A．B．C．D．9．（2019•常德）观察下列等式：70＝1，71＝7，72＝49，73＝343，74＝2401，75＝16807，…，根据其中的规律可得70+71+72+…+72019的结果的个位数字是（）A．0B．1C．7D．8 10．（2019•郴州）我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的三角形，如图所示，已知∠A＝90°，BD＝4，CF＝6，则正方形ADOF 的边长是（）A．B．2C．D．4二．填空题（共10小题）11．（2019•长沙）如图，函数y＝（k为常数，k＞0）的图象与过原点的O的直线相交于A，B两点，点M是第一象限内双曲线上的动点（点M在点A的左侧），直线AM分别交x轴，y轴于C，D两点，连接BM分别交x轴，y轴于点E，F．现有以下四个结论：①△ODM与△OCA的面积相等；②若BM⊥AM于点M，则∠MBA＝30°；③若M点的横坐标为1，△OAM为等边三角形，则k＝2+；④若MF＝MB，则MD＝2MA．其中正确的结论的序号是．（只填序号）12．（2019•永州）我们知道，很多数学知识相互之间都是有联系的．如图，图一是“杨辉三角”数阵，其规律是：从第三行起，每行两端的数都是“1”，其余各数都等于该数“两肩”上的数之和；图二是二项和的乘方（a+b）n的展开式（按b的升幂排列）．经观察：图二中某个二项和的乘方的展开式中，各项的系数与图一中某行的数一一对应，且这种关系可一直对应下去．将（s+x）15的展开式按x的升幂排列得：（s+x）15＝a0+a1x+a2x2+…+a15x15．依上述规律，解决下列问题：（1）若s＝1，则a2＝；（2）若s＝2，则a0+a1+a2+…+a15＝．13．（2019•衡阳）在平面直角坐标系中，抛物线y＝x2的图象如图所示．已知A点坐标为（1，1），过点A作AA1∥x轴交抛物线于点A1，过点A1作A1A2∥OA交抛物线于点A2，过点A2作A2A3∥x轴交抛物线于点A3，过点A3作A3A4∥OA交抛物线于点A4……，依次进行下去，则点A2019的坐标为．14．（2019•娄底）已知点P（x0，y0）到直线y＝kx+b的距离可表示为d＝，例如：点（0，1）到直线y＝2x+6的距离d＝＝．据此进一步可得两条平行线y＝x和y＝x﹣4之间的距离为．15．（2019•湘潭）《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章计算弧田面积所用的经验公式是：弧田面积＝（弦×矢+矢2）．孤田是由圆弧和其所对的弦围成（如图中的阴影部分），公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，运用垂径定理（当半径OC⊥弦AB时，OC平分AB）可以求解．现已知弦AB＝8米，半径等于5米的弧田，按照上述公式计算出弧田的面积为平方米．16．（2019•株洲）如图所示，在平面直角坐标系xOy中，在直线x＝1处放置反光镜Ⅰ，在y轴处放置一个有缺口的挡板Ⅱ，缺口为线段AB，其中点A（0，1），点B在点A上方，且AB＝1，在直线x＝﹣1处放置一个挡板Ⅲ，从点O发出的光线经反光镜Ⅰ反射后，通过缺口AB照射在挡板Ⅲ上，则落在挡板Ⅲ上的光线的长度为．17．（2019•岳阳）如图，AB为⊙O的直径，点P为AB延长线上的一点，过点P作⊙O的切线PE，切点为M，过A、B两点分别作PE的垂线AC、BD，垂足分别为C、D，连接AM，则下列结论正确的是．（写出所有正确结论的序号）①AM平分∠CAB；②AM2＝AC•AB；③若AB＝4，∠APE＝30°，则的长为；④若AC＝3，BD＝1，则有CM＝DM＝．18．（2019•邵阳）如图，将等边△AOB放在平面直角坐标系中，点A的坐标为（0，4），点B在第一象限，将等边△AOB绕点O顺时针旋转180°得到△A′OB′，则点B′的坐标是．19．（2019•常德）规定：如果一个四边形有一组对边平行，一组邻边相等，那么称此四边形为广义菱形．根据规定判断下面四个结论：①正方形和菱形都是广义菱形；②平行四边形是广义菱形；③对角线互相垂直，且两组邻边分别相等的四边形是广义菱形；④若M、N的坐标分别为（0，1），（0，﹣1），P是二次函数y＝x2的图象上在第一象限内的任意一点，PQ垂直直线y＝﹣1于点Q，则四边形PMNQ是广义菱形．其中正确的是．（填序号）20．（2019•郴州）如图，点A，C分别是正比例函数y＝x的图象与反比例函数y＝的图象的交点，过A点作AD⊥x轴于点D，过C点作CB⊥x轴于点B，则四边形ABCD的面积为．三．解答题（共19小题）21．（2019•长沙）已知抛物线y＝﹣2x2+（b﹣2）x+（c﹣2020）（b，c为常数）．（1）若抛物线的顶点坐标为（1，1），求b，c的值；（2）若抛物线上始终存在不重合的两点关于原点对称，求c的取值范围；（3）在（1）的条件下，存在正实数m，n（m＜n），当m≤x≤n时，恰好≤≤，求m，n的值．22．（2019•长沙）如图，抛物线y＝ax2+6ax（a为常数，a＞0）与x轴交于O，A两点，点B为抛物线的顶点，点D的坐标为（t，0）（﹣3＜t＜0），连接BD并延长与过O，A，B 三点的⊙P相交于点C．（1）求点A的坐标；（2）过点C作⊙P的切线CE交x轴于点E．①如图1，求证：CE＝DE；②如图2，连接AC，BE，BO，当a＝，∠CAE＝∠OBE时，求﹣的值．23．（2019•永州）某种机器使用若干年后即被淘汰，该机器有一易损零件，为调查该易损零件的使用情况，随机抽取了100台已被淘汰的这种机器，经统计：每台机器在使用期内更换的该易损零件数均只有8，9，10，11这四种情况，并整理了这100台机器在使用期内更换的该易损零件数，绘制成如图所示不完整的条形统计图．（1）请补全该条形统计图；（2）某公司计划购买一台这种机器以及若干个该易损零件，用上述100台机器更换的该易损零件数的频率代替一台机器更换的该易损零件数发生的概率．①求这台机器在使用期内共更换了9个该易损零件的概率；②若在购买机器的同时购买该易损零件，则每个200元；若在使用过程中，因备用该易损零件不足，再购买，则每个500元．请你帮该公司用花在该易损零件上的费用的加权平均数进行决策：购买机器的同时应购买几个该易损零件，可使公司的花费最少？24．（2019•永州）（1）如图1，在平行四边形ABCD中，∠A＝30°，AB＝6，AD＝8，将平行四边形ABCD分割成两部分，然后拼成一个矩形，请画出拼成的矩形，并说明矩形的长和宽．（保留分割线的痕迹）（2）若将一边长为1的正方形按如图2﹣1所示剪开，恰好能拼成如图2﹣2所示的矩形，则m的值是多少？（3）四边形ABCD是一个长为7，宽为5的矩形（面积为35），若把它按如图3﹣1所示的方式剪开，分成四部分，重新拼成如图3﹣2所示的图形，得到一个长为9，宽为4的矩形（面积为36）．问：重新拼成的图形的面积为什么会增加？请说明理由．25．（2019•衡阳）如图，二次函数y＝x2+bx+c的图象与x轴交于点A（﹣1，0）和点B（3，0），与y轴交于点N，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接CP，过点P作CP的垂线与y轴交于点E．（1）求该抛物线的函数关系表达式；（2）当点P在线段OB（点P不与O、B重合）上运动至何处时，线段OE的长有最大值？并求出这个最大值；（3）在第四象限的抛物线上任取一点M，连接MN、MB．请问：△MBN的面积是否存在最大值？若存在，求出此时点M的坐标；若不存在，请说明理由．26．（2019•衡阳）如图，在等边△ABC中，AB＝6cm，动点P从点A出发以1cm/s的速度沿AB匀速运动．动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动，当点P到达点B时，点P、Q同时停止运动．设运动时间为t（s）．过点P作PE⊥AC于E，连接PQ交AC边于D．以CQ、CE为边作平行四边形CQFE．（1）当t为何值时，△BPQ为直角三角形；（2）是否存在某一时刻t，使点F在∠ABC的平分线上？若存在，求出t的值，若不存在，请说明理由；（3）求DE的长；（4）取线段BC的中点M，连接PM，将△BPM沿直线PM翻折，得△B′PM，连接AB′，当t为何值时，AB'的值最小？并求出最小值．27．（2019•娄底）如图，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA（不包括端点）上运动，且满足AE＝CG，AH＝CF．（1）求证：△AEH≌△CGF；（2）试判断四边形EFGH的形状，并说明理由．（3）请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系，并说明理由．28．（2019•娄底）如图，抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），点B（3，0），与y轴交于点C，且过点D（2，﹣3）．点P、Q是抛物线y＝ax2+bx+c上的动点．（1）求抛物线的解析式；（2）当点P在直线OD下方时，求△POD面积的最大值．（3）直线OQ与线段BC相交于点E，当△OBE与△ABC相似时，求点Q的坐标．29．（2019•湘潭）如图一，抛物线y＝ax2+bx+c过A（﹣1，0）B（3.0）、C（0，）三点（1）求该抛物线的解析式；（2）P（x1，y1）、Q（4，y2）两点均在该抛物线上，若y1≥y2，求P点横坐标x1的取值范围；（3）如图二，过点C作x轴的平行线交抛物线于点E，该抛物线的对称轴与x轴交于点D，连结CD、CB，点F为线段CB的中点，点M、N分别为直线CD和CE上的动点，求△FMN周长的最小值．30．（2019•湘潭）如图一，在射线DE的一侧以AD为一条边作矩形ABCD，AD＝5，CD ＝5，点M是线段AC上一动点（不与点A重合），连结BM，过点M作BM的垂线交射线DE于点N，连接BN．（1）求∠CAD的大小；（2）问题探究：动点M在运动的过程中，①是否能使△AMN为等腰三角形，如果能，求出线段MC的长度；如果不能，请说明理由．②∠MBN的大小是否改变？若不改变，请求出∠MBN的大小；若改变，请说明理由．（3）问题解决：如图二，当动点M运动到AC的中点时，AM与BN的交点为F，MN的中点为H，求线段FH的长度．31．（2019•株洲）四边形ABCD是⊙O的圆内接四边形，线段AB是⊙O的直径，连结AC、BD．点H是线段BD上的一点，连结AH、CH，且∠ACH＝∠CBD，AD＝CH，BA的延长线与CD的延长线相交于点P．（1）求证：四边形ADCH是平行四边形；（2）若AC＝BC，PB＝PD，AB+CD＝2（+1）①求证：△DHC为等腰直角三角形；②求CH的长度．32．（2019•株洲）已知二次函数y＝ax2+bx+c（a＞0）（1）若a＝1，b＝﹣2，c＝﹣1①求该二次函数图象的顶点坐标；②定义：对于二次函数y＝px2+qx+r（p≠0），满足方程y＝x的x的值叫做该二次函数的“不动点”．求证：二次函数y＝ax2+bx+c有两个不同的“不动点”．（2）设b＝c3，如图所示，在平面直角坐标系Oxy中，二次函数y＝ax2+bx+c的图象与x轴分别相交于不同的两点A（x1，0），B（x2，0），其中x1＜0，x2＞0，与y轴相交于点C，连结BC，点D在y轴的正半轴上，且OC＝OD，又点E的坐标为（1，0），过点D作垂直于y轴的直线与直线CE相交于点F，满足∠AFC＝∠ABC．F A的延长线与BC的延长线相交于点P，若＝，求二次函数的表达式．33．（2019•岳阳）操作体验：如图，在矩形ABCD中，点E、F分别在边AD、BC上，将矩形ABCD沿直线EF折叠，使点D恰好与点B重合，点C落在点C′处．点P为直线EF 上一动点（不与E、F重合），过点P分别作直线BE、BF的垂线，垂足分别为点M和N，以PM、PN为邻边构造平行四边形PMQN．（1）如图1，求证：BE＝BF；（2）特例感知：如图2，若DE＝5，CF＝2，当点P在线段EF上运动时，求平行四边形PMQN的周长；（3）类比探究：若DE＝a，CF＝b．①如图3，当点P在线段EF的延长线上运动时，试用含a、b的式子表示QM与QN之间的数量关系，并证明；②如图4，当点P在线段FE的延长线上运动时，请直接用含a、b的式子表示QM与QN之间的数量关系．（不要求写证明过程）34．（2019•邵阳）如图1，已知⊙O外一点P向⊙O作切线P A，点A为切点，连接PO并延长交⊙O于点B，连接AO并延长交⊙O于点C，过点C作CD⊥PB，分别交PB于点E，交⊙O于点D，连接AD．（1）求证：△APO～△DCA；（2）如图2，当AD＝AO时①求∠P的度数；②连接AB，在⊙O上是否存在点Q使得四边形APQB是菱形．若存在，请直接写出的值；若不存在，请说明理由．35．（2019•邵阳）如图，二次函数y＝﹣x2+bx+c的图象过原点，与x轴的另一个交点为（8，0）（1）求该二次函数的解析式；（2）在x轴上方作x轴的平行线y1＝m，交二次函数图象于A、B两点，过A、B两点分别作x轴的垂线，垂足分别为点D、点C．当矩形ABCD为正方形时，求m的值；（3）在（2）的条件下，动点P从点A出发沿射线AB以每秒1个单位长度匀速运动，同时动点Q以相同的速度从点A出发沿线段AD匀速运动，到达点D时立即原速返回，当动点Q返回到点A时，P、Q两点同时停止运动，设运动时间为t秒（t＞0）．过点P 向x轴作垂线，交抛物线于点E，交直线AC于点F，问：以A、E、F、Q四点为顶点构成的四边形能否是平行四边形．若能，请求出t的值；若不能，请说明理由．36．（2019•常德）如图，已知二次函数图象的顶点坐标为A（1，4），与坐标轴交于B、C、D三点，且B点的坐标为（﹣1，0）．（1）求二次函数的解析式；（2）在二次函数图象位于x轴上方部分有两个动点M、N，且点N在点M的左侧，过M、N作x轴的垂线交x轴于点G、H两点，当四边形MNHG为矩形时，求该矩形周长的最大值；（3）当矩形MNHG的周长最大时，能否在二次函数图象上找到一点P，使△PNC的面积是矩形MNHG面积的？若存在，求出该点的横坐标；若不存在，请说明理由．37．（2019•常德）在等腰三角形△ABC中，AB＝AC，作CM⊥AB交AB于点M，BN⊥AC 交AC于点N．（1）在图1中，求证：△BMC≌△CNB；（2）在图2中的线段CB上取一动点P，过P作PE∥AB交CM于点E，作PF∥AC交BN于点F，求证：PE+PF＝BM；（3）在图3中动点P在线段CB的延长线上，类似（2）过P作PE∥AB交CM的延长线于点E，作PF∥AC交NB的延长线于点F，求证：AM•PF+OM•BN＝AM•PE．38．（2019•郴州）如图1，矩形ABCD中，点E为AB边上的动点（不与A，B重合），把△ADE沿DE翻折，点A的对应点为A1，延长EA1交直线DC于点F，再把∠BEF折叠，使点B的对应点B1落在EF上，折痕EH交直线BC于点H．（1）求证：△A1DE∽△B1EH；（2）如图2，直线MN是矩形ABCD的对称轴，若点A1恰好落在直线MN上，试判断△DEF的形状，并说明理由；（3）如图3，在（2）的条件下，点G为△DEF内一点，且∠DGF＝150°，试探究DG，EG，FG的数量关系．39．（2019•郴州）已知抛物线y＝ax2+bx+3与x轴分别交于A（﹣3，0），B（1，0）两点，与y轴交于点C．（1）求抛物线的表达式及顶点D的坐标；（2）点F是线段AD上一个动点．①如图1，设k＝，当k为何值时，CF＝AD？②如图2，以A，F，O为顶点的三角形是否与△ABC相似？若相似，求出点F的坐标；若不相似，请说明理由．2019年湖南省中考数学真题精选分类汇编：压轴题（含答案解析）参考答案与试题解析一．选择题（共10小题）1．（2019•长沙）如图，△ABC中，AB＝AC＝10，tan A＝2，BE⊥AC于点E，D是线段BE 上的一个动点，则CD+BD的最小值是（）A．2B．4C．5D．10【分析】如图，作DH⊥AB于H，CM⊥AB于M．由tan A＝＝2，设AE＝a，BE＝2a，利用勾股定理构建方程求出a，再证明DH＝BD，推出CD+BD＝CD+DH，由垂线段最短即可解决问题．【解答】解：如图，作DH⊥AB于H，CM⊥AB于M．∵BE⊥AC，∴∠AEB＝90°，∵tan A＝＝2，设AE＝a，BE＝2a，则有：100＝a2+4a2，∴a2＝20，∴a＝2或﹣2（舍弃），∴BE＝2a＝4，∵AB＝AC，BE⊥AC，CM⊥AB，∴CM＝BE＝4（等腰三角形两腰上的高相等））∵∠DBH＝∠ABE，∠BHD＝∠BEA，∴sin∠DBH＝＝＝，∴DH＝BD，∴CD+BD＝CD+DH，∴CD+DH≥CM，∴CD+BD≥4，∴CD+BD的最小值为4．方法二：作CM⊥AB于M，交BE于点D，则点D满足题意．通过三角形相似或三角函数证得BD＝DM，从而得到CD+BD＝CM＝4．故选：B．【点评】本题考查解直角三角形，等腰三角形的性质，垂线段最短等知识，解题的关键是学会添加常用辅助线，用转化的思想思考问题，属于中考常考题型．2．（2019•永州）若关于x的不等式组有解，则在其解集中，整数的个数不可能是（）A．1B．2C．3D．4【分析】先分别求出每一个不等式的解集，再根据不等式组有解，求出m＜4，然后分别取m＝2，0，﹣1，得出整数解的个数，即可求解．【解答】解：解不等式2x﹣6+m＜0，得：x＜，解不等式4x﹣m＞0，得：x＞，∵不等式组有解，∴＜，解得m＜4，如果m＝2，则不等式组的解集为＜x＜2，整数解为x＝1，有1个；如果m＝0，则不等式组的解集为0＜x＜3，整数解为x＝1，2，有2个；如果m＝﹣1，则不等式组的解集为﹣＜x＜，整数解为x＝0，1，2，3，有4个．故选：C．【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．3．（2019•衡阳）如图，在直角三角形ABC中，∠C＝90°，AC＝BC，E是AB的中点，过点E作AC和BC的垂线，垂足分别为点D和点F，四边形CDEF沿着CA方向匀速运动，点C与点A重合时停止运动，设运动时间为t，运动过程中四边形CDEF与△ABC的重叠部分面积为S．则S关于t的函数图象大致为（）A．B．C．D．【分析】根据已知条件得到△ABC是等腰直角三角形，推出四边形EFCD是正方形，设正方形的边长为a，当移动的距离＜a时，如图1S＝正方形的面积﹣△EE′H的面积＝a2﹣t2；当移动的距离＞a时，如图2，S＝S△AC′H＝（2a﹣t）2＝t2﹣2at+2a2，根据函数关系式即可得到结论；【解答】解：∵在直角三角形ABC中，∠C＝90°，AC＝BC，∴△ABC是等腰直角三角形，∵EF⊥BC，ED⊥AC，∴四边形EFCD是矩形，∵E是AB的中点，∴EF＝AC，DE＝BC，∴EF＝ED，∴四边形EFCD是正方形，设正方形的边长为a，如图1当移动的距离＜a时，S＝正方形的面积﹣△EE′H的面积＝a2﹣t2；当移动的距离＞a时，如图2，S＝S△AC′H＝（2a﹣t）2＝t2﹣2at+2a2，∴S关于t的函数图象大致为C选项，故选：C．【点评】本题考查动点问题的函数图象，正方形的性质、勾股定理等知识，解题的关键是读懂题意，学会分类讨论的思想，属于中考常考题型．4．（2019•娄底）如图，在单位长度为1米的平面直角坐标系中，曲线是由半径为2米，圆心角为120°的多次复制并首尾连接而成．现有一点P从A（A为坐标原点）出发，以每秒π米的速度沿曲线向右运动，则在第2019秒时点P的纵坐标为（）A．﹣2B．﹣1C．0D．1【分析】先计算点P走一个的时间，得到点P纵坐标的规律：以1，0，﹣1，0四个数为一个周期依次循环，再用2019÷4＝504…3，得出在第2019秒时点P的纵坐标为是﹣1．【解答】解：点运动一个用时为÷π＝2秒．如图，作CD⊥AB于D，与交于点E．在Rt△ACD中，∵∠ADC＝90°，∠ACD＝∠ACB＝60°，∴∠CAD＝30°，∴CD＝AC＝×2＝1，∴DE＝CE﹣CD＝2﹣1＝1，∴第1秒时点P运动到点E，纵坐标为1；第2秒时点P运动到点B，纵坐标为0；第3秒时点P运动到点F，纵坐标为﹣1；第4秒时点P运动到点G，纵坐标为0；第5秒时点P运动到点H，纵坐标为1；…，∴点P的纵坐标以1，0，﹣1，0四个数为一个周期依次循环，∵2019÷4＝504…3，∴第2019秒时点P的纵坐标为是﹣1．故选：B．【点评】本题考查了规律型中的点的坐标，解题的关键是找出点P纵坐标的规律：以1，0，﹣1，0四个数为一个周期依次循环．也考查了垂径定理．5．（2019•湘潭）现代互联网技术的广泛应用，催生了快递行业的高速发展．据调查，湘潭某家小型快递公司的分拣工小李和小江，在分拣同一类物件时，小李分拣120个物件所用的时间与小江分拣90个物件所用的时间相同，已知小李每小时比小江多分拣20个物件．若设小江每小时分拣x个物件，则可列方程为（）A．＝B．＝C．＝D．＝【分析】根据题意，可以列出相应的分式方程，本题得以解决．【解答】解：由题意可得，，故选：B．【点评】本题考查由实际问题抽象出分式方程，解答本题的关键是明确题意，列出相应的分式方程．6．（2019•株洲）从﹣1，1，2，4四个数中任取两个不同的数（记作a k，b k）构成一个数组M K＝{a k，b k}（其中k＝1，2…S，且将{a k，b k}与{b k，a k}视为同一个数组），若满足：对于任意的M i＝{a i，b i}和M j＝{a j，b j}（i≠j，1≤i≤S，1≤j≤S）都有a i+b i≠a j+b j，则S的最大值（）A．10B．6C．5D．4【分析】找出a i+b i的值，结合对于任意的M i＝{a i，b i}和M j＝{a i，b j}（i≠j，1≤i≤S，1≤j≤S）都有a i+b i≠a j+b j，即可得出S的最大值．【解答】解：∵﹣1+1＝0，﹣1+2＝1，﹣1+4＝3，1+2＝3，1+4＝5，2+4＝6，∴a i+b i共有5个不同的值．又∵对于任意的M i＝{a i，b i}和M j＝{a j，b j}（i≠j，1≤i≤S，1≤j≤S）都有a i+b i≠a j+b j，∴S的最大值为5．故选：C．【点评】本题考查了规律型：数字的变化类，找出a i+b i共有几个不同的值是解题的关键．7．（2019•岳阳）对于一个函数，自变量x取a时，函数值y也等于a，我们称a为这个函数的不动点．如果二次函数y＝x2+2x+c有两个相异的不动点x1、x2，且x1＜1＜x2，则c 的取值范围是（）A．c＜﹣3B．c＜﹣2C．c＜D．c＜1【分析】由函数的不动点概念得出x1、x2是方程x2+2x+c＝x的两个实数根，由x1＜1＜x2知△＞0且x＝1时y＜0，据此得，解之可得．【解答】解：由题意知二次函数y＝x2+2x+c有两个相异的不动点x1、x2是方程x2+2x+c ＝x的两个不相等实数根，且x1＜1＜x2，整理，得：x2+x+c＝0，由x2+x+c＝0有两个不相等的实数根，且x1＜1＜x2，知△＞0，令y＝x2+x+c，画出该二次函数的草图如下：则，解得c＜﹣2，故选：B．【点评】本题主要考查二次函数图象与系数的关系，解题的关键是理解并掌握不动点的概念，并据此得出关于c的不等式．8．（2019•邵阳）某出租车起步价所包含的路程为0～2km，超过2km的部分按每千米另收费．津津乘坐这种出租车走了7km，付了16元；盼盼乘坐这种出租车走了13km，付了28元．设这种出租车的起步价为x元，超过2km后每千米收费y元，则下列方程正确的是（）A．B．C．D．【分析】根据津津乘坐这种出租车走了7km，付了16元；盼盼乘坐这种出租车走了13km，付了28元可列方程组．【解答】解：设这种出租车的起步价为x元，超过2km后每千米收费y元，则所列方程组为，故选：D．【点评】本题主要考查由实际问题抽象出二元一次方程组，解题的关键是理解题意，找到题目蕴含的相等关系．9．（2019•常德）观察下列等式：70＝1，71＝7，72＝49，73＝343，74＝2401，75＝16807，…，根据其中的规律可得70+71+72+…+72019的结果的个位数字是（）A．0B．1C．7D．8【分析】首先得出尾数变化规律，进而得出70+71+72+…+72019的结果的个位数字．【解答】解：∵70＝1，71＝7，72＝49，73＝343，74＝2401，75＝16807，…，∴个位数4个数一循环，∴（2019+1）÷4＝505，∴1+7+9+3＝20，∴70+71+72+…+72019的结果的个位数字是：0．故选：A．【点评】此题主要考查了尾数特征，正确得出尾数变化规律是解题关键．10．（2019•郴州）我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的三角形，如图所示，已知∠A＝90°，BD＝4，CF＝6，则正方形ADOF 的边长是（）A．B．2C．D．4【分析】设正方形ADOF的边长为x，在直角三角形ACB中，利用勾股定理可建立关于x的方程，解方程即可．【解答】解：设正方形ADOF的边长为x，由题意得：BE＝BD＝4，CE＝CF＝6，∴BC＝BE+CE＝BD+CF＝10，在Rt△ABC中，AC2+AB2＝BC2，即（6+x）2+（x+4）2＝102，整理得，x2+10x﹣24＝0，解得：x＝2，或x＝﹣12（舍去），∴x＝2，即正方形ADOF的边长是2；故选：B．【点评】本题考查了正方形的性质、全等三角形的性质、一元二次方程的解法、勾股定理等知识；熟练掌握正方形的性质，由勾股定理得出方程是解题的关键．二．填空题（共10小题）11．（2019•长沙）如图，函数y＝（k为常数，k＞0）的图象与过原点的O的直线相交于A，B两点，点M是第一象限内双曲线上的动点（点M在点A的左侧），直线AM分别交x轴，y轴于C，D两点，连接BM分别交x轴，y轴于点E，F．现有以下四个结论：①△ODM与△OCA的面积相等；②若BM⊥AM于点M，则∠MBA＝30°；③若M点的横坐标为1，△OAM为等边三角形，则k＝2+；④若MF＝MB，则MD＝2MA．其中正确的结论的序号是①③④．（只填序号）【分析】①设点A（m，），M（n，），构建一次函数求出C，D坐标，利用三角形的面积公式计算即可判断．②△OMA不一定是等边三角形，故结论不一定成立．③设M（1，k），由△OAM为等边三角形，推出OA＝OM＝AM，可得1+k2＝m2+，推出m＝k，根据OM＝AM，构建方程求出k即可判断．④如图，作MK∥OD交OA于K．利用平行线分线段成比例定理解决问题即可．【解答】解：①设点A（m，），M（n，），则直线AC的解析式为y＝﹣x++，∴C（m+n，0），D（0，），∴S△ODM＝n×＝，S△OCA＝（m+n）×＝，∴△ODM与△OCA的面积相等，故①正确；∵反比例函数与正比例函数关于原点对称，∴O是AB的中点，∵BM⊥AM，∴OM＝OA，∴k＝mn，∴A（m，n），M（n，m），∴AM＝（n﹣m），OM＝，∴AM不一定等于OM，∴∠BAM不一定是60°，∴∠MBA不一定是30°．故②错误，∵M点的横坐标为1，∴可以假设M（1，k），∵△OAM为等边三角形，∴OA＝OM＝AM，1+k2＝m2+，∵m＞0，k＞0，∴m＝k，∵OM＝AM，∴（1﹣m）2+＝1+k2，∴k2﹣4k+1＝0，∴k＝2，∴k＝2+，故③正确，如图，作MK∥OD交OA于K．∵OF∥MK，∴＝＝，∴＝，∵OA＝OB，∴＝，∴＝，∵KM∥OD，∴＝＝2，∴DM＝2AM，故④正确．故答案为①③④．【点评】本题考查反比例函数与一次函数的交点问题，三角形的面积，平行线分线段成比例定理等知识，解题的关键是学会利用参数解决问题，学会构造平行线，利用平行线分线段成比例定理解决问题，属于中考填空题中的压轴题．12．（2019•永州）我们知道，很多数学知识相互之间都是有联系的．如图，图一是“杨辉三角”数阵，其规律是：从第三行起，每行两端的数都是“1”，其余各数都等于该数“两肩”上的数之和；图二是二项和的乘方（a+b）n的展开式（按b的升幂排列）．经观察：图二中某个二项和的乘方的展开式中，各项的系数与图一中某行的数一一对应，且这种关系可一直对应下去．将（s+x）15的展开式按x的升幂排列得：（s+x）15＝a0+a1x+a2x2+…依上述规律，解决下列问题：（1）若s＝1，则a2＝105；（2）若s＝2，则a0+a1+a2+…+a15＝315．【分析】（1）根据图形中的规律即可求出（1+x）15的展开式中第三项的系数为前14个数的和；（2）根据x的特殊值代入要解答，即把x＝1代入时，得到结论．【解答】解：（1）由图2知：（a+b）1的第三项系数为0，（a+b）2的第三项的系数为：1，（a+b）3的第三项的系数为：3＝1+2，（a+b）4的第三项的系数为：6＝1+2+3，…∴发现（1+x）3的第三项系数为：3＝1+2；（1+x）4的第三项系数为6＝1+2+3；（1+x）5的第三项系数为10＝1+2+3+4；不难发现（1+x）n的第三项系数为1+2+3+…+（n﹣2）+（n﹣1），∴s＝1，则a2＝1+2+3+…+14＝105．故答案为：105；（2）∵（s+x）15＝a0+a1x+a2x2+…+a15x15．当x＝1时，a0+a1+a2+…+a15＝（2+1）15＝315，故答案为：315．【点评】本题考查了完全平方式，也是数字类的规律题，首先根据图形中数字找出对应的规律，再表示展开式：对应（a+b）n中，相同字母a的指数是从高到低，相同字母b 的指数是从低到高．13．（2019•衡阳）在平面直角坐标系中，抛物线y＝x2的图象如图所示．已知A点坐标为（1，。
2019年中考数学压轴题 (1)
2019中考数学压轴题38．（2015三明）如图，已知点A 是双曲线2y x =在第一象限的分支上的一个动点，连接AO 并延长交另一分支于点B ，过点A 作y 轴的垂线，过点B 作x 轴的垂线，两垂线交于点C ，随着点A 的运动，点C 的位置也随之变化．设点C 的坐标为（m ，n ），则m ，n 满足的关系式为（ ）A ．2n m =-B ．2n m =-C ．4n m =-D ．4n m =-【答案】B ． 【解析】试题分析：∵点C 的坐标为（m ，n ），∴点A 的纵坐标是n ，横坐标是：2n ，∴点A 的坐标为（2n ，n ），∵点C 的坐标为（m ，n ），∴点B 的横坐标是m ，纵坐标是：2m ，∴点B 的坐标为（m ，2m ），又∵22n m mn =，∴22mn m n =⋅，∴224m n =，又∵m ＜0，n ＞0，∴2mn =-，∴2n m =-，故选B ．考点：反比例函数图象上点的坐标特征．39．（2015乌鲁木齐）如图，在直角坐标系xOy 中，点A ，B 分别在x 轴和y 轴，34OA OB =．∠AOB 的角平分线与OA 的垂直平分线交于点C ，与AB 交于点D ，反比例函数ky x =的图象过点C ．当以CD 为边的正方形的面积为27时，k 的值是（ ）A．2 B．3 C．5 D．7【答案】D．考点：1．反比例函数综合题；2．综合题；3．压轴题．40．（2015重庆市）如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为3，1．反比例函数3yx=的图象经过A，B两点，则菱形ABCD的面积为（）A．2 B．4 C．22．42【答案】D．【解析】试题分析：过点A作x轴的垂线，与CB的延长线交于点E，∵A，B两点在反比例函数3yx=的图象上且纵坐标分别为3，1，∴A ，B 横坐标分别为1，3，∴AE=2，BE=2，∴AB=22，S 菱形ABCD=底×高=22×2=42，故选D ．考点：1．菱形的性质；2．反比例函数图象上点的坐标特征；3．综合题． 41．（2015临沂）在平面直角坐标系中，直线2y x =-+与反比例函数1y x =的图象有唯一公共点，若直线y x b =-+与反比例函数1y x =的图象有2个公共点，则b 的取值范围是（ ）A ．b ＞2B ．﹣2＜b ＜2C ．b ＞2或b ＜﹣2D ．b ＜﹣2 【答案】C ．考点：反比例函数与一次函数的交点问题． 42．（2015滨州）如图，在x 轴的上方，直角∠BOA 绕原点O 按顺时针方向旋转，若∠BOA 的两边分别与函数1y x =-、2y x =的图象交于B 、A 两点，则∠OAB 的大小的变化趋势为（ ）A．逐渐变小 B．逐渐变大 C．时大时小 D．保持不变【答案】D．考点：1．相似三角形的判定与性质；2．反比例函数图象上点的坐标特征；3．综合题．二、填空题43．（2017云南省，第6题，3分）已知点A（a，b）在双曲线5yx=上，若a、b都是正整数，则图象经过B（a，0）、C（0，b）两点的一次函数的解析式（也称关系式）为．【答案】y=﹣5x+5或y=﹣15x+1．【分析】先根据反比例函数图象上点的坐标特征得出ab=5，由a、b都是正整数，得到a=1，b=5或a=5，b=1．再分两种情况进行讨论：当a=1，b=5；②a=5，b=1，利用待定系数法即可求解．【解析】∵点A（a，b）在双曲线5yx=上，∴ab=5，∵a、b都是正整数，∴a=1，b=5或a=5，b=1．设经过B（a，0）、C（0，b）两点的一次函数的解析式为y=mx+n．①当a=1，b=5时，由题意，得：5m nn+=⎧⎨=⎩，解得：55mn=-⎧⎨=⎩，∴y=﹣5x+5；②当a=5，b=1时，由题意，得：501m nn+=⎧⎨=⎩，解得：151mn⎧=-⎪⎨⎪=⎩，∴y=﹣15x+1．则所求解析式为y=﹣5x+5或y=﹣15x+1．故答案为：y=﹣5x+5或y=﹣15x+1．点睛：本题考查了反比例函数图象上点的坐标特征，待定系数法求一次函数的解析式．正确求出a、b 的值是解题的关键．考点：反比例函数图象上点的坐标特征；分类讨论．44．（2017内蒙古通辽市，第17题，3分）如图，直线333--=xy与x，y轴分别交于点A，B，与反比例函数xky=的图象在第二象限交于点C，过点A作x轴的垂线交该反比例函数图象于点D．若AD=AC，则点D的坐标为．【答案】（﹣3，3．【分析】过C作CE⊥x轴于E，求得A（﹣3，0），B（0，﹣3），解直角三角形得到∠OAB=30°，求得∠CAE=30°，设D（﹣3，3k-），得到AD=3k-，AC=3k-，于是得到C（33k-，6k-），列方程即可得到结论．【解析】过C作CE⊥x轴于E，∵直线333--=xy与x，y轴分别交于点A，B，∴A（﹣3，0），B （03，∴tan∠OAB=OBOA=3，∴∠OAB=30°，∴∠CAE=30°，设D（﹣3，3k-），∵AD⊥x轴，∴AD=3k-，∵AD=AC，∴AC=3k-，∴CE=6k-，AE=3k，∴C（33k，6k-），∵C在反比例函数x k y =的图象上，∴（336k -+）•（6k-）=k ，∴k=63-，∴D （﹣3，23），故答案为：（﹣3，23）．点睛：本题考查了反比例函数与一次函数的交点问题，解直角三角形，反比例函数图象上点的坐标特征，正确的点A 、B 、C 的坐标解题的关键． 考点：反比例函数与一次函数的交点问题． 45．（2017四川省成都市，第24题，4分）在平面直角坐标系xOy 中，对于不在坐标轴上的任意一点P （x ，y ），我们把点P （1x ，1y ），称为点P 的“倒影点”，直线1y x =-+ 上有两点A 、B ，它们的倒影点A ′，B ′均在反比例函数ky x =的图象上，若AB=22，则k= ．【答案】43-．【分析】设点A （a ，﹣a+1），B （b ，﹣b+1）（a ＜b ），则A′（1a ，11a -），B′（1b ，11b -），由AB=22可得出b=a+2，再根据反比例函数图象上点的坐标特征即可得出关于k 、a 、b 的方程组，解之即可得出k 值．【解析】设点A （a ，﹣a+1），B （b ，﹣b+1）（a ＜b ），则A′（1a ，11a -），B′（1b ，11b -），∵AB=22，∴b ﹣a=2，即b=a+2．∵点A′，B′均在反比例函数k y x =的图象上，∴211(1)(1)b a k a a b b =+⎧⎪⎨==⎪--⎩，解得：k=43-．故答案为：43-．点睛：本题考查了反比例函数图象上点的坐标特征、一次函数图象上点的坐标特征以及两点间的距离公式，根据反比例函数图象上点的坐标特征列出关于k 、a 、b 的方程组是解题的关键． 考点：反比例函数图象上点的坐标特征；一次函数图象上点的坐标特征．46．（2017山东省日照市，第16题，4分）如图，在平面直角坐标系中，经过点A 的双曲线ky x =（x＞0）同时经过点B ，且点A 在点B 的左侧，点A 2，∠AOB=∠OBA =45°，则k 的值为 ．．【答案】15【分析】过A作AM⊥y轴于M，过B作BD选择x轴于D，直线BD与AM交于点N，则OD=MN，DN=OM，∠AMO=∠BNA=90°，由等腰三角形的判定与性质得出OA=BA，∠OAB=90°，证出∠AOM=∠BAN，由AAS证明△AOM≌△BAN，得出AM=BN=2，OM=AN=2，求出B（2+2，2﹣2），得出方程（2+2）•（2﹣2）=k，解方程即可．点睛：本题考查了坐标与图形性质，全等三角形的判定与性质，等腰三角形的判定与性质等知识；本题综合性强，有一定难度．考点：反比例函数图象上点的坐标特征；综合题．47．（2017江苏省南通市，第18题，3分）如图，四边形OABC是平行四边形，点C在x轴上，反比例函数kyx=（x＞0）的图象经过点A（5，12），且与边BC交于点D．若AB=BD，则点D的坐标为．【答案】（8，15 2）．【分析】先根据点A（5，12），求得反比例函数的解析式为60yx=，可设D（m，60m），BC的解析式为y=125x+b，把D（m，60m）代入，可得b=60m﹣125m，进而得到BC的解析式为y=125x+60m﹣125m，据此可得OC=m﹣25m=AB，过D作DE⊥AB于E，过A作AF⊥OC于F，根据△DEB∽△AFO，可得DB=13﹣65m，最后根据AB=BD，得到方程m﹣25m=13﹣65m，进而求得D的坐标．【解析】∵反比例函数kyx=（x＞0）的图象经过点A（5，12），∴k=12×5=60，∴反比例函数的解析式为60yx=，设D（m，60m），由题可得OA的解析式为y=125x，AO∥BC，∴可设BC的解析式为y=125x+b，把D（m，60m）代入，可得125m+b=60m，∴b=60m﹣125m，∴BC的解析式为y=125x+60m﹣125m，令y=0，则x=m﹣25m，即OC=m﹣25m，∴平行四边形ABCO中，AB=m﹣25m，如图所示，过D作DE⊥AB于E，过A作AF⊥OC于F，则△DEB∽△AFO，∴DB AODE AF=，而AF=12，DE=12﹣60m，22512+ =13，∴DB=13﹣65m，∵AB=DB，∴m﹣25m=13﹣65m，解得m1=5，m2=8，又∵D在A的右侧，即m＞5，∴m=8，∴D的坐标为（8，152）．故答案为：（8，152）．点睛：本题主要考查了反比例函数图象上点的坐标特征以及平行四边形的性质的运用，解决问题的关键是作辅助线构造相似三角形，依据平行四边形的对边相等以及相似三角形的对应边成比例进行计算，解题时注意方程思想的运用．考点：反比例函数图象上点的坐标特征；平行四边形的性质；方程思想；综合题． 48．（2017江苏省宿迁市，第16题，3分）如图，矩形ABOC 的顶点O 在坐标原点，顶点B ，C 分别在x ，y 轴的正半轴上，顶点A 在反比例函数ky x =（k 为常数，k ＞0，x ＞0）的图象上，将矩形ABOC 绕点A 按逆时针方向旋转90°得到矩形AB′O′C′，若点O 的对应点O′恰好落在此反比例函数图象上，则C OBO 的值是 ．【答案】51-．【分析】设A （m ，n ），则OB=m ，OC=n ，根据旋转的性质得到O′C′=n，B′O′=m，于是得到O′（m+n ，n ﹣m ），于是得到方程（m+n ）（n ﹣m ）=mn ，求得512m n =，（负值舍去），即可得到结论．【解析】设A （m ，n ），则OB=m ，OC=n ，∵矩形ABOC 绕点A 按逆时针反向旋转90°得到矩形AB′O′C′，∴O′C′=n，B′O′=m，∴O′（m+n ，n ﹣m ），∵A ，O′在此反比例函数图象上，∴（m+n ）（n ﹣m ）=mn ，∴m2+mn ﹣n2=0，∴m=152-n ，∴512m n =，（负值舍去），∴C OBO 的值是512，故答案为：512．点睛：本题考查了坐标与图形变化﹣旋转，反比例函数图象上点的坐标特征，正确的理解题意是解题的关键．考点：坐标与图形变化﹣旋转；反比例函数图象上点的坐标特征；矩形的性质． 49．（2017江苏省常州市，第18题，2分）如图，已知点A 是一次函数12y x=（x ≥0）图象上一点，过点A作x轴的垂线l，B是l上一点（B在A上方），在AB的右侧以AB为斜边作等腰直角三角形ABC，反比例函数kyx=（x＞0）的图象过点B，C，若△OAB的面积为6，则△ABC的面积是．【答案】3．【分析】作辅助线，构建直角三角形，设AB=2a，根据直角三角形斜边中线是斜边一半得：BE=AE=CE=a，设A（x，12x），则B（x，kx），C（x+a，kx a+），因为B、C都在反比例函数的图象上，列方程组可得结论．【解析】如图，过C作CD⊥y轴于D，交AB于E，∵AB⊥x轴，∴CD⊥AB，∵△ABC是等腰直角三角形，∴BE=AE=CE，设AB=2a，则BE=AE=CE=a，设A（x，12x），则B B（x，kx），C（x+a，kx a+），∴11262212212OABS AB DE a xka xxka xa x∆⎧=⋅=⨯⨯=⎪⎪⎪=+⎨⎪⎪=+⎪+⎩①②③，由①得：ax=6，由②得：2k=4ax+x2，由③得：2k=2a（a+x）+x （a+x），2a2+2ax+ax+x2=4ax+x2，2a2=ax=6，a2=3，∵S△ABC=12AB•CE=12•2a•a=a2=3．故答案为：3．点睛：本题考查了反比例函数图象上点的坐标特征、等腰直角三角形的性质、三角形面积，熟练掌握反比例函数上的点符合反比例函数的关系式是关键．考点：反比例函数系数k的几何意义；反比例函数图象上点的坐标特征；等腰直角三角形；反比例函数综合题．50．（2017江苏省盐城市，第16题，3分）如图，曲线l是由函数6yx=在第一象限内的图象绕坐标原点O逆时针旋转45°得到的，过点A（42-，42），B（22，22）的直线与曲线l相交于点M、N，则△OMN的面积为．【答案】8．【分析】由题意A（42-，42），B（22，22），可知OA⊥OB，建立如图新的坐标系（OB为x′轴，OA为y′轴，利用方程组求出M、N的坐标，根据S△OMN=S△OBM﹣S△OBN计算即可．【解析】∵A（42-，42），B（22，22），∴OA⊥OB，建立如图新的坐标系（OB为x′轴，OA 为y′轴．在新的坐标系中，A（0，8），B（4，0），∴直线AB解析式为y′=﹣2x′+8，由'2'86''y xyx=-+⎧⎪⎨=⎪⎩，解得'1'6xy=⎧⎨=⎩或'3'2xy=⎧⎨=⎩，∴M（1.6），N（3，2），∴S△OMN=S△OBM﹣S△OBN=12×46﹣12×42=8，故答案为：8．点睛：本题考查坐标与图形的性质、反比例函数的性质等知识，解题的关键是学会建立新的坐标系解决问题，属于中考填空题中的压轴题．考点：坐标与图形变化﹣旋转；反比例函数系数k的几何意义．51．（2017江苏省连云港市，第15题，3分）设函数3yx=与y=﹣2x﹣6的图象的交点坐标为（a，b），则12a b+的值是．【答案】﹣2．【分析】由两函数的交点坐标为（a，b），将x=a，y=b代入反比例解析式，求出ab的值，代入一次函数解析式，得出2a+b的值，将所求式子通分并利用同分母分式的加法法则计算后，把ab及2a+b 的值代入即可求出值．点睛：此题考查了反比例函数与一次函数的交点问题，其中将x=a，y=b代入两函数解析式得出关于a 与b的关系式是解本题的关键．考点：反比例函数与一次函数的交点问题．52．（2017江苏省连云港市，第16题，3分）如图，已知等边三角形OAB与反比例函数kyx=（k＞0，x＞0）的图象交于A、B两点，将△OAB沿直线OB翻折，得到△OCB，点A的对应点为点C，线段CB交x轴于点D，则BDDC的值为．（已知sin15°=62-）【答案】31 2．【分析】作辅助线，构建直角三角形，根据反比例函数的对称性可知：直线y=x，求出∠BOF=15°，根据15°的正弦列式可以表示BF的长，证明△BDF∽△CDN，可得结论．【解析】如图，过O作OM⊥x轴于M，∵△AOB是等边三角形，∴AM=BM，∠AOM=∠BOM=30°，∴A、B关于直线OM对称，∵A、B两点在反比例函数kyx=（k＞0，x＞0）的图象上，且反比例函数关于直线y=x对称，∴直线OM的解析式为：y=x，∴∠BOD=45°﹣30°=15°，过B作BF⊥x轴于F，过C作CN⊥x轴于N，sin∠BOD=sin15°=BFOB=62-，∵∠BOC=60°，∠BOD=15°，∴∠CON=45°，∴△CNO是等腰直角三角形，∴CN=ON，设CN=x，则OC=2x，∴OB=2x，∴2x =62-，∴BF=(31)2x-，∵BF⊥x轴，CN⊥x轴，∴BF∥CN，∴△BDF∽△CDN，∴BD BFCD CN==(31)2xx-=312-，故答案为：312-．点睛：本题考查了反比例函数与一次函数的交点问题、等边三角形的性质、等腰直角三角形的性质和判定、三角函数、三角形相似的性质和判定、翻折的性质，明确反比例函数关于直线y=x对称是关键，在数学题中常设等腰直角三角形的直角边为未知数x，2倍表示斜边的长，从而解决问题．考点：反比例函数与一次函数的交点问题；等边三角形的性质；翻折变换（折叠问题）；解直角三角形．53．（2017浙江省宁波市，第17题，4分）已知△ABC的三个顶点为A（﹣1，﹣1），B（﹣1，3），C（﹣3，﹣3），将△ABC向右平移m（m＞0）个单位后，△ABC某一边的中点恰好落在反比例函数3 yx =的图象上，则m的值为．【答案】4或1 2．【分析】求得三角形三边中点的坐标，然后根据平移规律可得AB边的中点（﹣1，1），BC边的中点（﹣2，0），AC边的中点（﹣2，﹣2），然后分两种情况进行讨论：一是AB边的中点在反比例函数3yx=的图象上，二是AC边的中点在反比例函数3yx=的图象上，进而算出m的值．【解析】∵△ABC的三个顶点为A（﹣1，﹣1），B（﹣1，3），C（﹣3，﹣3），∴AB边的中点（﹣1，1），BC边的中点（﹣2，0），AC边的中点（﹣2，﹣2），∵将△ABC向右平移m（m＞0）个单位后，∴AB边的中点平移后的坐标为（﹣1+m，1），AC边的中点平移后的坐标为（﹣2+m，﹣2）．∵△ABC某一边的中点恰好落在反比例函数3yx=的图象上，∴﹣1+m=3或﹣2×（﹣2+m）=3，∴m=4或m=12．故答案为：4或12．点睛：此题主要考查了反比例函数图象上点的坐标特点，关键是掌握反比例函数图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．考点：反比例函数图象上点的坐标特征；坐标与图形变化﹣平移；分类讨论．54．（2017浙江省温州市，第15题，5分）如图，矩形OABC的边OA，OC分别在x轴、y轴上，点B 在第一象限，点D在边BC上，且∠AOD=30°，四边形OA′B′D与四边形OABD关于直线OD对称（点A′和A，B′和B分别对应）．若AB=1，反比例函数kyx=（k≠0）的图象恰好经过点A′，B，则k的值为．【答案】43．【分析】设B（m，1），得到OA=BC=m，根据轴对称的性质得到OA′=OA=m，∠A′OD=∠AOD=30°，求得∠A′OA=60°，过A′作A′E⊥OA于E，解直角三角形得到A′（12m，32m），列方程即可得到结论．【解析】∵四边形ABCO是矩形，AB=1，∴设B（m，1），∴OA=BC=m，∵四边形OA′B′D与四边形OABD 关于直线OD对称，∴OA′=OA=m，∠A′OD=∠AOD=30°，∴∠A′OA=60°，过A′作A′E⊥OA于E，∴OE=12m，A′E=3m，∴A′（12m，3m），∵反比例函数kyx=（k≠0）的图象恰好经过点A′，B，∴12m•3m=m，∴m=43，∴k=43．故答案为：43．点睛：本题考查了反比例函数图象上点的坐标特征，矩形的性质，轴对称的性质，解直角三角形，正确的作出辅助线是解题的关键．考点：反比例函数图象上点的坐标特征；矩形的性质；轴对称的性质；综合题．55．（2017浙江省湖州市，第16题，4分）如图，在平面直角坐标系xOy中，已知直线y=kx（k＞0）分别交反比例函数1yx=和9yx=在第一象限的图象于点A，B，过点B作 BD⊥x轴于点D，交1yx=的图象于点C，连结AC．若△ABC是等腰三角形，则k的值是．【答案】k=377或155．【分析】根据一次函数和反比例函数的解析式，即可求得点A、B、C的坐标（用k表示），再讨论①AB=BC，②AC=BC，即可解题．点睛：本题考查了点的坐标的计算，考查了一次函数和反比例函数交点的计算，本题中用k表示点A、B、C坐标是解题的关键．考点：反比例函数与一次函数的交点问题；等腰三角形的性质；分类讨论；综合题．56．（2017金华，第15题，4分）如图，已知点A （2，3）和点B （0，2），点A 在反比例函数ky x =的图象上，做射线AB ，再将射线AB 绕点A 按逆时针方向旋转45°，交反比例函数图象于点C ，则点C 的坐标为 ．【答案】（﹣1，﹣6）．【分析】先过A 作AE ⊥x 轴于E ，以AE 为边在AE 的左侧作正方形AEFG ，交AB 于P ，根据直线AB 的解析式为122y x =+，可得PF=32，将△AGP 绕点A 逆时针旋转90°得△AEH ，构造△ADP ≌△ADH ，再设DE=x ，则DH=DP=x+32，FD=1+2﹣x=3﹣x ，在Rt △PDF 中，根据PF2+DF2=PD2，可得方程22233()(3)()22x x +-=+，进而得到D （1，0），即可得出直线AD 的解析式为y=3x ﹣3，最后解方程组即可得到D 点坐标．【解析】如图所示，过A 作AE ⊥x 轴于E ，以AE 为边在AE 的左侧作正方形AEFG ，交AB 于P ，根据点A （2，3）和点B （0，2），可得直线AB 的解析式为122y x =+，由A （2，3），可得OF=1，当x=﹣1时，y=﹣12+2=32，即P （﹣1，32），∴PF=32，将△AGP 绕点A 逆时针旋转90°得△AEH ，则△ADP ≌△ADH ，∴PD=HD ，PG=EH=32，设DE=x ，则DH=DP=x+32，FD=1+2﹣x=3﹣x ，Rt △PDF 中，PF2+DF2=PD2，即22233()(3)()22x x +-=+，解得x=1，∴OD=2﹣1=1，即D （1，0），根据点A （2，3）和点D （1，0），可得直线AD 的解析式为y=3x ﹣3，解方程组：336y x y x =-⎧⎪⎨=⎪⎩，可得：23x y =⎧⎨=⎩或16x y =-⎧⎨=-⎩，∴C （﹣1，﹣6），故答案为：（﹣1，﹣6）．点睛：本题主要考查了反比例函数与一次函数图象交点问题，以及反比例函数图象上点的坐标特征的运用，解决问题的关键是作辅助线构造正方形以及全等三角形，依据勾股定理列方程进行求解．考点：坐标与图形变化﹣旋转；反比例函数图象上点的坐标特征；反比例函数与一次函数的交点问题；综合题．57．（2017湖北省孝感市，第16题，3分）如图，在平面直角坐标系中，OA=AB，∠OAB=90°，反比例函数kyx=（x＞0）的图象经过A，B两点．若点A的坐标为（n，1），则k的值为．【答案】512-．【分析】作AE⊥x轴于E，BF⊥x轴于F，过B点作BC⊥y轴于C，交AE于G，则AG⊥BC，先求得△AOE≌△BAG，得出AG=OE=n，BG=AE=1，从而求得B（n+1，1﹣n），根据k=n×1=（n+1）（1﹣n）得出方程，解方程即可．【解析】作AE⊥x轴于E，BF⊥x轴于F，过B点作BC⊥y轴于C，交AE于G，如图所示：则AG⊥BC，∵∠OAB=90°，∴∠OAE+∠BAG=90°，∵∠OAE+∠AOE=90°，∴∠AOE=∠GAB，在△AOE 和△BAG中，∵∠AOE=∠GAB，∠AOE=∠AGB，AO=AB，∴△AOE≌△BAG（AAS），∴OE=AG，AE=BG，∵点A（n，1），∴AG=OE=n，BG=AE=1，∴B（n+1，1﹣n），∴k=n×1=（n+1）（1﹣n），整理得：n2+n﹣1=0，解得：n=152-±（负值舍去），∴n=512-，∴k=512-；故答案为：512-．点睛：本题考查了全等三角形的判定与性质、反比例函数图象上点的坐标特征、解方程等知识；熟练掌握反比例函数图象上点的坐标特征，证明三角形全等是解决问题的关键．考点：反比例函数图象上点的坐标特征；全等三角形的判定与性质．58．（2017湖北省荆州市，第18题，3分）如图，在平面直角坐标系中，矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上，点B在第二象限．将矩形OABC绕点O顺时针旋转，使点B落在y轴上，得到矩形ODEF，BC与OD相交于点M．若经过点M的反比例函数kyx=（x＜0）的图象交AB于点N，S矩形OABC=32，tan∠DOE=12，则BN的长为．【答案】3．【分析】利用矩形的面积公式得到AB•BC=32，再根据旋转的性质得AB=DE，OD=OA，接着利用正切的定义得到an∠DOE=DEOD=12，所以DE•2DE=32，解得DE=4，于是得到AB=4，OA=8，同样在Rt△OCM中利用正切定义得到MC=2，则M（﹣2，4），易得反比例函数解析式为8yx=-，然后确定N点坐标，最后计算BN的长．【解析】∵S矩形OABC=32，∴AB•BC=32，∵矩形OABC绕点O顺时针旋转，使点B落在y轴上，得到矩形ODEF，∴AB=DE，OD=OA，在Rt△ODE中，tan∠DOE=DEOD=12，即OD=2DE，∴DE•2DE=32，解得DE=4，∴AB=4，OA=8，在Rt△OCM中，∵tan∠COM=MCOC=12，而OC=AB=4，∴MC=2，∴M（﹣2，4），把M（﹣2，4）代入kyx=得k=﹣2×4=﹣8，∴反比例函数解析式为8yx=-，当x=﹣8时，88y=--=1，则N（﹣8，1），∴BN=4﹣1=3．故答案为：3．点睛：本题考查了旋转图形的坐标：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．也考查了反比例函数图象上点的坐标特征和解直角三角形．考点：坐标与图形变化﹣旋转；反比例函数系数k的几何意义；解直角三角形；综合题．59．（2017湖北省鄂州市，第15题，3分）如图，AC⊥x轴于点A，点B在y轴的正半轴上，∠ABC=60°，AB=4，BC=3D为AC与反比例函数kyx=的图象的交点．若直线BD将△ABC的面积分成1：2的两部分，则k的值为．【答案】﹣4或﹣8．【分析】过C作CE⊥AB于E，根据∠ABC=60°，AB=4，BC=23，可求得△ABC的面积，再根据点D将线段AC分成1：2的两部分，分两种情况进行讨论，根据反比例函数系数k的几何意义即可得到k 的值．点睛：本题主要考查了反比例函数与一次函数交点问题，以及反比例函数系数k的几何意义的运用．过反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是12 |k|，且保持不变．解题时注意分类思想的运用．考点：反比例函数与一次函数的交点问题；数形结合；分类讨论．60．（2017湖南省株洲市，第17题，3分）如图所示是一块含30°，60°，90°的直角三角板，直角顶点O位于坐标原点，斜边AB垂直于x轴，顶点A在函数11kyx=（x＞0）的图象上，顶点B在函数22kyx=（x＞0）的图象上，∠ABO=30°，则12kk= ．【答案】13-．【分析】设AC=a ，则OA=2a ，OC=3a ，根据直角三角形30°角的性质和勾股定理分别计算点A 和B 的坐标，写出A 和B 两点的坐标，代入解析式求出k1和k2的值，相比即可．【解析】如图，Rt △AOB 中，∠B=30°，∠AOB=90°，∴∠OAC=60°，∵AB ⊥OC ，∴∠ACO=90°，∴∠AOC=30°，设AC=a ，则OA=2a ，OC=3a ，∴A （3a ，a ），∵A 在函数11k y x =（x ＞0）的图象上，∴k1=3a•a=23a ，Rt △BOC 中，OB=2OC=23a ，∴BC=22OB OC -=3a ，∴B （3a ，﹣3a ），∵B在函数22k y x =（x ＞0）的图象上，∴k2=﹣3a 3a=233a -，∴12k k =13-；故答案为：13-．点睛：本题考查了反比例函数图象上点的特征、直角三角形30°的性质，熟练掌握直角三角形30°角所对的直角边是斜边的一半，正确写出A 、B 两点的坐标是关键． 考点：反比例函数图象上点的坐标特征；综合题．61．（2017贵州省遵义市，第18题，4分）如图，点E ，F 在函数2y x =的图象上，直线EF 分别与x轴、y 轴交于点A 、B ，且BE ：BF=1：3，则△EOF 的面积是 ．【答案】8 3．【分析】证明△BPE∽△BHF，利用相似比可得HF=4PE，根据反比例函数图象上点的坐标特征，设E点坐标为（t，2t），则F点的坐标为（3t，23t），由于S△OEF+S△OFD=S△OEC+S梯形ECDF，S△OFD=S△OEC=1，所以S△OEF=S梯形ECDF，然后根据梯形面积公式计算即可．【解析】作EP⊥y轴于P，EC⊥x轴于C，FD⊥x轴于D，FH⊥y轴于H，如图所示：∵EP⊥y轴，FH⊥y轴，∴EP∥FH，∴△BPE∽△BHF，∴13PE BEHF BF==，即HF=3PE，设E点坐标为（t，2t），则F点的坐标为（3t，23t），∵S△OEF+S△OFD=S△OEC+S梯形ECDF，而S△OFD=S△OEC=12×2=1，∴S△OEF=S梯形ECDF=12（23t+2t）（3t﹣t）=83；故答案为：83．点睛：本题考查了反比例函数的几何意义、相似三角形的判定与性质；掌握反比例函数图象上点的坐标特征、反比例函数的比例系数的几何意义，证明三角形相似是解决问题的关键．考点：反比例函数系数k的几何意义．62．（2017辽宁省盘锦市，第16题，3分）在平面直角坐标系中，点P的坐标为（0，﹣5），以P为圆心的圆与x轴相切，⊙P的弦AB（B点在A点右侧）垂直于y轴，且AB=8，反比例函数kyx=（k≠0）经过点B，则k= ．【答案】﹣8或﹣32．【分析】设AB交y轴于点C，利用垂径定理可求得PC的长，则可求得B点坐标，代入反比例函数解析式可求得k的值．【解析】设线段AB 交y 轴于点C ，当点C 在点P 的上方时，连接PB ，如图，∵⊙P 与x 轴相切，且P （0，﹣5），∴PB=PO=5，∵AB=8，∴BC=4，在Rt △PBC 中，由勾股定理可得PC=22PB BC - =3，∴OC=OP ﹣PC=5﹣3=2，∴B 点坐标为（4，﹣2），∵反比例函数ky x =（k ≠0）经过点B ，∴k=4×（﹣2）=﹣8；当点C 在点P 下方时，同理可求得PC=3，则OC=OP+PC=8，∴B （4，﹣8），∴k=4×（﹣8）=﹣32； 综上可知k 的值为﹣8或﹣32，故答案为：﹣8或﹣32．点睛：本题主要考查切线的性质及反比例函数图象上点的坐标特征，利用垂径定理和切线的性质求得PC 的长是解题的关键，注意分两种情况．考点：反比例函数图象上点的坐标特征；切线的性质；分类讨论． 63．（2017黑龙江省齐齐哈尔市，第18题，3分）如图，菱形OABC 的一边OA 在x 轴的负半轴上，O是坐标原点，tan ∠AOC=43，反比例函数ky x =的图象经过点C ，与AB 交于点D ，若△COD 的面积为20，则k 的值等于 ．【答案】﹣24．【分析】易证S 菱形ABCO=2S △CDO ，再根据tan ∠AOC 的值即可求得菱形的边长，即可求得点C 的坐标，代入反比例函数即可解题．【解析】作DE ∥AO ，CF ⊥AO ，设CF=4x ，∵四边形OABC 为菱形，∴AB ∥CO ，AO ∥BC ，∵DE ∥AO ，∴S △ADO=S △DEO ，同理S △BCD=S △CDE ，∵S 菱形ABCO=S △ADO+S △DEO+S △BCD+S △CDE ，∴S 菱形ABCO=2（S △DEO+S △CDE ）=2S △CDO=40，∵tan ∠AOC=43，∴OF=3x ，∴22OF CF +，∴OA=OC=5x ，∵S 菱形ABCO=AO•CF=20x2，解得：2，∴OF=32CF=42C 坐标为（﹣3242），∵反比例函数ky x =的图象经过点C ，∴代入点C 得：k=﹣24，故答案为：﹣24．点睛：本题考查了菱形的性质，考查了菱形面积的计算，本题中求得S菱形ABCO=2S△CDO是解题的关键．考点：反比例函数系数k的几何意义；反比例函数图象上点的坐标特征；菱形的性质；解直角三角形；综合题．64．（2017山东省济南市，第20题，3分）如图，过点O的直线AB与反比例函数kyx=的图象交于A，B两点，A（2，1），直线BC∥y轴，与反比例函数3kyx-=（x＜0）的图象交于点C，连接AC，则△ABC的面积为．【答案】8．【分析】由A（2，1）求得两个反比例函数分别为2yx=，6yx-=，与AB的解析式y=12x，解方程组求得B的坐标，进而求得C点的纵坐标，即可求得BC，根据三角形的面积公式即可求得结论．点睛：本题主要考查了反比例函数于一次函数的交点问题，三角形的面积，正确的理解题意是解题的关键．考点：反比例函数与一次函数的交点问题；反比例函数及其应用．65．（2017山东省莱芜市，第15题，4分）直线y=kx+b与双曲线6 yx =-交于A（﹣3，m），B（n，﹣6）两点，将直线y=kx+b向上平移8个单位长度后，与双曲线交于D，E两点，则S△ADE= ．【答案】16．【分析】利用待定系数法求出平移后的直线的解析式，求出点D、E的左边，再利用分割法求出三角形的面积即可．【解析】由题意A（﹣3，2），B（1，﹣6），∵直线y=kx+b经过点A（﹣3，2），B（1，﹣6），∴326k bk b-+=⎧⎨+=-⎩，解得：24kb=-⎧⎨=-⎩，∴y=﹣2x﹣4，向上平移8个单位得到直线y=﹣2x+4，由624yxy x⎧=-⎪⎨⎪=-+⎩，解得：32xy=⎧⎨=-⎩和16xy=-⎧⎨=⎩，不妨设D（3，﹣2），E（﹣1，6），∴S△ADE=6×8﹣12×4×2﹣12×6×4﹣12×8×4=16，故答案为：16．点睛：本题考查反比例函数与一次函数的交点问题，解题的关键是熟练掌握待定系数法，学会利用分割法求三角形的面积．考点：反比例函数与一次函数的交点问题；一次函数图象与几何变换．66．（2016云南省昆明市）如图，反比例函数kyx=（k≠0）的图象经过A，B两点，过点A作AC⊥x 轴，垂足为C，过点B作BD⊥x轴，垂足为D，连接AO，连接BO交AC于点E，若OC=CD，四边形BDCE 的面积为2，则k的值为．【答案】163-．【分析】先设点B坐标为（a，b），根据平行线分线段成比例定理，求得梯形BDCE的上下底边长与高，再根据四边形BDCE的面积求得ab的值，最后计算k的值．【解析】设点B坐标为（a，b），则DO=﹣a，BD=b．∵AC⊥x轴，BD⊥x轴，∴BD∥AC．∵OC=CD，∴CE=12BD=12b，CD=12DO=12-a．∵四边形BDCE的面积为2，∴12（BD+CE）×CD=2，即12（b+12b）×（12-a）=2，∴ab=163-．将B（a，b）代入反比例函数kyx=（k≠0），得：k=ab=163-．故答案为：163-．考点：反比例函数系数k 的几何意义；平行线分线段成比例． 67．（2016内蒙古包头市）如图，在平面直角坐标系中，点A 在第二象限内，点B 在x 轴上，∠AOB=30°，AB=BO ，反比例函数ky x =（x ＜0）的图象经过点A ，若S △ABO=3，则k 的值为 ．【答案】33-．【分析】过点A 作AD ⊥x 轴于点D ，由∠AOB=30°可得出3AD OD=，由此可是点A 的坐标为（﹣3a ，3 a ），根据S △ABO=3结合三角形的面积公式可用a 表示出线段OB 的长，再由勾股定理可用含a的代数式表示出线段BD 的长，由此即可得出关于a 的无理方程，解方程即可得出结论．【解析】过点A 作AD ⊥x 轴于点D ，如图所示．∵∠AOB=30°，AD ⊥OD ，∴ADOD =tan ∠AOB=3，∴设点A 的坐标为（﹣3a 3）．∵S △ABO=123OB=2a ．在Rt △ADB 中，∠ADB=90°，AD=3a ，AB=OB=2a ，∴222BD AB AD =-=2243a a -，BD=2243a a -．∵OD=OB+BD=3a ，即222433a a a a =+-，解得：a=1或a=﹣1（舍去），∴点A 的坐标为（﹣3，3），∴k=﹣3×3=33-．故答案为：33-． 考点：反比例函数系数k 的几何意义． 68．（2016内蒙古呼和浩特市）已知函数1y x =-，当自变量的取值为﹣1＜x ＜0或x≥2，函数值y 的取值 ．【答案】y ＞1或12-≤y＜0．【分析】画出图形，先计算当x=﹣1和x=2时的对应点的坐标，并描出这两点，根据图象写出y 的取值．【解析】当x=﹣1时，y=11--=1，当x=2时，y=12-，由图象得：当﹣1＜x ＜0时，y ＞1，当x≥2时，12-≤y＜0，故答案为：y ＞1或12-≤y＜0．考点：反比例函数的性质．69．（2016四川省内江市）如图，点A 在双曲线5y x =上，点B 在双曲线8y x =上，且AB ∥x 轴，则△OAB 的面积等于 ．【答案】32．【分析】延长AB交y轴于点C，根据反比例函数系数的几何意义求出△BOC的面积与△AOC的面积，然后相减即可得解．【解析】延长AB交y轴于点C．S△OAC=12×5=52，S△OCB=12×8=4，则S△OAB=S△OCB﹣S△OAC=4﹣52=32．故答案为：32．考点：反比例函数系数k的几何意义．70．（2016四川省眉山市）如图，已知点A是双曲线6yx=在第三象限分支上的一个动点，连结AO 并延长交另一分支于点B，以AB为边作等边三角形ABC，点C在第四象限内，且随着点A的运动，点C的位置也在不断变化，但点C始终在双曲线kyx=上运动，则k的值是．【答案】36-【分析】根据反比例函数的性质得出OA=OB，连接OC，过点A作AE⊥y轴，垂足为E，过点C作CF⊥y轴，垂足为F，根据等边三角形的性质和解直角三角形求出3，求出△OFC∽△AEO，相似比OCOA3ΔOFCΔAEOSS=3，求出△OFC的面积，即可得出答案．。
2019中考数学压轴题分类复习之抛物线与三角形的综合问题
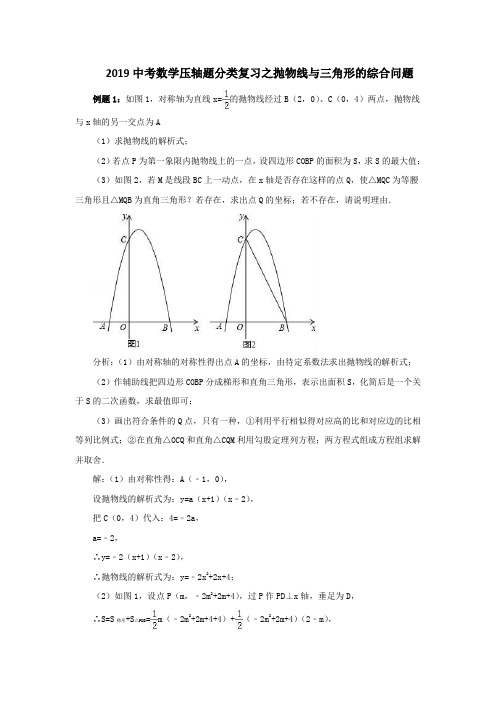
2019中考数学压轴题分类复习之抛物线与三角形的综合问题例题1：如图1，对称轴为直线x=的抛物线经过B（2，0）、C（0，4）两点，抛物线与x轴的另一交点为A（1）求抛物线的解析式；（2）若点P为第一象限内抛物线上的一点，设四边形COBP的面积为S，求S的最大值；（3）如图2，若M是线段BC上一动点，在x轴是否存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．分析：（1）由对称轴的对称性得出点A的坐标，由待定系数法求出抛物线的解析式；（2）作辅助线把四边形COBP分成梯形和直角三角形，表示出面积S，化简后是一个关于S的二次函数，求最值即可；（3）画出符合条件的Q点，只有一种，①利用平行相似得对应高的比和对应边的比相等列比例式；②在直角△OCQ和直角△CQM利用勾股定理列方程；两方程式组成方程组求解并取舍．解：（1）由对称性得：A（﹣1，0），设抛物线的解析式为：y=a（x+1）（x﹣2），把C（0，4）代入：4=﹣2a，a=﹣2，∴y=﹣2（x+1）（x﹣2），∴抛物线的解析式为：y=﹣2x2+2x+4；（2）如图1，设点P（m，﹣2m2+2m+4），过P作PD⊥x轴，垂足为D，∴S=S梯形+S△PDB=m（﹣2m2+2m+4+4）+（﹣2m2+2m+4）（2﹣m），S=﹣2m2+4m+4=﹣2（m﹣1）2+6，∵﹣2＜0，∴S有最大值，则S大=6；（3）如图2，存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形，理由是：设直线BC的解析式为：y=kx+b，把B（2，0）、C（0，4）代入得：，解得：，∴直线BC的解析式为：y=﹣2x+4，设M（a，﹣2a+4），过A作AE⊥BC，垂足为E，则AE的解析式为：y=x+，则直线BC与直线AE的交点E（1.4，1.2），设Q（﹣x，0）（x＞0），∵AE∥QM，∴△ABE∽△QBM，∴①，由勾股定理得：x2+42=2×[a2+（﹣2a+4﹣4）2]②，由①②得：a1=4（舍），a2=，当a=时，x=，∴Q（﹣，0）．同步练习：1.如图，已知二次函数y=﹣x2+bx+c（b，c为常数）的图象经过点A（3，1），点C（0，4），顶点为点M，过点A作AB∥x轴，交y轴于点D，交该二次函数图象于点B，连结BC．（1）求该二次函数的解析式及点M的坐标；（2）若将该二次函数图象向下平移m（m＞0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包括△ABC的边界），求m的取值范围；（3）点P是直线AC上的动点，若点P，点C，点M所构成的三角形与△BCD相似，请直接写出所有点P的坐标（直接写出结果，不必写解答过程）．。
中考压轴题二次函数与周长、面积综合题(解析版)
专题05 二次函数与周长、面积综合题1.（2019年湖北省黄石市中考数学试题）如图，已知抛物线经过点、.（1）求抛物线的解析式，并写出顶点的坐标；（2）若点在抛物线上，且点的横坐标为8，求四边形的面积（3）定点在轴上，若将抛物线的图象向左平移2各单位，再向上平移3个单位得到一条新的抛物线，点在新的抛物线上运动，求定点与动点之间距离的最小值（用含的代数式表示）【答案】（1），;（2）36;（3）【解析】【分析】（1）函数的表达式为：y=（x+1）（x-5），即可求解；（2）S四边形AMBC=AB（y C-y D），即可求解；（3）抛物线的表达式为：y=x2，即可求解．【详解】（1）函数的表达式为：y=（x+1）（x-5）=（x2-4x-5）=，点M坐标为（2，-3）；（2）当x=8时，y=（x+1）（x-5）=9，即点C（8，9），S四边形AMBC=AB（y C-y D）=×6×（9+3）=36；（3）y=（x+1）（x-5）=（x2-4x-5）=（x-2）2-3，抛物线的图象向左平移2个单位，再向上平移3个单位得到一条新的抛物线，则新抛物线表达式为：y=x2，则定点D 与动点P 之间距离PD =，∵＞0，PD 有最小值，当x 2=3m -时， PD 最小值d =．2.（2019年湖南省常德市中考数学试题）如图，已知二次函数图象的顶点坐标为(1,4)A ，与坐标轴交于B 、C 、D 三点，且B 点的坐标为(1,0)-． （1）求二次函数的解析式；（2）在二次函数图象位于x 轴上方部分有两个动点M 、N ，且点N 在点M左侧，过M 、N 作x 轴的垂线交x 轴于点G 、H 两点，当四边形MNHG 为矩形时，求该矩形周长的最大值； （3）当矩形MNHG 周长最大时，能否在二次函数图象上找到一点P ，使PNC ∆的面积是矩形MNHG 面积的916？若存在，求出该点的横坐标；若不存在，请说明理由．【答案】（1）2y x 2x 3=-++ （2）最大值为10（3）故点P 坐标为：315(,)24或或． 【解析】 【分析】（1）二次函数表达式为：()214y a x =-+，将点B 的坐标代入上式，即可求解；（2）矩形MNHG 的周长()()2222222223282C MN GM x x x x x =+=-+-++=-++，即可求解；（3）2711sin45822PNC S PK CD PH ∆==⨯⨯=⨯⨯︒⨯94PH HG ==，即可求解． 【详解】（1）二次函数表达式为：()214y a x =-+， 将点B 的坐标代入上式得：044a =+，解得：1a =-，的故函数表达式为：223y x x =-++…①；（2）设点M 的坐标为()2,23x x x -++，则点()22,23N x x x --++， 则222MN x x x =-+=-，223GM x x =-++，矩形MNHG 的周长()()2222222223282C MN GM x x x x x =+=-+-++=-++，∵20-<，故当22bx a=-=，C 有最大值，最大值为10， 此时2x =，点()0,3N 与点D 重合； （3）PNC ∆的面积是矩形MNHG 面积的916， 则99272316168PNCS MN GM ∆=⨯⨯=⨯⨯=， 连接DC ，在CD 得上下方等距离处作CD 的平行线m 、n ， 过点P 作y 轴的平行线交CD 、直线n 于点H 、G ，即PH GH =， 过点P 作PK CD ⊥于点K ，将()3,0C 、()0,3D 坐标代入一次函数表达式并解得： 直线CD 的表达式为：3y x =-+，OC OD =，∴45OCD ODC PHK ∠=∠=︒=∠，CD =设点()2,23P x x x -++，则点(),3H x x -+，2711sin45822PNC S PK CD PH ∆==⨯⨯=⨯⨯︒⨯ 解得：94PH HG ==，则292334PH x x x =-+++-=，解得：32x =，故点315,24P ⎛⎫⎪⎝⎭， 直线n 的表达式为：93344y x x =-+-=-+…②，联立①②并解得：32x ±=即点'P 、''P 的坐标分别为⎝⎭、⎝⎭；故点P 坐标为：315,24⎛⎫ ⎪⎝⎭或3324⎛+-- ⎝⎭或3324⎛--+ ⎝⎭． 【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．3．（2019年山东省烟台市中考）如图，顶点为M 的抛物线23y ax bx =++与x 轴交于(1,0)A -，B 两点，与y 轴交于点C ，过点C 作CD y ⊥轴交抛物线于另一点D ，作DE x ⊥轴，垂足为点E .双曲线6(0)y x x=>经过点D ，连接MD ，BD .(1)求抛物线的表达式；(2)点N ，F 分别是x 轴，y 轴上的两点，当以M ，D ，N ，F 为顶点的四边形周长最小时，求出点N ，F 的坐标；【答案】(1)2y x 2x 3=-++；(2)N 5,07⎛⎫ ⎪⎝⎭；F 50,3⎛⎫ ⎪⎝⎭； 【解析】 【分析】（1）先求D 的坐标，再代入二次函数解析式解析式求解；（2）分别作点M ，D 关于y 轴，x 轴的对称点M '，'D ，连接MD '交x 轴，y 轴于点N ，F .即M '，F ,N ，'D 在同一直线上时，四边形的周长最小，用待定系数法求直线MD '的表达式，再求N,F 的坐标； 【详解】解：(1)由题意，得点C 的坐标(0,3)，3OC =. ∵6k OC CD =⋅=， ∴2CD =.∴点D 的坐标(2,3).将点(1,0)A -，(2,3)D 分别代人抛物线23y ax bx =++，得30,423 3.a b a b -+=⎧⎨++=⎩解得1,2.a b =-⎧⎨=⎩∴抛物线的表达式为2y x 2x 3=-++.(2)分别作点M ，D 关于y 轴，x 轴的对称点M '，'D ， 连接MD '交x 轴，y 轴于点N ，F .由抛物线的表达式可知，顶点M 的坐标(1,4)， ∴点M 的坐标(1,4)-. 设直线MD '为y kx b =+， ∵点'D 的坐标(2,3)-， ∴4,2 3.k b k b -+=⎧⎨+=-⎩解得7,35.3a b ⎧=-⎪⎪⎨⎪=⎪⎩∴直线MD '的表达式为7533y x =-+. 令0y =，则75033x -+=，解得57x =，∴点N 的坐标5,07⎛⎫ ⎪⎝⎭.令0x =，则53y =，∴点F 的坐标50,3⎛⎫ ⎪⎝⎭.4．（广东省深圳市2019年中考数学试题）如图所示抛物线2y ax bx c =++过点()1,0A -，点()0,3C ，且OB OC =（1）求抛物线的解析式及其对称轴；（2）点,D E 在直线1x =上的两个动点，且1DE =，点D 在点E 的上方，求四边形ACDE 的周长的最小值；（3）点P 为抛物线上一点，连接CP ，直线CP 把四边形CBPA 的面积分为3∶5两部分，求点P 的坐标.【答案】（1）2y x 2x 3=-++，对称轴为直线1x =；（2）四边形ACDE 1；（3）12(4,5),(8,45)P P -- 【解析】 【分析】（1）OB =OC ，则点B （3，0），则抛物线的表达式为：y =a （x +1）（x -3）=a （x 2-2x -3）=ax 2-2ax -3a ，即可求解；（2）CD +AE =A ′D +DC ′，则当A ′、D 、C ′三点共线时，CD +AE =A ′D +DC ′最小，周长也最小，即可求解； （3）S △PCB ：S △PCA =12EB ×（y C -y P ）：12AE ×（y C -y P ）=BE ：AE ，即可求解． 【详解】（1）∵OB =OC ，∴点B （3，0），则抛物线的表达式为：y =a （x +1）（x -3）=a （x 2-2x -3）=ax 2-2ax -3a ， 故-3a =3，解得：a =-1，故抛物线的表达式为：y =-x 2+2x +3…①； 对称轴为：直线1x =（2）ACDE 的周长=AC +DE +CD +AE ，其中AC 、DE =1是常数， 故CD +AE 最小时，周长最小，取点C 关于函数对称点C （2，3），则CD =C ′D ， 取点A ′（-1，1），则A ′D =AE ，故：CD +AE =A ′D +DC ′，则当A ′、D 、C ′三点共线时，CD +AE =A ′D +DC ′最小，周长也最小，四边形ACDE 的周长的最小值=AC +DE +CD +AE +1+A ′D +DC +1+A ′C （3）如图，设直线CP 交x 轴于点E ，直线CP 把四边形CBP A 的面积分为3：5两部分， 又∵S △PCB ：S △PCA =12EB ×（y C -y P ）：12AE ×（y C -y P ）=BE ：AE ， 则BE ：AE ，=3：5或5：3， 则AE =52或32， 即：点E 的坐标为（32，0）或（12，0）， 将点E 、C 的坐标代入一次函数表达式：y =kx +3， 解得：k =-6或-2，故直线CP 的表达式为：y =-2x +3或y =-6x +3…② 联立①②并解得：x =4或8（不合题意值已舍去）， 故点P 的坐标为（4，-5）或（8，-45）．【点睛】本题考查的是二次函数综合运用，涉及到一次函数、图象面积计算、点的对称性等，其中（1），通过确定点A ′点来求最小值，是本题的难点．5.（湖南省益阳市2019年中考数学试题）在平面直角坐标系xOy 中，顶点为A 的抛物线与x 轴交于B 、C 两点，与y 轴交于点D ，已知A (1，4)，B (3，0)． (1)求抛物线对应二次函数表达式；(2)探究：如图1，连接OA ，作DE ∥OA 交BA 的延长线于点E ，连接OE 交AD 于点F ，M 是BE 的中点，则OM 是否将四边形OBAD 分成面积相等的两部分？请说明理由；(3)应用：如图2，P (m ，n )是抛物线在第四象限的图象上的点，且m +n ＝﹣1，连接P A 、PC ，在线段PC 上确定一点M ，使AN 平分四边形ADCP 的面积，求点N 的坐标．提示：若点A 、B 的坐标分别为(x 1，y 1)、(x 2，y 2)，则线段AB 的中点坐标为(122x x +，122y y +)．的【答案】(1)y＝﹣x2+2x﹣3；(2)OM将四边形OBAD分成面积相等的两部分，理由见解析；(3)点N(43，﹣73)．【解析】【分析】(1)函数表达式为：y＝a(x﹣1)2+4，将点B坐标的坐标代入上式，即可求解；(2)利用同底等高的两个三角形的面积相等，即可求解；(3)由(2)知：点N是PQ的中点，根据C,P点的坐标求出直线PC的解析式，同理求出AC,DQ的解析式，并联立方程求出Q点的坐标，从而即可求N点的坐标．【详解】(1)函数表达式为：y＝a(x﹣1)2+4，将点B坐标的坐标代入上式得：0＝a(3﹣1)2+4，解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+2x﹣3；(2)OM将四边形OBAD分成面积相等的两部分，理由：如图1，∵DE∥AO，S△ODA＝S△OEA，S△ODA+S△AOM＝S△OEA+S△AOM，即：S四边形OMAD＝S△OBM，∴S△OME＝S△OBM，∴S四边形OMAD＝S△OBM；(3)设点P(m，n)，n＝﹣m2+2m+3，而m+n＝﹣1，解得：m＝﹣1或4，故点P(4，﹣5)；如图2，故点D作QD∥AC交PC的延长线于点Q，由(2)知：点N 是PQ 的中点， 设直线PC 的解析式为y =kx +b ，将点C (﹣1，0)、P (4，﹣5)的坐标代入得：045k b k b -+=⎧⎨+=-⎩，解得：11k b =-⎧⎨=-⎩，所以直线PC 的表达式为：y ＝﹣x ﹣1…①， 同理可得直线AC 的表达式为：y ＝2x +2， 直线DQ ∥CA ，且直线DQ 经过点D (0，3)， 同理可得直线DQ 的表达式为：y ＝2x +3…②， 联立①②并解得：x ＝﹣43，即点Q (﹣43，13)， ∵点N 是PQ 的中点， 由中点公式得：点N (43，﹣73)． 【点睛】本题考查的是二次函数综合运用，涉及到一次函数、图形面积的计算等，其中(3)直接利用(2)的结论，即点N 是PQ 的中点，是本题解题的突破点． 最新模拟试题6.（2020年安徽省阜阳市太和县九年级第二次调研模拟预测试题）如图，在平面直角坐标系xoy 中，顶点为M 的抛物线1C ：2y ax bx =-(0a ＜)经过点A 和x 轴上的点B ，2AO OB ==，120AOB ∠=︒．（1）求该抛物线的表达式； （2）联结AM ，求AOM S △；（3）将抛物线1C 向上平移得到抛物线2C ，抛物线2C 与x 轴分别交于点E F 、(点E 在点F 的左侧)，如果△MBF 与AOM 相似，求所有符合条件的抛物线2C 的表达式．【答案】（1）2y x =+；（23）抛物线2C 为：2y x =++或23327y x x =-++ 【解析】【分析】（1）根据题意，可以写出点B 和点A 的坐标，从而可以得到该抛物线的表达式；（2）根据（1）中的函数解析式，可以求得点M 的坐标，从而可以求得直线AM 的函数解析式，从而可以求得S △AOM ；（3）根据题意，利用分类讨论的方法和三角形相似的知识可以求得点F 的坐标，从而可以求得抛物线C 2的表达式．【详解】解：（1）过A 作AH x ⊥轴，垂足为H ，∵2OB =，∴0(2)B ，∵120AOB ∠=︒∴60AOH ∠=︒，30HAO ∠=︒．∵2OA =， ∴112OH OA ==． 在Rt AHO 中，222OH AH OA +=，∴AH ==∴(1A --，∵抛物线1C ：2y ax bx =+经过点A B 、，∴可得：420a b a b -=⎧⎪⎨-=⎪⎩解得：a b ⎧=⎪⎪⎨⎪=⎪⎩∴这条抛物线的表达式为2y x x =；（2）过M 作MG x ⊥轴，垂足为G ，∵2y x x =+=21)x -∴顶点M是1,3⎛ ⎝⎭，得3MG =设直线AM 为y =kx +b ，把(A -，1,3M ⎛⎫ ⎪ ⎪⎝⎭代入得k b k b =-+=+，解得33k b ⎧=⎪⎪⎨⎪=-⎪⎩ ∴直线AM为y x =-令y =0，解得x =12∴直线AM 与x 轴的交点N 为1,02⎛⎫ ⎪⎝⎭∴111111×××22223223AOM S ON MG ON AH =⋅-⋅=+ （3）∵0(2)B ，、M ⎛ ⎝⎭，∴在Rt △BGM中，tan 3MG MBG BG ∠==， ∴30MBG ∠=︒．∴150MBF ∠=︒．由抛物线的轴对称性得：MO MB =，∴150MBO MOB ∠=∠=︒．∵120AOB ∠=︒，∴150AOM ∠=︒∴AOM MBF ∠=∠．∴当△MBF 与AOM 相似时，有：=OM BM OA BF 或=OM BF OA BM即332BF =或32=， ∴2BF =或23BF =． ∴0(4)F ，或803⎛⎫ ⎪⎝⎭， 设向上平移后的抛物线2C为：2y x x k =++， 当0(4)F ，时，3k =， ∴抛物线2C为：2y =+当803F ⎛⎫ ⎪⎝⎭，时，k =，∴抛物线2C 为：23327y x x =-++综上：抛物线2C 为：2y x =++或2y x x =++ 【点睛】本题是一道二次函数综合题，解答本题的关键是明确题意，求出相应的函数解析式，作出合适的辅助线，找出所求问题需要的条件，利用分类讨论和数形结合的思想解答．7.（2019年河南省中原名校中考第三次大联考数学试卷）如图，直线y ＝﹣x +5与x 轴交于点B ，与y 轴交于点C ，抛物线y ＝﹣x 2+bx +c 与直线y ＝﹣x +5交于B ，C 两点，已知点D 的坐标为（0，3） （1）求抛物线的解析式；（2）点M ，N 分别是直线BC 和x 轴上的动点，则当△DMN 的周长最小时，求点M ，N 的坐标，并写出△DMN 周长的最小值；（3）点P 是抛物线上一动点，在（2）的条件下，是否存在这样的点P ，使∠PBA ＝∠ODN ？若存在，请直接写出点P 的坐标；若不存在，请说明理由．【答案】（1）y ＝﹣x 2+4x +5；（2）点M 、N 的坐标分别为（85，175）、（34，0），△DMN 周长的最小；（3）点P （﹣23，73）． 【解析】（1）求出点B 、C 的坐标、将点B 、C 坐标代入二次函数表达式，即可求解；（2）过点D 分别作x 轴和直线BC 的对称点D ′（0，-3）、D ″，连接D ′D ″交x 轴、直线BC 于点N 、M ，此时△DMN 的周长最小，即可求解；（3）tan∠ODN=13ONOD==tan∠PBA，确定直线BP的表达式，即可求解．【详解】（1）y＝﹣x+5，令x＝0，则y＝5，令y＝0，则x＝5，故点B、C的坐标分别为（5，0）、（0，5），则二次函数表达式为：y＝﹣x2+bx+5，将点B坐标代入上式并解得：b＝4，故抛物线的表达式为：y＝﹣x2+4x+5…①，令y＝0，则x＝﹣1或5，故点A（﹣1，0），而OB＝OC＝2，故∠OCB＝45°；（2）过点D分别作x轴和直线BC的对称点D′（0，﹣3）、D″，∵∠OCB＝45°，则CD″∥x轴，则点D″（2，5），连接D′D″交x轴、直线BC于点N、M，此时△DMN的周长最小，将点D′、D″的坐标代入一次函数表达式：y＝mx+n并解得：直线D′D″的坐标代入一次函数表达式为：y＝4x﹣3，则点M、N的坐标分别为（85，175）、（34，0），△DMN周长的最小值＝DM+DN+MN；（3）如图2，tan∠ODN＝13ONOD=＝tan∠PBA，则直线BP 的表达式为：y ＝﹣13x +s ，将点B 的坐标代入上式并解得： 直线BP 的表达式为：y ＝﹣13x +53…②， 联立①②并解得：x ＝5或﹣23（舍去5） 故：点P （﹣23，73）． 【点睛】本题考查的是二次函数综合运用，涉及到一次函数、点的对称性等知识点，其中（2），通过点的对称性确定点M 、N 的位置，是此类题目的基本方法．8.(2019年河南省实验外国语学校中考数学模拟试卷)如图，直线y ＝-12x -3与x 轴，y 轴分别交于点A ，C ，经过点A ，C 的抛物线y ＝ax 2+bx ﹣3与x 轴的另一个交点为点B (2，0)，点D 是抛物线上一点，过点D 作DE ⊥x 轴于点E ，连接AD ，D C ．设点D 的横坐标为m ．(1)求抛物线的解析式；(2)当点D 在第三象限，设△DAC 的面积为S ，求S 与m 的函数关系式，并求出S 的最大值及此时点D 的坐标；(3)连接BC ，若∠EAD ＝∠OBC ，请直接写出此时点D 的坐标．【答案】(1)y ＝14x 2+x ﹣3；(2)S △ADC =﹣34(m +3)2+274；△ADC 的面积最大值为274；此时D (﹣3，﹣154)；(3)满足条件的点D 坐标为(﹣4，﹣3)或(8，21).【解析】（1）求出A 坐标，再用待定系数法求解析式；（2）设DE 与AC 的交点为点F .设点D 的坐标为：(m ，14m 2+m ﹣3)，则点F 的坐标为：(m ，﹣12m ﹣3)，根据S △ADC ＝S △ADF +S △DFC 求出解析式，再求最值；（3）①当点D 与点C 关于对称轴对称时，D (﹣4，﹣3)，根据对称性此时∠EAD ＝∠AB C ． ②作点D (﹣4，﹣3)关于x 轴的对称点D ′(﹣4，3)，直线AD ′的解析式为y ＝32x +9，解方程组求出函数图像交点坐标.【详解】解：(1)在y ＝﹣12x ﹣3中，当y ＝0时，x ＝﹣6， 即点A 的坐标为：(﹣6，0)，将A (﹣6，0)，B (2，0)代入y ＝ax 2+bx ﹣3得：366304230a b a b --=⎧⎨+-=⎩， 解得：141a b ⎧=⎪⎨⎪=⎩，∴抛物线的解析式为：y ＝14x 2+x ﹣3； (2)设点D 的坐标为：(m ，14m 2+m ﹣3)，则点F 的坐标为：(m ，﹣12m ﹣3)， 设DE 与AC 的交点为点F .∴DF ＝﹣12m ﹣3﹣(14m 2+m ﹣3)＝﹣14m 2﹣32m ， ∴S △ADC ＝S △ADF +S △DFC ＝12DF •AE +12•DF •OE ＝12DF •OA ＝12×(﹣14m 2﹣32m )×6 ＝﹣34m 2﹣92m ＝﹣34(m +3)2+274， ∵a ＝﹣34＜0， ∴抛物线开口向下，∴当m ＝﹣3时，S △ADC 存在最大值274， 又∵当m ＝﹣3时，14m 2+m ﹣3＝﹣154， ∴存在点D (﹣3，﹣154)，使得△ADC 的面积最大，最大值为274； (3)①当点D 与点C 关于对称轴对称时，D (﹣4，﹣3)，根据对称性此时∠EAD ＝∠AB C ．②作点D (﹣4，﹣3)关于x 轴的对称点D ′(﹣4，3)，直线AD ′的解析式为y ＝32x +9， 由2392134y x y x x ⎧=+⎪⎪⎨⎪=+-⎪⎩，解得60x y =-⎧⎨=⎩或821x y =⎧⎨=⎩， 此时直线AD ′与抛物线交于D (8，21)，满足条件，综上所述，满足条件的点D 坐标为(﹣4，﹣3)或(8，21)【点睛】本题属于二次函数综合题，考查了待定系数法，一次函数的应用，二次函数的性质等知识，解题的关键是学会构建二次函数解决最值问题，学会构建一次函数解决实际问题，属于中考压轴题．. 9.（广东省佛山市南海外国语学校2019-2020学年九年级下学期第一次月考数学试题）如图，已知抛物线2y ax bx c =++经过点0()3,A ﹣、()9,0B 和()0,4C ，CD 垂直于y 轴，交抛物线于点D ，DE 垂直于x 轴，垂足为E ，直线l 是该抛物线的对称轴，点F 是抛物线的顶点．(1)求出该二次函数的表达式及点D 的坐标；(2)若Rt △AOC 沿x 轴向右平移，使其直角边OC 与对称轴l 重合，再沿对称轴l 向上平移到点C 与点F 重合，得到11Rt AO F △，求此时11Rt AO F △与矩形OCDE 重叠部分图形的面积；(3)若Rt △AOC 沿x 轴向右平移t 个单位长度(06t <≤)得到222Rt A O C △，222Rt A O C △与Rt OED △重叠部分图形的面积记为S ，求S 与t 之间的函数表达式，并写出自变量t 的取值范围．【答案】(1)抛物线的解析式为2484279y x x =-++，点D 的坐标为()6,4；(2) 163；(3)221(03)3146(36)3t t S t t t ⎧<≤⎪⎪=⎨⎪-+-<≤⎪⎩. 【解析】【分析】（1）将点A （-3，0）、B （9，0）和C （0，4）代入y =ax 2+bx +c 即可求出该二次函数表达式，因为CD 垂直于y 轴，所以令y =4，求出x 的值，即可写出点D 坐标；（2）设A 1F 交CD 于点G ，O 1F 交CD 于点H ，求出顶点坐标，证△FGH ∽△F A 1O 1，求出GH 的长，因为Rt △A 1O 1F 与矩形OCDE 重叠部分的图形是梯形A 1O 1HG ，所以S 重叠部分=11A O F S ∆-S △FGH ，即可求出结果； （3）当0＜t ≤3时，设O 2C 2交OD 于点M ，证△OO 2M ∽△OED ，求出O 2M =23t ，可直接求出S =2OO M S ∆=12OO 2×O 2M =13t 2；当3＜t ≤6时，设A 2C 2交OD 于点M ，O 2C 2交OD 于点N ，分别求出直线OD 与直线A 2C 2的解析式，再求出其交点M 的坐标，证△DC 2N ∽△DCO ，求出C 2N =23（6-t ），由S =S 四边形A 2Q 2NM =2222A O C C MN S S ∆∆-，可求出S 与t 的函数表达式．【详解】(1)∵抛抛线2y ax bx c =++经过点()30A -,、()9,0B 和()0,4C ，∴抛物线的解析式为()()39y a x x =+-，∵点()0,4C 在抛物线上，∴427a =-， ∴427a =-， ∴抛物线的解析式为：2448(3)(9)427279y x x x x =-+-=-++， ∵CD 垂直于y 轴，()0,4C， 令24844279x x -++=， 解得，0x =或6x =，∴点D 的坐标为()6,4；(2)如图1所示，设1A F 交CD 于点G ，1O F 交CD 于点H ，∵点F 是抛物线2484279y x x =-++的顶点， ∴163,3F ⎛⎫ ⎪⎝⎭， ∴164433FH =-=， ∵11GH AO ，∴11FGH FAO △△∽， ∴111GH FH A O FO =， ∴4334GH =， 解得，1GH = ，∵11Rt AO F △与矩形OCDE 重叠部分的图形是梯形11A O HG ， ∴11A O F FGH S S S =-△△重叠部分 1111122AO O F GH FH =⋅-⋅ 114341223=⨯⨯-⨯⨯ 163=；(3)①当03t <≤时，如图2所示，设22O C 交OD 于点M ， ∵22C O DE ，∴2OO M OED △△∽， ∴22O DE EOO M O =， ∴246O M t =， ∴223O M t =， ∴22221121S 2233OO M S OO O M t t t ==⨯=⨯=△；②当36t <≤时，如图3所示，设22A C 交OD 于点M ，22O C 交OD 于点N ，将点()6,4D 代入y kx =， 得，23k =， ∴23OD y x =， 将点()3,0t -，(),4t 代入y kx b =+，得，(3)04k t b kt b -+=⎧⎨+=⎩， 解得，43k =，443b t =-+， ∴直线22A C 的解析式为：44433y x t =-+， 联立23OD y x =与44433y x t =-+， 得，2444333x x t =-+， 解得，62x t =-+，∴两直线交点M 坐标为462,43t t ⎛⎫-+-+⎪⎝⎭， 故点M 到2O C 2的距离为6t -，∵2C N OC ，∴2DC N DCO △△∽， ∴22DC C N CD OC=， ∴2664C N t -=， ∴22(6)3C N t =-， ∴222222A O C C MN A O NM S S S S ==-△△四边形211(6)22OA OC C N t =⋅-- 11234(6)(6)223t t =⨯⨯-⨯-- 21463t t =-+-； ∴S 与t 的函数关系式为：221(03)3146(36)3t t S t t t ⎧<≤⎪⎪=⎨⎪-+-<≤⎪⎩．【点睛】本题考查了待定系数法求解析式，相似三角形的判定与性质，三角形的面积等，解题关键是能够根据题意画图，知道有些不规则图形的面积可转化为几个规则图形的面积和或差来求出．。
专题02 二次函数与营销问题-2019年中考数学复习压轴题突破之二次函数(解析版)
【方法综述】此类问题以营销问题为背景，通过各种数学知识的结合，考察和二次函数最值和自变量取值范围有关的问题。
首先，考察有关利润的函数模型的构造，解答方法是通过利润公式根据题意找出等量关系；其次考察函数的最值计算、判断，解答方法是通过二次函数特性找到函数的最值或在一定自变量范围内函数值的最值；再次通常考察利润在一定范围内时对应的自变量取值范围，解答方法通常采用通过数形结合思想，画出函数图象根据题意找到答案。
【典例示范】类型一常规盈利问题例1：（2019湖北宜昌）某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利过程．下面的二次函数图象（部分）刻画了该公司年初以来累积利润（万元）与销售时间（月）之间的关系（即前个月的利润总和和之间的关系）．根据图象提供的信息，解答下列问题：由已知图象上的三点坐标，求累积利润（万元）与时间（月）之间的函数关系式；求截止到几月末公司累积利润可达到万元；求第个月公司所获利润是多少万元？【答案】（1）；（2）截止到月末公司累积利润可达万元；（3）万元．﹣2）2﹣2，即S=t2﹣2t．答：累积利润S与时间t之间的函数关系式为：S=t2﹣2t；（2）把S=30代入S=（t﹣2）2﹣2，得：（t﹣2）2﹣2=30．解得：t1=10，t2=﹣6（舍去）．*网答：截止到10月末公司累积利润可达30万元．针对训练1．(2018宁波)根据对宁波市相关的市场物价调研，某批发市场内甲种水果的销售利润y1（千元）与进货量x（吨）近似满足函数关系y1=0.25x，乙种水果的销售利润y2（千元）与进货量x（吨）之间的函数y2=ax2+bx+c 的图象如图所示．（1）求出y2与x之间的函数关系式；（2）如果该市场准备进甲、乙两种水果共8吨，设乙水果的进货量为t吨，写出这两种水果所获得的销售利润之和W（千元）与t（吨）之间的函数关系式，并求出这两种水果各进多少吨时获得的销售利润之和最大，最大利润是多少？【答案】（1）y2=﹣x2+x；（2）w=﹣（t﹣4）2+6，t=4时，w的值最大，最大值为6，∴两种水果各进4吨时获得的销售利润之和最大，最大利润是6千元．【解析】解：（1）∵函数y2=ax2+bx+c的图象经过（0，0），（1，2），（4，5），∴，解得：，∴y2=﹣x2+x．（2）w=y1+y2=（8﹣t）﹣t2+t=﹣（t﹣4）2+6，∴t=4时，w的值最大，最大值为6，∴两种水果各进4吨时获得的销售利润之和最大，最大利润是6千元．&网2．（2019泰州姜堰区期末）某水果店销售某品牌苹果，该苹果每箱的进价是40元，若每箱售价60元，每星期可卖180箱．为了促销，该水果店决定降价销售．市场调查反映:若售价每降价1元，每星期可多卖10箱．设该苹果每箱售价x元（40≤x≤60），每星期的销售量为y箱．（1）求y与x之间的函数关系式；（2）当每箱售价为多少元时，每星期的销售利润达到3570元？（3）当每箱售价为多少元时，每星期的销售利润最大，最大利润多少元?【答案】(1)y=-10x+780；(2)57；(3)当售价为59元时，利润最大，为3610元（3）设每星期的利润为w，W=（x-40）(-10x+780)=-10（x-59）2+3610,∵-100,二次函数向下,函数有最大值,当x=59时,利润最大，为3610元.3．（2019安徽阜阳期末）某企业生产了一款健身器材，可通过实体店和网上商店两种途径进行销售，销售了一段时间后，该企业对这种健身器材的销售情况进行了为期30天的跟踪调查，其中实体店的日销售量y1(套)与时间x(x为整数，单位:天)的部分对应值如下表所示:时间x(天)0510********日销售量y(套)025*********(1)求出y1与x的二次函数关系式及自变量x的取值范围(2)若网上商店的日销售量y2(套)与时间x(x为整数，单位:天)的函数关系为，则在跟踪调查的30天中，设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式；当x为何值时，日销售总量y达到最大，并写出此时的最大值.【答案】（1），（0≤x≤30，且为整数）；（2）当x=30时，y取得最大值360.（2）依题意有y=y1+y2，当0≤x≤10时，,∴当x=10时，y取得最大值80；当10<x≤30时，∴当x=30时，y取得最大值360；学&科网综上可知，当x=30时，y取得最大值360.4．（2018广东中山）某电商在购物平台上销售一款小电器，其进价为45元/件，每销售一件需缴纳平台推广费5元，该款小电器每天的销售量y（件）与每件的销售价格x（元）满足函数关系：y＝﹣2x+200．为保证市场稳定，供货商规定销售价格不得低于75元/件．（1）写出每天的销售利润w（元）与销售价格x（元）的函数关系式（不必写出x的取值范围）；（2）每件小电器的销售价格定为多少元时，才能使该款小电器每天获得的利润是1200元？【答案】（1）w＝﹣2x2+300x﹣10000；（2）每件小电器的销售价格定为90元时，才能使该款小电器每天获得的利润是1200元．【解析】解：（1）由题意可得：w＝（x﹣50）（﹣2x+200）＝﹣2x2+300x﹣10000；（2）由题意可得：1200＝﹣2x2+300x﹣10000，解得：x1＝60（不合题意舍去），x2＝90，学*科网答：每件小电器的销售价格定为90元时，才能使该款小电器每天获得的利润是1200元．5．（2019洛阳市月考）某公司为一工厂代销一种建筑材料（这里的代销是指厂家先免费提供货源，待货物售出后再进行结算，未售出的由厂家负责处理）．当每吨售价为260元时，月销售量为45吨．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7.5吨．综合考虑各种因素，每售出一吨建筑材料共需支付厂家及其它费用100元．设每吨材料售价为x（元），该经销店的月利润为y（元）．当每吨售价是240元时，计算此时的月销售量；（1）求出y与x的函数关系式（不要求写出x的取值范围）；（2）该经销店要获得最大月利润，售价应定为每吨多少元？（3）小静说：“当月利润最大时，月销售额也最大．”你认为对吗？请说明理由．【答案】（1）60吨．（2）y＝﹣x2+315x﹣24000．（3）利达经销店要获得最大月利润，材料的售价应定为每吨210元．（4）我认为，小静说的不对．（3）y＝﹣x2+315x﹣24000＝﹣（x﹣210）2+9075．利达经销店要获得最大月利润，材料的售价应定为每吨210元．（4）我认为，小静说的不对．理由：当月利润最大时，x为210元，而对于月销售额W＝x（45+×7.5）＝﹣（x﹣160）2+19200来说，当x为160元时，月销售额W最大．∴当x为210元时，月销售额W不是最大．∴小静说的不对．&网6．（2018重庆月考）某文具店购进A，B两种钢笔，若购进A种钢笔2支，B种钢笔3支，共需90元；购进A种钢笔3支，B种钢笔5支，共需145元．（1）求该文具店购进A、B两种钢笔每支各多少元？（2）经统计，B种钢笔售价为30元时，每月可卖64支；每涨价3元，每月将少卖12支，求该文具店B 种钢笔销售单价定为多少元时，每月获利最大？最大利润是多少元？【答案】（1）文具店购进A种钢笔每支15元，购进B种钢笔每支20元；（2）该文具店B种钢笔销售单价定为33元时，每月获利最大，最大利润是676元．（2）设B种钢笔每支售价为x元，每月获取的总利润为W，则W＝（x﹣20）（64﹣12）＝﹣4x2+264x﹣3680＝﹣4（x﹣33）2+676．学&科网∵a＝﹣4＜0，∴当x＝33时，W取得最大值，最大值为676．答：该文具店B种钢笔销售单价定为33元时，每月获利最大，最大利润是676元．7．（青岛市李沧区期末）某公司营销A，B两种产品，根据市场调研，确定两条信息：信息1：销售A种产品所获利润y（万元）与所售产品x（吨）之间存在二次函数关系，如图所示：信息2：销售B种产品所获利润y（万元）与销售产品x（吨）之间存在正比例函数关系y＝0.3x．根据以上信息，解答下列问题；(1)求二次函数的表达式；(2)该公司准备购进A、B两种产品共10吨，请设计一个营销方案，使销售A、B两种产品获得的利润之和最大，最大利润是多少万元？【答案】(1)销售A种产品所获利润y与销售产品x之间的函数关系式为y=﹣0.1x2+1.5x；(2)购进A产品6吨，购进B产品4吨，销售A、B两种产品获得的利润之和最大，最大利润是6.6万元（2）设购进A产品m吨，购进B产品（10﹣m）吨，销售A、B两种产品获得的利润之和为W元，则W=﹣0.1m2+1.5m+0.3（10﹣m），=﹣0.1m2+1.2m+3，=﹣0.1（m﹣6）2+6.6，∵﹣0.1＜0，学&科网∴当m=6时，W取得最大值，最大值为6.6万元，答：购进A产品6吨，购进B产品4吨，销售A、B两种产品获得的利润之和最大，最大利润是6.6万元．类型二一次函数与二次函数相结合的营销问题例2．（2019江苏东台）某校部分团员参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利润捐给慈善机构.根据市场调查，这种许愿瓶一段时间内的销售量y（个）与销售单价x（元/个）之间的对应关系如图所示：（1）试判断y与x之间的函数关系，并求出函数关系式；（2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润w（元）与销售单价x（元/个）之间的函数关系式；（3）在（2）的条件下，若许愿瓶的进货成本不超过900元，要想获得最大的利润，试确定这种许愿瓶的销售单价，并求出此时的最大利润.【答案】（1）y=-30x+600；（2）；（3）x=15时，利润最大1350元.（2）w=（x-6）（-30x+600）=-30x2+780x-3600，即w与x之间的函数关系式为w=-30x2+780x-3600；（3）由题意得：6（-30x+600）≤900，解得x≥15．w=-30x2+780x-3600图象对称轴为：x=-=-=13．∵a=-30＜0，∴抛物线开口向下，当x≥15时，w随x增大而减小，，∴当x=15时，w最大=1350即以15元/个的价格销售这批许愿瓶可获得最大利润1350元．针对训练1.国家推行“节能减排，低碳经济”政策后，某环保节能设备生产企业的产品供不应求．若该企业的某种环保设备每月的产量保持在一定的范围，每套产品的生产成本不高于50万元，每套产品的售价不低于80万元，已知这种设备的月产量x（套）与每套的售价y（万元）之间满足关系式y＝150﹣2x，月产量x（套）与生产总成本y2（万元）存在如图所示的函数关系．（1）直接写出y2与x之间的函数关系式；（2）求月产量x的范围；（3）当月产量x（套）为多少时，这种设备的利润W（万元）最大？最大利润是多少？【答案】（1）y2＝30x+500；（2）25≤x≤35；（3）月产量为30件时，利润最大，最大利润是1300万元．（2）依题意得：，解得：25≤x≤35；（3）∵W＝x•y1﹣y2＝x（150﹣2x）﹣（500+30x）＝﹣2x2+120x﹣500∴W＝﹣2（x﹣30）2+1300∵25＜30＜35，*网∴当x＝30时，W＝1300最大答：当月产量为30件时，利润最大，最大利润是1300万元．2．（2019天津南开期末）某商家独家销售具有地方特色的某种商品,每件进价为40元。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019中考数学压轴题解析3927．（2015黔西南州，第10题，4分）在数轴上截取从0到3的对应线段AB，实数m对应AB上的点M，如图1；将AB折成正三角形，使点A、B重合于点P，如图2；建立平面直角坐标系，平移此三角形，使它关于y轴对称，且点P的坐标为（0，2），PM的延长线与x轴交于点N（n，0），如图3，当m=3时，n的值为（）A．423- B．432- C．332-D．332【答案】A．【解析】试题分析：∵AB=3，△PDE是等边三角形，∴PD=PE=DE=1，以DE的垂直平分线为y轴建立直角坐标系，∵△PDE关于y轴对称，∴PF⊥DE，DF=EF，DE∥x轴，∴PF=32，∴△PFM∽△PON，∵m=3，∴332-，∴PF PMOP ON=，即333222ON-=，解得：ON=423-．故选A．考点：相似三角形的判定与性质；实数与数轴；等边三角形的性质；平移的性质；综合题；压轴题．二、填空题28．（2017湖南省常德市，第16题，3分）如图，有一条折线A1B1A2B2A3B3A4B4…，它是由过A1（0，0），B1（2，2），A2（4，0）组成的折线依次平移4，8，12，…个单位得到的，直线y=kx+2与此折线恰有2n（n≥1，且为整数）个交点，则k的值为．【答案】12n-．【分析】由点A1、A2的坐标，结合平移的距离即可得出点An的坐标，再由直线y=kx+2与此折线恰有2n（n≥1，且为整数）个交点，即可得出点An+1（4n，0）在直线y=kx+2上，依据依此函数图象上点的坐标特征，即可求出k值．【解析】∵A1（0，0），A2（4，0），A3（8，0），A4（12，0），…，∴An（4n﹣4，0）．∵直线y=kx+2与此折线恰有2n（n≥1，且为整数）个交点，∴点An+1（4n，0）在直线y=kx+2上，∴0=4nk+2，解得：k=12n-．故答案为：12n-．点睛：本题考查了一次函数图象上点的坐标特征以及坐标与图形变化中的平移，根据一次函数图象上点的坐标特征结合点An的坐标，找出0=4nk+2是解题的关键．考点：一次函数图象上点的坐标特征；坐标与图形变化﹣平移；规律型；综合题．29．（2017山东省菏泽市，第14题，3分）如图，AB⊥y轴，垂足为B，将△ABO绕点A逆时针旋转到△AB1O1的位置，使点B的对应点B1落在直线3y x=-上，再将△AB1O1绕点B1逆时针旋转到△A1B1O1的位置，使点O1的对应点O2落在直线33y x=-上，依次进行下去…若点B的坐标是（0，1），则点O12的纵坐标为．【答案】3【分析】观察图象可知，O12在直线33y x=-时，OO12=6OO2=6（3）3，由此即可解决问题．【解析】观察图象可知，O12在直线3y x=时，OO12=6OO2=6（3+2）3O12的横坐标=﹣（3•cos30°=﹣9﹣3，O12的纵坐标=123，∴O12（﹣9﹣33）．故答案为：3点睛：本题考查坐标与图形的变化、规律型：点的坐标、一次函数的性质等知识，解题的关键是学会从特殊到一般的探究方法，属于中考常考题型．考点：坐标与图形变化﹣旋转；规律型：点的坐标；一次函数图象上点的坐标特征；综合题．30．（2017湖南省张家界市，第14题，3分）如图，在正方形ABCD中，AD=23，把边BC绕点B逆时针旋转30°得到线段BP，连接AP并延长交CD于点E，连接PC，则三角形PCE的面积为．【答案】953-．【分析】根据旋转的想知道的PB=BC=AB，∠PBC=30°，推出△ABP是等边三角形，得到∠BAP=60°，AP=AB=23，解直角三角形得到CE=23﹣2，PE=4﹣23，过P作PF⊥CD于F，于是得到结论．【解析】∵四边形ABCD是正方形，∴∠ABC=90°，∵把边BC绕点B逆时针旋转30°得到线段BP，∴PB=BC=AB，∠PBC=30°，∴∠ABP=60°，∴△ABP是等边三角形，∴∠BAP=60°，AP=AB=23，∵AD=23，∴AE=4，DE=2，∴CE=23﹣2，PE=4﹣23，过P作PF⊥CD于F，∴PF=32PE=23﹣3，∴三角形PCE的面积=12CE•PF=12×（23﹣2）×（23﹣3）=953-，故答案为：953-．点睛：本题考查了旋转的性质，正方形的性质，等边三角形的判定和性质，解直角三角形，正确的作出辅助线是解题的关键．考点：旋转的性质；正方形的性质；综合题．31．（2017四川省内江市，第25题，6分）如图，已知直线l1∥l2，l1、l2之间的距离为8，点P到直线l1的距离为6，点Q到直线l2的距离为4，PQ=430，在直线l1上有一动点A，直线l2上有一动点B，满足AB⊥l2，且PA+AB+BQ最小，此时PA+BQ= ．【答案】16．【分析】作PE⊥l1于E交l2于F，在PF上截取PC=8，连接QC交l2于B，作BA⊥l1于A，此时PA+AB+BQ最短．作QD⊥PF于D．首先证明四边形ABCP是平行四边形，PA+BQ=CB+BQ=QC，利用勾股定理即可解决问题．【解析】作PE⊥l1于E交l2于F，在PF上截取PC=8，连接QC交l2于B，作BA⊥l1于A，此时PA+AB+BQ最短．作QD⊥PF于D．在Rt△PQD中，∵∠D=90°，PQ=430，PD=18，∴DQ=22PQ PD- =156，∵AB=PC=8，AB∥PC，∴四边形ABCP是平行四边形，∴PA=BC，CD=10，∴PA+BQ=CB+BQ=QC=22DQ CD+ =156100+=16．故答案为：16．点睛：本题考查轴对称﹣最短问题、平行线的性质、平行四边形的判定和性质、勾股定理等知识，解题的关键是学会构建平行四边形解决问题，属于中考常考题型．考点：轴对称﹣最短路线问题；平行线的性质；动点型；最值问题；综合题．32．（2017安徽省，第14题，5分）在三角形纸片ABC中，∠A=90°，∠C=30°，AC=30cm，将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD（如图1），减去△CDE后得到双层△BDE（如图2），再沿着过△BDE某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形，则所得平行四边形的周长为 cm．【答案】40或3 3．【分析】解直角三角形得到AB=3∠ABC=60°，根据折叠的性质得到∠ABD=∠EBD=12∠ABC=30°，BE=AB=3DE=10，BD=20，如图1，平行四边形的边是DF，BF，如图2，平行四边形的边是DE，EG，于是得到结论．【解析】∵∠A=90°，∠C=30°，AC=30cm，∴AB=3，∠ABC=60°，∵△ADB≌△EDB，∴∠ABD=∠EBD=12∠ABC=30°，BE=AB=103，∴DE=10，BD=20，如图1，平行四边形的边是DF，BF，且DF=BF=2033，∴平行四边形的周长=8033；如图2，平行四边形的边是DE，EG，且DF=BF=10，∴平行四边形的周长=40．综上所述：平行四边形的周长为40或8033，故答案为：40或8033．点睛：本题考查了剪纸问题，平行四边形的性质，解直角三角形，正确的理解题意是解题的关键．考点：剪纸问题；操作型；分类讨论；综合题．33．（2017山东省东营市，第15题，4分）如图，已知菱形ABCD的周长为16，面积为83，E为AB 的中点，若P为对角线BD上一动点，则EP+AP的最小值为．【答案】23．【分析】如图作CE′⊥AB于E′，甲BD于P′，连接AC、AP′．首先证明E′与E重合，因为A、C 关于BD对称，所以当P与P′重合时，PA′+P′E的值最小，由此求出CE即可解决问题．【解析】如图作C E′⊥AB于E′，甲BD于P′，连接AC、AP′．∵已知菱形ABCD的周长为16，面积为83，∴AB=BC=4，AB•CE′=83，∴CE′=23，在Rt△BCE′中，BE′=224(23)=2，∵BE=EA=2，∴E与E′重合，∵四边形ABCD是菱形，∴BD垂直平分AC，∴A、C关于BD对称，∴当P 与P′重合时，PA′+P′E的值最小，最小值为CE的长=23，故答案为：23．点睛：本题考查轴对称﹣最短问题、菱形的性质等知识，解题的关键是学会添加常用辅助线，本题的突破点是证明CE是△ABC的高，学会利用对称解决最短问题．考点：轴对称﹣最短路线问题；菱形的性质；动点型；最值问题．34．（2017山东省泰安市，第24题，3分）如图，∠BAC=30°，M为AC上一点，AM=2，点P是AB上的一动点，PQ⊥AC，垂足为点Q，则PM+PQ的最小值为．【答案】3．【分析】本题作点M关于AB的对称点N，根据轴对称性找出点P的位置，如图，根据三角函数求出MN，∠N，再根据三角函数求出结论．【解析】作点M关于AB的对称点N，过N作NQ⊥AC于Q交AB于P，则NQ的长即为PM+PQ的最小值，连接MN交AB于D，则MD⊥AB，DM=DN，∵∠NPB=∠APQ，∴∠N=∠BAC=30°，∵∠BAC=30°，AM=2，∴MD=12AM=1，∴MN=2，∴NQ=MN•cos∠N=2×32=3，故答案为：3．点睛：本题考查含30°直角三角形的性质、轴对称﹣﹣最短路线问题及三角函数，正确确定P点的位置是解题的关键．考点：轴对称﹣最短路线问题；最值问题；动点型．35．（2017浙江省温州市，第15题，5分）如图，矩形OABC的边OA，OC分别在x轴、y轴上，点B 在第一象限，点D在边BC上，且∠AOD=30°，四边形OA′B′D与四边形OABD关于直线OD对称（点A′和A，B′和B分别对应）．若AB=1，反比例函数kyx（k≠0）的图象恰好经过点A′，B，则k的值为．【答案】43 3．【分析】设B（m，1），得到OA=BC=m，根据轴对称的性质得到OA′=OA=m，∠A′OD=∠AOD=30°，求得∠A′OA=60°，过A′作A′E⊥OA于E，解直角三角形得到A′（12m，32m），列方程即可得到结论．【解析】∵四边形ABCO是矩形，AB=1，∴设B（m，1），∴OA=BC=m，∵四边形OA′B′D与四边形OABD 关于直线OD对称，∴OA′=OA=m，∠A′OD=∠AOD=30°，∴∠A′OA=60°，过A′作A′E⊥OA于E，∴OE=12m，A′E=32m，∴A′（12m，32m），∵反比例函数kyx（k≠0）的图象恰好经过点A′，B，∴12m•32m=m，∴m=433，∴k=433．故答案为：433．点睛：本题考查了反比例函数图象上点的坐标特征，矩形的性质，轴对称的性质，解直角三角形，正确的作出辅助线是解题的关键．考点：反比例函数图象上点的坐标特征；矩形的性质；轴对称的性质；综合题．36．（2016福建省南平市）如图，等腰△ABC中，CA=CB=4，∠ACB=120°，点D在线段AB上运动（不与A、B重合），将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，给出下列结论：①CD=CP=CQ；②∠PCQ的大小不变；③△PCQ面积的最小值为43 5；④当点D在AB的中点时，△PDQ是等边三角形，其中所有正确结论的序号是．【答案】①②④．【分析】①由折叠直接得到结论；②由折叠的性质求出∠ACP+∠BCQ=120°，再用周角的意义求出∠PCQ=120°；③先作出△PCQ的边PC上的高，用三角函数求出QE=3CQ，得到S△PCQ=23CD，判断出△PCQ面积最小时，点D的位置，求出最小的CD=CF，即可；④先判断出△APD是等边三角形，△BDQ是等边三角形，再求出∠PDQ=60°，即可．【解析】①∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，∴CP=CD=CQ，∴①正确；②∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，∴∠ACP=∠ACD，∠BCQ=∠BCD，∴∠ACP+∠BCQ=∠ACD+∠BCD=∠ACB=120°，∴∠PCQ=360°﹣（∠ACP+BCQ+∠ACB）=360°﹣（120°+120°）=120°，∴∠PCQ的大小不变；∴②正确；③如图，过点Q作QE⊥PC交PC延长线于E，∵∠PCQ=120°，∴∠QCE=60°，在Rt△QCE中，tan∠QCE=QECQ，∴QE=CQ×tan∠QCE=CQ×tan60°=3CQ，∵CP=CD=CQ，∴S△PCQ=12CP×QE=12CP×3CQ=23CD，∴CD最短时，S△PCQ最小，即：CD⊥AB时，CD最短，过点C作CF⊥AB，此时CF就是最短的CD，∵AC=BC=4，∠ACB=120°，∴∠ABC=30°，∴CF=12BC=2，即：CD最短为2，∴S△PCQ最小=232CD=2322=23，∴③错误；④∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，∴AD=AP，∠DAC=∠PAC，∵∠DAC=30°，∴∠APD=60°，∴△APD是等边三角形，∴PD=AD，∠ADP=60°，同理：△BDQ是等边三角形，∴DQ=BD，∠BDQ=60°，∴∠PDQ=60°，∵当点D在AB的中点，∴AD=BD，∴PD=DQ，∴△DPQ是等边三角形，∴④正确，故答案为：①②④．点睛：此题是几何变换综合题，主要考查了折叠的性质，等腰三角形的性质，等边三角形的判定，锐角三角函数，极值的确定，三角形的面积公式，解本题的关键是判断出∠PCQ=120°是个定值；（其实这个题目中还有∠PDQ=60°也是定值），解本题的难点是确定出△PCQ面积最小时，点D的位置．考点：几何变换综合题；定值问题；最值问题；综合题；翻折变换（折叠问题）．37．（2016山东省济南市）如图1，在矩形纸片ABCD中，AB=83AD=10，点E是CD中点，将这张纸片依次折叠两次；第一次折叠纸片使点A与点E重合，如图2，折痕为MN，连接ME/NE；第二次折叠纸片使点N与点E重合，如图3，点B落到B′处，折痕为HG，连接HE，则tan∠EHG= ．【答案】53 6．【分析】如图2中，作NF⊥CD于F．设DM=x，则AM=EM=10﹣x，利用勾股定理求出x，再利用△DME∽△FEN，得DE EMFN EN，求出EN，EM，求出tan∠AMN，再证明∠EHG=∠AMN即可解决问题．点睛：本题考查翻折变换、勾股定理、相似三角形的判定和性质等知识，解题的关键是学会把问题转化，证明∠AMN=∠EHG是关键，属于中考填空题中的压轴题．考点：翻折变换（折叠问题）；解直角三角形；综合题．38．（2016福建省宁德市4分）如图，在Rt△ABC中，∠BAC=90°，AB=4，AC=3，点D、E分别是AB、AC的中点，点G、F在BC边上（均不与端点重合），DG∥EF．将△BDG绕点D顺时针旋转180°，将△CEF绕点E逆时针旋转180°，拼成四边形MGFN，则四边形MGFN周长l的取值范围是【答案】495≤l ＜13． 【分析】如图，连接DE ，作AH ⊥BC 于H ．首先证明GF=DE=52，要求四边形MNFG 周长的取值范围，只要求出MG 的最大值和最小值即可．【解析】如图，连接DE ，作AH ⊥BC 于H ．在Rt △ABC 中，∵∠BAC=90°，AB=4，AC=3，∴BC=22AB AC =5，∵12•AB•AC=12•BC•AH，∴AH=125，∵AD=DB ，AE=EC ，∴DE ∥CB ，DE=12BC=52，∵DG ∥EF ，∴四边形DGFE 是平行四边形，∴GF=DE=52，由题意MN ∥BC ，GM ∥FN ，∴四边形MNFG 是平行四边形，∴当MG=NF=AH 时，可得四边形MNFG 周长的最小值=2×125+2×52=495，当G 与B 重合时可得周长的最大值为13，∵G 不与B 重合，∴495≤l ＜13．故答案为：495≤l ＜13．点睛：本题考查旋转变换、勾股定理、平行四边形的性质、三角形中位线定理等知识，解题的关键是灵活运用所学知识解决问题，学会取特殊点解决问题，属于中考常考题型．考点：旋转的性质；勾股定理；图形的剪拼；最值问题；综合题．39．（2016福建省宁德市4分）如图，在Rt △ABC 中，∠BAC=90°，AB=4，AC=3，点D 、E 分别是AB 、AC 的中点，点G 、F 在BC 边上（均不与端点重合），DG ∥EF ．将△BDG 绕点D 顺时针旋转180°，将△CEF 绕点E 逆时针旋转180°，拼成四边形MGFN ，则四边形MGFN 周长l 的取值范围是【答案】495≤l ＜13．【分析】如图，连接DE ，作AH ⊥BC 于H ．首先证明GF=DE=52，要求四边形MNFG 周长的取值范围，只要求出MG 的最大值和最小值即可．【解析】如图，连接DE ，作AH ⊥BC 于H ．在Rt △ABC 中，∵∠BAC=90°，AB=4，AC=3，∴BC=22AB AC +=5，∵12•AB•AC=12•BC•AH，∴AH=125，∵AD=DB ，AE=EC ，∴DE ∥CB ，DE=12BC=52，∵DG ∥EF ，∴四边形DGFE 是平行四边形，∴GF=DE=52，由题意MN ∥BC ，GM ∥FN ，∴四边形MNFG 是平行四边形，∴当MG=NF=AH 时，可得四边形MNFG 周长的最小值=2×125+2×52=495，当G 与B 重合时可得周长的最大值为13，∵G 不与B 重合，∴495≤l ＜13．故答案为：495≤l ＜13．点睛：本题考查旋转变换、勾股定理、平行四边形的性质、三角形中位线定理等知识，解题的关键是灵活运用所学知识解决问题，学会取特殊点解决问题，属于中考常考题型．考点：旋转的性质；勾股定理；图形的剪拼；最值问题；综合题．40．（2016内蒙古呼伦贝尔市，第17题，3分）如图，在Rt △ABC 中，∠C=90°，AC=3，BC=4，把△ABC 绕AB 边上的点D 顺时针旋转90°得到△A′B′C′，A′C′交AB 于点E ，若AD=BE ，则△A′DE 的面积是 ．【答案】32．【分析】在Rt △ABC 中，由勾股定理求得AB=5，由旋转的性质可知AD=A′D，设AD=A′D=BE=x，则DE=5﹣2x ，根据旋转90°可证△A′DE∽△ACB ，利用相似比求x ，再求△A′DE 的面积．【解析】Rt △ABC 中，由勾股定理求22AC BC +，由旋转的性质，设AD=A′D=BE=x，则DE=5﹣2x ，∵△ABC 绕AB 边上的点D 顺时针旋转90°得到△A′B′C′，∴∠A′=∠A ，∠A′DE=∠C=90°，∴△A′DE∽△ACB ，∴'DE BC A D AC =，即5243x x-=，解得x=32，∴S△A′DE=12DE ×A′D=12×（5﹣2×32）×32=32，故答案为：32．点睛：本题考查了相似三角形的判定与性质，勾股定理及旋转的性质．关键是根据旋转的性质得出相似三角形，利用相似比求解．考点：旋转的性质；相似三角形的判定与性质；综合题．41．（2015宁夏，第14题，3分）如图，在平面直角坐标系中，点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点A′是直线45y x=上一点，则点B与其对应点B′间的距离为．【答案】5．【解析】试题分析：如图，连接AA′、BB′．∵点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′，∴点A′的纵坐标是4．又∵点A的对应点在直线45y x=上一点，∴445x=，解得x=5．∴点A′的坐标是（5，4），∴AA′=5．∴根据平移的性质知BB′=AA′=5．故答案为：5．考点：一次函数图象上点的坐标特征；坐标与图形变化-平移；综合题．42．（2015泰州，第16题，3分）如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP 翻折至△EBP，PE与CD相交于点O，且OE=OD，则AP的长为．【答案】4.8．【解析】试题分析：如图所示：∵四边形ABCD是矩形，∴∠D=∠A=∠C=90°，AD=BC=6，CD=AB=8，根据题意得：△ABP≌△EBP，∴EP=AP，∠E=∠A=90°，BE=AB=8，在△ODP和△OEG中，∵∠D=∠E，OD=OE，∠DOP=∠EOG ，∴△ODP ≌△OEG （ASA ），∴OP=OG ，PD=GE ，∴DG=EP ，设AP=EP=x ，则PD=GE=6﹣x ，DG=x ，∴CG=8﹣x ，BG=8﹣（6﹣x ）=2+x ，根据勾股定理得：222BC CG BG +=，即2226(8)(2)x x +-=+，解得：x=4.8，∴AP=4.8；故答案为：4.8．考点：翻折变换（折叠问题）；勾股定理；矩形的性质；综合题．43．（2015攀枝花，第15题，4分）如图，在边长为2的等边△ABC 中，D 为BC 的中点，E 是AC 边上一点，则BE+DE 的最小值为 ．【答案】7．【解析】试题分析：作B 关于AC 的对称点B′，连接BB′、B′D，交AC 于E ，此时BE+ED=B′E+ED=B′D，根据两点之间线段最短可知B′D 就是BE+ED 的最小值，∵B 、B′关于AC 的对称，∴AC 、BB′互相垂直平分，∴四边形ABCB′是平行四边形，∵三角形ABC 是边长为2，∵D 为BC 的中点，∴AD ⊥BC ，∴AD=3，BD=CD=1，BB′=2AD=23，作B′G⊥BC 的延长线于G ，∴B′G=AD=3，在Rt △B′BG 中，BG=22''BB B G -=22(23)(3)-=3，∴DG=BG ﹣BD=3﹣1=2，在Rt △B′DG 中，BD=22'DG B G +=222(3)+=7．故BE+ED 的最小值为7．考点：轴对称-最短路线问题；等边三角形的性质；最值问题；综合题．44．（2015宜宾，第15题，3分）如图，一次函数的图象与x 轴、y 轴分别相交于点A 、B ，将△AOB沿直线AB翻折，得△ACB．若C（32，32），则该一次函数的解析式为．【答案】33y x=-+．【解析】试题分析：连接OC，过点C作CD⊥x轴于点D，∵将△AOB沿直线AB翻折，得△ACB，C（32，3），∴AO=AC，OD=32，DC=32，BO=BC，则tan∠COD=CDOD=33，故∠COD=30°，∠BOC=60°，∴△BOC是等边三角形，且∠CAD=60°，则sin60°=CDAC，即AC=sin60CD=1，故A（1，0），sin30°=CDOC=32CO=12，则CO=3，故BO=3，B点坐标为：（0，3），设直线AB的解析式为：y kx b=+，则3k bb+=⎧⎪⎨=⎪⎩，解得：33kb⎧=-⎪⎨=⎪⎩，即直线AB的解析式为：33y x=-+．故答案为：33y x=-+．考点：翻折变换（折叠问题）；待定系数法求一次函数解析式；综合题．45．（2015达州，第14题，3分）如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上，点D落在D′处，C′D′交AE于点M．若AB=6，BC=9，则AM的长为．【答案】94．【解析】试题分析：根据折叠的性质可知，FC=FC′，∠C=∠FC′M=90°，设BF=x ，则FC=FC′=9﹣x ，∵222''BF BC FC +=，∴2223(9)x x +=-，解得：x=4，∵∠FC′M=90°，∴∠AC′M+∠BC′F=90°，又∵∠BFC′+BC′F=90°，∴∠AC′M=∠BFC′，∵∠A=∠B=90°，∴△AMC′∽△BC′F，∴''AC AM BF BC =，∵BC′=AC′=3，∴AM=94．故答案为：94．考点：翻折变换（折叠问题）；综合题．46．（2015凉山州，第26题，5分）菱形ABCD 在平面直角坐标系中的位置如图所示，顶点B （2，0），∠DOB=60°，点P 是对角线OC 上一个动点，E （0，﹣1），当EP+BP 最短时，点P 的坐标为 ．【答案】（33，23）．【解析】试题分析：连接ED ，如图，∵点B 的对称点是点D ，∴DP=BP，∴ED 即为EP+BP 最短，∵四边形ABCD 是菱形，顶点B （2，0），∠DOB=60°，∴点D 的坐标为（1，3），∴点C 的坐标为（3，3），∴可得直线OC 的解析式为：33y x =，∵点E 的坐标为（﹣1，0），∴可得直线ED 的解析式为：(13)1y x =+-，∵点P 是直线OC 和直线ED的交点，∴点P 的坐标为方程组33(13)1y x y x ⎧=⎪⎨⎪=+-⎩的解，解方程组得：23323x y ⎧=-⎪⎨=-⎪⎩，所以点P 的坐标为（233-，23-），故答案为：（233-，23-）．考点：菱形的性质；坐标与图形性质；轴对称-最短路线问题；动点型；压轴题；综合题．47．（2015内江，第14题，5分）如图，在四边形ABCD 中，AD∥BC，∠C=90°，E 为CD 上一点，分别以EA ，EB 为折痕将两个角（∠D，∠C）向内折叠，点C ，D 恰好落在AB 边的点F 处．若AD=2，BC=3，则EF 的长为 ．【答案】6．【解析】试题分析：∵分别以AE ，BE 为折痕将两个角（∠D，∠C）向内折叠，点C ，D 恰好落在AB 边的点F 处，∴DE=EF，CE=EF ，AF=AD=2，BF=CB=3，∴DC=2EF，AB=5，作AH⊥BC 于H ，∵AD∥BC，∠B=90°，∴四边形ADCH 为矩形，∴AH=DC=2EF，HB=BC ﹣CH=BC ﹣AD=1，在Rt△ABH 中，AH=22AB BH -=26，∴EF=6．故答案为：6．考点：翻折变换（折叠问题）；综合题．48．（2015孝感，第16题，3分）如图，四边形ABCD 是矩形纸片，AB=2．对折矩形纸片ABCD ，使AD 与BC 重合，折痕为EF ；展平后再过点B 折叠矩形纸片，使点A 落在EF 上的点N ，折痕BM 与EF 相交于点Q ；再次展平，连接BN ，MN ，延长MN 交BC 于点G ．有如下结论：①∠ABN=60°；②AM=1；③QN=3；④△BMG 是等边三角形；⑤P 为线段BM 上一动点，H 是BN 的中点，则PN+PH 的最小值是3．其中正确结论的序号是 ．【答案】①④⑤．【解析】试题分析：如图1，连接AN ，∵EF 垂直平分AB ，∴AN=BN ，根据折叠的性质，可得：AB=BN ，∴AN=AB=BN ，∴△ABN 为等边三角形，∴∠ABN=60°，∠PBN=60°÷2=30°，即结论①正确；∵∠ABN=60°，∠ABM=∠NBM ，∴∠ABM=∠NBM=60°÷2=30°，∴AM=AB •tan30°=32=23，即结论②不正确；∵EF ∥BC ，QN 是△MBG 的中位线，∴QN=12BG ，∵BG=BM=AB ÷cos ∠ABM=322÷=33，∴QN=14323⨯=33，即结论③不正确； ∵∠ABM=∠MBN=30°，∠BNM=∠BAM=90°，∴∠BMG=∠BNM ﹣∠MBN=90°﹣30°=60°，∴∠MBG=∠ABG ﹣∠ABM=90°﹣30°=60°，∴∠BGM=180°﹣60°﹣60°=60°，∴∠MBG=∠BMG=∠BGM=60°，∴△BMG 为等边三角形，即结论④正确； ∵△BMG 是等边三角形，点N 是MG 的中点，∴BN ⊥MG ，∴BN=BG•sin60°=433=2，P 与Q 重合时，PN+PH 的值最小，∵P 是BM 的中点，H 是BN 的中点，∴PH ∥MG ，∵MG ⊥BN ，∴PH ⊥BN ，又∵PE ⊥AB ，∴PH=PE ，∴PN+PH=PN+PE=EN ，∵22BN BE -2221-3∴3，∴PN+PH 3，即结论⑤正确．故答案为：①④⑤．考点：几何变换综合题；翻折变换（折叠问题）；动点型；最值问题；和差倍分；综合题；压轴题．49．（2015鄂州，第16题，3分）如图，∠AOB=30°，点M、N分别是射线OA、OB上的动点，OP平分∠AOB，且OP=6，当△PMN的周长取最小值时，四边形PMON的面积为．．【答案】36354考点：轴对称-最短路线问题；最值问题；综合题．50．（2015随州，第16题，3分）在▱ABCD中，AB＜BC，已知∠B=30°，AB=23沿AC翻折至△AB′C，使点B′落在▱ABCD所在的平面内，连接B′D．若△AB′D是直角三角形，则BC的长为．【答案】4或6．【解析】试题分析：①当∠B′AD=90°AB＜BC时，如图1，∵AD=BC，BC=B′C，∴AD=B′C，∵AC∥B′D，∠B′AD=90°，∴∠B′GC=90°，∵∠B=30°，AB=23，∴∠AB′C=30°，∴GC=12B′C=12BC，∴G是BC的中点，在RT△ABG中，BG=3 2AB=3232⨯=3，∴BC=6；②当∠AB′D=90°时，如图2，∵AD=BC，BC=B′C，∴AD=B′C，∵AC∥B′D，∴四边形ACDB′是等腰梯形，∵∠AB′D=90°，∴四边形ACDB′是矩形，∴∠BAC=90°，∵∠B=30°，AB=23，∴BC=AB÷3=233⨯=4，∴当BC的长为4或6时，△AB′D是直角三角形．故答案为：4或6．考点：翻折变换（折叠问题）；平行四边形的性质；分类讨论；综合题；压轴题．51．（2015梅州，第14题，3分）如图，将矩形纸片ABCD折叠，使点A与点C重合，折痕为EF，若AB=4，BC=2，那么线段EF的长为．5【解析】试题分析：如图所示，AC交EF于点O，由勾股定理知AC=25C与A重合时有EF ⊥AC，则Rt△AOE∽Rt△ABC，∴OE：BC=AO：AB，∴OE=5，故55．考点：翻折变换（折叠问题）；综合题．52．（2015河南省，第15题，3分）如图，正方形ABCD的边长是16，点E在边AB上，AE=3，点F是边BC上不与点B，C重合的一个动点，把△EB F沿EF折叠，点B落在B′处．若△CDB′恰为等腰三角形，则DB′的长为．【答案】16或45．【解析】试题分析：（i ）当B′D=B′C 时，过B′点作GH ∥AD ，则∠B′GE=90°，当B′C=B′D 时，AG=DH=12DC=8，由AE=3，AB=16，得BE=13．由翻折的性质，得B′E=BE=13，∴EG=AG ﹣AE=8﹣3=5，∴ B′G=22'B E EG -=22135-=12，∴B′H=GH﹣B′G=16﹣12=4，∴DB′=22'B H DH +=2248+=45；（ii ）当DB′=CD 时，则DB′=16（易知点F 在BC 上且不与点C 、B 重合）；（iii ）当CB′=CD 时，∵EB=EB′，CB=CB′，∴点E 、C 在BB′的垂直平分线上，∴EC 垂直平分BB′，由折叠可知点F 与点C 重合，不符合题意，舍去；综上所述，DB′的长为16或45．故答案为：16或45．考点：翻折变换（折叠问题）；分类讨论．53．（2015牡丹江，第20题，3分）矩形纸片ABCD ，AB=9，BC=6，在矩形边上有一点P ，且DP=3．将矩形纸片折叠，使点B 与点P 重合，折痕所在直线交矩形两边于点E ，F ，则EF 长为 ．【答案】62或210．【解析】试题分析：①如图1，当点P 在CD 上时，∵PD=3，CD=AB=9，∴CP=6，∵EF 垂直平分PB ，∴四边形PFBE 是正方形，EF 过点C ，∴EF=62②如图2，当点P 在AD 上时，过E 作EQ ⊥AB 于Q ，∵PD=3，AD=6，∴AP=3，∴22AP AB +=2239+=310EF 垂直平分PB ，∴∠1=∠2，∵∠A=∠EQF ，∴△ABP ∽△EFQ ，∴EF EQPB AB=，∴69310EF=，∴EF=210，综上所述：EF长为62或210．故答案为：62或210．考点：翻折变换（折叠问题）；分类讨论；综合题；压轴题．54．（2015绥化，第21题，3分）在矩形ABCD中，AB=4，BC=3，点P在AB上．若将△DAP沿DP折叠，使点A落在矩形对角线上的A'处，则AP的长为__________．【答案】32或94．【解析】试题分析：①点A落在矩形对角线BD上，如图1，∵AB=4，BC=3，∴BD=5，根据折叠的性质，AD=A′D=3，AP=A′P，∠A=∠PA′D=90°，∴BA′=2，设AP=x，则BP=4﹣x，∵222''BP BA PA=+，∴222(4)2x x-=+，解得：x=32，∴AP=32；②点A落在矩形对角线AC上，如图2，根据折叠的性质可知DP⊥AC，∴△DAP∽△ABC，∴AD ABAP BC=，∴AP=AD BCAB⋅=334⨯=94．故答案为：32或94．考点：翻折变换（折叠问题）；分类讨论；综合题；压轴题．。