光学棱镜应用实例
利用棱镜实验探究光的折射

利用棱镜实验探究光的折射光是一种电磁波,它在传播过程中会遇到不同介质的边界,从而发生折射现象。
折射是光线从一种介质进入另一种介质时改变传播方向的现象。
为了深入了解光的折射规律,科学家们利用棱镜进行了一系列实验。
棱镜是一种具有三个或更多平面镜面的透明介质。
当光线射入棱镜时,由于光的速度在不同介质中的传播速度不同,光线会发生折射。
通过观察和测量光线的折射角度,我们可以探究光的折射规律。
在实验中,首先需要准备一块透明的三棱镜。
将光源放置在光源台上,调整光源位置,使得光线能够射入棱镜。
然后,将一个光屏放置在棱镜的另一侧,用于接收折射后的光线。
接下来,调整棱镜的位置和角度,观察光线在棱镜内的折射现象。
在实验中,我们可以观察到以下几个现象。
首先,当光线从空气射入棱镜时,会发生向棱镜内弯曲的折射。
这是因为光在从一种介质射入另一种介质时,传播速度的改变导致光线的折射。
其次,当光线从棱镜射出时,会再次发生折射,但这次是向外弯曲的折射。
最后,我们还可以观察到光线在棱镜内部发生多次反射和折射的现象,形成美丽的彩虹光谱。
通过对这些现象的观察和测量,我们可以得出一些有趣的结论。
首先,光线在折射时遵循斯涅尔定律,即入射角与折射角的正弦比等于两种介质的折射率之比。
这个定律描述了光在不同介质中传播时的折射规律。
其次,光线在从一种介质射入另一种介质时会发生偏折,这是由于不同介质的折射率不同导致的。
最后,光线在经过多次反射和折射后,会分离出不同颜色的光谱,形成彩虹。
通过这些实验,我们不仅可以了解光的折射规律,还可以深入探究光的性质和行为。
光的折射不仅在日常生活中有重要应用,如眼镜、棱镜等光学仪器,还在科学研究和技术领域中发挥着重要作用。
例如,利用光的折射原理,我们可以设计出光纤通信系统,实现高速的信息传输。
总之,利用棱镜实验可以帮助我们深入了解光的折射规律。
通过观察和测量光线的折射角度,我们可以得出斯涅尔定律等有关光的规律和性质。
手机棱镜的应用和原理

手机棱镜的应用和原理引言手机棱镜是一种在手机摄像头镜头上安装的透明棱镜,它可以改变光线的传播方向,从而实现一些有趣的效果。
手机棱镜在手机摄影和增强现实领域得到广泛应用,它能够为用户带来更丰富多样的拍摄体验。
本文将介绍手机棱镜的应用和原理。
手机棱镜的应用手机棱镜能够改变光线的传播方向,并且可以在手机摄像头的视野范围内进行操作。
下面列举了手机棱镜的一些应用:1.水下摄影:手机棱镜可以将之前无法触及的水下景物反射到摄像头的视野中,使用户能够拍摄出清晰的水下照片。
2.平面投影:通过将手机棱镜放置在手机摄像头上,并投射到平面上,可以实现增强现实技术中的虚拟物体显示。
3.光线折射:手机棱镜可以将光线经过折射后聚焦到特定位置,实现类似显微镜的放大效果,用于拍摄微观物体。
4.全景拍摄:通过将手机棱镜放置在摄像头上,可以实现拍摄全景照片或视频,将更多的场景信息捕捉到画面中。
5.特殊效果:手机棱镜可以用于制作特殊效果,比如光线分光、光斑效果等,使照片更加艺术化。
手机棱镜的原理手机棱镜的原理基于光线的折射和反射。
下面是手机棱镜的工作原理:1.光线折射:当光线从一种介质(如空气)进入另一种介质(如玻璃)时,会发生折射现象。
手机棱镜通常使用的是光密度不同的材料,如玻璃或塑料,通过使光线从一个介质折射到另一个介质来改变光线的传播方向。
2.光线反射:光线在折射后,可能会发生反射。
手机棱镜通常设计成具有一定的角度,使光线在折射后发生反射,达到特定的目的。
3.光的波长:不同颜色的光在介质中传播时,会发生不同程度的折射。
手机棱镜可以利用这一点,使特定的光线折射到特定的位置,实现特定的效果。
手机棱镜的设计和制造需要考虑光学参数和材料的选择,以便在特定的应用场景中实现预期的效果。
结论手机棱镜是一种能够改变光线传播方向的装置,具有丰富的应用场景。
通过应用手机棱镜,用户可以拍摄水下照片、实现增强现实投影、光线折射放大效果、全景拍摄和创造特殊效果等。
光学棱镜颜色实验报告

一、实验目的1. 了解光学棱镜的基本原理和特性。
2. 观察并分析不同波长光在棱镜中色散现象。
3. 掌握使用光学棱镜进行颜色实验的方法和技巧。
二、实验原理光学棱镜是一种利用光的折射原理,使光线发生偏折和色散的透明体。
当光线从一种介质进入另一种介质时,由于两种介质折射率的不同,光线会发生偏折。
在光学棱镜中,不同波长的光由于折射率不同,导致光线偏折角度不同,从而产生色散现象。
三、实验器材1. 光学棱镜(至少两个不同色散率的棱镜)2. 白光光源(如白炽灯、卤素灯等)3. 凸透镜4. 凹透镜5. 白屏6. 刻度尺7. 记录本四、实验步骤1. 准备实验装置,将光学棱镜、凸透镜、凹透镜和白屏依次放置在光具座上。
2. 打开白光光源,调节光源位置,使光线垂直照射到光学棱镜上。
3. 观察并记录白光通过光学棱镜后,在白屏上形成的彩色光带。
4. 重复步骤2,分别使用不同色散率的棱镜进行实验,观察并记录彩色光带的变化。
5. 在白光光源前放置一个凸透镜,观察并记录彩色光带的变化。
6. 在白光光源前放置一个凹透镜,观察并记录彩色光带的变化。
7. 对比不同实验条件下的彩色光带,分析实验结果。
五、实验结果与分析1. 在实验过程中,观察到白光通过光学棱镜后,在白屏上形成了彩色光带,这说明光在棱镜中发生了色散现象。
2. 当使用不同色散率的棱镜时,彩色光带的宽度、颜色和位置有所变化,这说明不同色散率的棱镜对光的色散效果不同。
3. 在白光光源前放置凸透镜时,彩色光带变得更宽,颜色更丰富,这说明凸透镜具有放大作用。
4. 在白光光源前放置凹透镜时,彩色光带变得更窄,颜色变浅,这说明凹透镜具有缩小作用。
六、实验结论1. 光学棱镜能够使光发生色散现象,不同色散率的棱镜对光的色散效果不同。
2. 凸透镜具有放大作用,能够使彩色光带变得更宽、颜色更丰富。
3. 凹透镜具有缩小作用,能够使彩色光带变得更窄、颜色变浅。
七、实验讨论1. 实验过程中,由于环境因素和仪器精度等因素的影响,实验结果可能存在一定误差。
光的折射揭示光在光学棱镜中的全反射现象

光的折射揭示光在光学棱镜中的全反射现象折射是光线从一种介质传播到另一种介质时改变传播方向的现象。
而在光学棱镜中,光线的折射现象尤为引人注目,尤其是全反射现象使得光在某些情况下完全发生反射。
本文将探讨光的折射如何揭示光学棱镜中的全反射现象。
一、折射现象及折射定律光线在从一种介质传播到另一种介质时,会发生折射现象。
其具体规律由折射定律描述,即入射光线、折射光线和法线在同一平面上,且入射角和折射角的正弦比等于两种介质的折射率之比。
这一定律可以用数学公式表示为:n₁sinθ₁ = n₂sinθ₂,其中n₁和n₂分别代表两种介质的折射率,θ₁和θ₂分别代表入射角和折射角。
折射定律的发现为我们理解光在光学棱镜中的行为提供了依据。
二、折射角的变化导致全反射现象光线从一种介质进入另一种折射率较小的介质时,折射角会大于入射角。
当入射角越大时,折射角也越大,直到达到临界角,此时折射光线会沿着介质边界发生全反射。
全反射的产生是因为折射介质无法将光线传导至折射率较小的介质,而使光线完全反射回折射介质。
三、光学棱镜中的折射和全反射现象光学棱镜是一种透明介质通过改变光线的传播方向来分离光的仪器。
当光线经过光学棱镜时,根据入射角和光学棱镜的折射率,光线会发生折射现象。
而当入射角大于临界角时,全反射现象会发生在光学棱镜的边界上。
这意味着光线无法透过光学棱镜,而是被完全反射回原介质中。
四、全反射的应用全反射现象在实际应用中有着广泛的用途。
其中一个例子是光纤通信技术。
光纤通过利用全反射现象来传输光信号。
光线以接近光纤轴的入射角进入光纤中,而光纤的折射率较小,使得光线在光纤内部发生全反射,并沿着光纤传输到目标地点。
这种传输方式具有高速、低损耗和抗干扰的特点,因此在现代通信领域中得到广泛应用。
结论:光的折射现象揭示了光学棱镜中的全反射现象。
通过折射定律的描述,我们理解了光线在不同介质中传播时发生的变化。
当光线遇到入射角大于临界角的情况时,会发生全反射现象,导致光线完全反射回原介质中。
光学实验利用棱镜解析光谱

棱镜的种类和选 择
平面棱镜
定义:平面棱镜是一种特殊的光学棱镜,其两个面都是平面,且相互垂直 特点:平面棱镜可以将入射光分为反射光和折射光,其中反射光和折射光分别沿不同的方向传播 应用:平面棱镜在光学实验中常被用于研究光的反射和折射现象,以及用于光谱分析等领域
选择:在选择平面棱镜时,需要考虑其材质、精度、表面质量等因素,以确保实验结果的准确性和可靠性
选择合适的棱镜
根据实验需求选择合适的棱镜类型,如分束棱镜、成像棱镜等。 考虑棱镜的材料和镀膜,以确保其光学性能和耐久性。 考虑棱镜的尺寸和形状,以满足实验中对光路和安装的需求。 参考相关的应用案例和研究文献,了解不同类型棱镜的特点和优缺点。
光学实验操作步 骤
准备实验器材
棱镜:用于分束 光线,形成光谱
结合其他光学仪器进行实验
可以结合显微镜观察棱镜 产生的光谱
结合光栅进行光谱分析
结合干涉仪研究光的干涉 现象
结合棱镜和透镜进行光学 实验
创新实验方法和应用领域
实验技术创新:引入计算机控 制技术,实现自动化光谱采集 与分析
实验方法改进:采用新型棱 镜材料,提高光谱解析精度
应用领域拓展:将光学实验棱 镜解析光谱技术应用于生物医
学、环境监测等领域
跨学科融合:结合其他学科技 术,开发多功能光谱分析系统
感谢您的观看
汇报人:
行星大气研究:分析行星的大 气光谱,研究行星的大气组成
和特性
星际物质研究:通过分析星际 物质的光谱,研究宇宙的起源
和演化
化学分析
确定物质的组成和结构
鉴别物质的真伪和纯度
添加标题
添加标题
检测物质的含量和浓度
添加标题
添加标题
研究物质的反应机理和动力学
《应用光学》第4章 平面镜棱镜系统1
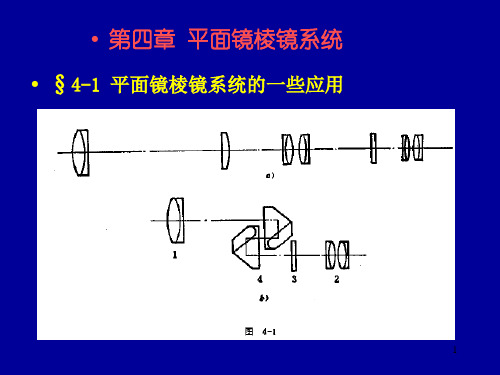
L ' d (1 tgI2 ) d (1 sin I2 )
• 图4-14所示为一个 三次反射棱镜,称为 斯密特棱镜。它使光 轴折转45°角。由于 棱镜中的光轴折叠, 因此,对缩小仪器的 体积非常有利。
图4-14
15
2)屋脊棱镜
光学系统中,光线经平面镜棱镜系统时的反射次数 可能为奇数,这时物体成镜像,为了获得和物相似 的像,在不宜再增加反射面的情况下,可以用两个 互相垂直的反射面代替其中的一个反射面,这两个 互相垂直的反射面叫作屋脊面。带有屋脊面的棱镜 叫屋脊棱镜。
• 第四章 平面镜棱镜系统 • §4-1 平面镜棱镜系统的一些应用
1
平面镜或棱镜、透镜组成的系统,则能满足系统改变 光束方向和物象间方位的要求。如目前使用的军用观 察望远镜,由于在系统中使用了棱镜,如图4-1b所示, 所以它在不加入导向透镜的情况下即可获得正像,同 时又大大地缩小了仪器的体积,减轻了仪器的重量。
下列关系:
由O1O2M得
2i1 2i2 或者 2(i1 i2 )
因二平面镜的法线交于N,
故由O1O2N得
i1 i2或 i1 i2
带入上式得 2
8
从上式可知, 与i角大小无关,只取决于两平面镜 间的夹角,因此,光线方向的改变可以根据设计需 要通过选择适当的角来实现。如果保持两平面镜间
和折射棱镜定义相同,反射棱镜的折射面和反射 面均称为棱镜的工作面,工作面的交线成反射棱镜的 棱,和各棱垂直的截面称为主截面,光学系统的光轴 位在棱镜中的 部分称为反射棱镜的光轴。
10
图4-10
11
图4-11
12
• 一、反射棱镜的分类
•常用的反射棱镜可分为三类:简单棱镜、屋脊 棱镜和复合棱镜。
眼用棱镜的应用

垂直棱镜允差 (△ )
±(0.25+0.05×Smax) ±(0.37+0.05×Smax) ±(0.50+0.05×Smax)
65
棱镜检测——GB10810.1-2005
例如:顶焦度:+0.50/-2.50×20。标称棱镜度不超过2.00△。其棱 镜度的计算方法如下:
本处方中,两主子午面顶焦度值分别为+0.50D和-2.00D,最大子
右眼镜片-2.00/+3.00×180的光心向30°方向移心6mm,求视轴处 的棱镜效果
36
球柱面透镜的移心
左眼镜片-6.00/+2.00×90要产生2 △B90°和1 △B180°的棱镜 效果,如何移心?
37
斜轴散光透镜的棱镜效果
求左眼镜片+2.00/+2.00×120在光心下方6mm偏内4mm处的棱镜效果
O
光学中心与瞳孔吻合
63
棱镜镜片的 检测
64
棱镜检测——GB10810.1-2005
5.1. 4 光学中心和棱镜度 眼镜片的光学中心偏差由镜片几何中心处的棱镜度表示。在棱镜基准点所测得的处方棱镜度和减
薄棱镜的总和偏差应符合表 4 的规定,按照 6.3 表述的方法进行测量。 单光镜片的标称棱镜度为零,其在镜片几何中心处所测得的棱镜度偏差应符合表 4 关于
48
近用有效棱镜度
有效棱镜度的计算
P 1 s
l
49
棱镜镜片的制造
50
棱镜的偏向角与顶角
(n 1)
51
棱镜的偏向角与顶角
棱镜的顶角、偏向角与棱镜度的关系
顶角 1° 1.1° 1.91°
偏向角 0.523° 0.573°
应用光学:第四章 平面镜和棱镜
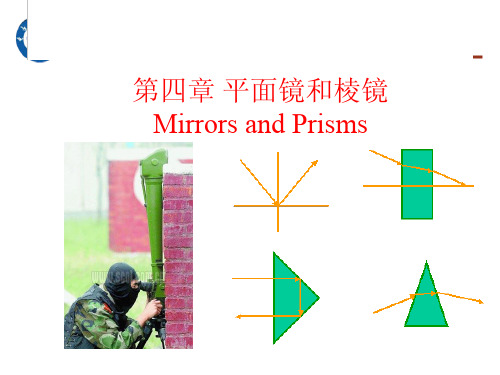
2、双面镜的旋转特性 β=2θ
P1
P2
I1
I1
I2 θ I2
θ
β
• 结论:
– 当两面镜夹角为θ时,出射光线和入射光线的夹角为2θ;其旋转
方向,与反射面按反射次序由P1转到P2的方向相同。
– 当两平面镜一起转动时,出射光线与入射光线的夹角不变,只是光 线位置发生了平移(入射光线方向不变)
– 若两平面镜相对移动α角,出射光线方向改变2α。所以在运输过
n1 n 2
(4)相对色散: (n1 n2 ) (nF n C )
③ 反射材料的光学特性
a.反射元件:抛光玻璃或金属表面镀上高反射率金属膜 或介质膜;
b.反射材料: (1)不存在色散; (2) 唯一光学特性是对各种色光的反射率: (3)金属反射膜的反射率随波长不同而不同:
–折射棱 —— 入射面与出射面的交 线
–顶角(折射角) ——α
–偏向角δ —— 入射光线与出射光 线的夹角从入射光线转到出射光线,
顺正逆负
I1
α
I1´ n -I2
-I2´ δ
①偏向角
sin I1 nsin I1'
sin
I2
n sin
I
' 2
sin
1 2
(
I1
I2'
)
cos
1 2
(
I1
I
' 2
)
n
sin
I2
n sin
I
' 2
cos I1dI1 n cos I1'dI1'
cos I2 dI2
n
cos
I
' 2
dI
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Optical Prism Application Examples
The angle, position, and number of surfaces of a prism help define the type and function. To understand how the most popular prisms work and how each can best be used in light reflection and refraction applications, consider right angle prisms, roof prisms, and combination prisms. For the theory of how prisms work and a selection guide with over ten unique geometries, view Introduction to Prisms.
RIGHT ANGLE PRISM
Figure 1: 45° - 90° - 45° as a Right Angle Prism Showing Inversion (Left) and Reversion (Right)
By far the mo st commonly used prism is the 45° - 90° - 45° prism, known popularly as the right angle prism. It can be used in many ways to achieve different results pertaining to image parity or deviation and is named so for the angles on its triangular faces. The most common application of the 45° - 90° - 45° prism is to treat it as a right angle prism, which has only a single reflection that deviates the incident ray by 90°. The produced image will then become left-handed, but depending upon the position of the prism, can be inverted or reverted (Figure 1).
Figure 2: Fixed 180° Rotation with a Porro System
Using the hypotenuse face of the prism rather than the leg faces allows for another configuration known as the porro prism. This produces a right-handed image since two reflections occur. The ray's direction is reversed when using a porro prism since the object enters and the image exits the same face. The position of the prism determines whether a rotation or just a deviation occurs (Figure 2).
Figure 3: 180° Rotation with a Pechan-Roof Prism
Lastly, a 45° - 90° - 45° p rism can also be used as a dove prism. A dove prism rotates the image 180°, but since only one reflection occurs, it will become either reverted or inverted depending on the position of the prism (Figure 3).
ROOF PRISM
A prism roof consists of two reflecti ng surfaces located 90° from each other. It is equivalent in function when compared to any other reflecting surface, except handedness does not change. A good example of this is the amici (roof) prism, which is basically a right angle prism with a roof. Under this configuration, a deviation of 90° still occurs, but without changing parity. A roof prism is often used in conjunction with other prisms in order to achieve the desired parity.
COMBINATION PRISMS
Many combination prisms are possible with slight adjustments to the orientation and/or coating applied to the surfaces of the individual prisms used. Ultimately, the application dictates the type of combination necessary. Consider the most well-known combination prisms: porro system, Pechan (roof) prism, and beamsplitters.
Figure 4: Fixed 180° Rotation with a Porro System
A porro prism is often used in combination with itself to create a porro system (Figure
4) with a total of four reflections. Due to its ability to produce an upside down image rotated 180° from the original while maintaining right-handedness, this type of image erection prism is extremely useful for binocular and telescope applications. It is important to keep in mind that the ray path does become displaced, a fact that must be taken into account when adjusting the rest of the optical components used with a porro system, such as an objective lens and eyepiece for binoculars.
Figure 5: 180° Rotation with a Pechan-Roof Prism
Figure 6: Cube Beamsplitter
Edmund Optics manufactures prisms in a range of geometries for simple dispersion to complex, multi optical element applications. Understanding the optical theories behind each specific geometry helps one select the best prism or combination of prisms for any application.。
