第四章 眼用棱镜和透镜的棱镜效果
合集下载
第四章--眼用棱镜和透镜的棱镜效果

+2.00DS OS +2.00DS 这副眼镜是用来阅读的,制作的时候也是按照近用瞳
距来制作的,但是患者阅读的时候视线是从镜片 光学中心下放5mm处通过的,请问此戴镜者在阅 读的时候每只眼睛产生的棱镜效果是多少?两只 眼睛总的棱镜效果是多少?
75
差异棱镜效果
基底0º合成一等效棱镜
34
解:(1)作图法: 用矢量加法
测量出, OR5 37
5B37
(2)计算法
O R O2 V O2 H 3 2 4 2 5
tan 3 0.75 36.87
4
所以 3△B90º()4△B0º=5ºB36.87º
35
例6-3 试合成3△B270º与4△B0º两棱镜 解:(1)作图6-12b
测量得OR=5, 37323
得到等效棱镜为5△B323º
(2)计算法:
O RO2V O2H 5
tan30.75 37323
4
所以3△B270º()与4△B0º=5△B323º
36
2、棱镜度的分解 例6-4:.试将5△B30º的棱镜分解为垂直与水平方向的两棱镜 解:(1)作图法
在坐标上沿30º方向作出OR=5。 过R点作RHOH,RV OV。测量 出OH=4.3,OV=2.5。 所以:5△B30º=2.5△B90º()4.3△B0º (2)计算法
偏向角与顶角的关系
(n1)
24
棱镜的偏向角与顶角
棱镜的顶角、偏向角与棱镜度的关系
顶角
偏向角
棱镜度
1°
0.523°
0.91△
1.1°
0.573°
1△
1.91°
1°
1.75△
25
棱镜的基底位置表示
距来制作的,但是患者阅读的时候视线是从镜片 光学中心下放5mm处通过的,请问此戴镜者在阅 读的时候每只眼睛产生的棱镜效果是多少?两只 眼睛总的棱镜效果是多少?
75
差异棱镜效果
基底0º合成一等效棱镜
34
解:(1)作图法: 用矢量加法
测量出, OR5 37
5B37
(2)计算法
O R O2 V O2 H 3 2 4 2 5
tan 3 0.75 36.87
4
所以 3△B90º()4△B0º=5ºB36.87º
35
例6-3 试合成3△B270º与4△B0º两棱镜 解:(1)作图6-12b
测量得OR=5, 37323
得到等效棱镜为5△B323º
(2)计算法:
O RO2V O2H 5
tan30.75 37323
4
所以3△B270º()与4△B0º=5△B323º
36
2、棱镜度的分解 例6-4:.试将5△B30º的棱镜分解为垂直与水平方向的两棱镜 解:(1)作图法
在坐标上沿30º方向作出OR=5。 过R点作RHOH,RV OV。测量 出OH=4.3,OV=2.5。 所以:5△B30º=2.5△B90º()4.3△B0º (2)计算法
偏向角与顶角的关系
(n1)
24
棱镜的偏向角与顶角
棱镜的顶角、偏向角与棱镜度的关系
顶角
偏向角
棱镜度
1°
0.523°
0.91△
1.1°
0.573°
1△
1.91°
1°
1.75△
25
棱镜的基底位置表示
棱镜片光学技术—棱镜效果(眼镜光学技术课件)

P cF 0.33 0.9 B0
左眼俯视图
• 例题二
– 计算左眼镜片-2.50DCX180在光心上方5mm 处的棱镜效果。
P cF 0.5 2.5 1.25 B90
左眼侧视图
二、球柱镜片的棱镜效果
球柱镜片可看成是球镜片与柱镜片或两个 正交的柱镜片叠加而成。所以,球柱镜片的棱 镜效果也可看作是球镜片与柱镜片棱镜效果的 叠加或相应两正交柱镜片效果的叠加。
P P12 P22 2.24
tan P2 1 0.5
P1 2
180 26.57 206.57
2.24 B206 .57
• 例题二
将右眼镜片-2.00DS/+3.00DCX180的光心向30°方向移心 6mm,求视轴处的棱镜效果。
解:将移心量分解: cV 6 sin 30 3mm
• 知识要求
– 像位移引起的旋转放大
• 能力要求
– 会将镜片的棱镜效果,运用到眼镜使用中,解 决配镜中的实际问题
• 素质要求
– 独立学习、独立思考 – 发现和总结实验现象及规律 – 团队合作 – 爱护实验仪器
通过远离镜片光心的位置看远方物体时,与不戴眼
镜看同一远方物体时,眼睛的旋转角度是不同的。不通
– 镜片上任意一点的棱镜效果
• 能力要求
– 会计算球镜片上任意一点的棱镜效果
• 素质要求
– 独立学习、独立思考 – 发现和总结实验现象及规律 – 团队合作 – 爱护实验仪器
一、棱镜效果的定义
– 球镜片上任一点对光线的偏折力称为该点的棱镜效果 (prism effect) 。
– 在光心(光轴上)位置,入射光是垂直于镜片两个表 面的,所以光心的棱镜效果等于零;其他位置则存在 棱镜。
左眼俯视图
• 例题二
– 计算左眼镜片-2.50DCX180在光心上方5mm 处的棱镜效果。
P cF 0.5 2.5 1.25 B90
左眼侧视图
二、球柱镜片的棱镜效果
球柱镜片可看成是球镜片与柱镜片或两个 正交的柱镜片叠加而成。所以,球柱镜片的棱 镜效果也可看作是球镜片与柱镜片棱镜效果的 叠加或相应两正交柱镜片效果的叠加。
P P12 P22 2.24
tan P2 1 0.5
P1 2
180 26.57 206.57
2.24 B206 .57
• 例题二
将右眼镜片-2.00DS/+3.00DCX180的光心向30°方向移心 6mm,求视轴处的棱镜效果。
解:将移心量分解: cV 6 sin 30 3mm
• 知识要求
– 像位移引起的旋转放大
• 能力要求
– 会将镜片的棱镜效果,运用到眼镜使用中,解 决配镜中的实际问题
• 素质要求
– 独立学习、独立思考 – 发现和总结实验现象及规律 – 团队合作 – 爱护实验仪器
通过远离镜片光心的位置看远方物体时,与不戴眼
镜看同一远方物体时,眼睛的旋转角度是不同的。不通
– 镜片上任意一点的棱镜效果
• 能力要求
– 会计算球镜片上任意一点的棱镜效果
• 素质要求
– 独立学习、独立思考 – 发现和总结实验现象及规律 – 团队合作 – 爱护实验仪器
一、棱镜效果的定义
– 球镜片上任一点对光线的偏折力称为该点的棱镜效果 (prism effect) 。
– 在光心(光轴上)位置,入射光是垂直于镜片两个表 面的,所以光心的棱镜效果等于零;其他位置则存在 棱镜。
眼镜学光学棱镜

9
透镜的棱镜效果
双眼的棱镜效果
5△
5△
5△
5△
0
10△BO
透镜的棱镜效果
双眼的棱镜效果
Z如果双眼前都加棱镜时: Z基底方向相同的,棱镜度互相抵消 Z基底方向相反的,棱镜度互相叠加 Z举例
要使双眼获得10△BO的棱镜效果 方法三:右眼加5△BO,左眼加5△BO 方法四:右眼加7△BO,左眼加3△BO 方法五:右眼加12△BO,左眼加2△BI …………
透镜的棱镜效果
透镜可以想象为无数棱镜的组合 透镜上任一点对光线的偏折力称为该点的棱镜效
果
7
透镜的棱镜效果
如何计算透镜在特定位置的棱镜效果?
Z球镜上任意点的棱镜效果
c f
P = c = cF f
透镜的棱镜效果
球镜上任意点的棱镜效果
Z基底方向 凸透镜光心上方3mm处: BD 凹透镜光心上方3mm处: BU 凸透镜光心内侧3mm处: BO 凹透镜光心内侧3mm处: B I
眼通过棱镜视物,像向棱镜顶角的方向偏移
棱镜的光学作用
眼通过棱镜视物的原理
棱镜的表示方式
棱镜使光线偏折的程度
Z棱镜度 Z厘弧度
棱镜的方向
Z以棱镜底的方向来表示
棱镜的单位
棱镜度
Z在1m处使光线偏移1cm,作为1△
1m
1△ = 0.573 ° 10△ = 5.71 °
1cm 10cm
棱镜的单位
厘弧度
2
棱镜的基底位置
棱镜的基底位置
老式英国标记法 新式英国标记法
棱镜的基底位置
四个主要的基底方向
上
上
外
内
外
下
下
棱镜的基底位置
透镜的棱镜效果
双眼的棱镜效果
5△
5△
5△
5△
0
10△BO
透镜的棱镜效果
双眼的棱镜效果
Z如果双眼前都加棱镜时: Z基底方向相同的,棱镜度互相抵消 Z基底方向相反的,棱镜度互相叠加 Z举例
要使双眼获得10△BO的棱镜效果 方法三:右眼加5△BO,左眼加5△BO 方法四:右眼加7△BO,左眼加3△BO 方法五:右眼加12△BO,左眼加2△BI …………
透镜的棱镜效果
透镜可以想象为无数棱镜的组合 透镜上任一点对光线的偏折力称为该点的棱镜效
果
7
透镜的棱镜效果
如何计算透镜在特定位置的棱镜效果?
Z球镜上任意点的棱镜效果
c f
P = c = cF f
透镜的棱镜效果
球镜上任意点的棱镜效果
Z基底方向 凸透镜光心上方3mm处: BD 凹透镜光心上方3mm处: BU 凸透镜光心内侧3mm处: BO 凹透镜光心内侧3mm处: B I
眼通过棱镜视物,像向棱镜顶角的方向偏移
棱镜的光学作用
眼通过棱镜视物的原理
棱镜的表示方式
棱镜使光线偏折的程度
Z棱镜度 Z厘弧度
棱镜的方向
Z以棱镜底的方向来表示
棱镜的单位
棱镜度
Z在1m处使光线偏移1cm,作为1△
1m
1△ = 0.573 ° 10△ = 5.71 °
1cm 10cm
棱镜的单位
厘弧度
2
棱镜的基底位置
棱镜的基底位置
老式英国标记法 新式英国标记法
棱镜的基底位置
四个主要的基底方向
上
上
外
内
外
下
下
棱镜的基底位置
眼用棱镜和透镜的棱镜效果

六、柱面镜的移心
柱面镜移心方向在与轴垂直方向上。
例: 左眼处方+2.00×90°要产生1 △B180 ° 的棱镜效果,求移心量和方向。
解: c=P/F=1/2=0.5cm (向内移5mm)
27
可编辑课件PPT
七、球柱面镜的棱镜效果
球柱面镜的棱镜效果可看作是球面镜与柱 面镜棱镜效果的叠加或相应两正交柱面透 镜棱镜效果的叠加。
29
可编辑课件PPT
九、在临床中的应用
1.球镜棱镜效果应用的前提 2.隐斜 3.矫正辐辏功能的不足 4.其他: 解释临床上的一些现象
30
可编辑课件PPT
第五节 Fresnel棱镜
1. Fresnel棱镜: 由一系列缩小的习用棱镜紧密排列 于平板之上构成。
2. 原理: 去除习用棱镜或透镜的非屈光部分,以减 轻重量,增大口径。
旋转棱镜 透镜的棱镜效果 Fresnel棱镜
3
可编辑课件PPT
第一节 眼用棱镜
一、棱镜的构造
4
可编辑课件PPT
相关概念
1.棱镜: 两个平面相交形成的三角形透明柱。 2.顶角: 两个折射面相交的角,大小决定了
棱镜对光线偏折的能力的大小。 3.底: 与顶角相对的一面。 4.底顶线: 垂直于底和顶边的线,用于表示
棱镜的方向。 5.主截面: 与定线和两个平面垂直的切面
5
可编辑课件PPT
二、棱镜的两个重要性质
1.光线通过棱镜后向基底方向偏折。 d=i1+i2’-a 2.人眼通过棱镜视物, 像要向顶的方向偏折。
6
可编辑课件PPT
白光通过棱镜后发生色散
红 橙 黄 绿 青 蓝 紫
7
可编辑课件PPT
三、棱镜的单位和测量
棱镜片—棱镜效果(眼镜光学技术课件)

+2.00 X180 / +4.00 X 90 第一柱镜 P1 c1F1 0.5 2 1 B270
第二柱镜 P2 c2F2 0.5 4 2 B180
总: P PH / PV 2 B180 /1 B270
+4.00
二、球柱镜片的棱镜效果
例3:试求右眼镜片+2.00+2.00X90在光心上方
tan 3.2 1.6 58
2
即:合成棱镜效果为是 3.77 B122
四、镜片移心所产生的棱镜效果
移心法则
• 正球镜片移心的方向应与所需棱镜之底的方向相同 • 负球镜片移心的方向应与所需棱镜之底的方向相反
要想产生底朝内的棱镜效果,就将正球镜 片光心向鼻侧移,或将负球镜片光心向颞 侧移。
四、镜片移心所产生的棱镜效果
球+柱
柱+柱
二、球柱镜片的棱镜效果
例3:试求右眼镜片+2.00+2.00X90在光心上方
5mm及光心偏内5mm处的棱镜效果。
解一:看成是球镜片+柱镜片
球镜片
PHs cHsFHs 0.5 2 1 B180 PVs cVsFVs 0.5 2 1 B270
+2.00 +2.00
柱镜片
总:
P——棱镜度 c——该点到光心的距离,cm F——镜片屈光力
三、球镜片上任意点的棱镜效果
•例1:一个镜片+5.00DS,问在其上方5mm处A点 的棱镜如何?
解:如图所示,在A点,
棱镜大小:P cF 0.55 2.5
棱镜基底方向:向下
故在A点棱镜为 2.5 BD
A
5mm
+5.00D
三、球镜片上任意点的棱镜效果
《应用光学》第4章 平面镜棱镜系统1
L ' d (1 tgI2 ) d (1 sin I2 )
• 图4-14所示为一个 三次反射棱镜,称为 斯密特棱镜。它使光 轴折转45°角。由于 棱镜中的光轴折叠, 因此,对缩小仪器的 体积非常有利。
图4-14
15
2)屋脊棱镜
光学系统中,光线经平面镜棱镜系统时的反射次数 可能为奇数,这时物体成镜像,为了获得和物相似 的像,在不宜再增加反射面的情况下,可以用两个 互相垂直的反射面代替其中的一个反射面,这两个 互相垂直的反射面叫作屋脊面。带有屋脊面的棱镜 叫屋脊棱镜。
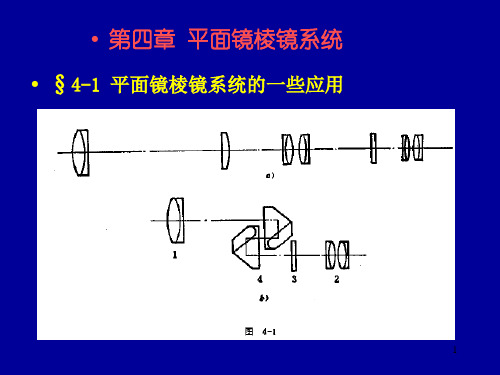
• 第四章 平面镜棱镜系统 • §4-1 平面镜棱镜系统的一些应用
1
平面镜或棱镜、透镜组成的系统,则能满足系统改变 光束方向和物象间方位的要求。如目前使用的军用观 察望远镜,由于在系统中使用了棱镜,如图4-1b所示, 所以它在不加入导向透镜的情况下即可获得正像,同 时又大大地缩小了仪器的体积,减轻了仪器的重量。
下列关系:
由O1O2M得
2i1 2i2 或者 2(i1 i2 )
因二平面镜的法线交于N,
故由O1O2N得
i1 i2或 i1 i2
带入上式得 2
8
从上式可知, 与i角大小无关,只取决于两平面镜 间的夹角,因此,光线方向的改变可以根据设计需 要通过选择适当的角来实现。如果保持两平面镜间
和折射棱镜定义相同,反射棱镜的折射面和反射 面均称为棱镜的工作面,工作面的交线成反射棱镜的 棱,和各棱垂直的截面称为主截面,光学系统的光轴 位在棱镜中的 部分称为反射棱镜的光轴。
10
图4-10
11
图4-11
12
• 一、反射棱镜的分类
•常用的反射棱镜可分为三类:简单棱镜、屋脊 棱镜和复合棱镜。
眼用棱镜的应用

垂直棱镜允差 (△ )
±(0.25+0.05×Smax) ±(0.37+0.05×Smax) ±(0.50+0.05×Smax)
65
棱镜检测——GB10810.1-2005
例如:顶焦度:+0.50/-2.50×20。标称棱镜度不超过2.00△。其棱 镜度的计算方法如下:
本处方中,两主子午面顶焦度值分别为+0.50D和-2.00D,最大子
右眼镜片-2.00/+3.00×180的光心向30°方向移心6mm,求视轴处 的棱镜效果
36
球柱面透镜的移心
左眼镜片-6.00/+2.00×90要产生2 △B90°和1 △B180°的棱镜 效果,如何移心?
37
斜轴散光透镜的棱镜效果
求左眼镜片+2.00/+2.00×120在光心下方6mm偏内4mm处的棱镜效果
O
光学中心与瞳孔吻合
63
棱镜镜片的 检测
64
棱镜检测——GB10810.1-2005
5.1. 4 光学中心和棱镜度 眼镜片的光学中心偏差由镜片几何中心处的棱镜度表示。在棱镜基准点所测得的处方棱镜度和减
薄棱镜的总和偏差应符合表 4 的规定,按照 6.3 表述的方法进行测量。 单光镜片的标称棱镜度为零,其在镜片几何中心处所测得的棱镜度偏差应符合表 4 关于
48
近用有效棱镜度
有效棱镜度的计算
P 1 s
l
49
棱镜镜片的制造
50
棱镜的偏向角与顶角
(n 1)
51
棱镜的偏向角与顶角
棱镜的顶角、偏向角与棱镜度的关系
顶角 1° 1.1° 1.91°
偏向角 0.523° 0.573°
眼用棱镜的应用

25
棱镜度的计算
26
透镜的棱镜效果
• 公式
P = C*F P:棱镜度 C:入射点到光心的距离 F:透镜的屈光度
28
球镜上任意一点的棱镜效果
• 举例: ➢ 右眼透镜+3.50D,求以下位置的棱镜效果: – 光心下方5mm处 – 光心内侧4mm处 – 光心下方5mm且内侧4mm处
30
透镜的移心
• 为了获得一定的棱镜效果,可以将透镜的光心向特定方向移动 特定的距离,这个过程称为移心
• 一个右眼前戴镜为+4.00DCⅹ90,如果通过光心内侧3mm且上方 4mm处注视,求棱镜效果
34
球柱透镜的棱镜效果
• 两种途径 – 分别计算球镜和柱镜产生的棱镜效果,之后再合成即可 – 将处方变换成柱镜形式,分别计算两个柱镜的棱镜效果,之 后再合成
35
球柱透镜的棱镜效果
• 右眼镜片为+2.00DS/+2.00DCⅹ90°当眼睛从光心上方5偏内5看 近物体时产生怎样的棱镜效果
• 右眼镜片-2.00/+3.00×180的光心向30°方向移心6mm,求视轴 处的棱镜效果
36
球柱面透镜的移心
• 左眼镜片-6.00/+2.00×90要产生2 △B90°和1 △B180°的棱 镜效果,如何移心?
37
斜轴散光透镜的棱镜效果
• 求左眼镜片+2.00/+2.00×120在光心下方6mm偏内4mm处的棱镜效果
心凹与另一眼中心凹以外的点建立点点对应关系。以消除复视现 象。
• 4. 偏心注视(eccentric fixation):单眼注视时使用中心凹外一点注 视目标。
• 5. 弱视(amblyopia):
棱镜度的计算
26
透镜的棱镜效果
• 公式
P = C*F P:棱镜度 C:入射点到光心的距离 F:透镜的屈光度
28
球镜上任意一点的棱镜效果
• 举例: ➢ 右眼透镜+3.50D,求以下位置的棱镜效果: – 光心下方5mm处 – 光心内侧4mm处 – 光心下方5mm且内侧4mm处
30
透镜的移心
• 为了获得一定的棱镜效果,可以将透镜的光心向特定方向移动 特定的距离,这个过程称为移心
• 一个右眼前戴镜为+4.00DCⅹ90,如果通过光心内侧3mm且上方 4mm处注视,求棱镜效果
34
球柱透镜的棱镜效果
• 两种途径 – 分别计算球镜和柱镜产生的棱镜效果,之后再合成即可 – 将处方变换成柱镜形式,分别计算两个柱镜的棱镜效果,之 后再合成
35
球柱透镜的棱镜效果
• 右眼镜片为+2.00DS/+2.00DCⅹ90°当眼睛从光心上方5偏内5看 近物体时产生怎样的棱镜效果
• 右眼镜片-2.00/+3.00×180的光心向30°方向移心6mm,求视轴 处的棱镜效果
36
球柱面透镜的移心
• 左眼镜片-6.00/+2.00×90要产生2 △B90°和1 △B180°的棱 镜效果,如何移心?
37
斜轴散光透镜的棱镜效果
• 求左眼镜片+2.00/+2.00×120在光心下方6mm偏内4mm处的棱镜效果
心凹与另一眼中心凹以外的点建立点点对应关系。以消除复视现 象。
• 4. 偏心注视(eccentric fixation):单眼注视时使用中心凹外一点注 视目标。
• 5. 弱视(amblyopia):
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
OH OR cos 5 cos30 4.3 B0
OV OR sin 5 sin 30 2.5 B90
例6-5 把3△B225º 棱镜分解为B180º 与B270º 两棱镜
解:(1)作图法(图6-13b) OV=2.1, OH=2.1
3 B225 2.1 B180
解:按题意,该棱镜底在180º 方向,顶 在0º 方向,且在 45 方向打孔 (如图6-11),因该棱镜直径为60mm, 半径为30mm,孔距边缘5mm,故孔与棱 镜中心距25mm。 故该孔中心与棱镜中心的厚度差为:
g 45
5 25cos45 1.69m m 100(1.523 1)
角,且该 如果某一棱镜可使出射光线相对入射光线偏折一个 角的正切值为0.01时,该棱镜度为1△
棱镜度可表示为: P△= 100 tan 即,棱镜度是偏向角正切的100倍
tan 显然,当长度为1m,偏移5cm时, 5 0.05 ,10P=0×0.05 100
= 5△
1△ = 0.5729º = 34.376′
1、棱镜度的合成 例6-2 两眼用棱镜3△基底90º (3△B90º )与4△ 基底0º 合成一等效棱镜
解:(1)作图法:
用矢量加法 测量出, OR 5
37
5 B37
(2)计算法
OR OV 2 OH 2 32 42 5 3 tan 0.75 36.87 4
棱镜的两个重要性质:
(1)光线通过棱镜后, 向基底方向偏折; (2)人眼通过棱镜视物, 其像要向顶方向偏移。
通常小于10º
超过15º 更为少见
棱镜的光学作用
改变光束的方向,不改变聚散度 光线向棱镜底方向偏折
棱镜的重要性质
棱镜的重要性质(一)
棱镜的重要性质(二)
棱镜的重要性质(二)
棱镜的重要性质(二)
所以 3△B90º ()4△B0º =5º B36.87º
例6-3 试合成3△B270º 与4△B0º 两棱镜
解:(1)作图6-12b
37 323 测量得OR=5,
得到等效棱镜为5△B323º
(2)计算法:
OR OV 2 OH 2 5
3 tan 0.75 4
顶角 偏向角 棱镜度 厘弧度
棱镜的分解和合成
底的朝向相同的 底的朝向相反的 底的朝向垂直的 斜轴相交的
棱镜的合成
任意基底方向的两棱镜叠加
• 先分解-后叠加-再合成
求3ΔB30°联合4ΔB140°的效果
旋转棱镜
总的棱镜效果=2psinθ
旋转棱镜
旋转棱镜的组成 旋转棱镜的棱镜度效果
老式英国标记法
新式英国标记法
360º 标记法
棱镜各参数之间的关系
。当一条 一个棱镜,其顶角为 光线垂直入射于该棱镜的第一面 时,光线不发生折射,入射至第 二面时,入射光线与该面法线成I 角,出射光线与法线成角 i ,故 偏向角为 ,棱镜材料折射率为n
i i
i
i
• 镜架的大小 • 镜片的大小 • 透镜的屈光度
球面透镜的移心
一个患者戴镜右眼为+2.00DS,要产生1
底朝下和1.5 底朝内需要如何移心 一个患者戴镜左眼为-2.00DS,要产生 1Δ 底朝下和1.5Δ 底朝内须如何移心
柱面透镜的棱镜效果
一右眼为-2.00DCⅹ180°,如通过光心 上方3mm注视时,求棱镜效果及方向 一个右眼前戴镜为+4.00DCⅹ30,他的 右眼瞳距大了3mm,求此右眼将产生多大 的棱镜效果及方向
g tan d
(n 1)
g (n 1) tan d
g P 100 tan 100 (n 1) d Pd
g
100(n 1)
Pd cos g 100(n 1)
n 1.523 。今在与棱镜中心 例6-1 一眼用棱镜5△B180º 直径为60mm, 成45º 方向且距棱镜边5mm处打一螺钉孔,已知孔厚度为3mm。试求 该棱镜最薄边厚度。
2.1 B270
(2)计算法:由图6-13b可知
OH OR cos 3 cos225 2.12 △B180º OV OR sin 3 sin 225 2.12
△B270º
3 B225 2.12 B180 2.12 B 270
棱镜的单位
n sin sin( )
sin (n 1)
0.532
n sin i sin i
sin
n
n 1.532
, , P
顶角
1º
偏向角 0.523º
棱镜度P△
0.91△
1.1º
0.573º
1△
1.91º
1º
1.75△
棱镜的厚度差
公式:
g=
Pd 100( n 1)
棱镜的厚度差
如果要求的厚度差的两点不在底顶线方向, 与底顶线成β角,则:
Pd cos g 100(n 1)
棱镜的厚度差
棱镜底顶线方向某两点间的厚度之差为棱镜的厚度差。有时, 在制作眼用棱镜的时候需要考虑其厚度差
通常眼用棱镜很薄,故顶角很小
差异棱镜效果
一个患者的近用处方是 OD +2.00DS OS +2.00DS 这副眼镜是用来阅读的,制作的时候也是按照近用 瞳距来制作的,但是患者阅读的时候视线是从镜 片光学中心下放5mm处通过的,请问此戴镜者在 阅读的时候每只眼睛产生的棱镜效果是多少?两 只眼睛总的棱镜效果是多少?
差异棱镜效果
球柱透镜的移心
一个患者戴镜右眼为+2.00DS/4.00DCⅹ180°要使其产生2Δ底朝下和 2Δ底朝内的棱镜效果该如何移心
棱镜对眼的效果
视觉移动 集合移动 分离移动 差异棱镜效果
棱镜底的临床应用
R:2ΔBO L:2ΔBO R:2ΔBU L:2ΔBD R:3ΔBO L:1ΔBO R:3ΔBU L:1ΔBD R:0 L:4ΔBO R:0 L:4ΔBD
眼球震颤
同时伴有斜视
有确切中间带者 暂时不能手术者
三棱镜的临床适应症
目的
消除复视
改善头位
获得一定双眼单视功能
三棱镜的诊断作用
测量斜视角
测量融合范围 三棱镜适应试验(Prism
adaptation test)
压帖式三棱镜矫正眼位+worth四点试验
双眼平衡:棱镜分离
右眼:3 BU
4.69 mm
即中心厚度为: 1.69 3
因棱镜最薄处在顶方向。故中心与顶的厚度差为:
5 30 g 2.87m m 所以最薄边厚度为:4.69-2.87=1.82mm 100(n 1)
第二节 棱镜度的合成与分解
如果棱镜A与棱镜B的棱镜效果可以由另一棱镜C代替,则 可以说C棱镜是棱镜A与棱镜B的合成。反之,C棱镜也可 分解为A、B两棱镜 。
第四章 眼用棱镜和透 镜的棱镜效果
棱镜的概念
由两个作用面相交所成的三角形透明体
眼用棱镜
牛顿棱镜(大于15-20度)
薄的棱镜(小于10-15度
)
棱镜的术语
棱(顶) 顶角
主截面 底
棱镜的术语
棱镜的特性
任何一棱镜必须至少有两个相交的平面
ABC
主截面
以主截面代表一个棱镜
角称为棱镜的顶角 底顶线
37 323
所以3△B270º ()与4△B0º =5△B323º
2、棱镜度的分解
例6-4:.试将5△B30º 的棱镜分解为垂直与水平方向的两棱镜 解:(1)作图法 在坐标上沿30º 方向作出OR=5。 过R点作RH OH,RVOV。测量 出OH=4.3,OV=2.5。 所以:5△B30º =2.5△B90º ()4.3△B0º (2)计算法
球柱透镜的棱镜效果
两种途径
• 分别计算球镜和柱镜产生的棱镜效果,之后再 合成即可 • 将处方变换成柱镜形式,分别计算两个柱镜的 棱镜效果,之后再合成
球柱透镜的棱镜效果
一个患者戴镜右眼为 +3.00DS/+1.00DCⅹ90°当眼睛从光心 下方2偏内2看近物体时产生怎样的棱镜效 果 一个左眼镜片为-2.00/-1.50ⅹ70°,求 它在180方向的屈光度,如此镜片光心向鼻 侧移心3mm,产生的棱镜效果是多少
原理
棱镜的单位
棱镜度
• 在1m处使光线偏移1cm,作为1△
厘弧度
• 在半径为1m的圆周上,使光线偏移1cm弧度
棱镜的单位
棱镜度 此单位系C.F.Prentice于1888年所倡导,其符号为P△。1△屈 光力的棱鏡是指当光线通过该棱镜时,使出射光线相对入射光线在 100单位距离处,偏移l单位的距离。 即在lm处能使光线偏移lcm的棱镜为1△,若能偏移3cm即为3△, 偏移lm为100△
公式
P= Cf P:棱镜度 C:入射点到光心的距离 F:透镜的屈光度
球镜上任意一点的棱镜效果
计算:R:+3.50DS L:-4.00DS 1、在光心 2、在光心下方5mm 3、在光学内侧4mm 的棱镜效果移心法则
凸透镜的移心方向与所需棱镜底的方向相同 凹透镜的移心方向与所需棱镜底的方向相反 关系式:c=P/F 取决于
压贴三棱镜的主要缺点
视敏度有所下降
OV OR sin 5 sin 30 2.5 B90
例6-5 把3△B225º 棱镜分解为B180º 与B270º 两棱镜
解:(1)作图法(图6-13b) OV=2.1, OH=2.1
3 B225 2.1 B180
解:按题意,该棱镜底在180º 方向,顶 在0º 方向,且在 45 方向打孔 (如图6-11),因该棱镜直径为60mm, 半径为30mm,孔距边缘5mm,故孔与棱 镜中心距25mm。 故该孔中心与棱镜中心的厚度差为:
g 45
5 25cos45 1.69m m 100(1.523 1)
角,且该 如果某一棱镜可使出射光线相对入射光线偏折一个 角的正切值为0.01时,该棱镜度为1△
棱镜度可表示为: P△= 100 tan 即,棱镜度是偏向角正切的100倍
tan 显然,当长度为1m,偏移5cm时, 5 0.05 ,10P=0×0.05 100
= 5△
1△ = 0.5729º = 34.376′
1、棱镜度的合成 例6-2 两眼用棱镜3△基底90º (3△B90º )与4△ 基底0º 合成一等效棱镜
解:(1)作图法:
用矢量加法 测量出, OR 5
37
5 B37
(2)计算法
OR OV 2 OH 2 32 42 5 3 tan 0.75 36.87 4
棱镜的两个重要性质:
(1)光线通过棱镜后, 向基底方向偏折; (2)人眼通过棱镜视物, 其像要向顶方向偏移。
通常小于10º
超过15º 更为少见
棱镜的光学作用
改变光束的方向,不改变聚散度 光线向棱镜底方向偏折
棱镜的重要性质
棱镜的重要性质(一)
棱镜的重要性质(二)
棱镜的重要性质(二)
棱镜的重要性质(二)
所以 3△B90º ()4△B0º =5º B36.87º
例6-3 试合成3△B270º 与4△B0º 两棱镜
解:(1)作图6-12b
37 323 测量得OR=5,
得到等效棱镜为5△B323º
(2)计算法:
OR OV 2 OH 2 5
3 tan 0.75 4
顶角 偏向角 棱镜度 厘弧度
棱镜的分解和合成
底的朝向相同的 底的朝向相反的 底的朝向垂直的 斜轴相交的
棱镜的合成
任意基底方向的两棱镜叠加
• 先分解-后叠加-再合成
求3ΔB30°联合4ΔB140°的效果
旋转棱镜
总的棱镜效果=2psinθ
旋转棱镜
旋转棱镜的组成 旋转棱镜的棱镜度效果
老式英国标记法
新式英国标记法
360º 标记法
棱镜各参数之间的关系
。当一条 一个棱镜,其顶角为 光线垂直入射于该棱镜的第一面 时,光线不发生折射,入射至第 二面时,入射光线与该面法线成I 角,出射光线与法线成角 i ,故 偏向角为 ,棱镜材料折射率为n
i i
i
i
• 镜架的大小 • 镜片的大小 • 透镜的屈光度
球面透镜的移心
一个患者戴镜右眼为+2.00DS,要产生1
底朝下和1.5 底朝内需要如何移心 一个患者戴镜左眼为-2.00DS,要产生 1Δ 底朝下和1.5Δ 底朝内须如何移心
柱面透镜的棱镜效果
一右眼为-2.00DCⅹ180°,如通过光心 上方3mm注视时,求棱镜效果及方向 一个右眼前戴镜为+4.00DCⅹ30,他的 右眼瞳距大了3mm,求此右眼将产生多大 的棱镜效果及方向
g tan d
(n 1)
g (n 1) tan d
g P 100 tan 100 (n 1) d Pd
g
100(n 1)
Pd cos g 100(n 1)
n 1.523 。今在与棱镜中心 例6-1 一眼用棱镜5△B180º 直径为60mm, 成45º 方向且距棱镜边5mm处打一螺钉孔,已知孔厚度为3mm。试求 该棱镜最薄边厚度。
2.1 B270
(2)计算法:由图6-13b可知
OH OR cos 3 cos225 2.12 △B180º OV OR sin 3 sin 225 2.12
△B270º
3 B225 2.12 B180 2.12 B 270
棱镜的单位
n sin sin( )
sin (n 1)
0.532
n sin i sin i
sin
n
n 1.532
, , P
顶角
1º
偏向角 0.523º
棱镜度P△
0.91△
1.1º
0.573º
1△
1.91º
1º
1.75△
棱镜的厚度差
公式:
g=
Pd 100( n 1)
棱镜的厚度差
如果要求的厚度差的两点不在底顶线方向, 与底顶线成β角,则:
Pd cos g 100(n 1)
棱镜的厚度差
棱镜底顶线方向某两点间的厚度之差为棱镜的厚度差。有时, 在制作眼用棱镜的时候需要考虑其厚度差
通常眼用棱镜很薄,故顶角很小
差异棱镜效果
一个患者的近用处方是 OD +2.00DS OS +2.00DS 这副眼镜是用来阅读的,制作的时候也是按照近用 瞳距来制作的,但是患者阅读的时候视线是从镜 片光学中心下放5mm处通过的,请问此戴镜者在 阅读的时候每只眼睛产生的棱镜效果是多少?两 只眼睛总的棱镜效果是多少?
差异棱镜效果
球柱透镜的移心
一个患者戴镜右眼为+2.00DS/4.00DCⅹ180°要使其产生2Δ底朝下和 2Δ底朝内的棱镜效果该如何移心
棱镜对眼的效果
视觉移动 集合移动 分离移动 差异棱镜效果
棱镜底的临床应用
R:2ΔBO L:2ΔBO R:2ΔBU L:2ΔBD R:3ΔBO L:1ΔBO R:3ΔBU L:1ΔBD R:0 L:4ΔBO R:0 L:4ΔBD
眼球震颤
同时伴有斜视
有确切中间带者 暂时不能手术者
三棱镜的临床适应症
目的
消除复视
改善头位
获得一定双眼单视功能
三棱镜的诊断作用
测量斜视角
测量融合范围 三棱镜适应试验(Prism
adaptation test)
压帖式三棱镜矫正眼位+worth四点试验
双眼平衡:棱镜分离
右眼:3 BU
4.69 mm
即中心厚度为: 1.69 3
因棱镜最薄处在顶方向。故中心与顶的厚度差为:
5 30 g 2.87m m 所以最薄边厚度为:4.69-2.87=1.82mm 100(n 1)
第二节 棱镜度的合成与分解
如果棱镜A与棱镜B的棱镜效果可以由另一棱镜C代替,则 可以说C棱镜是棱镜A与棱镜B的合成。反之,C棱镜也可 分解为A、B两棱镜 。
第四章 眼用棱镜和透 镜的棱镜效果
棱镜的概念
由两个作用面相交所成的三角形透明体
眼用棱镜
牛顿棱镜(大于15-20度)
薄的棱镜(小于10-15度
)
棱镜的术语
棱(顶) 顶角
主截面 底
棱镜的术语
棱镜的特性
任何一棱镜必须至少有两个相交的平面
ABC
主截面
以主截面代表一个棱镜
角称为棱镜的顶角 底顶线
37 323
所以3△B270º ()与4△B0º =5△B323º
2、棱镜度的分解
例6-4:.试将5△B30º 的棱镜分解为垂直与水平方向的两棱镜 解:(1)作图法 在坐标上沿30º 方向作出OR=5。 过R点作RH OH,RVOV。测量 出OH=4.3,OV=2.5。 所以:5△B30º =2.5△B90º ()4.3△B0º (2)计算法
球柱透镜的棱镜效果
两种途径
• 分别计算球镜和柱镜产生的棱镜效果,之后再 合成即可 • 将处方变换成柱镜形式,分别计算两个柱镜的 棱镜效果,之后再合成
球柱透镜的棱镜效果
一个患者戴镜右眼为 +3.00DS/+1.00DCⅹ90°当眼睛从光心 下方2偏内2看近物体时产生怎样的棱镜效 果 一个左眼镜片为-2.00/-1.50ⅹ70°,求 它在180方向的屈光度,如此镜片光心向鼻 侧移心3mm,产生的棱镜效果是多少
原理
棱镜的单位
棱镜度
• 在1m处使光线偏移1cm,作为1△
厘弧度
• 在半径为1m的圆周上,使光线偏移1cm弧度
棱镜的单位
棱镜度 此单位系C.F.Prentice于1888年所倡导,其符号为P△。1△屈 光力的棱鏡是指当光线通过该棱镜时,使出射光线相对入射光线在 100单位距离处,偏移l单位的距离。 即在lm处能使光线偏移lcm的棱镜为1△,若能偏移3cm即为3△, 偏移lm为100△
公式
P= Cf P:棱镜度 C:入射点到光心的距离 F:透镜的屈光度
球镜上任意一点的棱镜效果
计算:R:+3.50DS L:-4.00DS 1、在光心 2、在光心下方5mm 3、在光学内侧4mm 的棱镜效果移心法则
凸透镜的移心方向与所需棱镜底的方向相同 凹透镜的移心方向与所需棱镜底的方向相反 关系式:c=P/F 取决于
压贴三棱镜的主要缺点
视敏度有所下降
