数形结合找规律试题集锦
找规律试题题型及答案大全

找规律试题题型及答案大全一、选择题1. 观察下列数列:2, 4, 8, 16, 32, ()A. 64B. 128C. 256D. 512答案:A2. 找出下列数列的规律并填空:1, 2, 4, 8, ()A. 16B. 10C. 12D. 15答案:A3. 根据数列规律,下一个数字是:1, 3, 6, 10, ()A. 15B. 18C. 21D. 24答案:C二、填空题1. 根据数列规律,下一个数字是:2, 4, 8, 16, ()答案:322. 找出下列数列的规律并填空:1, 3, 6, 10, ()答案:153. 根据数列规律,下一个数字是:2, 6, 12, 20, ()答案:30三、解答题1. 观察下列数列:1, 2, 4, 7, 11, (), (), 26请找出规律并填写空缺的数字。
答案:16, 222. 根据数列规律:1, 1, 2, 3, 5, 8, (), ()请找出规律并填写空缺的数字。
答案:13, 213. 观察下列数列:2, 4, 8, 16, (), (), 128请找出规律并填写空缺的数字。
答案:32, 64四、应用题1. 一个数列的规律是每个数字是前一个数字的两倍,如果数列的前两个数字是1和2,那么第10个数字是多少?答案:10242. 一个数列的规律是每个数字是前一个数字加上一个递增的整数,数列的前两个数字是1和3(即第二个数字是第一个数字加上2),那么第5个数字是多少?答案:133. 一个数列的规律是每个数字是前一个数字加上一个递增的奇数,数列的前两个数字是2和5(即第二个数字是第一个数字加上3),那么第4个数字是多少?答案:12。
数形结合找规律试题集锦
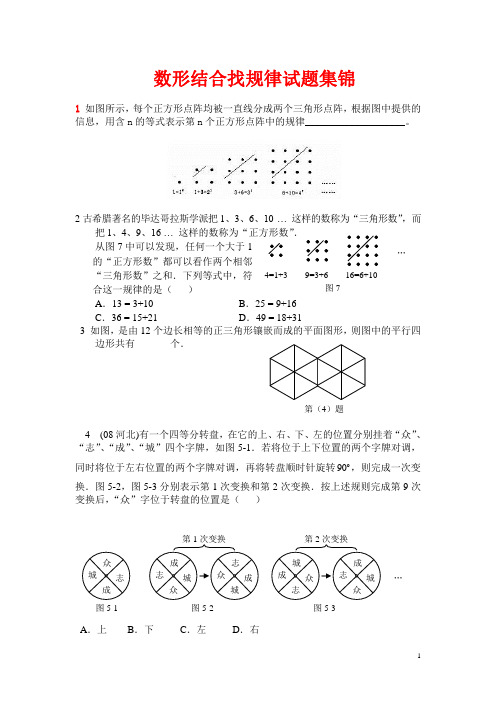
4=1+3 9=3+616=6+10图7 … 数形结合找规律试题集锦1 如图所示,每个正方形点阵均被一直线分成两个三角形点阵,根据图中提供的信息,用含n 的等式表示第n 个正方形点阵中的规律____________________。
2古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图7中可以发现,任何一个大于1 的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符 合这一规律的是( )A .13 = 3+10B .25 = 9+16C .36 = 15+21D .49 = 18+313 如图,是由12个边长相等的正三角形镶嵌而成的平面图形,则图中的平行四边形共有_______个.4 (08河北)有一个四等分转盘,在它的上、右、下、左的位置分别挂着“众”、“志”、“成”、“城”四个字牌,如图5-1.若将位于上下位置的两个字牌对调,同时将位于左右位置的两个字牌对调,再将转盘顺时针旋转90 ,则完成一次变换.图5-2,图5-3分别表示第1次变换和第2次变换.按上述规则完成第9次变换后,“众”字位于转盘的位置是( )A .上B .下C .左D .右第(4)题图5-1图5-2图5-3 …5 如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个,若这样铺成一个10×10的正方形图案,则其中完整的圆共有个.6把长方形的纸条对折一次可得1条折痕,对折两次可得3条折痕,那么对折6次可得条折痕。
对折n次可得条折痕。
7如图第二个三角形是由第一个三角形连接三边的中点而得到的,猜想第四个图形中有个三角形,………,第n个图形共有个三角形(1 )( 2 )( 3 )这n个图形共有个三角形。
初二数学图形找规律练习题

初二数学图形找规律练习题(正文内容)1. 矩形面积规律小明正在学习数学中的图形找规律。
他发现了一组矩形图形,如下所示:矩形1:长为3,宽为2,面积为6矩形2:长为5,宽为3,面积为15矩形3:长为7,宽为4,面积为28小明观察这个序列,发现每个矩形的面积都是其长乘以宽的结果。
小明找到了规律:矩形的面积等于长乘以宽。
这个规律可以用公式表示为 S = L × W,其中 S代表矩形的面积,L代表矩形的长,W代表矩形的宽。
请你根据这个规律,计算以下矩形的面积:矩形4:长为9,宽为6,面积为?矩形5:长为12,宽为8,面积为?矩形6:长为15,宽为10,面积为?2. 正方形周长规律除了矩形,小明还发现了一组正方形图形,如下所示:正方形1:边长为2,周长为8正方形2:边长为4,周长为16正方形3:边长为6,周长为24小明观察这个序列,发现每个正方形的周长都是其边长乘以4的结果。
小明找到了规律:正方形的周长等于边长乘以4。
这个规律可以用公式表示为 P = 4 × S,其中 P代表正方形的周长,S代表正方形的边长。
请你根据这个规律,计算以下正方形的周长:正方形4:边长为8,周长为?正方形5:边长为10,周长为?正方形6:边长为12,周长为?3. 三角形面积规律在继续观察图形时,小明发现了一组三角形图形,如下所示:三角形1:底边长为3,高为2,面积为3三角形2:底边长为5,高为3,面积为7.5三角形3:底边长为7,高为4,面积为14小明观察这个序列,发现每个三角形的面积都是其底边长乘以高再除以2的结果。
小明找到了规律:三角形的面积等于底边长乘以高再除以2。
这个规律可以用公式表示为 S = (B × H) / 2,其中 S代表三角形的面积,B 代表三角形的底边长,H代表三角形的高。
请你根据这个规律,计算以下三角形的面积:三角形4:底边长为9,高为6,面积为?三角形5:底边长为12,高为8,面积为?三角形6:底边长为15,高为10,面积为?(文章结束)。
2022-2023学年小升初数学专项备考高频考点一轮复习系列之:数形结合规律(解析版)

2022-2023学年小升初数学专项备考高频考点一轮复习系列之:数形结合规律(解析版)一、单选题1.如下图,小明用相同的小棒搭房子,他搭3间房子用了13根小棒,搭10间房子用()根小棒。
A.41B.52C.45D.50【答案】A【解析】【解答】搭1间房子用的木棒为:5=4×1+1;搭2间房子用的木棒为:9=4×2+1;搭3间房子用的木棒为:13=4×3+1;……搭n间房子用的木棒为:4n+1;所以搭10间房子用的木棒为:4×10+1=41。
故答案为:A。
【分析】根据所给的图形,可得出搭1间房子、2间房子、3件房子用的木棒的数量,即5、9、13,可得出规律为4n+1,再将n=10代入即可得出搭10间房子用木棒的数量。
2.某餐厅里,一张桌子可坐6人,如图所示:按照上面的规律,n张桌子能坐()人。
A.6n+4B.4n+4C.4n+2D.6n+6【答案】C【解析】【解答】解:按照上面的规律,n张桌子能坐4n+2人。
故答案为:C。
【分析】第一个桌子上坐的人数:6=4+2;第二个桌子上坐的人数:10=4×2+2;第三个桌子上坐的人数:14=4×3+2;……第n个桌子上坐的人数:4n+2。
3.下图的阶梯有三级,是由6个长方体砖组成的,若组成类似的八级台阶,需要()个长方体。
A.8B.14C.36D.64【答案】C【解析】【解答】1+2+3+4+5+6+7+8=36(个)故答案为:C【分析】由题图可知,从上往下观察,第4级台阶由4个长方体组成,第5级台阶由5个长方体组成,第6级台阶由6个长方体组成,第7级台阶由7个长方体组成,第8级台阶由8个长方体组成,组成级台阶一共需要36个长方体。
4.把正方形边长扩大到原来的2倍,所得到的图形周长是原图形周长的倍,面积是原图形的倍.()A.2,4B.2,1C.2,2D.4,4【答案】A【解析】【解答】根据正方形的周长和面积公式可知,正方形的边长扩大到原来的2倍,所得到的图形周长是原图形周长的2倍,面积是原图形的4倍.故答案为:A【分析】正方形周长=边长×4,正方形面积=边长×边长,正方形边长扩大的倍数与周长扩大的倍数相同,面积扩大的倍数是边长扩大倍数的平方倍.5.把一些规格相同的杯子叠起来(如图),4个杯子叠起来高20厘米,6个杯子叠起来高26厘米。
数形结合找规律试题集锦.doc

判断题1.销售统计表毛利成本分析不正确的可能是由于“销售出库单”在存货系统已审核,但在销售系统中发货单还未生成“销售发票”,从而造成销售与成本不匹配。
答案:False2.销售管理中发货开票勾对表统计出客户的收款情况,作为客户信用的评估依据。
答案:False3.发货开票勾对表可以统计发货、开票、收款情况等,其中收款情况来自应收系统的核销数据。
答案:True4.发货统计表只能统计发货的数量,但不能统计发货已结算(开票)部分的数量。
答案:False5.销售统计表能够提供销售金额、折扣、成本、毛利等数据,其存货成本数据来自存货系统。
答案:True6.退货明细表与销售综合统计表均有是否退货过滤项,劳务收入统计表和发货统计表具有按按劳务过滤的功能。
答案:False7.存货核算中填制出库调整单,在收发存汇总表金额已被调整,但此单据未回写到销售统计分析表中去。
可能的原因是由于销售出库调整单上的部门、客户等信息不全。
答案:True8.销售统计表中以前各月都可以显示本期成本,但是本与月不能显示成本金额,可能是存货中单据没有记账,全月平均的仓库未进行期末处理。
答案:True9.发货统计表中可以查询到去年已发货未开票的发货单。
答案:True10.销售账表,对于其中的数字型栏目,系统默认按照一定的数字格式显示,但可以修改。
答案:True11.销售综合统计表可以按货物、客户、部门三种方式进行货龄分析,分析。
答案:False12.查询发货单开票情况的做法还可通过发货单列表,设置出结算数量来查询相关数据。
答案:True13.销售成本只有到存货核算系统月末结账后才能取得准确的数据。
答案:True14.发货统计表可以统计存货的发货、开票、结存业务数据信息,其开票数据来自与发货单相关联的销售发票、销售调拨单、零售日报及其红字单据。
答案:True15.销售统计表能够提供销售金额、折扣、成本、毛利信息,其成本来源于《存货核算》的存货明细账。
小学数形结合的规律精选文档

小学数形结合的规律精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-2016小学数形结合的规律一.选择题(共30小题)1.(2016春?灵武市期末)摆一个三角形用3根小棒,摆两个三角形是5根,摆9个三角形要()根小棒.A.15 B.17 C.192.(2016春?盐都区期末)用火柴按照如图的方法摆正方形(每条边摆1根火柴),照这样,摆15个正方形共需要()根火柴.A.45 B.46 C.603.(2015?如皋市模拟)下面的三角形是用小棒拼成的,根据图形排列的规律,第100个图形要()根小棒.A.300 B.299 C.201 D.2404.(2015?永宁县模拟)小明用小棒搭房子,他搭的三间房子用了13根小棒.搭10间房子用()根小棒.A.40 B.41 C.45 D.505.(2015秋?扬中市校级期末)按下面点阵中的规律继续画,第11个点阵应该画()个点.A.64 B.81 C.100 D.1216.(2015秋?海淀区校级期末)木材厂将木头按下图堆放,第五堆有()个.A.15 B.21 C.28 D.347.(2015春?博罗县期末),第8个点阵中的点数是()A.12 B.14 C.16 D.188.(2015秋?宜兴市校级月考)根据下面几幅图的排列规律,第四幅图是()A.B.C.D.9.(2014?公安县)按下列规律印刷笑脸图案,第8幅图案有()个笑脸.A.8 B.32 C.3610.(2014?石家庄)古希腊着名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()A.13=3+10 B.25=9+16 C.36=15+21 D.49=18+3111.(2014?深圳)观察如图所示的图形.你认为选项中与+…+(共10个相乘),最接近的数值是()A.B.C.D.12.(2014?贵阳校级自主招生)如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律,则第(6)个图形中面积为1的正方形的个数为()A.20 B.27 C.35 D.4013.(2014秋?深圳校级期末)下面的3个图形都是由相同的小棒拼成,根据前3个图形的排列规律,第5个图形由()根小棒拼成.A.20 B.18 C.16 D.1414.(2014秋?东平县期末)如图,用火柴棍拼成一排由三角形组成的图形,如果图形中含有16个三角形,则需要()根火柴棍.A.30根 B.31根 C.32根 D.33根15.(2014秋?东平县期末)《棋盘上的米粒》故事中,皇帝往棋盘的第一格中放1粒米,第二格中放2粒米,在第三格上加倍至4粒,…,依此类推,每一格均是前一格的双倍,那么他在第12格中所放的米粒是()A.22粒 B.24粒 C.211粒 D.212粒16.(2013?泉州)按图中的规律接着画下去,第(5)个图形一共有()个这样的圆点.A.20 B.21 C.23 D.2617.(2013?宜昌)如果按照下面的画法,画到第10个正方形时,图中共有()个直角三角形.A.28 B.32 C.36 D.4018.(2013?永昌县)用6根小棒可以拼成1个正六边形,用11根小棒可以拼成2个正六边形,用16根小棒可以拼3个正六边形,照这样拼下去,用46根可以拼()个正方形.A.6 B.7 C.8 D.919.(2013?郑州)一个由一些小平行四边形组成的装饰链,段去了一部分,剩下的部分如图所示,则断去部分中的小平行四边形的个数可能是()A.9 B.10 C.11 D.1220.(2013?罗平县校级模拟)如图,摆一摆,摆10个图形需()根小棒.A.26 B.28 C.3121.(2013秋?绥宁县期末)如图,是蜂巢的一部分,假如从中间到外面有6层,每个小正六边形中有一只幼蜂,那么这个蜂巢里共有()只幼蜂.A.7 B.37 C.75 D.9122.(2012?金牛区)笑笑用火柴按照右面的方法摆正方形,按这样的方法摆6个正方形共需要()根火柴.A.19 B.20 C.2423.(2012?淮安校级自主招生)将整数1,2,3,…,按如图所示的方式排列.这样,第1次转弯的是2,第2次转弯的是3,第3次转弯的是5,第4次转弯的是7,….则第16次转弯的是()A.71 B.72 C.73 D.7424.(2012?东莞市校级自主招生)按下面的规律印制笑脸图案,第⑦幅图案有()个笑脸.A.13 B.21 C.28 D.3625.(2012?南海区自主招生)为庆祝“六一”儿童节,某幼儿阅举行用火桨棒摆“金鱼”比赛,如图所示:按照以上的规律,摆n个“金鱼”需要火柴棒的根数为()A.2+6n B.8+6n C.4+4n D.8n26.(2012?郑州校级自主招生)按如图所示的方式排列点阵,则第六个点阵中有()个点.A.36 B.25 C.1627.(2012?北京校级自主招生)意大利着名数学家裴波那契在研究兔子繁殖问题时,发现有这样一组数:0、1、2、3、5、8、13…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图,再分别依次从左到右取2个,3个,4个,5个正方形拼成如下长方形并记为①、②、③、④,相应长方形的周长如下表所示序号①②③④周长6101626若按此规律继续作长方形,则序号为⑧的长方形周长是()A.288 B.178 C.128 D.11028.(2012?东城区校级自主招生)用火柴按照下图的方法摆正方形(每条边摆l根火柴),照这样,摆l5个正方形共需要()根火柴.A.45 B.46 C.59 D.6029.(2012?西安校级模拟)观察图中每一个大三角形中白色的三角形的排列规律,则第5个大三角形中白色的三角形有()A.82个 B.154 C.83个 D.121个30.(2012秋?灌南县校级月考)下面的4个图形都是用相同的小棒拼成.根据前4个图形的排列规律,第5个图形由()根小棒拼成.A.9 B.11 C.12 D.152016小学数形结合的规律参考答案与试题解析一.选择题(共30小题)1.(2016春?灵武市期末)摆一个三角形用3根小棒,摆两个三角形是5根,摆9个三角形要()根小棒.A.15 B.17 C.19【解答】解:根据题意,可得摆一个三角形用3根小棒,摆两个三角形用:2×2+1=5根小棒,摆3个三角形用7根小棒,摆10个三角形用:2×9+1=19根小棒;故选:C.2.(2016春?盐都区期末)用火柴按照如图的方法摆正方形(每条边摆1根火柴),照这样,摆15个正方形共需要()根火柴.A.45 B.46 C.60【解答】解:根据题干分析可得:摆n个正方形需要1+3n根火柴棒,当n=15时,1+3×15=1+45=46(根)答:摆15个正方形共需要46根火柴;故选:B.3.(2015?如皋市模拟)下面的三角形是用小棒拼成的,根据图形排列的规律,第100个图形要()根小棒.A.300 B.299 C.201 D.240【解答】解:因为3=2×1+1,5=2×2+1,7=×3+1,…,所以当三角形的个数是n时,需要的小棒的数量是2n+1个,所以n=100时,2n+1=2×100+1=201(个)答:第100个图形要201根小棒.故选:C.4.(2015?永宁县模拟)小明用小棒搭房子,他搭的三间房子用了13根小棒.搭10间房子用()根小棒.A.40 B.41 C.45 D.50【解答】解:根据题干分析可得:1+10×4=41(根)答:搭10间房子用 41根小棒.故选:B.5.(2015秋?扬中市校级期末)按下面点阵中的规律继续画,第11个点阵应该画()个点.A.64 B.81 C.100 D.121【解答】解:根据题干分析可得,第n个图形中就有n2个点,当n=11时,112=121;答:第11个点阵应该画121个点.故选:D.6.(2015秋?海淀区校级期末)木材厂将木头按下图堆放,第五堆有()个.A.15 B.21 C.28 D.34【解答】解:观察图形可知,第1堆有1+2个第2堆有1+2+3个第3堆有1+2+3+4个,…则第n堆就是1+2+3+…+(n+1)=个若n=5,则==21(个)答:第五堆有21个.故选:B.7.(2015春?博罗县期末),第8个点阵中的点数是()A.12 B.14 C.16 D.18【解答】解:根据题干分析可得,第八个图形中有8×2=16(个)答:第八个点阵中的点数是16.故选:C.8.(2015秋?宜兴市校级月考)根据下面几幅图的排列规律,第四幅图是()A.B.C.D.【解答】解:第一和第三幅图的箭头是相反的,所以第二和第四幅图的箭头也应该是相反的,所以第四幅图的箭头应该向下.故选:A.9.(2014?公安县)按下列规律印刷笑脸图案,第8幅图案有()个笑脸.A.8 B.32 C.36【解答】解:1+2+3+4+5+6+7+8,=(1+8)+(2+7)+(3+6)+(4+5),=9×4,=36;答:第8副图案有36个笑脸.故选:D.10.(2014?石家庄)古希腊着名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()A.13=3+10 B.25=9+16 C.36=15+21 D.49=18+31【解答】解:这些三角形数的规律是1,3,6,10,15,21,28,36,45,…,且正方形数是这串数中相邻两数之和,很容易看到:恰有36=15+21.故选:C.11.(2014?深圳)观察如图所示的图形.你认为选项中与+…+(共10个相乘),最接近的数值是()A.B.C.D.【解答】解:每个三角形的面积都是三角形所在梯形面积的,所以阴影部分的面积是整个图形面积的.故选:B.12.(2014?贵阳校级自主招生)如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律,则第(6)个图形中面积为1的正方形的个数为()A.20 B.27 C.35 D.40【解答】解:第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的图象有2+3=5个,第(3)个图形中面积为1的正方形有2+3+4=9个,…,按此规律,第n个图形中面积为1的正方形有2+3+4+…+(n+1)=个,则第(6)个图形中面积为1的正方形的个数为2+3+4+5+6+7=27个.故选:B.13.(2014秋?深圳校级期末)下面的3个图形都是由相同的小棒拼成,根据前3个图形的排列规律,第5个图形由()根小棒拼成.A.20 B.18 C.16 D.14【解答】解:第一个正方体需要4根火柴棒;第二个正方体需要4+3×1=7根火柴棒;第三个正方体需要4+3×2=10根火柴棒;…摆n个正方形需4+3×(n﹣1)=3n+1根火柴棒.当n=5时,3n+1=3×5+1=16(根)答:第5个图形由16根小棒拼成.故选:C.14.(2014秋?东平县期末)如图,用火柴棍拼成一排由三角形组成的图形,如果图形中含有16个三角形,则需要()根火柴棍.A.30根 B.31根 C.32根 D.33根【解答】解:摆16个共需要:3+(16﹣1)×2=3+30=33(根),答:拼成16个三角形,需要33根火柴棍.故选:D.15.(2014秋?东平县期末)《棋盘上的米粒》故事中,皇帝往棋盘的第一格中放1粒米,第二格中放2粒米,在第三格上加倍至4粒,…,依此类推,每一格均是前一格的双倍,那么他在第12格中所放的米粒是()A.22粒 B.24粒 C.211粒 D.212粒,【解答】解:设第n格中所放的米粒数是an则有a=2n﹣1n=212﹣1a12=211故选:C.16.(2013?泉州)按图中的规律接着画下去,第(5)个图形一共有()个这样的圆点.A.20 B.21 C.23 D.26【解答】解:根据分析可得:第(5)个图形一共有圆点的个数是:1+(5﹣1)×5=1+20=21(个)故选:B.17.(2013?宜昌)如果按照下面的画法,画到第10个正方形时,图中共有()个直角三角形.A.28 B.32 C.36 D.40【解答】解:根据观察的数据可知:1个正方形有0个三角形,可以写成(1﹣1)×4个;2个正方形有4个三角形,可以写成(2﹣1)×4个;3个正方形有8个三角形,可以写成(3﹣1)×4个;4个正方形有12个三角形,可以写成(4﹣1)×4个;所以当正方形的个数为a时,三角形的个数可以写成:(a﹣1)×4个;第10个正方形时:(10﹣1)×4=36(个)答:按照上面的画法,如果画到第10个正方形,能得到36个直角三角形.故选:C.18.(2013?永昌县)用6根小棒可以拼成1个正六边形,用11根小棒可以拼成2个正六边形,用16根小棒可以拼3个正六边形,照这样拼下去,用46根可以拼()个正方形.A.6 B.7 C.8 D.9【解答】解:根据题干分析可得:摆n个六边形需要:5n+1根小棒,据此完成表格如下:六边形/12345n个小棒/根6111621265n+1照这样摆下去:当5n+1=46时,5n=45n=9;答:46根小棒可以摆9个六边形.故选:D.19.(2013?郑州)一个由一些小平行四边形组成的装饰链,段去了一部分,剩下的部分如图所示,则断去部分中的小平行四边形的个数可能是()A.9 B.10 C.11 D.12【解答】解:仔细观察图象会发现断去的为3n+2个小平行四边形,最少为2个,当n=3时,3n+2=3×3+2=11.故选:C.20.(2013?罗平县校级模拟)如图,摆一摆,摆10个图形需()根小棒.A.26 B.28 C.31【解答】解:1个小平行四边形需要1+1×3根小棒,2个小平行四边形需要1+2×3根小棒,3个小平行四边形需要1+3×3根小棒…,所以n个小正方形需要1+3n根小棒,当n=10时,1+3n=1+3×10=31(根),答:摆10个图形需31根小棒;故选:C.21.(2013秋?绥宁县期末)如图,是蜂巢的一部分,假如从中间到外面有6层,每个小正六边形中有一只幼蜂,那么这个蜂巢里共有()只幼蜂.A.7 B.37 C.75 D.91【解答】解:观察可知:第一层,正六边形总数为1,第二层,正六边形总数为1+6×1,第三层,正六边形总数为1+6×1+6×2,…第n层,正六边形总数为:1+6×1+6×2+…+6(n一1)=1+3n(n一1).当n=6时,1+3×6×(6﹣1)=91,所以这个蜂巢总计可以放91只幼蜂.故选:D.22.(2012?金牛区)笑笑用火柴按照右面的方法摆正方形,按这样的方法摆6个正方形共需要()根火柴.A.19 B.20 C.24【解答】解:3×6+1=18+1=19(根)答:按这样的方法摆6个正方形共需要19根火柴.故选:A.23.(2012?淮安校级自主招生)将整数1,2,3,…,按如图所示的方式排列.这样,第1次转弯的是2,第2次转弯的是3,第3次转弯的是5,第4次转弯的是7,….则第16次转弯的是()A.71 B.72 C.73 D.74【解答】解:16÷2=8;第16次转弯是第8个偶数项,这一项上的数字是:8×9+1=73;即第16次转弯处的数字是73.故选:C.24.(2012?东莞市校级自主招生)按下面的规律印制笑脸图案,第⑦幅图案有()个笑脸.A.13 B.21 C.28 D.36【解答】解:1+2+3+4+5+6+7,=(1+7)+(2+6)+(3+5)+4,=8×3+4,=28(个);答:第7副图案有28个笑脸.故选:C.25.(2012?南海区自主招生)为庆祝“六一”儿童节,某幼儿阅举行用火桨棒摆“金鱼”比赛,如图所示:按照以上的规律,摆n个“金鱼”需要火柴棒的根数为()A.2+6n B.8+6n C.4+4n D.8n【解答】解:由图形可知:第一个金鱼需用火柴棒的根数为:2+6=8;第二个金鱼需用火柴棒的根数为:2+2×6=14;第三个金鱼需用火柴棒的根数为:2+3×6=20;…;第n个金鱼需用火柴棒的根数为:2+n×6=2+6n.故选:A.26.(2012?郑州校级自主招生)按如图所示的方式排列点阵,则第六个点阵中有()个点.A.36 B.25 C.16【解答】解:第6个点阵有点的个数是:1+3+5+7+9+11=36(个);故选:A.27.(2012?北京校级自主招生)意大利着名数学家裴波那契在研究兔子繁殖问题时,发现有这样一组数:0、1、2、3、5、8、13…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图,再分别依次从左到右取2个,3个,4个,5个正方形拼成如下长方形并记为①、②、③、④,相应长方形的周长如下表所示序号①②③④周长6101626若按此规律继续作长方形,则序号为⑧的长方形周长是()A.288 B.178 C.128 D.110【解答】解:由分析可得:第⑤个的周长为:2×(8+13),第⑥的周长为:2×(13+21),第⑦个的周长为:2×(21+34),第⑧个的周长为:2×(34+55)=178,故选:B.28.(2012?东城区校级自主招生)用火柴按照下图的方法摆正方形(每条边摆l根火柴),照这样,摆l5个正方形共需要()根火柴.A.45 B.46 C.59 D.60【解答】解:根据题干分析可得:摆n个正方形需要1+3n根火柴棒,当n=15时,1+3×15=46(根),答:需要46根火柴棒.故选:B.29.(2012?西安校级模拟)观察图中每一个大三角形中白色的三角形的排列规律,则第5个大三角形中白色的三角形有()A.82个 B.154 C.83个 D.121个【解答】分析:分别数出第一、第二、第三个图中白色三角形的个数,总结出白色三角形的增长规律,即可推出第5个大三角形中白色的三角形的个数.解答:解:第一个图形的白色三角形个数为1,第二个图形的白色三角形个数为1+3,第三个图形的白色三角形个数为1+3+9,第四个图形的白色三角形个数为1+3+9+27=30+31+32+33,第五个图形的白色三角形个数为1+3+9+27+81=30+31+32+33+34=121.故选:D30.(2012秋?灌南县校级月考)下面的4个图形都是用相同的小棒拼成.根据前4个图形的排列规律,第5个图形由()根小棒拼成.A.9 B.11 C.12 D.15【解答】解:根据前4个图形的排列规律,第5个图形由11根小棒拼成.故选:B.。
小学数学数形结合练习题

小学数学数形结合练习题题目一:数形结合的认知训练1. 看图填空:(a) 在图中,将所有的三角形标记一下。
(b) 将你周围的物体,如书桌、椅子等尽可能多地找出正方形、长方形和圆形,并分别写下它们的名称。
2. 计算下列各图形的周长和面积:(a) 根据提供的边长,计算正方形的周长和面积。
(b) 根据提供的长和宽,计算长方形的周长和面积。
(c) 根据提供的半径,计算圆形的周长和面积。
(d) 尝试设计一个你认为面积最大的正方形,画出它的示意图,并计算周长和面积。
3. 图形转换:(a) 请将以下图形按照标号进行旋转,并写出每个旋转后的图形名称。
图1:正方形图2:长方形图3:三角形图4:圆形(b) 请将以下图形按照标号进行翻转,并写出每个翻转后的图形名称。
图1:正方形图2:长方形图3:三角形图4:圆形4. 找规律:(a) 请观察以下数字序列,找出其规律,并写出下一个数字:1, 4, 9, 16, ...(b) 请观察以下形状序列,找出其规律,并画出下一个形状:△, □, ○, ▽, ...5. 图形拼凑:(a) 使用提供的拼图块,组合成一个正方形。
(b) 使用提供的拼图块,组合成一个长方形。
(c) 使用提供的拼图块,组合成一个圆形。
6. 图形推理:给出以下图形的排列顺序,请写出图形编号,并解释其排列规律。
图1:▽图2:□ 图3:○ 图4:△题目二:数形结合的实际应用1. 实际问题运用:(a) 小明家花园的形状是长方形,长为8米,宽为5米,他要在花园的四周围上一圈砖。
砖的规格是2米长、1米宽,请问他需要多少块砖?如果砖的价格是每块20元,他需要多少钱?(b) 小红的家有一个圆形的花坛,直径是3米。
她想在花坛周围种植一圈花草,每株花草之间的间距是20厘米。
她需要多少株花草?题目三:数形结合的解决问题能力训练1. 智力题:(a) 小明手上有12枚硬币,其中有一个是假币,假币的重量比真币轻。
小明有一个天平,最多能使用3次天平,能否找出假币?如果能,请写出解决方法;如果不能,请解释原因。
六年级数学上册专项复习-数形结合规律试题含解析

六年级上册专项复习:数形结合规律一、选择题(共3题;共6分)1.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是().A. 86B. 52C. 38D. 742.用火柴棒按下图的方式摆放第12个图形需要()根小棒.A. 30B. 36C. 393.把一些规格相同的杯子叠起来(如图),4个杯子叠起来高20厘米,6个杯子叠起来高26厘米.n个杯子叠起来的高度可以用下面()的关系式来表示.A. 6n-10B. 3n+11C. 6n-4D. 3n+8二、填空题(共9题;共14分)4.下图是小明用火柴搭成的1条、2条、3条“金鱼”……则搭6条“金鱼”需要火柴________根.5.一些小棒按下面的方式摆放.摆第7个图形需要________根小棒;摆第10个图形需要________根小棒.6.如图,用同样大小的黑色棋子按如图所示的方式摆图案,按照这样的规律摆下去,第20个图案需棋子________枚.7.若=1,=2,=3,则=________.8.如图,有一座四层楼房,每个窗户有4块玻璃,分别涂上灰色和白色,每个窗户代表一个数字.每层楼有三个窗户,从左向右表示一个三位数.四个楼层表示的三位数有791,275,362,612.第三层楼表示的三位数是________.9.观察如图,第6个图有________个圆点,第n个图比它前一个图多________个圆点.图序 1 2 3 4 ……点群……圆点数1 5 14 30 ……10.下列图中有大小不同的平行四边形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个……第5幅图中有________个,第n幅图中有________个.11.将一些▲按一定的规律摆放,(如图所示).图中▲的个数依次是6、10、16 、24……第8个图形共有________个▲.第n个图形中共有________个▲.12.小明用吸管和图钉钉三角形形状(如下图,线段表示吸管,黑点表示图钉).(1)照样子钉4个三角形,需要________个图钉和________个吸管.(2)小明用100个图钉,同时要再用________根吸管,就能钉成________个三角形.三、解答题(共2题;共9分)13.1张长方形桌子可坐6人,按下图方式将桌子拼在一起.(1)2张桌子拼在一起可坐多少人?3张桌子呢?n张桌子呢?(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐________人.(3)在(2)中,若改成每8张桌子拼成1张大桌子,则共可坐________人.14.探索规律.(1)按小方块的摆放规律把表格填写完整.层数 1 2 3 4 …7 …n方块个数5 15 30 ________ …________ …________(2)当所用的小方块达到330个时,搭成的台阶共有________层.答案解析部分一、选择题1.【答案】 A【考点】数形结合规律【解析】【解答】解:8×10+6=86,所以m的值是86.故答案为:A.【分析】从已给的规律可以得出,右上角的数=左上角的数+4,左下角的数=左上角的数+2,右下角的数=右上角的数×左上角的数-左上角的数.据此作答即可.2.【答案】 C【考点】数形结合规律【解析】【解答】6+3×(12-1)=6+33=39(根)故答案为:C【分析】观察图可知,如果把图形的序数设为n,小棒的个数与图形的序数间的关系为:小棒的个数=6+3×(n-1),以此即可解答.3.【答案】 D【考点】数形结合规律【解析】【解答】1个杯子重叠部分的高度:(26-20)÷2=6÷2=3(厘米)下面没有重叠部分的高度是:20-3×4=20-12=8(厘米)n个杯子叠起来的高度可以用3n+8来表示.故答案为:D.【分析】根据条件“4个杯子叠起来高20 厘米,6个杯子叠起来高26厘米”可知,2个杯子叠起来重叠部分的高度是:26-20=6(厘米),也就是一个杯子上面的重叠部分是3厘米,有几个杯子重叠,就有几个3厘米,再加上下面未重叠的高度就是总高度,据此分析解答.二、填空题4.【答案】 38【考点】数形结合规律【解析】【解答】解:搭6条“金鱼”需要火柴38根.故答案为:38.【分析】1条鱼需要火柴6+2根,2条鱼需要火柴6×2+2=14根,3条鱼需要火柴6×3+2=20根,……n条鱼需要火柴6n+2根.据此作答即可.5.【答案】 15;21【考点】数形结合规律【解析】【解答】7×2+1=15(根);10×2+1=21(根).故答案为:15;21.【分析】此题主要考查了数形结合的规律,观察图形可得规律:摆第n个图形需要2n+1根小棒,据此列式解答.6.【答案】 62【考点】数形结合规律【解析】【解答】解:2+3×20=2+60=62(枚)故答案为:62.【分析】规律:棋子的枚数=2+图案个数×3,按照这样的规律计算即可.7.【答案】 9【考点】数形结合规律【解析】【解答】解:(10+8)÷2=9故答案为:9.【分析】观察已知三个图形中的三个数字,发现用左边两个数字的和除以右边的数字来计算,所以用左边的8与10的和除以2即可.8.【答案】 791【考点】数形结合规律【解析】【解答】解:第三层楼表示的三位数是791.故答案为:791.【分析】从下往上数,一层和四层最右边的窗户形状相同,那么表示这两层的数字的最后一位相同,所以“362和612”表示这两层,且表示2,那么一层左边的数字就是2,所以一层用275表示.那么第三层楼表示的三位数就是791.9.【答案】 91;【考点】数形结合规律【解析】【解答】观察如图,第6个图有=91个圆点,第n个图比它前一个图多个圆点.故答案为:91;.【分析】此题主要考查了数形结合的知识,关键是找出图形的变化规律,观察可得规律:第n个图比它前一个图多个圆点,据此解答.10.【答案】 9;2n-1【考点】数形结合规律【解析】【解答】解:第5幅图中:5×2-1=9(个),第n幅图中:(2n-1)个.故答案为:9;2n-1.【分析】规律:平行四边形的个数=图形的个数×2-1,根据规律计算即可.11.【答案】 76;n2+n+4【考点】数形结合规律【解析】【解答】根据分析可知,第8个图形共有4+8×(8+1)=76个▲.第n个图形中共有4+n×(n+1)=n2+n+4个▲.故答案为:76;n2+n+4.【分析】先观察每个图形的最外侧都有4个▲,再观察每个图形内部▲的行数和列数,则有第1个图形中有4+1×2=6个▲,第2个图形中有4+2×3=10个▲,第3个图形中有4+3×4=16个▲,则第n个图形中有4+n×(n+1)=n2+n+4个▲,据此规律解答.12.【答案】(1)6;9(2)197;98【考点】数形结合规律【解析】【解答】解:(1)照样子钉4个三角形,需要6个图钉和9个吸管;(2)小明用100个图钉,同时要再用197根吸管,就能钉成98个三角形.故答案为:(1)6;9;(2)197;98【分析】图中要钉成n个三角形,需要2n+1根吸管和n+2个图钉.(1)将n=4代入公式作答即可;(2)现在是100个图钉,所以n+2=100,解得n=98,所以可以钉成98个三角形,然后再将n=98代入2n+1就可以得出需要吸管的根数.三、解答题13.【答案】(1)解:2张桌子拼在一起可坐8人,3张桌子拼在一起可坐10人,n张桌子拼在一起可坐2n+4人.(2)112(3)100【考点】数形结合规律【解析】【解答】解:(2)5×2+4=10+4=14(人)14×(40÷5)=14×8=112(人)(2)8×2+4=16+4=20(人)20×(40÷8)=20×5=100(人)故答案为:(2)112;(3)100.【分析】(1)规律:能坐的人数=桌子张数×2+4,根据规律用字母表示;(2)根据规律先计算出5张桌子拼成的1张大桌子能坐的人数,40张桌子能拼成8张大桌子,这样用1张大桌子能坐的人数乘8即可求出坐的总人数;(3)先计算出8张桌子拼成的1张大桌子能坐的人数,40张桌子能拼成5张大桌子,用1张大桌子能坐的人数乘5即可求出可以坐的总人数.14.【答案】(1)50;140;(1+2+3+4+……+n)×5或(1+n)×n× 或1×5+2×5+3×5++n×5(2)11【考点】数形结合规律【解析】【解答】(1)按小方块的摆放规律,填表如下:层数 1 2 3 4 …7 …n方块个数 5 15 30 50 …140 …(1+n)×n×(2)(1+n)×n×=330解:(1+n)×n×5=330×2(1+n)×n×5÷5=660÷5(1+n)×n=132因为11×12=132,所以n=11.【分析】(1)观察图形排列可得规律:当小方块摆放n层时,方块的个数是:(1+n)×n×;(2)根据题意,要求搭成的台阶一共有几层,直接将数据代入字母式子中求值,据此解答.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4=1+3 9=3+6
16=6+10
图7 …
数形结合找规律试题集锦
1 如图所示,每个正方形点阵均被一直线分成两个三角形点阵,根据图中提供的信息,用含n 的等式表示第n 个正方形点阵中的规律____________________。
2古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而
把1、4、9、16 … 这样的数称为“正方形数”. 从图7中可以发现,任何一个大于1
的“正方形数”都可以看作两个相邻
“三角形数”之和.下列等式中,符 合这一规律的是( )
A .13 = 3+10
B .25 = 9+16
C .36 = 15+21
D .49 = 18+31 3 如图,是由12个边长相等的正三角形镶嵌而成的平面图形,则图中的平行四
边形共有_______个.
4 (08河北)有一个四等分转盘,在它的上、右、下、左的位置分别挂着“众”、“志”、“成”、“城”四个字牌,如图5-1.若将位于上下位置的两个字牌对调,同时将位于左右位置的两个字牌对调,再将转盘顺时针旋转90,则完成一次变换.图5-2,图5-3分别表示第1次变换和第2次变换.按上述规则完成第9次变换后,“众”字位于转盘的位置是( )
A .上
B .下
C .左
D .右
第(4)题
图5-1
图5-2
图5-3 …
5 如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个,若这样铺成一个10×10的正方形图案,则其中完整的
圆共有个.
6把长方形的纸条对折一次可得1条折痕,对折两次可得3条折痕,那么对折6次可得条折痕。
对折n次可得条折痕。
7如图第二个三角形是由第一个三角形连接三边的中点而得到的,猜想第四个图形中有个三角形,………,第n个图形共有个三角形
(1 )( 2 )( 3 )这n个图形共有个三角形。
8 一块正方形的地板,由相同的小正方形瓷砖铺满,若地板对角线上的瓷砖是黑色的,其余瓷砖是白色的,如果用了黑色瓷砖101块,那么白色瓷砖的总数是
块。
9 (2008年山东省临沂市)如图,以等腰三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA
1
,再以等腰直角三角形ABA
1
的斜边为直角边向外作第3个等
腰直角三角形A
1
BB
1
,……,如此作下去,若OA=OB=1,则第n个等腰直角三角形
的面积S
n
=________。
B1
B2
A1
A
O B
10 如图所示,图(1)是一个水平摆放的小正方体木块,图(2),(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,•至第七个叠放的图形中,小正方体木块总数应是 ( )
A 25
B 66
C 91
D 120
11 .在数学活动中,小明为了求 23411111
22222n
+++++
的值(结果用n 表示),设计如图1所示的几何图形.
(1)请你利用这个几何图形求
23411111
22222n
+++++
的值为 ;
(2)请你利用图2,再设计一个能求23411111
22222n
+++++
的值的几何图形.
12 如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,依此递推,第8层中含有正三角形个数是________
,第n 层中含有正三角形个数是________
12
212图2图1
13 用同样规格的黑白两种颜色的正方形瓷砖铺地板,按如下第(1)至第(7)个图的方
式铺设,则第(30)个图形中黑色的瓷砖有 块.
14 15.如图,每个图形均是由单位1的小正方形组成的,其中第一个图形的面积为2个平
方单位,第二个图形的面积为7个平方单位,第三个图形的面积为14个平方单位,…,由此规律第七个图形的面积为___________平方单位.
15 右图为手的示意图,在各个手指间标记字母A B C D ,,,.
请你按图中箭头所指方向(即A B C D C B A B →→→→→→→
C →→…的方式)从A 开始数连续的正整数1234,
,,,…,当数到12时,对应的字母是________;当字母C 第201次出现时,恰
好数到的数是_________;当字母C 第21n +次出现时(n 为正整数),恰好数到的数是_____________(用含n 的代数式表示).
16.请你将一根细长的绳子,沿中间对折,再沿对折后的绳子中间再对折,这样连续对折5次,最后用剪刀沿对折5次后的绳子的中间将绳子剪断,此时绳子将被剪成__________段.
17.(2009年四川省内江市)把一张纸片剪成4块,再从所得的纸片中任取若干块,每块又剪成4块,像这样依次地进行下去,到剪完某一次为止。
那么2007,2008,2009,2010这四个数中______________可能是剪出的纸片数
18.(2009武汉)14.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有 个小圆.
第1个图形
第2个图形
第3个图形
第4个图形
…
⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ 第38题图 ......
19.(2009年铁岭市)如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n 个图形需要黑色棋子的个数是 .
【答案】(2)n n +或2
2n n +或2
(1)1n +-
答案
15 B 603 36+n 16 (提示 21n
+ ) 17 【答案】2008 18 【答案】46
19。
