高中数学选修2-3概率同步练习

合集下载

北师大版高中数学选修2-3精练：第二章概率测评 Word版含答案

第二章测评( 时间:120分钟满分:150分)一、选择题( 本大题共12小题，每小题5分，共60分)1、若随机变量ξ的分布列如下表所示，则p1=( )ξ-124P p1A、0B、C、D、1详细解析:由分布列性质p i=1，n=1，2，3，…，n，得+p1=1、所以p1=、正确答案:B2、已知事件A，B发生的概率都大于零，则( )A、如果A，B是互斥事件，那么A与也是互斥事件B、如果A，B不是相互独立事件，那么它们一定是互斥事件C、如果A，B是相互独立事件，那么它们一定不是互斥事件D、如果A∪B是必然事件，那么它们一定是对立事件详细解析:对A，若A，B互斥，则A与不互斥;对B，若A，B不相互独立，则它们可能互斥，也可能不互斥;对C，是正确的、对D，当A∪B是必然事件，A∩B是不可能事件时，A，B才是对立事件、正确答案:C3、( 2016·山东青岛教学质量调研)某校高考的数学成绩近似服从正态分布N( 100，100 )，则该校成绩位于( 80，120 )内的人数占考生总人数的百分比约为( )A、22、8%B、45、6%C、95、4%D、97、22%详细解析:设该校高考数学成绩为X，由X~N( 100，100 )知，正态分布的两个参数为μ=100，σ=10，所以P( 80<X<120 )=P( 100-20<X<100+20 )=P( μ-2σ<X<μ+2σ )=0、954、正确答案:C4、若Y~B( n，p )，且EY=3、6，DY=2、16，则此二项分布是( )A、B( 4，0、9 )B、B( 9，0、4 )C、B( 18，0、2 )D、B( 36，0、1 )详细解析:由题意得np=3、6，np( 1-p )=2、16，所以n=9，p=0、4、正确答案:B5、某普通高校招生体育专业测试合格分数线确定为60分、甲、乙、丙三名考生独立参加测试，他们能达到合格的概率分别是0、9，0、8，0、75，则三人中至少有一人达标的概率为( ) A、0、015 B、0、005 C、0、985 D、0、995详细解析:三人都不合格的概率为( 1-0、9 )×( 1-0、8 )×( 1-0、75 )=0、005、所以至少有一人合格的概率为1-0、005=0、995、正确答案:D6、设由“0”“1”组成的三位数组中，若用A表示“第二位数字为‘0’的事件”，用B表示“第一位数字为‘0’的事件”，则P( A|B )=( )A、B、C、D、详细解析:∵P( B )=，P( A∩B )=，∴P( A|B )=、正确答案:C7、在4次独立重复试验中，随机事件A恰好发生1次的概率不大于其恰好发生2次的概率，则事件A在1次试验中发生的概率p的取值范围是( )A、[0、4，1 )B、( 0，0、4]C、( 0，0、6]D、[0、6，1 )详细解析:由题意知p( 1-p )3≤p2( 1-p )2，化简得2( 1-p )≤3p，解得p≥0、4，又因为0<p<1，所以0、4≤p<1、故选A、正确答案:A8、由正方体ABCD-A1B1C1D1的8个顶点中的任意3个顶点构成的所有三角形中，任取其中的两个，这两个三角形不共面的概率为( )A、B、C、D、详细解析:从8个顶点中任选3个顶点组成三角形的个数为=56，从56个三角形中任选2个有种选法、正方体中四点共面的情况共有12种，每共面的四个顶点可组成=4个三角形，在4个三角形中任取2个的取法有=6种，所以8个顶点中的任意3个顶点构成的所有三角形中，任取其中的两个，这两个三角形共面的概率为，所以所求概率为1-、正确答案:A9、设集合A={1，2}，B={1，2，3}，分别从集合A和集合B中随机取一个数a和b，确定平面上的一个点P( a，b )，记“点P( a，b )落在直线x+y=n上”为事件C n( 2≤n≤5，n∈N+ )，当事件C n发生的概率最大时，n的所有可能取值为( )A、3B、4C、2和5D、3和4详细解析:由题意知点P的坐标可能为( 1，1 )，( 1，2 )，( 1，3 )，( 2，1 )，( 2，2 )，( 2，3 )，故事件C2发生的概率为，事件C3发生的概率为，事件C4发生的概率为，事件C5发生的概率为，故选D、正确答案:D10、利用下列盈利表中的数据进行决策，应选择的方案是( )自然状况方案盈利概率A1A2A3A4S10、255070-2098S20、3065265282S30、45261678-10A、A1B、A2C、A3D、A4详细解析:分别求出方案A1，A2，A3，A4盈利的均值，得EA1=43、7，EA2=32、5，EA3=45、7，EA4=44、6，故选C、正确答案:C11、( 2016·四川绵阳市高二月考)设10≤x1<x2<x3<x4≤104，x5=105、随机变量ξ1取值x1，x2，x3，x4，x5的概率均为0、2，随机变量ξ2取值的概率也均为0、2、若记Dξ1，Dξ2分别为ξ1，ξ2的方差，则( )A、Dξ1>Dξ2B、Dξ1=Dξ2C、Dξ1<Dξ2D、Dξ1与Dξ2的大小关系与x1，x2，x3，x4的取值有关详细解析:因为Eξ1和Eξ2相等，且第二组数据是第一组数据的两两平均值，所以比第一组更“集中”、更“稳定”，根据方差的概念，可得Dξ1>Dξ2、正确答案:A12、( 2016·甘肃天水一中高二段考)一袋中有大小、形状、质地相同的4个红球和2个白球，给出下列结论:①从中任取3球，恰有一个白球的概率是;②从中有放回的取球6次，每次任取一球，则取到红球次数的方差为;③现从中不放回的取球2次，每次任取1球，则在第一次取到红球后，第二次再次取到红球的概率为;④从中有放回的取球3次，每次任取一球，则至少有一次取到红球的概率为、其中所有正确的结论是( )A、①②④B、①③④C、②③④D、①②③④详细解析:①恰有一个白球的概率P=，故①正确;②每次任取一球，取到红球次数X~B，其方差为6×，故②正确;③设A={第一次取到红球}，B={第二次取到红球}，则P( A )=，P( AB )=，所以P( B|A )=，故③错;④每次取到红球的概率P=，所以至少有一次取到红球的概率为1-，故④正确、正确答案:A二、填空题( 本大题共4小题，每小题5分，共20分)13、( 2016·湖北省孝感高中高二上学期期中考试)已知离散型随机变量X的分布列为:X012P0、51-2q q2则常数q=、详细解析:由离散型随机变量的分布列意义得得q=1-、正确答案:1-14、在等差数列{a n}中，a4=2，a7=-4、现从{a n}的前10项中随机取数，每次取出一个数，取后放回，连续抽取3次，假定每次取数互不影响，那么在这三次取数中，取出的数恰好为两个正数和一个负数的概率为( 用数字作答)、详细解析:由a4=2，a7=-4可得等差数列{a n}的通项公式为a n=10-2n( n=1，2，…，10 )、由题意，三次取数相当于三次独立重复试验，在每次试验中取得正数的概率为，取得负数的概率为，在三次取数中，取出的数恰好为两个正数和一个负数的概率为、正确答案:15、某射手射击所得环数ξ的分布列如下:ξ78910P x0、10、3y已知ξ的期望Eξ=8、9，则y的值为、详细解析:依题意得即解得正确答案:0、416、甲、乙两人进行一场比赛，已知甲在一局中获胜的概率为0、6，无平局，比赛有3种方案:①比赛3局，先胜2局者为胜者;②比赛5局，先胜3局者为胜者;③比赛7局，先胜4局者为胜者、则方案对乙最有利、详细解析:设三种方案中乙获胜的概率分别为P1，P2，P3，每种方案都可以看成独立重复试验，则P1=×0、42+×0、6×0、42=0、352，P2=×0、43+×0、6×0、43+×0、62×0、43≈0、317，P3=×0、44+×0、44×0、6+×0、44×0、62+×0、44×0、63≈0、290、由于P1>P2>P3，所以方案①对乙最有利、正确答案:①三、解答题( 本大题共6小题，共70分)17、( 本小题满分10分)一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1，3张卡片上的数字是2，2张卡片上的数字是3、从盒中任取3张卡片、( 1 )求所取3张卡片上的数字完全相同的概率;( 2 )X表示所取3张卡片上的数字的中位数，求X的分布列与均值、( 注:若三个数a，b，c满足a≤b≤c，则称b为这三个数的中位数、)解( 1 )由古典概型中的概率计算公式知所求概率为P=、( 2 )X的所有可能值为1，2，3，且P( X=1 )=，P( X=2 )=，P( X=3 )=，故X的分布列为X123P从而EX=1×+2×+3×、18、( 本小题满分12分)某高校设计了某实验学科的考核方案:考生从6道备选题中一次性随机抽取3题，按照题目要求独立完成全部实验操作、规定:至少正确完成其中2题才可提交通过、已知6道备选题中，考生甲有4道题能正确完成，2道题不能正确完成;考生乙每题正确完成的概率都是，且每题正确完成与否互不影响、( 1 )分别写出甲、乙两考生正确完成题数的概率分布列，并计算数学期望;( 2 )试从两位考生正确完成题数的数学期望及至少正确完成2道题的概率分析比较两位考生的实验操作能力、解( 1 )设考生甲、乙正确完成实验操作的题数分别为ξ，η，则ξ的所有可能取值为1，2，3，η的所有可能取值为0，1，2，3、∵P( ξ=1 )=，P( ξ=2 )=，P( ξ=3 )=，∴考生甲正确完成题数的概率分布列为ξ123PEξ=1×+2×+3×=2、∵P( η=0 )=，P( η=1 )=，P( η=2 )=，P( η=3 )=，∴考生乙正确完成题数的分布列为η0123PEη=0×+1×+2×+3×=2、( 2 )∵P( ξ≥2 )==0、8，P( η≥2 )=≈0、74，∴P( ξ≥2 )>P( η≥2 )、从做对题数的数学期望考核，两人水平相当;从至少正确完成2道题的概率考核，甲获得通过的可能性大、因此可以判断甲的实验操作能力较强、19、( 本小题满分12分)某班从6名班干部( 其中男生4人，女生2人)中，任选3人参加学校的义务劳动、( 1 )设所选3人中女生人数为X，求X的分布列;( 2 )求男生甲或女生乙被选中的概率;( 3 )设“男生甲被选中”为事件A，“女生乙被选中”为事件B，求P( B )和P( A|B )、解( 1 )X的所有可能取值为0，1，2，依题意得P( X=0 )=，P( X=1 )=，P( X=2 )=、∴X的分布列为X012P( 2 )设“男生甲、女生乙都不被选中”为事件C，则P( C )=，∴所求概率为P( )=1-P( C )=1-、( 3 )由题意得P( B )=，又∵P( AB )=，∴P( A|B )=、20、导学号43944048( 本小题满分12分)某球类总决赛采取7局4胜制，预计本次比赛两队的实力相当，每场比赛组织者可获利200万元、( 1 )求组织者在本次比赛中获利不低于1 200万元的概率;( 2 )组织者在本次比赛中获利的期望为多少万元?解设本次比赛组织者获利为X万元，当X=800时，这两队只进行四场比赛，两队有一队全胜，P( X=800 )=2×=0、125;当X=1 000时，这两队进行五场比赛，两队中有一队前四场比赛是胜三场，败一场，第五场胜，P( X=1 000 )=2=0、25;当X=1 200时，这两队进行六场比赛，P( X=1 200 )=2=0、312 5;当X=1 400时，这两队比赛满七场，P( X=1 400 )=2=0、312 5、所以X的分布列为X800 1 000 1 200 1 400P0、1250、250、312 50、312 5( 1 )组织者在本次比赛中获利不低于1 200万元的概率是0、312 5×2=0、625、( 2 )EX=800×0、125+1 000×0、25+1 200×0、312 5+1 400×0、312 5=1 162、5、故组织者在本次比赛中获利的期望为1 162、5万元、21、导学号43944049( 本小题满分12分)一家面包房根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图，如图所示、将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立、( 1 )求在未来连续3天里，有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;( 2 )用X表示在未来3天里日销售量不低于100个的天数，求随机变量X的分布列，均值EX 及方差DX、解( 1 )设A1表示事件“日销售量不低于100个”，A2表示事件“日销售量低于50个”，B表示事件“在未来连续3天里，有连续2天的日销售量都不低于100个且另1天的日销售量低于50个”，因此P( A1 )=( 0、006+0、004+0、002 )×50=0、6，P( A2 )=0、003×50=0、15，P( B )=0、6×0、6×0、15×2=0、108、( 2 )X可能取的值为0，1，2，3，相应的概率为P( X=0 )=×( 1-0、6 )3=0、064，P( X=1 )=×0、6×( 1-0、6 )2=0、288，P( X=2 )=×0、62×( 1-0、6 )=0、432，P( X=3 )=×0、63=0、216、分布列为X0123P0、0640、2880、4320、216因为X~B( 3，0、6 )，所以EX=3×0、6=1、8，方差DX=3×0、6×( 1-0、6 )=0、72、22、导学号43944050( 本小题满分12分)某厂用鲜牛奶在某台设备上生产A，B两种奶制品，生产1吨A产品需鲜牛奶2吨，使用设备1小时，获利1 000元;生产1吨B产品需鲜牛奶1、5吨，使用设备1、5小时，获利1 200元，要求每天B产品的产量不超过A产品产量的2倍，设备每天生产A，B两种产品时间之和不超过12小时，假定每天可获取的鲜牛奶数量W( 单位:吨)是一个随机变量，其分布列为W121518P0、30、50、2该厂每天根据获取的鲜牛奶数量安排生产，使其获利最大，因此每天的最大获利Z( 单位:元)是一个随机变量、( 1 )求Z的分布列和均值;( 2 )若每天可获取的鲜牛奶数量相互独立，求3天中至少有1天的最大获利超过10 000元的概率、解( 1 )设每天A，B两种产品的生产数量分别为x，y，相应的获利为z，则有①目标函数为z=1 000x+1 200y、当W=12时，①表示的平面区域如图1，三个顶点分别为A( 0，0 )，B( 2、4，4、8 )，C( 6，0 )、将z=1 000x+1 200y变形为y=-x+，当x=2、4，y=4、8时，直线l:y=-x+在y轴上的截距最大，最大获利Z=z max=2、4×1 000+4、8×1 200=8 160、当W=15时，①表示的平面区域如图2，三个顶点分别为A( 0，0 )，B( 3，6 )，C( 7、5，0 )、图1图2将z=1 000x+1 200y变形为y=-x+，当x=3，y=6时，直线l:y=-x+在y轴上的截距最大，最大获利Z=z max=3×1 000+6×1 200=10 200、当W=18时，①表示的平面区域如图3、图3四个顶点分别为A( 0，0 )，B( 3，6 )，C( 6，4 )，D( 9，0 )、将z=1 000x+1 200y变形为y=-x+，当x=6，y=4时，直线l:y=-x+在y轴上的截距最大，最大获利Z=z max=6×1 000+4×1 200=10 800、故最大获利Z的分布列为Z8 16010 20010 800P0、30、50、2因此，EZ=8 160×0、3+10 200×0、5+10 800×0、2=9 708、( 2 )由( 1 )知，一天最大获利超过10 000元的概率p1=P( Z>10 000 )=0、5+0、2=0、7，由二项分布，得3天中至少有1天最大获利超过10 000元的概率为p=1-( 1-p1 )3=1-0、33=0、973、。

北师大版高中数学选修2-3第二章概率同步练习(一).docx

第二章概率同步练习(一)一、选择题：（本大题共10小题，每小题5分，共50分）1．将一颗骰子抛掷两次，设抛掷的最大点数为ξ，则)3(≤ξP 的值是（） A ．32B ．21 C ．31 D ． 412．已知：),,(~2δμN X 且,5=X E ,4=X D 则≈≤<)73(x P （）A ．0．045 6B ．0.50C ．0.682 6D ．0.95443．数字1、2、3、4、5任意排成一列，如果数字)5,4,3,2,1(=k k 恰好排在第k 个位置，则称为一个巧合数，设巧合数为ξ，则)1(=ξP 的值是（）A ．3011B ． 61C ．83D ．121 4．如图，这是一个城镇的街道网络图，某人从A 到B 最短的行走方式是向东或向北行走，经过哪个街道都是等可能的，则这个人经过线段CD 的概率是（）A ．285 B ．31C ．51D ．41 AD CB向东→←向北5．某厂生产电子元件，其产品的次品率为%p ,现从一大批这类产品中任意地连续取出3件，奖品数为ξ，则)2(≤ξP 的值是（）A ．223)1(3)1(3)1(p p p p p -+-+-B ．3)%]100[(1p --C ．2%))%](100[(3p p -D ．3%)(1p -6．在5道题中有2道选修题和3道必修题.如果不放回地依次取出2道题，则第1次和第2次都抽到必修题的概率是（）A ．259 B ．53 C ．103 D ．104 7．某人的“QQ ”密码共7位数字，每位数字都是从0~9中任选的一个，他上网时忘记了中间的一位数字，他任意选数字，则不超过3次选对的概率是（）A ．103 B ．72 C ．31 D ．528．有8张卡片，其中6张标有数字2，有2张标有数字5，从中随机抽取3张卡片，设3张卡片上的数字之和为X ，则随机变量X 的均值EX 是（）A ．7.80B ．8.25C ．9.02D ．8.249．某篮球运动员罚球命中率为0.8，命中得1分，没有命中得0分，则他罚球1次的得分X 的方差为（）A ．0.20B ．0.18C ．0.16D ．0.14 10．根据气象预报，在某地区近期有小沙尘暴的概率为41，有大沙尘暴的概率为1001，该地区某勘探工地上有一台大型勘探设备，遇到大沙尘暴时要损失60 000元，遇到小沙尘暴时要损失10 000元，为了保护勘探设备，有三种应急方案：方案措施、费用损失（元）方案1 运走勘探设备，搬运费用为3 800元1X 方案2 建防护帐篷，建设费用为2 000元，但防护帐篷只能防小沙尘暴2X 方案3 不采取任何措施，但愿不发生沙尘暴3X这三种方案的平均损失分别为E 1X 、E 2X 、E 3X ，则它们的大小关系是（） A ．E 3X <E 2X <E 1X B ． E 3X <E 1X <E 2XC ．E 2X <E 1X <E 3XD ．E 2X <E 3X < E 1X二、填空题（本大题共4小题，每小题6分，共24分）11．某篮球运动员的罚球命中率为0.7，若连续罚球三次，则得分的概率为 .12．盒中有6个白球和4个黑球，从中任意取出3个，设X 是其中的黑球数，则=≥)1(X P .13．设离散型随机变量),1,4.0(~N X 则=≤)4.0(X P .14．在一副扑克牌的13张梅花中，不放回地连续抽取2次，每次抽1张牌，则恰好在第2次抽取到梅花Q 的概率为 .三、解答题（本大题共5题，共76分）15．对某种抗禽流感的抗生素进行临床试验，试验表明抗生素对禽流感患者的治愈率为75%，现给12名患者同时用这种抗生素，求至少有10人被治愈的概率. (15分)16．某旅游城市有甲、乙两个五星级宾馆，根据多年来的业绩记录显示：甲、乙两个宾馆一年中满员（出租率%称为满员）的天数所占比例分别是18%和9024%，两个宾馆同时满员的天数的比例为12%，求（1）乙宾馆满员时，甲宾馆也满员的概率；（2）甲宾馆满员时，乙宾馆不满员的概率.(15分)17．如图，由三个同心圆组成的靶子，它们的半径比为1：2：3，制定如下法则：第一次射击只要在大圆范围内，称为命中；第二次射击时，只要在中圆范围内，称为命中；第三次射击必须在小圆范围内，才称为命中，已知某射手第一次射击的命中率为0.5，如果第一次未射中，则要进行第二次射击；如果第二次还未射中，则要进行第三次射击.已知射击的命中率与环的半径的平方成正比，求该射手命中靶子的概率.（射击命中后射击立即停止）（15分）18．售票窗口有10台电脑各自独立地运行，因修理协调等原因，每台电脑停机的概率为0.2 求：（1）电脑同时停机的台数X的分布列；（2）10台电脑恰好有1台停机的概率；（3）10台电脑至多有2台停机的概率.（15分）19．某学校高二年级进行数学∙选修2-3模块考试评价，考试成绩拟合正态分布，且X~N).75(2如果规定考试成绩低于60分为考试评价不合格，对低于60不,15低于45的学生再组织本模块补考；对低于45分的学生本模块必须重修.(1) 模块考试评价不合格的人数占多少？(2) 重修数学∙选修2-3的学生的人数占多少？(3) 若本年级选修数学∙选修2-3的学生是1 000名学生，则至少要准备补考试卷多少份？（16分）参考答案一、选择题1．D 2．C 3．C 4．A 5．D 6．C 7．A 8．B 9．C 10．D 二、填空题11．0．973 12．65 13．0.5 14．131 三、解答题15．解：设“一患者被治愈”的事件为A ，则P （A ）=0.75，则 )12()11()10()10(=+=+==≥ξξξξP P P P12121211111122101012)43()41()43()41()43(C C C ++=3907.00317.01267.02323.0=++≈16．设“甲宾馆满员”事件为A ，“乙宾馆满员”事件为B ，依题意；18.0)(=A P24.0)(=B P ，12.0)(=AB P .所以：（1）5.024.012.0)()()|(===B P AB P B A P （2）33.067.01)|(,67.018.012.0)()()|(=-≈∴≈==A B P A P AB P A B P 17．设三次射中靶子的事件依次为321,,A A A ，则,1815.03)(21=⇒=⋅=k k A P ,922)(22=⋅=k A P 5.03)(23=⋅=k A P 因此，该射手命中靶子的概率为：6327.01819721922121)()()(321211=⨯⨯+⨯+=++=A A A P A A P A P P18．解：依题意：随机变量),2.0,10(~B X 则（1）电脑同时停机的台数X 的分布列是：)10,...,2,1,0(8.02.0)(1010=⨯==-k C k X P k k k（2）10台电脑恰好有恰好有1台停机的概率是：2684.08.02.0)1(91110≈⨯==C X P （3）10台电脑至多有2台停机的概率是：82210911101000108.02.08.02.08.02.0)2(⨯+⨯+⨯=≤C C C X P6778.03020.02684.01074.0=++=19．设学生的考试成绩为随机变量X ，且)15,75(~2N X ，则,15,75==σμ （1）考试成绩在60~90分的人数所占的比例为,6826.0)15751575(=+≤≤-X P 考试不合格的人数所占的比例是：)60(<X P %87.15)6826.01(21=-=（2）考试成绩在45~105分的人数所占的比例为,9544.0)10545(=≤≤X P 所以重修数学∙选修2-3的学生的人数所占的比例是：)60(<X P %28.2)9544.01(21=-=（3）至少准备补考试卷的份数是：1000136%)28.2%87.15(≈-⨯份.。

北师大版高中数学选修2-3第二章概率同步练习(二).docx

高中数学学习材料马鸣风萧萧*整理制作第二章概率同步练习(二)一、选择题：（本大题共10小题，每小题5分，共50分）1．从装有6个白球、4个红球的盒子中，不放回地一个一个地摸出球，则第3次才摸出红球的概率为（）A ．61 B ． 52 C ．12518 D ． 63102．从一批有3件次品与10件正品的产品中，等可能地一件一件地抽取产品，每次取出的产品都不放回，取到正品为止时所需抽取次数为ξ，则)3(=ξP 的值是（）A ．265 B ．1435 C ．286285 D ．1310)133(2⨯ 3．有甲、乙两位篮球运动员，甲罚球进球数4.121+=ξX ，其中),8.0,6(~B ξ 乙罚球进球数2X ),9.0,12(~B 则（）A ．甲罚球进球的平均数比乙罚球进球的平均数少B ．甲罚球进球的平均数比乙罚球进球的平均数多C ．甲罚球进球的平均数与乙罚球进球的平均数相同D ． 4.0||21=-EX EX4．如图，曲线),(21)(:21212)(11R x ex f C x ∈=--δμδπ曲线),(21)(:22222)(22R x e x C x ∈=--δμδπϕ则（）A ．21μμ<B ．曲线1C 与x 轴相交 C ．21δδ>D ．曲线1C 、2C 分别与x 轴所夹的面积相等5．交4元钱，可以参加摸奖一次，暗箱中装有大小一样的10个小球，其中有8个标有1元钱，2个标有5元钱，一次摸奖只能从中任摸2个球，所获奖励是两球上的钱数之和，则获利的数学期望是（）A ．3.6B ．4.0-C ．2.6D ．4.1-6．设随机变量),2(~p B X 和),,4(~p B Y 若,167)1(=≥X P 则=≤)3(Y P （）A ．256175B ．12841 C ．256255D ．256817．设随机变量ξ的概率分布列为下表所示，则)2(+ξE 的值是（）A ．625 B ．313 C ．311 D ．4ξ123i P121 61 41 121 （第7题图）（第8题图）AB CxyoC 1C 28．如图，设A 、B 、C 表示三种开关，若在某段时间内它们正常工作的概率分别为0.8、0.9、0.7，则该系统的可靠性是（）A ．0.504B ．0.994C ．0.496D ．0.0609．在数学单元测试中，有12道选择题，每道选择题有4个选项，其中仅有一个选项正确.每题选对得5分，不选、多选或选错不得分，选择题的满分是60分，某个学生选对任意一题的概率为0.75，设该学生在这次单元测试中选对的题数为X ，则DX 是（）A ．0.20B ．0.18C ．0.16D ．0.1410．假定生男孩和生女孩的概率是相等的，一个家庭有两个小孩，已知这个家庭有一个女孩，则这时另一个是男孩的概率是（）A ．43 B ．21 C ．52 D ． 32 二、填空题（本大题共4小题，每小题6分，共24分）11．若随机变量X 的分布列为下表所示，则=X δ . X 123P51 103 21 （第11题）（第12题）12．已知随机变量X 的分布列如上表所示，则=-)12(X D . 13．根据统计资料，某地高二学生中男生的身高X （单位：cm ）服从正态分布N （174，9），若该地共有高二男生3000人，则该地高二男生中身高在（174，180]范围内的有 .14．5名同学站成一排，已知甲同学不能站在第1位，则任意站成一排时，乙同学没有排在第2位的概率为 .三、解答题（本大题共5题，共76分） 15．一个暗箱里放着6个黑球、4个白球.(1) 依次取出3个球，不放回，若第1次取出的是白球，求第3次取到黑球的概率； (2) 有放回地依次取出3个球，若第1次取出的是白球，求第3次取到黑球的概率；X 1 2 3 4 5 P0.20.20.30.20.1(3) 有放回地依次取出3个球，求取到白球个数ξ的分布列.(15分)16．有甲、乙两个材料厂生产型号相同的材料，都参加了某项重点工程的投标，为了对重点工程负责，相关部门对两个厂提供的材料进行抽样检查，各取等量的样品检查它们的抗拉强度指标，检测如下表：其中ξ和η（单位：mm）分别表示甲、乙两个厂生产材料的抗拉强度，在使用时要求抗拉强度的均值不低于120mm，试比较甲、乙两厂生产的材料的稳定性. (15分)ξ100 115 125 130 145 η110 120 125 130 135 P 0.1 0.2 0.4 0.1 0.2 P 0.1 0.2 0.4 0.1 0.217．某射手有6发子弹，射击一次命中概率为0.9，如果命中就停止射击，否则一直到子弹用尽，求消耗子弹数X的分布列，并求该射手命中的概率.（15分）18．某商店有100台相同型号的冰箱待售，其中60台是甲厂生产的，25台是乙厂生产的，15台是丙厂生产的.已知这三个厂生产的不合格率分别为0.1、0.4、0.2.（1）试求该顾客取到不合格冰箱的概率；（2）顾客开箱测试后发现冰箱不合格，但这台冰箱的厂标已经脱落，试问这台冰箱是甲厂、乙厂、丙厂生产的概率各是多少？（15分）19．分析人才成长资料表明：因小学成绩优秀而最终导致成为精英（相互独立）的比例占0.2% .求目前正在读小学的成绩优秀的1000人中：(1) 最终恰有4人成为精英的概率（列成算式）；(2) 最终成为精英的人数不超过2个的概率（列成算式）。

人教b版选修2-3第2章概率同步练测(人教实验B版选修2-3)2

高中数学学习材料金戈铁骑整理制作第2章概率（人教实验B版选修2-3）一、选择题（本题包括10小题，每小题5分，共50分，每小题给出的四个选项中，只有一个选项正确）1.在所有两位数中，任取一个数，则这个数能被3 整除的概率是A. B.C. D.2.四边形ABCD为长方形，AB＝2，BC＝1，O为AB的中点，在长方形ABCD内随机取一点，取到的点到O的距离大于1的概率为A. B.1-C. D.1-3.三人独立破译同一份密码，已知三人各自破译出密码的概率分别为 , , ，且他们是否破译出密码互不影响，设“密码被破译”的概率为，“密码未被破译”的概率为，则，的大小关系为A.＞B.=C.＜D.无法判断4.设随机变量XN（2，4），且P（X≤0）＝P（X≥a-2），则实数a的值为A.4B.5C.6D.75.若X是离散型随机变量，P（X=）= ,P（X=）= ，且<，又已知E（X）= ，D（X）= ，则+的值为（）A. B.C.3D.6.有一批书共100本，其中文科书40本，理科书60本，分为精装、平装两种，精装书70本，某人从这100本书中任取一书，恰是文科书，放回后再任取1本，恰是精装书，这一事件的概率是（）A. B.C. D.7.将一枚骰子抛掷两次，若先后出现的点数分别为b，c，则方程+bx+c=0有实根的概率为建议用时实际用时满分实际得分120分钟150分A. B.C. D.8.下列四个游戏盘（各正方形边长和圆的直径都是单位1），如果撒一粒黄豆落在阴影部分，则可中奖.小明希望中奖，他应选择的游戏盘是9. 设随机变量X~B(n，0.5)，且D(X)＝2，则事件“X＝1”的概率为（）A. B.C. D.10.已知椭圆 +=1的焦点为、，在长轴上任取一点M，过点M作垂直于的直线交椭圆于点P，则使得·＜0的点M的概率为A. B.C. D.二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中横线上）11.将一骰子连续抛掷三次，它落地时向上的点数依次成等差数列的概率为 .12.罐中有6个红球，4个白球，从中任取1球，记下颜色后再放回，连续摸取4次，设为取得红球的次数，则ξ的数学期望E（）＝ .13.在圆周上有10个等分点，以这些点为顶点，每3个点可以构成一个三角形，如果随机选择3个点，则刚好构成直角三角形的概率为 .14.设l为平面上过点（0,1）的直线,l的斜率等可能地取-2 ，- ，- ，0，，，2 ，用X表示坐标原点到l的距离，则随机变量X的数学期望E（X）＝ .三、解答题（本大题共5小题，共80分.解答应写出文字说明，证明过程或演算步骤）15.（14分）一袋中有6个黑球，4个白球.（1）依次取出3个球，不放回，已知第一次取出的是白球，求第三次取到黑球的概率；（2）有放回地依次取出3个球，已知第一次取出的是白球，求第三次取到黑球的概率.16.（14分）已知关于x的一元二次函数f(x)=-4bx+1.（1）设集合P＝{1,2,3}和Q＝{-1，1，2，3，4}，分别从集合P和Q中随机取一个数作为a和b，求函数y=f(x)在区间［1,+∞）上是增函数的概率；（2）设点（a,b）是区域内的随机点，求函数y=f(x)在区间［1,+∞）上是增函数的概率.17.(16分）某城市有甲、乙、丙三个旅游景点，一位游客游览这三个景点的概率分别是0.4、0.5、0.6，且游客是否游览哪个景点互不影响，用ξ表示该游客离开该城市时游览的景点数与没有游览的景点数之差的绝对值.（1）求ξ的分布列及期望；（2）记“f（x）=2ξx+4在［-3,-1］上存在,使f（）=0”为事件A，求事件A的概率.18.（18分）设关于x的一元二次方程+2ax+=0. （1）若a是从0,1,2,3四个数中任取的一个数，b是从0,1,2三个数中任取的一个数，求上述方程有实根的概率；（2）若a 是从区间［0，3］中任取的一个数，b 是从区间［0，2］中任取的一个数，求上述方程有实根的概率.19.(18分)如图所示，某学校要用鲜花布置花圃中A ，B ，C ，D ，E 五个不同区域，要求同一区域上用同一种颜色的鲜花，相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择. （1）当A ，D 区域同时用红色鲜花时，求布置花圃的不同方法的种数；（2）求恰有两个区域用红色鲜花的概率；（3）记ξ为花圃中用红色鲜花布置的区域的个数，求随机变量ξ的分布列及数学期望E （ξ）.第2章概率（人教实验B 版选修2-3）答题纸得分：一、选择题题号 1 2 3 4 5 6 7 8 9 10答案二、填空题11． 12． 13. 14.三、解答题15.16.17.18.19.第2章概率（人教实验B版选修2-3）参考答案一、选择题1.D解析：两位数从10到99共有99-10+1＝90（个），其中能被3整除的数为12，15，18，…，99组成以12为首项，以3为公差的等差数列.由12+（n-1）×3=99得n=30，即能被3整除的两位数有30个，所以概率为P＝＝ .故选D.2.B 解析：如图，要使图中的点到O的距离大于1，则该点需取在图中阴影部分，故概率为P＝ =1- .故选B.3.A解析：记“第i个人破译出密码”为事件（i=1，2，3），依题意有P（）＝，P（）＝，P（）＝，且，，相互独立.设“密码被破译”为事件B，“密码未被破译”为事件C，则C＝··，且，，相互独立，故＝P（C）＝P·P·P＝×× = ，而=P（B）=1-P（C）= ，故.故选A.4.C解析：由正态曲线的对称性得 =2,∴a=6.故选C.5.C解析：分析已知条件，利用离散型随机变量的均值和方差的计算公式得解得或又∵ ,∴∴ =3.6.A解析：设“任取一书是文科书”的事件为A，“任取一书是精装书”的事件为B，则A、B是相互独立的事件，所求概率为P（AB）.据题意可知P（A）= = ,P（B）= = ,∴P（AB）=P（A）P（B）= × = .7.A解析：若方程有实根，则Δ＝-4c≥0，当有序实数对（b,c）的取值为（6,6）,(6,5),…,(6,1),（5，6），(5,5)，…，（5，1），（4，4），…，（4，1），（3，2），（3，1），（2，1）时方程有实根，共19 种情况，而（b,c）等可能的取值共有36种情况，所以方程有实根的概率为P＝ .故选A.8.A解析：P（A）＝ ,P(B)= ,P(C)= ＝1- ,P（D）＝ ,P(A)最大，故选A.9.C 解析：D(X)＝n×0.5×(1-0.5)＝2，∴n=8，则P(X＝1)＝×0.5×＝故选C.10.C 解析：设点M的坐标为（,0），点P的坐标为（,)，则有∈［-2,2］，由题知两焦点为（- ,0）,( ,0),∴·＝-3+=-3+1- = -2＜0，解得- ＜＜ ,即点M的几何度量为 .又｜｜=4,∴P= = .故选C.二、填空题11. 解析：基本事件有6×6×6=216（个），点数依次成等差数列的有：（1）当公差d=0时，1，1，1及2，2，2;…，共6个.（2）当公差d=±1时，1，2，3及2，3，4；3，4，5；4，5，6；…，共4×2个.（3）当公差d=±2时，1，3，5；2，4，6；…，共2×2个.∴P＝ = .12. 解析：因为是有放回地摸球，所以每次摸球（试验）摸得红球（成功）的概率均为，连续摸4次（做4次试验），ξ为取得红球（成功）的次数，则ξB (4， ) ，从而有E（ξ）＝np=4× = .13. 解析：∵直角三角形的斜边是圆的直径，而圆周上的10个等分点能组成5条直径，∴直角三角形的个数为＝40个.而每3个点能构成的三角形有＝120（个），∴所求概率为P＝＝ .14. 解析：当k=±2 时，直线方程为±2 x-y+1＝0= ；当k=±时，= ；当k=±时，= ；当k=0时，=1.由等可能性事件的概率可得分布列如下：X 1P∴E（）＝× + × + × +1×＝ .三、解答题15. 解：（1）设A=“第一次取到白球”，B=“第二次取到白球”，C=“第三次取到白球”，则在A发生的条件下，袋中只剩下6个黑球和3个白球，则P（C |A）= = = .（2）∵每次取之前袋中球的情况不变，∴n次取球的结果互不影响，∴P（C）= = .16.解：（1）∵函数f（x）=-4bx+1的图象的对称轴为x= ，要使f（x）=-4bx+1在区间［1，+∞）上为增函数，当且仅当a＞0且≤1，即2b≤a.若a=1，则b=-1，若a=2，则b=-1，1，若a=3，则b=-1，1，∴所求事件包含基本事件的个数是1+2+2=5.而试验中包含的基本事件总数为3×5=15，∴所求事件的概率为 = .（2）由（1）知当且仅当2b≤a且a＞0时函数f（x）＝-4bx+1在区间［1，+∞）上为增函数，依条件可知试验的全部结果所构成的区域为{（a，b）|}，则构成所求事件的区域为三角形阴影部分，如图所示，由得交点P ( ， ) .∴所求事件的概率为P= = .17.解：（1）设游客游览甲、乙、丙三个景点分别记为事件、、，已知、、相互独立，且P（）=0.4，P（）=0.5，P（）=0.6.游客游览的景点数可能取值为0、1、2、3，相应的游客没有游览的景点数可能取值为3、2、1、0，所以ξ的可能取值为1、3.则P（ξ=3）=P（··）+P（··）=P（）·P（）·P（）+P·P·P=2×0.4×0.5×0.6=0.24.P（ξ=1）=1-0.24=0.76.所以ξ的分布列为ξ 1 3P0.76 0.24∴E（ξ）＝1×0.76+3×0.24=1.48.（2）∵f（x）=2ξx+4在［-3，-1］上存在，使得f（）=0，∴f（-3）·f（-1）≤0,即（-6ξ+4）（-2ξ+4）≤0,解得≤ξ≤2.∴P（A）=P ( ≤ξ≤2) =P（ξ=1）=0.76.18.解：设事件A为“方程+2ax+=0有实根”.当a≥0，b≥0时，方程+2ax+=0有实根的充要条件是a≥b.(1)基本事件共有12个：（0,0）,(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)，其中第一个数表示a的取值，第二个数表示b的取值.事件A中包含9个基本条件，事件A发生的概率为P（A）＝＝ .（2）试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}.构成事件A的区域为{（a，b)|0≤a≤3,0≤b≤2，a≥b}.所以所求的概率为P（A）＝ = .19.解：（1）当A，D区域同时用红色鲜花时，其他区域不能用红色鲜花，因此，布置花圃的不同方法的种数为4×3×3=36（种）.（2）设M表示事件“恰有两个区域用红色鲜花”，当区域A，D同色时，共有5×4×3×1×3＝180（种）；当区域A，D不同色时，共有5×4×3×2×2＝240（种）.因此，所有基本事件共有180+240＝420（种）（是等可能的）.又因为A，D为红色时，共有4×3×3=36（种）；B，E为红色时，共有4×3×3＝36（种）.因此事件M包含的基本事件有36+36＝72（种），所以P（M）＝＝ .（3）随机变量ξ的分布列为ξ0 1 2P所以E（ξ）＝0× +1× +2× =1.。

高中数学选修2-3 2.2.1 条件概率同步课时练附参考答案

A.1
B.1
C.2
D.1
8
4
5
2
4．某地一农业科技实验站，对一批新水稻种子进行试验，已知这批水稻种子的发芽
率为 0.8，出芽后的幼苗成活率为 0.9，在这批水稻种子中，随机地抽取一粒，则这粒水稻
种子能成长为幼苗的概率为( )
A．0.02
B．0.08
C．0.18
D．0.72
二、填空题(每小题 5 分，共 10 分)
6．6 位同学参加百米短跑初赛，赛场共有 6 条跑道，已知甲同学排在第一跑道，则乙同学排在第二跑道的概率是________．
三、解答题(每小题 10 分，共 30 分) 7．袋中有 3 个白球，2 个黑球，现每次取一个，不放回地取 2 次．求在第 1 次取到白球的条件下，第 2 次取到白球的概率．
则 B ＝{三个数互不同行且不同列}，依题意得
n(A)＝C28＝28，n( AB )＝2.
故 P
B
A
n AB
n A
2 1 ，则 28 14
P(B|A)＝1－ P B A ＝1－ 1 ＝13. 14 14
即已知取到
a22
的条件下，至少有两个数位于同行或同列的概率为13. 14
P B A 表示甲厂生产的产品的不合格率，即 P B A 1－P(B|A)＝1－95%＝5%＝0.05.
P B A 表示乙厂生产的产品的合格率，即 P B A 80%＝0.8.
P B A 表示乙厂生产的产品的不合格率，即 P B A 1－ P B A 20%＝0.2
答案： 0.95 0.05 0.8 0.2
6.解析：甲同学排在第一跑道后，还剩 5 个跑道，则乙排在第二跑道的概率为1. 5

高中数学选修2-3第二章概率单元测试试题2

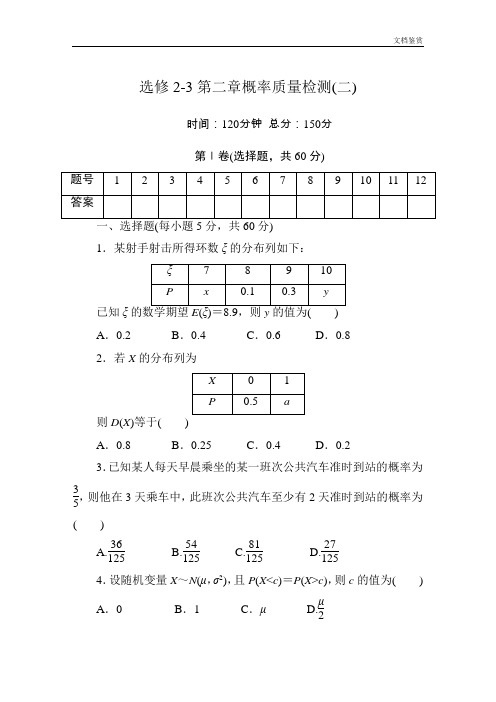
选修2-3第二章概率质量检测(二)时间：120分钟总分：150分第Ⅰ卷(选择题，共60分)1．某射手射击所得环数ξ的分布列如下：已知ξA．0.2 B．0.4 C．0.6 D．0.82．若X的分布列为则D(X)等于(A．0.8 B．0.25 C．0.4 D．0.23．已知某人每天早晨乘坐的某一班次公共汽车准时到站的概率为35，则他在3天乘车中，此班次公共汽车至少有2天准时到站的概率为()A.36125 B.54125 C.81125 D.271254．设随机变量X～N(μ，σ2)，且P(X<c)＝P(X>c)，则c的值为()A．0 B．1 C．μ D.μ25．将三颗骰子各掷一次，记事件A ＝“三个点数都不同”，B ＝“至少出现一个6点”，则条件概率P (A |B )，P (B |A )分别是( )A.6091，12B.12，6091C.518，6091D.91216，12 6.箱中装有标号为1,2,3,4,5,6且大小相同的6个球．从箱中一次摸出两个球，记下号码后放回，如果两球号码之积是4的倍数，则获奖．现有4人参与摸奖，恰好有3人获奖的概率是( )A.16625B.96625C.624625D.4625 7．已知X 的分布列为且Y ＝aX ＋3，E (Y )＝73，则a 为( )A ．－1B ．－12C ．－13D ．－148．已知变量x 服从正态分布N (4，σ2)，且P (x >2)＝0.6，则P (x >6)＝( )A ．0.4B ．0.3C ．0.2D ．0.19．设由“0”，“1”组成的三位数组中，若用A 表示“第二位数字为‘0’的事件”，用B 表示“第一位数字为‘0’的事件”，则P (A |B )等于( )A.25B.34C.12D.1810．把10个骰子全部投出，设出现6点的骰子的个数为X ，则P (X ≤2)＝( )A ．C 210×⎝⎛⎭⎪⎫162×⎝ ⎛⎭⎪⎫568 B ．C 110×16×⎝ ⎛⎭⎪⎫569＋⎝ ⎛⎭⎪⎫5610C ．C 110×16×⎝ ⎛⎭⎪⎫569＋C 210×162×⎝ ⎛⎭⎪⎫568D ．以上都不对 11．已知随机变量X ～B (6,0.4)，则当η＝－2X ＋1时，D (η)＝( ) A ．－1.88 B ．－2.88 C ．5.76 D ．6.76 12．节日期间，某种鲜花的进价是每束2.5元，售价是每束5元，节后对没售出的鲜花以每束1.6元处理．据前5年节日期间这种鲜花销售情况得需求量ξ(单位：束)的统计如下表，若进这种鲜花500束在今年节日期间销售，则期望利润是( )A.706D ．720元第Ⅱ卷(非选择题，共90分)二、填空题(每小题5分，共20分)13．加工某一零件需经过三道工序，设第一、二、三道工序的次品率分别为170，169，168，且各道工序互不影响，则加工出来的零件的次品率为________．14.已知正态总体的数据落在区间(－3，－1)内的概率和落在区间(3,5)内的概率相等，那么这个正态总体的数学期望为________．15．如果一个随机变量ξ～B ⎝ ⎛⎭⎪⎫15，12，则使得P (ξ＝k )取得最大值的k 的值为________．16．某一部件由三个电子元件按下图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作．设三个电子元件的使用寿命(单位：小时)均服从正态分布N (1 000,502)，且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1 000小时的概率为________．三、解答题(写出必要的计算步骤，只写最后结果不得分，共70分)17．(10分)设进入某商场的每一位顾客购买甲种商品的概率为0.5，购买乙种商品的概率为0.6，且购买甲种商品与购买乙种商品相互独立，各顾客之间购买商品也是相互独立的．(1)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率；(2)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数，求ξ的分布列及期望．18．(12分)某同学参加3门课程的考试．假设该同学第一门课程取得优秀成绩的概率为45，第二、第三门课程取得优秀成绩的概率分别为p ，q (p >q )，且不同课程是否取得优秀成绩相互独立．记ξ为该生取得优秀成绩的课程数，其分布列为(1)求该生至少有1门课程取得优秀成绩的概率；(2)求p，q的值；(3)求数学期望E(ξ)．19.(12分)一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3.从盒中任取3张卡片．(1)求所取3张卡片上的数字完全相同的概率；(2)X表示所取3张卡片上的数字的中位数，求X的分布列与数学期望．(注：若三个数a，b，c满足a≤b≤c，则称b为这三个数的中位数．)20.(12分)一家面包房根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图，如图所示．将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立．(1)求在未来连续3天里，有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率；(2)用X 表示在未来3天里日销售量不低于100个的天数，求随机变量X 的分布列，期望E (X )及方差D (X )．21.(12分)某企业有甲、乙两个研发小组，他们研发新产品成功的概率分别为23和35.现安排甲组研发新产品A ，乙组研发新产品B .设甲、乙两组的研发相互独立．(1)求至少有一种新产品研发成功的概率；(2)若新产品A 研发成功，预计企业可获利润120万元；若新产品B 研发成功，预计企业可获利润100万元．求该企业可获利润的分布列和数学期望．22.(12分)设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4，各人是否需使用设备相互独立．(1)求同一工作日至少3人需使用设备的概率；(2)X 表示同一工作日需使用设备的人数，求X 的数学期望．答案1．B ∵E (ξ)＝7x ＋8×0.1＋9×0.3＋10y ＝7(0.6－y )＋10y ＋3.5＝7.7＋3y ，∴7.7＋3y ＝8.9，∴y ＝0.4.2．B 由题意知0.5＋a ＝1，E (X )＝0×0.5＋a ＝a ＝0.5，所以D (X )＝0.25.3．C 设此班次公共汽车准时到站的天数为随机变量X ，则此班次公共汽车至少有2天准时到站的概率为P (X ＝2)＋P (X ＝3)＝C 23⎝⎛⎭⎪⎫352×25＋C 33⎝ ⎛⎭⎪⎫353＝81125.4．C 因为P (X <c )＝P (X >c )，由正态曲线的对称性知μ＝c . 5．A 由题意得事件A 包含的基本事件个数为6×5×4＝120，事件B 包含的基本事件个数为63－53＝91，在B 发生的条件下A 发生包含的基本事件个数为C 13A 25＝60，在A 发生的条件下B 发生包含的基本事件个数为C 13A 25＝60，所以P (A |B )＝6091，P (B |A )＝60120＝12.故正确答案为A.6．B 若摸出的两球中含有4，必获奖，有5种情形；若摸出的两球是2,6，也能获奖．故获奖的情形共6种，获奖的概率为6C 26＝25.现有4人参与摸奖，恰有3人获奖的概率是C 34⎝⎛⎭⎪⎫253×35＝96625. 7．C E (X )＝1×16＋2×23＋3×16＝2，由Y ＝aX ＋3，得E (Y )＝aE (X )＋3. 所以73＝2a ＋3，解得a ＝－13.8．A 因为P (x >2)＝0.6，所以P (x <2)＝1－0.6＝0.4.因为N (4，σ2)，所以此正态曲线关于x ＝4对称，所以P (x >6)＝P (x <2)＝0.4.故选A.9．C 因为P (B )＝1×2×22×2×2＝12，P (A ∩B )＝1×1×22×2×2＝14，所以P (A |B )＝P (A ∩B )P (B )＝12.10．DP (X ≤2)＝P (X ＝0)＋P (X ＝1)＋P (X ＝2)＝C 010×⎝⎛⎭⎪⎫160×⎝ ⎛⎭⎪⎫5610＋C 110×16×⎝ ⎛⎭⎪⎫569＋C 210×⎝ ⎛⎭⎪⎫162×⎝ ⎛⎭⎪⎫568.11．C 由已知D (X )＝6×0.4×0.6＝1.44，则D (η)＝4D (X )＝4×1.44＝5.76.12．A 节日期间这种鲜花需求量的均值E (ξ)＝200×0.20＋300×0.35＋400×0.30＋500×0.15＝340(束)．设利润为η，则η＝5ξ＋1.6(500－ξ)－500×2.5＝3.4ξ－450，则E (η)＝E (3.4ξ－450)＝3.4E (ξ)－450＝3.4×340－450＝706(元)．13.370解析：加工出来的零件的合格品率为 ⎝⎛⎭⎪⎫1－170×⎝ ⎛⎭⎪⎫1－169×⎝ ⎛⎭⎪⎫1－168＝6770，所以次品率为1－6770＝370. 14．1解析：区间(－3，－1)和区间(3,5)关于x ＝1对称(－1的对称点是3，－3的对称点是5)，所以正态分布的数学期望就是1.15．7,8解析：P (ξ＝k )＝C k 15⎝ ⎛⎭⎪⎫1215，则只需C k 15最大即可，此时k ＝7,8. 16.38解析：设元件1,2,3的使用寿命超过1 000小时的事件分别记为A ，B ，C ，显然P (A )＝P (B )＝P (C )＝12，所以该部件的使用寿命超过1 000的事件为(A B ＋A B ＋AB )C .所以该部件的使用寿命超过1 000小时的概率为⎝ ⎛⎭⎪⎫12×12＋12×12＋12×12×12＝38. 17．解：(1)由题可得，至少购买甲、乙两种商品中的一种的概率为p ＝1－(1－0.5)(1－0.6)＝0.8.(2)ξ可能的取值有0,1,2,3， p (ξ＝0)＝(1－0.8)3＝0.008，p (ξ＝1)＝C 13(1－0.8)20.8＝0.096， p (ξ＝2)＝C 23(1－0.8)10.82＝0.384，p (ξ＝3)＝0.83＝0.512. 故ξ的分布列为ξ18．解：记事件A i 表示“该生第i 门课程取得优秀成绩”，i ＝1,2,3. 由题意知P (A 1)＝45，P (A 2)＝p ，P (A 3)＝q .(1)由于事件“该生至少有1门课程取得优秀成绩”与事件“ξ＝0”是对立的，所以该生至少有1门课程取得优秀成绩的概率是1－P (ξ＝0)＝1－6125＝119125.(2)由题意知P (ξ＝0)＝P (A 1A 2A 3)＝15(1－p )(1－q )＝6125， P (ξ＝3)＝P (A 1A 2A 3)＝45pq ＝24125. 整理得pq ＝625，p ＋q ＝1. 由p >q ，可得p ＝35，q ＝25.(3)由题意知a ＝P (ξ＝1)＝P (A 1A 2A 3)＋P (A 1A 2A 3)＋P (A 1A 2A 3)＝45(1－p )(1－q )＋15p (1－q )＋15(1－p )q ＝37125，b ＝P (ξ＝2)＝1－P (ξ＝0)－P (ξ＝1)－P (ξ＝3)＝58125.所以E (ξ)＝0×P (ξ＝0)＋1×P (ξ＝1)＋2×P (ξ＝2)＋3×P (ξ＝3)＝95.19.解：(1)由古典概型中的概率计算公式知所求概率为P ＝C 34＋C 33C 39＝584.(2)X 的所有可能值为1,2,3，且P (X ＝1)＝C 24C 15＋C 34C 39＝1742，P (X ＝2)＝C 13C 14C 12＋C 23C 16＋C 33C 39＝4384， P (X ＝3)＝C 22C 17C 39＝112，故X 的分布列为从而E (X )＝1×1742＋2×4384＋3×112＝4728.20．解：(1)设A 1表示事件“日销售量不低于100个”，A 2表示事件“日销售量低于50个”，B 表示事件“在未来连续3天里有连续2天日销售量不低于100个且另一天销售量低于50个”．因此P (A 1)＝(0.006＋0.004＋0.002)×50＝0.6， P (A 2)＝0.003×50＝0.15， P (B )＝0.6×0.6×0.15×2＝0.108. (2)X 可能取的值为0,1,2,3，相应的概率为P (X ＝0)＝C 03·(1－0.6)3＝0.064，P (X ＝1)＝C 13·0.6(1－0.6)2＝0.288，P (X ＝2)＝C 23·0.62(1－0.6)＝0.432，P (X ＝3)＝C 33·0.63＝0.216.分布列为因为X ～B ，方差D (X )＝3×0.6×(1－0.6)＝0.72.21.解：记E ＝{甲组研发新产品成功}，F ＝{乙组研发新产品成功}．由题设知P (E )＝23，P (E )＝13，P (F )＝35，P (F )＝25，且事件E 与F ，E 与F ，E 与F ，E 与F 都相互独立．(1)记H ＝{至少有一种新产品研发成功}，则H ＝E F ，于是P (H )＝P (E )P (F )＝13×25＝215，故所求的概率为P (H )＝1－P (H )＝1－215＝1315.(2)设企业可获利润为X (万元)，则X 的可能取值为0,100,120,220.因P (X ＝0)＝P (E F )＝13×25＝215，P (X ＝100)＝P (E F )＝13×35＝315，P (X ＝120)＝P (E F )＝23×25＝415，P (X ＝220)＝P (EF )＝23×35＝615，故所求的分布列为数学期望为E (X )＝0×215＋100×315＋120×415＋220×615＝300＋480＋1 32015＝2 10015＝140.22．解：记A i 表示事件：同一工作日乙、丙中恰有i 人需使用设备，i ＝0,1,2，B 表示事件：甲需使用设备，C 表示事件：丁需使用设备，D 表示事件：同一工作日至少3人需使用设备．(1)D ＝A 1·B ·C ＋A 2·B ＋A 2·B ·C .P (B )＝0.6，P (C )＝0.4，P (A i )＝C i 2×0.52，i ＝0,1,2，所以P (D )＝P (A 1·B ·C ＋A 2·B ＋A 2·B ·C )＝P (A 1·B ·C )＋P (A 2·B )＋P (A 2·B ·C )＝P (A 1)P (B )P (C )＋P (A 2)P (B )＋P (A 2)P (B )P (C ) ＝0.31.(2)X 的可能取值为0,1,2,3,4，其分布列为 P (X ＝0)＝P (B ·A 0·C )＝P (B )P (A 0)P (C )＝(1－0.6)×0.52×(1－0.4)＝0.06，P (X ＝1)＝P (B ·A 0·C ＋B ·A 0·C ＋B ·A 1·C )＝P (B )P (A 0)P (C )＋P (B )P (A 0)P (C )＋P (B )P (A 1)P (C )＝0.6×0.52×(1－0.4)＋(1－0.6)×0.52×0.4＋(1－0.6)×2×0.52×(1－0.4)＝0.25，P(X＝4)＝P(A2·B·C)＝P(A2)P(B)P(C)＝0.52×0.6×0.4＝0.06，P(X＝3)＝P(D)－P(X＝4)＝0.25，P(X＝2)＝1－P(X＝0)－P(X＝1)－P(X＝3)－P(X＝4)＝1－0.06－0.25－0.25－0.06＝0.38，数学期望E(X)＝0×P(X＝0)＋1×P(X＝1)＋2×P(X＝2)＋3×P(X ＝3)＋4×P(X＝4)＝0.25＋2×0.38＋3×0.25＋4×0.06＝2.。

人教版高中数学必修三第三章概率选修2-3概率-高考题(3)

选修2-3概率-高考题 (3)一、选择题1.下列说法中，正确的是A ．不可能事件发生的概率为B ．随机事件发生的概率为21C ．概率很小的事件不可能发生D ．投掷一枚质地均匀的硬币100次，正面朝上的次数一定为50次【答案】A【逐步提示】本题考查了概率的意义和事件发生的概率，根据概率的意义和事件发生的概率，依次判断各个选项是否正确．【详细解答】解： A.不可能事件发生的概率为0，所以A 选项正确；B.随机事件发生的概率在0与1之间，所以B 选项错误；C.概率很小的事件不是不可能发生，而是发生的机会较小，所以C 选项错误；D.投掷一枚质地均匀的硬币100次，正面朝上的次数可能为50次，所以D 选项错误，故选择 A. 【解后反思】概率的意义：一般地，在大量重复实验中，如果事件A 发生的频率会稳定在某个常数p 附近，那么这个常数p 就叫做事件A 的概率，记为P （A ）=p ；概率是频率（多个）的波动稳定值，是对事件发生可能性大小的量的表现．必然发生的事件的概率P （A ）=1；不可能发生事件的概率P （A ）=0．【关键词】不可能事件；随机事件；概率的意义；2.（2016甘肃省天水市，3，4分）下列事件中，必然事件是（）A ．抛掷1枚骰子，出现6点向上B ．两条直线被第三条直线所截，同位角相等C ．366人中至少有2个人的生日相同D ．实数的绝对值是非负数【答案】D【逐步提示】本题考查事件的分类，解题的关键是认识到在一定条件下，有些事件必然会发生，这样的事件称为必然事件；在一定条件下，可能发生也可能不发生的事件称为随机事件，只有分清各种事件才能做出正确的判断.【详细解答】解：抛掷1枚骰子，可能出现6点向上，也可能出现其它点数向上，所以A 中事件是随机事件．只有两条平行直线被第三条直线所截，同位角才一定相等，所以B 中事件是随机事件．由于闰年有366天，有可能出现这366人的生日一人占一天的情况，所以C 中事件不是必然事件．对于D ，由于正实数的绝对值是正数，0的绝对值是0，负实数的绝对值是正数，所以实数的绝对值一定是非负数，属于必然事件．故选择D ．【解后反思】对于B 中事件，由于阅读不细致、认真，易受思维定势的影响误认为是两条平行直线被第三条直线所截，从而认定同位角必定相等而错误地判断为必然事件．另外，本题难点在于对C 中事件的认识，可以按照“一个萝卜一个坑”的现实原理加强理解．【关键词】必然事件；随机事件．3.（2016广东省广州市，4，3分）某个密码锁的密码由三个数字组成，每个数字都是0－9这十个数字中的一个，只有当三个数字与所设定的密码及顺序完全相同时，才能将锁打开，如果仅忘记了所设密码的最后那个数字，那么一次就能打开该密码锁的概率是（）A ．101B ．91C ．31D ．21【答案】A【逐步提示】所设密码最后那个数字是0－9这十个数字中的一个，即共有10种可能，密码数字只有1种，据此可根据概率的计算公式求解结果．【详细解答】解：根据题意可知，密码锁所设密码的最后那个数字是0－9这十个数字中的一个，因此，一次就能打开该密码锁的概率是101，故选择A ．【解后反思】（1）一般地，如果在一次试验中，有n 种可能的结果，并且它们发生的可能性相等，事件A包含其中的m 种结果，那么事件A 发生的概率nm A P )(．（2）求较复杂随机事件的概率时，常用画树状图或列表法不重不漏地列出所有等可能结果．【关键词】概率的计算公式4.（2016广东茂名，4，3分）下列事件中，是必然事件的是（）A．两条线段可以组成一个三角形B．400人中有两个人的生日在同一天C．早上的太阳从西方升起D．打开电视机，它正在播放动画片【答案】B【逐步提示】本题考查了必然事件的概念，解题的关键是正确区分必然事件与不可能事件、随机事件．事先能肯定它一定会发生的事件称为必然事件.事先能肯定它一定不会发生的事件称为不可能事件，必然事件和不可能事件都是确定的．而不确定事件（即随机事件）是在一定条件下，可能发生也可能不发生的事件．【详细解答】解：三角形是由三条不在同一直线上的线段首尾顺次相接组成的，两条线段不能组成一个三角形，选项A中的事件属于不可能事件；一年有365天或366天，由于400>365，400＞366，因此400人中必有两个人的生日在同一天，选项B中的事件属于必然事件；根据自然规律，早上的太阳从东方升起，选项C中的事件属于不可能事件；打开电视机，它不一定正在播放动画片，选项D中的事件属于随机事件. 故选择 B .【解后反思】事件分为确定事件和不确定事件（随机事件），确定事件又分为必然事件和不可能事件，其中，①必然事件发生的概率为1，即P（必然事件）＝1；②不可能事件发生的概率为0，即P（不可能事件）＝0；③如果A为不确定事件（随机事件），那么0＜P（A）＜1．【关键词】不可能事件；必然事件；随机事件5.（2016湖北宜昌，6，3分）在课外实践活动中，甲、乙、丙、丁四个小组用投掷一元硬币的方法来估算正面朝上的概率，其实验次数分别为10次，50次，100次，200次，其中实验相对科学的是（）A．甲组B．乙组C．丙组D．丁组【答案】D【逐步提示】本题考查了用频率估计概率，解题的关键是根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．【详细解答】解：甲组实验了10次，乙组实验了50次，丙组实验了100次，丁组实验了200次，实验次数多的频率往往接近事件发生的概率，故选择 D .【解后反思】在一次试验中，若共有n次等可能的结果，其中事件A包含m个等可能的结果，则事件A的概率为P(A)=mn．随机事件的频率，指此事件发生的次数与试验总次数的比值，当试验次数很多时，它具有一定的稳定性，即稳定在某一常数附近，而偏离的它可能性很小．为了说明这种规律，我们把这个常数称为这个随机事件的概率．它从数量上反映了随机事件发生的可能性的大小，而频率在大量重复试验的前提下可近似地作为这个事件的概率．【关键词】概率公式；用频率估计概率6（2016湖南常德，5，3分）下列说法正确的是A．袋中有形状、大小、质地完全一样的5个红球和1个白球，从中随机取出一个球，一定是红球．B．天气预报“明天降水概率10%”，是指明天有10%的时间会下雨．C．某地发行一种福利彩票，中奖概率是千分之一．那么，买这种彩票1000张，一定会中奖．D．连续掷一枚均匀硬币，若5次都是正面朝上，则第六次仍然可能正面朝上．【答案】D【逐步提示】本题考查的是概率的含义．概率是反映事件发生机会的大小的概念，只是表示发生的机会的大小，机会大也不一定发生，机会小也有可能．【详细解答】解：选项A、“取到红球”是随机事件，且可能性较大，但不是必然事件，所以从中随机取出一个球，不一定是红球，所以A选项错误；选项B、“明天降水概率10%”，是指下雨的可能性为10%，而不是10%的时间会下雨，所以B选项错误；选项C、“中奖概率是千分之一”是指这批彩票总体平均每1000张有一张中奖，而不是买这种彩票1000张，一定会中奖，所以C选项错误；选项D、“投掷一枚质地均匀的硬币正面朝上”是随机事件，所以第六次仍然可能正面朝上，所以D选项正确．故选D．【解后反思】事件分为确定事件和不确定事件，确定事件分为必然事件和不可能事件；也就是说一定发生的事件是必然事件，一定不会发生的事件是不可能事件；可能发生，也可能不发生的事件是不确定事件；必然事件发生的概率是1，不可能发生的事件发生的概率是0，不确定事件发生的概率大于零小于1，偶然事件0到1之间【关键词】概率的含义；随机事件；7.（2016湖南湘西，15，4分）在一个不透明的口袋中装有6个红球，2个绿球，这些球除颜色外无其它差别，从这个袋子中随机摸出一个球，摸到红球的概率为A ．43B ．41C ．21D ．1【答案】A【逐步提示】本题考查了概率的定义，熟悉定义是解题的关键.口袋中共8个球，其中有6个红球，根据概率定义解题即可．【详细解答】解：P(摸到红球)=86=43，故答案为43.故选择 A .【解后反思】一般地，在试验中，如果各种结果发生的可能性都相同，那么一个事件A 发生的概率计算公式为P(A)=A 事件可能发生的结果数所有等可能结果的总数．【关键词】摸球；简单事件的概率二、填空题1.（2016福建福州，15，4分）已知四个点的坐标分别是（－1，1），（2，2），（32，23），（－5，－51），从中随机选取一个点，在反比例函数y ＝x1图象上的概率是．【答案】12【逐步提示】本题考查了概率的计算和反比例函数的性质，解题的关键是掌握等可能事件概率的计算公式．先判断四个点的坐标是否在反比例函数y ＝x1图象上，再用在反比例函数y ＝x1图象上点的个数除以点的总数即为在反比例函数y ＝x1图象上的概率．【详细解答】解：∵﹣1×1=﹣1，2×2=4，×=1，（﹣5）×（﹣）=1，∴2个点的坐标在反比例函数y ＝x1图象上，∴在反比例函数y ＝x1图象上的概率是2÷4=12，故答案为12.【解后反思】此类问题容易出错的地方是不能正确判断所关注事件可能出现的结果数，以及所有等可能出现的结果数．等可能性事件的概率的计算公式：P(A)＝n m，其中m 是总的结果数，n 是该事件成立包含的结果数．【关键词】反比函数的图像；概率的计算公式；2.（2016贵州省毕节市，18，5分）掷两枚质地均匀的骰子，其点数之和大于10的概率为_________．【答案】112【逐步提示】本题考查了求简单随机事件的概率，解题的关键掌握用列表法或画树状图的方法进行计算．本题用列表法更方便，表中也可只用两种符号来表示点数之和大于10和不大于10，这样能一目了然，不易出错．【详细解答】解：设点数之和小于或等于10用○表示，大于10用√表示不，列表如下：1 2 3 4 5 6 1 ○○○○○○2 ○○○○○○3 ○○○○○○4 ○○○○○○5 ○○○○○√6○○○○√√由表可知，掷两枚骰子，共有36种等可能的情况出现，其中点数之和大于10的结果共有3种，所以P （点数之和大于10）＝336＝112，故答案为112.【解后反思】此类问题的易错点是没有列表或画树状图，只凭想象列举出所有可能的结果，造成丢掉一些情况，如把（1，2）和（2，1）当作一种情况，从而致错．【关键词】求概率的方法；3.（2016河南省，12，3分）在“阳光体育”活动期间，班主任将全班同学随机分成了4组进行活动，则该班小明和小亮被分在同一组的概率是_________.【答案】41【逐步提示】本题考查的是用列表法或画树状图法求概率，解题的关键是合理选择方法求概率．思路：选择树状图或列表法解题，通过分析看出，小明和小亮任意分在各组的可能情况为16种，两次抽出卡片所标数字不同占4种，则利用公式可求出事件的概率．【详细解答】解：列表得：设分A 、B 、C 、D 四个组AB C D A （A ，A ）（A ，B ）（A ，C ）（A ，D ）B （B ，A ）（B ，B ）（B ，C ）（B ，D ）C （C ，A ）（C ，B ）（C ，C ）（C ，D ）D（D ，A ）（D ，B ）（D ，C ）（D ，D ）所有等可能的情况有16种，其中小明和小亮分在同一组的情况有4种，则P=41164，故答案为41.【解后反思】此类问题容易出错的地方是抽象不出基本概型，事件发生的可能情况列举不出来．一般方法规律是用数值来刻画事件发生的可能性大小，这个数值就是概率．一般地，如果一个实验有n 个等可能的结果，而事件A 包含其中m 个结果，我们可计算概率P(A)=m n=A 事件包含的可能结果数所有可能结果数．运用列举法（包括列表、画树状图）计算简单事件发生的概率的能力，有利于提高学生的数学意识、应用数学的能力和数学素养．【关键词】求概率方法——树状图法和列表法4.（2016湖南省郴州市，13，3分）同时掷两枚均匀的硬币，则两枚都出现反面朝上的概率是．【答案】14【逐步提示】本题考查的是概率问题，解题的关键是弄清事件发生的所有可能的情况，然后看事件发生的概率．抛两枚硬币有四种情况：即（正正）（正反）（反反）（反正），然后判断两个反面朝上的概率就可以了．【详细解答】解：设两枚硬币分别为甲、乙：共有四种结果：（正正）（正反）（反正）（反反）∴14P 两个反面朝上＝．反面硬币甲硬币乙开始正面反面正面正面反面【解后反思】此类问题容易出错的地方是列举所有可能性事件时重复或遗漏．(1)运用公式P(A)=nm 求简单事件发生的概率，在确定各种事件等可能性的基础上，关键是求事件所有可能的结果种数n 和使事件A 发生的结果种数m.(2)求简单随机事件的概率有两种方法．①在做了大量试验的基础上，可以用频率的近似地估计概率；②可以用列表或画树状图，列举出所有可能事件，再求概率．(3)列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．【关键词】概率；树状图；.6（2016湖南省怀化市，14，4分）一个不透明的袋子，装了除颜色不同，其它没有任何区别的红色球3个，绿色球4个，黑色球7个，黄色球2个，从袋子中随机摸出一个球，摸到黑色球的概率是______________.【答案】716【逐步提示】在等可能的条件下，袋共有球3＋4＋7＋2＝16个，其中黑色球7个，从袋子中随机摸出一个球，摸到黑色球的概率是黑色球数：总球数.【详细解答】解：P黑色球＝73472＝716，故答案为716.【解后反思】此题考查概率，难度不大，解题的关键是掌握概率的计算公式.【关键词】概率的计算公式7.（2016湖南省湘潭市，12，3分）从2015年12月26日起，一艘载满湘潭历史和文化的“航船——湘潭市规划展示馆、博物馆和党史馆（以下简称‘三馆’）”正式起航，市民可以免费到三馆参观.听说这个好消息，小张同学准备星期天去参观其中一个馆，假设参观者选择每一个馆参观的机会均等，则小张同学选择参观博物馆的概率为.【答案】13【逐步提示】本题考查了概率的计算，解题的关键是知道某事件发生的概率等于该事件出现的可能次数与所有可能次数之间的比．因此先确定参观博物馆的可能次数和参观三个馆总数，再根据概率公式计算即可．【详细解答】解：∵共有3个馆，参观博物馆的可能性为1，∴小张同学选择参观博物馆的概率为13，故答案为13.【解后反思】掌握此类问题，需熟练掌握以下知识：（1）公式法：P(A)=nm，其中n 为所有事件的总数，m 为事件A 发生的总次数；（2）列举（列表或画树状图）法的一般步骤为：①判断使用列表或画树状图方法：列表法一般适用于两步计算；画树状图法适合于两步及两步以上求概率；②不重不漏的列举出所有事件出现的可能结果，并判定每种事件发生的可能性是否相等；③确定所有可能出现的结果数n 及所求事件A 出现的结果m ；④用公式P(A)=nm ，求事件A 发生的概率．【关键词】概率初步8.（2016年湖南省湘潭市，12，3分）从2015年12月26日起，一艘载满湘潭历史和文化的“航船——湘潭市规划展示馆、博物馆和党史馆（以下简称‘三馆’）”正式起航，市民可以免费到三馆参观。

新课标高中数学选修23(统计与概率)测试题

新课标高中数学选修2—3（统计与概率）测试题命题：广东省汕头市潮阳林百欣中学许吟裕（2006-4-8）一、选择题（本题共10小题，每小题5分，共50分，在每小题给出的4个选项中，只有1项是符合题目要求的。

） 1．从总体中抽得的样本数据为3.8，6.8，7.4则样本平均数x 为：（）A. 6.5B. 6C. 5D. 5.52．高三年级有12个班，每班50人按1—50排学号，为了交流学习经验，要求每班学号为 18的同学留下进行交流，这里运用的是（）抽样法：A.抽签法B.系统抽样C.分层抽样D.随机数表法3．如果数据x 1,x 2,x 3,…,x n 的平均数为 ,方差为62，则数据3x 1+5,3x 2+5,…,3x n +5的平均数和方差分别是（） A ． B ． C ． D ． 4．甲、乙两个水文站同时作水文预报，如果甲站、乙站各自预报的准确率为0.8和0.7，那么，在一次预报中两站都准确预报的概率为（） A ．0.7 B ．0.56 C ．0.7 D ．0.85．从分别写有A 、B 、C 、D 、E 的5张卡片中，任取两张，这两张卡片上的字母恰好是按字母顺序相邻的概率为（）A ．B ．C ．D ．6．已知盒子中有散落的围棋棋子15粒，其中6粒黑子，9粒白子，从中任意取出2粒恰好是同一色的概率（）A ．B ．C ．D ．7）A ．B ．C ．D ．8．甲、乙两人独立解答某道题，解不出来的概率分别为a 和b ，那么甲、乙两人都解出这道题的概率是（） A ．1-ab B ．(1-a )(1-b ) C ．1-(1-a )(1-b ) D ．a (1-b )+b (1-a ) 9．有3个相识的人某天各自乘火车外出，假设火车有10节车厢，那么至少有两人在车厢内相遇的概率为（）A ．B ．C ．D ．26和x 2653和+x 29653和+x 2363和x 51521031073517711051635342014121107200292571442918710．一患者服用某种药品后被治愈的概率是95%，则患有相同症状的四位病人中至少有3人被治愈的概率为（） A ．0.86 B ．0.90 C ．0.95 D ．0.99二，填空题（本题共4小题，每小题5分，共20分）11．甲投篮的命中率为0.7，乙投篮的命中率为0.8，每人各投3次，每人恰好都投中2次的概率为___________。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

概率同步练习
一、选择题（第小题5分）
1．在某一试验中事件A 出现的概率为p ，则在n 次试验中A 出现k 次的概率为（）
A 1－k p
B ()k n k
p p --1 C 1－()k
p -1 D ()k n k k
n p p C --1
2.设随机变量ξ服从分布B(n,p),且E(ξ)=1.6,V(ξ)=1.28则( )
A n=8,p=0.2
B n=4,p=0.4
C n=5,p=0.32
D n=7,p=0.45 3、在10个球中有个6红球和4个白球（各不相同），不放回地依次摸出2个球，在第一次摸
出红球的条件下，第二次也摸到红球的概率是（） A 53 B 52 C 101 D 9
5
4、箱中有5个黑球，4个白球，每次随机取出一个球，若取出黑球，则放回箱中，重新取球；若取出白球，则停止取球，那么在第四次取球之后停止的概率为（）
A.C 35 ·C 14C 45
B.(59)3×(49)
C. 35 ×14
D.C 14(59)3×(4
9) 5、某射手命中目标的概率为P ，则在三次射击中至少有1次未命中目标的概率为（）
A 、P 3
B 、(1—P)3
C 、1—P 3
D 、1—(1-P)3 6．一射手对同一目标独立地射击四次，已知至少命中一次的概率为8081
，则此射手每次击中
的概率是( ）
A 、13
B 、23
C 、14
D 、25
7、已知在6个电子元件中，有2个次品，4个合格品，每次任取一个测试，测试完后不再放回，直到两个次品都找到为止，则经过4次测试恰好将2个次品全部找出的概率（）
A.5
1 B.
154 C.52 D.15
14 8、一台X 型号自动机床在一小时内不需要工人照看的概率为0.8000,有四台这种型号的自动
机床各自独立工作,则在一小时内至多有2台机床需要工人照看的概率是( )
1536.0.A 1808.0.B 5632.0.C 9728.0.D
二、填空题（第小题5分）
9、在含有5件次品的100件产品中，任取3件，则取到的次品数X 的分布列为 .
10、某自然保护区内有n 只大熊猫，从中捕捉t 只体检并加上标志再放回保护区，1年后再从这个保护区内捕捉m 只大熊猫（设该区内大熊猫总数不变）则其中有s 只大熊猫是第2次接受体检的概率是。

11、已知10件产品，其中3件次品，不放回抽取3次，已知第一次抽到是次品，则第三次抽次品的概率。

12、已知每个人的血清中含有乙型肝炎病毒的概率为3‰，混合100人的血清，则混合血清
中有乙型肝炎病毒的概率约为 .
(参考数据：0.996100≈0.6698，0.997100≈0.7405，0.998100≈0.8186) 三、解答题（注：一定要有必要的文字叙述） 13、（本小题12分）
(1)抛掷一颗骰子两次,定义随机变量
⎩⎨
⎧=)(,1)(,0的点数数等于第二次向上一面当第一次向上一面的点
面的点数数不等于第二次向上一当第一次向上一面的点
ξ
试写出随机变量ξ的分布列;
(2)抛掷一颗骰子两次,在第一次掷得向上一面点数是偶数的条件下,求第二次掷得向上一面
点数也是偶数的概率． 14、（本小题12分）
甲、乙两人玩套圈游戏，套中的概率分别为0.7和0.8，如果每人都扔两个圈。

（Ⅰ）求甲套中两次而乙只套中一次的概率；
（Ⅱ）若套中一次得1分，套不中得0分，求甲、乙两人得分相同的概率。

15、（本小题12分）
有一批数量很大的产品，其次品率是10％。

（Ⅰ）连续抽取两件产品，求两件产品均为正品的概率；
（Ⅱ）对这批产品进行抽查，每次抽出一件，如果抽出次品，则抽查终止，否则继续抽查，直到抽出次品，但抽查次数最多不超过4次，求抽查次数ξ的分布列及期望。

16、（本小题12分）
某汽车在前进途中要经过4个路口，但由于路况不同，汽车在前两个路口遇到绿灯的概率为43，在后两个路口遇到绿灯的概率为.32
假定汽车只在遇到红灯或到达目的地时才停止前进，ξ表示停车时已经通过的路口数，求：（1）停车时已通过2个路口的概率；（2）停车时至多已通过3个路口的概率；（3） ξ的概率分布列，数学期望E ξ. 17、（本小题12分）
某校一个研究性学习团队从网上查得，某种植物种子在一定条件下的发芽成功的概率为1
2
，
于是该学习团队分两个小组进行验证性实验.
（Ⅰ）第一小组做了5次这种植物种子的发芽实验（每次均种下一粒种子），求他们的实验至
少有3次成功的概率；
（Ⅱ）第二小组做了若干次发芽实验（每次均种下一粒种子），如果在一次实验中种子发芽成功就停止实验，否则就继续进行下次实验.直到种子发芽成功为止，但实验的次数不超过5次.求这一小组所做的种子发芽实验次数的分布列和期望.
18、（本小题12分）在一次抗洪抢险中，准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知只有5发子弹备用，且首次命中只能使汽油流出，再次命中才能引爆成功，每次射击命中率都是3
2
.，每次命中与否互相独立. (Ⅰ)求油罐被引爆的概率.
(Ⅱ)如果引爆或子弹打光则停止射击，设射击次数为ξ，求ξ的分布列及ξ的数学期望； 19、（本小题14分）
甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为0.6，被甲或乙解出的概率
为0.92.
（1）求该题被乙独立解出的概率；（2）求解出该题的人数ξ的数学期望和方差.
20、（本小题14分）
下表为某班英语及数学成绩的分布.学生共有50人，成绩分为5个档次，如表中所示英语成绩为5分、数学成绩为4分的学生有3人。

若在全班学生中任选一人，其英语语成绩记为x ，数学成绩记为y .
(1) 1=x 的概率是多少？3≥x 且3=y 的概率是多少？ (2) 若y 的期望为50
133
，试确定a ,b 的值.。