奥数鸟头模型课件
第三讲 鸟头模型

F A B D
学而思培优北京分校·小学理科教研组出品 3
1 C
E
2013-2014 学年·秋季五年级知识点总结 【答案】7
S△DBE BD BE 2, 【分析】 这道题是对应第二单元例 2 的作业. 由鸟头模型, 故 S△BDE 2S△ABC 2 , S△ABC BA BC
12 34 12 34 3 1 2 1 2 1 2 1 2 1 1 ; ; ;下 4 题: (12 56) (34 78) 68 112 56 (1 3) 4 4 4 8 (2 4) 3 6 3 9 67 67 3 34 12 34 12 34 ; (6 8) 5 14 5 5 (34 56) 78 90 78 585
【点评】注意某些夹边需要将已知线段长度相加;注意在计算时一定要先约后乘.
【第一单元 3】 (2)如图,园林小路由白色正方形石板和红、青两色的三角形石板铺成. 问:内圈 红色三角形石板的总面积大,还是外圈青色三角形石板的总面积大?
【答案】一样大 【分析】本题即为例 3(1)的多次重复;每一个红色三角形,均和与其有公共顶点的青色三角形构成 有互补内角的鸟头模型,其面积相等,故知 S红 S青 . 【基础、 提高作业 3】 如图, 已知三角形 ABC 面积为 1, 分别延长 AB、 BC、 CA 至 D、 E、 F, 使 BD AB ,
【点评】把条件中的 2、3 改为 x、y,就将是鸟头模型的一般证明. 从证明过程可以看出,鸟头模型是 使用两次等高模型得来的,进一步地说:共角模型的基础是共边模型. 三道小题的证明方法完全相同,这正是因为鸟头模型的特征是角(相等或互补的角) ,而不是 位置. 这一点在第一单元的例 3 中体现得最为明显. 例 2 对寻找夹边长度给出了相应练习,这一类题目是重要的,在这里提供几道练习题:
六年级奥数专题-4几何五大模型——鸟头模型
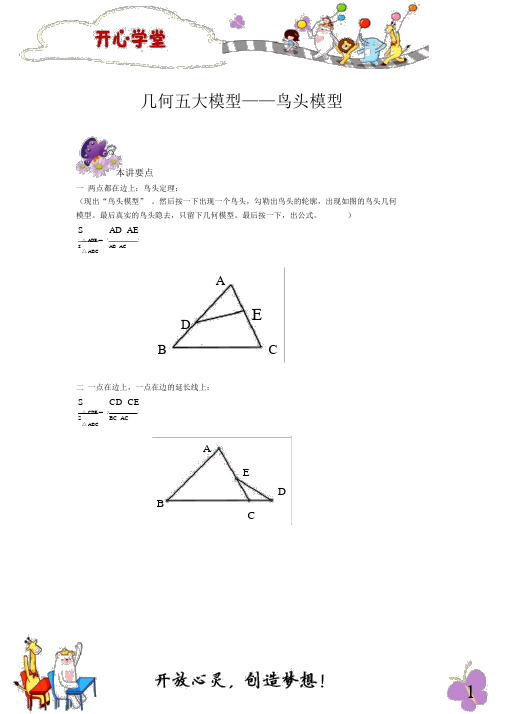
几何五大模型——鸟头模型本讲要点一两点都在边上:鸟头定理:(现出“鸟头模型” 。
然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。
最后真实的鸟头隐去,只留下几何模型。
最后按一下,出公式。
)S AD×AE△ADE =S AB×AC△ABCAEDB C二一点在边上,一点在边的延长线上:S CD×CE△CDE =S BC×AC△ABCAEDBC例 1如图, AD=DB,AE=EF=FC,已知阴影部分面积为 5 平方厘米,△ABC 的面积是平方厘米.例 2例 2 ( 1)如图在△ ABC中, D、E 分别是 AB,AC上的点,且 AD:AB=2:5, AE:AC=4:7,△ ABC 的面积是 16 平方厘米,求△ ABC的面积。
(2)如图在△ ABC中, D 在 BA 的延长线上, E 在 AC上,且 AB:AD=5:2, AE:EC=3:2,△ ADE 的面积是12 平方厘米,求△ABC的面积。
例3已知△ DEF的面积为12 平方厘米, BE=CE,AD=2BD,CF=3AF,求△ ABC的面积。
例4三角形 ABC面积为 1, AB 边延长一倍到 D, BC 延长 2 倍到 E, CA延长 3 倍到 F,问三角形DEF的面积为多少?FAECBD例5长方形 ABCD面积为 120, EF 为 AD上的三等分点, G、 H、 I 为 DC上的四等分点,阴影面积是多大?例 6如图,过平行四边形 ABCD内的一点 P 作边AD、BC的平行线 EF 、GH,若 PBD 的面积为 8 平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米?AG DPEFB H C家庭作业1.如下左图,在△ABC 中,D、E分别是BC、AB的三等分点,且△ABC 的面积是54,求△CDE 的面积。
AEB D C2. 如图,长方形 ABCD 的面积是1,M是AD边的中点,N在AB边上,且AN 1 BN .那2么,阴影部分的面积等于.A M DNB C图13.如图以△ABC 的三边分别向外做三个正方形ABIH 、 ACFG 、 BCED ,连接 HG 、 EF 、ID ,又得到三个三角形,已知六边形 DEFGHI 的面积是 77 平方厘米,三个正方形的面积分别是 9、 16、 36 平方厘米,则三角形ABC的面积是多少?HGIAFBCD E4.如图,已知三角形ABC 面积为 1 ,延长AB 至 D ,使 BD AB ;延长 BC 至 E ,使CE 2BC ;延长 CA 至 F ,使 AF 3AC ,求三角形DEF 的面积。
六年级下册数学小学奥数几何模块鸟头模型ppt(31页PPT)全国通用标准课件

目 录
专题解析 例题讲解 总结归纳 巩固提升
专题解析
专题解析
鸟头模型 鸟头模型(共角模型)作为比例模型中基础的一种,可以通过等高模型进行推导,其主要研究的 是三角形面积比与对应线段乘积比之间的关系.
基本要求 存在公共角或互补角,总共有四种基本形式,下面分类列出,并进行证明.
例题讲解
例题讲解
例1:如图,三角形ABC的面积是1,B、C、D在同一条直线上,且CD:BC=1:3,E为AC的中点, 求图中阴影部分的面积.
例题讲解
练一练1:如图,D、E分别在BA、CA的延长线上,AD:AB=1:2,AE:AC=1:3,已知阴影部分 的面积是10,求三角形ABC的面积.
例题讲解
例题讲解
例4:如图,三角形ABC的面积是1,D、E、F分别在AB、BC、CA的延长线上,且BD=2BA, CE=2CB,AF=3AC,求三角形DEF的面积.
例题讲解
练一练4:如图,平行四边形ABCD的面积是2,E、F、G、H分别在AB、BC、CD、DA的延长线 上,且BE=BA,CF=2CB,DG=2DC,AH=3AD,求四边形EFGH的面积.
例题讲解
练一练2:如图,三角形ABC中,D、G分别是AB、AC的中点,E、F为BC的三等分点,已知阴影 部分的面积是5,求三角形ABC的面积.
例题讲解
例3:如图,四边形ABCD、DEFG是正方形,试判断三角形CDE与三角形ADG面积的大小关系, 并说明原因.
例题讲解
练一练3:如图,以三角形ABC的三条边分别为边长作正方形,已知AB=8厘米,AC=6厘米,求图 中阴影面积的总和.
专题解析
基本形式
练一练5:如图,四边形ABCD的面积是2,E、F、G、H分别在AB、BC、CD、DA的延长线上,且BE=2BA,CF=2CB,DG=2DC,AH=2AD,求四边形EFGH的面积. 练一练6:如图,三角形ABC的面积是2,D、F分别在AB、BC的延长线上,且BD=BA,CB=2CF,E是AC的中点,求三角形DEF的面积. 鸟头模型(共角模型)作为比例模型中基础的一种,可以通过等高模型进行推导,其主要研究的是三角形面积比与对应线段乘积比之间的关系. 例7:如图,正六边形ABCDEF中,G、H、I、J、K、L分别是各边的四等分点,求图中阴影部分面积与正六边形ABCDEF的面积比. 例1:如图,三角形ABC的面积是1,B、C、D在同一条直线上,且CD:BC=1:3,E为AC的中点,求图中阴影部分的面积. 例1:如图,三角形ABC的面积是1,B、C、D在同一条直线上,且CD:BC=1:3,E为AC的中点,求图中阴影部分的面积. 作业2:如图,三角形ABC的面积是5,D、E、F分别在BA、AC、CB的延长线上,且AD=AB,CE=CA,BF=BC,求三角形DEF的面积. 例5:如图,四边形ABCD的面积是1,E、F、G、H分别在AB、BC、CD、DA的延长线上,且BE=BA,CF=CB,DG=DC,AH=AD,求四边形EFGH的面积. 练一练5:如图,四边形ABCD的面积是2,E、F、G、H分别在AB、BC、CD、DA的延长线上,且BE=2BA,CF=2CB,DG=2DC,AH=2AD,求四边形EFGH的面积. 存在公共角或互补角,总共有四种基本形式,下面分类列出,并进行证明. 练一练7:如图,正六边形ABCDEF的面积是1,G为AB的三等分点,H为CD的中点,求图中阴影部分面积. 练一练5:如图,四边形ABCD的面积是2,E、F、G、H分别在AB、BC、CD、DA的延长线上,且BE=2BA,CF=2CB,DG=2DC,AH=2AD,求四边形EFGH的面积. 主讲老师:癸酉0311 作业3:如图,平行四边形ABCD的面积是2,E、F、G、H分别在BA、CB、DC、AD的延长线上,且AE=3AB,BF=BC,CG=2CD,DH=DA,求四边形EFGH的面积. 练一练3:如图,以三角形ABC的三条边分别为边长作正方形,已知AB=8厘米,AC=6厘米,求图中阴影面积的总和. 练一练1:如图,D、E分别在BA、CA的延长线上,且AD:AB=1:2,AE:AC=1:3,已知阴影部分的面积是10,求三角形ABC的面积. 主讲老师:癸酉0311 例4:如图,三角形ABC的面积是1,D、E、F分别在AB、BC、CA的延长线上,且BD=2BA,CE=2CB,AF=3AC,求三角形DEF的面积.
六年级奥数专题几何五大模型鸟头模型
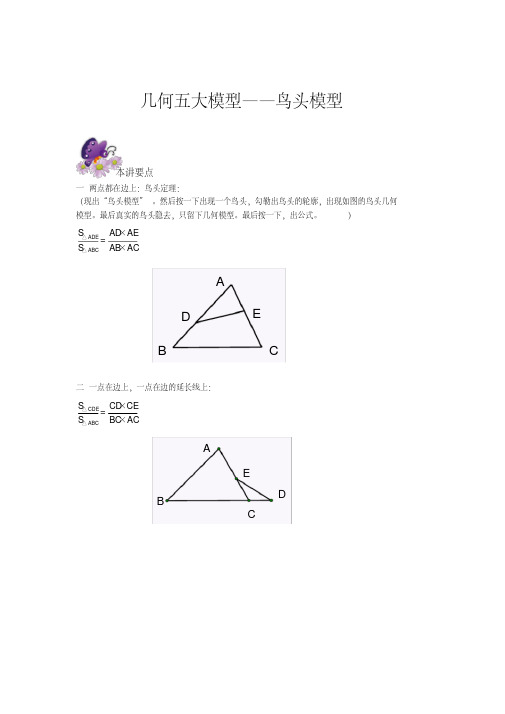
几何五大模型——鸟头模型一两点都在边上:鸟头定理:(现出“鸟头模型”。
然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。
最后真实的鸟头隐去,只留下几何模型。
最后按一下,出公式。
)△ADE△ABC S AD ×AE=S AB ×ACED CB A二一点在边上,一点在边的延长线上:△CDE △ABC S CD ×CE=S BC ×ACEDC B A本讲要点例1如图,AD=DB ,AE=EF=FC ,已知阴影部分面积为5平方厘米,△ ABC的面积是平方厘米.例2例2 (1)如图在△ABC中,D、E分别是AB,AC上的点,且AD:AB=2:5, AE:AC=4:7,△ABC 的面积是16平方厘米,求△ABC的面积。
(2)如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE 的面积是12平方厘米,求△ABC的面积。
已知△DEF 的面积为12平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC 的面积。
三角形ABC 面积为1,AB 边延长一倍到D ,BC 延长2倍到E ,CA 延长3倍到F,问三角形DEF 的面积为多少?FED C BA 例4例3长方形ABCD 面积为120,EF 为AD 上的三等分点,G 、H 、I 为DC 上的四等分点,阴影面积是多大?如图,过平行四边形ABCD 内的一点P 作边AD 、BC 的平行线EF 、GH ,若PBD 的面积为8平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米?AB CDE F G H P例6例51.如下左图,在ABC △中,D 、E 分别是BC 、AB 的三等分点,且ABC △的面积是54,求CDE △的面积。
2.如图,长方形ABCD 的面积是1,M 是AD 边的中点,N在AB 边上,且12AN BN .那么,阴影部分的面积等于.A B C DM N图1家庭作业B ACD E3.如图以ABC △的三边分别向外做三个正方形ABIH 、ACFG 、BCED ,连接HG 、EF 、ID ,又得到三个三角形,已知六边形DEFGHI 的面积是77平方厘米,三个正方形的面积分别是9、16、36平方厘米,则三角形ABC 的面积是多少?IHGFED CB A 4.如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB ;延长BC 至E ,使2CE BC ;延长CA 至F ,使3AFAC ,求三角形DEF 的面积。
小学奥数几何五大模型鸟头模型.

三角形等高模型与鸟头模型模型二鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角 )两夹边的乘积之比.如图在△ABC中,D,E分别是AB,AC上的点如图⑴(或D在BA的延伸线上,E在AC上如图2),则S△ABC:S△ADE(AB AC):(AD AE)ADADEEB C B C图⑴图⑵【例1】如图在△ABC中,D,E分别是AB,AC上的点,且AD:AB2:5,AE:AC4:7,S△ADE16平方厘米,求△ABC的面积.AAD DE EB C B C【分析】连结BE,S△ADE:S△ABE AD:AB2:5(24):(54),S△ABE:S△ABC AE:AC4:7(45):(75),所以S△ADE:S△ABC(24):(75),设S△ADE8份,则△35份,△16平方厘米,所以1份是2平方厘米,35份就是70平方厘米,△ABC的SABC SADE面积是平方厘米.由此我们获得一个重要的共角定理:共角三角形的面积比等于(相70定理,对应角等角或互补角)两夹边的乘积之比.page1of7【坚固】如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,假如三角形ADE的面积等于1,那么三角形ABC的面积是多少?A ADE D EB CB C【分析】连结BE.∵EC3AE∴S ABC3S ABE又∵AB5AD∴S ADE S ABE5 S ABC 15,∴S ABC15S ADE15.【坚固】如图,三角形ABC被分红了甲(暗影部分)、乙两部分,BD DC 4,BE 3,AE6,乙部分面积是甲部分面积的几倍?A AEB甲【分析】连结AD.∵BE3,AE6∴AB3BE,SABD乙E乙甲C B CD D3S BDE又∵BD DC4,∴S ABC2S ABD,∴S ABC6S BDE,S乙5S甲.【例2】如图在△ABC中,D在BA的延伸线上,E在AC上,且AB:AD5:2,AE:EC3:2,S△ADE12平方厘米,求△ABC的面积.D DA AEEB C B C【分析】连结BE,S△ADE:S△ABE AD:AB2:5(23):(53)S△ABE:S△ABC AE:AC3:(32)(35):(32)5,所以S△ADE:S△ABC(32):5(32)6:25,设S△ADE6份,则S△ABC25份,S△ADE12平方厘米,所以1份是2平方厘米,25份就是50平方厘米,△ABC的面积是50平方厘米.由此我们获得一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例3】以以下图,在平行四边形ABCD中,E为AB的中点,AF2CF,三角形AFE(图中暗影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?page2of7D CFAEB【分析】连结FB .三角形AFB 面积是三角形CFB 面积的 2倍,而三角形 AFB 面积是三角形 AEF 面积的2倍,所以三角形ABC 面积是三角形 AEF 面积的3倍;又因为平行四边形的面积是三角形 ABC 面积的2倍,所以平行四边形的面积是三角形AFE面积的(32) 6倍.所以,平行四边形的面积为648(平方厘米).【例 4】已知△DEF 的面积为7平方厘米,BE CE,AD2BD,CF 3AF ,求△ABC 的面积.AFDBCE【分析】S △BDE :S △ABC(BD BE):(BABC)(1 1):(2 3) 1:6,S△CEF:S△ABC(CE CF):(CBCA)(1 3):(2 4) 3:8S △ADF :S △ABC(AD AF):(AB AC)(21):(3 4)1:6设△ ABC 24份,则 △BDE 4份,△ 4份,△ CEF 9份,△24 4 497份,恰巧是7S S S ADFSS DEF平方厘米,所以S △ABC 24平方厘米【例 5】如图,三角形ABC 的面积为 3平方厘米,此中 AB:BE2:5,BC:CD3:2 ,三角形BDE 的面积是多少?ABEABEC CDD【分析】因为ABC DBE 180,所以能够用共角定理,设 AB2份,BC3份,则BE5份,BD 3 25份,由共角定理 S △ABC :S △BDE (AB BC):(BE BD)(23):(55)6:25,设S△ABC6份,恰巧是 3平方厘米,所以1份是0.5平方厘米,25份就是250.5 12.5平方厘米,三角形BDE 的面积是12.5 平方厘米【例 6】(2007年”走美”五年级初赛试题)以以下图,正方形ABCD 边长为6厘米,AE1AC ,CF1BC .三角形DEF 的面积为_______平方厘米.3 3ADEBF Cpage3of7【分析】由题意知AES △CEF :S △ABC11 2AC .依据”共角定理”可得,AC 、CFBC ,可得CE333(CFCE):(CB AC)12:(3 3)2:9;而△ABC662 18;所以△CEF4;SS同理得,S △CDE :S △ACD 2:3;,S △CDE 18 3212,S △CDF 6故△ △ △ △4 126 10(平方厘米).S DEF S CEF S DEC S DFC【例 7】如图,已知三角形 ABC 面积为1 ,延伸AB 至D ,使BDAB ;延伸BC 至E ,使CE2BC ;延伸CA 至F ,使AF 3AC ,求三角形DEF 的面积.FFA EAEBCBCDD【分析】(法1)此题是性质的频频使用.连结AE 、CD .S ABC 11 ,∵,S ABCS DBC 1∴S DBC1.同理可得其他,最后三角形 DEF 的面积18.(法2)用共角定理∵在 ABC 和CFE 中,ACB 与FCE 互补,S ABC AC BC 1 11∴FC CE 4 2.SFCE8又S ABC1,所以S FCE 8 .同理可得S ADF 6,S BDE3.所以S DEF S ABCSFCESADFSBDE 186318.【例 8】如图,平行四边形ABCD ,BE AB ,CF 2CB ,GD 3DC ,HA 4AD ,平行四边形ABCD 的面积是2,求平行四边形 ABCD 与四边形 EFGH 的面积比.HHA B EABEGDCGDCFF【分析】连结AC 、BD .依据共角定理∵在△ABC 和△BFE 中, ABC 与 FBE 互补,S△ABC AB BC 1 1 1.∴BE BF 1 3 3S△FBE又S △ABC 1,所以S △FBE 3.同理可得S△GCF8,S △DHG 15,S △AEH 8.page4of7所以S EFGH S△AEH S△CFG S△DHG S△BEF S ABCD8815+3+236.SABCD21所以36.SEFGH18【例9】如图,四边形EFGH的面积是66平方米,EAAB,CB BF,DC CG,HD DA,求四边形ABCD 的面积.H HD C GDC GA BF A BFE E【分析】连结BD.由共角定理得S△BCD:S△CGF(CDCB):(CG CF)1:2,即S△CGF2S△CDB同理S△ABD:S△AHE1:2,即S△AHE2S△ABD所以S△AHE S△CGF2(S△CBDS△ADB)2S四边形ABCD连结AC,同理能够获得S△DHG S△BEF2S四边形ABCDS四边形EFGH S△AHES△CGFS△HDGS△BEFS四边形ABCD5S四边形ABCD所以S四边形ABCD66513.2平方米【例10】如图,将四边形ABCD的四条边AB、CB、CD、AD分别延伸两倍至点E、F、G、H,若四边形ABCD的面积为5,则四边形EFGH的面积是.F FE B A E B AG C GCD DH H【分析】连结AC、BD.因为BE2AB,BF2BC,于是S BEF4S ABC,同理S HDG4S ADC.于是S BEF S HDG4S ABC4S ADC4S ABCD.再因为AE3AB,AH3AD,于是S AEH9S ABD,同理S CFG9S CBD.于是S AEH S CFG9S ABD9S CBD9S ABCD.那么S EFGH S BEF S HDG S AEH S CFG S ABCD4S ABCD9S ABCD S ABCD12S ABCD60.【例11】如图,在△ABC中,延伸AB至D,使BD AB,延伸BC至E,使CE 1,F是AC的BC中点,若△ABC的面积是2,则△DEF的面积是多少?2AFB C ED【分析】∵在△ABC和△CFE中,ACB与FCE互补,page5of7∴S△ABC AC BC224.S△FCE FC CE111又S ABC2,所以S FCE0.5.同理可得S△ADF2,S△BDE3.所以S△DEF S△ABC S△CEF S△DEB S△ADF20.5323.5【例12】如图,S△ABC1,BC5BD,AC4EC,DG GS SE,AF FG.求S FGS.AFG SEB CD【分析】此题题目自己很简单,但它把本讲的两个重要知识点交融到一同,既能够看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的频频运用,也能够看作是找点,最妙的是此中包括了找点的3种状况.最后求得S△432111.FGS的面积为△S FGS4322105【例13】以以下图,正方形ABCD边长为8厘米,E是AD的中点,F是CE的中点,G是BF的中点,三角形ABG的面积是多少平方厘米?A ED AEDF FB GC BGC【分析】连结AF、EG.因为S△BCF1216,依据”当两个三角形有一个角相等或互补时,这两个三角形的面积S△CDE84比等于夹这个角的两边长度的乘积比”SAEF8,S EFG8,再依据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,获得S BFC16,S ABFE32,SABF24,所以S ABG12平方厘米.【例14】四个面积为1的正六边形如图摆放,求暗影三角形的面积.F HA EBG CD【分析】如图,将原图扩展成一个大正三角形DEF,则AGF与CEH都是正三角形.假定正六边形的边长为为a,则AGF与CEH的边长都是4a,所以大正三角形DEF的边长为4 2 1 7,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角page6of7形构成的,所以一个单位小正三角形的面积为1,三角形DEF 的面积为49.66因为FA 4a ,FB3a ,所以AFB 与三角形DEF 的面积之比为4 3 12.77 49同理可知BDC 、AEC 与三角形DEF 的面积之比都为12,所以ABC 的面积占三角形DEF 面积49的112 313,所以ABC 的面积的面积为 49 13 13.49 49649 6【坚固】已知图中每个正六边形的面积都是 1,则图中虚线围成的五边形 ABCDE 的面积是.EA DB C【分析】从图中能够看出,虚线AB 和虚线CD 外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC 和虚线DE 外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE 外的图形是两个三角形,从右图中能够看出,每个三角形都是一个正六边 形面积的 1,所以虚线外图形的面积等于 1 3 1 2 31,所以五边形的面积是10 3162.6 6 333精选文档page7of7。
小学奥数-鸟头模型含解析

模型二 鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .三角形等高模型与鸟头模型【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?E D C B A A B C D E【解析】 连接BE .∵3EC AE = ∴3ABC ABE S S = 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==.【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAA BCDE甲乙【解析】 连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S = 又∵4BD DC ==,∴2ABC ABD S S =,∴6ABC BDE S S =,5S S =乙甲.【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【解析】 :():()(11):(23)1:6BDE ABCS S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米【例 5】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米【例 6】 如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.A【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△ 故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【例 7】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.F EDCB AABCDEF【解析】 (法1)本题是性质的反复使用.连接AE 、CD . ∵11ABC DBC S S =,1ABC S =, ∴S 1DBC =.同理可得其它,最后三角形DEF 的面积18=.(法2)用共角定理∵在ABC 和CFE 中,ACB ∠与FCE ∠互补, ∴111428ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯. 又1ABCS=,所以8FCES=.同理可得6ADFS =,3BDES=.所以186318DEFABCFCEADFBDESS SS S=+++=+++=.【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【例 9】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD的面积.H GFED CB A A B CDEFGH【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【例 10】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CD EF GH【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=.于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==.【例 11】如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABCS=,所以0.5FCES=.同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【例 12】如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGSS.SGF E DCB【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【例 13】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCDEF GABCDEF G【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =,8EFG S =,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFCS =,32ABFE S =,24ABFS=,所以12ABGS=平方厘米.【例 14】四个面积为1的正六边形如图摆放,求阴影三角形的面积.【解析】 如图,将原图扩展成一个大正三角形DEF ,则AGF ∆与CEH ∆都是正三角形.假设正六边形的边长为为a ,则AGF ∆与CEH ∆的边长都是4a ,所以大正三角形DEF 的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF 的面积为496.由于4FA a =,3FB a =,所以AFB ∆与三角形DEF 的面积之比为43127749⨯=.同理可知BDC ∆、AEC ∆与三角形DEF 的面积之比都为1249,所以ABC ∆的面积占三角形DEF 面积的1213134949-⨯=,所以ABC ∆的面积的面积为4913136496⨯=.【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE 的面积是 .BDCA【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.。
数学中的鸟头模型

数学中的鸟头模型数学中的鸟头模型,这名字一听就挺有意思的,对吧?光听名字你就能想象出一只鸟的头,睁着大眼睛,带着一丝机灵和好奇,像是在看着你,想问你点什么。
其实这个模型啊,跟它的名字一样,看起来挺简单,实际上一点也不简单。
你是不是也在想,鸟头跟数学有什么关系呢?看似毫不相关的东西,竟然能碰到一起。
嘿,说实话,刚开始我也觉得这个模型一定跟一些复杂的公式啥的扯上关系,结果呢,一点也不那么回事。
它说的其实是一个特别直观、特别形象的数学模型,虽然名字让人有点摸不着头脑,但一了解,哎呀,原来这么有趣!所谓鸟头模型,其实是指在某些数学场景中,我们可以用一个形象化的“鸟头”来代表问题的结构。
这鸟头模型最早是用来描述一些数学图形的,尤其是在组合数学和图论方面。
简单说来,假如你有个图形,点和线就像是小小的颗粒,点之间相连的线就是桥梁。
而这个鸟头模型就像是在描述这些点与线的排列,像是给它们画了个小框框,给数学问题找个形象的家。
是不是觉得有点抽象?那你可得慢慢听。
我得给你讲个例子。
想象一下,你在街头看到了两个小朋友正准备玩跳绳,他们站在不同的地方,绳子一端在一个小朋友手里,另一端则在另一个小朋友手里。
这个绳子就是两点之间的连线,而小朋友就像是“点”。
他们之间的“连线”是不是就像是一个数学模型里的线条?这个鸟头模型的神奇之处就在于,它能帮助我们把这种关系表达得更加简洁而又准确。
你看,数学不就是这么神奇吗?它能把一堆看似杂乱无章的东西,用简简单单的语言表达出来。
你要是理解了这个鸟头模型,它其实并不神秘。
咱们就把它当作一个画图工具,帮助我们更好地了解和分析数学对象之间的关系。
这些点和线,可以说是数学的基本元素,经过鸟头模型的加工、组合,突然间变得有了生命,像是一个个活跃的小家伙在纸上舞动。
是不是觉得又好玩又有点可爱?再说到这鸟头模型的应用,哎呀,那可真不少。
比如在网络结构的分析中,咱们就常常用这种模型来帮助理解和优化网络的连接情况。
小学的奥数-几何五大模型(鸟头模型)

模型二鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图⑴(或D 在BA 的延长线上,E 在AC 上如图 2),则:():()ABC ADES S AB AC AD AE △△EDCBAEDCBA图⑴图⑵【例1】如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB,:4:7AE AC,16ADES △平方厘米,求ABC △的面积.EDCBAEDCB A【解析】连接BE ,::2:5(24):(54)ADE ABES S AD AB △△,::4:7(45):(75)ABE ABC S S AE AC△△,所以:(24):(75)ADE ABCS S △△,设8ADES △份,则35ABCS △份,16ADE S △平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.三角形等高模型与鸟头模型【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?E D CBA A BCD E【解析】连接BE .∵3EC AE ∴3ABCABESS又∵5AB AD ∴515ADEABEABCSSS,∴1515ABCADESS.【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ,3BE,6AE,乙部分面积是甲部分面积的几倍?乙甲E D CBAABCDE甲乙【解析】连接AD .∵3BE ,6AE ∴3AB BE ,3ABDBDES S又∵4BD DC ,∴2ABCABDSS,∴6ABCBDE SS ,5S S 乙甲.【例2】如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD,:3:2AE EC ,12ADE S △平方厘米,求ABC △的面积.EDC B A EDCB A【解析】连接BE ,::2:5(23):(53)ADE ABES S AD AB △△::3:(32)(35):(32)5ABE ABCS S AE AC△△,所以:(32):5(32)6:25ADE ABC S S △△,设6ADES △份,则25ABCS △份,12ADES △平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例3】如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AFCF ,三角形AFE(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?EFDCBA【解析】连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326()倍.因此,平行四边形的面积为8648(平方厘米).【例4】已知DEF △的面积为7平方厘米,,2,3BECE AD BD CF AF ,求ABC △的面积.FED CBA【解析】:():()(11):(23)1:6BDE ABCS S BD BE BA BC △△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA △△:():()(21):(34)1:6ADF ABC S S ADAF ABAC △△设24ABCS △份,则4BDES △份,4ADF S △份,9CEFS △份,244497DEFS △份,恰好是7平方厘米,所以24ABCS △平方厘米【例5】如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE,:3:2BC CD,三角形BDE 的面积是多少?AB EC DDC EB A【解析】由于180ABC DBE,所以可以用共角定理,设2AB 份,3BC份,则5BE 份,325BD 份,由共角定理:():()(23):(55)6:25ABC BDES S ABBC BE BD △△,设6ABCS △份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5平方厘米,三角形BDE 的面积是12.5平方厘米【例6】(2007年”走美”五年级初赛试题)如图所示,正方形ABCD 边长为6厘米,13AEAC ,13CF BC .三角形DEF 的面积为_______平方厘米.FED C BA【解析】由题意知13AEAC 、13CFBC ,可得23CEAC .根据”共角定理”可得,:():()12:(33)2:9CEF ABC S S CF CE CB AC △△;而66218ABCS △;所以4CEF S △;同理得,:2:3CDE ACD S S △△;,183212CDE S △,6CDF S △故412610DEFCEFDECDFCS S S S △△△△(平方厘米).【例7】如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB ;延长BC 至E ,使2CEBC ;延长CA 至F ,使3AF AC ,求三角形DEF 的面积.F EDCB A AB CDEF【解析】(法1)本题是性质的反复使用.连接AE 、CD .∵11ABC DBC S S ,1ABCS ,∴S1DBC.同理可得其它,最后三角形DEF 的面积18.(法2)用共角定理∵在ABC 和CFE 中,ACB 与FCE 互补,∴111428ABC FCES AC BC SFC CE .又1ABCS,所以8FCES.同理可得6ADFS ,3BDES.所以186318DEFABCFCEADFBDESS SSS.【例8】如图,平行四边形ABCD ,BE AB ,2CF CB ,3GD DC ,4HA AD ,平行四边形ABCD 的面积是2,求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CDEF【解析】连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC 与FBE 互补,∴111133ABC FBES AB BC S BE BF△△.又1ABC S △,所以3FBES △.同理可得8GCF S △,15DHGS △,8AEH S △.所以8815+3+236EFGH AEH CFG DHGBEFABCDS S S S S S △△△△.所以213618ABCD EFGHS S .【例9】如图,四边形EFGH 的面积是66平方米,EAAB ,CBBF ,DCCG ,HD DA ,求四边形ABCD 的面积.H GFED CB A A BCDEFG H 【解析】连接BD .由共角定理得:():()1:2BCD CGFS S CD CB CGCF △△,即2CGFCDBS S △△同理:1:2ABD AHE S S △△,即2AHE ABDS S △△所以2()2AHECGFCBDADB ABCDS S S S S △△△△四边形连接AC ,同理可以得到2DHGBEFABCDS S S △△四边形5AHECGFHDGBEFEFGHABCDABCDS S S S S S S △△△△四边形四边形四边形所以66513.2ABCDS 四边形平方米【例10】如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是.A B CD EF GHA B CD EFGH【解析】连接AC 、BD .由于2BE AB ,2BFBC ,于是4BEFABCS S,同理4HDGADCSS.于是444BEFHDGABC ADCABCD SS S SS .再由于3AE AB ,3AH AD ,于是9AEHABDSS,同理9CFGCBDSS.于是999AEHCFG ABDCBDABCD SS S S S .那么491260EFGHBEFHDG AEHCFGABCDABCD ABCDABCDABCDS SSSSS S S S S .【例11】如图,在ABC △中,延长AB 至D ,使BD AB ,延长BC 至E ,使12CEBC ,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【解析】∵在ABC △和CFE △中,ACB 与FCE 互补,∴224111ABC FCES AC BC S FC CE △△.又2ABCS,所以0.5FCES.同理可得2ADF S △,3BDES △.所以20.532 3.5DEFABC CEF DEB ADF S S S S S △△△△△【例12】如图,1ABCS △,5BCBD ,4AC EC ,DGGSSE ,AFFG .求FGSS.SGF E DCBA 【解析】本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGSS △.【例13】如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCDEF GABCDEF G【解析】连接AF 、EG .因为218164BCFCDES S △△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEFS,8EFGS,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFCS,32ABFE S ,24ABFS,所以12ABGS平方厘米.【例14】四个面积为1的正六边形如图摆放,求阴影三角形的面积.HGFEDCB A【解析】如图,将原图扩展成一个大正三角形DEF ,则AGF 与CEH 都是正三角形.假设正六边形的边长为为a ,则AGF 与CEH 的边长都是4a ,所以大正三角形DEF 的边长为4217,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF 的面积为496.由于4FAa ,3FBa ,所以AFB 与三角形DEF 的面积之比为43127749.同理可知BDC、AEC与三角形DEF的面积之比都为1249,所以ABC的面积占三角形DEF面积的1213134949,所以ABC的面积的面积为4913136496.【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE的面积是.BDCEA【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363,所以五边形的面积是12103633.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021/3/7
CHENLI
7
例2
如图,ABCD和DEFG都是正方形,问三角形ADG和三角形CDE的面 积比是多少
【分析】
1、观察,图片中存在三角形和四边形,并
且三图角形中AD存G的在面鸟积 头模AD型×D;G
1
三角形CDE的面积
CD×DE
2、三角形ADG和三角形CDE构成鸟头模型,
三答角:形三角A形DAGDG的和三面角积形CDE的面积A比D是×1 DG
3、二图三角形两角互补;(互补)
4、三图三角形两角对顶;(相等)
5、四图三角形两角和为180度(互补)
2021/3/7
CHENLI
3
鸟头模型
•鸟头定理是若两三角形有一组对应角相等或互补,则它们的面积 比等于对应角两边乘积的比。
•字母表达:
SADE AD AE SABC AB AC
2021/3/7
鸟头模型
2021/3/7
CHENLI
1
想一想
•刚才封面书房有哪些东西
窗户、书桌、足球、书架、书、尺子、笔筒、笔、魔方、金字塔
•有哪些平面图形、有什么特点
长方形、圆、正方形、三角形
列一列
2021/3/7
CHENLI
2
看一看
• 以下图形由什么特点
1、都是由两个三角形组成
2、一图三角形两角共角;(相等)
CHENLI
4
鸟头模型公式证明
【解析】 连接BE,根据等高模型,
,
所以,
例2 2021/3/7
CHENLI
5
例1
如图,在三角形ABC中,D、E是AB和AC上的点,且AD:AB=2:5 AE:AC=4:7,三角形ADE的面积是16平方厘米,求三角形ABC的面 积。 分析: 1、先观察图形是否是鸟头模型 2、回忆鸟头模型的公式 136、×带35入÷8准=1确6÷计8算×35=2×35=70
答:三角形ABC的面积是70 Nhomakorabea2021/3/7
CHENLI
6
练习1
如图,三角形ABC的面积是3平方厘米,期中AB:BE=2:5,BC: CD=3:2,三角形BDE的面积是多少
三角形ABC和三角形DBE构成鸟头模型 BD=BC+CD=5
3×25÷6=75÷6=12.5(平方厘米) 答:三角形BDE的面积是12.5平方厘米。
所以角D=90度,所以角A+角C=180度,
根据鸟头模型,三角形ABD和三角形BCD
的面积比等于,
(AD×AB)÷(CD×CB)=1:7
答:三角形ABC和三角形BCD的面积比是1:7。
2021/3/7
CHENLI
9
课后作业
课后习题
2021/3/7
CHENLI
10
三角形CDE的面积
CD×DE
3、因为两个四边形是正方形,所以AD=CD,DG=DE。
2021/3/7
CHENLI
8
练习2
四边形ABCD中,AB与BC垂直,各边长度已在图中标出,求三角 形ABD和三角形BCD的面积比。
连接AC交BD于点E,
AB×AB+BC×BC=AC×AC=50 ,
AD×AD+DC×DC=AC×AC=50,
