自动控制原理(非自动化类)习题答案_第二版(孟庆明)
自动控制原理第二版课后答案孟华

自动控制原理第二版课后答案孟华【篇一:自动控制原理_孟华_习题答案】t>第二章2.1 试分别写出图2.68中各无源电路的输入ur(t)与输出uc(t)之间的微分方程。
图2.68 习题2.1图解:(a)ur?ucu?r?u?c)?i2,i1?i2?c?i1,c(ur1r2,r1r2rrr2?c?uc?12cu?r?cuurr1?r2r1?r2r1?r2(b)?r?u?c)?i1,c1(uur?u1?1,uc?i1r2?u1, ?i2,i1?i2?c2ur1??c?(r1c1?r1c2?r2c1)u?c?uc?r1r2c1c2u??r?(r1c1?r2c1)u?r?u r r1r2c1c2u(c)uur?uc?i1,c1(ur?u1)?i2,i1?i2?1r1r2,uc?1i1dt?u1, ?c2??c?(rc????r1r2c1c2u12?r2c2?r2c1)uc?uc?r1r2c1c2ur?(r2c2?r2c1)ur?ur2.2 试证明图2.69(a)所示电路与图2.69(b)所示的机械系统具有相同的微分方程。
图2.69(b)中xr(t)为输入,xc(t)为输出,均是位移量。
(a)(b)图2.69 习题2.2图(a)1ur?uc?r?u?c)?i2,i1?i2?i,uc??i1,c1(uidt?ir2,r1c2???c?(r1c1?r1c2?r2c2)u?c?uc?r1r2c1c2u??r?(r1c1?r2c2)u?r?u r r1r2c1c2u(b)?c?x?1)?k2x1,b1(x?r?x?c)?k1(xr?xc)?b2(x?c?x?1), b2(xb1b2bbbbbbb??c?(1?2?2)x?c?xc?12??r?(1?2)x?r?xrxxk1k2k1k2k1k1k2k1k22.3 试分别求出图2.70中各有源电路的输入ur(t)与输出uc(t)之间的微分方程。
(a) (b)(c)图2.70 习题2.3图解:(a)uur?r??c?cur1r2,uc?r???r2cur2ur r1(b)uurr?c,r2cu?c?uc??2ur ??c?cur1r2r1uc??ur1u?c??r2cu?r?ur r2??rdt,r1cur1cr1(c)2.4 某弹簧的力-位移特性曲线如图2.71所示。
自动控制原理(第二版)

自动控制原理
孟庆明 主编
高等教育出版社
注意事项
1. 请在 请在CPU450MHz,内存 ,内存256M以上的计算机上使用 以上的计算机上使用 多 媒 体 教 学 课 件 , Windows 2000 操 作 系 统 , 安 装 Office 2000软件,或更高版本. 软件,或更高版本. 软件 2. 使用时请安装MathType5及以上版本,否则课件中 使用时请安装 及以上版本, 及以上版本 的部分公式不能正确显示. 的部分公式不能正确显示. 3. 将字体文件 将字体文件LZFonts.ttf拷贝到计算机操作系统安装 拷贝到计算机操作系统安装 目录下的Fonts子目录中,以显示两个花体字符. 子目录中, 目录下的 子目录中 以显示两个花体字符. 4. 显示器的最佳分辨率为 显示器的最佳分辨率为1024×768. × .
�
自动控制原理
孟庆明 主编
高等教育出版社
帮
助
1. 点击目录页各项,可进入相应章节;由于使用了超 点击目录页各项,可进入相应章节; 级链接, 请将所有多媒体课件的ppt文件拷贝到同一 级链接 , 请将所有多媒体课件的 文件拷贝到同一 个文件夹中使用. 个文件夹中使用. 2. 使用键盘上的↓,↑箭头键或鼠标上的滚轮可以实现 使用键盘上的↓,↑箭头键或鼠标上的滚轮可以实现 幻灯片的向下,向上翻页. 幻灯片的向下,向上翻页. 3.使用键盘上的 键,可以回到总目录页. 使用键盘上的Esc键 可以回到总目录页. 使用键盘上的
自动控制原理
第1章 绪论 章
孟庆明 主编
高等教 第3章 时域分析法 章 第4章 复域分析法——根轨迹法 章 复域分析法 根轨迹法 第5章 频域分析法 章 频域分析法——频率法 频率法 第6章 自动控制系统的设计与校正 章 第7章 采样数据控制系统分析 章 采样数据控制系统分析 第8章 状态空间分析法 章
自动控制原理答案_第二版(孟庆明)讲解

课后答案网,用心为你服务!大学答案--- 中学答案--- 考研答案--- 考试答案最全最多的课后习题参考答案,尽在课后答案网()!Khdaw团队一直秉承用心为大家服务的宗旨,以关注学生的学习生活为出发点,旨在为广大学生朋友的自主学习提供一个分享和交流的平台。
爱校园()课后答案网()淘答案()自动控制原理(非自动化类)习题答案第一章 习题1-1(略) 1-2(略) 1-3 解:受控对象:水箱液面。
被控量:水箱的实际水位 h c 执行元件:通过电机控制进水阀门开度,控制进水流量。
比较计算元件:电位器。
测量元件:浮子,杠杆。
放大元件:放大器。
工作原理:系统的被控对象为水箱。
被控量为水箱的实际水位 h 。
给定值为希望水位 h (与电位器设定 c r 电压 u r 相对应,此时电位器电刷位于中点位置)。
当 h c = h r 时,电位器电刷位于中点位置,电动机不工作。
一但 h c ⎺ h r 时,浮子位置相应升高(或降低),通过杠杆作用使电位器电刷从中点位置下移(或上移),从而给电动机提供一定的工作电压,驱动 电动机通过减速器使阀门的开度减小(或增大),以使水箱水位达到希望值 h r 。
水位自动控制系统的职能方框图1-4 解:受控对象:门。
执行元件:电动机,绞盘。
放大元件:放大器。
受控量:门的位置 测量比较元件:电位计工作原理:系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时,桥式电位器测量电路产生偏差电压,经放大器放大后,驱动电动机带动绞盘转动, 使大门向上提起。
同时,与大门连在一起的电位器电刷上移,直到桥式电位器达到平衡,电动机停转,开 门开关自动断开。
反之,当合上关门开关时,电动机带动绞盘反转,使大门关闭。
开(闭)门门实际 仓库大门自动控制开(闭)的职能方框图1-5 解:系统的输出量:电炉炉温 给定输入量:加热器电压 被控对象:电炉放大元件:电压放大器,功率放大器,减速器 比较元件:电位计 测量元件:热电偶 职能方框图:第二章 习题2-1 解:对微分方程做拉氏变换:♣ X 1 (s ) = R (s ) C (s ) + N 1 (s ) ♠ ♠ X 2(s ) = K 1 X 1 (s )♠ X 3 (s ) = X 2 (s ) X 5 (s )♦ ♠TsX 4 (s ) = X 3 (s )♠ X 5 (s ) = X 4 (s ) K 2 N 2 (s )♠ ♠K X (s ) = s 2C (s ) + sC (s ) ♥3 5 绘制上式各子方程的方块图如下图所示:1(s)3(s)5(s)K 1K 3C (s ) / R (s ) = , Ts 3 + (T + 1)s 2+ s + K K 1 3C (s ) / N 1 (s ) = C (s ) / R (s ) ,K 2 K 3Ts C (s ) / N (s ) = 2Ts 3 + (T + 1)s 2 + s + K K 1 32-2 解:对微分方程做拉氏变换♣ X 1 (s ) = K [R (s ) C (s )] ♠♠ X 2 (s ) = ⎜ sR (s )♠(s + 1) X 3 (s ) = X 1 (s ) + X 2 (s )♦♠(Ts + 1) X 4 (s ) = X 3 (s ) + X 5 (s ) ♠C (s ) = X (s ) N (s ) 4 ♠ ♠♥ X 5 (s ) = (Ts + 1) N (s )绘制上式各子方程的方块如下图:⎜ s K+ K + ⎜ s = (s + 1)(Ts + 1) (s + 1)(Ts + 1) = C (s ) R (s ) k Ts 2+ (T + 1)s + (K + 1) 1 + (s + 1)(Ts + 1)C (s ) N (s ) =2-3 解:(过程略) C (s ) 1 C (s ) =G 1 + G 2 (a)= R (s ) ms 2+ fs + K(b)R (s ) 1 + G G G G + G G G G 1 3 1 4 2 3 2 4C (s ) =G 2 + G 1G 2C (s ) = G 1G 2 (c)(d)R (s ) 1 + G 1 + G 2G 1R (s ) 1 G 2G 3C (s ) =G 1G 2G 3G 4 (e)R (s ) 1 + G 1G 2 + G 2G 3 + G 3G 4 + G 1G 2G 3G 42-4 解 :(1)求 C/R ,令 N=0G (s ) = K 1K 2 K3s (Ts + 1)K 1K 2 K 3 G (s )C (s ) / R (s ) = = 1 + G (s ) Ts 2 + s + K K K 1 2 3求 C/N ,令 R=0,向后移动单位反馈的比较点K 3K 2 ) Ts + 1 = K n K 3s K 1K 2 K 3G n C (s ) / N (s ) = (K G K n n 1K K Ts 2 + s + K K K s 1 + 3 2K 1 2 3 1 Ts + 1 s(2)要消除干扰对系统的影响C (s ) / N (s ) = K n K 3 s K 1K 2 K 3G n= 0Ts 2 + s + K K K 1 2 3K n sG (s ) = nK 1K 22-5 解:(a )(1)系统的反馈回路有三个,所以有3La= L 1 + L 2 + L 3 = G 1G 2G 5 G 2G 3G 4 + G 4G 2G 5a =1三个回路两两接触,可得 ⊗ = 1La= 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5(2)有两条前向通道,且与两条回路均有接触,所以P 1 = G 1G 2G 3 , ⊗1 = 1 P 2 = 1, ⊗2 = 1(3)闭环传递函数 C/R 为C =G 1G 2G 3 + 1 R 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5(b )(1)系统的反馈回路有三个,所以有3La= L 1 + L 2 + L 3 = G 1G 2 G 1 G 1a =1三个回路均接触,可得 ⊗ = 1La= 1 + G 1G 2 + 2G 1(2)有四条前向通道,且与三条回路均有接触,所以P 1 = G 1G 2 , ⊗1 = 1 P 2 = G 1 , ⊗2 = 1 P 3 = G 2 , ⊗3 = 1 P 4 = G 1 , ⊗4 = 1(3)闭环传递函数 C/R 为C = G 1G 2 + G 1 + G 2 G 1 = G 1G 2 + G 2 R 1 + G 1G 2 + 2G 1 1 + G 1G 2 + 2G 12-6 解:用梅逊公式求,有两个回路,且接触,可得 ⊗ = 1La= 1 + G 1G 2G 3 + G 2 ,可得C (s ) = G 1G 2G 3+ G 2G 3 C (s ) = C (s ) / R (s )R (s ) 1 + G 1G 2G 3 + G 2 N 1 (s )(1 + G 2 )G 3C(s ) = 1⋅ (1 + G 1G 2G 3 + G 2 )= 1C(s ) = N 2 (s ) 1 + G 1G 2G 3 + G 2 1 + G 1G 2G 3 + G 2 N 3 (s )E (s ) =1 + G2 G 2G3 E (s )= C (s ) = G 2G 3 G 1G 2G 3 R (s ) 1 + G 1G 2G 3 + G 2N 1 (s ) N 1 (s ) 1 + G 1G 2G 3 + G 2 E(s ) = C (s ) (1 + G 2 )G 3E (s ) = C (s )= = 1 N 2 (s ) N 2 (s ) 1 + G 1G 2G 3 + G 2 N 3 (s ) N 3 (s )第三章 习题103-1 解:(原书改为 G (s ) =)0.2s + 1采用 K 0 , K H 负反馈方法的闭环传递函数为10K 0⎫ (s ) = C (s ) = K G (s )1 + 10K H = R (s ) 01 + G (s )K 0.2 s + 1H 1 + 10K H要使过渡时间减小到原来的 0.1 倍,要保证总的放大系数不变,则:(原放大系数为 10,时 间常数为 0.2)10K 0♣ = 10 ♣ K = 10 ♠0 ♦1 + 10K ® ♦ H♥K = 0.9♠ H 1 + 10K = 10 ♥H 3-2 解:系统为欠阻尼二阶系统(书上改为“单位负反馈……”,“已知系统开环传递函数”)⎛ % = e⎩⋅100% = 1.3 1 ⋅100%1t p == 0.1解得:⎤n = 33.71 ⎩ = 0.358所以,开环传递函数为:1136 47.1G (s ) = = s (s + 24.1) s (0.041s + 1)3-3 解:(1) K = 10s 1时:100G (s ) = s 2+ 10s⎤ 2 =100 n 2⎩⎤n = 10解得:⎤n = 10, ⎩ = 0.5, ⎛ % = 16.3%, t p = 0.363 (2) K = 20s 1 时:200 G (s ) = s 2+ 10s⎤ 2 = 200n 2⎩⎤n = 10解得:⎤n = 14.14, ⎩ = 0.354, ⎛ %=30%, t p = 0.238结论,K 增大,超调增加,峰值时间减小。
《自动控制原理》第二版课后习题答案
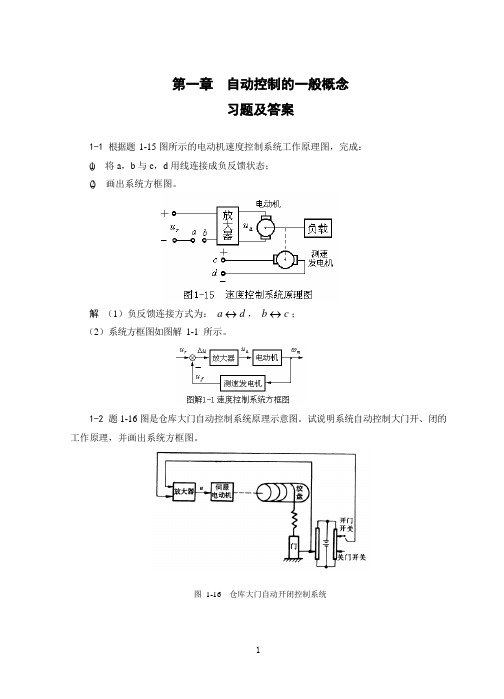
动电位器 P2 的滑臂转过一定的角度 o ,直至 o i 时, ui uo ,偏差电压ue 0 ,电动 机停止转动。这时,导弹发射架停留在相应的方位角上。只要 i o ,偏差就会产生调节作
3
用,控制的结果是消除偏差 e ,使输出量 o 严格地跟随输入量 i 的变化而变化。 系统中,导弹发射架是被控对象,发射架方位角 o 是被控量,通过手轮输入的角度 i 是
大,提高发电机的端电压,使发电机 G 的端电压回升,偏差电压减小,但不可能等于零,因
为当偏差电压为 0 时, i f =0,发电机就不能工作。即图(b)所示系统的稳态电压会低于 110
伏。 1-8 图 1-22 为水温控制系统示意图。冷水在热交换器中由通入的蒸汽加热,从而得到一
定温度的热水。冷水流量变化用流量计测量。试绘制系统方块图,并说明为了保持热水温度 为期望值,系统是如何工作的?系统的被控对象和控制装置各是什么?
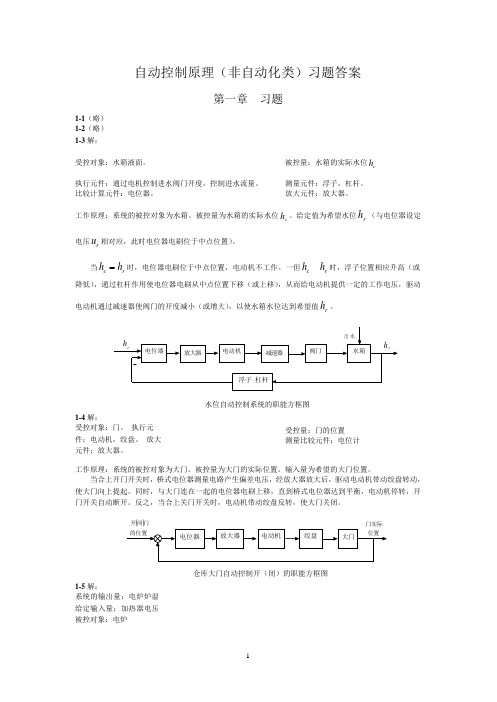
图 1-16 仓库大门自动开闭控制系统
1
解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏 差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。与此同时,和大 门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开 启位置。反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离 开闭自动控制。系统方框图如图解 1-2 所示。
征炉温的希望值)。系统方框图见图解 1-3。
1-4 图 1-18 是控制导弹发射架方位的电位器式随动系统原理图。图中电位器 P1 、 P2 并 联后跨接到同一电源 E0 的两端,其滑臂分别与输入轴和输出轴相联结,组成方位角的给定元件
自动控制原理第二版课后答案(孟庆明)

自动控制原理第二版课后答案(孟庆明)目录第一章 (1)第二章 (2)第三章 (5)第四章 (15)第五章 (18)第六章 (27)1-1(略) 1-2(略) 1-3 解:受控对象:水箱液面。
被控量:水箱的实际水位 h c 执行元件:通过电机控制进水阀门开度,控制进水流量。
比较计算元件:电位器。
测量元件:浮子,杠杆。
放大元件:放大器。
工作原理:系统的被控对象为水箱。
被控量为水箱的实际水位 h 。
给定值为希望水位 h (与电位器设定 c r 电压 u r 相对应,此时电位器电刷位于中点位置)。
当 h c = h r 时,电位器电刷位于中点位置,电动机不工作。
一但 h c ⎺ h r 时,浮子位置相应升高(或降低),通过杠杆作用使电位器电刷从中点位置下移(或上移),从而给电动机提供一定的工作电压,驱动 电动机通过减速器使阀门的开度减小(或增大),以使水箱水位达到希望值 h r 。
水位自动控制系统的职能方框图1-4 解:受控对象:门。
执行元件:电动机,绞盘。
放大元件:放大器。
受控量:门的位置 测量比较元件:电位计工作原理:系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时,桥式电位器测量电路产生偏差电压,经放大器放大后,驱动电动机带动绞盘转动, 使大门向上提起。
同时,与大门连在一起的电位器电刷上移,直到桥式电位器达到平衡,电动机停转,开 门开关自动断开。
反之,当合上关门开关时,电动机带动绞盘反转,使大门关闭。
开(闭)门门实际 仓库大门自动控制开(闭)的职能方框图1-5 解:系统的输出量:电炉炉温 给定输入量:加热器电压 被控对象:电炉第一章放大元件:电压放大器,功率放大器,减速器比较元件:电位计 测量元件:热电偶 职能方框图: 2-1 解:对微分方程做拉氏变换:♣ X 1 (s ) = R (s ) C (s ) + N 1 (s ) ♠ ♠ X 2(s ) = K 1 X 1 (s )♠ X 3 (s ) = X 2 (s ) X 5 (s ) ♦♠TsX 4 (s ) = X 3 (s )♠ X 5 (s ) = X 4 (s ) K 2 N 2 (s ) ♠ ♠K X (s ) = s 2C (s ) + sC (s ) ♥3 5 绘制上式各子方程的方块图如下图所示:(s)3(s)5(s)K 1K 3C (s ) / R (s ) = , Ts 3 + (T + 1)s 2+ s + K K 1 3第二章C (s ) / N 1 (s ) = C (s ) / R (s ) ,K 2 K 3Ts C (s ) / N (s ) = 2Ts 3 + (T + 1)s 2 + s + K K 1 32-2 解:对微分方程做拉氏变换♣ X 1 (s ) = K [R (s ) C (s )]♠♠ X 2 (s ) = ⎜ sR (s )♠(s + 1) X 3 (s ) = X 1 (s ) + X 2 (s ) ♦♠(Ts + 1) X 4 (s ) = X 3 (s ) + X 5 (s ) ♠C (s ) = X (s ) N (s ) 4 ♠ ♠♥ X 5 (s ) = (Ts + 1) N (s )绘制上式各子方程的方块如下图:⎜ s K+ K + ⎜ s = (s + 1)(Ts + 1) (s + 1)(Ts + 1) = C (s ) R (s ) k Ts 2+ (T + 1)s + (K + 1) 1 + (s + 1)(Ts + 1)C (s )N (s ) =0 2-3 解:(过程略) C (s ) 1 C (s ) =G 1 + G 2 (a)=R (s ) ms 2 + fs + K(b)R (s ) 1 + G G G G + G G G G 1 3 1 4 2 3 2 4C (s ) = G 2 + G 1G 2 C (s ) = G 1 G 2 (c)(d)R (s ) 1 + G 1 + G 2G 1R (s ) 1 G 2G 3C (s ) =G 1G 2G 3G 4 (e)R (s ) 1 + G 1G 2 + G 2G 3 + G 3G 4 + G 1G 2G 3G 42-4 解 :(1)求 C/R ,令 N=0G (s ) =K 1K 2 K 3s (Ts + 1)K 1K 2 K 3 G (s )C (s ) / R (s ) = = 1 + G (s ) Ts 2 + s + K K K 1 2 3 求 C/N ,令 R=0,向后移动单位反馈的比较点K 3K 2 ) Ts + 1 = K n K 3 s K 1K 2 K 3G n C (s ) / N (s ) = (K G K n n1 K K Ts2 + s + K K K s 1 +3 2 K 1 2 31Ts + 1 s(2)要消除干扰对系统的影响C (s ) / N (s ) = K n K 3 s K 1K 2 K 3G n= 0Ts 2 + s + K K K 1 2 3K n sG (s ) = nK 1K 22-5 解:(a )(1)系统的反馈回路有三个,所以有3La= L 1 + L 2 + L 3 = G 1G 2G 5 G 2G 3G 4 + G 4G 2G 5a =1三个回路两两接触,可得 ⊗ = 1La= 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5(2)有两条前向通道,且与两条回路均有接触,所以P 1 = G 1G 2G 3 , ⊗1 = 1 P 2 = 1, ⊗2 = 1(3)闭环传递函数 C/R 为C =G 1G 2G 3 + 1 R 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5(b )(1)系统的反馈回路有三个,所以有3La= L 1 + L 2 + L 3 = G 1G 2 G 1 G 1a =1三个回路均接触,可得 ⊗ = 1La= 1 + G 1G 2 + 2G 1(2)有四条前向通道,且与三条回路均有接触,所以P 1 = G 1G 2 , ⊗1 = 1 P 2 = G 1 , ⊗2 = 1 P 3 = G 2 , ⊗3 = 1 P 4 = G 1 , ⊗4 = 1(3)闭环传递函数 C/R 为C = G 1G 2 + G 1 + G 2 G 1 = G 1G 2 + G 2 R 1 + G 1G 2 + 2G 1 1 + G 1G 2 + 2G 12-6 解:用梅逊公式求,有两个回路,且接触,可得 ⊗ = 1La= 1 + G 1G 2G 3 + G 2 ,可得C (s ) = G 1G 2G 3 + G 2G 3C (s ) = C (s ) / R (s )R (s ) 1 + G 1G 2G 3 + G 2 N 1 (s ) (1 + G 2 )G 3C(s ) = 1⋅ (1 + G 1G 2G 3 + G 2 )= 1C(s ) = N 2 (s ) 1 + G 1G 2G 3 + G 2 1 + G 1G 2G 3 + G 2 N 3 (s )E (s ) =1 + G2 G 2G3 E (s ) = C (s ) =G 2G 3 G 1G 2G 3 R (s ) 1 + G 1G 2G 3 + G 2N 1 (s ) N 1 (s ) 1 + G 1G 2G 3 + G 2E(s ) = C (s )(1 + G 2 )G 3 E (s )= C (s )= = 1 N 2 (s ) N 2 (s ) 1 + G 1G 2G 3 + G 2 N 3 (s ) N 3 (s )103-1 解:(原书改为 G (s ) =)0.2s + 1采用 K 0 , K H 负反馈方法的闭环传递函数为10K 0⎫ (s ) =C (s ) = K G (s )1 + 10K H = R (s ) 0 1 + G (s )K 0.2s + 1H1 + 10K H要使过渡时间减小到原来的 0.1 倍,要保证总的放大系数不变,则:(原放大系数为 10,时 间常数为 0.2)10K 0♣ = 10 ♣ K = 10 ♠0 ♦1 + 10K ® ♦ H♥K = 0.9 ♠ H 1 + 10K = 10 ♥ H3-2 解:系统为欠阻尼二阶系统(书上改为“单位负反馈……”,“已知系统开环传递函数”)⎛ % = e⎩⋅100% = 1.3 1 ⋅100%1t p == 0.1第三章解得:⎤n = 33.71 ⎩ = 0.358所以,开环传递函数为:1136 47.1G (s ) = = s (s + 24.1) s (0.041s + 1)3-3 解:(1) K = 10s 1时:100G (s ) = s 2+ 10s⎤ 2 =100 n 2⎩⎤n = 10解得:⎤n = 10, ⎩ = 0.5, ⎛ % = 16.3%, t p = 0.363 (2) K = 20s 1 时:200 G (s ) = s 2+ 10s⎤ 2 = 200 n2⎩⎤n = 10解得:⎤n = 14.14, ⎩ = 0.354, ⎛ %=30%, t p = 0.238结论,K 增大,超调增加,峰值时间减小。
自动控制原理(非自动化类)答案_第二版(孟庆明)
自动控制原理(非自动化类)习题答案第一章 习题1-1(略) 1-2(略) 1-3 解:受控对象:水箱液面。
被控量:水箱的实际水位 h c 执行元件:通过电机控制进水阀门开度,控制进水流量。
比较计算元件:电位器。
测量元件:浮子,杠杆。
放大元件:放大器。
工作原理:系统的被控对象为水箱。
被控量为水箱的实际水位 h 。
给定值为希望水位 h (与电位器设定 c r 电压 u r 相对应,此时电位器电刷位于中点位置)。
当 h c = h r 时,电位器电刷位于中点位置,电动机不工作。
一但 h c ⎺ h r 时,浮子位置相应升高(或降低),通过杠杆作用使电位器电刷从中点位置下移(或上移),从而给电动机提供一定的工作电压,驱动电动机通过减速器使阀门的开度减小(或增大),以使水箱水位达到希望值 h r 。
水位自动控制系统的职能方框图1-4 解:受控对象:门。
执行元件:电动机,绞盘。
放大元件:放大器。
受控量:门的位置测量比较元件:电位计工作原理:系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时,桥式电位器测量电路产生偏差电压,经放大器放大后,驱动电动机带动绞盘转动, 使大门向上提起。
同时,与大门连在一起的电位器电刷上移,直到桥式电位器达到平衡,电动机停转,开 门开关自动断开。
反之,当合上关门开关时,电动机带动绞盘反转,使大门关闭。
仓库大门自动控制开(闭)的职能方框图1-5 解:系统的输出量:电炉炉温 给定输入量:加热器电压 被控对象:电炉放大元件:电压放大器,功率放大器,减速器 比较元件:电位计 测量元件:热电偶 职能方框图:第二章 习题2-1 解:对微分方程做拉氏变换:♣ X 1 (s ) = R (s )C (s ) + N 1 (s ) ♠ ♠ X 2(s ) = K 1 X 1 (s )♠ X 3 (s ) = X 2 (s )X 5 (s )♦ ♠TsX 4 (s ) = X 3 (s ) ♠ X 5 (s ) = X 4 (s ) K 2 N 2 (s )♠ ♠K X (s ) = s 2C (s ) + sC (s ) ♥ 3 5绘制上式各子方程的方块图如下图所示:1(s)3(s)5(s)K 1K 3C (s ) / R (s ) = , Ts 3+ (T + 1)s 2+ s + K K 1 3C (s ) / N 1 (s ) = C (s ) / R (s ) ,K 2 K 3Ts C (s ) / N (s ) = 2Ts 3 + (T + 1)s 2 + s + K K 1 32-2 解:对微分方程做拉氏变换♣ X 1 (s ) = K [R (s )C (s )] ♠♠ X 2 (s ) = ⎜ sR (s )♠(s + 1) X 3 (s ) = X 1 (s ) + X 2 (s ) ♦♠(Ts + 1) X 4 (s ) = X 3 (s ) + X 5 (s ) ♠C (s ) = X (s ) N (s ) 4 ♠ ♠♥ X 5 (s ) = (Ts + 1) N (s )绘制上式各子方程的方块如下图:⎜s K + K + ⎜ s = (s + 1)(Ts + 1) (s + 1)(Ts + 1) =C (s ) R (s ) k Ts 2 + (T + 1)s + (K + 1) 1 +(s + 1)(Ts + 1)C (s )N (s ) = 02-3 解:(过程略) C (s ) 1 C (s ) =G 1 + G 2(a)= R (s ) ms 2+ fs + K(b)R (s ) 1 + G G G G + G G G G 1 3 1 4 2 3 2 4C (s ) =G 2 +G 1G 2 C (s ) = G1G 2 (c)(d)R (s ) 1 + G 1 + G 2G 1R (s ) 1 G 2G 3C (s ) =G 1G 2G 3G 4 (e)R (s ) 1 + G 1G 2 + G 2G 3 + G 3G 4 + G 1G 2G 3G 42-4 解 :(1)求 C/R ,令 N=0G (s ) = K 1K 2 K3s (Ts + 1)K 1K 2 K 3G (s ) C (s ) / R (s ) = = 1 + G (s ) Ts 2 + s + K K K 1 2 3求 C/N ,令 R=0,向后移动单位反馈的比较点K 3K 2 ) Ts + 1 = K n K 3 s K 1K 2 K 3G n C (s ) / N (s ) = (K G K n n 1 K K Ts 2 + s + K K K s 1 + 3 2K 1 2 3 1 Ts + 1 s(2)要消除干扰对系统的影响C (s ) / N (s ) = K n K 3 s K 1K 2 K 3G n = 0Ts 2 + s + K K K 1 2 3K n sG (s ) =n K 1K 22-5 解:(a )(1)系统的反馈回路有三个,所以有3La= L 1 + L 2 + L 3 = G 1G 2G 5 G 2G 3G 4 + G 4G 2G 5a =1三个回路两两接触,可得 ⊗ = 1La= 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5(2)有两条前向通道,且与两条回路均有接触,所以P 1 = G 1G 2G 3 , ⊗1 = 1 P 2 = 1, ⊗2 = 1(3)闭环传递函数 C/R 为C =G 1G 2G 3 + 1 R 1 + G 1G 2G 5 + G 2G 3G 4 G 4G 2G 5(b )(1)系统的反馈回路有三个,所以有3La= L 1 + L 2 + L 3 = G 1G 2 G 1 G 1a =1三个回路均接触,可得 ⊗ = 1La= 1 + G 1G 2 + 2G 1(2)有四条前向通道,且与三条回路均有接触,所以P 1 = G 1G 2 , ⊗1 = 1 P 2 = G 1 , ⊗2 = 1 P 3 = G 2 , ⊗3 = 1 P 4 = G 1 , ⊗4 =1 (3)闭环传递函数 C/R 为C = G 1G 2 + G 1 + G 2 G 1 = G 1G 2 + G 2 R 1 + G 1G 2 + 2G 1 1 + G 1G 2 + 2G 12-6 解:用梅逊公式求,有两个回路,且接触,可得 ⊗ = 1La= 1 + G 1G 2G 3 + G 2 ,可得C (s ) = G 1G 2G 3+ G 2G 3 C (s )= C (s ) / R (s ) R (s ) 1 + G 1G 2G 3 + G 2 N 1 (s )(1 + G 2 )G 3C(s ) =1⋅ (1+ G 1G 2G 3 + G 2 ) = 1C(s ) = N 2 (s ) 1 + G 1G 2G 3 + G 2 1 + G 1G 2G 3 + G 2 N 3 (s )E (s )= 1 + G 2 G 2G 3E (s )= C (s ) = G 2G 3 G 1G 2G 3R (s ) 1 + G 1G 2G 3 + G 2N 1 (s ) N 1 (s ) 1 + G 1G 2G 3 + G 2E (s ) =C (s ) (1 + G 2 )G 3 E (s )=C (s ) = = 1 N 2 (s ) N 2 (s ) 1 + G 1G 2G 3 + G 2 N 3 (s ) N 3 (s )第三章 习题10 3-1 解:(原书改为 G (s ) =)0.2s + 1采用 K 0 , K H 负反馈方法的闭环传递函数为10K 0⎫ (s ) =C (s )= K G (s ) 1 + 10K H = R (s ) 0 1 + G (s )K 0.2s + 1H 1 + 10K H要使过渡时间减小到原来的 0.1 倍,要保证总的放大系数不变,则:(原放大系数为 10,时 间常数为 0.2)10K 0♣ = 10 ♣ K = 10 ♠0 ♦1 + 10K ® ♦ H ♥K = 0.9 ♠ H 1 + 10K = 10 ♥H 3-2 解:系统为欠阻尼二阶系统(书上改为“单位负反馈……”,“已知系统开环传递函数”)⎛ % = e⎩⋅100% = 1.31 ⋅100%1 t p == 0.1解得:⎤n = 33.71 ⎩ = 0.358所以,开环传递函数为:1136 47.1G (s ) = = s (s + 24.1) s (0.041s + 1)3-3 解:(1) K = 10s 1时:100G (s ) =s 2 + 10s⎤ 2 = 100 n 2⎩⎤n = 10解得:⎤n = 10, ⎩ = 0.5, ⎛ % = 16.3%, t p = 0.363 (2) K = 20s 1时:200 G (s ) = s 2+ 10s⎤ 2 = 200 n 2⎩⎤n = 10解得:⎤n = 14.14, ⎩ = 0.354, ⎛ %=30%, t p = 0.238结论,K 增大,超调增加,峰值时间减小。
自动控制原理孟华第二版课后答案

自动控制原理孟华第二版课后答案【篇一:自动控制原理_孟华_习题答案大连理工】t>第一章(略)第二章2.1 试分别写出图2.68中各无源电路的输入ur(t)与输出uc(t)之间的微分方程。
图2.68 习题2.1图解:(a)ur?ucurrrrr2?c?uc?12cu?r??r?u?c)?i2,i1?i2?c,12cu?i1,c(uurr1r2r1?r2r1?r2r1?r2(b)?r?u?c)?i1,c1(uur?u1?1,uc?i1r2?u1, ?i2,i1?i2?c2ur1??c?(r1c1?r1c2?r2c1)u?c?uc?r1r2c1c2u??r?(r1c1?r2c1)u?r?u r r1r2c1c2u(c)u1ur?uc?i1,c1(ur?u1)?i2,i1?i2?1,uc?i1dt?u1, r1r2c2???c?(rc????r1r2c1c2u12?r2c2?r2c1)uc?uc?r1r2c1c2ur?(r2c2?r2c1)ur?ur2.2 试证明图2.69(a)所示电路与图2.69(b)所示的机械系统具有相同的微分方程。
图2.69(b)中xr(t)为输入,xc(t)为输出,均是位移量。
(a)(b)图2.69 习题2.2图解:(a)1ur?uc?r?u?c)?i2,i1?i2?i,uc??i1,c1(uidt?ir2,r1c2???c?(r1c1?r1c2?r2c2)u?c?uc?r1r2c1c2u??r?(r1c1?r2c2)u?r?u r r1r2c1c2u(b)?c?x?1)?k2x1,b1(x?r?x?c)?k1(xr?xc)?b2(x?c?x?1), b2(x b1b2bbbbbbb??c?(1?2?2)x?c?xc?12??r?(1?2)x?r?xrxxk1k2k1k2k1k1k2k1k22.3 试分别求出图2.70中各有源电路的输入ur(t)与输出uc(t)之间的微分方程。
自动控制原理第二版课后答案第二章精选全文完整版

x kx ,简记为
y kx 。
若非线性函数有两个自变量,如 z f (x, y) ,则在
平衡点处可展成(忽略高次项)
f
f
z xv
|( x0 , y0 )
x y |(x0 , y0 )
y
经过上述线性化后,就把非线性关系变成了线性 关系,从而使问题大大简化。但对于如图(d)所示的 强非线性,只能采用第七章的非线性理论来分析。对于 线性系统,可采用叠加原理来分析系统。
Eb (s) Kbsm (s)
Js2 m(s) Mm fsm(s)
c
(s)
1
i
m
(s)
45
系统各元部件的动态结构图
传递函数是在零初始条件下建立的,因此,它只 是系统的零状态模型,有一定的局限性,但它有现 实意义,而且容易实现。
26
三、典型元器件的传递函数
1. 电位器
1 2
max
E
Θs
U s
K
U
K E
max
27
2. 电位器电桥
1
2
E
K1p1
K1 p 2
U
Θ 1
s
Θ
K1 p
Θ 2
s
U s
28
3.齿轮
传动比 i N2 N1
G2(s)
两个或两个以上的方框,具有同一个输入信号,并 以各方框输出信号的代数和作为输出信号,这种形
式的连接称为并联连接。
41
3. 反馈连接
R(s)
-
C(s) G(s)
H(s)
一个方框的输出信号输入到另一个方框后,得 到的输出再返回到这个方框的输入端,构成输 入信号的一部分。这种连接形式称为反馈连接。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制原理(非自动化类)习题答案第一章习题1-1(略)1-2(略)1-3解:受控对象:水箱液面。
被控量:水箱的实际水位h c 执行元件:通过电机控制进水阀门开度,控制进水流量。
比较计算元件:电位器。
测量元件:浮子,杠杆。
放大元件:放大器。
工作原理:系统的被控对象为水箱。
被控量为水箱的实际水位h 。
给定值为希望水位h (与电位器设定c r 电压u r 相对应,此时电位器电刷位于中点位置)。
当h c =h r 时,电位器电刷位于中点位置,电动机不工作。
一但h c ≠h r 时,浮子位置相应升高(或电动机通过减速器使阀门的开度减小(或增大),以使水箱水位达到希望值h r 。
出水h rh c水位自动控制系统的职能方框图1-4解:受控对象:门。
执行元件:电动机,绞盘。
放大元件:放大器。
受控量:门的位置测量比较元件:电位计工作原理:系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时,桥式电位器测量电路产生偏差电压,经放大器放大后,驱动电动机带动绞盘转动,使大门向上提起。
同时,与大门连在一起的电位器电刷上移,直到桥式电位器达到平衡,电动机停转,开门开关自动断开。
反之,当合上关门开关时,电动机带动绞盘反转,使大门关闭。
开(闭)门的位置门实际仓库大门自动控制开(闭)的职能方框图1-5解:系统的输出量:电炉炉温给定输入量:加热器电压被控对象:电炉_大门位置绞盘电动机放大器电位器_浮子杠杆水箱阀门减速器电动机放大器电位器放大元件:电压放大器,功率放大器,减速器比较元件:电位计测量元件:热电偶职能方框图:给定炉温炉温—第二章习题2-1解:对微分方程做拉氏变换:⎧X 1(s )=R (s )−C (s )+N 1(s )⎪⎪X 2(s )=K 1X 1(s )⎪X 3(s )=X 2(s )−X 5(s )⎨⎪TsX 4(s )=X 3(s )⎪X 5(s )=X 4(s )−K 2N 2(s )⎪⎪K X (s )=s 2C (s )+sC (s )⎩35绘制上式各子方程的方块图如下图所示:N 1(s)R(s)+X 1(s)X 2(s)X 3(s)X 1(s)X 2(s)--C(s)X 5(s)N 2(s)X 3(s)X 4(s)X 5(s)C(s)X 4(s)-X 5(s)将方块图连接起来,得出系统的动态结构图:N 2(s)N 1(s)+X 1(s)_C(s)R(s)X 2(s)X 3(s)X 4(s)X 5(s)K 1K 3C (s )/R (s )=,Ts 3+(T +1)s 2+s +K K 13--K 3K 11s 2+s1TsK 2K 31Ts1s 2+sK 2K 1热电偶电炉加热器电机功率放大电压放大电位器C (s )/N 1(s )=C (s )/R (s ),K 2K 3TsC (s )/N (s )=−2Ts 3+(T +1)s 2+s +K K 132-2解:对微分方程做拉氏变换⎧X 1(s )=K [R (s )−C (s )]⎪⎪X 2(s )=⎜sR (s )⎪(s +1)X 3(s )=X 1(s )+X 2(s )⎨⎪(Ts +1)X 4(s )=X 3(s )+X5(s )⎪C (s )=X (s )−N (s )4⎪⎪⎩X 5(s )=(Ts +1)N (s )绘制上式各子方程的方块如下图:X 2(s)R(s)X 1(s)R(s)X 2(s)X 1(s)X 3(s)-C(s)X 5(s)N(s)N(s)X 5(s)—X 3(s)X 4(s)X 4(s)C(s)将方块图连接得出系统的动态结构图:N(s)X 2(s)X 5(s)—C(s)R(s)X 1(s)X 3(s)X 4(s)⎜s K+K +⎜s =(s +1)(Ts +1)(s +1)(Ts +1)=C (s )R (s )k Ts 2+(T +1)s +(K +1)1+(s +1)(Ts +1)C (s )N (s )=02-3解:(过程略)C (s )1C (s )=G 1+G 2(a)=R (s )ms 2+fs +K(b)R (s )1+G G −G G +G G −G G 13142324-K1Ts +11s +1τsTs+1Ts1Ts +1τsK1s +1C (s )=G 2+G 1G 2C (s )=G 1−G 2(c)(d)R (s )1+G 1+G 2G 1R (s )1−G 2G 3C (s )=G 1G 2G 3G 4(e)R (s )1+G 1G 2+G 2G 3+G 3G 4+G 1G 2G 3G 42-4解:(1)求C/R ,令N=0G (s )=K 1K 2K 3s (Ts +1)K 1K 2K 3G (s )C (s )/R (s )==1+G (s )Ts 2+s +K K K 123求C/N ,令R=0,向后移动单位反馈的比较点K 3K 2)Ts +1=K n K 3s −K 1K 2K 3G n C (s )/N (s )=(K −G K n n 1K K Ts 2+s +K K K s 1+32K 1231Ts +1s(2)要消除干扰对系统的影响C (s )/N (s )=K n K 3s −K 1K 2K 3G n=0Ts 2+s +K K K 123K n s G (s )=n K 1K 22-5解:(a )(1)系统的反馈回路有三个,所以有3∑La=L 1+L 2+L 3=−G 1G 2G 5−G 2G 3G 4+G 4G 2G 5a =1三个回路两两接触,可得⊗=1−∑La=1+G 1G 2G 5+G 2G 3G 4−G 4G 2G 5(2)有两条前向通道,且与两条回路均有接触,所以P 1=G 1G 2G 3,⊗1=1P 2=1,⊗2=1(3)闭环传递函数C/R 为C =G 1G 2G 3+1R 1+G 1G 2G 5+G 2G 3G 4−G 4G 2G 5(b )(1)系统的反馈回路有三个,所以有3∑La=L 1+L 2+L 3=−G 1G 2−G 1−G 1a =1三个回路均接触,可得⊗=1−∑L a=1+G 1G 2+(2)有四条前向通道,且与三条回路均有接触,所以P 1=G 1G 2,⊗1=1P 2=G 1,⊗2=1P 3=G 2,⊗3=1P 4=−G 1,⊗4=1(3)闭环传递函数C/R 为C =G 1G 2+G 1+G 2−G 1=G 1G 2+G 2R 1+G 1G 2+2G 11+G 1G 2+2G 12-6解:用梅逊公式求,有两个回路,且接触,可得⊗=1−∑La=1+G 1G 2G 3+G 2,可得C (s )=G 1G 2G 3+G 2G 3C (s )=C (s )/R (s )R (s )1+G 1G 2G 3+G 2N 1(s )(1+G 2)G 3C (s )=−1⋅(1+G 1G 2G 3+G 2)=−1C (s )=N 2(s )1+G 1G 2G 3+G 21+G 1G 2G 3+G 2N 3(s )E (s )=1+G 2−G 2G 3E (s )=−C (s )=−G 2G 3−G 1G 2G 3R (s )1+G 1G 2G 3+G 2N 1(s )N 1(s )1+G 1G 2G 3+G 2E (s )=−C (s )−(1+G 2)G 3E (s )=−C (s )==1N 2(s )N 2(s )1+G 1G 2G 3+G 2N 3(s )N 3(s )第三章习题103-1解:(原书改为G (s )=)0.2s +1采用K 0,K H 负反馈方法的闭环传递函数为10K 0⎫(s )=C (s )=K G (s )1+10K H =R (s )01+G (s )K 0.2s +1H1+10K H要使过渡时间减小到原来的0.1倍,要保证总的放大系数不变,则:(原放大系数为10,时间常数为0.2)10K 0⎧=10⎧K =10⎪0⎨1+10K ⇒⎨H⎩K =0.9⎪H 1+10K =10⎩H3-2解:系统为欠阻尼二阶系统(书上改为“单位负反馈……”,“已知系统开环传递函数”)⎛%=e −⎩/1−⎩⋅100%=1.3−1⋅100%21t p ==0.11−⎩2⎤n解得:⎤=33.71n⎩=0.358所以,开环传递函数为:113647.1G(s)==s(s+24.1)s(0.041s+1) 3-3解:(1)K=10s−1时:100G(s)=s2+10s⎤2=100n2⎩⎤=10n解得:⎤n=10,⎩=0.5,⎛%=16.3%,t p=0.363(2)K=20s−1时:200G(s)=s2+10s⎤2=200n2⎩⎤=10n解得:⎤n=14.14,⎩=0.354,⎛%=30%,t p=0.238结论,K增大,超调增加,峰值时间减小。
3-4解:(1)a.⎩=0.1,⎤=5s−1时,n2⎛%=e−⎩/1−⎩⋅100%=72.8%3.5t==7ss⎩⎤nb.⎩=0.1,⎤=10s−1时,n2⎛%=e−⎩/1−⎩⋅100%=72.8%3.5t==3.5ss⎩⎤nc.⎩=0.1,⎤=1s−1时,n2⎛%=e−⎩/1−⎩⋅100%=72.8%3.5t==35ss⎩⎤n⎩=0.5,⎤=5s−1时,(2)n2⎛%=e−⎩/1−⎩⋅100%=16.3%3.5t==1.4ss⎩⎤n(3)讨论系统参数:⎩不变,⎛%不变;⎩不变,⎤n增加,则t s减小;⎤n不变,⎩增加,则⎛%减小,t s减小3-5解:(1)(a)用劳思判据s3 s2 s1 s012041009100系统稳定。
(b)用古尔维茨判据20 1100 9D1=20,D2==8020 1 0100920100D3==8000系统稳定。
(2)(a)用劳思判据s4 s3 s2 s1 s03104.7−3.2553252102系统不稳定。
(b)用古尔维茨判据1015100101D 1=10,D 2==47,D =532=−1533031(其实D 4不必计算,因为D 3<0)1015103021503000D 4==−30602系统不稳定。
3-6解:(1)系统闭环特征方程为0.2S 3+0.8S 2−s +K =0劳思表s 3s 2s 1s 00.2−10.8K −K −14K若系统稳定,则:−K−1>0,K >0。
无解4(2)系统闭环特征方程为0.2S 3+0.8S 2+(K −1)s +K =0劳思表s 3s 2s 1s 0K −1K0.20.83K −14K3若系统稳定,则:K −1>0,K >044解得K >33-7解:10(s +1)(a)系统传递函数:s 3+21s 2+10s +10劳斯表:s3 s2 s1 s0121200/21 101010系统稳定。
