实验3 Matlab 符号运算及求函数极值-推荐下载
matlab函数求极限

matlab函数求极限使用Matlab函数求极限极限是数学中的一个重要概念,它描述了函数在某个点无限接近某个值的情况。
求解极限可以帮助我们理解函数的性质和行为,对于数学建模和问题求解也具有重要意义。
在Matlab中,我们可以利用一些函数来求解极限,本文将介绍一些常用的方法和技巧。
一、符号计算工具箱Matlab中的符号计算工具箱(Symbolic Math Toolbox)提供了一系列函数,可以用于进行符号计算和代数运算。
在求解极限时,可以使用其中的limit函数。
limit函数的调用格式为:limit(f, x, a)其中,f是要求极限的函数,x是自变量,a是自变量趋近的点。
通过调用limit函数,我们可以得到函数f在x趋近于a时的极限值。
例如,我们要求函数f(x) = sin(x)/x 在x趋近于0时的极限。
可以使用以下代码:syms xf = sin(x)/x;limit(f, x, 0)运行以上代码,可以得到极限值为1。
这是由于当x趋近于0时,sin(x)/x的值趋近于1。
二、数值计算工具箱除了符号计算工具箱,Matlab还提供了数值计算工具箱(Numerical Computing Toolbox),可以进行数值计算和数值优化。
在求解极限时,我们可以利用数值计算工具箱中的一些函数来进行近似计算。
例如,我们要求函数f(x) = (1+x)^(1/x) 在x趋近于0时的极限。
由于这个函数在x趋近于0时的极限不存在,我们可以通过数值计算来逼近这个极限值。
可以使用以下代码:x = linspace(-1, 1, 1000);f = (1+x).^(1./x);limit_value = f(end)运行以上代码,可以得到极限值为2.7183。
这是通过将x取一个足够小的范围,并计算函数在该范围内的取值来进行近似计算得到的。
三、图形方法除了数值计算,我们还可以利用图形方法来求解极限。
在Matlab中,可以使用plot函数绘制函数的图像,并观察函数在某个点附近的行为。
matlab 实验3 函数的极值以及符号表达式的计算
实验3 函数的极值以及符号表达式的计算一、实验目的1、求函数的极值;2、符号表达式的分解、展开与化简;3、求符号表达式的极限;4、级数的求和与泰勒级数展开。
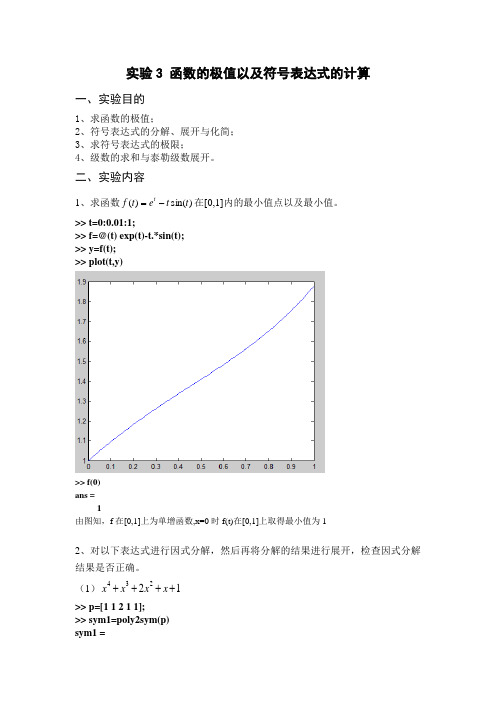
二、实验内容1、求函数)sin()(t t e t f t -=在[0,1]内的最小值点以及最小值。
>> t=0:0.01:1;>> f=@(t) exp(t)-t.*sin(t);>> y=f(t); >> plot(t,y)>> f(0)ans =1由图知,f 在[0,1]上为单增函数,x=0时f(t)在[0,1]上取得最小值为12、对以下表达式进行因式分解,然后再将分解的结果进行展开,检查因式分解结果是否正确。
(1)12234++++x x x x>> p=[1 1 2 1 1];>> sym1=poly2sym(p)sym1 =x^4 + x^3 + 2*x^2 + x + 1>> sym2=factor(sym1)sym2 =(x^2 + 1)*(x^2 + x + 1)>> sym3=expand(sym2)sym3 =x^4 + x^3 + 2*x^2 + x + 1(2)6555234-++-x x x x>> p=[1 -5 5 5 -6];>> sym1=poly2sym(p)sym1 =x^4 - 5*x^3 + 5*x^2 + 5*x - 6>> sym2=factor(sym1)sym2 =(x - 1)*(x - 2)*(x - 3)*(x + 1)>> sym3=expand(sym2)sym3 =x^4 - 5*x^3 + 5*x^2 + 5*x – 63、对以下表达式进行化简。
(1)123842+++x x x >> syms x>> y=(4*x.^2+8*x+3)/(2*x+1); >> simple(y)ans =2*x + 3(2)x x 22sin cos 2->> syms x>> y=2*cos(x).^2-sin(x).^2y =2*cos(x)^2 - sin(x)^2>> simple(y)ans =2 - 3*sin(x)^24、求下列函数的极限。
高等数学:MATLAB实验

MATLAB实验
2.fplot绘图命令 fplot绘图命令专门用于绘制一元函数曲线,格式为:
fplot('fun',[a,b]) 用于绘制区间[a,b]上的函数y=fun的图像.
MATLAB实验 【实验内容】
MATLAB实验
由此可知,函数在点x=3处的二阶导数为6,所以f(3)=3为 极小值;函数在点x= 1处的二阶导数为-6,所以f(1)=7为极大值.
MATLAB实验
例12-10 假设某种商品的需求量q 是单价p(单位:元)的函 数q=12000-80p,商 品的总成本C 是需求量q 的函数 C=25000+50q.每单位商品需要纳税2元,试求使销售 利润达 到最大的商品单价和最大利润额.
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验 实验九 用 MATLAB求解二重积分
【实验目的】 熟悉LAB中的int命令,会用int命令求解简单的二重积分.
MATLAB实验
【实验M步A骤T】 由于二重积分可以化成二次积分来进行计算,因此只要
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
实验七 应用 MATLAB绘制三维曲线图
【实验目的】 (1)熟悉 MATLAB软件的绘图功能; (2)熟悉常见空间曲线的作图方法.
【实验要求】 (1)掌握 MATLAB中绘图命令plot3和 mesh的使用; (2)会用plot3和 mesh函数绘制出某区间的三维曲线,线型
实验3Matlab符号运算及求函数极值

实验3 Matlab 符号运算及求函数极值一、实验目的和要求掌握用Matlab软件进行符号运算以及求函数的极值。
二、实验环境Windows系列操作系统,Matlab软件。
三、实验内容1.用MATLAB进行符号运算;2.编程求函数的极值。
四、实验步骤1.开启软件平台——Matlab,开启Matlab编辑窗口;2.根据求解步骤编写M文件;3.保存文件并运行;4.观察运行结果(数值或图形);5.根据观察到的结果和体会写出实验报告。
五、示例1.计算一元函数的极值例1求223441x xyx x++=++的极值解首先建立函数关系:s yms xy=(3*x^2+4*x+4)/( x^2+x+1); 然后求函数的驻点:dy=diff(y);xz=solve(dy)xz=[0] [-2]知道函数有两个驻点x1=0和x2=-2,接下来我们通过考察函数的图形,则它的极值情况和许多其它特性是一目了然的。
而借助MATLAB的作图功能,我们很容易做到这一点。
例2 画出上例中函数的图形解 syms xy=(3*x^2+4*x+4)/( x^2+x+1); 得到如下图形ezplot(y)2.计算二元函数的极值MATLAB 中主要用diff 求函数的偏导数,用jacobian 求Jacobian 矩阵。
diff(f,x,n) 求函数f 关于自变量x 的n 阶导数。
jacobian(f,x) 求向量函数f 关于自变量x(x 也为向量)的jacobian 矩阵。
例1 求函数42823z x xy y =-+-的极值点和极值.首先用diff 命令求z 关于x,y 的偏导数>>clear; syms x y;>>z=x^4-8*x*y+2*y^2-3;>>diff(z,x)>>diff(z,y)结果为ans =4*x^3-8*yans =-8*x+4*y即348,84z z x y x y x y∂∂=-=-+∂∂再求解方程,求得各驻点的坐标。
Matlab求解方程和函数极值

Matlab求解方程和函数极值一.线性方程组求解1.直接解法①利用左除运算符的直接解法对于线性方程组Ax=b,可以利用左除运算符“\”求解:x=A\b例用直接解法求解下列线性方程组。
命令如下:A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';x=A\b②利用矩阵的分解求解线性方程组矩阵分解是指根据一定的原理用某种算法将一个矩阵分解成若干个矩阵的乘积。
常见的矩阵分解有LU分解、QR分解、Cholesky分解,以及Schur分解、Hessenberg分解、奇异分解等。
(1) LU分解矩阵的LU分解就是将一个矩阵表示为一个交换下三角矩阵和一个上三角矩阵的乘积形式。
线性代数中已经证明,只要方阵A是非奇异的,LU分解总是可以进行的。
MATLAB提供的lu函数用于对矩阵进行LU分解,其调用格式为:[L,U]=lu(X):产生一个上三角阵U和一个变换形式的下三角阵L(行交换),使之满足X=LU。
注意,这里的矩阵X必须是方阵。
[L,U,P]=lu(X):产生一个上三角阵U和一个下三角阵L以及一个置换矩阵P,使之满足PX=LU。
当然矩阵X同样必须是方阵。
实现LU分解后,线性方程组Ax=b的解x=U\(L\b)或x=U\(L\Pb),这样可以大大提高运算速度。
例用LU分解求解例7-1中的线性方程组。
命令如下:A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';[L,U]=lu(A);x=U\(L\b)或采用LU分解的第2种格式,命令如下:[L,U ,P]=lu(A);x=U\(L\P*b)(2) QR分解对矩阵X进行QR分解,就是把X分解为一个正交矩阵Q和一个上三角矩阵R的乘积形式。
QR分解只能对方阵进行。
MATLAB的函数qr可用于对矩阵进行QR分解,其调用格式为:[Q,R]=qr(X):产生一个一个正交矩阵Q和一个上三角矩阵R,使之满足X=QR。
用MATLAB求极值

用MATLAB求极值灵活的运用MATLAB的计算功能,可以很容易地求得函数的极值。
例3.6.1 求223441x xyx x++=++的极值解首先建立函数关系:s yms sy=(3*x^2+4*x+4)/( x^2+x+1); ↙然后求函数的驻点:dy=diff(y); ↙xz=solve(dy) ↙xz=[0] [-2]知道函数有两个驻点x1=0和x2=-2,考察函数在驻点处二阶导数的正负情况:d2y=diff(y,2); ↙z1=limit(d2y,x,0) ↙z1=-2z2=limit(d2y,x,-2) ↙z2=2/9于是知在x1=0处二阶导数的值为z1=-2,小于0,函数有极大值;在x2=-2处二阶导数的值为z2=2/9,大于0,函数有极小值。
如果需要,可顺便求出极值点处的函数值:y1=limit(y,x,0) ↙y1=4y2=limit(y,x,-2) ↙y2=8/3事实上,如果知道了一个函数的图形,则它的极值情况和许多其它特性是一目了然的。
而借助MA TLAB的作图功能,我们很容易做到这一点。
例3.6.2画出上例中函数的图形解syms x ↙y=(3*x^2+4*x+4)/( x^2+x+1); ↙得到如下图形ezplot(y) ↙如何用MATLAB求函数的极值点和最大值比如说y=x^3+x^2+1,怎样用matlab来算它的极值和最大值?求极值:syms x y>> y=x^3+x^2+1>> diff(y) %求导ans =3*x^2 + 2*x>> solve(ans)%求导函数为零的点ans =-2/3极值有两点。
求最大值,既求-y的最小值:>> f=@(x)(-x^3-x^2-1)f = @(x)(-x^3-x^2-1)>> x=fminunc(f,-3,3)% 在-3;-3范围内找Warning: Gradient must be provided for trust-region method;using line-search method instead.> In fminunc at 354Optimization terminated: relative infinity-norm of gradient less than options.TolFun.x =-0.6667>> f(x)ans =-1.1481在规定范围内的最大值是1.1481由于函数的局限性,求出的极值可能是局部最小(大)值。
MATLAB求函数零点与极值
MATLAB求函数零点与极值
1. roots函数
针对多项式求零点(详见MATLAB多项式及多项式拟合)
2. fzero函数
返回⼀元函数在某个区间内的的零点.
x0 = fzero(@(x)x.^2-3*x-4,[1,5]);
只能求区间⾥⾯的⼀个零点,并且要求在给定区间端点函数值异号,所以使⽤之前应该先作图,得出单个零点分布的区间,然后使⽤该函数求零点.若有多个零点,则需多次使⽤该函数.
如需求上例中的全部零点,先作图
fplot(@(x)x.^2-3*x-4,[-10,10]);
得知两个零点的分布区间,然后两次使⽤fzero函数求对应区间的零点.
x1 = fzero(@(x)x.^2-3*x-4,[-2,0]);
x2 = fzero(@(x)x.^2-3*x-4,[2,6]);
3. solve函数
求⼀元函数(⽅程)的零点.
x0 = solve('x^2-3*x-4=0','x');
注意⽅程需包含’=0’部分,另外,不建议直接将⽅程写在函数solve的参数部分,可以⽤符号运算的⽅法.
4. fminbnd函数
求⼀元函数在某个区间内的最⼩值和对应的最⼩值点.
[x0,fmin]=fminbnd(@(x)x+1/(x+1),-0.5,2);
求极值与极值点之前须估计极值点的区间,保证在该区间没有使得函数值趋于⽆穷的点.。
实验三 用matlab求极限和导数
实验三 用matlab 求极限和导数1.求极限、导数的MATLAB 命令MATLAB 中主要用limit,diff 分别求函数的极限与导数。
可以用help limit, help diff 查阅有关这些命令的详细信息例1首先分别作出函数x y 1cos=在区[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=cos(1./x); plot(x,y) 结果如图2.1图2.1函数x y 1cos=的图形根据图形,能否判断出极限x x x x 1sinlim ,1cos lim 00→→的存在性? 当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:>>clear;>>syms x; %说明x 为符号变量>>limit(sin(1/x),x,0)结果为ans = -1 .. 1,即极限值在-1,1之间,而极限如果存在则必唯一,故极限x x 1sinlim 0→不存在,同样,极限x x 1coslim 0→也不存在。
例2 首先分别作出函数x xy sin =在区间[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=sin(x)./x; plot(x,y) 结果如图2.2图2.2 函数x xy sin =的图形根据图形,能否判断出极限1sin lim0=→x xx 的正确性?当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:>>clear; >>syms x;>>limit(sin(x)/x,x,0) 结果为ans =1.例3 观测当n 趋于无穷大时,数列n n n a )11(+=和1)11(++=n n n A 的变化趋势。
Matlab求解方程和函数极值.docx
Mat lab求解方程和函数极值The fifth chapter, 22010-03-31 22:50Two. Matlab for solving equations and function extremumI. solving linear equations1. direct solutionThe direct solution to the use of the left division operatorFor linear equations Ax=b, we can use the left division operator to solve: X=A\bFor example, the following linear equations are solved by direct solution. The commands are as follows:A=[2, 1, -5, 1; 1; -5,0,7; 0,2, 1; -1; 1,6; -1; —4];B=[13, -9,6,0],;X=A\bSolving linear equations by the decomposition of matrixMatrix decomposition is the product of decomposing a matrix into several matrices according to certain principles・ Common matrix decomposition includes LU decomposition, QR decomposition, Cholesky decomposition, and Schur decomposition, Hessenberg decomposition, singular decomposition,and so on.(1)LU decompositionThe LU decomposition of a matrix means that a matrix is expressed as a product of a commutative lower triangular matrix and an upper triangular matrix・Linear algebra has proved that LU decomposition is always possible as long as the square A is nonsingular・\IATLAB provides the Lu function for LU decomposition of the matrix, the call format for:[L, U]二lu (X): produces an upper triangular array U and a transform form of lower triangular array L (row exchange) to satisfy X二LU. Note that the matrix X here must be square・[L, U, P]二lu (X): produces an upper triangular array U and a lower triangular matrix L, and a permutation matrix P, which satisfies PX=LU ・ Of course, the matrix X must also be square・After the LU decomposition, the solution of the linear equations Ax二b (L\b) or x二U\ (L\Pb), which can greatly improve the speed of operation x二U\・For example, LU is used to solve the linear equations in example 7-1. The commands are as follows:A二[2,1, -5, 1; 1; -5,0,7; 0,2, 1; T; 1,6; -1; -4];B二[13, -9, 6,0]';[L, U]二lu (A);X二U\ (L\b)Or using LU decomposition of the second formats, as follows:[L, U, P]二lu (A);X二U\ (L\P*b)(2)QR decompositionQR decomposition of the matrix X, is the decomposition of X into an orthogonal matrix Q and an upper triangular matrix R product form. QR decomposition can only be carried out by the opponent,s array. MATLAB function QR can be used for QR decomposition of the matrix, the call format for:[Q, R]=qr (X): produces an orthogonal matrix Q and an upper triangular matrix R so that it satisfies X二QR・[Q, R, E]=qr (X): produce an orthogonal matrix Q, an upper triangular matrix, R, and a permutation matrix E, so that it satisfies XE二QR.After the QR decomposition, the solution of the linear equation Ax二b is x二R\ (Q\b) or x二E (R\ (Q\b))・For example, QR is used to solve the linear equations in example 7-1.The commands are as follows:A二[2,1, -5, 1; 1; -5,0,7; 0,2, 1; T; 1,6; -1; -4];B二[13, -9, 6,0]';[Q, R]二qr (A);X二R\ (Q\b)Or using QR decomposition of the second formats, as follows:[Q, R, E] =qr (A):X二E* (R\ (Q\b))(3)Cholesky decompositionIf the matrix X is symmetric and positive definite, the Cholesky decomposition decomposes the matrix X into the product of a lower triangular matrix and upper triangular matrix・ Set the triangle matrix to R,Then the lower triangular matrix is transposed, that is, X二R' R・ The MATLAB function Choi (X) is used for Cholesky decompositionof the matrix X, and its call format is:R二chol (X): produces an upper triangular array R that makes R'R二X ・If the X is an asymmetric positive definite, an error message is output ・[R, p]二chol (X): this command format will not output error messages・ When X is symmetric positive definite, then p二0 and R are the same as those obtained in the above format: otherwise, P is a positive integer ・If X is a full rank matrix, then R is an upper triangular matrix of order q=p-l and satisfies R'R二X (l:q, l:q)・After the Cholesky decomposition, the linear equation group Ax二b becomes R 'Rx二b, so x二R\ (R, \b ')・Example 4 decomposes the system of linear equations in example 7-1 by Cholesky decomposition.The commands are as follows:A二[2,1, -5, 1; 1; -5, 0,7; 0,2, 1; T; 1,6; -1; -4];B 二[13, —9,6,0]';R二chol (A)Error using Chol =>???Matrix, must, be, positive, definiteWhen the command is executed, an error message appears indicating that the A is a non positive definite matrix・2. iteration methodIterative method is very suitable for solving large coefficient matrix equations・ In numerical analysis, the iterative methods mainly include Jacobi iterative method, Gauss-Serdel iterative method, over relaxationiterative method and two step iterative method・Jacobi iteration methodFor linear equations Ax二b, if A is a nonsingular square, that is, (i=l, 2,・・・(n), A can be decomposed into A 二D-L-U, where D is a diagonal matrix, and its elements are diagonal elements of A, L and U are lower triangular and upper triangular matrices of A, so Ax二b becomes・・:The corresponding iteration formula is:This is the Jacobi iteration formula・If the sequence converges to x, then x must be the solution of equation Ax二b・The MATLAB function file of the Jacobi iteration method Jacobi.m is as follows:Function, [y, n]二jacobi (A, B, xO, EPS)If nargin=3Eps=1.Oe-6;Elseif nargin〈3ErrorReturnEndD=diag (diag (A)) -% A diagonal matrixL=-tril (A, -1); the lower triangular array of% AU二-triu (A, 1); the upper triangular array of% AB二D\ (L+U);F二D\b;Y二B*xO+f:N二1;% iterationsWhile norm (y-xO) 〉=epsXO二y;Y二B*xO+f:N二n+1;EndExample 5 uses the Jacobi iterative method to solve the following linear equations・The initial value of iteration is 0, and the iteration accuracy is 10-6・Call the function file "Jacobi.nT in the command. The command is as follows:A二[10, -1,0; -1, 10; -2; 0; -2, 10];B二[9, 7,6]';[x, n]二jacobi (A, B, [0,0,0]', 1. Oe-6)Gauss-Serdel iteration methodIn the Jacobi iteration process, the calculations have been obtained and need not be reused, i.e., the original iterative formula Dx (k+1)二(L+U) x (k) +b can be improved to Dx (k+1) 二Lx (k+1) +Ux (k) +b and thus obtained:X (k+1)二(D-L) -lUx (k) + (D-L) TbThis formula is the Gauss-Serdel iterative formula・ Compared with the Jacobi iteration,The Gauss-Serdel iteration replaces the old components with new ones, with higher accuracy・The MATLAB function f订e of the Gauss-Serdel iteration method gauseidel.m is as follows:Function, [y, n]=gauseidel (A, B, xO, EPS)If nargin=3Eps二1. 0e-6;Elseif nargin<3ErrorReturnEndD=diag (diag (A)) -% A diagonal matrixL=-tril (A, -1); the lower triangular array of% AU=-triu (A, 1); the upper triangular array of% AG二(D-L) \U;F二(D-L) \b;Y二G*xO+f;N=l;% iterationsWhile norm (y-xO) >=epsXO二y;Y二G*xO+f:N二n+1;EndExample 6 uses the Gauss-Serdel iterative method to solve the followinglinear equations・The initial value of iteration is 0, and the iteration accuracy is 10-6・Call the function file z,gauseidel.m" in the command. The command is as follows:A二[10, -1,0; -1, 10; -2; 0; -2, 10];B二[9, 7,6]';[x, n]二gauseidel (A, B, [0,0,0]', 1.0e~6)Example 7, Jacobi iteration and Gauss-Serdel iteration method are used to solve the following linear equations, to see whether convergence・The commands are as follows:A二[1,2, -2; 1, 1, 1; 2, 2,11;B二[9; 7; 6];[x, n]=jacobi (a, B, [0; 0; 0])[x, n]=gauseidel (a, B, [0; 0; 0])Two. Numerical solution of nonlinear equations1 solving the single variable nonlinear equationIn MATLAB, a fzero function is provided that can be used to find the roots of a single variable nonlinear equation. The call format of this functionis: z二fzero ('fname', xO, tol, trace)Where fname is the root to be a function of the file name, xO as the search starting point・ A function may have more than one root, but the fzero function only gives the root nearest to the x0・ The relative accuracy of the TOL control results, by default, take tol二eps, trace, specify whether the iteration information is displayed in the operation, and when 1 is displayed, 0 is not displayed, and the trace=0 is taken by default・Example 8 ask for roots in the neighborhood.Steps are as follows:(1) establishment of function file funx・m.Function fx二funx (x)Fx二xTO. x+2;(2) fzero function call root.Z=fzero (' funx', 0. 5)二ZZero point three seven five eight2. solving nonlinear equationsFor nonlinear equations F (X) =0, the numerical solution is obtained by using the fsolve function. The call format of the fsolve function is:X二fsolve (' fun,, X0, option)Where X is the return of the solution, fun is used to define the demand for solutions of nonlinear equations function of the file name, X0 is the initial rooting process, option optimization toolbox options・ The Optimization Toolbox provides more than 20 options that users can display using the optimset command・If you want to change one of the options, you can call the optimset () function to complete it. For example, Display display option decision function calls intermediate results, in eluding 〃off〃does not show, 〃ITER〃said each show,'final5 shows only the final results・ Optimset ('Display', 'off') will set the Display option to 'off'.Example 9 find the numerical solution of the following nonlinear equations in (0.5,0.5) neighborhood・(1)establishment of function file myfun. m.Function q=myfun (P)X二p (1);Y二p (2);Q (1) =x-0・6*sin (x) -0.3*cos (Y);Q (2)二y-0・6*cos (x) +0. 3*sin (Y);(2)under the given initial value x0=0・5 and y0=0・5, call the fsolve function to find the root of the equation.X二fsolve C myfun,, [0.5,0. 5]', optimset ('Display'off'))二xZero point six three five fourZero point three seven three fourThe solution is returned to the original equation, and it can be checked whether the result is correct or not:Q二myfun (x)1.0e-009 *0. 2375, 0. 2957We can see the result of higher precision.Three・ Numerical solution of initial value problems for ordinary differential equations1. introduction of Runge Kutta method2., the realization of Runge Kutta methodBased on Runge Kutta method, MATLAB provides the function of finding numerical solutions of ordinary differential equations:[t, y]二ode23 C fname,, tspan, Y0)[t, y]二ode45 C fname,, tspan, Y0)Where fname is the function file name that defines f (T, y), and the function file must return a column vector・ The tspan form is [tO, tf], which represents the solution interva. 1. Y0 is the initial state column vector ・ The time vectors and corresponding state vectors are given by T and Y respectively.Example 10 has an initial value problem,Try to find the numerical solution and compare it with the exact solution (the exact solution is y (T)二).(1)establishment of function file funt. m.Function yp二funt (T, y)Yp= (y"2-t-2) /4/ (t+1);(2)solving differential equations・TOO; tf二10;¥0=2;[t, y]=ode23 ('funt', [tO, tf], Y0) ;% for numerical solutionYl=sqrt (t+1) +1;% refinement; exact solutionPlot (T, y, 'B・',t, Yl, ?)% are compared by graphThe numerical solution is represented by a blue dot, and the exact solution is expressed in red solid lines・ As shown. It can be seen that the two results approximate・ CloseFour. Function extremumMATLAB provides functions based on the simplex algorithm for solving extremal functions Fmin and fmins, which are used respectively for minimum values of univariate functions and multivariate functions:X二fmin (' fname,, xl, x2)X二fmins (' fname' , xO)The call formats of the two functions are similar・ Among them, the Fmin function is used to find the minimum point of a single variable function. Fname is the object function name that is minimized, and XI and X2 limit the range of arguments・ The fmins function is used to find the minimum point of a multivariable function, and xO is the initial value vector of the solution.MATLAB provides no special function to find the maximum function, but as long as the attention to -f (x) in the interval (a, b) is the minimum value of F (x) in (a, b) of the maximum value, so Fmin (F, xl, x2) f (x) function in the interval (xl the maximum value, X2)・Example 13 asks in [0,Minimum point in 5]・(1)establishment of function file mymin. m.Function fx二mymin (x)Fx=x.八3-2*x-5;(2)call the Fmin function to find the minimum point・Zero point eight one six fiveThree・Matlab numerical integration and differentiationI. numerical integration1.basic principles of numerical integrationNumerical methods for solving definite integration are various, such as simple trapezoidal method, Xin Pusheng (Simpson) method, Newton Cortes (Newton-Cotes) method, etc・,are often used・Their basic idea is to divide the whole integral interval [a and b] into n sub intervals [[, ], i=l, 2],・・・ N, in which,・ In this way, the problem of determining integral is decomposed into summation problem・2.realization method of numerical integrationVariable step symplectic methodBased on the variable step long Xin Pusheng method, MATLAB gives the quad function to find the definite integra 1. The call format of this function is:[I, n]二quad ('fname', a, B, tol, trace)Where fname is the product function name・A and B are the lower bound and upper bound of the definite integra 1. TOL is used to control the integration accuracy, and the tol=0.001 is taken by default・ Does the trace control show the integration process? If you take the non 0, it will show the integral process, take 0 instead of the default, and take the trace=0 bydefault・ Returns the parameter I, the fixed integral value, and the call number of n for the integrand・Finding definite integral(1)establish the integrand function file fesin.m.Function f二fesin (x)F二exp (一0.5*x)・ *sin (x+pi/6);(2)call the numerical integral function quad to find the definite integra1.[S, n]二quad ('fesin', 0, 3*pi)二SZero point nine Zero Zero eight二nSeventy-sevenThe Newton Cotes methodNewton Cotes method based on MATLAB, gives the quad8 function to find the definite integra 1. The call format of this functionis: [I, n]=quad8 C fname,, a, B, tol, trace)The meaning of the parameter is similar to that of the quad function, but only the default value of the tol. The function can more accurately calculate the value of the definite integral, and in general, the number of steps of the function call is less than the quad function, thus ensuring the higher efficiency to find the required integral value・Finding definite integral(1)the integrand function file fx. m・Function f二fx (x)F二x. *sin (x) / (1+cos (x)・*cos (x));(2)call the function quad8 to find the definite integral.I二quad8 (' fx' , 0, PI)二ITwo point four six seven fourExample 3 uses the quad function and the quad8 function respectively to find the approximate value of the integral, and compares the number of calls of the function under the same integral accuracy.Call the function quad to find the definite integral:Format long;Fx二inline ('exp (-x));[I, n]二quad ('FX', 1,2. 5, le-10)二IZero point two eight five seven nine four four four two fivefour seven six six二nSixty-fiveCall the function quad8 to find the definite integral:Format long;Fx二inline ('exp (-x));[I, n] =quad8 (FX, 1,2. 5, le-10)二IZero point two eight five seven nine four four four two fivefour seven five fourThirty-threeThe integrand is defined by a tableIn MATLAB, the problem of determining the function relations defined in tabular form is called trapz (X, Y) functions. The vector X, Y defines the function relation Y二f (X).Example 8-4 calculates definite integral with trapz function.The commands are as follows:X=l:0. 01:2.5:Y二exp (-X);% generated function relational data vectorTrapz (X, Y)二ansZero point two eight five seven nine six eight two four one six three nine threeNumerical solution of 3. double definite integralConsider the following double definite integral problem:By using the dblquad function provided by MATLAB, the numerical solution of the above double definite integral can be obtaineddirectly. The call format of this function is:I=dblquad (F, a, B, C, D, tol, trace)The function asks f (x, y) to double definite integral on the [a, b] * [c, d] regions・The parameter tol, trace is used exactly the same as function quad・Example 8~5 calculates the double definite integral(1)build a function file fxy.m:Function f二fxy (x, y)Global ki;Ki=ki+1:%ki is used to count the number of calls to the integrandF二exp (-x.八2/2). *sin (x. 2+y);(2)call the dblquad function to solve・Global ki; ki二0;I二dblquad (' fxy' , -2, 2, -1, 1)Ki1.57449318974494 (data format related)二kiOne thousand and thirty-eightTwo. Numerical differentiation1numerical difference and difference quotient2the realization of numerical differentiationIn MATLAB, there is no function that provides direct numerical derivatives・ Only the function diff, which calculates the forward difference, is called:DX二diff (X) : calculates the forward difference of vector X, DX (I), =X (i+1), -X (I), i二1,2,・・.N-l.DX二diff (X, n) : calculates the forward difference of the n order of X. For example, diff (X, 2)二diff (diff (X)).DX二diff (A, N, dim): calculates the n order difference of the matrix A, the dim=l (default state), calculates the difference by column, and dim=2 calculates the difference by line・6 cases of Vandermonde matrix generation based on vectorV= [ 1, 2, 3, 4, 5, 6], according to the column difference operation. The commands are as follows:V=vander (1:6)DV二diff (V)% calculates the first order difference of V 二V111111321684212438127931102425664164131256251252551777612962163661二DV31157310211 65 19 5 1 0781 175 37 7 1 02101 369 61 9 1 04651 671 91 11 1 0用不同的方法求函数f(X)的数值导数,并在同一个坐标系中做出f (X)的图像。
matlab计算函数最大值及最小值
matlab计算函数最大值及最小值在MATLAB中,有几种方法可以计算一个函数的最大值和最小值。
下面将介绍几种常用的方法。
1.通过绘制函数图像找到最大值和最小值:首先,可以通过绘制函数图像来观察函数的最大值和最小值所在的位置。
可以使用plot函数来绘制函数的图像。
例如,我们想计算函数y=x^3-2x的最大值和最小值:```x=-10:0.1:10;y=x.^3-2*x;plot(x, y)```通过观察图像,可以确定函数的最大值和最小值的位置。
2. 使用fminbnd函数找到函数的最小值:MATLAB中的fminbnd函数可以用于寻找函数的最小值。
该函数使用了黄金分割算法。
例如,我们想计算函数y=x^3-2x的最小值:```[x, y] = fminbnd(f, -10, 10);```这段代码将返回函数的最小值y以及对应的x值。
3. 使用fmincon函数找到函数的最小值(约束最优化):如果函数有特定的约束条件,可以使用fmincon函数来计算函数的最小值。
fmincon函数基于无约束的最优化算法,并添加了约束条件。
例如,我们想计算函数y=x^2的最小值,但限制x的范围在0到1之间:```x0=0.5;%初始解A=[];b=[];Aeq = [];beq = [];lb = 0; % x的下限ub = 1; % x的上限[x, y] = fmincon(f, x0, A, b, Aeq, beq, lb, ub);```这段代码将返回函数的最小值y以及对应的x值。
4. 使用max和min函数找到向量或矩阵的最大值和最小值:如果需要计算向量或矩阵的最大值和最小值,可以使用MATLAB中的max和min函数。
例如,计算向量x=[1,2,3,4,5]的最大值和最小值:```x=[1,2,3,4,5];max_value = max(x);min_value = min(x);```这段代码将返回向量x的最大值和最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验3 Matlab 符号运算及求函数极值
一、实验目的和要求掌握用Matlab 软件进行符号运算以及求函数的极值。
二、实验环境Windows 系列操作系统,Matlab 软件。
三、实验内容1.用MATLAB 进行符号运算; 2.编程求函数的极值。
四、实验步骤1.
开启软件平台——Matlab ,开启Matlab 编辑窗口; 2.
根据求解步骤编写M 文件; 3.
保存文件并运行; 4.
观察运行结果(数值或图形); 5.
根据观察到的结果和体会写出实验报告。
五、示例1.计算一元函数的极值
例1 求的极值223441x x y x x ++=++解 首先建立函数关系:
s yms x
y=(3*x^2+4*x+4)/( x^2+x+1);
然后求函数的驻点:
dy=diff(y);
xz=solve(dy)
xz=
[0] [-2]
知道函数有两个驻点x =0和x =-2,12接下来我们通过考察函数的图形,则它的极值情况和许多其它特性是一目了然的。
而借助MATLAB 的作图功能,我们很容易做到这一点。
例2 画出上例中函数的图形
解 syms x y=(3*x^2+4*x+4)/( x^2+x+1); 得到如下图形ezplot(y)
2.计算二元函数的极值MATLAB 中主要用diff 求函数的偏导数,用jacobian 求Jacobian 矩阵。
diff(f,x,n) 求函数f 关于自变量x 的n 阶导数。
jacobian(f,x) 求向量函数f 关于自变量x(x 也为向量)的jacobian 矩阵。
可以用help diff, help jacobian 查阅有关这些命令的详细信息例1 求函数的极值点和极值.42823z x xy y =-+-首先用diff 命令求z 关于x,y 的偏导数>>clear; syms x y;>>z=x^4-8*x*y+2*y^2-3;>>diff(z,x)>>diff(z,y)结果为ans =4*x^3-8*y ans =-8*x+4*y 即再求解方程,求得各驻点的坐标。
一般方程组的符号解用348,84z z x y x y x y
∂∂=-=-+∂∂solve 命令,当方程组不存在符号解时,solve 将给出数值解。
求解方程的MATLAB 代码为:
>>clear;
>>[x,y]=solve('4*x^3-8*y=0','-8*x+4*y=0','x','y')
结果有三个驻点,分别是P(-2,-4),Q(0,0),R(2,4).
我们仍然通过画函数图形来观测极值点与鞍点。
>>clear;
>>x=-5:0.2:5; y=-5:0.2:5;
>>[X,Y]=meshgrid(x,y);
>>Z=X.^4-8*X.*Y+2*Y.^2-3;
>>mesh(X,Y,Z)
>>xlabel('x'),ylabel('y'),zlabel('z')
结果如图1
图1 函数曲面图
可见在图1中不容易观测极值点,这是因为z的取值范围为[-500,100],是一幅远景图,局部信息丢失较多,观测不到图像细节.可以通过画等值线来观测极值.
>>contour(X,Y,Z, 600)
>>xlabel('x'),ylabel('y')
结果如图2
图2 等值线图由图2可见,随着图形灰度的逐渐变浅,函数值逐渐减小,图形中有两个明显的极小值点和.根据提梯度与等高线之间的关系,梯度的方向是等高线的法方向,且指(2,4)P --(2,4)Q 向函数增加的方向.由此可知,极值点应该有等高线环绕,而点周围没有等高线环绕,不
(0,0)Q 是极值点,是鞍点.六、实验任务:1.求的极值,并画出函数图形。
12sin sin 33y x x =+2.求的极值,并对图形进行观测。
4441z x y xy =+-+七、 程序代码及运行结果(经调试后正确的源程序)1.
2.
八、实验总结
通过本节课让我学会了怎样计算一元函数的极值和二元函数的极值。
并知道了diff(f,x,n) 是求函数f关于自变量x的n 阶导数。
jacobian(f,x) 是求向量函数f关于自变量x(x也为向量)的jacobian矩阵。
