【材料力学课件】广义胡克定律.docx
材料学 胡克定律

l
b=50mm h=100mm
解: 梁为拉伸与弯曲的组合变形. A点有拉伸引起的正应力和弯曲 引起的切应力.
(拉伸) (负)
(1)A点处的主应变1, 2 , 3
A
x = 20
x = 30
(2)A点处的线应变 x , y , z
例题14 简支梁由18号工字钢制成. 其上作用有力F= 15kN, 已知
2.三向等值应力单元体的体积应变(The volumetric strain of triaxial-equal stress element body)
三个主应力为
m
单元体的体积应变
m
m
这两个单元体的体积应变相同 单元体的三个主应变为
2
1
dy
3
dz dx
m
m
m
如果变形前单元体的三个棱边成某种比例,由于三个棱边应 变相同,则变形后的三个棱边的长度仍保持这种比例. 所以在三向
因此,该圆筒变形后的厚度并无变化,仍然为 d =10mm .
例题13 已知矩形外伸梁受力F1,F2作用. 弹性模量E=200GPa,泊
松比m= 0.3, F1=100KN,F2=100KN. 求:(1)A点处的主应变 1,2 , 3 (2)A点处的线应变 x , y , z
F1
b
F2 A
F2 z
a
例题10 边长 a = 0.1m 的铜立方块,无间隙地放入体积较大,变形
可略去不计的钢凹槽中,如图所示. 已知铜的弹性模量E=100GPa,
泊松比μ=0.34,当受到F=300kN的均布压力作用时,求该铜块的主
应力,体积应变以及最大切应力.
解:铜块横截面上的压应力
Fa
13-2广义胡克定律与变形能-材料力学

1 m 形状改变
3 m
②形状改变比能:
证明在:
' 1
1
m
,
' 2
2
m
,
' 3
3
m
作用下,体积没有变化 。
3(1
2)
1'
' 2
' 3
E
3
1 2
E
(1'
' 2
' 3
)
1 2
E
[(1
m
)
(
2
1
该单元体所储存的应变
能为:
3
U
1 2
(
1e1
2
e
2
3e
3
)dxdydz
②比能:
u
U V
1 2
(
1e1
2e2
3e
3
)
③代入虎克定律:
u
1 2E
[12
2 2
2 3
2
(1
2
2
3
31
)]
(二)、体积改变比能 ut 与形状改变比能 u x
1.有关概念:
三、复杂应力状态下的变形比能 (一)、总应变比能
1.有关概念: ①应变能(变形能):伴随弹性体的变 形而储存在弹性体的能量。用U表示;
广义胡克定律、强度理论、组合变形

1 2 3
b
n
最大切应力理论(第三强度理论)
理论要点
引起材料屈服的主要因素-最大切应力 max
当 max s,单拉 时, 材料屈服
max
1
3
2
s,单拉
s 0 2
s
2
1 3 s -材料的屈服条件
强度条件
r,3 1 3 [ ]
1 , 3 - 构件危险点处的工作应力 - 材料单向拉伸时的许用应力
2
2 x
max min
CK
x
2
y
2
2 x
回顾 极值应力的方位
min
y
x
最大正应力方位:
max与min所在截面正交
tan2α0 = -
τx σx - σy
2
tan
0
x
x
min
x max
y
极值与 极值所在截面, 成 45 夹角
回顾 主平面与主应力 (类似单向应力状态)
2
min
2
xy x
min
所在方位切应变为零的正 应变-主应变
主应变位于互垂方位,
主应变表示:1 2 3
Cε
εx
+ 2
εy
,0
Rε =
εx
- εy 2
2
+
γ xy 2
2
广义胡克定律(三向应力状态)
因切应力不引起正应变, 故只考虑正应力引起的正应变之和
x
x
E
x
y
E
x
z
(适用于脆性材料) ❖ 最大拉应变理论 (第2强度理论)
屈服强度理论 最大切应力理论 (第3强度理论)
广义胡克定律
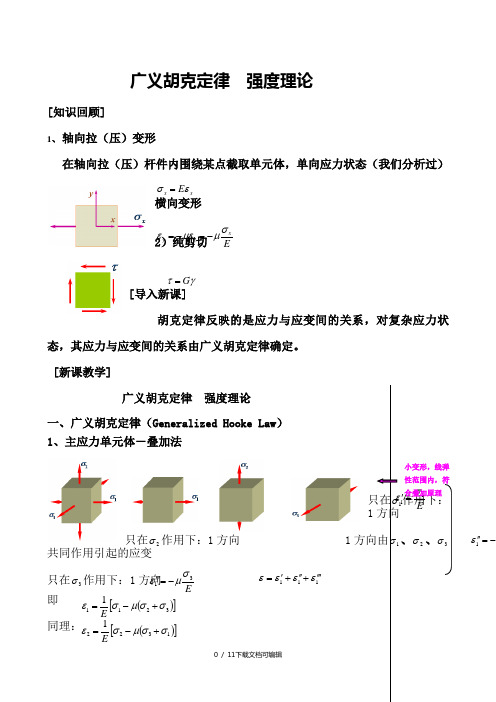
广义胡克定律 强度理论[知识回顾]1、 轴向拉(压)变形在轴向拉(压)杆件内围绕某点截取单元体,单向应力状态(我们分析过)横向变形2)纯剪切[导入新课]胡克定律反映的是应力与应变间的关系,对复杂应力状态,其应力与应变间的关系由广义胡克定律确定。
[新课教学]广义胡克定律 强度理论一、广义胡克定律(Generalized Hooke Law ) 1、主应力单元体-叠加法只在σ作用下:1方向只在2σ作用下:1方向 1方向由σ、2σ、3σ共同作用引起的应变只在3σ作用下:1方向 即同理: E11σ='1ε-=''E31σμε-='''111εεεε'''+''+'=()[]32111σσμσε+-=E()[]13221σσμσε+-=Exx E εσ=Exx y σμμεε-=-=γτG =小变形,线弹性范围内,符合叠加原理2、非主应力单元体 可以证明:对于各向同性材料,在小变形及线弹性范围内,线应变只与正应力有关,而与剪应力无关; 剪应变只与剪应力有关,而与正应力无关,满足应用叠加原理的条件。
3、体积应变 单元体,边长分别为dx 、dy 和dz 。
在三个互相垂直的面上有主应力1σ、2σ和3σ。
变形前单元体的体积为变形后,三个棱边的长度变为由于是单元体,变形后三个棱边仍互相垂直,所以,变形后的体积为dxdydz V )1)(1)(1(3211εεε+++=将上式展开,略去含二阶以上微量的各项,得 dxdydz V )1(3211εεε+++= 于是,单元体单位体积的改变为 3211εεεθ++=-=VVV θ称为体积应变(或体应变)。
它描述了构件内一点的体积变化程度。
5、体积应变与应力的关系将广义虎克定律(8-22)代入上式,得到以应力表示的体积应变()[]21331σσμσε+-=E[][][]⎪⎪⎪⎭⎪⎪⎪⎬⎫+-=+-=+-=)(1)(1)(1y x z z x z y y z y x x E E E σσμσεσσμσεσσμσε⎪⎪⎪⎭⎪⎪⎪⎬⎫===zx zx yz yz xy xy G G G τγτγτγ111dxdydzV =dz dz dz dydy dy dx dx dx )1()1()1(332211εεεεεε+=++=++=+K E m σσσσμθ=++⋅-==3)21(3321)(21321321σσσμεεεθ++-=++=E式中K 称为体积弹性模量,m σ是三个主应力的平均值。
秦飞编著《材料力学》 第9章 应力状态分析与广义胡克定律

秦飞 编著《材料力学》 第9章 应力状态分析与广义胡克定律 2
9.1 应力状态
(1)单元体与应力状态
应力是比较特殊的量(张量):
• 哪一点?
应力
要明确
• 在哪一个面上(面的方位)? • 面的哪个方向?
过一点不同方向面上应力的集合称为这一点的应力状态。 通常用包围该点的正六面体—单元体(element volume)的 各个面上的应力表示该点的应力状态。
α =60˚斜截面上的应力为
x y
2 x y
x y
2
cos 2 xy sin 2 16.3MPa
2
sin 2 xy cos 2 3.66MPa
25
秦飞 编著《材料力学》 第9章 应力状态分析与广义胡克定律
9.2 二向应力状态分析
秦飞 编著《材料力学》PPT 讲义
第9章 应力状态分析与广义胡克定律
Stress Analysis and Generalized
Hook’s Law
第9章 应力状态分析与广义胡克定律
9.1 应力状态
9.2 二向应力状态分析
9.3 三向应力状态分析简介
9.4 广义胡克定律
*9.5 由测点处的正应变确定应力状态
秦飞 编著《材料力学》 第9章 应力状态分析与广义胡克定律
8
9.1 应力状态
例题9–2
解:该悬臂梁承受扭矩、剪力和弯矩,由 内力图,固定端截面内力分别为
T Me
FS F
M Fl
A点处的单元体如图所示,单元体上各应力的大 小为 M 32Fl T 16M e A A Wz πd 3 W πd 3
材料力学广义胡克定律公式

材料力学广义胡克定律公式好的,以下是为您生成的关于“材料力学广义胡克定律公式”的文章:在我们探索材料力学这个神奇的领域时,广义胡克定律公式就像一把神奇的钥匙,能帮助我们打开很多未知的大门。
咱先来说说啥是广义胡克定律公式。
简单来讲,它描述了材料在复杂应力状态下的应变与应力之间的关系。
这就好比我们去拉一根橡皮筋,拉得越用力,它就伸得越长,这个伸长的程度和我们用力的大小是有关系的。
广义胡克定律公式就是在告诉我们这个“关系”到底是咋样的。
比如说,有一次我在实验室里做材料力学的实验。
那是一根金属棒,我们要通过施加不同的力来观察它的变形情况。
我小心翼翼地调整着仪器,眼睛紧紧盯着那根金属棒,心里还挺紧张,就怕出啥差错。
当我逐渐增加力的大小,那金属棒开始慢慢地发生了细微的弯曲。
我赶紧记录下每一个数据,心里想着,这不就是广义胡克定律公式在现实中的体现嘛!广义胡克定律公式可以用数学表达式来表示,对于各向同性材料,它通常可以写成这样:\(\epsilon_{x} = \frac{1}{E}[\sigma_{x} - \nu (\sigma_{y} +\sigma_{z})]\)\(\epsilon_{y} = \frac{1}{E}[\sigma_{y} - \nu (\sigma_{x} +\sigma_{z})]\)\(\epsilon_{z} = \frac{1}{E}[\sigma_{z} - \nu (\sigma_{x} +\sigma_{y})]\)这里面的\(\epsilon\)表示应变,\(\sigma\)表示应力,\(E\)是材料的弹性模量,\(\nu\)是材料的泊松比。
可别小看这些公式,它们在工程领域的作用那可大了去了。
就拿建筑来说吧,设计师们在设计高楼大厦的时候,就得靠这些公式来计算材料在各种力的作用下会发生多大的变形,从而确保建筑的安全和稳定。
想象一下,如果没有广义胡克定律公式,那盖出来的房子说不定哪天就歪了或者塌了,多吓人啊!再比如说汽车制造。
材料力学广义胡克定律

材料力学广义胡克定律引言材料力学是研究物质在外力作用下的力学行为和性能的学科。
其中,广义胡克定律是材料力学中的重要定律之一。
本文将详细介绍材料力学广义胡克定律的定义、应用以及相关的概念和公式。
胡克定律的定义胡克定律是描述弹性体材料的应力-应变关系的定律。
它的基本假设是当材料受到小应力作用时,其应变是线性的。
根据胡克定律,应力与应变之间的关系可以表示为:σ=E⋅ε其中,σ是材料的应力,单位是帕斯卡(Pa);E是材料的弹性模量,单位是帕斯卡(Pa);ε是材料的应变,无单位。
广义胡克定律的引入广义胡克定律是对胡克定律的扩展和推广,它考虑了材料在大应力下的非线性行为。
在实际应用中,材料通常会遭受较大的应力,此时线性胡克定律不再适用。
为了描述材料在大应力下的力学行为,引入了广义胡克定律。
广义胡克定律的表达式广义胡克定律可以表示为:σ=E⋅ε+K⋅εn其中,σ是材料的应力,单位是帕斯卡(Pa);E是材料的弹性模量,单位是帕斯卡(Pa);ε是材料的应变,无单位;K是材料的非线性系数,单位是帕斯卡(Pa);n是材料的非线性指数,无单位。
广义胡克定律的应用广义胡克定律可以描述材料在大应力下的非线性力学行为。
它广泛应用于工程领域中的材料设计、结构分析和强度计算等方面。
材料设计在材料设计中,广义胡克定律可以帮助工程师选择合适的材料和确定其力学性能。
通过测量材料的弹性模量和非线性系数,可以评估材料的强度和稳定性,从而选择最适合的材料。
结构分析在结构分析中,广义胡克定律可以用来计算结构在大应力下的变形和应力分布。
通过将广义胡克定律应用于结构的力学模型,可以预测结构在实际工作条件下的性能和安全性。
强度计算在强度计算中,广义胡克定律可以用来评估材料和结构的承载能力。
通过将广义胡克定律应用于强度分析,可以确定材料和结构在受到外力时的破坏点和失效机制,从而进行强度设计和优化。
广义胡克定律的实验验证广义胡克定律的有效性可以通过实验进行验证。
广义胡克定律

广义胡克定律1. 概述广义胡克定律是描述材料在受到外力作用下变形的力学定律,是胡克定律的一种扩展形式。
广义胡克定律表示了材料的应力与应变之间的线性关系。
根据广义胡克定律,应力与应变的关系可以通过材料的弹性模量来描述,弹性模量是材料特性的重要参数之一。
2. 胡克定律的表达式根据广义胡克定律,应力与应变之间的线性关系可以用以下表达式表示:σ = Eε其中,σ表示应力,单位为Pa(帕斯卡),E表示材料的弹性模量,单位为Pa,ε表示应变,无单位。
3. 弹性模量的定义弹性模量是衡量材料抵抗变形的能力的物理量,表示单位应力下材料的相对应变。
根据胡克定律,弹性模量E可以表示为应力与应变的比值:E = σ/ε这里E为弹性模量,σ为应力,ε为应变。
4. 弹性恢复能力根据广义胡克定律,材料在受到应力作用时,会发生弹性变形,即当外力撤除时,材料会恢复到原始形状。
这是因为材料具有弹性的特性,能够在受到外力作用后恢复原状,这种能力称为弹性恢复能力。
弹性恢复能力可以通过材料的弹性模量来衡量。
弹性模量越大,材料的弹性恢复能力就越强,反之则弹性恢复能力较弱。
5. 应力与应变的关系根据广义胡克定律,应力与应变之间的关系是线性的。
当材料受到外力作用时,会发生应力的产生,应力与应变的关系可以表示为:σ = Eε这里σ表示应力,E表示弹性模量,ε表示应变。
根据这个关系,应变是由应力和弹性模量决定的。
6. 应力应变曲线应力应变曲线是描述材料在受力过程中应力与应变关系的曲线。
根据广义胡克定律,应力应变曲线为直线,与应力与应变的线性关系相对应。
在应力应变曲线上,通常有三个重要点:比例极限点、弹性极限点和断裂点。
比例极限点表示材料可以承受的最大应力,弹性极限点表示材料开始发生塑性变形的点,断裂点表示材料完全破坏的点。
7. 应用广义胡克定律在工程领域有着广泛的应用。
它是材料力学的基础,可以帮助工程师分析和设计结构的性能。
在材料选择和设计过程中,根据材料的弹性模量可以选择合适的材料,以满足工程需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-8广义胡克定律
已知简单W力状态的胡克定律和横向效应:
备向同性材料,弹性范围内,线弹性材料,小变形。
由此:
1)在复杂丿2力状态下,应变分最可市备丿、'、/:力分最引起的丿、'、Z变分最吾加得到。
2)正丿'V变只与正戒力冇关,剪应变只与剪丿、''/「力冇关,线变形与角变形的相互影
响可
以略去。
广义胡克定肄ey
1)对空间一般应力状态
r 1
耳=万1务一虽(CF” +巳)[
1
1
2)主应力形式
r]
习=万[6一“92 +6)]
« 叼=-^[^2 _“(6 +6)]
习=+[內一虽(6+內)]
3)对平面一般应力状态
1
耳=_ w
° 1 _ % E厂丘(空-“务)=—
(8-11)
(8-12)
F = 一壬(耳+空)其
余»= Yzx
(8-13)
4)考虑热应力的广义胡克定律
耳=-[^ -吩y +匕)]+必« 弓=£[巧_“©+
〔)] +仏
务+勺)卜加
(8-14) 此处,。
一各向同性材料的线膨胀系数。
8-9微元体的体积改变与形状改变
1・体积改变与静水应力
体积应变定义(如图8-29&、b):
受力前微元体体积: V = dxdydz
(8-15)
受力后微元体体积:r"(1 +如° +习)初(1 +恥。
由于叼,习,习,略去正应变的二次,三次项后得:
7’ = (1 + £1 + 叼 + s3 )dxdydz
由定义式(8—15)即得
3(1 - 2v) o-! + a2 + CF3
~E 3
定义材料的体积模量久1" 2v) o
片=?(巧+丐+屯)微元体的静水应力(平均正应力)3
△7 旷一7
体积改变定律:
微元体的体积改变与静水应力(平均正应力)b"成正比,与反映材料弹性性能的体积模量&成反比。
2. 形状改变与应力偏;
处于空间一般应力状态的微元体的变形可以分为只产生体积改变和只产生形状改
对于(c),不存在体积改变,且偏应力状态可分解为几个纯剪应力状态。
8-10复杂应力状态的变形比能
1. 一般表达式
对线弹性材料,在弹性范围内,在缓慢加载条件下,由能量守恒定理,弹性变形能的储备等于外载所做的功,它的大小只与外载和变形的最终状态有关,与加载次序无关。
对微元体,则用比能(变形比能,应变能密度)来描写。
对空间一般应力状态:
_____________ (8-17a)
引入广义胡克定律,用应力分量表示:
(8-17b)
用主应力,主应变表示:
(8-18)
・体积改变比能与形状改变比能
对备向同性材料,弹性范囤内,貝有将应力状态分解为静水应力状态和侃应力状态,
其能景才可以吾加(如图8-30: _______________ )
对于图8-30b,将三个平均应力代入式(8-18):
对于图8-30c,将三个偏应力代入式(8-18):
(8-19)
体积改变比能;
形状改变比能。
(8-20)
可以证明:
【例8-4]将单向应力状态下的比能分解为体积改变比能与形状改变比能。
图8-31a, b, c
对图8-31 (a):
对图8-31 (b):
对图8-31 (c):
可证:。
