中考数学复习第二部分空间与图形第二十四课时正方形练习

合集下载

中考数学复习----《正方形的性质》知识点总结与专项练习题(含答案解析)

中考数学复习----《正方形的性质》知识点总结与专项练习题（含答案解析）知识点总结1.正方形的定义：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形2.正方形的性质：①具有平行四边形的一切性质。

②具有矩形与菱形的一切性质。

所以正方形的四条边都相等，四个角都是直角。

对角线相互平分且相等，且垂直，且平分每一组对角，把正方形分成了四个全等的等腰直角三角形。

正方形既是中心对称图形，也是轴对称图形。

对角线交点是对称中心，对角线所在直线是对称轴，过每一组对边中点的直线也是对称轴。

练习题1．（2022•黄石）如图，正方形OABC的边长为，将正方形OABC绕原点O顺时针旋转45°，则点B的对应点B1的坐标为（）A．（﹣2，0）B．（2，0）C．（0，2）D．（0，2）【分析】连接OB，由正方形的性质和勾股定理得OB＝2，再由旋转的性质得B1在y轴正半轴上，且OB1＝OB＝2，即可得出结论．【解答】解：如图，连接OB，∵正方形OABC的边长为，∴OC＝BC＝，∠BCO＝90°，∠BOC＝45°，∴OB＝＝＝2，∵将正方形OABC绕原点O顺时针旋转45°后点B旋转到B1的位置，∴B 1在y 轴正半轴上，且OB 1＝OB ＝2，∴点B 1的坐标为（0，2），故选：D ．2．（2022•广州）如图，正方形ABCD 的面积为3，点E 在边CD 上，且CE ＝1，∠ABE 的平分线交AD 于点F ，点M ，N 分别是BE ，BF 的中点，则MN 的长为（）A ．26B ．23C ．2﹣3D ．226− 【分析】连接EF ，由正方形ABCD 的面积为3，CE ＝1，可得DE ＝﹣1，tan ∠EBC ＝＝＝，即得∠EBC ＝30°，又AF 平分∠ABE ，可得∠ABF ＝∠ABE ＝30°，故AF ＝＝1，DF ＝AD ﹣AF ＝﹣1，可知EF ＝DE ＝×（﹣1）＝﹣，而M ，N 分别是BE ，BF 的中点，即得MN ＝EF ＝．【解答】解：连接EF ，如图：∵正方形ABCD 的面积为3，∴AB ＝BC ＝CD ＝AD ＝，∵CE ＝1，∴DE＝﹣1，tan∠EBC＝＝＝，∴∠EBC＝30°，∴∠ABE＝∠ABC﹣∠EBC＝60°，∵AF平分∠ABE，∴∠ABF＝∠ABE＝30°，在Rt△ABF中，AF＝＝1，∴DF＝AD﹣AF＝﹣1，∴DE＝DF，△DEF是等腰直角三角形，∴EF＝DE＝×（﹣1）＝﹣，∵M，N分别是BE，BF的中点，∴MN是△BEF的中位线，∴MN＝EF＝．故选：D．3．（2022•贵阳）如图，“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形．若图中的直角三角形的两条直角边的长分别为1和3，则中间小正方形的周长是（）A．4B．8C．12D．16【分析】根据题意和题目中的数据，可以计算出小正方形的边长，然后即可得到小正方形的周长．【解答】解：由题意可得，小正方形的边长为3﹣1＝2，∴小正方形的周长为2×4＝8，故选：B．4．（2022•青岛）如图，O为正方形ABCD对角线AC的中点，△ACE为等边三角形．若AB＝2，则OE 的长度为（）A ．26B ．6C ．22D ．23【分析】首先利用正方形的性质可以求出AC ，然后利用等边三角形的性质可求出OE ．【解答】解：∵四边形ABCD 为正方形，AB ＝2，∴AC ＝2，∵O 为正方形ABCD 对角线AC 的中点，△ACE 为等边三角形，∴∠AOE ＝90°，∴AC ＝AE ＝2，AO ＝，∴OE ＝×＝．故选：B ．5．（2022•泰州）如图，正方形ABCD 的边长为2，E 为与点D 不重合的动点，以DE 为一边作正方形DEFG ．设DE ＝d 1，点F 、G 与点C 的距离分别为d 2、d 3，则d 1+d 2+d 3的最小值为（）A ．2B ．2C ．22D ．4【分析】连接AE ，那么，AE ＝CG ，所以这三个d 的和就是AE +EF +FC ，所以大于等于AC ，故当AEFC 四点共线有最小值，最后求解，即可求出答案．【解答】解：如图，连接AE ，∵四边形DEFG 是正方形，∴∠EDG ＝90°，EF ＝DE ＝DG ，∵四边形ABCD 是正方形，∴AD ＝CD ，∠ADC ＝90°，∴∠ADE ＝∠CDG ，∴△ADE ≌△CDG （SAS ），∴AE ＝CG ，∴d 1+d 2+d 3＝EF +CF +AE ，∴点A ，E ，F ，C 在同一条线上时，EF +CF +AE 最小，即d 1+d 2+d 3最小，连接AC ，∴d 1+d 2+d 3最小值为AC ，在Rt △ABC 中，AC ＝AB ＝2，∴d 1+d 2+d 3最小＝AC ＝2，故选：C ．6．（2022•黔东南州）如图，在边长为2的等边三角形ABC 的外侧作正方形ABED ，过点D 作DF ⊥BC ，垂足为F ，则DF 的长为（）A ．23+2B ．5﹣33C ．3﹣3D ．3+1【分析】方法一：如图，延长DA 、BC 交于点G ，利用正方形性质和等边三角形性质可得：∠BAG ＝90°，AB ＝2，∠ABC ＝60°，运用解直角三角形可得AG ＝2，DG ＝2+2，再求得∠G ＝30°，根据直角三角形性质得出答案．方法二：过点E 作EG ⊥DF 于点G ，作EH ⊥BC 于点H ，利用解直角三角形可得EH ＝1，BH ＝，再证明△BEH ≌△DEG ，可得DG ＝BH ＝，即可求得答案．【解答】解：方法一：如图，延长DA、BC交于点G，∵四边形ABED是正方形，∴∠BAD＝90°，AD＝AB，∴∠BAG＝180°﹣90°＝90°，∵△ABC是边长为2的等边三角形，∴AB＝2，∠ABC＝60°，∴AG＝AB•tan∠ABC＝2×tan60°＝2，∴DG＝AD+AG＝2+2，∵∠G＝90°﹣60°＝30°，DF⊥BC，∴DF＝DG＝×（2+2）＝1+，故选D．方法二：如图，过点E作EG⊥DF于点G，作EH⊥BC于点H，则∠BHE＝∠DGE＝90°，∵△ABC是边长为2的等边三角形，∴AB＝2，∠ABC＝60°，∵四边形ABED是正方形，∴BE＝DE＝2，∠ABE＝∠BED＝90°，∴∠EBH＝180°﹣∠ABC﹣∠ABE＝180°﹣60°﹣90°＝30°，∴EH＝BE•sin∠EBH＝2•sin30°＝2×＝1，BH＝BE•cos∠EBH＝2cos30°＝，∵EG⊥DF，EH⊥BC，DF⊥BC，∴∠EGF＝∠EHB＝∠DFH＝90°，∴四边形EGFH是矩形，∴FG＝EH＝1，∠BEH+∠BEG＝∠GEH＝90°，∵∠DEG+∠BEG＝90°，∴∠BEH＝∠DEG，在△BEH和△DEG中，，∴△BEH≌△DEG（AAS），∴DG＝BH＝，∴DF＝DG+FG＝+1，故选：D．7．（2022•随州）七巧板是一种古老的中国传统智力玩具，如图，在正方形纸板ABCD中，BD为对角线，E，F分别为BC，CD的中点，AP⊥EF分别交BD，EF于O，P两点，M，N分别为BO，DO的中点，连接MP，NF，沿图中实线剪开即可得到一副七巧板．则在剪开之前，关于该图形，下列说法正确的有（）①图中的三角形都是等腰直角三角形；②四边形MPEB是菱形；③四边形PFDM的面积占正方形ABCD面积的．A．只有①B．①②C．①③D．②③【分析】①利用正方形的性质和中位线的性质可以解决问题；②利用①的结论可以证明OM≠MP解决问题；③如图，过M作MG⊥BC于G，设AB＝BC＝x，利用正方形的性质与中位线的性质分别求出BE和MG即可判定是否正确．【解答】解：①如图，∵E，F分别为BC，CD的中点，∴EF为△CBD的中位线，∴EF∥BD，∵AP⊥EF，∴AP⊥BD，∵四边形ABCD为正方形，∴A、O、P、C在同一条直线上，∴△ABC、△ACD、△ABD、△BCD、△OAB、△OAD、△OBC、△OCD、△EFC都是等腰直角三角形，∵M，N分别为BO，DO的中点，∴MP∥BC，NF∥OC，∴△DNF、△OMP也是等腰直角三角形．故①正确；②根据①得OM＝BM＝PM，∴BM≠PM∴四边形MPEB不可能是菱形．故②错误；③∵E，F分别为BC，CD的中点，∴EF∥BD，EF＝BD，∵四边形ABCD是正方形，且设AB＝BC＝x，∴BD＝x，∵AP⊥EF，∴AP⊥BD，∴BO＝OD，∴点P在AC上，∴PE＝EF，∴PE＝BM，∴四边形BMPE是平行四边形，∴BO＝BD，∵M为BO的中点，∴BM＝BD＝x，∵E为BC的中点，∴BE＝BC＝x，过M作MG⊥BC于G，∴MG＝BM＝x，∴四边形BMPE的面积＝BE•MG＝x2，∴四边形BMPE的面积占正方形ABCD面积的．∵E、F是BC，CD的中点，∴S△CEF＝S△CBD＝S四边形ABCD，∴四边形PFDM的面积占正方形ABCD面积的（1﹣﹣﹣）＝．故③正确．故选：C．8．（2022•宁波）将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内，其中矩形纸片和正方形纸片的周长相等．若知道图中阴影部分的面积，则一定能求出（）A．正方形纸片的面积B．四边形EFGH的面积C．△BEF的面积D．△AEH的面积【分析】根据题意设PD＝x，GH＝y，则PH＝x﹣y，根据矩形纸片和正方形纸片的周长相等，可得AP＝x+y，先用面积差表示图中阴影部分的面积，并化简，再用字母分别表示出图形四个选项的面积，可得出正确的选项．【解答】解：设PD＝x，GH＝y，则PH＝x﹣y，∵矩形纸片和正方形纸片的周长相等，∴2AP+2（x﹣y）＝4x，∴AP＝x+y，∵图中阴影部分的面积＝S矩形ABCD﹣2△ADH﹣2S△AEB＝（2x+y）（2x﹣y）﹣2×•（x﹣y）（2x+y）﹣2×•（2x﹣y）•x＝4x2﹣y2﹣（2x2+xy﹣2xy﹣y2）﹣（2x2﹣xy）＝4x2﹣y2﹣2x2+xy+y2﹣2x2+xy＝2xy，A、正方形纸片的面积＝x2，故A不符合题意；B、四边形EFGH的面积＝y2，故B不符合题意；C、△BEF的面积＝•EF•BQ＝xy，故C符合题意；D、△AEH的面积＝•EH•AM＝y（x﹣y）＝xy﹣y2，故D不符合题意；故选：C．9．（2022•重庆）如图，在正方形ABCD中，AE平分∠BAC交BC于点E，点F是边AB上一点，连接DF，若BE＝AF，则∠CDF的度数为（）A．45°B．60°C．67.5°D．77.5°【分析】根据正方形的性质和全等三角形的判定和性质，可以得到∠ADF的度数，从而可以求得∠CDF的度数．【解答】解：∵四边形ABCD是正方形，∴AD＝BA，∠DAF＝∠ABE＝90°，在△DAF和△ABE中，，△DAF≌△ABE（SAS），∠ADF＝∠BAE，∵AE平分∠BAC，四边形ABCD是正方形，∴∠BAE＝∠BAC＝22.5°，∠ADC＝90°，∴∠ADF＝22.5°，∴∠CDF＝∠ADC﹣∠ADF＝90°﹣22.5°＝67.5°，故选：C．10．（2022•重庆）如图，在正方形ABCD中，对角线AC、BD相交于点O．E、F分别为AC、BD上一点，且OE＝OF，连接AF，BE，EF．若∠AFE＝25°，则∠CBE的度数为（）A．50°B．55°C．65°D．70°【分析】利用正方形的对角线互相垂直平分且相等，等腰直角三角形的性质，三角形的内角和定理和全等三角形的判定与性质解答即可．【解答】解：∵四边形ABCD是正方形，∴∠AOB＝∠AOD＝90°，OA＝OB＝OD＝OC．∵OE＝OF，∴△OEF为等腰直角三角形，∴∠OEF＝∠OFE＝45°，∵∠AFE＝25°，∴∠AFO＝∠AFE+∠OFE＝70°，∴∠F AO＝20°．在△AOF和△BOE中，，∴△AOF ≌△BOE （SAS ）．∴∠F AO ＝∠EBO ＝20°，∵OB ＝OC ，∴△OBC 是等腰直角三角形，∴∠OBC ＝∠OCB ＝45°，∴∠CBE ＝∠EBO +∠OBC ＝65°．故选：C ．11．（2022•益阳）如图，将边长为3的正方形ABCD 沿其对角线AC 平移，使A 的对应点A ′满足AA ′＝31AC ，则所得正方形与原正方形重叠部分的面积是．【分析】由正方形边长为3，可求AC ＝3，则AA ′＝AC ＝，由平移可得重叠部分是正方形，根据正方形的面积公式可求重叠部分面积．【解答】解：∵正方形ABCD 的边长为3，∴AC ＝3，∴AA ′＝AC ＝， ∴A ′C ＝2，由题意可得重叠部分是正方形，且边长为2，∴S 重叠部分＝4．故答案为：4．12．（2022•海南）如图，正方形ABCD 中，点E 、F 分别在边BC 、CD 上，AE ＝AF ，∠EAF ＝30°，则∠AEB ＝ °；若△AEF 的面积等于1，则AB 的值是．【分析】利用“HL”先说明△ABE与△ADF全等，得结论∠BAE＝∠DAF，再利用角的和差关系及三角形的内角和定理求出∠AEB；先利用三角形的面积求出AE，再利用直角三角形的边角间关系求出AB．【解答】解：∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝∠B＝∠D＝90°．在Rt△ABE和Rt△ADF中，，∴Rt△ABE≌Rt△ADF（HL）．∴∠BAE＝∠DAF．∴∠BAE＝（∠BAD﹣∠EAF）＝（90°﹣30°）＝30°．∴∠AEB＝60°．故答案为：60．过点F作FG⊥AE，垂足为G．∵sin∠EAF＝，∴FG＝sin∠EAF×AF．∵S△AEF＝×AE×FG＝×AE×AF×sin∠EAF＝1，∴×AE2×sin30°＝1．即×AE2×＝1．∴AE＝2．在Rt△ABE中，∵cos∠BAE＝，∴AB＝cos30°×AE＝×2＝．故答案为：．13．（2022•广西）如图，在正方形ABCD中，AB＝42，对角线AC，BD相交于点O．点E是对角线AC上一点，连接BE，过点E作EF⊥BE，分别交CD，BD于点F，G，连接BF，交AC于点H，将△EFH沿EF翻折，点H的对应点H′恰好落在BD上，得到△EFH′．若点F为CD的中点，则△EGH′的周长是．【分析】作辅助线，构建全等三角形，先根据翻折的性质得△EGH'≌△EGH，所以△EGH′的周长＝△EGH的周长，接下来计算△EGH的三边即可；证明△BME≌△FNE（ASA）和△BEO≌△EFP（AAS），得OE＝PF＝2，OB＝EP＝4，利用三角函数和勾股定理分别计算EG，GH和EH的长，相加可得结论．【解答】解：如图，过点E作EM⊥BC于M，作EN⊥CD于N，过点F作FP⊥AC于P，连接GH，∵将△EFH沿EF翻折得到△EFH′，∴△EGH'≌△EGH，∵四边形ABCD是正方形，∴AB＝CD＝BC＝4，∠BCD＝90°，∠ACD＝∠ACB＝45°，∴BD＝BC＝8，△CPF是等腰直角三角形，∵F是CD的中点，∴CF＝CD＝2，∴CP＝PF＝2，OB＝BD＝4，∵∠ACD＝∠ACB，EM⊥BC，EN⊥CD，∴EM＝EN，∠EMC＝∠ENC＝∠BCD＝90°，∴∠MEN＝90°，∵EF⊥BE，∴∠BEF＝90°，∴∠BEM＝∠FEN，∵∠BME＝∠FNE，∴△BME≌△FNE（ASA），∴EB＝EF，∵∠BEO+∠PEF＝∠PEF+∠EFP＝90°，∴∠BEO＝∠EFP，∵∠BOE＝∠EPF＝90°，∴△BEO≌△EFP（AAS），∴OE＝PF＝2，OB＝EP＝4，∵tan∠OEG＝＝，即＝，∴OG＝1，∴EG＝＝，∵OB∥FP，∴∠OBH＝∠PFH，∴tan∠OBH＝tan∠PFH，∴＝，∴＝＝2，∴OH＝2PH，∵OP＝OC﹣PC＝4﹣2＝2，∴OH＝×2＝，在Rt△OGH中，由勾股定理得：GH＝＝，∴△EGH′的周长＝△EGH的周长＝EH+EG+GH＝2+++＝5+．故答案为：5+．14．（2022•无锡）如图，正方形ABCD的边长为8，点E是CD的中点，HG垂直平分AE 且分别交AE、BC于点H、G，则BG＝．【分析】设CG＝x，则BG＝8﹣x，根据勾股定理可得AB2+BG2＝CE2+CG2，可求得x 的值，进而求出BG的长．【解答】解：连接AG，EG，∵E是CD的中点，∴DE＝CE＝4，设CG＝x，则BG＝8﹣x，在Rt△ABG和Rt△GCE中，根据勾股定理，得AB2+BG2＝CE2+CG2，即82+（8﹣x）2＝42+x2，解得x＝7，∴BG＝BC﹣CG＝8﹣7＝1．故答案是：1．15．（2022•江西）沐沐用七巧板拼了一个对角线长为2的正方形，再用这副七巧板拼成一个长方形（如图所示），则长方形的对角线长为．【分析】根据图形可得长方形的长是正方形的对角线为2，长方形的宽是正方形对角线的一半为1，然后利用勾股定理即可解决问题．【解答】解：根据图形可知：长方形的长是正方形的对角线为2，长方形的宽是正方形对角线的一半为1，则长方形的对角线长＝＝．故答案为：．。

中考数学复习第二部分空间与图形第二十四课时正方形课件

∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,∴∠ABE=∠
ECD=30°,
=
在△ABE 和△DCE 中, ∠ = ∠ ,∴△ABE≌△DCE(SAS).
=
1
(2)∵BA=BE,∠ABE=30°,∴∠BAE= (180°-30°
3.分值:3~7 分
4.热点和趋势:
(1)利用正方形的性质进
行运算;
(2)利用正方形的性质和
判Hale Waihona Puke 进行证明.-3-1.正方形定义:(1)四条边相等,
正方形既是矩形
,又是
四个角都是直角的四边形,叫做正方形.
菱形
.
(2)顺次连接正方形各边中点得到(dédào) 正方形 .
2.正方形性质:边:(1)正方形的对边平行且
答案D只满足“垂直”,无法判定四边形为正方形,属假命题.故选D.
【题型感悟】此题主要考查了正方形的判定以及平行四边形、矩形、菱形
的性质(xìngzhì),正确掌握正方形的判定方法是解题关键.
第九页，共十八页。
-10-
【考点变式】
(2017·青岛)已知:如图,在菱形ABCD 中,点E,O,F 分别是边AB,AC,AD的中点,
B.对角线互相垂直的矩形是正方形
C.对角线相等的菱形是正方形
D.对角线互相垂直的四边形是正方形
【名师点拨】此题考点为正方形的判定.利用平行四边形、矩形、菱形、正
方形之间的关系与区别,结合正方形的判定方法分别判断得出即可.
【我的解法】解:根据“对角线互相垂直、平分且相等的四边形是正
方形”,可知答案A、B、C满足“垂直、平分且相等”,均为真命题,

第24课时正方形课件 2025年中考数学一轮总复习

（2）求证：EF＋EG＝ CE.
解：（2）证明：如图，过点C作CM⊥CE交BE于点M. ∵△CBG≌△CDF，∴CG＝CF，∠CGB＝∠F. ∵CM⊥CE，∠DCF＝90°，∴∠MCG＋∠DCE＝∠ECF＋∠DCE＝
90°，∴∠MCG＝∠ECF，
∴△MCG≌△ECF（ASA），∴MG＝EF，CM＝CE，
为 .
2
例2 如图1，在正方形ABCD中，点E
在边BC上，点F在CD的延长线上，且
DF＝BE，连接AE，AF，EF. （1）求证：△AEF是等腰直角三角形；
图1 图2
[答案] （1）证明：∵四边形ABCD为正
为H，交CD于点G，连接BH.
①求证：BE＝ BH－AB；
图1 图2
[答案]解：（2）①证明：如答案图，过点H作HM⊥BH交BC的延长线于点M，∴∠BHE＋∠EHM＝90°.∵△AEF是等腰直角三角形，AH⊥EF，∴AH＝EH，∠AHE＝90°，∴∠BHE＋∠AHB＝90°，∴∠EHM＝∠AHB. ∵∠ABE＝∠AHE＝90°，
AB⊥BC
3. （2024·内蒙古）如图，边长为2的正
方形ABCD的对角线AC与BD相交于点
O. E是BC边上一点，F是BD上一点，
连接DE，EF. 若△DEF与△DEC关于
直线DE对称，则△BEF的周长是 .
2
4. 如图，在正方形ABCD中，点F是BC
AC，AB，BO，CO的中点，∠BOC＝
90°.若AO＝3，BO＝4，CO＝3，则四
边形DEFG的周长为 .
8
1. 如图，F是正方形ABCD的对角线BD
上一点，连接AF，CF，并延长CF交
AD于点E. 若∠AFC＝140°，则∠DEC的度数为（ D ）

2019重庆中考数学第24题专题训练---正方形(含答案)

2019重庆中考数学第24题专题训练---正方形201902121、重庆第一中学2018-2019学年初2019级初三年级上学期第二次定时作业数学试题如图，点M 是正方形ABCD 的边BC 上一点，连接AM ，点E 是线段AM 上一点，CDE ∠的平分线交AM 延长线于点F .（1）如图1，若点E 为线段AM 的中点，:1:2BM CM =，BE =AB 的长；（2）如图2，若G 为AE 中点，延长DG 至N ，使DG NG =，连接EN ，且EDG ENG ∠=∠，求证：BF DF +=．2、在正方形ABCD 中，点F 是BC 延长线上一点，过点B 作BE ⊥DF 于点E ，交CD 于点G ，连接CE . （1）若正方形ABCD 边长为3，DF =4，求CG 的长；（2）求证：EF+EG =2CE .GEA B CDF3、如图1，在正方形ABCD 中，对角线AC 与BD 交于点,O H 为CD 边上一点，连接BH 交AC 于K ,E 为BH 上一点，连接AE 交BD 于点.F（1）若AE BH ⊥于E ,且6,CK ==求AF 的长；（2）如图2，若=AE BE ,且,BEO EAO ∠=∠求证：.AEH图1 图24、重庆市南开（融侨）中学初2019级暑假作业数学综合练习如图，正方形ABCD 中，CB 的延长线上有一点E,连接AC 、AE. (1)如图1，若AC=4，∠CAE=75°，求△ACE 的面积； (2)如图2，连接BD 交AC 于点O ，在线段AB 上取点F ，使BE=BF ，连接CF ，过点B 作BG ∥CF ，交AE 于点G ，连接OG 、BG.求证：.BG AG +=5、重庆市南岸区11中、二外、珊瑚2018-2019学年度上期三校期末联考九年级数学如图1,以正方形ABCD 边AD 为边作等边三角形ADE ,EF ⊥AD 于点F ,连接BE 交AD 于G . (1)若正方形的边长为2,求AG 的长；(2)如图2，∠EAD 的平分线交BE 于点P ，连接CP ，求证:AP +PC6、在正方形ABCD 中,对角线AC,BD 交于点O,E 为OB 上一点,连接CE,F 为CE 的中点.(1)如图1,连接AE,OF,若 AB=6,求OF 的长；(2)如图2,连接BF,作BG ⊥BF 交CA 的延长线于点G ，求证：.CG BE =7、已知正方形ABCD如图所示，连接其对角线AC，∠BCA的平分线CF交AB于点F，过点B作BM⊥C F于点N，交AC于点M，过点C作CP⊥CF，交AD延长线于点P．（1）若正方形ABCD的边长为4，求△ACP的面积；（2）求证：CP=BM+2FN．8、重庆巴蜀中学初2018届九年级下第二次周考如图1,正方形ABCD中,AE为过顶点A的任意一条射线,过C作CE⊥AE于E.(1)己知AB=6.AE=8,求CE的长；(2)如图2,过D作DF⊥AE于F,求证:DF=EF.图1 图29、重庆一中初2018级初三下期期中如图，在正方形ABCD 中，点M 是边BC 上一点，连接AM ，过点C 作CH ⊥AM 交AM 的延长线于点H ，延长CH 于点M 连接MN 、BN ．（1）若AB =4，AH =528，求线段CH 的长度；（2）若∠MAD =∠BMN ，求证：AM =MN +CN ．2019重庆中考数学第24题专题训练---正方形答案1、重庆第一中学2018-2019学年初2019级初三年级上学期第二次定时作业数学试题如图，点M 是正方形ABCD 的边BC 上一点，连接AM ，点E 是线段AM 上一点，CDE ∠的平分线交AM 延长线于点F .（3）如图1，若点E 为线段AM 的中点，:1:2BM CM =，BE =AB 的长；（4）如图2，若G 为AE 中点，延长DG 至N ，使DG NG =，连接EN ，且EDG ENG ∠=∠，求证：BF DF +=．（1）:1:2BM CM ==,2BM x CM x ∴=设则∵正方形ABCD 3,90AB x ABC ∴=∠=︒Rt ABM AM ∆在中，∵点E 为线段AM 的中点2AM BM ∴== 2x ∴=36AB x ∴==（2）G AE 为中点AG EG ∴=AGD EGN AG EG AGD EGN DG NG ∆∆=⎧⎪∠=∠⎨⎪=⎩在和中AGD EGN ∴∆≅∆ 4N ∴∠=∠ EDG ENG ∠=∠,34ED EN ∴=∠=∠ DG NG = 90EGD ∴∠=︒AF CDE ∠平分12∴∠=∠123452FDG CDA ∴∠=∠+∠=∠=︒,90A AH AF FD H FAH ⊥∠=︒过作交延长线于即//DG AH ∴45H FDG ∴∠=∠=︒AHF ∴∆为等腰直角三角形,AH AF FH ∴=90DAB HAF ∴∠=∠=︒ DAH BAF ∴∠=∠DAH BAF AH AF DAH BAF AD AB DAH BAF DH BF∆∆=⎧⎪∠=∠⎨⎪=⎩∴∆≅∆∴=在和中BF DF DH DF FH ∴+=+==2、在正方形ABCD 中，点F 是BC 延长线上一点，过点B 作BE ⊥DF 于点E ，交CD 于点G ，连接CE . （1）若正方形ABCD 边长为3，DF =4，求CG 的长；（2）求证：EF+EG =2CE .解答：（1）∵四边形ABCD 是正方形∴∠BCG =∠DCB=∠DCF=90°，BC=DC .∵BE ⊥DF∴∠CBG+∠F=∠CDF+∠F .∴∠CBG=∠CDF . ∴△CBG ≌△CDF .∴BG=DF=4.∴在Rt △BCG 中，222BG BC CG =+∴CG =73422=-. …………………………4分（2）过点C 作CM ⊥CE 交BE 于点M∵∠BCG=∠MCE =∠DCF =90° ∴∠BCM=∠DCE ，∠MCG=∠ECF ∵BC=DC ，∠CBG=∠CDF∴△CBM ≌△CDE ∴CM=CE∴△CME 是等腰直角三角形∴ME=CE 2 ，即MG+EG=CE 2 又∵△CBG ≌△CDF ∴CG=CF∴△CMG ≌△FCE ∴MG=EF∴EF+EG =2CEGEA B CDFM3、如图1，在正方形ABCD 中，对角线AC 与BD 交于点,O H 为CD 边上一点，连接BH 交AC 于K ,E 为BH 上一点，连接AE 交BD 于点.F（1）若AE BH ⊥于E ,且6,CK ==求AF 的长；（2）如图2，若=AE BE ,且,BEO EAO ∠=∠求证：.AEH图1图2解答：4、重庆市南开（融侨）中学初2019级暑假作业数学综合练习如图，正方形ABCD中，CB的延长线上有一点E,连接AC、AE.(1)如图1，若AC=4，∠CAE=75°，求△ACE的面积；(2)如图2，连接BD交AC于点O，在线段AB上取点F，使BE=BF，连接CF，过点B作BG∥CF，交AE于点G，连接OG、BG.求证：.+=BG AG5、重庆市南岸区11中、二外、珊瑚2018-2019学年度上期三校期末联考九年级数学如图1,以正方形ABCD边AD为边作等边三角形ADE,EF⊥AD于点F,连接BE交AD于G.(1)若正方形的边长为2,求AG的长；(2)如图2，∠EAD的平分线交BE于点P，连接CP，求证解法一：解法二：6、在正方形ABCD 中,对角线AC,BD 交于点O,E 为OB 上一点,连接CE,F 为CE 的中点.(1)如图1,连接AE,OF,若 AB=6,求OF 的长；(2)如图2,连接BF,作BG ⊥BF 交CA 的延长线于点G ，求证：.CG BE =7、已知正方形ABCD 如图所示，连接其对角线AC ，∠BCA 的平分线CF 交AB 于点F ，过点B 作BM⊥C F 于点N ，交AC 于点M ，过点C 作CP⊥CF，交AD 延长线于点P ．（1）若正方形ABCD 的边长为4，求△ACP 的面积；（2）求证：CP=BM+2FN ．解：∵∠1=∠2=22.5°，又CP⊥CF，∴∠3+∠FCD=∠1+∠FCD=90°∴∠3=∠1=22.5°∴∠P=67.5°又∵四边形ABCD 为正方形，∴∠ACP=45+22.5=67.5°∴∠P=∠ACP∴AP=AC又∵AB=4 ∴AP=42 ∴S △A P C =12AP•CD=82（2）∵在△PDC 和△FBC 中，{ ∠PDC=∠FBCCD=BC∠1=∠3∴△PDC≌△FBC∴CP=CF 在CN 上截取NH=FN ，连接BH∵FN=NH，且BN⊥FH∴BH=BF∴∠4=∠5∴∠4=∠1=∠5=22.5°又∠4+∠BFC=∠1+∠BFC=90°∴∠HBC=∠BAM=45°在△AMB 和△BHC 中，{ ∠1=∠4AB=BC∠HBC=∠BAM，∴△AMB≌△BHC，∴CH=BM∴CF=BM+2FN∴CP=BM+2FN．8、重庆巴蜀中学初2018届九年级下第二次周考如图1,正方形ABCD 中,AE 为过顶点A 的任意一条射线,过C 作CE ⊥AE 于E.(1)己知AB=6.AE=8,求CE 的长；(2)如图2,过D 作DF ⊥AE 于F,求证:DF=EF.图1 图29、重庆一中初2018级初三下期期中如图，在正方形ABCD 中，点M 是边BC 上一点，连接AM ，过点C 作CH ⊥AM 交AM 的延长线于点H ，延长CH 于点M 连接MN 、BN ．（1）若AB =4，AH =528，求线段CH 的长度；（2）若∠MAD =∠BMN ，求证：AM =MN +CN ．。

福建省2022中考数学第5章四边形第24课时正方形(课后练本)课件

第五章四边形第24课时正方形
教材梳理篇
01 02 03

04
05 06 07
08 09 10
11
12 13 14
清基础 1．正方形具有而菱形不具有的性质是( B ) A．对角线互相平分 B．对角线相等 C．对角线互相垂直 D．每一条对角线平分一组对角
2．四边形ABCD中，点O是对角线的交点，下列条件中，能判定它是正方形的是( C )
(3)类比迁移：如图②，在菱形ABCD中，点E，F分别在 AB ， BC 边上， DE 与 AF 相交于点 G ， DE ＝ AF ， ∠AED＝60°，AE＝6，BF＝2，求DE的长．
解：如图，延长CB到点H，使BH＝AE，连接AH， ∵四边形ABCD是菱形，∴AD∥BC，AB＝AD，∴∠ABH＝ ∠BAD.又∵BH＝AE，∴△DAE≌△ABH(SAS)， ∴AH＝DE，∠AHB＝∠DEA＝60°.∵DE＝AF， ∴AH＝AF，∴△AHF是等边三角形， ∴AH＝HF＝HB＋BF＝AE＋BF ＝6＋2＝8，∴DE＝AH＝8.
∴四边形 BEDF 的周长为 8 5.
提能力 9．【2021·重庆】如图，把含30°角的直角三角板PMN放
置在正方形ABCD中，直角顶点P在正方形ABCD的对角线BD上，点M，N分别在AB和CD边上，MN与BD交于点O，且点O为MN的中点，则∠AMP的度数为( C ) A．60° B．65° C．75° D．80°
∵DC＝AB＝3，∴DP＝DC－CP＝3－x，在 Rt△DPF 中，DF＝ DP2＋PF2，
∴DF＝（3－x）2＋x2＝
2x2－6x＋9.
14．【2021·白银】问题解决：如图①，在矩形ABCD中，点E，F分别在AB，BC边上，DE＝AF，DE⊥AF于点 G.

九年级- 正方形知识点典型例题及练习

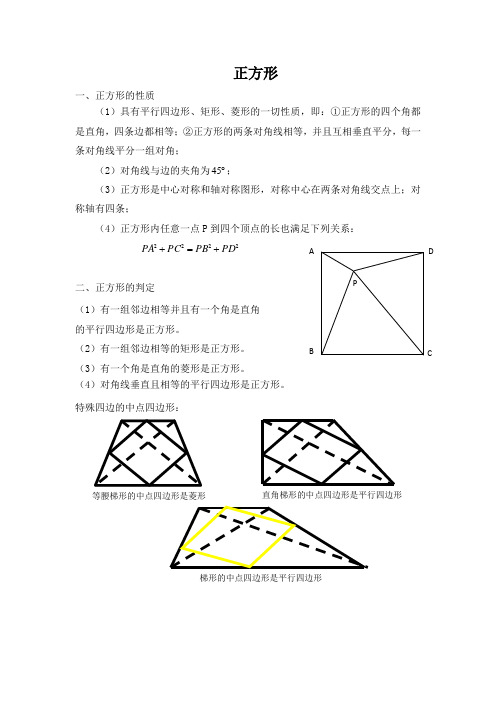
正方形一、正方形的性质（1）具有平行四边形、矩形、菱形的一切性质，即：①正方形的四个角都是直角，四条边都相等；②正方形的两条对角线相等，并且互相垂直平分，每一条对角线平分一组对角；（2）对角线与边的夹角为︒45；（3）正方形是中心对称和轴对称图形，对称中心在两条对角线交点上；对称轴有四条；（4）正方形内任意一点P 到四个顶点的长也满足下列关系： 2222PD PB PC PA +=+二、正方形的判定（1）有一组邻边相等并且有一个角是直角的平行四边形是正方形。

（2）有一组邻边相等的矩形是正方形。

（3）有一个角是直角的菱形是正方形。

（4）对角线垂直且相等的平行四边形是正方形。

特殊四边的中点四边形：ABCDP等腰梯形的中点四边形是菱形直角梯形的中点四边形是平行四边形梯形的中点四边形是平行四边形平行四边形的中点四边形是平行四边形矩形的中点四边形是菱形菱形的中点四边形是矩形正方形的中点四边形是正方形归纳：特殊四边形的中点四边形：◆平行四边形的中点四边形是平行四边形◆矩形的中点四边形是菱形◆菱形的中点四边形是矩形◆正方形的中点四边形是正方形◆等腰梯形的中点四边形是菱形◆直角梯形的中点四边形是平行四边形◆梯形的中点四边形是平行四边形一般四边形的中点四边形：决定中点四边形EFGH的形状的主要因素是原四边形ABCD的对角线的长度和位置关系例题分析例1 下列叙述错误的是（）A.既是矩形又是菱形的四边形是正方形B.有一组邻边相等的矩形是正方形C.有一个角是直角的菱形是正方形D.对角线相等且互相垂直的四边形是正方形例2 如图1-3-1，正方形ABCD 的面积为256，点E 在AD 上，点F 在AB 的延长线上，EC ⊥FC ，∆CEF 的面积是200，则BF 的长是 .例 3 已知E 为边长是1的正方形ABCD 内一点，且AEB S ∆=0.1999，则CED S ∆= .例4 如图1-3-2，正方形ABCD 的边长AB=20，F 为AD 上的一点，连接CF ，作CE ⊥CF 交AB 的延长线于E ，作DG ⊥CF 交CF 于G ，若BE=15，则DG 的长为 .例5 如图1-3-3，正方形ABCD 中，E ，F 为BC ，CD 上的点，且∠EAF=45°，求证EF=BE+DF .1-3-11-3-21-3-3例6 如图1-3-4，正方形ABCD 的边长为4，E ，F 分别为AD ，BC 上的两个点，且BF=DE=1，从EF 的中点O 作EF 的垂直平分线，交CD 于G ，则OG = .例7 如图1-3-5，正方形ABCD 的边长为a ，E ，F ，G ，H 分别在正方形的四条边上，已知EF//GH ，EF=GH ，（1）若AE=AH=13a ，求四边形EFGH 的周长和面积；（2）求四边形EFGH 的周长的最小值.例8 如图1-3-6，已知E 是正方形ABCD 内一点，且∠ECD=∠EDC=15°，则AEB ∠= .90.DEC D DE A DE A AD AEB ∆︒''∆∆∠分析：利用旋转将以为中心顺时针旋转得到，再将以为轴对称即可得出度数1-3-41-3-61-3-51-3-81.在正方形ABCD 内有点P ，使∆PAB 、 ∆PBC 、∆PCD 、∆PDA 都是等腰三角形，那么具有这样性质的点是个2.已知边长为4的正方形ABCD 中，F 是AD 的中点，E 点在AB 边上，且AE:EB=1:3，那么EFC S ∆= .3.一张边长为6的长方形纸片，按图1-3-7加以折叠，使得一角顶点落在对边上，则折痕长为 .4.若P 是边长为1的正方形ABCD 内一点，且0.31ABP S ∆=，则DCP S ∆= .5.边长为10的正方形，把边长增加同样的长度后，所得面积是625，则边长增加了 .6.如图1-3-8将正方形内接于等腰Rt ABC ∆，如果按照图甲的放法，可求得该正方形的面积是441，如果按照图乙的放法，那么只能放边长为的正方形1-3-77.如图1-3-9，在面积为1的正方形ABCD 内取一点P ，使PBC ∆为等边三角形，求∆BPD 的面积.8.如图1-3-10，正方形OPQR 内接于∆ABC .已知∆AOR 、∆BOP 和∆CRQ 的面积分别是1、3和1.试求正方形OPQR 的面积.9.如图1-3-11，已知正方形AC 、BD 相交于点O ，BE 平分∠OBA ，CF ⊥BE 与F ，交OB 于G ，求证OE=OG.10.如图1-3-12，点P 在正方形ABCD 内，若PA:PB:PC=1：2：3，求∠APB 的度数.1-3-91-3-101-3-111-3-1211.如图1-3-13，过正方形ABCD 的顶点B 作直线l ，过,A C 作l 的垂线，垂足分别为,E F .若1AE =，3CF =，则AB 的长度为 .练习12（中，折叠与正方形的性质）如图1-3-14，在正方形纸片ABCD 中，对角线AC 、BD 交于点O ，折叠正方形纸片ABCD ，使AD 落在BD 上，点A 恰好与BD 上的点F 重合。

2024海南中考数学二轮重点专题研究第24课时正方形(课件)

例 2 题图②
(3)如图③，在正方形 ABCD 中，AB＝4，点 G 为 DC 边上的一点，将正方形 ABCD 沿线段 BG 对折后，若∠ABH 比∠GBH 大 15°，则∠GBH 的度数为___2_5_°___；若 G 为 CD 的中点，则 BG 的长为___2__5___；
例 2 题图③
(4)如图④，点 P 是正方形 ABCD 内的一点，点 Q 是正方形外的一点，连接 BP，BQ，若 BQ＝BP 且 BQ⊥BP，连接 AP，CQ.求证：△ABP≌△ CBQ.
海南近年真题及拓展
正方形的性质及相关计算(10 年 6 考)
1．如图，P 是正方形 ABCD 对角线 AC 上一点，点 E 在 BC 上，且 PE ＝PB，连接 PD、DE，若 PD＝ 3 ，则 DE 的长为____6____．
第 1 题图
2．如图，已知正方形ABCD的边长为8，点E、F分别在边BC、CD上，连接AE，以EF为边在正方形ABCD内作正方形EFGH，点H恰好落在AE 上，连接AG，若BE＝6，则AG＝__5__21_0___．
例 2 题图①
(1)若 BE＝1，EC＝3，则正方形 ABCD 的边长为__2__2____，正方形 ABCD 的周长为___8__2___，正方形 ABCD 的面积为____8____；
例2题图①
(2)如图②，连接 AC、BD，交于点 O，若点 E 是 AB 的中点． ①连接 OE，若 BE＝4，则 OE 的长为____4____； ②若 CE 交 BD 于点 F，BF＝3，CF＝ 17 ，则 AC 的长为____8____；
__是__正__方__形____；
(2)请添加一个条件_A__B_＝__A_D__或__A_B__＝__B_C_或__A__D_＝__D__C_或__B_C__＝__C_D____(写出一个即可)，使矩形ABCD为正方形； (2)【判定依据】___有__一__组__邻__边__相__等__的__矩__形__是__正__方__形___________； AC⊥BD；【判定依据】对角线互相垂直的矩形是正方形．

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第24正方形
备考演练
一、精心选一选
1.(2016·海南)面积为2的正方形的边长在( B )
A.0和1之间
B.1和2之间
C.2和3之间
D.3和4之
间
2.( 2016·陕西)如图,在正方形ABCD中,连接BD,点O是BD的中
点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于
两点M'、N',则图中的全等三角形共有( C )
A.2对
B.3对
C.4对
D.5对
第2题图第3题图第4题图
3.(2016·郴州)如图,在正方形ABCD中,△ABE和△CDF为直角三
角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( C )
A.7
B.8
C.7
D.7
4.(2016·贵州)如图,正方形ABCD的边长为9,将正方形折叠,使顶
点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH
的长是( B )
A.3
B.4
C.5
D.6
二、细心填一填
5.(2015·怀化)如图,在正方形AB CD中,如果AF=BE,那么∠AOD 的度数是90°.
第5题图第6题图
6.(2015·北海)如图,已知正方形ABCD的边长为4,对角线AC与BD相交于点O,点E在DC边的延长线上.若∠CAE=15°,则AE=8.
三、用心解一解
7.(2017·上海)已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形
(2)如果BE=BC,且∠CBE∶∠BCE=2∶3,求证:四边形ABCD是正方形.
解:( 1)在△ADE与△CDE中,,
∴△ADE≌△CDE,∴∠ADE=∠CDE,
∵AD∥BC,∴∠ADE=∠CBD,∴∠CDE=∠CBD,∴BC=CD,
∵AD=CD,∴BC=AD,∴四边形ABCD为平行四边形,
∵AD=CD,∴四边形ABCD是菱形
(2)∵BE=BC,∴∠BCE=∠BEC,
∵∠CBE∶∠BCE=2∶3,∴∠CBE=180°×=45°,
∵四边形ABCD是菱形,∴∠ABE=45°,∴∠ABC=90°,∴四边形ABCD是正方形.。

中考数学复习第二部分空间与图形第二十四课时正方形练习

中考数学复习----《正方形的性质》知识点总结与专项练习题(含答案解析)

中考数学复习 第二部分 空间与图形 第二十四课时 正方形课件

第24课时 正方形 课件 2025年中考数学一轮总复习

2019重庆中考数学第24题专题训练---正方形(含答案)

最新人教版初中九年级下册数学【总复习第二十四讲 正方形】教学课件

福建省2022中考数学 第5章 四边形第24课时 正方形(课后练本)课件

九年级- 正方形知识点典型例题及练习

2024海南中考数学二轮重点专题研究 第24课时 正方形(课件)

中考数学复习第二部分空间与图形第二十四课时正方形课件

第24课时正方形课件 2025年中考数学一轮总复习

最新人教版初中九年级下册数学【总复习第二十四讲正方形】教学课件

福建省2022中考数学第5章四边形第24课时正方形(课后练本)课件

2024海南中考数学二轮重点专题研究第24课时正方形(课件)