专题五 第二讲 战考场
最新部编版中考语文考点复习第二部分阅读专题五 非连续性文本阅读

上一页
目录
下一页
个收集卫星信号的喇叭式装置,称得上是目前世界上最金贵的接收器。 与之前世界上最先进的望远镜相比,“中国天眼”的综合观测能力提高了 大约 10 倍,将在未来 10-20 年保持世界领先地位,为我国天文学跻身 世界一流创造了条件。
上一页
目录
下一页
材料二:“中国天眼”是我国科学道路上的一个里程碑。“中国天 眼”的功能、探究成果打开了人类天文学的新征程。2021 年 3 月 31 日起, “中国天眼”向全世界天文学家征集观测权利的申请,以全开放的方式 促进人类科学多维度研究,为人类文明做出包容性贡献。这标志着中国 智慧与世界全人类智慧融合汇聚,将在不久的未来打开一片探索宇宙奧 秘的新天地。
建成使用,将让我国天文学在未来 10-20 年保持世界领先地位。
B.“中国天眼”的启用是我国射电天文学发展史上的一个里程碑。
C.“中国天眼”是世界上最强大的脉冲星搜寻利器,截至 2021 年 5 月,
“中国天眼”已发现脉冲星超过 370 颗。
D.正因为卓越的综合性能,“中国天眼”对于天文观测的重要性不言而喻。
各国政府应对模式产生了激烈的矛盾冲突。
D.帕慕克认为笛福和加缪的作品还有着政治之外的有关人类文明的反
思。
上一页
目录
下一页
4.新冠肺炎疫情带给我们许多反思,根据材料,梳理和概括对这场疫情 我们不应该忘记什么。 示例:客观冷静认识灾难,积极探索战胜灾难的方法,强化正确的舆论 导向。
上一页
目录
下一页
上一页
上一页
目录
下一页
(B)
上一页
目录
下一页
2.根据材料二的内容,下列理解准确的一项是
(D )
中考物理 专题讲解 第二讲 声现象(含解析)(2021年整理)

2018年中考物理专题讲解第二讲声现象(含解析)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018年中考物理专题讲解第二讲声现象(含解析))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018年中考物理专题讲解第二讲声现象(含解析)的全部内容。
声现象【考纲要求】(1)声音的产生和传播,声速;(2)声音的三种特性;(3)噪声的来源及控制;(4)声的利用;(5)与声相关的探究实验;(6)联系与声相关的实际问题。
【命题趋势】近年来对声现象的考查主要集中在声音的产生和传播、怎样防治噪声、超声波(次声波)的应用、乐音的特征等内容上,其中噪声污染、超声波及次声波是新课标考试的热点,值得关注。
【考点精析】一.选择题(共5小题)1.关于声现象,下列说法不正确的是( )A.声音是由物体的振动产生的B.声音不可以在真空中传播C.声源振动的频率越高,音调越高D.音调越高,说明声源振动的幅度越大【考点】91:声音的产生;92:声音的传播条件;9D:频率及音调的关系.【分析】①声音是由物体的振动产生的,一切发声体都在振动;②声音传播需要介质,声音传播的速度与介质种类和温度有关,真空不能传声;③音调是指声音的高低,由频率决定,响度是指声音的强弱,与振幅有关;【解答】解:A、声音是由物体振动产生的,振动停止,发声也就停止.故A叙述正确;B、声音传播需要介质,真空不能传声.故B叙述正确;C、声源振动的频率越高,音调越高.故C叙述正确;D、声音的强弱叫响度,声源振动的幅度越大,响度越大,故D叙述错误.故选D.2.下列各图关于声现象的说法中,正确的是()A.敲击编钟能发声说明声音是由物体的振动产生的B.钢尺振动的越快、响度越大C.街头设置噪声监测仪可以控制噪声D.B型超声波诊断仪可以传递能量【考点】91:声音的产生;9D:频率及音调的关系;9L:防治噪声的途径;9M:声与信息.【分析】①声音的传播需要介质,它可以在气体中传播,也可以在固体和液体中传播,但不能在真空中传播;②声音的高低叫音调,音调决定于发声体振动的快慢;声音的强弱叫响度,响度决定于发声体的振幅和距离发声体的远近;③噪声监测仪可以监控噪声的分贝,但不能控制噪声污染;④声音能够传递信息,也能够传递能量.【解答】解:A、敲击编钟时编钟振动发声,说明声音是由于物体的振动而产生的.故A正确;B、钢尺振动的越快音调越高.故B错误;C、噪声监测仪可以监控噪声污染,但不能控制噪声污染.故C错误;D、超声波具有很强的穿透性,所以B型超声波诊断仪可以用于医疗观察,利用的是声音传递信息.故D错误.故选A.3.如图所示,是小明探究“看”到自己的声音的实验.把两个纸杯底部用细棉线连接起来,固定其中一个纸杯,在纸杯口上蒙上胶膜,膜上粘一小片平面镜,拉紧棉线,将激光笔发出的光照射在平面镜上,小明对另一纸杯说话(不接触纸杯).会看到墙上反射的光点在晃动.在下列说法中正确的是( )A.小明发出的声音是由声带振动产生的B.该实验说明声音不能传递能量C.两个纸杯间声音的传播主要是通过空气实现的D.在月球上做该实验也能看到光点的晃动【考点】91:声音的产生;92:声音的传播条件;9N:声与能量.【分析】(1)声音由物体的振动产生;(2)声音能够传递信息和能量;(3)声音的传播靠介质;固体、液体、气体都可作为传播声音的介质,不同介质中声速不同;真空不能传声;【解答】解:A、声音由物体的振动产生;小明发出的声音是由声带振动产生的;故A正确;B、看到墙上反射的光点在晃动,说明声音能够传递能量;故B错误;C、两个纸杯间声音的传播主要是通过固体棉线传播的;故C错误;D、在月球上是真空,真空不能传声;故做该实验不能成功,不能看到光点的晃动;故D错误;4.物理老师自制了“探究真空是否可以传声”的简易装置如图所示,实验时将正在发声的音乐卡芯固定在拔罐器内,用抽气枪逐步抽出罐内空气,关于该实验下列说法正确的是()A.音乐卡芯发出的声音不是由振动产生的B.音乐卡芯发出的声音尖锐刺耳,说明其声音响度大C.抽气时听到的声音越来越小是由于音调变低的缘故D.由实验可推理出声音不能在真空中传播【考点】91:声音的产生;92:声音的传播条件;9I:音调、响度与音色的区分.【分析】(1)声音是由物体的振动产生;(2)三个特征:音调、响度和音色.音调指声音的高低;响度指声音的大小;音色指声音的音质好坏.(3)在探究真空是否能传声的实验中,采取了实验推理法,即通过不断抽气来减少介质(空气),再根据声音的大小变化来分析得出结论.【解答】解:A、声音都是由物体的振动产生,故A错误;B、声音尖锐刺耳,说明声音的音调高,故B错误;C、抽气时听到的声音越来越小是由于响度变小的缘故,故C错误;D、将正在发声的音乐卡芯固定在拔罐器内,用抽气机抽去空气,声音由大变小,由此我们可以得出声音在真空中无法传播.但现有的抽气设备总是很难将玻璃罩内抽成真空状态,即实验无法达到绝对的真空.在这种情况下,我们是在实验基础上加科学的推理得出的结论.故D正确.5.为了同学们顺利进行中考,考务工作非常细致,用物理知识解释相关做法,正确的是( ) A.用广播指令,说明声音的传播不需要介质B.调节广播音量,是调节音调的高低C.用广播指令,说明声音可以传递信息D.禁止喧哗,是在传播途径中控制噪声【考点】92:声音的传播条件;9L:防治噪声的途径;9M:声与信息.【分析】(1)声音的传播需要介质,电磁波的传播不需要介质;(2)响度指的是声音的大小;(3)声音可以传递信息;(4)有效防治噪声的途径有三条:①在声源处;②在传播过程中;③在人耳处.【解答】解:A、用广播指令,说明声音可以在空气中传播,故A错误;B、调节广播音量,是调节声音的大小,即响度,故B错误;C、用广播指令传达一些信息,说明声音可以传递信息,故C正确;D、禁止喧哗,是在声源处控制噪声,故D错误.故选C.二.填空题(共5小题)6.考场内翻阅试卷的声音是由纸张的振动产生的.倒车雷达利用超声波(选填“超声波”或“次声波”)探测障碍物,帮助司机倒车.【考点】91:声音的产生;9E:超声波与次声波.【分析】声音是由物体的振动产生的;人们可以利用超声波传递信息,如利用回声定位制造的倒车雷达.【解答】解:翻阅试卷的声音是由纸张的振动产生的;倒车雷达是利用超声波传递信息来确定障碍物的远近.故答案为:振动;超声波.7.音乐小组的几位同学自己动手制作了各自的乐器,乐器发声的波形图如下图所示:根据波形图可以知道:三种乐器具有相同的音调,不同的音色.(选填“音色”、“音调")【考点】9I:音调、响度与音色的区分.【分析】声音的三个特性:音调、响度和音色,并能够搞清影响它们的因素.音调与发声体的振动频率有关;响度与振幅有关;音色与发声体有关.【解答】解:频率表示物体振动的快慢,物体振动的越快,频率越大,音调越高.观察图形,相同时间内,经过的周期越多,频率越大.振动物体往返一次叫一个周期.观察图示可知发声体振动的频率相同,所以音调相同;不同乐器、不同发声体的材料和结构不同,产生的音色会不同,我们是靠音色来辨别乐器的种类,所以音乐小组的几位同学的各自的乐器音色不同.故答案为:音调;音色.8.声音是由物体的振动产生的;医生常利用超声波振动粉碎人体内的结石,这说明声音可以传递能量(选填“信息”或“能量”).【考点】91:声音的产生;9N:声与能量.【分析】声音是由物体的振动产生的;声音能够传递信息,声音也能够传递能量.【解答】解:声音是由物体的振动产生的;医生可以利用超声波振动除去人体内的结石,这是由于声音能够传递能量.故答案为:振动;能量.9.小敏在表演二胡时,二胡声是通过空气传递过来的;小敏不断用手指去控制琴弦长度,这样做的目的是为了改变声音的音调;日常生活中,我们常说声音“震耳欲聋”,这是指它的响度很大.【考点】92:声音的传播条件;9D:频率及音调的关系;9F:响度.【分析】音调的高低与发声体振动快慢有关,物体振动越快,音调就越高;声音的传播是需要介质的,它既可以在气体中传播,也可以在固体和液体中传播.【解答】解:小敏在表演二胡时,二胡声是通过空气传到我们的耳朵里;小敏不断用手指去控制琴弦长度时,琴弦振动的快慢会不一样,所以变声音的音调就会发生变化;“震耳欲聋”是说声音的振幅较大,声音的响度也会很大.故答案为:空气;音调;响度.10.如表记录了声波在五种气体中不同温度条件下的传播速度,请依据表中的相关数据回答下列问题:空气氢气氦气氮气二氧化碳03311261891337269103371284908343273203431306924349279303491328939355283①当温度为20℃时,声波在氢气中的传播速度为1306 米/秒.②声波的传播速度与温度的关系是:在同种气体中,声波的传播速度随气体温度升高变快.③根据表格中的数据,最大飞行速度一定的飞机要在空气中实现超音速飞行,在温度较低的条件下更容易成功.(选填“较高”或“较低”)【考点】95:声速的大小跟介质温度的关系.【分析】分析表中数据,对比声音在不同介质中的速度以及在同种介质不同温度时的速度,可以得出结论.【解答】解:①由表中的数据知:当温度为20℃时,声波在氢气中的传播速度为1306m/s;②对比表中声音在不同温度的气体中传播速度,可以得出:声音的传播速度与温度有关.③在同种气体中,声波的传播速度随气体温度降低而减慢,故飞机要在空气中实现超音速飞行,在温度较低的条件下更容易成功.故答案是:①1306;②在同种气体中,声波的传播速度随气体温度升高变快;③较低.三.计算题(共1小题)11.每年到正月十五的时候,小梦家总能看到附近广场上有很多市民放烟花,他在家看到烟花后 2。
中考语文考点专题训练——专题5:标点符号(含答案)

专题五:标点符号一、选择题1、下列句子标点符号使用完全正确的一项是()A“是现在的学校好呢?还是原来的学校好?”老师问一位新转校来的学生。
B《红色歌曲,唱响广安》活动,表达了广安人民对红色历史的缅怀,对革命英雄的崇敬,对幸福生活的赞美……C“我的朋友们啊。
”他说。
”我——我——”D这一小步,对一个人来说,是小小的一步;对整个人来来说,是巨大的飞跃。
2、下死各句中,标点符号的使用合乎规范的一项是()A.“最美司机”昊斌用大爱阐释了生命的价值:76秒,吴斌用生命履行了职责;76秒,吴斌用平凡成就了伟大;76秒,吴斌用行动诠释了人间大爱。
B.在一场暴风雨后,因家庭变故而失学的杜小康觉得自己“突然地长大了,坚强了。
”C.“冰塔儿”既简洁又生动,把葫芦形容得晶莹可人(不管是山楂还是荸荠)。
D.我追想为什么会有那样大的感情震荡,是为了民族而自豪?还是为了稼先而骄傲?3.下列语句中标点符号使用正确的一项是()A.周作人看中国书有一条标准十分独特,就是看作者“对待人的态度”,特别是“对待女人、儿童的态度”。
B.徐悲鸿熟练地运用解剖、透视、和记忆形象的非凡能力,捕捉动物最为传神的瞬间,把猫的娇敏、牛的敦厚、鹰的雄健描绘得淋漓尽致。
C.《记钱钟书与〈围城〉》给我们详尽地介绍了《围城》这部脍炙人口的作品是如何创作出来的?D.微博上,不同群体表现出来的特征各异:“70后”好为人师,制造深度话题,“80后”从不袖手旁观,参与度较高,“90后”则基本上是娱乐。
4、下面这段话,填入括号中的标点符号正确..的一项是()池沼或河道的边沿很少砌齐整的石岸,总是高低屈曲任其自然。
还在那儿布置几块玲珑的石头()或者种些花草()这也是为了取得从各个角度看都成一幅画的效果()池沼里养着金鱼或各色鲤鱼,夏秋季节荷花或睡莲开放,游览者看()鱼戏莲叶间()又是入画的一景。
A、,:。
“ ”,B、,;。
《》C、。
:,,。
D、。
:。
《》5、下列各句标点符号使用正确的一项是()A.仰之弥高,越高,攀得越起劲,钻之弥坚,越坚,钻得越锲而不舍。
中考历史开卷考场速查——高频专题五:世界古代科技思想成就

中考考场速查高频专题五:世界古代科技思想成就【考点链接】(1)东方四大文明古国及文明成果:古代埃及、古代两河流域、古代中国、古代印度(2)古希腊文明:古雅典民主政治(3)古老的文字、世界三大宗教(4)古代文学、科技、建筑成就(5)古代文明的交流与传播【考点速查】◆独家视角:古老的亚非文明是在什么样的地理环境中发生和发展的?为什么?都产生于大河流域。
因为大河流域气候湿润,光热充足,地势平坦,适合人类生存;而且大河河水定期泛滥,提供了充沛的水源和肥沃的土壤,有利于农业生产的发展。
◆独家视角:简析《汉谟拉比法典》和种姓制度的影响。
前18世纪,古巴比伦王国汉谟拉比王为了维护奴隶主阶级的专政,制定了法典,严格维护奴隶主阶级的利益,是目前所知的人类历史上第一部较完备的成文法典,是了解和研究古巴比伦社会的重要资料。
种姓制度是古印度在向奴隶社会过渡的过程中逐渐形成的一种等级制度,是统治者为维护奴隶主统治而采用的措施,激化了当时的社会矛盾,并对后来印度社会的发展带来了不良的影响。
2.西方文明的源头在哪里?有什么文明成果?西方文明发源于古希腊。
其文明成果的代表是公元前5世纪后半期伯利克里执政时期,雅典城邦的奴隶主民主政治发展到古代世界的高峰。
◆独家视角:如何评价伯利克里时代高度发达的奴隶制民主政治?伯利克里改革政治制度,规定一切官职向所有等级的公民开放,公民大会成为最高权力机构。
这种制度下,公民享有比较广泛的权力,为雅典的昌盛提供了政治上的条件和保障,把古代世界的民主政治发展到顶峰,成为一种典型范例,对近代西方民主政治也产生一定影响。
但它是奴隶制民主政治,本质上仍然是少数奴隶主对广大奴隶的专政,能够享受到民主权利的成年男性公民只占雅典人口的1/6。
落。
4.古代文明的交流与传播有哪些方式?请举出实例。
史例1、希波战争:前5世纪,东方帝国波斯与西方希腊城邦在各自发展过程中的一次碰撞,也是早期东西方文明的一次重要冲突。
史例2、亚历山大大帝东征:前4世纪,亚历山大建立起地跨欧亚非三洲的大帝国,促进了东西方文化的交流。
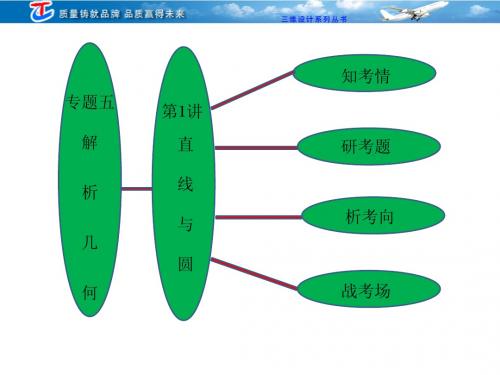
专题五 第一讲 直线与圆
(x-1)2+y2=1
点评:本题主要考查平面图形的折叠问题、二面角以及利 用代入法求圆的方程等知识,涉及空间与平面直角坐标系 与斜坐标系的转化.综合性强、创新角度新颖.
已知圆C:x2+y2=12.直线l:4x+3y=25.圆C上任意一点 A到直线l的距离小于2的概率为________.
解析:如图,设与直线 4x+3y=25 距离为 2 且与该直线平行的直线与 圆交于 P、Q 两点.因为点 O 到直线 PQ 的距离 d=3.又 r=2 3,∴∠ OPQ=60° .若点 A 到直线 l 的距离小于 2,则点 A 只能在弧 PQ 上,∴ P= 60° 1 = . 360° 6
[考题
查漏补缺]
(2011· 重庆高考)设圆C位于抛物线y2=2x与直线x
=3所围成的封闭区域(包含边界)内,则圆C的半径能取到
的最大值为________.
[解析]
依题意,结合图形的对称性可知,要使满足题目约束条件
的圆的半径最大,需圆与抛物线及直线 x=3 同时相切,可设圆心 坐标是(a,0)(0<a<3), 则由条件知圆的方程是(x-a)2+y2=(3-a)2.
结论:
l1∥l2⇔k1=k2且b1≠b2;l1⊥l2⇔k1· 2=-1. k (2)若给定的方程是一般式,即l1:A1x+B1y+C1=0和l2: A2x+B2y+C2=0,则有下列结论: l1∥l2⇔A1B2-A2B1=0且B1C2-B2C1≠0;
l1⊥l2⇔A1A2+B1B2=0.
[做考题
查漏补缺]
答案:D
7.(2011· 湖北高考)过点(-1,-2)的直线 l 被圆 x2+y2-2x-2y +1=0 截得的弦长为 2,则直线 l 的斜率为________.
专题六 第二讲 战考场

一、选择题1.(2011·合肥模拟)某单位在一次春游踏青中,开展有奖答题活动.从2道文史题和3道理科题中不放回地依次抽取2道题,当2道题都是理科题时获奖,则获奖的概率为( )A.925B.625C.310D.12解析:从5道题中抽取2道有A 25种抽法,都是理科题有A 23种抽法,故所求概率为A 23A 25=310. 答案:C2.[理](2011·东北三校)一个篮球运动员投篮一次得3分的概率为a ,得2分的概率为b ,不得分的概率为c ,a 、b 、c ∈(0,1),且无其他得分情况,已知他投篮一次得分的数学期望为1,则ab 的最大值为( )A.148 B.124 C.112D.16解析:依题意得3a +2b +0×c =1,∵a >0,b >0, ∴3a +2b ≥26ab ,即26ab ≤1,∴ab ≤124. 答案:B[文] (2011·郑州质量检测)一个盒子内部有如图所示的六个小格子,现有桔子、苹果和香蕉各两个,将这六个水果随机地放入这六个格子里,每个格子放一个,放好之后每行、每列的水果种类各不相同的概率是( )A.215 B.29 C.15D.13解析:依题意,将这六个不同的水果分别放入这六个格子里,每个格子放入一个,共有A 66=720种不同的放法,其中满足放好之后每行、每列的水果种类各不相同的放法共有96种(此类放法进行分步计数:第一步,确定第一行的两个格子的水果放法,共有C 23·C 12·C 12·A 22=24种放法;第二步,确定第二行的两个格子的水果放法,有C 12·C 12=4种放法,剩余的两个水果放入第三行的两个格子),因此所求的概率等于96720=215.答案:A3.[理](2011·广州模拟)设随机变量ξ服从正态分布N (3,4),若P (ξ<2a -3)=P (ξ>a +2),则a 的值为( )A.73B.53 C .5D .3解析:∵ξ~N (3,4),P (ξ<2a -3)=P (ξ>a +2), ∴2a -3与a +2关于μ=3对称, ∴2a -3+a +22=3,解得a =73. 答案:A[文](2011·重庆高考)从一堆苹果中任取10只,称得它们的质量如下(单位:克): 125 120 122 105 130 114 116 95 120 134 则样本数据落在[114.5,124.5)内的频率为( ) A .0.2 B .0.3 C .0.4D .0.5解析:依题意得,样本数据落在[114.5,124.5)内的频率为410=0.4.答案:C4.(2011·陕西高考)甲乙两人一起去游“2011西安世园会”,他们约定,各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后一小时他们同在一个景点的概率是( )A.136 B.19 C.536D.16解析:若用{1,2,3,4,5,6}代表6处景点,显然甲、乙两人选择结果为{1,1}、{1,2}、{1,3}、…、{6,6},共36种;其中满足题意的“同一景点相遇”包括{1,1}、{2,2}、{3,3}、…、{6,6},共6个基本事件,所以所求的概率值为16.答案:D 二、填空题5.(2011·重庆高考)将一枚均匀的硬币抛掷6次,则正面出现的次数比反面出现的次数多的概率为________.解析:依题意得所求的概率为C 46(12)6+C 56(12)6+C 66·(12)6=1132. 答案:11326.已知函数f (x )=6x -4(x =1,2,3,4,5,6)的值域为集合A ,函数g (x )=2x -1(x =1,2,3,4,5,6)的值域为集合B ,任意x ∈A ∪B ,则x ∈A ∩B 的概率是________.解析:根据已知条件可得A ={2,8,14,20,26,32}, B ={1,2,4,8,16,32}.∴A ∪B ={1,2,4,8,14,16,20,26,32},A ∩B ={2,8,32}. 所以任取x ∈A ∪B ,则x ∈A ∩B 的概率是39=13.答案:137.(2011·江苏高考)某老师从星期一到星期五收到的信件数分别为10,6,8,5,6,则该组数据的方差s 2=________.解析:5个数据的平均数x -=10+6+8+5+65=7,所以s 2=15×[(10-7)2+(6-7)2+(8-7)2+(5-7)2+(6-7)2]=3.2.答案:3.2 三、解答题8.[理]有一种旋转舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为0.5.若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面.(1)求恰好有两个面需要维修的概率; (2)求至少三个面需要更换的概率. 解:(1)因为一个面不需要维修的概率为P 5(3)+P 5(4)+P 5(5)=C 35+C 45+C 5525=12, 所以一个面需要维修的概率为12.因此,六个面中恰好有两个面需要维修的概率为P 6(2)=C 2626=1564. (2)设需要更换的面为ξ个, 则ξ~B (6,12),又P 6(0)=C 0626=164,P 6(1)=C 1626=332,P 6(2)=C 2626=1564,故至少有三个面需要更换的概率是1-P 6(0)-P 6(1)-P 6(2) =1-164-332-1564=2132. 至少三个面需要更换的概率是2132.[文](2011·全国大纲卷)根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立.(1)求该地1位车主至少购买甲、乙两种保险中的1种的概率;(2)求该地的3位车主中恰有1位车主甲、乙两种保险都不购买的概率. 解:记A 表示事件:该地的1位车主购买甲种保险;B 表示事件:该地的1位车主购买乙种保险但不购买甲种保险;C 表示事件:该地的1位车主至少购买甲、乙两种保险中的一种;D 表示事件:该地的1位车主甲、乙两种保险都不购买;E 表示事件:该地的3位车主中恰有1位车主甲、乙两种保险都不购买. (1)P (A )=0.5,P (B )=0.3,C =A +B , P (C )=P (A +B )=P (A )+P (B )=0.8. (2)D =C ,P (D )=1-P (C )=1-0.8=0.2,P (E )=C 13×0.2×0.82=0.384.9.[理]某科技公司遇到一个技术难题,紧急成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期满就攻克技术难题的小组给予奖励.已知这个技术难题在攻关期满时被甲小组攻克的概率为23,被乙小组攻克的概率为34.(1)设ξ为攻关期满时获奖的攻关小组数,求ξ的分布列及Eξ;(2)设η为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数f (x )=⎪⎪⎪⎪η-72x 在定义域内单调递减”为事件C ,求事件C 的概率. 解:记“甲攻关小组获奖”为事件A ,则P (A )=23,记“乙攻关小组获奖”为事件B ,则P (B )=34.(1)由题意,ξ的所有可能取值为0,1,2, P (ξ=0)=P (A ·B )=(1-23)×(1-34)=112,P (ξ=1)=P (A ·B )+P (A ·B )=(1-23)×34+23×(1-34)=512,P (ξ=2)=P (A ·B )=23×34=12,∴ξ的分布列为Eξ=0×112+1×512+2×12=1712.(2)∵获奖攻关小组数的可能取值为0、1、2,相对应没有获奖的攻关小组的取值为2、1、0,∴η的可能取值为0、4.当η=0时,f (x )=⎪⎪⎪⎪η-72x =(72)x , 在定义域内是增函数;当η=4时,f (x )=⎪⎪⎪⎪η-72x =(12)x , 在定义域内是减函数,∴P (C )=P (η=4)=P (A ·B )+P (A ·B )=12+112=712. [文]有一种旋转舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为0.5.若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面.(1)求恰好有两个面需要维修的概率; (2)求至少三个面需要更换的概率.解:(1)因为一个面不需要维修的概率为P 5(3)+P 5(4)+P 5(5)=C 35+C 45+C 5525=12, 所以一个面需要维修的概率为12.因此,六个面中恰好有两个面需要维修的概率为P 6(2)=C 2626=1564. (2)P 6(0)=C 0626=164,P 6(1)=C 1626=332,P 6(2)=C 2626=1564,故至少有三个面需要更换的概率是 1-P 6(0)-P 6(1)-P 6(2) =1-164-332-1564=2132. 至少三个面需要更换的概率是2132. 10.[理]某种家用电器每台的销售利润与该电器的无故障使用时间T (单位:年)有关.若T ≤1,则销售利润为0元;若1<T ≤3,则销售利润为100元;若T >3,则销售利润为200元.设每台该种电器的无故障使用时间T ≤1,1<T ≤3及T >3这三种情况发生的概率分别为p 1,p 2,p 3,又知p 1,p 2是方程25x 2-15x +a =0的两个根,且p 2=p 3.(1)求p 1,p 2,p 3的值;(2)记ξ表示销售两台这种家用电器的销售利润总和,求ξ的分布列; (3)求销售两台这种家用电器的销售利润总和的平均值. 解:(1)由已知得p 1+p 2+p 3=1. ∵p 2=p 3,∴p 1+2p 2=1.p 1,p 2是方程25x 2-15x +a =0的两个根, ∴p 1+p 2=35.∴p 1=15,p 2=p 3=25.(2)ξ的可能取值为0,100,200,300,400. p (ξ=0)=15×15=125,p (ξ=100)=2×15×25=425,p (ξ=200)=2×15×25+25×25=825,p (ξ=300)=2×25×25=825,p (ξ=400)=25×25=425.随机变量ξ的分布列为(3)销售利润总和的平均值为Eξ=0×125+100×425+200×825+300×825+400×425=240.∴销售两台这种家用电器的利润总和的平均值为240元.[文]每进行一次游戏,赢的话可领取1 000元,输的话则要罚300元,在这种游戏中某人赢的概率是13,输的概率是23,如果这个人连续8次进行这种游戏.(1)在这8次游戏中,求赢了多少次才能保证在扣除罚款后至少可得6 000元; (2)试求在这8次游戏中,扣除罚款后至少可得到6 000元的概率. 解:(1)设在这8次游戏中赢了x 次,则输了8-x 次, 依题意1 000x -300(8-x )≥6 000,x ≥6613,故x =7或8,因此在这8次游戏中赢7次或8次,才能保证在扣除罚款后至少可得6 000元. (2)在这8次游戏中,至少要赢7次,才能使扣除罚款后至少可得到6 000元,即必须在这8次游戏中赢7次或8次,由于这两个事件互不相容,因此所求的概率为 P =C 88(13)8+C 78(13)7(23)1=176 561.。
人民版历史必修3:专题五专题过关检测
(时间:90分钟,满分:100分)一、选择题(每题4分,共60分)1.下列说法体现了“双百”方针内涵的是()A.“要革命派,不要流派”B.“争论会引起党内思想不一致”C.“让样板戏占领革命舞台”D.“不打棍子、不戴帽子、不抓辫子”解析:选D。
“双百”方针的基本含义是在艺术问题上百花齐放,在学术问题上百家争鸣,其目的是调动一切积极因素,更好的为人民服务,为社会主义建设服务。
A、B、C三项显然不符合这一精神。
答案为D。
2.在“文化大革命”时期,中国文艺界出现了“八亿人口八个戏”的现象,下图属于“革命样板戏”的是()解析:选D。
注意题干中的限制词“样板戏”,结合教材可知只有京剧《智取威虎山》是“八大样板戏”之一。
3.“文化大革命”时期,许多知识分子受到了伤害;而“文化大革命”后文艺创作重现繁荣。
这最能说明()A.文艺创作有一个兴衰交替的反复过程B.文艺的繁荣不会持久C.文艺的兴衰受制于一定时期的政治环境D.“文化大革命”对文艺有重大的影响解析:选C。
此题考查对文艺与政治环境关系的理解。
一定时期的政治环境决定那个时期文艺的发展方向和程度。
题中所述史实证明了这一结论。
4.艺术创作反映了时代特征,右图“上山下乡光荣”可以直接用于研究的主题是()A.三大改造和“双百方针”的贯彻B.“三下乡”活动C.“文化大革命”的历史D.邓小平全面整顿思想解析:选C。
“文革”期间为解决城市青年就业问题,毛泽东发出知识青年上山下乡的号召。
5.“国运兴衰,系于教育。
”下列有关新中国教育的表述,按出现先后排列正确的是()①实施“科教兴国”战略②面向工农“开门”,开办工农学校③恢复高考④教育要面向现代化,面向世界,面向未来A.②④①③B.②③④①C.④③②①D.④①②③解析:选B。
建国初期,教育开基创业,建立人民教育;1977年恢复高考;20世纪80年代邓小平提出了“三个面向”;90年代中期实施“科教兴国”的战略,故②③④①排序正确,符合题意。
作文专题5——议论文主体段写作教案
精心打造主体段考场写作不畏难——材料议论文主体段落技巧彭爱明学习目标:掌握和熟练写作议论文主体段一、论据分析练习回顾挑战高考——2015福建高考作文阅读下面的材料,根据要求作文。
(70分)地上本没有路,走的人多了,便也成了路。
有时,走错路也是一件有意思的事情,如果没有走错了路,就不会发现新的路。
世上没有走不通的路,只有不敢走的人。
上面三则材料,引发你怎样的感悟和联想?请就此写一篇不少于800字的议论文或记叙文。
要求:(1)必须符合文体要求;(2)角度自选,立意自定,标题自拟;(3)不要脱离材料内容及含意的范围;(4)不得抄袭,不得套作。
(一)审题立意:1、材料显然暗示着思辩,体现了对立中有统一。
三句话虽不同,但有核心词——路,抓住共同点和不同点进行题分析。
(1)共同点:路——围绕“路”进行阐释,根据“不要脱离材料内容及含意的范围”,写作的话题或范围最好是“路”。
(2)不同点:对立中辩证统一第一句:地上没有路——后来有了路第二句:走错路——发现新路第三句:走不通的路——不敢走的人三句话内部看似对立,实则一分为二,矛盾(对立面)在一定条件下是可以转化的。
第一句,没有路,变成有路,条件是,走的人多了。
这是辩证思维的起码规律。
第二句,走错路,也就是走不通了,没有路,但是,可以变成“发现新路”,从错路到新路,这也是对立面的转化。
第三句,“世上没有走不通的路,只有不敢走的人”,仍然矛盾对立的转化。
路走不通是结果,不敢走是原因。
反过来说,只要敢走,联系到前面所说,走错路,走不通,恰恰是发现新路,走通一切路的条件。
三句话都谈的是人生态度。
这个命题的思辩性很明显,而且不是一般的思辩性,而是直接的以抽象的话语,而不是感性经验材料作思辨的基础。
表现上是三句话,实际上包含着三个方面,三个层次有机统一。
这是一个水平极高的命题,更有思维的深处和发挥的空间。
2、确定立意——论点(写作的主旨)三条路有不同的含义,要理解路的象征意义,围绕面对困难、创新、信仰、理想等来立意,找准材料命题的中心,选择自己熟悉的知识、文化背景,贴近思想实际,才能避免空洞。
第一轮第三册专题五第二课人民教育事业的发展
B
A
B
10.我国形成比较完整的国民教育体系是在 A、建国初期 B.“文革”期间 C.20世纪80年代D.20世纪90年代 11.毛泽东提出人民教育事业发展的指导方针是在 A.1 949年 B.1 954年 C.1 957年 D.1 965年 12.刘少奇提出“两种教育制度”是在 A、建国后初期 B.社会主义改造完成后 C.“文革"初期 D、“文革"后期 13.毛泽东号召“知识青年到农村去,接受贫下中农 再教育"的直接原因是 A、知识青年缺乏劳动知识 B.“文化大革命”的需要 C.面临中学毕业生就业压力 D.劳动人民要求 学习科学文化知识
三、新时期教育事业的蓬勃发展
1、背景:“文化大革命”结束后,中国 教育界经过拨乱反正,平反大批冤假错 案,广大教育工作者在政治上获得了新 生。十三大后,教育成为国家优先发展 的战略目标 。
2、恢复发展教育的措施
⑴恢复高考(1977年);建立起中小学教师参评高级 职称等制度。 ⑵坚持“三个面向”,深化教育改革------新时期教育 事业发展的指导方针。(1983年邓小平) ⑶加强教育立法、依法治教: 颁行了《学位条例》、《义务教育法》、《教师 法》、《教育法》、《职业教育法》、《高等教育 法》、《民办教育促进法》等,到20世纪90年代,初 步建立起中国教育法律法规体系的基本框架。为中国 教育的发展提供了有力的法律保障。 (4)1995年《关于加强科学技术进步的决定》明确提出 “科教兴国”战略。
教育法律法规体系的基本框架初步建立 教育法律法规 《学位条例》 《义务教育法》 《教师法》 《教育法》 《职业教育法》 《高等教育法》 《民办教育促进法》 开始正式实施的时间 1981年 1986年 1994年 1995年 1996年 1999年 2003年
【新步步高】2017年人教版语文一轮复习讲义:写作专题训练 专题训练五 Word版含答案
专题训练五善设分论点[专题引语] 考场上绝大多数考生会选择写议论文,而不是记叙文。
可是,面对议论文,考生又多不会“分解”与“剖析”,尤其不会设置分论点和安排分论点,以致文章除了中心论点还是中心论点。
如果能巧妙地设置一些分论点,并很好地安排它们,那么,不仅可以使论证结构更清晰,还可以多角度、多侧面地论述中心论点,使说理更丰实、更深入。
本训练就试图教你一些分论点的设置方法及安排技巧。
真题回放(2016·全国乙)题目见专题训练二“品读佳作”部分。
满分佳作教育之道,不可任性福建一考生标题即中心论点。
《大学》中写道:“大学之道,在明明德。
”诚如斯言,教育的最终目的是培养健全的人格,弘扬美好的德行,而漫画中的孩子脸上的一记巴掌却违背了《大学》的精神。
指出教育之道的内涵,漫画中的“巴掌”违背了教育精神。
从55分进步到61分值得嘉许,但孩子得到55分时的一记巴掌是他进步的关键因素吗?倘若是,那么分数上的进步也不意味着心智和人格上的进步。
再者,从100分退步到98分,可能不只是个人因素,更有试卷难度差异等诸多因素的叠加,那么一记巴掌怎能在学生心中留下积极向上的印记?分析漫画材料,印证观点。
分论点一:教育的手段是情感上的感化与人格上的孕育。
应当看到,教育的手段不应只有“亲吻”和“耳光”两个非黑即白的工具,而应是更多情感上的感化与人格上的孕育。
社会心理学家扎乔克曾言:“人是‘情感优先’的动物。
”人对于事物的认识首先是情感上的直觉判断,在此之后才有事后诸葛亮式的论证。
因此,对学生的情感教育才是更为长久而又有深远意义的育人之道。
一个微笑、一些积极正确的指引能够在学生心中种下健全心灵的植株,在春风化雨下开出希望之花。
分论点二:耳光(代指惩罚)打落的是学生的自信心和自尊心。
况且,一记耳光扬起的是学生的成绩,打落的是学生的自信心和自尊心。
福柯在《规训与惩罚》中写道:“强力惩罚迫使人服从社会意志,进而失去自我。
”由此观之,即使教育者的动机是好的,他采取的手段也不能是任性的一记耳光,正如《发条橙》中“上发条的玩具”,恰是惩戒过度之后的心灵写照。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.(2011·杭州五校质检)在三棱柱ABC-A1B1C1中,底面ABC为边长等于2的等边三角形,AA1⊥底面ABC,AA1=3,那么直线AB与平面A1BC所成角的正弦值为()A.34 B.54C.74 D.34解析:如图,设D为BC的中点,连接A1D,AD,容易得到A1D ⊥BC,AD⊥BC,于是,过A作AH⊥A1D于H,易得AH⊥平面A1BC,连接BH,则∠ABH就是直线AB与平面A1BC所成的角,在Rt△A1AD中,AA1=3,AD=3,A1D=23,∴AH=32,sin∠ABH=34.答案:D2.(2011·重庆高考)到两互相垂直的异面直线的距离相等的点()A.只有1个B.恰有3个C.恰有4个D.有无穷多个解析:在长方体ABCD-A1B1C1D1中建立如图所示的空间直角坐标系,易知直线AD与D1C1是异面且垂直的两条直线,过直线AD与D1C1平行的平面是平面ABCD,因此考虑在平面ABCD内到直线AD与D1C1的距离相等的动点M(x,y,0)的坐标所满足的条件,作MM1⊥AD于点M1,MN⊥CD于点N,NP⊥D1C1于点P,连接MP,易知MN⊥平面CDD1C1,MP⊥D1C1,若MM1=MP,则有y2=x2+a2(其中a是异面直线AD与D1C1间的距离),即有y2-x2=a2,从而可知在平面ABCD内动点M的轨迹是双曲线的一部分,故满足题意的点有无穷多个.答案:D3.(2011·唐山一模)正方体ABCD-A1B1C1D1中,直线A1B与平面A1ACC1所成的角为() A.30°B.45°C.60°D.90°解析:连接BD,设BD∩AC=O,连接A1O,则有BD⊥AC.又AA1⊥平面ABCD,BD ⊂平面ABCD ,因此有BD ⊥AA 1,BD ⊥平面A 1ACC 1,则∠OA 1B 是直线A 1B 与平面A 1ACC 1所成的角.设正方体的棱长为a .在Rt △OA 1B 中,sin ∠OA 1B =OB A 1B =22a 2a =12,所以∠OA 1B =30°, 直线A 1B 与平面A 1ACC 1所成的角是30°.答案:A4.在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,M 为AB 的中点,则点A 到平面A 1DM 的距离为( )A.63a B.66a C.22a D.12a 解析:作AN ⊥DM ,N 为垂足,连接A 1N ,作AG ⊥A 1N ,G为垂足,正方体中AA 1⊥平面ABCD 则AA 1⊥DM ,从而DM ⊥平面AA 1N ,则有DM ⊥AG .又AG ⊥A 1N得AG ⊥平面A 1DM ,AG 即为点A 到平面A 1DM 的距离,在Rt △ADM 中,DA =a ,AM =a 2,DM =52a , AN =AD ·AM DM =55a .在Rt △AA 1N 中, A 1N =AN 2+AA 21=305a , 则AG =AN ·AA 1A 1N =66a . 答案:B二、填空题5.在三棱锥P -ABC 中,∠ABC =90°,PB ⊥平面ABC ,AB =BC =22,PB =2,则点B 到平面PAC 的距离是________.解析:建立空间直角坐标系B -xyz ,如图,则A (22,0,0),C (0,22,0),P (0,0,2)则PA =(22,0,-2).PC =(0,22,-2)设平面PAC 的法向量为n =(x ,y ,z )则⎩⎨⎧ 22x -2z =0,22y -2z =0.取x =1得平面PAC 的一个法向量为n =(1,1,2).又BP =(0,0,2), ∴B 到平面PAC 的距离d =|BP ·n ||n |=222= 2. 答案: 26.(2011·石家庄一检)已知矩形ABCD ,AB =4,BC =3,若将其沿对角线AC 折成直二面角,则异面直线AB 与CD 所成角的余弦值为________.解析:作DE ⊥AC 于点E ,作BF ⊥AC 于点F ,则DE ⊥平面ABC ,BF ⊥平面ADC .且AF =CE =165, AB ·CD =(AF +FB )·(CE +ED )=AF ·CE +AF ·ED +FB ·CE +FB ·ED =-(165)2, 故cos 〈AB ,CD 〉=AB ·CD | AB |·|CD |=-1625, 故异面直线AB ,CD 所成角的余弦值为1625.答案:16257.(2011·广西阶段性检测)如图,已知α-l -β是60°的二面角,A∈l ,射线AC ⊂β,AC 与l 成45°角,线段AP ⊂α,AP ⊥l ,且AP =4,PH ⊥AC 交AC 于H ,则AH =________.解析:过P 作PB ⊥β,垂足为B ,连接AB 、BH ,易知∠PAB 就是二面角α-l -β的平面角,即∠PAB =60°,易得BH ⊥AC ,BA ⊥l ,那么∠BAH =45°.在Rt △PAB 中,可得AB =2,在Rt △HAB 中,可得AH = 2.答案: 2三、解答题8.(2011·新课标全国卷)如图,四棱锥P -ABCD 中,底面ABCD为平行四边形,∠DAB =60°,AB =2AD ,PD ⊥底面ABCD .(1)证明:PA ⊥BD ;(2)若PD =AD ,求二面角A -PB -C 的余弦值.解:(1)证明:因为∠DAB =60°,AB =2AD ,由余弦定理得BD =3AD .从而BD 2+AD 2=AB 2,故BD ⊥AD .又PD ⊥底面ABCD ,可得BD ⊥PD .所以BD ⊥平面PAD .故PA ⊥BD .(2)如图,以D 为坐标原点,AD 的长为单位长,射线DA 为x 轴的正半轴建立空间直角坐标系D -xyz ,则A (1,0,0),B (0,3,0),C (-1,3,0),P (0,0,1). AB =(-1,3,0),PB =(0,3,-1), BC =(-1,0,0).设平面PAB 的法向量为n =(x ,y ,z ),则⎩⎨⎧ n ·AB =0,n ·PB =0,即⎩⎨⎧-x +3y =0,3y -z =0, 因此可取n =(3,1,3). 设平面PBC 的法向量为m ,则⎩⎨⎧m ·PB =0,m ·BC =0, 可取m =(0,-1,-3).则cos 〈m ,n 〉=-427=-277. 故二面角A -PB -C 的余弦值为-277.9.(2011·西城模拟)如图,ABCD 是边长为3的正方形,DE ⊥平面ABCD ,AF ∥DE ,DE =3AF ,BE 与平面ABCD 所成角为60°.(1)求证:AC ⊥平面BDE ;(2)求二面角F -BE -D 的余弦值;(3)设点M 是线段BD 上一个动点,试确定M 的位置,使得AM ∥平面BEF ,并证明你的结论.解:(1)证明:因为DE ⊥平面ABCD ,所以DE ⊥AC .因为ABCD 是正方形,所以AC ⊥BD ,从而AC ⊥平面BDE .(2)因为DA ,DC ,DE 两两垂直,所以建立空间直角坐标系D -xyz 如图所示.因为BE 与平面ABCD 所成角为60°,即∠DBE =60°,所以ED DB = 3. 因为正方形ABCD 的边长为3,所以BD =32,所以DE =36,AF = 6.则A (3,0,0),F (3,0,6),E (0,0,36),B (3,3,0),C (0,3,0),所以BF =(0,-3,6),EF =(3,0,-26),设平面BEF 的法向量为n =(x ,y ,z ),则⎩⎨⎧ n ·BF =0,n ·EF =0,即⎩⎨⎧-3y +6z =0,3x -26z =0, 令z =6,则n =(4,2,6).因为AC ⊥平面BDE ,所以CA 为平面BDE 的一个法向量,CA =(3,-3,0),所以cos 〈n ,CA 〉=n ·CA |n ||CA |=626×32=1313. 因为二面角为锐角,所以二面角F -BE -D 的余弦值为1313. (3)点M 是线段BD 上一个动点,设M (t ,t,0).则AM =(t -3,t,0),因为AM ∥平面BEF ,所以AM ·n =0,即4(t -3)+2t =0,解得t =2.此时,点M 坐标为(2,2,0),BM =13BD ,符合题意. 10.(2011·东莞模拟)如图,在四棱锥P -ABCD 中,侧面PAD ⊥底面ABCD ,侧棱PA =PD =2,底面ABCD 为直角梯形,其中BC ∥AD ,AB ⊥AD ,AD =2AB =2BC =2,O 为AD 中点.(1)求证 :PO ⊥平面ABCD ;(2)求直线BD 与平面PAB 所成角的正弦值;(3)线段AD 上是否存在点Q ,使得它到平面PCD 的距离为32. 解:法一:(1)证明:在△PAD 中,PA =PD ,O 为AD 的中点,∴PO ⊥AD .又侧面PAD ⊥底面ABCD ,平面PAD ∩平面ABCD =AD ,PO ⊂平面PAD ,∴PO ⊥平面ABCD .(2)由(1)知PO ⊥平面ABCD ,∴PO ⊥AB .又AB ⊥AD ,PO ∩AD =O ,∴AB ⊥平面PAD .∴AB ⊥PD .∵PA =PD =2,AD =2,∴在Rt △APD 中,PD ⊥PA ,PA ∩AB =A ,∴PD ⊥平面PAB .∴∠DBP 为直线BD 与平面PAB 所成的角.在Rt △DPB 中,BD =5,PD =2,∴sin ∠DBP =PD BD =25=105.∴直线BD 与平面PAB 所成角的正弦值为105.(3)假设存在点Q ,使得它到平面PCD 的距离为32.设QD =x ,则S △DQC =12x ,由(2)得CD =OB =2,在Rt △POC 中,PC =OC 2+OP 2=2,∴PC =CD =DP = 2.∴S △PCD =34·(2)2=32.由V P -DQC =V Q -PCD ,得13PO ·S △DQC =13·32·S △PDC ,∴x =32.∴存在点Q 满足题意,此时QD =32.法二:(1)同法一(1).(2)由(1)知可以以OC 所在直线为x 轴,OD 所在直线为y 轴,OP 所在直线为z 轴建立空间直角坐标系,得A (0,-1,0),D (0,1,0),B (1,-1,0),C (1,0,0),P (0,0,1), BD =(-1,2,0),AB =(1,0,0),AP =(0,1,1),设平面PAB 的一个法向量为n =(x ,y ,z ),由n ·AP =0,n ·AB =0可以求得n=(0,1,-1),cos〈BD,n〉=10 5,∴直线BD与平面PAB所成角的正弦值为10 5.(3)设平面PCD的一个法向量为m=(a,b,c),DC=(1,-1,0),PD=(0,1,-1),可求得m=(1,1,1).设Q(0,q,0)(-1≤q≤1),QD=(0,1-q,0),那么Q到平面PCD的距离为d=|QD·m||m|=32,解得q=-12,∴在线段AD上存在Q(0,-12,0),使得它到平面PCD的距离为3 2.。
