选修2-2合情推理课时作业
高中数学 课时跟踪检测(十二)合情推理(含解析)新人教A版选修2-2-新人教A版高二选修2-2数学试

课时跟踪检测(十二) 合情推理一、题组对点训练对点练一 数(式)中的归纳推理1.已知数列{a n }的前n 项和S n =n 2·a n (n ≥2),且a 1=1,通过计算a 2,a 3,a 4,猜想a n等于( )A .2(n +1)2B .2n (n +1)C .22n -1D .22n -1解析:选B 由a 1=1,S 2=22·a 2=a 1+a 2得a 2=13,由a 1+a 2+a 3=9×a 3得a 3=16,由a 1+a 2+a 3+a 4=42·a 4得a 4=110,…,猜想a n =2n (n +1),故选B.2.将正整数排列如下图: 12 3 4 5 6 7 8 910 11 12 13 14 15 16 …则2 018出现在 A .第44行第81列 B .第45行第81列 C .第44行第82列D .第45行第82列解析:选D 由题意可知第n 行有2n -1个数,则前n 行的数的个数为1+3+5+…+(2n -1)=n 2,因为442=1 936,452=2 025,且1 936<2 018<2 025,所以2 018在第45行,又第45行有2×45-1=89个数,2018-1 936=82,故2 018在第45行第82列,选D.3.观察下列各式:1=12,2+3+4=32,3+4+5+6+7=52,4+5+6+7+8+9+10=72,…可以得出的一般结论是( )A .n +(n +1)+(n +2)+…+(3n -2)=n 2B .n +(n +1)+(n +2)+…+(3n -2)=(2n -1)2C .n +(n +1)+(n +2)+…+(3n -1)=n 2D .n +(n +1)+(n +2)+…+(3n -1)=(2n -1)2解析:选B 观察各等式的构成规律可以发现,各等式的左边是2n -1(n ∈N *)项的和,其首项为n ,右边是项数的平方,故第n 个等式首项为n ,共有2n -1项,右边是(2n -1)2,即n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2,故选B.4.设f(x)=13x+3,先分别求f(0)+f(1),f(-1)+f(2),f(-2)+f(3),然后归纳出一个一般结论,并给出证明.解:f(0)+f(1)=130+3+13+3=11+3+13+3=3-12+3-36=33.同理f(-1)+f(2)=33,f(-2)+f(3)=33.由此猜想:当x1+x2=1时,f(x1)+f(x2)=33.证明:设x1+x2=1,则f(x1)+f(x2)=13x1+3+13x2+3=3x1+3x2+233x1+x2+3(3x1+3x2)+3=3x1+3x2+233(3x1+3x2)+2×3=3x1+3x2+233(3x1+3x2+23)=33.故猜想成立.对点练二归纳推理在几何中的应用5.如图为一串白黑相间排列的珠子,按这种规律往下排起来,那么第36颗珠子应是什么颜色( )A.白色B.黑色C.白色可能性大D.黑色可能性大解析:选A 由图,知三白二黑周期性排列,36=5×7+1,故第36颗珠子的颜色为白色.6.如图所示,第n个图形是由正n+2边形拓展而来(n=1,2,…),则第n-2个图形共有________个顶点.解析:第一个图有3+3×3=4×3个顶点;第二个图有4+4×4=5×4个顶点;第三个图有5+5×5=6×5个顶点;第四个图有6+6×6=7×6个顶点;……;第n 个图有(n +3)×(n +2)个顶点. 第n -2个图有(n +1)×n =(n 2+n )个顶点. 答案:n 2+n7.某少数民族的刺绣有着悠久的历史,如图(1),(2),(3),(4)为最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮. 现按同样的规律刺绣(小正方形的摆放规律相同),设第n 个图形包含f (n )个小正方形.(1)求出f (5)的值;(2)利用合情推理的“归纳推理思想”,归纳出f (n +1)与f (n )之间的关系式,并根据你得到的关系式求出f (n )的表达式;(3)求1f (1)+1f (2)-1+1f (3)-1+…+1f (n )-1的值. 解:(1)f (5)=41.(2)因为f (2)-f (1)=4=4×1,f (3)-f (2)=8=4×2, f (4)-f (3)=12=4×3, f (5)-f (4)=16=4×4,…由上面规律,得出f (n +1)-f (n )=4n . 因为f (n +1)-f (n )=4n ⇒f (n +1)=f (n )+4n ⇒f (n )=f (n -1)+4(n -1)=f (n -2)+4(n -1)+4(n -2)=f (n -3)+4(n -1)+4(n -2)+4(n -3) =…=f (1)+4(n -1)+4(n -2)+4(n -3)+…+4 =2n 2-2n +1. (3)当n ≥2时,1f (n )-1=12n (n -1)=12⎝ ⎛⎭⎪⎫1n -1-1n .所以1f (1)+1f (2)-1+1f (3)-1+…+1f (n )-1=1+12×⎝ ⎛⎭⎪⎫1-12+12-13+13-14+…+1n -1-1n=1+12⎝ ⎛⎭⎪⎫1-1n =32-12n .对点练三 类比推理8.已知{b n }为等比数列,b 5=2,且b 1b 2b 3…b 9=29.若{a n }为等差数列,a 5=2,则{a n }的类似结论为( )A .a 1a 2a 3…a 9=29B .a 1+a 2+…+a 9=29C .a 1a 2…a 9=2×9D .a 1+a 2+…+a 9=2×9解析:选D 等比数列中的积(乘方)类比等差数列中的和(积),得a 1+a 2+…+a 9=2×9. 9.在平面中,△ABC 的∠ACB 的平分线CE 分△ABC 面积所成的比S △AEC S △BEC =ACBC,将这个结论类比到空间:在三棱锥A BCD 中,平面DEC 平分二面角A CD B 且与AB 交于E ,则类比的结论为________.解析:平面中的面积类比到空间为体积,故S △AEC S △BEC 类比成V A CDEV B CDE.平面中的线段长类比到空间为面积,故ACBC 类比成S △ACD S △BDC .故有V A CDE V B CDE =S △ACDS △BDC. 答案:V A CDE V B CDE =S △ACDS △BDC10.在矩形ABCD 中,对角线AC 与两邻边所成的角分别为α,β,则cos 2α+cos 2β=1,在立体几何中,通过类比,给出猜想并证明.解:如图①,在矩形ABCD 中,cos 2α+cos 2β=⎝ ⎛⎭⎪⎫a c 2+⎝ ⎛⎭⎪⎫b c 2=a 2+b 2c 2=c2c 2=1.于是类比到长方体中,猜想其体对角线与共顶点的三条棱所成的角分别为α,β,γ, 则cos 2α+cos 2β+cos 2γ=1,证明如下:如图②,cos 2α+cos 2β+cos 2γ=⎝ ⎛⎭⎪⎫m l 2+⎝ ⎛⎭⎪⎫n l 2+⎝ ⎛⎭⎪⎫g l 2=m 2+n 2+g 2l 2=l 2l 2=1.二、综合过关训练1.观察下列各式:72=49,73=343,74=2 401,…,则72 018的末两位数字为( )A .01B .43C .07D .49解析:选D 因为71=7,72=49,73=343,74=2 401,75=16 807,76=117 649,…, 所以这些数的末两位数字呈周期性出现,且周期T =4.又2 018=4×504+2, 所以72 018的末两位数字与72的末两位数字相同,为49.2.定义A *B ,B *C ,C *D ,D *B 依次对应下列4个图形:那么下列4个图形中,可以表示A *D ,A *C 的分别是( ) A .(1),(2) B .(1),(3) C .(2),(4)D .(1),(4)解析:选C 由①②③④可归纳得出:符号“*”表示图形的叠加,字母A 代表竖线,字母B 代表大矩形,字母C 代表横线,字母D 代表小矩形,∴A *D 是(2),A *C 是(4).3.古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:他们研究过图(1)中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图(2)中的1,4,9,16,…,这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )A .289B .1 024C .1 225D .1 378解析:选C 记三角形数构成的数列为{a n },则a 1=1,a 2=3=1+2,a 3=6=1+2+3,a 4=10=1+2+3+4,可得通项公式为a n =1+2+3+…+n =n (n +1)2.同理可得正方形数构成的数列的通项公式为b n =n 2.将四个选项的数字分别代入上述两个通项公式,使得n 都为正整数的只有1 225.4.将正偶数2,4,6,8,…按下表的方式进行排列,记a ij 表示第i 行和第j 列的数,若a ij=2 018,则i +j 的值为( )第1 列 第2列 第3列 第4列 第5列 第1行2 4 6 8 第2行 1614 12 10 第3行18 20 22 24 第4行 3230 28 26 第5行34 36 38 40 ………………A .257B .256C .255D .254解析:选C 由表所反映的信息来看,第n 行的最大偶数为S n =8n (n ∈N *),则8(i -1)<2 018≤8i ,由于i ∈N *,解得i =253;另一方面,奇数行的最大数位于第5列,偶数行的最大数位于第1列,第252行最大数为8×252=2 016,此数位于第252行第1列,因此2 018位于第253行第2列,所以i =253,j =2,故i +j =253+2=255,故选C.5.设等差数列{a n }的前n 项和为S n ,则S 4,S 8-S 4,S 12-S 8,S 16-S 12成等差数列.类比以上结论有:设等比数列{b n }的前n 项积为T n ,则T 4,________,________,T 16T 12成等比数列. 解析:等差数列类比于等比数列时,和类比于积,减法类比于除法,可得类比结论为:设等比数列{b n }的前n 项积为T n ,则T 4,T 8T 4,T 12T 8,T 16T 12成等比数列. 答案:T 8T 4T 12T 86.如图(1),在三角形ABC 中,AB ⊥AC ,若AD ⊥BC ,则AB 2=BD ·BC .若类比该命题,如图(2),三棱锥A BCD 中,AD ⊥平面ABC ,若A 点在三角形BCD 所在平面内的射影为M ,则有什么结论?命题是不是真命题.解:命题是:三棱锥A BCD 中,AD ⊥平面ABC ,若A 点在三角形BCD 所在平面内的射影为M ,则有S 2△ABC =S △BCM ·S △BCD .此命题是一个真命题.证明如下:在图(2)中,延长DM 交BC 于E ,连接AE ,则有DE ⊥BC . 因为AD ⊥平面ABC , 所以AD ⊥AE .又AM ⊥DE ,所以AE 2=EM ·ED .于是S 2△ABC =⎝ ⎛⎭⎪⎫12BC ·AE 2=⎝ ⎛⎭⎪⎫12BC ·EM ·⎝ ⎛⎭⎪⎫12BC ·ED =S △BCM ·S △BCD .7.如图所示为m 行m +1列的士兵方阵(m ∈N *,m ≥2).(1)写出一个数列,用它表示当m 分别是2,3,4,5,…时,方阵中士兵的人数; (2)若把(1)中的数列记为{a n },归纳该数列的通项公式; (3)求a 10,并说明a 10表示的实际意义; (4)已知a n =9 900,问a n 是数列第几项?解:(1)当m =2时,表示一个2行3列的士兵方阵,共有6人,依次可以得到当m =3,4,5,…时的士兵人数分别为12,20,30,….故所求数列为6,12,20,30,….(2)因为a 1=2×3,a 2=3×4,a 3=4×5,…,所以猜想a n =(n +1)(n +2),n ∈N *. (3)a 10=11×12=132.a 10表示11行12列的士兵方阵的人数为132.(4)令(n +1)(n +2)=9 900,所以n =98,即a n 是数列的第98项,此时方阵为99行100列.。
【人教A版高中数学复习精练及解析】选修2-2 第二章 2.1.1 合情推理 复习练习

选修2-2 第二章 2.1.1 合情推理 复习练习[A 基础达标]1.观察数列1,5,14,30,x ,…,则x 的值为( ) A .22 B .33 C .44D .552.如图,观察图形规律,在其右下角的空格处画上合适的图形,应为( )3.把下列在平面内成立的结论类比到空间,结论不成立的是( ) A .如果一条直线与两条平行线中的一条相交,则必与另一条相交 B .如果一条直线与两条平行线中的一条垂直,则必与另一条垂直 C .如果两条直线与第三条直线都不相交,则这两条直线不相交 D .如果两条直线同时与第三条直线垂直,则这两条直线平行4.《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术.得诀自诩无所阻,额上坟起终不悟.”在这里,我们称以下形式的等式具有“穿墙术”:223=223,338=338,4415=4415,5524=5524,…. 按照以上规律,若88n =88n具有“穿墙术”,则n =( ) A .7 B .35 C .48D .635. 如图,椭圆的中心在坐标原点,F 为其左焦点,当FB →⊥AB →时,椭圆的离心率为5-12,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”可得“黄金双曲线”的离心率为( )A.5+12B.5-12C.5-1D.5+16.在平面直角坐标系xOy 中,二元一次方程Ax +By =0(A ,B 不同时为0)表示过原点的直线.类似地,在空间直角坐标系Oxyz 中,三元一次方程Ax +By +Cz =0(A ,B ,C 不同时为0)表示________.7.观察下列等式: 1+1=2×1,(2+1)(2+2)=22×1×3,(3+1)(3+2)(3+3)=23×1×3×5, …照此规律,第n 个等式可为________________________.8.根据图(1)的面积关系:S △PA ′B ′S △PAB =PA ′PA ·PB ′PB ,可猜想图(2)有体积关系:V P A ′B ′C ′V P ABC=________.9.已知数列{a n }的前n 项和S n =n 2·a n (n ≥2),而a 1=1,通过计算a 2,a 3,a 4,猜想a n .10.在公比为4的等比数列{b n }中,若T n 是数列{b n }的前n 项积,则有T 20T 10,T 30T 20,T 40T 30也是等比数列,且公比为4100;类比上述结论,相应地在公差为3的等差数列{a n }中,若S n 是{a n }的前n 项和,写出相应的结论,判断该结论是否正确,并加以证明.[B能力提升]11.将正奇数按如图所示的规律排列,则第21行从左向右的第5个数为()135791113151719212325272931…A.809 B.853C.785 D.89312.如图,在等腰直角三角形ABC中,斜边BC=22,过点A作BC的垂线,垂足为A1,过点A1作AC的垂线,垂足为A2;过点A2作A1C的垂线,垂足为A3;…,以此类推,设BA=a1,AA1=a2,A1A2=a3,…,A5A6=a7,则a7=________.13.如图所示为m行m+1列的士兵方阵(m∈N*,m≥2).(1)写出一个数列,用它表示当m分别是2,3,4,5,…时,方阵中士兵的人数;(2)若把(1)中的数列记为{a n},①归纳猜想该数列的通项公式;②求a10,并说明a10表示的实际意义;③若a m=9 900,求a m是数列{a n}的第几项,此时的方阵为几行几列.14.(选做题)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:①sin2 13°+cos2 17°-sin 13°cos 17°;②sin2 15°+cos2 15°-sin 15°cos 15°;③sin2 18°+cos2 12°-sin 18°cos 12°;④sin2 (-18°)+cos2 48°-sin (-18°)cos 48°;⑤sin2 (-25°)+cos2 55°-sin (-25°)cos 55°.(1)试从上述五个式子中选择一个,求出这个常数;(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.选修2-2 第二章 2.1.1 合情推理 复习练习[A 基础达标]1.解析:选D.观察归纳得出,从第2项起,每一项都等于它的前一项与它本身项数的平方的和,即a n =a n -1+n 2,所以x =30+52=55. 2.解析:选 A.观察题图中每一行、每一列的规律,从形状和颜色入手,每一行、每一列中三种图形都有,故填长方形;又每一行、每一列中的图形的颜色应有二黑一白,故选A.3.解析:选D.类比A 的结论为:如果一个平面与两个平行平面中的一个相交,则必与另一个相交,成立.类比B 的结论为:如果一个平面与两个平行平面中的一个垂直,则必与另一个垂直,成立. 类比C 的结论为:如果两个平面与第三个平面都不相交,则这两个平面不相交,成立. 类比D 的结论为:如果两个平面同时与第三个平面垂直,则这两个平面平行,不成立. 4. 解析:选D.223=2222-1=223,338=3 332-1=338,4415=4442-1=4415,5524=5 552-1=5524,…,按照以上规律可得n =82-1=63. 5.解析:选A.设双曲线方程为x 2a 2-y 2b 2=1(a >0,b >0),F (-c ,0),B (0,b ),A (a ,0),则FB →=(c ,b ),AB →=(-a ,b ).因为FB →⊥AB →,所以FB →·AB →=-ac +b 2=0.又b 2=c 2-a 2,所以c 2-ac -a 2=0,即e 2-e -1=0,解得e =1±52.又e >1,所以e =1+52.故选A. 6.解析:由方程的特点可知:平面几何中的直线类比到立体几何中应为平面,“过原点”类比仍为“过原点”,因此应得到:在空间直角坐标系Oxyz 中,三元一次方程Ax +By +Cz =0(A ,B ,C 不同时为0)表示过原点的平面.答案:过原点的平面 7.解析:观察规律可知,左边为n 项的积,最小项和最大项依次为(n +1),(n +n ),右边为连续奇数之积乘以2n ,则第n 个等式为:(n +1)(n +2)…(n +n )=2n ×1×3×…×(2n -1).答案:(n +1)(n +2)…(n +n )=2n ×1×3×…×(2n -1) 8.解析:题干两图中,与△PAB ,△PA ′B ′相对应的是三棱锥P -ABC ,P A ′B ′C ′;与△PA ′B ′两边PA ′,PB ′相对应的是三棱锥P -A ′B ′C ′的三条侧棱PA ′,PB ′,PC ′.与△PAB 的两条边PA ,PB 相对应的是三棱锥P -ABC 的三条侧棱PA ,PB ,PC .由此,类比题图(1)的面积关系,得到题图(2)的体积关系为V P A ′B ′C ′V P ABC=PA ′PA ·PB ′PB ·PC ′PC . 答案:PA ′PA ·PB ′PB ·PC ′PC9.解:因为S n =n 2·a n (n ≥2),a 1=1, 所以S 2=4·a 2=a 1+a 2,a 2=13=23×2.S 3=9a 3=a 1+a 2+a 3,a 3=a 1+a 28=16=24×3. S 4=16a 4=a 1+a 2+a 3+a 4,a 4=a 1+a 2+a 315=110=25×4.所以猜想a n =2n (n +1). 10.解:结论:S 20-S 10,S 30-S 20,S 40-S 30也是等差数列且公差为300.此结论是正确的,证明如下: 因为数列{a n }的公差d =3.所以(S 30-S 20)-(S 20-S 10)=(a 21+a 22+…+a 30)-(a 11+a 12+…+a 20)==100d =300.同理:(S 40-S 30)-(S 30-S 20)=300,所以S 20-S 10,S 30-S 20,S 40-S 30是等差数列且公差为300.[B 能力提升]11.解析:选A.前20行共有正奇数1+3+5+…+39=202=400(个),则第21行从左向右的第5个数是第405个正奇数,所以这个数是2×405-1=809.12.解析:根据题意易得a 1=2,a 2=2,a 3=1, 所以{a n }构成以a 1=2,q =22的等比数列, 所以a 7=a 1q 6=2×⎝⎛⎭⎫226=14.答案:1413.解:(1)当m =2时,表示一个2行3列的士兵方阵,共有6人,同理可以得到当m =3,4,5,…时的士兵人数分别为12,20,30,…,故所求数列为6,12,20,30,….(2)①因为a 1=2×3,a 2=3×4,a 3=4×5,…, 所以猜想a n =(n +1)(n +2),n ∈N *. ②a 10=11×12=132.a 10表示11行12列的士兵方阵的人数为132.③令(m +1)(m +2)=9 900,所以m =98,即a m 是数列{a n }的第98项,此时的方阵为99行100列. 14.解:(1)选择②式,计算如下:sin 2 15°+cos 2 15°-sin 15°cos 15°=1-12sin 30°=1-14=34.(2)三角恒等式为sin 2 α+cos 2(30°-α)-sin αcos(30°-α)=34.证明如下:sin 2 α+cos 2(30°-α)-sin αcos(30°-α)=sin 2 α+(cos 30°cos α+sin 30° sin α)2-sin α(cos 30°cos α+sin 30°sin α)=sin 2 α+34cos 2 α+32sin αcos α+14sin 2 α-32sin αcos α-12sin 2 α=sin 2 α+34cos 2 α-14sin 2 α =34sin 2 α+34cos 2 α=34.。
高中数学 2.1《合情推理与演绎推理》测试(1) 新人教B版选修2-2

合情推理与演绎推理一、归纳推理 例1.(1)观察圆周上n 个点之间所连的弦,发现两个点可以连一条弦,3个点可以连3条弦,4个点可以连6条弦,5个点可以连10条弦,你由此可以归纳出什么规律?变式1.设平面内有n 条直线)3(≥n ,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用)(n f 表示这n 条直线交点的个数,则)4(f =____________;当4>n 时,=)(n f .(用n 表示)变式2.在圆内画一条线段,将圆分成两部分;画两条线段,彼此最多分割成4条线段,同时将圆分割成4部分;画三条线段,彼此最多分割成9条线段,同时将圆分割成7部分.那么 (1)在圆内画四条线段,彼此最多分割成 条线段?同时将圆分割成 部分?(2)猜想:圆内两两相交的n (n ≥2)条线段,彼此最多分割成 条线段?同时将圆分割成 部分?强化训练1.某同学在电脑上打下了一串黑白圆,如图所示,○○○●●○○○●●○○○…,按这种规律往下排,那么第36个圆的颜色应是 .2.由107>85,119>108,2513>219,…若a >b >0,m >0,则m a m b ++与a b 之间的大小关系为 .3.下列推理是归纳推理的是 (填序号).①A ,B 为定点,动点P 满足|PA |+|PB |=2a >|AB |,得P 的轨迹为椭圆 ②由a 1=1,a n =3n -1,求出S 1,S 2,S 3,猜想出数列的前n 项和S n 的表达式 ③由圆x 2+y 2=r 2的面积πr 2,猜想出椭圆2222b y a x +=1的面积S =πab④科学家利用鱼的沉浮原理制造潜艇4.已知整数的数对列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…则第60个数对是 .二、类比推理(一)数列中的类比例1.在等差数列{}n a 中,若010=a ,则有等式n a a a +⋅⋅⋅++21),19(1921+-∈<+⋅⋅⋅++=N n n a a a n 成立,类比上述性质,相应地:在等比数列{}n b 中,若19=b ,则有等式 成立.强化练习1.定义“等和数列”,在一个数列中,如果每一项与它的后一项的和都为同一常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。
【人教B版】选修2-2:2.1.1《合情推理》课时作业及答案

【成才之路】高中数学 第2章 2.1第1课时 合情推理课时作业 新人教B 版选修2-2一、选择题1.下面使用类比推理正确的是( )A .“若a ·4=b ·4,则a =b ”类比推出“若a ·0=b ·0,则a =b ”B .“(a +b )c =ac +bc ”类比推出“(a ·b )c =ac ·bc ”C .“(a +b )c =ac +bc ”类比推出“a +bc =a c +bc(c ≠0)” D .“(ab )n=a n b n”类比推出“(a +b )n=a n+b n” [答案] C2.已知数列{a n }满足a 1=0,a n +1=a n -33a n +1(n ∈N +),则a 20=( ) A .0 B .- 3 C. 3 D .32[答案] B[解析] ∵a 1=0,∴a 2=-3,a 3=-3-3-2=3,a 4=0,…,由此可以看出周期为3,∴a 20=a 3×6+2=a 2=- 3.3.下面几种推理是合情推理的是( ) ①由圆的性质类比出球的有关性质;②由直角三角形、等腰三角形、等边三角形的内角和是180°,归纳出所有三角形的内角和都是180°;③教室内有一把椅子坏了,则该教室内的所有椅子都坏了;④三角形内角和是180°,四边形内角和是360°,五边形内角和是540°,由此得凸多边形内角和是(n -2)·180°.A .①②B .①③④C .①②④D .②④[答案] C[解析] ①是合情推理中的类比法,排除D ;②是归纳推理,排除B ;④是归纳推理.故选C.4.已知数列{a n }中,a 1=1,当n ≥2时,a n =2a n -1+1,依次计算a 2,a 3,a 4后,猜想a n的一个表达式是( )A.n2-1 B.(n-1)2+1C.2n-1 D.2n-1+1[答案] C[解析]a2=2a1+1=2×1+1=3,a3=2a2+1=2×3+1=7,a4=2a3+1=2×7+1=15,利用归纳推理,猜想a n=2n-1,故选C.5.观察(x2)′=2x,(x4)′=4x3,(cos x)′=-sin x,由归纳推理可得:若定义在R 上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)=( ) A.f(x) B.-f(x)C.g(x) D.-g(x)[答案] D[解析]本题考查了推理证明及函数的奇偶性内容,由例子可看出偶函数求导后都变成了奇函数,∴g(-x)=-g(x),选D,体现了对学生观察能力,概括归纳推理能力的考查.6.我们把4,9,16,25,…这些数称做正方形数,这是因为这些数目的点子可以排成一个正方形(如下图),则第n-1个正方形数是( )A.n(n-1) B.n(n+1)C.n2D.(n+1)2[答案] C[解析]第n-1个正方形数的数目点子可排成n行n列,即每边n个点子的正方形,∴点数为n2.故选C.7.根据给出的数塔猜测123456×9+7等于( )1×9+2=1112×9+3=111123×9+4=11111234×9+5=1111112345×9+6=111111…A.1111110 B.1111111C.1111112 D.1111113[答案] B[解析]由数塔猜测应是各位都是1的七位数,即1111111.8.观察图所示图形规律,在其右下角的空格内画上合适的图形为( )A. B.△C. D .○[答案] A[解析] 由每行或每列均有2个黑色图形知,本题选A. 二、填空题9.甲、乙、丙三位同学被问到是否去过A ,B ,C 三个城市时, 甲说:我去过的城市比乙多,但没去过B 城市; 乙说:我没去过C 城市; 丙说:我们三人去过同一城市; 由此可判断乙去过的城市为________. [答案] A[解析] 利用逻辑推理的知识求解.由题意可推断:甲没去过B 城市,但比乙去的城市多,而丙说“三人去过同一城市”,说明甲去过A ,C 城市,而乙“没去过C 城市”,说明乙去过城市A ,由此可知,乙去过的城市为A .10.对于等差数列{a n }有如下命题:“若{a n }是等差数列,a 1=0,s 、t 是互不相等的正整数,则有(s -1)a t -(t -1)a s =0”.类比此命题,给出等比数列{b n }相应的一个正确命题是________.[答案] 若{b n }是等比数列,b 1=1,s 、t 是互不相等的正整数,则有b s -1tb t -1s=1[解析] 这是一个从等差数列到等比数列的平行类比,等差数列中的加、减、乘、除类比到等比数列经常是乘、除、乘方、开方,类比方法的关键在于善于发现不同对象之间的“相似”,“相似”是类比的基础.∴b s -1t b t -1s =b 1·q t -1s -1b 1·q s -1t -1=1.11.观察下列等式: (1+1)=2×1;(2+1)(2+2)=22×1×3;(3+1)(3+2)(3+3)=23×1×3×5; ……照此规律,第n 个等式可为______________________. [答案] (n +1)(n +2)…(n +n )=2n×1×3×…×(2n -1)[解析] 观察规律,等号左侧第n 个等式共有n 项相乘,从n +1到n +n ,等式右端是2n与等差数列{2n -1}前n 项的乘积,故第n 个等式为(n +1)(n +2)…(n +n )=2n×1×3×…×(2n -1).三、解答题12.已知等差数列{a n }的公差为d ,前n 项和为S n ,有如下的性质: (1)通项a n =a m +(n -m )·d (n >m ,n ,m ∈N *)(2)若m +n =p +q ,其中,m 、n 、p 、q ∈N *,则a m +a n =a p +a q . (3)若m +n =2p ,m ,n ,p ∈N *,则a m +a n =2a p . (4)S n ,S 2n -S n ,S 3n -S 2n 构成等差数列.类比上述性质,在等比数列{b n }中,写出相类似的性质. [解析] 等比数列{b n }中,设公比为q ,前n 项和为S n . (1)a n =a m ·qn -m(n >m ,n ,m ∈N *).(2)若m +n =p +q ,其中m ,n ,p ,q ∈N *, 则a m ·a n =a p ·a q .(3)若m +n =2p ,其中,m ,n ,p ∈N *,则a 2p =a m ·a n . (4)S n ,S 2n -S n ,S 3n -S 2n (各项均不为零)构成等比数列.一、选择题1.设0<θ<π2,已知a 1=2cos θ,a n +1=2+a n ,则猜想a n =( )A .2cos θ2nB .2cos θ2n -1 C .2cos θ2n +1D .2sin θ2n[答案] B[解析] ∵a 1=2cos θ,a 2=2+2cos θ=21+cos θ2=2cos θ2,a 3=2+2a 2=21+cos θ22=2cos θ4……,猜想a n =2cos θ2n -1.故选B.2.类比平面内正三角形的“三边相等,三内角相等”的性质,可推知正四面体的下列哪些性质,你认为比较恰当的是( )①各棱长相等,同一顶点上的任两条棱的夹角都相等;②各个面都是全等的正三角形,相邻两个面所成的二面角都相等; ③各个面都是全等的正三角形,同一顶点上的任两条棱的夹角都相等. A .① B .①② C .①②③ D .③[答案] C[解析] 正四面体的面(或棱)可与正三角形的边类比,正四面体的相邻两面成的二面角(或共顶点的两棱的夹角)可与正三角形相邻两边的夹角类比,故①②③都对.故选C.3.把3、6、10、15、21、…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如下图),试求第六个三角形数是( )A .27B .28C .29D .30[答案] B[解析] 观察归纳可知第n -1个三角形数共有点数:1+2+3+4+…+n =n n +12个,∴第六个三角形数为7×7+12=28.故选B. 4.(2015·甘肃省会宁一中高二期中)如图,椭圆中心在坐标原点,F 为左焦点,当FB →⊥AB →时,其离心率为5-12,此类椭圆被称为“黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率为( )A.5+12B .5-12C.5+1 D .5-1[答案] A[解析] 类比“黄金椭圆”,在黄金双曲线中,|OA |=a ,|OB |=b ,|OF |=c , 当FB →⊥AB →时,|BF |2+|AB |2=|AF |2, ∴b 2+c 2+c 2=a 2+c 2+2ac , ∵b 2=c 2-a 2,整理得c 2=a 2+ac , ∴e 2-e -1=0,解得e =5+12,或e =-5+12(舍去). 故黄金双曲线的离心率e =5+12. 二、填空题5.在平面上,若两个正三角形的边长比为12,则它们的面积比为14.类似地,在空间中,若两个正四面体的棱长比为12,则它们的体积比为________.[答案] 18[解析] V 1V 2=13S 1h 113S 2h 2=S 1S 2·h 1h 2=14×12=18.6.(2015·陕西文,16)观察下列等式 1-12=121-12+13-14=13+141-12+13-14+15-16=14+15+16 ……据此规律,第n 个等式可为_________________________________. [答案] 1-12+13-14+…+12n -1-12n =1n +1+1n +2+…+12n[解析] 观察等式知:第n 个等式的左边有2n 个数相加减,奇数项为正,偶数项为负,且分子为1,分母是1到2n 的连续正整数,等式的右边是 1n +1+1n +2+…+12n.故答案为1-12+13-14+…+12n -1-12n =1n +1+1n +2+…+12n三、解答题7.在△ABC 中,不等式1A +1B +1C ≥9π成立,在四边形ABCD 中,不等式1A +1B +1C +1D ≥162π成立,在五边形ABCDE 中,不等式1A +1B +1C +1D +1E ≥253π成立,猜想在n 边形A 1A 2…A n 中,有怎样的不等式成立?[解析] 根据已知特殊的数值:9π、162π、253π,…,总结归纳出一般性的规律:n2n -2π(n ≥3且n ∈N *).∴在n 边形A 1A 2…A n 中:1A 1+1A 2+…+1A n≥n 2n -2π(n ≥3且n ∈N *).8.已知等式sin 210°+cos 240°+sin10°cos40°=34,sin 26°+cos 236°+sin6°cos36°=34.请写出一个具有一般性的等式,使你写出的等式包含已知的等式,并证明结论的正确性.[解析] 等式为sin 2α+cos 2(30°+α)+sin αcos(30°+α)=34.证明如下:sin 2α+cos 2(30°+α)+sin αcos(30°+α) =sin 2α+1+cos 60°+2a2+sin α(cos30°·cos α-sin30°·sin α)=12+sin 2α+cos60°+2α2+34sin2α-12sin 2α=12+sin 2α+12(12cos2α-32sin2α)+34sin2α-12sin 2α=12+sin 2α+14cos2α-34sin2α+34sin2α-12sin 2α=12+12sin 2α+14(1-2sin 2α)=34.。
人教版新课标A版高中选修2-2数学2.1合情推理与演绎推理同步练习A卷

人教版新课标A版选修2-2数学2.1合情推理与演绎推理同步练习A卷姓名:________ 班级:________ 成绩:________一、选择题 (共15题;共30分)1. (2分)下列命题中正确的是()A . 类比推理是一般到特殊的推理B . 演绎推理的结论一定是正确的C . 合情推理的结论一定是正确的D . 演绎推理在前提和推理形式都正确的前提下,得到的结论一定是正确的2. (2分)下图是某光缆的结构图,其中数字为某段的最大信息量,则从M到N的最大信息量为()A . 6B . 7C . 12D . 213. (2分) (2016高二上·衡阳期中) 在实数集R中定义一种运算“*”,对任意a,b∈R,a*b为唯一确定的实数,且具有性质:①对任意a∈R,a*0=a;②对任意a,b∈R,a*b=ab+(a*0)+(b*0).则函数f(x)=(ex)* 的最小值为()A . 2B . 3C . 6D . 84. (2分)我们知道,在边长为a的正三角形内任一点到三边的距离之和为定值a,类比上述结论,在棱长为a的正四面体内任一点到其四个面的距离之和为定值,此定值为()A . aB . aC . aD . a5. (2分)观察下列各式:,则的末四位数为()A . 3125B . 5624C . 0625D . 81256. (2分)北京市为了缓解交通压力实行机动车辆限行政策,每辆机动车周一到周五都要限行一天,周末不限行.某公司有A、B、C、D、E五辆车,保证每天至少有四辆车可以上路行驶.已知:E车周四限行,B车昨天限行,从今天算起,A、C两车连续四天都能上路行驶,E车明天可以上路.由此可知,下列推测一定正确的是()A . 今天是周六B . 今天是周四C . A车周三限行D . C车周五限行7. (2分)根据下边给出的数塔猜测1234569+8=()19+2=11129+3=1111239+4=111112349+5=11111A . 1111110B . 1111111C . 1111112D . 11111138. (2分) (2016高二下·钦州期末) “因为偶函数的图象关于y轴对称,而函数f(x)=x2+x是偶函数,所以f(x)=x2+x的图象关于y轴对称”,在上述演绎推理中,所得结论错误的原因是()A . 大前提错误B . 小前提错误C . 推理形式错误D . 大前提与推理形式都错误9. (2分)下面说法正确的有()(1)演绎推理是由一般到特殊的推理;(2)演绎推理得到的结论一定是正确的;(3)演绎推理一般模式是“三段论”形式;(4)演绎推理的结论的正误与大前提、小前提和推理形式有关。
高中数学2.1.1合情推理课时作业(含解析)新人教A版选修22
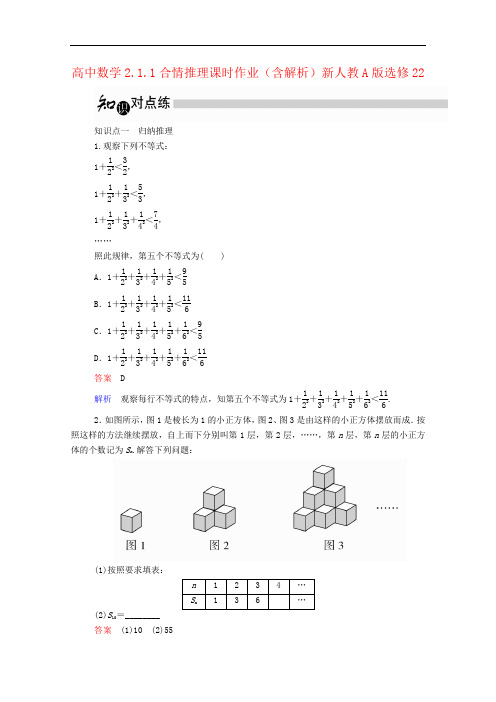
高中数学2.1.1合情推理课时作业(含解析)新人教A版选修22知识点一归纳推理1.观察下列不等式:1+122<32,1+122+132<53,1+122+132+142<74,……照此规律,第五个不等式为( )A.1+122+132+142+152<95B.1+122+132+142+152<116C.1+122+132+142+152+162<95D.1+122+132+142+152+162<116答案 D解析观察每行不等式的特点,知第五个不等式为1+122+132+142+152+162<116.2.如图所示,图1是棱长为1的小正方体,图2、图3是由这样的小正方体摆放而成.按照这样的方法继续摆放,自上而下分别叫第1层,第2层,……,第n层,第n层的小正方体的个数记为S n.解答下列问题:(1)按照要求填表:n 1234…S n136…(2)S10=________答案(1)10 (2)55解析 S 1=1,S 2=3=1+2,S 3=6=1+2+3, 推测S 4=1+2+3+4=10,S 10=1+2+3+…+10=55.知识点二 类比推理3.在公比为4的等比数列{b n }中,若T n 是数列{b n }的前n 项积,则有T 20T 10,T 30T 20,T 40T 30也成等比数列,且公比为4100;类比上述结论,相应地,在公差为3的等差数列{a n }中,若S n 是{a n }的前n 项和.可类比得到的结论是______________________.答案 数列S 20-S 10,S 30-S 20,S 40-S 30也是等差数列,且公差为300 解析 因为等差数列{a n }的公差d =3, 所以(S 30-S 20)-(S 20-S 10)=(a 21+a 22+…+a 30)-(a 11+a 12+…+a 20)=100d =300,同理可得:(S 40-S 30)-(S 30-S 20)=300,所以数列S 20-S 10,S 30-S 20,S 40-S 30是等差数列,且公差为300. 即结论为:数列S 20-S 10,S 30-S 20,S 40-S 30也是等差数列,且公差为300. 4.在Rt △ABC 中,AB ⊥AC ,AD ⊥BC 于D ,求证:1AD2=1AB2+1AC 2,那么在四面体ABCD 中,类比上述结论,你能得到怎样的猜想,并说明理由.解 如图①所示,由射影定理得AD 2=BD ·DC ,AB 2=BD ·BC ,AC 2=CD ·BC ,所以1AD2=1BD ·DC=BC 2BC ·BC ·BD ·DC =BC 2AB 2·AC 2.又BC 2=AB 2+AC 2, 所以1AD2=1AB2+1AC 2.类比猜想:四面体ABCD 中,AB ,AC ,AD 两两垂直,AE ⊥平面BCD ,则1AE2=1AB2+1AC2+1AD 2.如图②,连接BE 交CD 于F ,连接AF ,因为AB ⊥AC ,AB ⊥AD ,AC ∩AD =A , 所以AB ⊥平面ACD ,而AF ⊂平面ACD ,所以AB ⊥AF , 在Rt △ABF 中,AE ⊥BF , 所以1AE2=1AB2+1AF 2,易知在Rt △ACD 中,AF ⊥CD , 所以1AF 2=1AC2+1AD 2, 所以1AE2=1AB2+1AC2+1AD 2,猜想正确.知识点三 归纳和类比推理的应用5.鲁班发明锯子的思维过程为:带齿的草叶能割破行人的腿,“锯子”能“锯”开木材,它们在功能上是类似的.因此,它们在形状上也应该类似,“锯子”应该是齿形的.该过程体现了( )A .归纳推理B .类比推理C .胡乱推理D .没有推理 答案 B解析 推理是根据一个或几个已知的判断来确定一个新的判断的思维过程,上述过程是推理,由性质类比可知是类比推理.6.若数列{a n }(n ∈N *)是等差数列,则有数列b n =a 1+a 2+a 3+…+a n n(n ∈N *)也是等差数列.类比上述性质,相应地:若数列{c n }(n ∈N *)是等比数列,且c n >0,则数列d n =________(n ∈N *)也是等比数列. 答案nc 1·c 2·c 3·…·c n解析 由等差、等比数列之间运算的相似特征知, “和――→类比积,商――→类比开方”.容易得出d n =nc 1·c 2·c 3·…·c n 也是等比数列.一、选择题1.归纳推理和类比推理的相似之处为( ) A .都是从一般到一般 B .都是从一般到特殊 C .都是从特殊到特殊 D .所得结论都不一定正确 答案 D解析 归纳推理是由特殊到一般的推理,其结论不一定正确.类比推理是从特殊到特殊的推理,结论具有推测性,不一定可靠,故选D.2.下列平面图形与空间的平行六面体作为类比对象比较合适的是( ) A .三角形 B .梯形C .平行四边形D .矩形答案 C解析 由类比推理的定义和特点判断,易知选C.3.观察下列事实|x |+|y |=1的不同整数解(x ,y )的个数为4,|x |+|y |=2的不同整数解(x ,y )的个数为8,|x |+|y |=3的不同整数解(x ,y )的个数为12,…,则|x |+|y |=20的不同整数解(x ,y )的个数为 ( )A .76B .80C .86D .92 答案 B解析 由已知条件得,|x |+|y |=n (n ∈N *)的整数解(x ,y )个数为4n ,故|x |+|y |=20的整数解(x ,y )的个数为80.4.如图,在所给的四个选项中,最适合填入问号处,使之呈现一定的规律性的为( )答案 A解析 观察第一组中的三个图,可知每一个黑色方块都从右向左循环移动,每次移动一格,由第二组图的前两个图,可知选A.5.把下列在平面内成立的结论类比到空间,结论不成立的是( ) A .如果一条直线与两条平行线中的一条相交,则必与另一条相交 B .如果一条直线与两条平行线中的一条垂直,则必与另一条垂直 C .如果两条直线与第三条直线都不相交,则这两条直线不相交 D .如果两条直线同时与第三条直线垂直,则这两条直线平行 答案 D解析 类比A 的结论为:如果一个平面与两个平行平面中的一个相交,则必与另一个相交.成立.类比B 的结论为:如果一个平面与两个平行平面中的一个垂直,则必与另一个垂直.成立.类比C 的结论为:如果两个平面与第三个平面都不相交,则这两个平面不相交.成立.类比D 的结论为:如果两个平面同时与第三个平面垂直,则这两个平面平行.不成立.二、填空题 6.已知 2+23=223, 3+38=338, 4+415=4415,…,若 6+a b=6ab(a ,b ∈R ),则a +b =________. 答案 41解析 根据题意,由于2+23=223, 3+38=338, 4+415=4415,…那么可知 6+a b =6ab,a =6,b =6×6-1=35,所以a +b =41. 7.如图,直角坐标系中每个单元格的边长为1,由下往上的6个点1,2,3,4,5,6的横纵坐标(x i ,y i )(i =1,2,3,4,5,6)分别对应数列{a n }(n ∈N *)的前12项,如下表所示:a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 a 10 a 11 a 12 x 1y 1x 2y 2x 3y 3x 4y 4x 5y 5x 6y 6按如此规律下去,则a 2013+a 2014+a 2015的值为______. 答案 1007解析 由题图知a 1=x 1=1,a 3=x 2=-1,a 5=x 3=2,a 7=x 4=-2,…,则a 1+a 3=a 5+a 7=…=a 2013+a 2015=0.又a 2=y 1=1,a 4=y 2=2,a 6=y 3=3,…,则a 2014=1007,所以a 2013+a 2014+a 2015=1007.答案sin x 1+sin x 22<sin x 1+x 22解析 运用类比推理与数形结合,可知y =sin x (x ∈(0,π))的图象是上凸的,因此线段AB 的中点的纵坐标sin x 1+sin x 22总是小于函数y =sin x (x ∈(0,π))图象上的点⎝⎛⎭⎪⎫x 1+x 22,sin x 1+x 22的纵坐标,即有sin x 1+sin x 22<sin x 1+x 22成立. 三、解答题9.某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数. ①sin 213°+cos 217°-sin13°cos17°; ②sin 215°+cos 215°-sin15°cos15°; ③sin 218°+cos 212°-sin18°cos12°; ④sin 2(-18°)+cos 248°-sin(-18°)cos48°; ⑤sin 2(-25°)+cos 255°-sin(-25°)cos55°.(1)试从上述五个式子中选择一个,求出这个常数;(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论. 解 (1)选择②式计算如下:sin 215°+cos 215°-sin15°cos15° =1-12sin30°=34.(2)sin 2α+cos 2(30°-α)-sin αcos(30°-α)=34.证明:sin 2α+cos 2(30°-α)-sin αcos(30°-α)=sin 2α+(cos30°cos α+sin30°sin α)2-sin α(cos30°cos α+sin30°·sin α)=sin 2α+34cos 2α+32sin αcos α+14sin 2α-32sin α·cos α-12sin 2α=34sin 2α+34cos 2α=34.10.已知椭圆具有性质:若M ,N 是椭圆C 上关于原点对称的两个点,点P 是椭圆上任意一点,当直线PM ,PN 的斜率都存在,并记为k PM ,k PN 时,k PM 与k PN 之积是与点P 的位置无关的定值.试对双曲线x 2a 2-y 2b2=1写出具有类似特征的性质,并加以证明.解 类似的性质为:若M ,N 是双曲线x 2a 2-y 2b2=1上关于原点对称的两个点,点P 是双曲线上任意一点,当直线PM ,PN 的斜率都存在,并记为k PM ,k PN 时,那么k PM 与k PN 之积是与点P 的位置无关的定值.证明:设点M ,P 的坐标分别为(m ,n ),(x ,y ), 则N (-m ,-n ).因为点M (m ,n )在已知的双曲线上,所以n 2=b 2a 2m 2-b 2,同理,y 2=b 2a2x 2-b 2.则k PM ·k PN =y -n x -m ·y +n x +m =y 2-n 2x 2-m 2=b 2a 2·x 2-m 2x 2-m 2=b 2a 2(定值).。
(必考题)高中数学高中数学选修2-2第一章《推理与证明》测试题(包含答案解析)(3)

一、选择题1.数学归纳法证明*1111(1,)n 1n 2n 2n n N n +++>>∈+++,过程中由n k =到1n k =+时,左边增加的代数式为( )A .122k +B .121k + C .11+2122++k k D .112k 12k 2++- 2.正四面体ABCD 的棱AD 与平面α所成角为θ,其中02πθ<<,点D 在平面α内,则当四面体ABCD 转动时( )A .存在某个位置使得BC α,也存在某个位置使得BC α⊥B .存在某个位置使得BC α,但不存在某个位置使得BC α⊥ C .不存在某个位置使得BC α,但存在某个位置使得BC α⊥D .既不存在某个位置使得BC α,也不存在某个位置使得BC α⊥ 3.用反证法证明某命题时,对其结论“a ,b 都是正实数”的假设应为( ) A .a ,b 都是负实数B .a ,b 都不是正实数C .a ,b 中至少有一个不是正实数D .a ,b 中至多有一个不是正实数4.给出下面四个推理:①由“若a b 、是实数,则+≤+a b a b ”推广到复数中,则有“若12z z 、是复数,则1212z z z z +≤+”;②由“在半径为R 的圆内接矩形中,正方形的面积最大”类比推出“在半径为R 的球内接长方体中,正方体的体积最大”;③以半径R 为自变量,由“圆面积函数的导函数是圆的周长函数”类比推出“球体积函数的导函数是球的表面积函数”;④由“直角坐标系中两点11(,)A x y 、22(,)B x y 的中点坐标为1212(,)22x x y y ++”类比推出“极坐标系中两点11(,)C ρθ、22(,)D ρθ的中点坐标为1212(,)22ρρθθ++”.其中,推理得到的结论是正确的个数有( )个 A .1B .2C .3D .45.“杨辉三角形”是古代重要的数学成就,它比西方的“帕斯卡三角形”早了300多年,如图是三角形数阵,记n a 为图中第n 行各个数之和,则411a a +的值为A .528B .1032C .1040D .20646.有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说:“是乙或丙获奖.”乙说:“甲、丙都未获奖.”丙说:“我获奖了.”丁说:“是乙获奖.”四位歌手的话只有两句是对的,则获奖的歌手是( ) A .甲B .乙C .丙D .丁7.圆有6条弦,两两相交,这6条弦将圆最多分割成( )个部分 A .16 B .21 C .22 D .238.数学老师给同学们出了一道证明题,以下四人中只有一人说了真话,只有一人会证明此题,甲:我不会证明;乙:丙会证明;丙:丁会证明;丁:我不会证明.根据以上条件,可以判定会证明此题的人是( ) A .甲B .乙C .丙D .丁9.定义*A B ,*B C ,*C D ,*D A 的运算分别对应下面图中的⑴,⑵,⑶,⑷,则图中⑸,⑹对应的运算是( )A .*B D ,*A D B .*B D ,*AC C .*B C ,*AD D .*C D ,*A D10.由圆心与弦(非直径)中点的连线垂直于弦,想到球心与截面圆(不经过球心的小截面圆)圆心的连线垂直于截面,用的是( )A .类比推理B .三段论推理C .归纳推理D .传递性推理 11.根据给出的数塔猜测12345697⨯+( )19211⨯+=1293111⨯+= 123941111⨯+= 12349511111⨯+= 1234596111111⨯+=…A .1111111B .1111110C .1111112D .111111312.设十人各拿一只水桶,同到水龙头前打水,设水龙头注满第i (i =1,2,…,10)个人的水桶需T i 分钟,假设T i 各不相同,当水龙头只有一个可用时,应如何安排他(她)们的接水次序,使他(她)们的总的花费时间(包括等待时间和自己接水所花费的时间)最少( ) A .从T i 中最大的开始,按由大到小的顺序排队B .从T i 中最小的开始,按由小到大的顺序排队C .从靠近T i 平均数的一个开始,依次按取一个小的取一个大的的摆动顺序排队D .任意顺序排队接水的总时间都不变二、填空题13.观察如图等式,照此规律,第n 个等式为______.11234934567254567891049=++=++++=++++++=14.在圆中:半径为r 的圆的内接矩形中,以正方形的面积最大,最大值为22r .类比到球中:半径为R 的球的内接长方体中,以正方体的体积最大,最大值为__________. 15.某次高三英语听力考试中有5道选择题,每题1分,每道题在三个选项中只有一个是正确的.下表是甲、乙、丙三名同学每道题填涂的答案和这5道题的得分:1 2 3 4 5 得分甲 4 乙 3 丙2则甲同学答错的题目的题号是__________.16.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:则第个图案中有白色地面砖 块.17.在探究实系数一元二次方程的根与系数的关系时,可按下述方法进行: 设实系数一元二次方程22100a x a x a ++=……①在复数集C 内的根为1x ,2x ,则方程①可变形为()()2120a x x x x --=, 展开得()222122120a x a x x x a x x -++=.……②比较①②可以得到:11220122a x x a a x x a ⎧+=-⎪⎪⎨⎪=⎪⎩类比上述方法,设实系数一元n 次方程11100nn n n a x a xa x a --++++=(2n ≥且*N n ∈)在复数集C 内的根为1x ,2x ,…,n x ,则这n 个根的积1ni i x ==∏ __________.18.观察下列等式: (1)24sin sin 033ππ+= (2)2468sin sin sin sin 05555ππππ+++= (3)2468sinsin sin sin 7777ππππ+++1012sin sin 077ππ++= …… …… …… …… …… ……由以上规律推测,第n 个等式为:__________.19.小明在做一道数学题目时发现:若复数111cos i?sin ?,z αα=+222 cos i?sin ,z αα=+,333cos i?sin z αα=+(其中123,,R ααα∈), 则121212cos()i?sin(+)z z αααα⋅=++,232323cos()i?sin(+)z z αααα⋅=++ ,根据上面的结论,可以提出猜想: z 1·z 2·z 3=__________________. 20.观察下列各式:0014C =011334C C +=01225554;C C C ++=0123377774C C C C +++=……照此规律,当n ∈N 时,012121212121n n n n n C C C C -----++++=______________.三、解答题21.设数列{}n a 的前n 项和为n S ,对任意*n ∈N 都有2132n n S n a =+. (1)求数列{}n a 的通项公式;(2)记*4()n n b a n N =+∈*1)nn N b ++<∈ 22.已知数列{}n a 满足11a =,1(5)5n n n a a a ++=. (1)计算234,,a a a 的值,猜想数列{}n a 的通项公式; (2)用数学归纳法证明(1)中的猜想. 23.已知数列1111,,,,,112123123n+++++++,其前n 项和为n S ;(1)计算1234,,,S S S S ;(2)猜想n S 的表达式,并用数学归纳法进行证明.24.(1)当1x >时,求2()1x f x x =-的最小值.(2)用数学归纳法证明:11111222n n n +++≥++*()n N ∈. 25.在数列{}n a 中,111,21nn n a a a a +==+,其中1,2,3,n =.(Ⅰ)计算234,,a a a 的值;(Ⅱ)猜想数列{}n a 的通项公式,并用数学归纳法加以证明. 26.已知()()()()20121111nnn x a a x a x a x +=+-+-++-(2,*n n N ≥∈),(1)当5n =时,求12345a a a a a ++++的值; (2)设2233,2n n n n a b T b b b -==+++,试用数学归纳法证明:当2n ≥时,()()113n n n n T +-=。
人教a版数学【选修2-2】备选练习:2.1.1 合情推理(含答案)

选修2-2第二章 2.1 2.1.1第1课时1.如图所示的是一串黑白相间排列的珠子,若按这种规律排列下去,那么第36颗珠子的颜色是()A.白色B.黑色C.白色的可能性大D.黑色的可能性大[答案] A[解析]由图知,这串珠子的排列规律是:每5个一组(前3个是白色珠子,后2个是黑色珠子)呈周期性排列,而36=5×7+1,即第36颗珠子正好是第8组中的第1颗珠子,其颜色与第一颗珠子的颜色相同,故它的颜色一定是白色.2.四个小动物换座位,开始是鼠、猴、兔、猫分别坐1、2、3、4号位子上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…,这样交替进行下去,那么第2011次互换座位后,小兔的座位对应的是()A.编号1 B.编号2C.编号3 D.编号4[答案] D[解析]归纳得,四个小动物在换座过程中,每换座四次与原来的一样,即以4为周期,因此在2011次换座后,四个小动物的位置应该和第三次换座后的位置一样,即小兔的座位对应的编号为4,故选D.3.平面内的小圆形按照下图中的规律排列,每个图中的圆的个数构成一个数列{a n},则下列结论正确的是()①a5=15;②数列{a n}是一个等差数列;③数列{a n}是一个等比数列;④数列{a n}的递推关系是a n=a n-1+n(n∈N*).A.①②④B.①③④C.①②D.①④[答案] D[解析] 由于a 1=1,a 2=3,a 3=6,a 4=10,所以有a 2-a 1=2,a 3-a 2=3,a 4-a 3=4.因此必有a 5-a 4=5,即a 5=15,故①正确.同时④正确,而{a n }显然不是等差数列也不是等比数列,故②③错误,故选D.4.在一容器内装有浓度为r %的溶液a 升,注入浓度为p %的溶液14a 升,搅匀后再倒出溶液14a 升,这叫一次操作,设第n 次操作后容器内溶液的浓度为b n (每次注入的溶液浓度都是p %),计算b 1、b 2、b 3,并归纳出b n 的计算公式.[解析] b 1=a ·r 100+a 4·p 100a +a 4=1100⎝⎛⎭⎫45r +15p ,b 2=ab 1+a 4·p 100a +a 4=1100⎣⎡⎦⎤⎝⎛⎭⎫452r +15p +452p . b 3=a ·b 2+a 4·p 100a +a 4=1100⎣⎡⎦⎤⎝⎛⎭⎫453r +15p +452p +4253p , ∴归纳得b n =1100⎣⎡⎦⎤⎝⎛⎭⎫45n r +15p +452p +…+4n -15n p .5.(2014·洛阳市高二期中)观察等式: sin50°+sin20°=2sin35°cos15° sin66°+sin32°=2sin49°cos17°猜想符合以上两式规律的一般结论,并进行证明. [解析] 猜想:sin α+sin β=2sin α+β2cos α-β2.下面证明:左边=sin(α+β2+α-β2)+sin(α+β2-α-β2)=(sin α+β2cos α-β2+cos α+β2sin α-β2)+(sin α+β2cos α-β2-cos α+β2sin α-β2)=2sin α+β2cos α-β2=右边.所以原等式成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业11合情推理
时间:45分钟满分:100分
一、选择题(每小题5分,共30分)
1.下列哪个平面图形与空间的平行六面体作为类比对象较为合适()
A.三角形B.梯形
C.平行四边形D.矩形
【答案】C
【解析】只有平行四边形与平行六面体较为接近,故选C.
|
2.下列类比推理恰当的是()
A.把a(b+c)与log a(x+y)类比,则有:log a(x+y)=log a x+log a y B.把a(b+c)与sin(x+y)类比,则有:sin(x+y)=sin x+sin y
C.把(ab)n与(a+b)n类比,则有:(a+b)n=a n+b n
D.把a(b+c)与a·(b+c)类比,则有:a·(b+c)=a·b+a·c
【答案】D
【解析】A,B,C三个选项没有从本质上类比,是简单类比,从而出现错误.
3.如图所示,在杨辉三角中,斜线AB上方箭头所示的数组成一个锯齿形的数列:1,2,3,3,6,4,10,…,记这个数列前n项的和为S(n),则S(16)等于()
?
A.128 B.144
C.155 D.164
【答案】D
【解析】由题意可知该数列的前16项为:1,2,3,3,6,4,10,5,15,6,21,7,28,8,36,9.故S(16)=1+2+3+…+36+9=164.
4.观察右图图形规律,在其右下角的空格内画上合适的图形为
()
~
A.■B.△
C.□ D.○
【答案】A
【解析】每一行、每一列的图形都有两个黑色.
5.观察下列事实:|x|+|y|=1的不同整数解(x,y)的个数为4, |x|
+|y|=2的不同整数解(x,y)的个数为8, |x|+|y|=3的不同整数解(x,y)的个数为12,…,则|x|+|y|=20的不同整数解(x,y)的个数为() A.76 B.80
C.86 D.92
【答案】B
…
【解析】由已知条件知|x|+|y|=n的不同整数解(x,y)个数为4n,所以|x|+|y|=20不同整数解(x,y)的个数为4×20=80.归纳体现了由特殊到一般的思维过程.
6.定义A*B、B*C、C*D、D*B分别对应下列图形
那么下列图形中,
可以表示A*D、A*C的分别是()
A.(1)、(2) B.(2)、(3)
|
C.(2)、(4) D.(1)、(4)
【答案】C
【解析】由A*B、B*C、C*D、D*B的定义图形知A为,B为,
C为——,D为.
二、填空题(每小题10分,共30分)
7.(2014·陕西理)观察分析下表中的数据:
.【答案】F+V-E=2
【解析】本题考查归纳推理.
,
5+6-9=2,
6+6-10=2,
6+8-12=2,
∴F+V-E=2.
8.观察下列等式:13+23=(1+2)2,13+23+33=(1+2+3)2,13+23+33+43=(1+2+3+4)2,…,根据上述规律,第四个等式为__________________.
【答案】13+23+33+43+53=(1+2+3+4+5)2(或152)
【解析】根据已知条件,第四个等式应为13+23+33+43+53=(1+2+3+4+5)2(或152).
9.如图所示,已知命题:若矩形ABCD的对角线BD与边AB和BC所成的角分别为α,β,则cos2α+cos2β=1,则在长方体ABCD-A1B1C1D1中,写出类似的命题:________.
<
【答案】 长方体ABCD -A 1B 1C 1D 1中,若对角线BD 1与棱AB 、BB 1、BC 所成的角分别为α、β、γ,则cos 2α+cos 2β+cos 2γ=1或sin 2α+sin 2β+sin 2γ=2
(或:长方体ABCD -A 1B 1C 1D 1中,若对角线BD 1与平面ABCD 、ABB 1A 1、BCC 1B 1所成的角分别为α、β、γ,则cos 2α+cos 2β+cos 2γ=2或sin 2α+sin 2β+sin 2γ=1)
三、解答题(本题共3小题,共40分.解答应写出必要的文字说明、证明过程或演算步骤)
10.(13分)已知{a n }满足a 1=1,4a n +1-a n ·a n +1+2a n =9,写出a 1、a 2、a 3、a 4,试猜想出这个数列的通项公式.
【解析】 由4a n +1-a n a n +1+2a n =9 得a n +1=2-1a n -4
,
,
∴a 2=2-1a 1-4=2+13,a 3=2-1a 2-4=2+3
5,
a 4=2-1a 3-4=2+5
7,猜想:a n =2+2n -32n -1
.
11.(13分)在平面几何里有勾股定理:“若三角形有两条边垂直,
则这两条直角边的平方和等于第三边的平方.”拓展到空间中,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积之间的关系,可以得出什么结论请你证明.
【分析】 在平面上是线的关系,在空间就有可能是面的关系.类
比一下:直角顶点所对的边的平方是另外两边的平方和,那么直角顶点所对的面的面积就可能具有类似的关系.
【解析】“若三棱锥有三个面,两两互相垂直,则这三个面的面积的平方和等于这三个面相交的顶点所对面的面积的平方.”
证明如下:如图,在三棱锥A-BCD中,平面ABC,平面ACD,平面ABD两两垂直,则AB⊥AC,AB⊥AD,AC⊥AD.
过点A作AE⊥CD于点E,连接BE.
|
由题,易得BE⊥CD,AB⊥AE.
∴S2△BCD=1
4CD2·BE2
=1
4CD2(AB2+AE2)
=1
4(AC2+AD2)AB2+
1
4CD2·AE2
=S2△ABC+S2△ADB+S2△ACD.
【规律方法】类比推理是根据两个对象有一部分属性类似,推出这两个对象其他属性亦类似的一种推理方法.类比推理时有可能出现错误,如:由命题“在平面内,已知直线a,b,c,若a⊥b,b⊥c,则a,c平行.”类比推理得到“在空间,已知三个平面α,β,γ,若α⊥β,β⊥γ,则α∥γ.”但实际上,α,γ之间可能平行,也可能相交,所以这里类比推理得到的结论为假.
12.(14分)把正整数排列成如图所示的数阵.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
……
(1)求数阵中前10行所有的数的个数; (2)求数阵中第n 行的第一个数;
(3)2 007是数阵中第几行的第几个数(从左向右数)
【解析】 (1)数阵中第n 行有n 个数,所以前10行所有的数的个数为1+2+3+…+10=55.
(2)数阵中前n 行所有的数的个数为1+2+3+…+n =1
2n (n +1),所以第n 行最后一个数为12n (n +1),则第n 行第一个数为1
2n (n +1)-(n -1)=12n 2-1
2n +1.
(3)当n =63时,数阵中第63行最左边的数为1
2×63×64-62=1 954.数阵中第63行最右边的数为1
2×64×63=2 016,所以2 007位于数阵中第63行.又因为2 007-1 954=53,故2 007是数阵中第63行的第54个数.。
