求图示平面图形的形心坐标
惯性矩、静矩,形心坐标公式
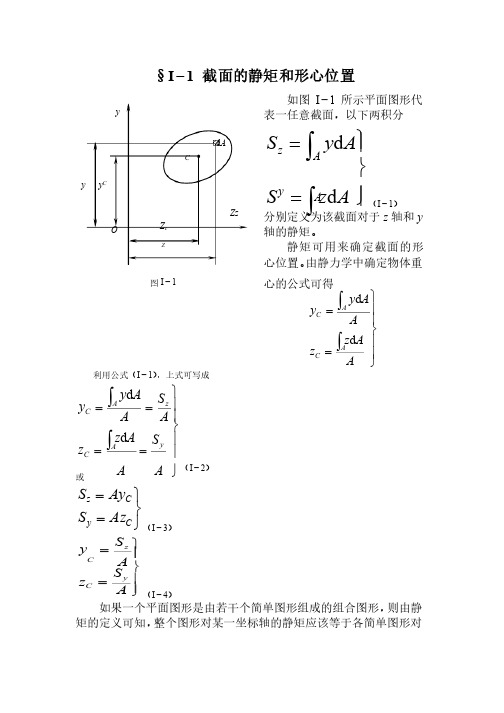
§I −1 截面的静矩和形心位置如图I −1所示平面图形代表一任意截面,以下两积分表一任意截面,以下两积分ïþïýü==òòA z S A y S A y Az d d (I −1)分别定义为该截面对于z 轴和y 轴的静矩。
轴的静矩。
静矩可用来确定截面的形心位置。
由静力学中确定物体重心的公式可得心的公式可得ïïþïïýü==òòA A z z A A y y AC ACd d利用公式(I −1),上式可写成,上式可写成ïïþïïýü====òòA S A A z z A SA Ay y y A C z A C d d (I −2) 或þýü==C y C z Az S Ay S (I −3)ïïþïýü==A S z A S y y C z C(I −4)如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对d A C Zz y y y C Z c O 图I −1 Z 同一坐标轴的静矩的代数和。
即:同一坐标轴的静矩的代数和。
即:ïïþïïýü==åå==ni ci i y ni ci i z z A S y A S 11(I −5)式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。
单图形的个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标的计算公式为ïïïïïþïïïïýü==åååå====ni ini c iic ni ini c i i c AzA z A y A y 1111(I −6)例题I −1 图a 所示为对称T 型截面,求该截面的形心位置。
求图示平面图形的形心位置及形心主惯性矩
σ x +σ y
2
± (
σ x −σ y
2
) 2 + τ xy 2
j
= 2v A , kd = 1 + 1 +
2H
j
= 1+ 1+
H vA
σ max = ⎨
min
⎧130MPa ⎩30MPa
σ d max = kd i2σ B max
vd = kd
⎛ H⎞ = 2 ⎜1 + 1 + ⎟ σ B max ⎜ vA ⎟ ⎝ ⎠
(δ B )水平
M ∂M 1 = [∫ ds ]Pf =0 = s EI ∂P EI f
∫
π
2 0
PR 3 PR cos ϕ i R(1 − sin ϕ )i Rdϕ = 2 EI
共 10 页;第 8 页
共 10 页;第 7 页
六、图示传动轴。直径为 d,轮 C、轮 E 直径均为 D。轮 C 受铅垂力 P。轮 E 受水平力 P。试求:⑴作轴的扭矩图,弯矩图。⑵指出危险截面的位置。⑶ 用第三强度理论写出校核该轴强度的相当应力表达式。 10 分) (
δ 22 =
1 ⎛l ⎞ 3l ⎜ × 1 + l × 1⎟ = EI ⎝ 2 ⎠ 2 EI
应用卡氏定理
将以上系数代入式(1) ,经简化可得
l Pl 1 ⎫ X1 − X 2 + = 0⎪ ⎪ 3 2 8 ⎬ 5Pl lX 1 − 3 X 2 + =0⎪ ⎪ 8 ⎭ X1 = − P 8 X2 = P Pl H A = HB = 6 8 RA = RB = P 2 MA = MB = Pl 24
2 3 2 2 2
∂M = R cos ϕ ∂P (δ B )竖直 M ∂M 1 =∫ ds = s EI ∂P EI
材料力学形心计算公式(一)

材料力学形心计算公式(一)材料力学形心计算公式1. 面积形心计算公式面积形心是用来描述一个平面图形相对于一个参考点的几何特征。
下面是计算不同平面图形的面积形心的公式:•长方形:面积形心的x坐标为长方形中心点的x坐标,y坐标为长方形中心点的y坐标。
•圆形:面积形心的x坐标为圆形中心点的x坐标,y坐标为圆形中心点的y坐标。
•三角形:面积形心的x坐标为三角形各顶点x坐标的平均值,y 坐标为三角形各顶点y坐标的平均值。
•多边形:对于不规则多边形,可以使用叠加面积形心的方法计算。
将多边形分解成若干个三角形或四边形,然后计算每个小形状的面积形心,最后取加权平均值作为整个多边形的面积形心。
2. 体积形心计算公式体积形心是用来描述一个立体图形相对于一个参考点的几何特征。
下面是计算不同立体图形的体积形心的公式:•长方体:体积形心的x坐标为长方体中心点的x坐标,y坐标为长方体中心点的y坐标,z坐标为长方体中心点的z坐标。
•圆柱体:体积形心的x坐标为圆柱体中心点的x坐标,y坐标为圆柱体中心点的y坐标,z坐标为圆柱体高度的一半。
•球体:体积形心的x坐标为球体中心点的x坐标,y坐标为球体中心点的y坐标,z坐标为球体中心点的z坐标。
•其他立体图形:对于其他不规则立体图形,可以使用积分的方法计算体积形心。
将图形切割成无穷小的微元,然后对每个微元求解体积形心,最后求解加权平均值得到整个图形的体积形心。
3. 弯曲形心计算公式弯曲形心是用来描述一个截面相对于一个参考轴线的几何特征。
下面是计算不同截面的弯曲形心的公式:•矩形截面:弯曲形心的x坐标为矩形截面中心点的x坐标,y坐标为矩形截面中心点的y坐标。
•圆形截面:弯曲形心的x坐标为圆形截面中心点的x坐标,y坐标为圆形截面中心点的y坐标。
•其他截面:对于其他不规则截面,可以使用积分的方法计算弯曲形心。
将截面分解成无穷小的微元,然后对每个微元求解弯曲形心,最后求解加权平均值得到整个截面的弯曲形心。
参数方程的形心坐标公式

参数方程的形心坐标公式形心,也称作质心或重心,是指一个平面图形或三维空间图形的重心位置,即该图形的所有质点的平均位置。
在几何学中,求解形心坐标是一个重要的问题,可以通过参数方程来计算。
参数方程是一种表示曲线或曲面的方程,其中自变量通常表示为参数。
在二维平面上,一个曲线的参数方程可以表示为x = f(t), y = g(t),其中t是参数,f(t)和g(t)是关于t的函数。
同样,在三维空间中,一个曲面的参数方程可以表示为x = f(u, v), y = g(u, v), z = h(u, v),其中u和v是参数,f(u, v), g(u, v)和h(u, v)是关于u和v 的函数。
对于一个平面图形的形心,可以使用参数方程的形心坐标公式来计算。
对于一个曲线,形心坐标公式可以表示为:x̄= (1/L) ∫[a,b] x(t)ρ(t)dtȳ= (1/L) ∫[a,b] y(t)ρ(t)dt其中L是曲线的弧长,[a,b]是参数t的取值范围,x(t)和y(t)分别是曲线上点的x坐标和y坐标的函数,ρ(t)是曲线上点的单位质量。
同样地,对于一个曲面,形心坐标公式可以表示为:x̄ = (1/S) ∬[D] x(u, v)ρ(u, v)dAȳ = (1/S) ∬[D] y(u, v)ρ(u, v)dAz̄ = (1/S) ∬[D] z(u, v)ρ(u, v)dA其中S是曲面的面积,[D]是参数u和v所确定的曲面上的区域,x(u, v),y(u, v)和z(u, v)分别是曲面上点的x坐标、y坐标和z坐标的函数,ρ(u, v)是曲面上点的单位质量,dA是曲面上的面积元素。
形心坐标公式的推导可以通过对参数t、u和v进行积分来得到。
在计算形心时,需要确定曲线或曲面上每个点的密度分布,即单位质量。
通常情况下,可以假设质量均匀分布在曲线或曲面上,即单位质量在整个曲线或曲面上是恒定的。
形心坐标公式的应用非常广泛。
在工程学中,形心坐标公式可以用于计算物体的质心位置,从而确定物体的平衡状态。
材料力学附录I 平面图形的几何性质2形心主轴和形心主惯性矩

i1
i1
i1
材料力学 附录I 平面图形的几何性质
例I-4-1:已知三角形对底边(x1轴)的惯性矩为bh3/12,
求其对过顶点的与底边平行的x2轴的惯性矩。
解:由于x1、x2轴均非形心轴,所以不
x2
能直接使用平行移轴公式,需先求出 三角形对形心轴xC的惯性矩,再求对
h xC
h/3
x1
x2轴的惯性矩,即进行两次平行移轴
3.求截面形心主惯性矩的方法
①建立坐标系
②计算面积和面积矩 ③求形心位置
x
Sy A
xi Ai A
y
Sx A
yi Ai A
④建立形心坐标系;求:IyC , IxC , IxCyC
⑤求形心主轴方向 — 0
tg2
0
2I xCyC I xC I yC
⑥求形心主惯性矩
I I
xC0 yC0
I
x
C
I 2
b
:
I xC
I x1
a12 A
bh3 12
h 2 3
bh 2
bh3 36
I x2
I xC
a22 A
bh3 36
2h 2 3
bh 2
bh3 4
材料力学 附录I 平面图形的几何性质
例I-4-2:求图示T型截面对形心轴的惯性矩。
30
5
30
5
材料力学 附录I 平面图形的几何性质
30
求T形截面对形心轴的惯性矩
C O
10 150yC x1
x
由于对称知: xC=0
材料力学 附录I 平面图形的几何性质
§I-2 惯性矩和惯性半径
一、惯性矩
工程力学材料力学-知识点-及典型例题
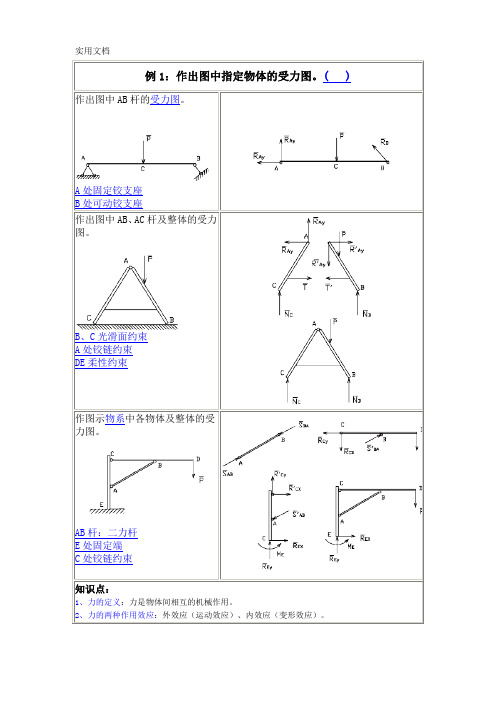
作出图中AB杆的受力图。
A处固定铰支座B处可动铰支座作出图中AB、AC杆及整体的受力图。
B、C光滑面约束A处铰链约束DE柔性约束作图示物系中各物体及整体的受力图。
AB杆:二力杆E处固定端C处铰链约束(1)运动效应:力使物体的机械运动状态发生变化的效应。
(2)变形效应:力使物体的形状发生和尺寸改变的效应。
3、力的三要素:力的大小、方向、作用点。
4、力的表示方法:(1)力是矢量,在图示力时,常用一带箭头的线段来表示力;(注意表明力的方向和力的作用点!)(2)在书写力时,力矢量用加黑的字母或大写字母上打一横线表示,如F、G、F1等等。
5、约束的概念:对物体的运动起限制作用的装置。
6、约束力(约束反力):约束作用于被约束物体上的力。
约束力的方向总是与约束所能限制的运动方向相反。
约束力的作用点,在约束与被约束物体的接处7、主动力:使物体产生运动或运动趋势的力。
作用于被约束物体上的除约束力以外的其它力。
8、柔性约束:如绳索、链条、胶带等。
(1)约束的特点:只能限制物体原柔索伸长方向的运动。
(2)约束反力的特点:约束反力沿柔索的中心线作用,离开被约束物体。
()9、光滑接触面:物体放置在光滑的地面或搁置在光滑的槽体内。
(1)约束的特点:两物体的接触表面上的摩擦力忽略不计,视为光滑接触面约束。
被约束的物体可以沿接触面滑动,但不能沿接触面的公法线方向压入接触面。
(2)约束反力的特点:光滑接触面的约束反力沿接触面的公法线,通过接触点,指向被约束物体。
()10、铰链约束:两个带有圆孔的物体,用光滑的圆柱型销钉相连接。
约束反力的特点:是方向未定的一个力;一般用一对正交的力来表示,指向假定。
()11、固定铰支座(1)约束的构造特点:把中间铰约束中的某一个构件换成支座,并与基础固定在一起,则构成了固定铰支座约束。
(2)约束反力的特点:固定铰支座的约束反力同中间铰的一样,也是方向未定的一个力;用一对正交的力来表示,指向假定。
()12、可动铰支座(1)约束的构造特点把固定铰支座的底部安放若干滚子,并与支撑连接则构成活动铰链支座约束,又称锟轴支座。
求图示平面图形的形心坐标

求图示平面图形的形心坐标
试求图示组合平面图形的形心坐
标。
(单位:mm)
解:1、将图示组合平面图形分成如右图所示的矩形I和矩形II组合后再减去圆III(认为其面积为负的)
2、I、II、III的面积和形心坐标分别为:
A1=(100-20)×20=1600mm2X1=10mm Y1=20+40=60mm
A2=80×20=1600mm2X2=40mm Y2=10mm
A3=-πR2=3.14×52=-78.5mm2X3=10mm Y3=90mm
3、利用形心坐标公式计算形心坐标
知识点:
1、重心:物体的重力的合力作用点称为物体的重心。
(与组成该物体的物质有关)
2、形心:物体的几何中心。
(只与物体的几何形状和尺寸有关,与组成该物体的物质无关)
一般情况下重心和形心是不重合的,只有物体是由同一种均质材料构成时,重心和形心才重合。
3、平面图形的形心坐标公式:
(1)、分割法:
工程中的零部件往往是由几个简单基本图形组合而成的,在计算它们的形心时,可先将其分割为几个基本图形,利用查表法查出每个基本图形的形心位置与面积,然后利用形心计算公式求出整体的形心位置。
此法称为分割法。
(2)、负面积法:
仍然用分割法的公式,只不过去掉部分的面积用负值。
上式中的A
i 是每一个基本图形的面积;X
i
、Y
i
分别是每一个基本图形的形心的
X、Y坐标。
上述两种方法可以分别使用,也可以同时使用。
建筑力学习题,详解答案
y
0: FAy FB 0
FB 1.5kN
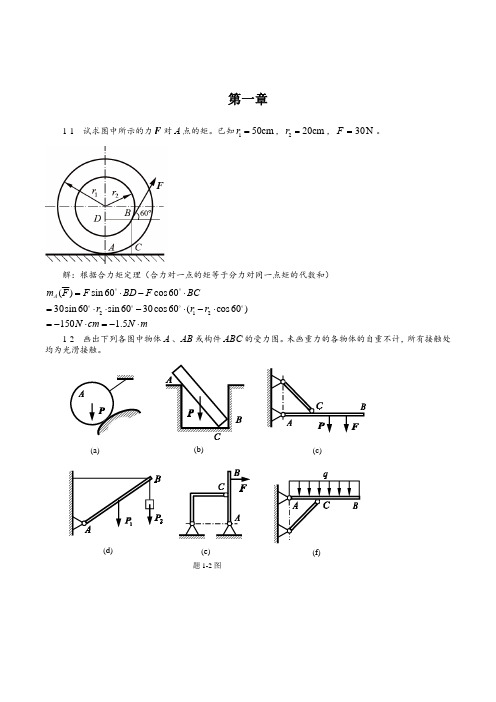
3-5 求图示各梁的支座反力。
q A
3m 3m 3m
B
A
5m
A
B
1m
M
3m 3m
B
3m
(a )
(b )
(c )
A
M1
2m 4m
M2
2m
B A
q
l
(e ) 题 3-5 图
q B A
(f)
l
B
(d )
解:以梁 AB 为研究对象。采用数学中一般平面直角坐标系。 设所有的垂直反力向上的画,水平反力指向右。反力偶逆时针画。 (a)
yC
A x
i
i
第三章 3-1 用两根绳子 AC 和 BC 悬挂一个重 G = 1kN 的物体。绳 AC 长 0.8 m,绳 BC 长 1.6 m,A、B 点在 同一水平线上,相距 2 m。求这两根绳子所受的拉力。
【解】以整体为研究对象
cos
0.82 22 1.62 0.6500 2 0.8 2 1.62 22 0.82 cos 0.9250 2 1.6 2
F4 100kN 。
解:1.计算每个力在 x 轴上的投影,并求和。
F F
x
F1 60
1 1 3 1
2 2
F2 80
1 1 1 1
2 2
F3 F4 50 100
2 1 22 2
2
x
12 32
12 12
12 22
-1.848
解【分析】求力系合力的题目的一般步骤如下: 选定一点为简化中心。建立坐标系(一般以简化中心为坐标原点) ; 计算所有力在 x 轴上投影并求和,即主知在 x 轴上的投影 Fx; 计算所有力在 y 轴上投影并求和,即主知在 y 轴上的投影 Fy; 根据公式: F '
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识点:
1、重心:物体的重力的合力作用点称为物体的重心。(与组成该物体的物质有关)
2、形心:物体的几何中心。(只与物体的几何形状和尺寸有关,与组成该物体的物 质无关)
一般情况下重心和形心是不重合的,只有物体是由同一种均质材料构成时, 重心和形心才重合。
3、平面图形的形心坐标公式 :
求图示平面图形的形心坐标
试求图示组合平面图形的形心坐 标。(单位:mrj)
解:1、将图示组合平面图形分成如右图所示的矩形I和矩形II组合
后再减去圆III(认为其面积为负的)
2、I、II、III的面积和形心坐标分别为:
2
A=(100-20)x20=1600mmXi=10mm Yi=20+40=60mm
上式中的A]是每一个基本图形的面积;分别是每一个基本图形的形心的X、
Y坐标。
上述两种方法可以分别使用,也可以同时使用。
2
A=80x20=1600mmX2=40mm Y2=10mm
A=-n氏=3.14X 52=-78.5mm X=10mm Ya=90mm
3、利用形心坐标公式计算形心坐标
艺4兀屈第4■風x广4沁 [购如0苟跑""卜衲3溟用
y;<4-y广止“y卢屈乳i枫你和+160弘1也1<-幣5)注o…
V■-- --—
£Ai< xi
工A~=
EAi-yi
E—A
(1)、分割法:
工程中的零部件往往是由几个简单基本图形组合而成的,在计算它们的形心时,
可先将其分割为几个基本图形,利用查表法查岀每个基本图形的形心位置与面积,
然后利用形心计算公式求岀整体的形心位置。此,只不过去掉部分的面积用负值。
