【高考】用平面的法向量解高考立体几何试题
用平面法向量解立体几何题

用平面法向量解立体几何题张家瑞(江苏省苏州市迅达培训学校,215005) 收稿日期:2005-07-04 (本讲适合高中)数学竞赛试题中,立体几何题占有一定数量.立体几何题的证明和求解方法很多,本文介绍用平面法向量解立体几何题.1 证明直线与平面平行证明这类题的基本思路是:要证平面外的直线l 与平面α平行,只须确定平面α的一个法向量n ,证明n ⊥l 即可推出l ∥α.例1 已知正三棱柱ABC -A 1B 1C 1中,D 为AC 的中点.求证:AB 1∥平面DBC 1.图1证明:建立如图1的空间直角坐标系.则A (0,0,0).设B 1(0,a ,b )、B (0,a ,0)、D 3a 4,a4,0、C 13a 2,a2,b .于是,AB 1=(0,a ,b ),BD =3a 4,-3a4,0,DC 1=3a 4,a4,b .设平面BC 1D 的法向量为n =(x ,y ,z ).由n ⊥BD ,n ⊥DC 1,得3a 4x -3a 4y =0,3a 4x +a4y +bz =0.令y =3,则x =3,z =-3ab,即n =3,3,-3a b.考虑到n ・AB 1=3,3,-3a b・(0,a ,b )=0且AB 1⁄平面BC 1D ,AB 1⊥n ,所以,AB 1∥平面BC 1D.2 证明两平面平行证明这类题的基本思路是:(1)若平面α、β的法向量n 1、n 2共线,则α∥β.(2)若平面α、β有相同的法向量n ,则α∥β.例2 求证:单位正方体ABCD -A 1B 1C 1D 1中,平面A 1BC 1∥平面D 1AC.证明:建立如图2的空间直角坐标系.图2则 D (0,0,0)、A 1(1,0,1)、B (1,1,0)、C (0,1,0)、C 1(0,1,1)、D 1(0,0,1)、A (1,0,0).于是,A 1C 1=(-1,1,0),A 1B =(0,1,-1),AD 1=(-1,0,1),AC =(-1,1,0).设平面A 1BC 1、平面D 1AC 的法向量分别为n 1=(x 1,y 1,z 1)、n 2=(x 2,y 2,z 2).由n 1⊥A 1C 1,n 1⊥A 1B ,n 2⊥AC ,n 2⊥AD 1,得-x 1+y 1=0,y 1-z 1=0,-x 2+y 2=0,-x 2+z 2=0.令x 1=a ,x 2=b ,则n 1=(a ,a ,a ),n 2=(b ,b ,b ).易知n 1=ab n 2,故n 1、n 2为共线向量.由此推出平面A 1BC 1∥平面D 1AC.注:在上述证明过程中,若令x 1=x 2=a ,则n 1=n 2=(a ,a ,a ).这说明平面A 1BC 1与平面D 1AC 有公共法向量,所以它们平行.3 证明直线与平面垂直证明这类题的基本思路是:确定平面α的法向量n ,若直线l 与n 共线,则可推出l ⊥α.例3 已知正方体ABCD -A 1B 1C 1D 1的棱长为1,M 、N 、P 分别是棱CC 1、BC 、CD 的中点.求证:A 1P ⊥平面DMN.(2004,山东省数学竞赛)图3证明:建立如图3的空间直角坐标系,联结DM 、DN.则D (0,0,0)、N12,1,0、M 0,1,12.于是,DN =12,1,0,DM =0,1,12.设平面DMN 的法向量为n =(x ,y ,z ).由n ⊥DN ,n ⊥DM ,得12x +y =0,y +12z =0.令y =-1,则x =z =2.故n =(2,-1,2).又A 1(1,0,1)、P 0,12,0,则A 1P =-1,12,-1.易知n =-2A 1P ,这说明n 与A 1P 共线.所以,A 1P ⊥平面DMN.4 证明两直线垂直证明这类题的基本思路是:要证l 1⊥l 2,若直线l 2<平面α,可确定平面α的法向量n .如果n 与直线l 1共线,则可推出l 1⊥l 2.例4 已知单位正方体ABCD -A 1B 1C 1D 1中,E 是BC 上的动点,F 是AB 的中点.试确定点E 的位置,使得C 1F ⊥A 1E.图4证明:联结A 1D 、DE ,建立如图4的空间直角坐标系.则D (0,0,0)、A 1(1,0,1)、E (a ,1,0)、F 1,12,0、C 1(0,1,1).于是,DA 1=(1,0,1),D E =(a ,1,0).设平面A 1DE 的法向量为n =(x ,y ,z ).若C 1F ⊥平面DA 1E ,则n 与C 1F 共线.故n =λ(C 1F )=λ1,-12,-1=λ,-12λ,-λ.由n ⊥D E ,得λ,-12λ,-λ・(a ,1,0)=0.由此得aλ=12λ,即a =12.这说明E 为BC 的中点.此时,C 1F ⊥平面A 1DC ,则C 1F ⊥A 1E.5 证明两平面垂直证明这类题的基本思路是:(1)确定两个平面α、β的法向量n 1、n 2.若n 1⊥n 2,则α⊥β;(2)在平面α内找出向量a ,若a 与β的法向量共线,则可推出α⊥β.例5 已知单位正方体ABCD -A 1B 1C 1D 1中,E 为CC 1的中点.求证:平面A 1BD ⊥平面E BD.图5证法1:建立如图5的空间直角坐标系.则D (0,0,0)、A 1(1,0,1)、B (1,1,0)、E 0,1,12.于是,D E =0,1,12,DB =(1,1,0),DA 1=(1,0,1),DB =(1,1,0).设平面E BD 的法向量为n 1=(x 1,y 1,z 1).由n 1⊥DB ,n 1⊥DE ,得y 1+12z 1=0,x 1+y 1=0.令x 1=1,则y 1=-1,z 1=2.所以,n 1=(1,-1,2).设平面A 1BD 的法向量为n 2=(x 2,y 2,z 2).由n 2⊥DA 1,n 2⊥DB ,得x 2+z 2=0,x 2+y 2=0.令x 2=1,则y 2=z 2=-1.所以,n 2=(1,-1,-1).故n 1・n 2=(1,-1,2)・(1,-1,-1)=0.因此,n 1⊥n 2.由此推出平面A 1BD ⊥平面E BD.证法2:设BD 的中点为O12,12,0,则OA 1=12,-12,1,平面E BD 的法向量为n 1=(1,-1,2).易知n 1=2OA 1,这说明OA 1与n 1共线,且OA 1<平面A 1BD.所以,OA 1⊥平面E BD.故平面A 1BD ⊥平面E BD.6 求直线与平面所成的角解这类题的基本思路是:图6如图6,直线l ∩平面α=A ,B 是直线l 上的一点,BC ⊥α于C ,则∠BAC 为直线l 与平面α所成的角.设平面法向量为n ,则cos ∠ABC =|n ・AB ||n ||AB |,∠BAC =π2-∠ABC.所以,∠BAC =arcsin|n ・AB ||n ||AB |.例6 在长方体ABCD -A 1B 1C 1D 1中,AB=2,AA 1=AD =1.求AB 与平面AB 1C 所成的角.图7解:建立如图7的空间直角坐标系.则D (0,0,0)、A (1,0,0)、C (0,2,0)、B 1(1,2,1).于是,AC =(-1,2,0),AB 1=(0,2,1).设平面AB 1C 的法向量为n =(x ,y ,z ).由n ⊥AC ,n ⊥AB 1,得-x +2y =0,2y +z =0.令x =2,则y =1,z =-2.所以,n =(2,1,-2).又AB =(0,2,0),AB 与平面AB 1C 所成的角为θ=arcsin |AB ・n ||n ||AB |=arcsin |(0,2,0)・(2,1,-2)|2×3=arcsin 13.故AB 与平面A 1B 1C 所成的角为arcsin 13.7 求二面角解这类题的基本思路是:图8如图8,二面角α-l -β,平面α、β的法向量分别为n 1、n 2,它们的夹角与二面角的平面角相等或互补.P 为空间一点,P A ⊥α于A ,P B ⊥β于B ,AC ⊥l 于C ,则BC ⊥l ,∠ACB 为平面角,PA ∥n 1,PB ∥n 2.易知∠A P B 与∠ACB 互补.例7 正方体ABCD -A 1B 1C 1D 1中,二面角A -BD 1-A 1的度数是.(2004,全国高中数学联赛)图9解:设正方体为单位正方体.建立如图9的空间直角坐标系,则D (0,0,0)、A (1,0,0)、D 1(0,0,1)、B (1,1,0)、A 1(1,0,1).于是,AD 1=(-1,0,1),AB =(0,1,0),A 1B =(0,1,-1),A 1D 1=(-1,0,0).设平面ABD 1和平面A 1BD 1的法向量分别为n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2).由n 1⊥AB ,n 1⊥AD 1,n 2⊥A 1B ,n 2⊥A 1D 1,得y 1=0,-x 1+z 1=0,y 2-z 2=0,-x 2=0.令x 1=a ,则z 1=a ;令y 2=b ,则z 2=b.于是,n 1=(a ,0,a ),n 2=(0,b ,b ),设n 1、n 2的夹角为α.故cos α=n 1・n 2|n 1|・|n 2|=(a ,0,a )・(0,b ,b )2a ・2b=12.所以,α=60°.又易知二面角A -BD 1-A 1的平面角为θ=α.因此,二面角A -D 1B -A 1为60°.注:求二面角时,应注意法向量n 1、n 2的夹角是与其平面角相等还是互补,这可根据图形实际加以判定.8 求点到平面的距离解这类题的基本思路是:如图6,点B 到平面α的距离d =|BC |,设∠ABC =θ1,∠BAC =θ2,θ1+θ2=π2,且cos θ1=|n ・AB ||n ||AB |.在Rt △ABC 中,|BC |=|AB |cos θ1=|n ・AB ||n |.则d =|n ・AB ||n |.例8 在单位正方体ABCD -A 1B 1C 1D 1中,E 、F 分别是AB 、BC 的中点.求点D 到平面B 1EF 的距离.(2002,湖南省高中数学竞赛)图10解:建立如图10的空间直角坐标系,则D (0,0,0)、B 1(1,1,1)、E 1,12,0、F 12,1,0.于是,B 1E =0,-12,-1,B 1F =-12,0,-1.设平面B 1EF 的法向量为n =(x ,y ,z ).由n ⊥B 1E ,n ⊥B 1F ,得-12y -z =0,-12x -z =0.令z =1,则x =-2,y =-2.所以,n =(-2,-2,1).又D E =1,12,0,则点D 到平面B 1EF的距离为d =|n ・DE ||n |=(-2,-2,1)・1,12,03=1.9 求平行平面之间的距离解这类题的基本思路是:若平面α∥平面β,求平面α和平面β之间的距离可转化为求平面α内一点到平面β的距离.例9 已知长方体ABCD -A 1B 1C 1D 1中,AB =a ,BC =b ,CC 1=c.求平面A 1BD 和平面B 1D 1C 的距离.图11解:建立如图11的空间直角坐标系,则D (0,0,0)、A 1(b ,0,c )、B (b ,a ,0)、C (0,a ,0).于是,DA 1=(b ,0,c ),DB =(b ,a ,0),DC =(0,a ,0).设平面A 1BD 的法向量为n =(x ,y ,z ).由n ⊥DA 1,n ⊥DB ,得bx +cz =0,bx +ay =0.令x =ac ,则y =-bc ,z =-ab.所以,n =(ac ,-bc ,-ab ).要求平面A 1BD 与平面B 1D 1C 的距离,只须求点C 到平面A 1BD 的距离,则d =|n ・DC ||n |=|(ac ,-bc ,-ab )・(0,a ,0)|a 2b 2+b 2c 2+c 2a2.故平面A 1BD 与平面B 1D 1C 的距离为abca 2b 2+b 2c 2+a 2c2.10 求异面直线的距离解这类题的基本思路是:求异面直线l 1、l 2的距离,只须过直线l 2作平面α∥l 1,则可转化为求直线l 1上任一点到平面α的距离.例10 已知单位正方体ABCD -A 1B 1C 1D 1中,M 、N 分别是BB 1、B 1C 1的中点,P 是线段MN 的中点.求DP 与AC 1的距离.(1982,上海市高中数学竞赛)图12解:建立如图12的空间直角坐标系,则B 1(0,0,0)、A (0,1,1)、C 1(1,0,0)、D (1,1,1)、P14,0,14.设过DP 且平行于AC 1的平面α的方程为A 2x +B 2y +C 2z +e =0.因为DP ∈α,所以,A 2+B 2+C 2+e =0,14A 2+14C 2+e =0.又因为α∥AC 1,则AC 1⊥α的法向量n .于是,A 2-B 2-C 2=0.由以上各式可求得A 2=-12e ,B 2=3e ,C 2=-72e ,平面α的方程为x -6y +7z -2=0.因此,点C 1到平面α的距离为d =|1×1-6×0+7×0-2|12+(-6)2+72=8686.11 求直线与平面的距离解这类题的基本思路是:求直线l 与平行平面α的距离,可转化为求直线l 上一点到平面α的距离.例11 在直四棱柱ABCD -A 1B 1C 1D 1中,底面为直角梯形ABCD ,CD ⊥AD ,AB =2,AD =3,DC =6,AA 1=6,M 、N 分别是C 1D 1、CC 1的中点.求MN 与平面AD 1C 的距离.图13解:建立如图13的空间直角坐标系,则D (0,0,0)、A (3,0,0)、C (0,6,0)、D 1(0,0,6)、M (0,3,6)、N (0,6,3).于是,AC =(-3,6,0),AD 1=(-3,0,6).设平面AD 1C 的法向量为n =(x ,y ,z ).由n ⊥AC ,n ⊥AD 1,得-3x +6y =0,-3x +6z =0.令x =2,则y =z =1.所以,n =(2,1,1),NC =(0,0,-3).要求MN 与平面AD 1C 之间的距离,只须求点N 到平面AD 1C 的距离,则d =|n ・NC ||n |=36=62.故MN 与平面AD 1C 的距离为62.最后指出,确定平面的法向量,一般说来有两种方法:(1)待定系数法.设法向量n =(x ,y ,z ),由向量间垂直关系来确定x 、y 、z 的值.(2)求出平面的方程Ax +By +Cz +D =0,则该平面的法向量即为(A ,B ,C )(见例10).练习题1.已知正四面体ABCD 中,AB 、BC 、CD 的中点依次为E 、F 、G.求二面角C -FG -E 的大小.答案:π-arccos 33.2.正方体ABCD -A 1B 1C 1D 1中,M 、N 分别是AB 1、BC 1上的点,且AM =BN.求证:MN ⊥AA 1.3.正方体ABCD -A 1B 1C 1D 1中,E 、F 分别是BD 、B 1C 上的点,B E =13BD ,CF =13B 1C.求证:EF ∥AC 1.4.正方体ABC D -A 1B 1C 1D 1中,棱BB 1、CC 1的中点分别为M 、N.求A 1D 与平面D 1MN 所成的角.答案:arcsin105.5.已知正方体ABCD -A 1B 1C 1D 1中,CC 1、BC 、CD上各有一点M 、N 、P ,且CM =CN.要使A 1P ⊥平面DMN ,试确定点P 的位置.(提示:DP =CM.)。
2023年高考数学----立体几何解答题常考全归类真题练习题(含答案解析)

2023年高考数学----立体几何解答题常考全归类真题练习题(含答案解析)1.(2022·天津·统考高考真题)直三棱柱111ABC A B C -中,112,,AA AB AC AA AB AC AB ===⊥⊥,D 为11A B 的中点,E 为1AA 的中点,F 为CD 的中点.(1)求证://EF 平面ABC ;(2)求直线BE 与平面1CC D 所成角的正弦值; (3)求平面1ACD 与平面1CC D 所成二面角的余弦值. 【解析】(1)证明:在直三棱柱111ABC A B C -中,1AA ⊥平面111A B C ,且AC AB ⊥,则1111AC A B ⊥以点1A 为坐标原点,1A A 、11A B 、11AC 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则()2,0,0A 、()2,2,0B 、()2,0,2C 、()10,0,0A 、()10,0,2B 、()10,0,2C 、()0,1,0D 、()1,0,0E 、11,,12F ⎛⎫⎪⎝⎭,则10,,12EF ⎛⎫= ⎪⎝⎭, 易知平面ABC 的一个法向量为()1,0,0m =,则0EF m ⋅=,故EF m ⊥,EF ⊄平面ABC ,故//EF 平面ABC .(2)()12,0,0C C =,()10,1,2C D =−,()1,2,0EB =,设平面1CC D 的法向量为()111,,u x y z =,则111112020u C C x u C D y z ⎧⋅==⎪⎨⋅=−=⎪⎩,取12y =,可得()0,2,1u =,4cos ,5EB u EB u EB u⋅<>==⋅. 因此,直线BE 与平面1CC D 夹角的正弦值为45.(3)()12,0,2AC =,()10,1,0A D =, 设平面1ACD 的法向量为()222,,v x y z =,则122122200v AC x z v A D y ⎧⋅=+=⎪⎨⋅==⎪⎩,取21x =,可得()1,0,1v =−,则1cos ,5u v u v u v⋅<>==−=⨯⋅因此,平面1ACD 与平面1CC D 2.(2022·全国·统考高考真题)如图,四面体ABCD 中,,,AD CD AD CD ADB BDC ⊥=∠=∠,E 为AC 的中点.(1)证明:平面BED ⊥平面ACD ;(2)设2,60AB BD ACB ==∠=︒,点F 在BD 上,当AFC △的面积最小时,求CF 与平面ABD 所成的角的正弦值.【解析】(1)因为AD CD =,E 为AC 的中点,所以AC DE ⊥; 在ABD △和CBD △中,因为,,B A C D CD ADB DB DB D ∠=∠==,所以ABD CBD ≌△△,所以AB CB =,又因为E 为AC的中点,所以AC BE ⊥; 又因为,DE BE ⊂平面BED ,DE BE E ⋂=,所以AC ⊥平面BED ,因为AC ⊂平面ACD ,所以平面BED ⊥平面ACD .(2)连接EF ,由(1)知,AC ⊥平面BED ,因为EF ⊂平面BED , 所以AC EF ⊥,所以1=2AFC S AC EF ⋅△, 当EF BD ⊥时,EF 最小,即AFC △的面积最小. 因为ABD CBD ≌△△,所以2CB AB ==, 又因为60ACB ∠=︒,所以ABC 是等边三角形, 因为E 为AC 的中点,所以1AE EC ==,BE 因为AD CD ⊥,所以112DE AC ==, 在DEB 中,222DE BE BD +=,所以BE DE ⊥.以E 为坐标原点建立如图所示的空间直角坐标系E xyz −,则()()()1,0,0,,0,0,1A B D ,所以()()1,0,1,AD AB =−=−, 设平面ABD 的一个法向量为(),,n x y z =,则00n AD x z n AB x ⎧⋅=−+=⎪⎨⋅=−+=⎪⎩,取y =()3,3,3n =, 又因为()31,0,0,4C F ⎛⎫− ⎪ ⎪⎝⎭,所以31,4CF ⎛⎫= ⎪ ⎪⎝⎭,所以cos ,21n CF n CF n CF⋅===设CF 与平面ABD 所成的角的正弦值为02πθθ⎛⎫≤≤ ⎪⎝⎭,所以4sin cos ,7nCF θ==所以CF 与平面ABD3.(2022·浙江·统考高考真题)如图,已知ABCD 和CDEF 都是直角梯形,//AB DC ,//DC EF ,5AB =,3DC =,1EF =,60BAD CDE ∠=∠=︒,二面角F DC B −−的平面角为60︒.设M ,N 分别为,AE BC 的中点.(1)证明:FN AD ⊥;(2)求直线BM 与平面ADE 所成角的正弦值.【解析】(1)过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点G 、H . ∵四边形ABCD 和EFCD 都是直角梯形,//,//,5,3,1AB DC CD EF AB DC EF ===,60BAD CDE ∠=∠=︒,由平面几何知识易知,2,90DG AH EFC DCF DCB ABC ==∠=∠=∠=∠=︒,则四边形EFCG 和四边形DCBH 是矩形,∴在Rt EGD 和Rt DHA ,EG DH == ∵,DC CF DC CB ⊥⊥,且CF CB C ⋂=,∴DC ⊥平面,BCF BCF ∠是二面角F DC B −−的平面角,则60BCF ∠=, ∴BCF △是正三角形,由DC ⊂平面ABCD ,得平面ABCD ⊥平面BCF ,∵N 是BC 的中点,∴FN BC ⊥,又DC ⊥平面BCF ,FN ⊂平面BCF ,可得FN CD ⊥,而BC CD C ⋂=,∴FN ⊥平面ABCD ,而AD ⊂平面ABCD FN AD ∴⊥.(2)因为FN ⊥平面ABCD ,过点N 做AB 平行线NK ,所以以点N 为原点, NK ,NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N xyz −,设(3,(1,0,3)A B D E,则32M ⎛⎫ ⎪ ⎪⎝⎭,333,,,(2,23,0),(2,22BM AD DE ⎛⎫∴=−=−−=− ⎪ ⎪⎝⎭ 设平面ADE 的法向量为(,,)nx y z =由00n AD n DE ⎧⋅=⎨⋅=⎩,得20230x x z ⎧−−=⎪⎨−+=⎪⎩,取(3,n =−,设直线BM 与平面ADE 所成角为θ,∴3||sin cos ,|||3n BM n BM n BMθ⋅=〈〉====⋅4.(2022·全国·统考高考真题)如图,PO 是三棱锥−P ABC 的高,PA PB =,AB AC ⊥,E 是PB 的中点.(1)证明://OE 平面PAC ;(2)若30ABO CBO ∠=∠=︒,3PO =,5PA =,求二面角C AE B −−的正弦值. 【解析】(1)证明:连接BO 并延长交AC 于点D ,连接OA 、PD ,因为PO 是三棱锥−P ABC 的高,所以PO ⊥平面ABC ,,AO BO ⊂平面ABC , 所以PO AO ⊥、PO BO ⊥,又PA PB =,所以POA POB ≅△△,即OA OB =,所以OAB OBA ∠=∠,又AB AC ⊥,即90BAC ∠=︒,所以90OAB OAD ∠+∠=︒,90OBA ODA ∠+∠=︒, 所以ODA OAD ∠=∠所以AO DO =,即AO DO OB ==,所以O 为BD 的中点,又E 为PB 的中点,所以//OE PD , 又OE ⊄平面PAC ,PD ⊂平面PAC , 所以//OE 平面PAC(2)过点A 作//Az OP ,如图建立平面直角坐标系, 因为3PO =,5AP =,所以4OA =,又30OBA OBC ∠=∠=︒,所以28BD OA ==,则4=AD,AB = 所以12AC =,所以()O,()B,()P ,()0,12,0C ,所以32E ⎛⎫ ⎪⎝⎭,则332AE ⎛⎫= ⎪⎝⎭,()43,0,0AB =,()0,12,0AC =,设平面AEB 的法向量为(),,n x y z =,则33302430n AE y z n AB ⎧⋅=++=⎪⎨⎪⋅==⎩,令2z =,则=3y −,0x =,所以()0,3,2n =−;设平面AEC 的法向量为(),,m a b c =,则33302120m AE a bc m AC b ⎧⋅=++=⎪⎨⎪⋅==⎩,令a =6c =−,0b =,所以()3,0,6m =−;所以cos ,13n m n m n m⋅−===设二面角C AE B −−的大小为θ,则43cos cos ,=13n m θ=, 所以11sin 13θ=,即二面角C AE B −−的正弦值为1113.5.(2022·全国·统考高考真题)如图,四面体ABCD 中,,,AD CD AD CD ADB BDC ⊥=∠=∠,E 为AC 的中点.(1)证明:平面BED ⊥平面ACD ;(2)设2,60AB BD ACB ==∠=︒,点F 在BD 上,当AFC △的面积最小时,求三棱锥F ABC −的体积.【解析】(1)由于AD CD =,E 是AC 的中点,所以AC DE ⊥.由于AD CDBD BD ADB CDB =⎧⎪=⎨⎪∠=∠⎩,所以ADB CDB ≅△△,所以AB CB =,故AC BD ⊥,由于DE BD D ⋂=,,DE BD Ì平面BED , 所以AC ⊥平面BED ,由于AC ⊂平面ACD ,所以平面BED ⊥平面ACD . (2)[方法一]:判别几何关系依题意2AB BD BC ===,60ACB ∠=︒,三角形ABC 是等边三角形,所以2,1,AC AE CE BE ===由于,AD CD AD CD =⊥,所以三角形ACD 是等腰直角三角形,所以1DE =. 222DE BE BD +=,所以DE BE ⊥,由于AC BE E ⋂=,,AC BE ⊂平面ABC ,所以DE ⊥平面ABC . 由于ADB CDB ≅△△,所以FBA FBC ∠=∠,由于BF BF FBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩,所以FBA FBC ≅,所以AF CF =,所以EF AC ⊥, 由于12AFCSAC EF =⋅⋅,所以当EF 最短时,三角形AFC 的面积最小 过E 作EF BD ⊥,垂足为F ,在Rt BED △中,1122BE DE BD EF ⋅⋅=⋅⋅,解得EF =所以13,222DF BF DF ===−=, 所以34BF BD =过F 作FH BE ⊥,垂足为H ,则//FH DE ,所以FH ⊥平面ABC ,且34FH BF DE BD ==, 所以34FH =,所以111323324F ABC ABCV SFH −=⋅⋅=⨯⨯=[方法二]:等体积转换AB BC =,60ACB ∠=︒,2AB =ABC ∴∆是边长为2的等边三角形,BE ∴=连接EFADB CDB AF CF EF ACBED EF BD ∆≅∆∴=∴⊥∴∆⊥∆在中,当时,AFC 面积最小222,,2,,BED EF AD CD AD CD AC E AC DE BE BD BE EDBE DE EF BD BD ⊥==∴+=∴⊥⋅⊥∆==为中点DE=1若在中,32113222BEFBF S BF EF ∆∴=⋅=⋅11233F ABC A BEF C BEF BEF V V V S AC −−−∆∴=+=⋅=6.(2022·全国·统考高考真题)在四棱锥P ABCD −中,PD ⊥底面,,1,2,ABCD CD AB AD DC CB AB DP ====∥(1)证明:BD PA ⊥;(2)求PD 与平面PAB 所成的角的正弦值.【解析】(1)证明:在四边形ABCD 中,作DE AB ⊥于E ,CF AB ⊥于F , 因为//,1,2CD AB AD CD CB AB ====, 所以四边形ABCD 为等腰梯形, 所以12AE BF ==,故DE =BD = 所以222AD BD AB +=, 所以AD BD ⊥,因为PD ⊥平面ABCD ,BD ⊂平面ABCD , 所以PD BD ⊥, 又=PD AD D ⋂, 所以BD ⊥平面PAD , 又因为PA ⊂平面PAD , 所以BD PA ⊥;(2)如图,以点D 为原点建立空间直角坐标系,BD =则()()(1,0,0,,A B P ,则()()(1,0,3,0,3,3,AP BP DP =−=−=,设平面PAB 的法向量(),,n x y z =,则有0{30n AP x n BP ⋅=−=⋅=−=,可取()3,1,1n =, 则5cos ,5n DPn DP n DP ⋅==所以PD 与平面PAB7.(2022·北京·统考高考真题)如图,在三棱柱111ABC A B C -中,侧面11BCC B 为正方形,平面11BCC B ⊥平面11ABB A ,2AB BC ==,M ,N 分别为11A B ,AC 的中点.(1)求证:MN ∥平面11BCC B ;(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB 与平面BMN 所成角的正弦值.条件①:AB MN ⊥;条件②:BM MN =.注:如果选择条件①和条件②分别解答,按第一个解答计分.【解析】(1)取AB 的中点为K ,连接,MK NK ,由三棱柱111ABC A B C -可得四边形11ABB A 为平行四边形,而11,B M MA BK KA ==,则1//MK BB ,而MK ⊄平面11BCC B ,1BB ⊂平面11BCC B ,故//MK 平面11BCC B ,而,CN NA BK KA ==,则//NK BC ,同理可得//NK 平面11BCC B ,而,,NK MK K NK MK =⊂平面MKN ,故平面//MKN 平面11BCC B ,而MN ⊂平面MKN ,故//MN 平面11BCC B ,(2)因为侧面11BCC B 为正方形,故1CB BB ⊥,而CB ⊂平面11BCC B ,平面11CBB C ⊥平面11ABB A ,平面11CBB C ⋂平面111ABB A BB =,故CB ⊥平面11ABB A ,因为//NK BC ,故NK ⊥平面11ABB A ,因为AB ⊂平面11ABB A ,故NK AB ⊥,若选①,则AB MN ⊥,而NK AB ⊥,NK MN N =,故AB ⊥平面MNK ,而MK ⊂平面MNK ,故AB MK ⊥,所以1AB BB ⊥,而1CB BB ⊥,CB AB B ⋂=,故1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()()()()0,0,0,0,2,0,1,1,0,0,1,2B A N M , 故()()()0,2,0,1,1,0,0,1,2BA BN BM ===,设平面BNM 的法向量为(),,n x y z =,则00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取1z =−,则()2,2,1n =−−, 设直线AB 与平面BNM 所成的角为θ,则42sin cos ,233n AB θ===⨯. 若选②,因为//NK BC ,故NK ⊥平面11ABB A ,而KM ⊂平面MKN , 故NK KM ⊥,而11,1B M BK NK ===,故1B M NK =,而12B B MK ==,MB MN =,故1BB M MKN ≅,所以190BB M MKN ∠=∠=︒,故111A B BB ⊥,而1CB BB ⊥,CB AB B ⋂=,故1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()()()()0,0,0,0,2,0,1,1,0,0,1,2B A N M , 故()()()0,2,0,1,1,0,0,1,2BA BN BM ===,设平面BNM 的法向量为(),,n x y z =,则00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取1z =−,则()2,2,1n =−−, 设直线AB 与平面BNM 所成的角为θ,则42sin cos ,233n AB θ===⨯.8.(2022·全国·统考高考真题)如图,直三棱柱111ABC A B C -的体积为4,1A BC 的面积为(1)求A 到平面1A BC 的距离;(2)设D 为1AC 的中点,1AA AB =,平面1A BC ⊥平面11ABB A ,求二面角A BD C −−的正弦值. 【解析】(1)在直三棱柱111ABC A B C -中,设点A 到平面1A BC 的距离为h , 则111111112211433333A A BC A A ABC A ABC AB BC C C B V S h h V S A A V −−−=⋅===⋅==,解得h =所以点A 到平面1A BC (2)取1A B 的中点E ,连接AE ,如图,因为1AA AB =,所以1AE A B ⊥, 又平面1A BC ⊥平面11ABB A ,平面1A BC ⋂平面111ABB A A B =, 且AE ⊂平面11ABB A ,所以⊥AE 平面1A BC , 在直三棱柱111ABC A B C -中,1BB ⊥平面ABC , 由BC ⊂平面1A BC ,BC ⊂平面ABC 可得AE BC ⊥,1BB BC ⊥,又1,AE BB ⊂平面11ABB A 且相交,所以BC ⊥平面11ABB A , 所以1,,BC BA BB 两两垂直,以B 为原点,建立空间直角坐标系,如图,由(1)得AE 12AA AB ==,1A B =2BC =, 则()()()()10,2,0,0,2,2,0,0,0,2,0,0A A B C ,所以1AC 的中点()1,1,1D , 则()1,1,1BD =,()()0,2,0,2,0,0BA BC ==,设平面ABD 的一个法向量(),,m x y z =,则020m BD x y z m BA y ⎧⋅=++=⎨⋅==⎩, 可取()1,0,1m =−,设平面BDC 的一个法向量(),,n a b c =,则020n BD a b c n BC a ⎧⋅=++=⎨⋅==⎩, 可取()0,1,1n =−r , 则11cos ,22m nm n m n ⋅===⨯⋅,所以二面角A BD C −−=本课结束。
高三数学平面向量的几何运算试题答案及解析

高三数学平面向量的几何运算试题答案及解析1.在平面直角坐标中,的三个顶点A、B、C,下列命题正确的个数是()(1)平面内点G满足,则G是的重心;(2)平面内点M满足,点M是的内心;(3)平面内点P满足,则点P在边BC的垂线上;A.0B.1C.2D.3【答案】B【解析】对(2),M为的外心,故(2)错.对(3),,所以点P在的平分线上,故(3)错.易得(1)正确,故选B.【考点】三角形与向量.2.如图所示,、、是圆上的三点,的延长线与线段交于圆内一点,若,则()A.B.C.D.【答案】C【解析】由于、、三点共线,设,则,由于、、三点共线,且点在圆内,点在圆上,与方向相反,则存在,使得,因此,,所以,选C.【考点】1.共线的平面向量;2.平面向量的线性表示3. [2014·牡丹江模拟]设e1,e2是两个不共线的向量,且a=e1+λe2与b=-e2-e1共线,则实数λ=()A.-1B.3C.-D.【答案】D【解析】∵a=e1+λe2与b=-e2-e1共线,∴存在实数t,使得b=ta,即-e2-e1=t(e1+λe2),- e2-e1=te1+tλe2,由题意,e1,e2不共线,∴t=-1,tλ=-,即λ=,故选D.4.在平行四边形中,,,为中点,若,则的长为.【答案】6【解析】根据题意可得:,则,化简得:,解得:.【考点】向量的运算5.若向量=(1,2),=(1,﹣1),则2+与的夹角等于()A.﹣B.C.D.【答案】C【解析】∵=(1,2),=(1,﹣1),∴2+=(3,3)=(0,3)则(2+)•()=9|2|=,||=3∴cosθ==∴θ=故选C6.在△ABC中,过中线AD中点E任作一条直线分别交边AB、AC于M、N两点,设=x,=y (xy≠0),则4x+y的最小值是________.【答案】【解析】因为D是BC的中点,E是AD的中点,所以== ( +).又=,=,所以=+.因为M、E、N三点共线,所以=1,所以4x+y=(4x+y)7.已知=(2,0),,的夹角为60°,则.【答案】【解析】.【考点】向量的基本运算.8.在所在的平面内,点满足,,且对于任意实数,恒有,则()A.B.C.D.【答案】C【解析】过点作,交于,是边上任意一点,设在的左侧,如图,则是在上的投影,即,即在上的投影,,令,,,,故需要,,即,为的中点,又是边上的高,是等腰三角形,故有,选C.【考点】共线向量,向量的数量积.9.如图所示的方格纸中有定点O,P,Q,E,F,G,H,则=()A.B.C.D.【答案】D【解析】在方格纸上作出,如下图,则容易看出,故选D.【考点】1.向量的加法运算.10.在中,已知是边上的一点,若,,则()A.B.C.D.【答案】A【解析】,即,解得,,故选A.【考点】平面向量的线性表示11.设点为三角形ABC的外心,则.【答案】【解析】出边AB,AC的垂线,利用向量的运算将用表示,利用向量的数量积的几何意义将向量的数量积表示成一个向量与另个向量的投影的乘积.解:过O作OS⊥AB,OT⊥AC 垂足分别为S,T 则S,T分别是AB,AC的中点,则=【考点】向量的运算法则点评:本题考查向量的运算法则、向量数量积的几何意义.12.的外接圆的圆心为,半径为,且,则向量在上的射影的数量为()A.B.C.D.【答案】A【解析】解:由题意因为△ABC的外接圆的圆心为O,半径为2,OA + AB + AC =" 0" 且| OA |="|" AB |,对于 OA + AB + AC =" 0" ⇔ OB =" CA" ,所以可以得到图形为:因为 CA =" OB" ,所以四边形ABOC为平行四边形,又由于| OA |="|" AB |,所以三角形OAB为正三角形且边长为2,所以四边形ABOC为边长为2且角ABO为60°的菱形,所以向量 CA 在 CB 方向上的投影为:| CA |cos< CA , CB >=2×cos30°= 故选:A13.设向量,若a//b,则实数t的值是_______.【答案】 9【解析】考查平面向量的坐标运算及共线性质。
专题5:向量法做立体几何的线面角问题(解析版)

专题5:理科高考中的线面角问题(解析版)求直线和平面所成的角求法:设直线l 的方向向量为a ,平面α的法向量为u ,直线与平面所成的角为θ,a 与u 的夹角为ϕ, 则θ为ϕ的余角或ϕ的补角的余角.即有:cos s .in a u a u ϕθ⋅== 1.如图,在三棱锥A BCD -中,ABC 是等边三角形,90BAD BCD ∠=∠=︒,点P 是AC 的中点,连接,BP DP .(1)证明:平面ACD ⊥平面BDP ;(2)若6BD =,且二面角A BD C --为120︒,求直线AD 与平面BCD 所成角的正弦值.【答案】(1)见解析(2)22 【分析】(1)由ABC 是等边三角形,90BAD BCD ∠=∠=︒,得AD CD =.再证明PD AC ⊥,PB AC ⊥,从而和证明AC ⊥平面PBD ,故平面ACD ⊥平面BDP 得证. (2)作CE BD ⊥,垂足为E 连接AE .由Rt Rt ABD CBD ⊆,证得,AE BD ⊥,AE CE =结合二面角A BD C --为120︒,可得2AB =,23AE =,6ED =.建立空间直角坐标系,求出点的坐标则60,,03D ⎛⎫ ⎪ ⎪⎝⎭,3,0,13A ⎛⎫- ⎪ ⎪⎝⎭,向量36,,133AD ⎛⎫=- ⎪ ⎪⎝⎭,即平面BCD 的一个法向量(0,0,1)m =,运用公式cos ,m ADm AD m AD ⋅〈〉=和sin cos ,m AD θ=〈〉,即可得出直线AD 与平面BCD 所成角的正弦值.【详解】解:(1)证明:因为ABC 是等边三角形,90BAD BCD ∠=∠=︒,所以Rt Rt ABD CBD ≅,可得AD CD =.因为点P 是AC 的中点,则PD AC ⊥,PB AC ⊥,因为PD PB P =,PD ⊂平面PBD ,PB ⊂平面PBD ,所以AC ⊥平面PBD ,因为AC ⊂平面ACD ,所以平面ACD ⊥平面BDP .(2)如图,作CE BD ⊥,垂足为E 连接AE .因为Rt Rt ABD CBD ⊆,所以,AE BD ⊥,AE CE =AEC ∠为二面角A-BD-C 的平面角.由已知二面角A BD C --为120︒,知120AEC ∠=︒.在等腰三角形AEC 中,由余弦定理可得3AC =.因为ABC 是等边三角形,则AC AB =,所以3AB =.在Rt △ABD 中,有1122AE BD AB AD ⋅=⋅,得3BD =, 因为6BD =所以2AD =. 又222BD AB AD =+,所以2AB =. 则23AE =,6ED =. 以E 为坐标原点,以向量,EC ED 的方向分别为x 轴,y 轴的正方向,以过点E 垂直于平面BCD 的直线为z 轴,建立空间直角坐标系E xyz -, 则6D ⎛⎫ ⎪ ⎪⎝⎭,3A ⎛⎫ ⎪ ⎪⎝⎭,向量361AD ⎛⎫=- ⎪ ⎪⎝⎭, 平面BCD 的一个法向量为(0,0,1)m =,设直线AD 与平面BCD 所成的角为θ,则2cos ,221m ADm AD m AD ⋅〈〉===-⨯,2sin |cos ,|2m AD θ=〈〉= 所以直线AD 与平面BCD 所成角的正弦值为22. 【点睛】本题考查面面垂直的证明和线面所成角的大小,考查空间想象力和是数形结合的能力,属于基础题.2.如图,直四棱柱ABCD –A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ;(2)求AM 与平面A 1MD 所成角的正弦值.【答案】(1)见解析(2)105 【分析】要证线面平行,先证线线平行建系,利用法向量求解。
(完整版)高考立体几何大题及答案(理)

故AD=AF。又AD⊥AF,所以四边形ADEF为正方形。
因为BC⊥AF,BC⊥AD,AF∩AD=A,故BC⊥平面DEF,因此平面BCD⊥平面DEF。
连接AE、DF,设AE∩DF=H,则EH⊥DF,EH⊥平面BCD。
连接CH,则∠ECH为 与平面BCD所成的角。
因ADEF为正方形,AD= ,故EH=1,又EC= =2,
(II)设线段 、 的中点分别为 、 ,
求证: ∥
(III)求二面角 的大小。
10.如题(18)图,在五面体 中, ∥ , , ,四边形 为平行四边形, 平面 , .求:
(Ⅰ)直线 到平面 的距离;
(Ⅱ)二面角 的平面角的正切值.
11.如图,四棱锥PABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅱ)设平面BCD的法向量 则
又 =(-1,1,0),
=(-1,0,c),故
令x=1,则y=1,z= , =(1,1, ).
又平面 的法向量 =(0,1,0)
由二面角 为60°知, =60°,
故 °,求得
于是 ,
,
°
所以 与平面 所成的角为30°
3、(Ⅰ)证明:连接 ,在 中, 分别是 的中点,所以 ,又 ,所以 ,又 平面ACD,DC 平面ACD,所以 平面ACD
(1)证明:PA⊥BD;
(2)设PD=AD,求二面角A-PB-C的余弦值.
12(本小题满分12分)
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB CD,AC BD,垂足为H,
PH是四棱锥的高,E为AD中点
(1)证明:PE BC
(2)若 APB= ADB=60°,求直线PA与平面PEH所成角的正弦值
2021年高考数学经典例题专题七立体几何与空间向量含解析

专题七 立体几何与空间向量一、单项选择题1.假如棱长为A .12πB .24πC .36πD .144π【答案】C【解析】求出正方体的体对角线的一半,即为球的半径,利用球的外表积公式,即可得解.【详解】这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即3R ==,所以,这个球的外表积为2244336S R πππ==⨯=.应当选:C.【点睛】此题考查正方体的外接球的外表积的求法,求出外接球的半径是此题的解题关键,属于根底题.求多面体的外接球的面积和体积问题,常用方法有:〔1〕三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;〔2〕直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;〔3〕如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心.2.某三棱柱的底面为正三角形,其三视图如下列图,该三棱柱的外表积为〔〕.A .63+B .623+C .123+D .1223+【答案】D【解析】首先确定几何体的结构特征,然后求解其外表积即可.【详解】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,如此其外表积为:()1322222sin 60122S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+ ⎪⎝⎭应当选:D.3.某几何体的三视图〔单位:cm 〕如下列图,如此该几何体的体积〔单位:cm 3〕是〔〕A .73B .143C .3D .6 【答案】A【解析】根据三视图复原原图,然后根据柱体和锥体体积计算公式,计算出几何体的体积.【详解】由三视图可知,该几何体是上半局部是三棱锥,下半局部是三棱柱,且三棱锥的一个侧面垂直于底面,且棱锥的高为1,棱柱的底面为等腰直角三角形,棱柱的高为2,所以几何体的体积为:11117211212232233⎛⎫⎛⎫⨯⨯⨯⨯+⨯⨯⨯=+= ⎪ ⎪⎝⎭⎝⎭. 应当选:A4.,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,假如⊙1O 的面积为4π,1AB BC AC OO ===,如此球O 的外表积为〔〕A .64πB .48πC .36πD .32π【答案】A【解析】由可得等边ABC 的外接圆半径,进而求出其边长,得出1OO 的值,根据球的截面性质,求出球的半径,即可得出结论.【详解】设圆1O 半径为r ,球的半径为R ,依题意,得24,2r r ππ=∴=,ABC 为等边三角形,由正弦定理可得2sin60AB r =︒=1OO AB ∴==1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥====,∴球O 的外表积2464S R ππ==.应当选:A5.如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M ,在俯视图中对应的点为N ,如此该端点在侧视图中对应的点为〔〕A .EB .FC .GD .H【答案】A【解析】根据三视图,画出多面体立体图形,即可求得M 点在侧视图中对应的点.【详解】根据三视图,画出多面体立体图形,14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N,∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E .应当选:A6.四面体ABCD 的顶点A ,B ,C ,D 在同个球面上,AD ⊥平面ABC ,3AD =,2AB =,3AC =,60CAB ∠=︒,如此该四面体的外接球的外表积为〔〕A .6πB .143πC .12πD .163π 【答案】C【解析】过ABC 外接圆1O ,作直线l ⊥平面ABC ,可得1123OO AD ==,在ABC 中,利用余弦定理求出BC =ABC 外接圆半径,利用勾股定理求出外接球半径,根据球的外表积公式即可求解.【详解】如下列图,作ABC 外接圆1O ,过1O 作直线l ⊥平面ABC ,又DA ⊥平面ABC ,//DA l ∴,连接1AO ,并延长交球O 于H ,连接DH ,与l 的交点为球心O ,OH OD R ==,如此112OO AD ==, 在ABC 中,由余弦定理得2222cos60BC AB AC AB AC =+-⋅⋅︒14922372=+-⨯⨯⨯=,BC ∴=,又由正弦定理得12sin 60BC O H =︒(1O H 为外接圆半径),13O H ∴= 222211621399R OH OO O H ∴==+=+=, 2412S R ππ∴==.应当选:C.7.日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OAA处放置一个日晷,假如晷面与赤道所在平面平行,点A处的纬度为北纬40°,如此晷针与点A处的水平面所成角为〔〕A.20°B.40°C.50°D.90°【答案】B【解析】画出过球心和晷针所确定的平面截地球和晷面的截面图,根据面面平行的性质定理和线面垂直的定义判定有关截线的关系,根据点A 处的纬度,计算出晷针与点A 处的水平面所成角.【详解】画出截面图如如下图所示,其中CD 是赤道所在平面的截线;l 是点A 处的水平面的截线,依题意可知OA l ⊥;AB 是晷针所在直线.m 是晷面的截线,依题意依题意,晷面和赤道平面平行,晷针与晷面垂直, 根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥..由于40,//AOC m CD ∠=︒,所以40OAG AOC ∠=∠=︒,由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒,所以40BAE OAG ∠=∠=︒,也即晷针与点A 处的水平面所成角为40BAE ∠=︒.应当选:B8.△ABC 的等边三角形,且其顶点都在球OO 的外表积为16π,如此O 到平面ABC 的距离为〔〕A .32C .1D .2【答案】C【解析】根据球O 的外表积和ABC 的面积可求得球O 的半径R 和ABC 外接圆半径r ,由球的性质可知所求距离d =【详解】设球O 的半径为R ,如此2416R ππ=,解得:2R =.设ABC 外接圆半径为r ,边长为a ,ABC 的等边三角形,212a ∴=,解得:3a =,2233r ∴===∴球心O 到平面ABC 的距离1d ===.应当选:C.9.在三棱锥P ABC -中,BC ⊥平面PAB ,AP AB ⊥,D 是BC 的中点.假如45APB ∠=︒,60APC ∠=︒,如此直线PD 与平面ABC 所成角的正弦值为〔〕A .3B .2C D 【答案】C【解析】根据线面角的定义找到直线PD 与平面ABC 所成角的平面角,法一:应用几何法,根据线面垂直的性质、勾股定理求对应边,在直角三角形中求线面角的正弦值;法二:应用向量法,构建空间直角坐标系,并确定线面角两边所在直线的方向向量坐标,进而求其余弦值,由同角三角函数关系求正弦值.【详解】在三棱锥P ABC -中,BC ⊥平面PAB ,AP ⊂面PAB ,∴BC AP ⊥,又AP AB ⊥,AB BC B ⋂=,∴PA ⊥平面ABC ,即PDA ∠即直线PD 与平面ABC 所成角.法一:设PA a =,由45APB ∠=︒,60APC ∠=︒,得AB PA a ==,∴AC =,BC =.又D 是BC 的中点,如此2BD =,∴在Rt ABD △中,2AD a ==.又易知PA AD ⊥,在Rt PAD 中,PD ==,∴sin 5AP PDA PD ∠==.法二:过点A 在平面ABC 内作//Ax BC .易知直线AP ,AB ,Ax 两两垂直,可建立如下列图的空间直角坐标系A xyz -.不妨设1PA =,如此1AB =,ACBC =2BD =,有()0,0,0A ,()0,0,1P,2D ⎛⎫ ⎪ ⎪⎝⎭,∴1,0DA ⎛⎫=--⎪ ⎪⎝⎭,1,1DP ⎛⎫=-- ⎪ ⎪⎝⎭,如此3cos ,3DA DP DA DP DA DP ⋅===,∴10sin ,5DA DP =.应当选:C.,,,是同一个半径为4的球的球面上四点,ABC为等边三角形且其面积为,如10.设A B C D体积的最大值为〔〕此三棱锥D ABCA...D.【答案】B【解析】如下列图,点M 为三角形ABC 的中心,E 为AC 中点,当DM ⊥平面ABC 时,三棱锥D ABC -体积最大此时,OD OB R 4===2ABC S AB == AB 6∴=,点M 为三角形ABC 的中心2BM 3BE ∴==Rt OMB ∴中,有OM 2==DM OD OM 426∴=+=+=()max 163D ABC V -∴=⨯=应当选B.二、多项选择题11.矩形ABCD 中,4AB =,3BC =,将ABD △沿BD 折起,使A 到A '的位置,A '在平面BCD 的射影E 恰落在CD 上,如此〔〕A .三棱锥A BCD '-的外接球直径为5B .平面A BD '⊥平面A BC 'C .平面A BD '⊥平面ACD 'D .A D '与BC 所成角为60【答案】AB【解析】根据面面垂直的判定定理以与面面垂直的性质定理结合对选项BCD 逐一进展分析,对A 选项注意确定球心位置,然后利用勾股定理求解外接球的直径.【详解】由题意,A E '⊥平面BCD BC A E '⇒⊥,又BC CD ⊥,A E CD E '=,∴BC ⊥平面A CD BC A D ''⇒⊥.故D 错误;又A B A D ''⊥,A BBC B '=,可得A D '⊥平面A BC ',又A D '⊂平面A BD '⇒平面A BD '⊥平面A BC '.故B 正确; 对C ,假如平面A BD '⊥平面ACD ',如此由A B A D A B '''⊥⇒⊥平面90A CD BA C ''⇒∠=︒与90A CB '∠=︒矛盾,故C 错误;取BD 中点为O .如此OA OB OC OD '===,故O 为三棱锥A BCD '-的外接球球心,所以直径5d BD ===,故A 正确.应当选:AB三、填空题12.正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为BB 1、AB 的中点,如此三棱锥A -NMD 1的体积为____________ 【答案】13【解析】利用11A NMD D AMN V V --=计算即可.【详解】因为正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为BB 1、AB 的中点 所以11111112323A NMD D AMN V V --==⨯⨯⨯⨯= 故答案为:1313.如图,将正方体沿交于同一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的棱长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.假如用一小桶油漆刚好可以涂该二十四等边体的外表一遍,如此用该小桶油漆去涂与该二十四等边体棱长相等的正四面体魔方外表(也是涂一遍),那么至少可以涂___________个这样的正四面体魔方.(结果取整数)【答案】5【解析】设二十四等边体的棱长为1,计算其外表积,再计算正四面体魔方的外表积,即可解得.【详解】设该二十四等边体的棱长为1,如此正四面体魔方的棱长也为1,如此该二十四等边体的外表积为2218161622⨯⨯⨯+⨯=,正四面体的外表积为214122⨯⨯⨯=2 5.46=+≈,所以至少可以涂5个这样正四面体魔方. 故答案为:5.14.三棱锥P ABC -中,AP 、AB 、AC 三条棱两两垂直,且长度均为P 为球心,4为半径作一个球,如此该球面被三棱锥四个外表截得的所有弧长之和为______.【答案】3π【解析】采用数形结合,然后利用弧长公式计算即可.【详解】由题可知:AP 、AB 、AC 三条棱两两垂直,且长度均为如图:所以PC PB BC ====2AM AF ===,所以tan tanAPF APM ∠=∠==6APF APM π∠=∠= 所以12EPF CPM π∠=∠=,如此4123EF MN ππ==⨯=44,2332NE MF ππππ=⨯==⨯= 所以球面被三棱锥四个外表截得的所有弧长之和为42333ππππ⨯++= 故答案为:3π 15.直四棱柱ABCD –A1B 1C 1D 1的棱长均为2,∠BAD =60°.以1D BCC 1B 1的交线长为________.. 【解析】根据条件易得1D E =1D E ⊥侧面11BC CB ,可得侧面11BC CB 与球面的交线上的点到E 可得侧面11BC CB 与球面的交线是扇形EFG 的弧FG ,再根据弧长公式可求得结果.【详解】如图:取11B C 的中点为E ,1BB 的中点为F ,1CC 的中点为G ,因为BAD ∠=60°,直四棱柱1111ABCD A BC D -的棱长均为2,所以△111D B C 为等边三角形,所以1D E=111D E B C ⊥,又四棱柱1111ABCD A BC D -为直四棱柱,所以1BB ⊥平面1111D C B A ,所以111BB B C ⊥, 因为1111BB B C B =,所以1D E ⊥侧面11BC CB ,设P 为侧面11BC CB 与球面的交线上的点,如此1DE EP ⊥,1D E =||EP === 所以侧面11BC CB 与球面的交线上的点到E因为||||EF EG =11BC CB 与球面的交线是扇形EFG 的弧FG ,因为114B EF C EG π∠=∠=,所以2FEG π∠=,所以根据弧长公式可得22FG π==.. 16.圆锥的底面半径为1,母线长为3,如此该圆锥内半径最大的球的体积为_________.【解析】将原问题转化为求解圆锥内切球的问题,然后结合截面确定其半径即可确定体积的值.【详解】易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如下列图,其中2,3BC AB AC ===,且点M 为BC 边上的中点,设内切圆的圆心为O ,由于AM =122S =⨯⨯△ABC设内切圆半径为r ,如此:ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯ ()13322r =⨯++⨯=解得:22r ,其体积:3433V r π==.. 【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出适宜的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.17.中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体〞〔图1〕.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体表现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的外表上,且此正方体的棱长为1.如此该半正多面体共有________个面,其棱长为_________.【答案】共26个面.1.【解析】由图可知第一层与第三层各有9个面,计18个面,第二层共有8个面,所以该半正多面体共有18826+=个面.如图,设该半正多面体的棱长为x ,如此AB BE x ==,延长BC 与FE 交于点G ,延长BC 交正方体棱于H ,由半正多面体对称性可知,BGE ∆为等腰直角三角形,,21)1BG GE CH x GH x x x ∴===∴=+==,1x ∴==1.18.四面体ABCD 的顶点A 、B 、C 、D 在同个球面上,AD ⊥平面ABC ,3AD =,2AB =,3AC =,60CAB ∠=,如此该四面体的外接球的外表积为___________.【答案】12π【解析】利用余弦定理计算出AB ,利用正弦定理计算出ABC 的外接圆半径r ,利用公式R =可计算出四面体ABCD 的外接球半径R ,利用球体面积可求得结果. 【详解】如如下图所示:圆柱12O O 的底面圆直径为2r ,母线长为h ,如此12O O 的中点 O 到圆柱底面圆上每点的距离都相等,如此O 为圆柱12O O 的外接球球心.可将三棱锥D ABC -放在圆柱12O O 内 ,使得圆2O 为ABC 的外接圆,点D 在圆1O 上,由余弦定理可得2222cos 7BC AB AC AB AC BAC =+-⋅∠=,如此BC =所以,ABC 的外接圆直径为2sin 3BC r BAC ==∠,r ∴=,AD ∴⊥平面ABC ,所以,四面体ABCD 的外接球半径为R ==因此,四面体ABCD 的外接球的外表积为2412R ππ=.故答案为:12π.【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以复原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径;③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,如此球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.四、解答题19.如图,四棱锥P ABCD 的底面为正方形,PD ⊥底面ABCD .设平面PAD 与平面PBC 的交线为l .〔1〕证明:l⊥平面PDC;〔2〕PD AD1,Q为l上的点,QB2PB与平面QCD所成角的正弦值.【答案】〔1〕证明见解析;〔26【解析】AD l,利用线面垂直的判定定理证得AD⊥平面PDC,〔1〕利用线面平行的判定定理以与性质定理,证得//从而得到l⊥平面PDC;Q m,之后求得平面QCD 〔2〕根据题意,建立相应的空间直角坐标系,得到相应点的坐标,设出点(,0,1)<>,即可得到直线PB与平面QCD所成角的正弦值.的法向量以与向量PB的坐标,求得cos,n PB【详解】〔1〕证明:AD BC,在正方形ABCD中,//因为AD⊄平面PBC,BC⊂平面PBC,AD平面PBC,所以//又因为AD ⊂平面PAD ,平面PAD平面PBC l =,所以//AD l , 因为在四棱锥P ABCD -中,底面ABCD 是正方形,所以,,AD DC l DC ⊥∴⊥且PD ⊥平面ABCD ,所以,,AD PD l PD ⊥∴⊥因为CD PD D =所以l ⊥平面PDC ;〔2〕如图建立空间直角坐标系D xyz -,因为1PD AD ==,如此有(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)D C A P B ,设(,0,1)Q m ,如此有(0,1,0),(,0,1),(1,1,1)DC DQ m PB ===-,因为QB 1m ==设平面QCD 的法向量为(,,)n x y z =,如此00DC n DQ n ⎧⋅=⎨⋅=⎩,即00y x z =⎧⎨+=⎩,令1x =,如此1z =-,所以平面QCD 的一个法向量为(1,0,1)n =-,如此2cos ,1n PBn PB n PB ⋅<>==== 根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,所以直线与平面所成角的正弦值等于6|cos ,|3n PB <>=所以直线PB 与平面QCD 20.如图,在四棱锥P ABCD -中,底面ABCD 为正方形.且PA ⊥平面ABCD ,M ,N 分别为,PB PD 的中点.〔1〕求证://MN 平面ABCD ;〔2〕假如2PA AB ==,求CN 与平面PBD 所成角的正弦值.【答案】〔1〕详见解析;〔2【解析】〔1〕要证明线面平行,需证明线线平行,即转化为证明//MN BD ;〔2〕首先建立空间直角坐标系,求平面PBD 的法向量,利用线面角的向量公式求解.【详解】〔1〕连结BD ,,M N 分别是,PB PD 的中点,//MN BD ∴,MN ⊄平面ABCD ,BD ⊂平面ABCD ,//MN ∴平面ABCD ;〔2〕如图,以点A 为原点,,,AB AD AP 为,,x y z 轴的正方向建立空间直角坐标系, ()002P ,,,()2,0,0B ,()0,2,0D ()2,2,0C ,()0,1,1N ,()2,0,2PB =-,()2,2,0PD =-,()2,1,1CN =--,设平面PBD 的法向量(),,n x y z =,如此00PB n PD n ⎧⋅=⎨⋅=⎩,即220220x z x y -=⎧⎨-+=⎩,令1x =,如此1,1y z ==, ∴平面PBD 的法向量()1,1,1n =,如此21sin cos ,3CN nCN n CN n θ⋅-⨯-=<>===, 所以CN 与平面PBD 21.如图,在三棱柱111ABC A B C -中,1CC ⊥平面,,2ABC AC BC AC BC ⊥==,13CC =,点,D E 分别在棱1AA 和棱1CC 上,且12,AD CE M ==为棱11AB 的中点.〔Ⅰ〕求证:11C M B D ⊥;〔Ⅱ〕求二面角1B B E D --的正弦值; 〔Ⅲ〕求直线AB 与平面1DB E 所成角的正弦值.【答案】〔Ⅰ〕证明见解析;【解析】以C 为原点,分别以1,,CA CB CC 的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系.〔Ⅰ〕计算出向量1C M 和1B D 的坐标,得出110C M B D ⋅=,即可证明出11C M B D ⊥; 〔Ⅱ〕可知平面1BB E 的一个法向量为CA ,计算出平面1B ED 的一个法向量为n ,利用空间向量法计算出二面角1B B E D --的余弦值,利用同角三角函数的根本关系可求解结果; 〔Ⅲ〕利用空间向量法可求得直线AB 与平面1DB E 所成角的正弦值.【详解】依题意,以C 为原点,分别以CA 、CB 、1CC 的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系〔如图〕,可得()0,0,0C 、()2,0,0A 、()0,2,0B 、()10,0,3C 、 ()12,0,3A 、()10,2,3B 、()2,0,1D 、()0,0,2E 、()1,1,3M . 〔Ⅰ〕依题意,()11,1,0C M =,()12,2,2B D =--, 从而112200C M B D ⋅=-+=,所以11C M B D ⊥; 〔Ⅱ〕依题意,()2,0,0CA =是平面1BB E 的一个法向量,()10,2,1EB =,()2,0,1ED =-.设(),,n x y z =为平面1DB E 的法向量,如此100n EB n ED ⎧⋅=⎪⎨⋅=⎪⎩,即2020y z x z +=⎧⎨-=⎩, 不妨设1x =,可得()1,1,2n =-.2cos ,2C CA nA C n A n ⋅<>===⋅⨯, 230sin ,1cos ,6CA n CA n ∴<>=-<>=. 所以,二面角1B B E D --的正弦值为6 〔Ⅲ〕依题意,()2,2,0AB =-. 由〔Ⅱ〕知()1,1,2n =-为平面1DB E 的一个法向量,于是cos ,322AB nAB n ABn ⋅<>===-⋅. 所以,直线AB 与平面1DB E 22.如图,在正方体1111ABCD A BC D -中,E 为1BB 的中点.〔Ⅰ〕求证:1//BC 平面1AD E ;〔Ⅱ〕求直线1AA 与平面1AD E 所成角的正弦值.【答案】〔Ⅰ〕证明见解析;〔Ⅱ〕23. 【解析】〔Ⅰ〕证明出四边形11ABC D 为平行四边形,可得出11//BC AD ,然后利用线面平行的判定定理可证得结论; 〔Ⅱ〕以点A 为坐标原点,AD 、AB 、1AA 所在直线分别为x 、y 、z 轴建立空间直角坐标系A xyz ,利用空间向量法可计算出直线1AA 与平面1AD E 所成角的正弦值.【详解】〔Ⅰ〕如如下图所示:在正方体1111ABCD A BC D -中,11//AB A B 且11AB AB =,1111//A BCD 且1111A B C D =, 11//AB C D ∴且11AB C D =,所以,四边形11ABC D 为平行四边形,如此11//BC AD ,1BC ⊄平面1AD E ,1AD ⊂平面1AD E ,1//BC ∴平面1AD E ;〔Ⅱ〕以点A 为坐标原点,AD 、AB 、1AA 所在直线分别为x 、y 、z 轴建立如如下图所示的空间直角坐标系A xyz -,设正方体1111ABCD A BC D -的棱长为2,如此()0,0,0A 、()10,0,2A 、()12,0,2D 、()0,2,1E ,()12,0,2AD =,()0,2,1AE =,设平面1AD E 的法向量为(),,n x y z =,由100n AD n AE ⎧⋅=⎨⋅=⎩,得22020x z y z +=⎧⎨+=⎩, 令2z =-,如此2x =,1y =,如此()2,1,2n =-. 11142cos ,323n AA n AA n AA ⋅<>==-=-⨯⋅. 因此,直线1AA 与平面1AD E 所成角的正弦值为23. 23.如图,三棱台ABC —DEF 中,平面ACFD ⊥平面ABC ,∠ACB =∠ACD =45°,DC =2BC .〔I 〕证明:EF ⊥DB ;〔II 〕求DF 与面DBC 所成角的正弦值.【答案】〔I 〕证明见解析;〔II 【解析】〔I 〕作DH AC ⊥交AC 于H ,连接BH ,由题意可知DH ⊥平面ABC ,即有DH BC ⊥,根据勾股定理可证得BC BH ⊥,又//EF BC ,可得DH EF ⊥,BH EF ⊥,即得EF ⊥平面BHD ,即证得EF DB ⊥;〔II 〕由//DF CH ,所以DF 与平面DBC 所成角即为CH 与平面DBC 所成角,作HG BD ⊥于G ,连接CG ,即可知HCG ∠即为所求角,再解三角形即可求出DF 与平面DBC 所成角的正弦值.【详解】〔Ⅰ〕作DH AC ⊥交AC 于H ,连接BH .∵平面ADFC ⊥平面ABC ,而平面ADFC 平面ABC AC =,DH ⊂平面ADFC ,∴DH ⊥平面ABC ,而BC ⊂平面ABC ,即有DH BC ⊥.∵45ACB ACD ∠=∠=︒, ∴2CD BC CH =⇒=.在CBH 中,22222cos45BH CH BC CH BC BC =+-⋅︒=,即有222BH BC CH +=,∴BH BC ⊥. 由棱台的定义可知,//EF BC ,所以DH EF ⊥,BH EF ⊥,而BH DH H =,∴EF ⊥平面BHD ,而BD ⊂平面BHD ,∴EF DB ⊥.〔Ⅱ〕因为//DF CH ,所以DF 与平面DBC 所成角即为与CH 平面DBC 所成角.作HG BD ⊥于G ,连接CG ,由〔1〕可知,BC ⊥平面BHD ,因为所以平面BCD ⊥平面BHD ,而平面BCD 平面BHD BD =,HG ⊂平面BHD ,∴HG ⊥平面BCD .即CH 在平面DBC 内的射影为CG ,HCG ∠即为所求角.在Rt HGC △中,设BC a =,如此CH =,BH DH HG a BD ⋅===,∴sin3HG HCG CH ∠===..故DF与平面DBC所成角的正弦值为324.如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.〔1〕证明:l⊥平面PDC;〔2〕PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.【答案】〔1〕证明见解析;〔2【解析】AD l,〔1〕利用线面垂直的判定定理证得AD⊥平面PDC,利用线面平行的判定定理以与性质定理,证得//从而得到l⊥平面PDC;Q m,之后求得平面QCD 〔2〕根据题意,建立相应的空间直角坐标系,得到相应点的坐标,设出点(,0,1)<>的最大值,即为直线PB与平面QCD所成角的正弦值的的法向量以与向量PB的坐标,求得cos,n PB最大值.【详解】〔1〕证明:在正方形ABCD 中,//AD BC ,因为AD ⊄平面PBC ,BC ⊂平面PBC ,所以//AD 平面PBC ,又因为AD ⊂平面PAD ,平面PAD平面PBC l =, 所以//AD l ,因为在四棱锥P ABCD -中,底面ABCD 是正方形,所以,,AD DC l DC ⊥∴⊥且PD ⊥平面ABCD ,所以,,AD PD l PD ⊥∴⊥因为CD PD D =所以l ⊥平面PDC ;〔2〕如图建立空间直角坐标系D xyz -,因为1PD AD ==,如此有(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)D C A P B ,设(,0,1)Q m ,如此有(0,1,0),(,0,1),(1,1,1)DC DQ m PB ===-,设平面QCD 的法向量为(,,)n x y z =,如此00DC n DQ n ⎧⋅=⎨⋅=⎩,即00y mx z =⎧⎨+=⎩, 令1x =,如此z m =-,所以平面QCD 的一个法向量为(1,0,)n m =-,如此1cos ,3n PBn PB n PB ⋅+<>==根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,所以直线与平面所成角的正弦值等于|cos ,|n PB <>===≤≤=1m =时取等号,所以直线PB 与平面QCD25.在三棱锥A —BCD 中,CB =CD BD =2,O 为BD 的中点,AO ⊥平面BCD ,AO =2,E 为AC 的中点.〔1〕求直线AB 与DE 所成角的余弦值;〔2〕假如点F 在BC 上,满足BF =14BC ,设二面角F —DE —C 的大小为θ,求sin θ的值.【答案】〔12 【解析】〔1〕建立空间直角坐标系,利用向量数量积求直线向量夹角,即得结果;〔2〕先求两个平面法向量,根据向量数量积求法向量夹角,最后根据二面角与向量夹角关系得结果.【详解】〔1〕连,CO BC CD BO OD CO BD ==∴⊥以,,OB OC OA 为,,x y z 轴建立空间直角坐标系,如此(0,0,2),(1,0,0),(0,2,0),(1,0,0)(0,1,1)A B C D E -∴(1,0,2),(1,1,1)cos ,AB DE AB DE ∴=-=∴<>==从而直线AB 与DE〔2〕设平面DEC 一个法向量为1(,,),n x y z =11200(1,2,0),00x y n DC DC x y z n DE ⎧+=⋅=⎧⎪=∴⎨⎨++=⋅=⎪⎩⎩ 令112,1(2,1,1)y x z n =∴=-=∴=- 设平面DEF 一个法向量为2111(,,),n x y z =11221117100171(,,0),4244200x y n DF DF DB BF DB BC n DE x y z ⎧⎧+=⋅=⎪⎪=+=+=∴⎨⎨⋅=⎪⎩⎪++=⎩ 令111272,5(2,7,5)yx z n =-∴==∴=- 12cos ,n n ∴<>==因此sin 13θ== 26.如图,在长方体1111ABCD A BC D -中,点,E F分别在棱11,DD BB 上,且12DE ED =,12BF FB =.〔1〕证明:点1C 在平面AEF 内; 〔2〕假如2AB =,1AD =,13AA =,求二面角1A EF A--的正弦值.【答案】〔1〕证明见解析;〔2〕7. 【解析】〔1〕连接1C E 、1C F ,证明出四边形1AEC F 为平行四边形,进而可证得点1C 在平面AEF 内; 〔2〕以点1C 为坐标原点,11C D 、11C B 、1C C 所在直线分别为x 、y 、z 轴建立空间直角坐标系1C xyz -,利用空间向量法可计算出二面角1A EF A --的余弦值,进而可求得二面角1A EF A --的正弦值.【详解】〔1〕在棱1CC 上取点G ,使得112C G CG =,连接DG 、FG 、1C E 、1C F ,在长方体1111ABCD A BC D -中,//AD BC 且AD BC =,11//BB CC 且11BB CC =,112C G CG =,12BF FB =,112233CG CC BB BF ∴===且CG BF =, 所以,四边形BCGF 为平行四边形,如此//AF DG 且AF DG =,同理可证四边形1DEC G 为平行四边形,1//C E DG ∴且1C E DG =,1//C E AF ∴且1C E AF =,如此四边形1AEC F 为平行四边形,因此,点1C 在平面AEF 内;〔2〕以点1C 为坐标原点,11C D 、11C B 、1C C 所在直线分别为x 、y 、z 轴建立如如下图所示的空间直角坐标系1C xyz -,如此()2,1,3A 、()12,1,0A 、()2,0,2E 、()0,1,1F , ()0,1,1AE =--,()2,0,2AF =--,()10,1,2A E =-,()12,0,1A F =-,设平面AEF 的法向量为()111,,m x y z =,由00m AE m AF ⎧⋅=⎪⎨⋅=⎪⎩,得11110220y z x z --=⎧⎨--=⎩取11z =-,得111x y ==,如此()1,1,1m =-, 设平面1A EF 的法向量为()222,,n x y z =,由1100n A E n A F ⎧⋅=⎪⎨⋅=⎪⎩,得22222020y z x z -+=⎧⎨-+=⎩,取22z =,得21x =,24y =,如此()1,4,2n =,3cos ,3m nm n m n ⋅<>===⨯⋅设二面角1A EF A --的平面角为θ,如此cos θ=,sin 7θ∴==.因此,二面角1A EF A --. 27.如图,在长方体1111ABCD A BC D -中,点E ,F 分别在棱1DD ,1BB 上,且12DE ED =,12BF FB =.证明:〔1〕当AB BC =时,EF AC ⊥;〔2〕点1C 在平面AEF 内.【答案】〔1〕证明见解析;〔2〕证明见解析.【解析】〔1〕根据正方形性质得AC BD ⊥,根据长方体性质得1AC BB ⊥,进而可证AC ⊥平面11BB D D ,即得结果; 〔2〕只需证明1//EC AF 即可,在1CC 上取点M 使得12CM MC =,再通过平行四边形性质进展证明即可.【详解】〔1〕因为长方体1111ABCD A BC D -,所以1BB ⊥平面ABCD ∴1AC BB ⊥,因为长方体1111,ABCD A B C D AB BC -=,所以四边形ABCD 为正方形AC BD ∴⊥因为11,BB BD B BB BD =⊂、平面11BB D D ,因此AC ⊥平面11BB D D ,因为EF ⊂平面11BB D D ,所以AC EF ⊥;〔2〕在1CC 上取点M 使得12CM MC =,连,DM MF ,因为111112,//,=D E ED DD CC DD CC =,所以11,//,ED MC ED MC =所以四边形1DMC E 为平行四边形,1//DM EC ∴因为//,=,MF DA MF DA 所以M F A D 、、、四点共面,所以四边形MFAD 为平行四边形,1//,//DM AF EC AF ∴∴,所以1E C A F 、、、四点共面,因此1C 在平面AEF 内28.如图,D 为圆锥的顶点,O 是圆锥底面的圆心,ABC 是底面的内接正三角形,P 为DO 上一点,∠APC =90°.〔1〕证明:平面PAB ⊥平面PAC ;〔2〕设DO,求三棱锥P −ABC 的体积.【答案】〔1〕证明见解析;〔2【解析】〔1〕根据可得PA PB PC ==,进而有PAC △≌PBC ,可得90APC BPC ∠=∠=,即PB PC ⊥,从而证得PC ⊥平面PAB ,即可证得结论;〔2〕将条件转化为母线l 和底面半径r 的关系,进而求出底面半径,由正弦定理,求出正三角形ABC 边长,在等腰直角三角形APC 中求出AP ,在Rt APO 中,求出PO ,即可求出结论.【详解】〔1〕连接,,OA OB OC ,D 为圆锥顶点,O 为底面圆心,OD ∴⊥平面ABC , P 在DO 上,,OA OB OC PA PB PC ==∴==, ABC 是圆内接正三角形,AC BC ∴=,PAC △≌PBC ,90APC BPC ∴∠=∠=︒,即,PB PC PA PC ⊥⊥,,PA PB P PC =∴⊥平面,PAB PC ⊂平面PAC ,∴平面PAB ⊥平面PAC ;〔2〕设圆锥的母线为l ,底面半径为r ,圆锥的侧面积为,rl rl π==2222OD l r =-=,解得1,r l ==2sin 603AC r ==在等腰直角三角形APC 中,2AP AC ==在Rt PAO 中,2PO ===,∴三棱锥P ABC -的体积为11333P ABC ABC V PO S -=⋅==△.29.如图,D 为圆锥的顶点,O 是圆锥底面的圆心,AE 为底面直径,AE AD =.ABC 是底面的内接正三角形,P 为DO 上一点,PO =.〔1〕证明:PA ⊥平面PBC ;〔2〕求二面角B PC E --的余弦值.【答案】〔1〕证明见解析;〔2. 【解析】〔1〕要证明PA ⊥平面PBC ,只需证明PA PB ⊥,PA PC ⊥即可;〔2〕以O 为坐标原点,OA 为x 轴,ON 为y 轴建立如下列图的空间直角坐标系,分别算出平面PCB 的法向量为n ,平面PCE 的法向量为m ,利用公式cos ,||||n m m n n m ⋅<>=计算即可得到答案. 【详解】〔1〕由题设,知DAE △为等边三角形,设1AE =,如此2DO =,1122CO BO AE ===,所以64PO DO ==,PC PB ====又ABC 为等边三角形,如此2sin 60BA OA =,所以2BA =, 22234PA PB AB +==,如此90APB ∠=,所以PA PB ⊥, 同理PA PC ⊥,又PC PB P =,所以PA ⊥平面PBC ;〔2〕过O 作ON ∥BC 交AB 于点N ,因为PO ⊥平面ABC ,以O 为坐标原点,OA 为x 轴,ON 为y 轴建立如下列图的空间直角坐标系,如此111(,0,0),(,(,244444E P B C ----,1(,4PC =-,1(4PB =-,1(,0,2PE =-, 设平面PCB 的一个法向量为111(,,)n x y z =,由00n PC n PB ⎧⋅=⎨⋅=⎩,得11111100x x ⎧-=⎪⎨-+=⎪⎩,令1x =111,0z y =-=, 所以(2,0,1)n =-,设平面PCE 的一个法向量为222(,,)m x y z =由00m PC m PE ⎧⋅=⎨⋅=⎩,得22222020x x ⎧--=⎪⎨-=⎪⎩,令21x =,得223z y ==,所以3(1,3m =故2cos ,||||3n m mn n m ⋅<>===⋅⨯ 设二面角B PC E --的大小为θ,如此cos θ=30.四棱锥P ABCD -中,//AB CD ,90PDA BAD ∠=∠=︒,12PD DA AB CD ===,S 为PC 中点,BS CD ⊥.〔1〕证明:PD ⊥平面ABCD ;〔2〕平面SAD 交PB 于Q ,求CQ 与平面PCD 所成角的正弦值.【答案】〔1〕证明见解析;〔2. 【解析】〔1〕取CD 中点为M ,得到BM CD ⊥,由BS CD ⊥,证得CD ⊥平面BSM ,得到CD SM ⊥,再根据CD PD ⊥,结合线面垂直的判定定理,证得PD ⊥平面ABCD ;〔2〕以,,DA DC DP 方向为,,x y z 轴的正方向,建立空间直角坐标系O xyz -,设1AB =,根据2PQ QB =,求得CQ 坐标,再求得平面PCD 的法向量,结合向量的夹角公式,即可求解.【详解】〔1〕取CD 中点为M ,如此DM AB =且//DM AB ,所以四边形ABMD 为平行四边形,可得//BM AD ,所以BM CD ⊥,又由BS CD ⊥,BM BS B ⋂=,所以CD ⊥平面BSM ,又因为SM ⊂平面BSM ,所以CD SM ⊥,又由//SM PD ,所以CD PD ⊥,AD PD ⊥,CD AD D =,所以PD ⊥平面ABCD .〔2〕延长CB ,DA 交于N ,连SN 与PB 交点即为Q ,因为B 为CN 中点,S 为PC 中点,故Q 为PNC △的重心,故2PQ QB =,以D 为原点,,,DA DC DP 方向为,,x y z 轴的正方向,建立空间直角坐标系O xyz -,不妨设1AB =,如此()1,1,0B ,()0,0.1P ,。
高考数学的立体几何多选题及答案
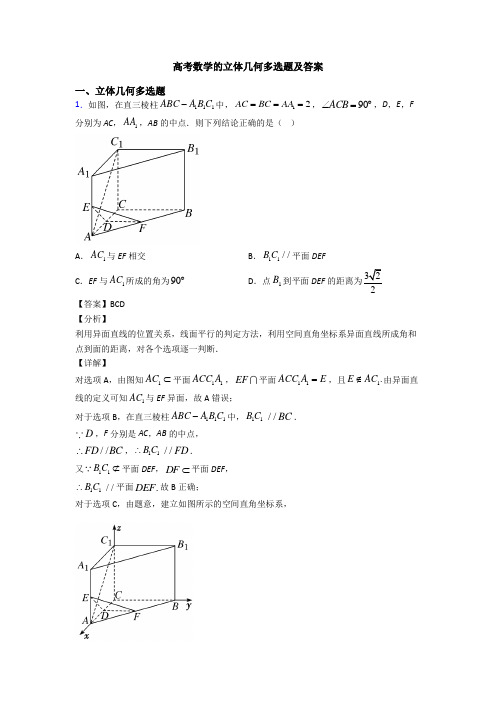
高考数学的立体几何多选题及答案一、立体几何多选题1.如图,在直三棱柱111ABC A B C -中,12AC BC AA ===,90ACB ∠=︒,D ,E ,F分别为AC ,1AA ,AB 的中点.则下列结论正确的是( )A .1AC 与EF 相交B .11//BC 平面DEF C .EF 与1AC 所成的角为90︒D .点1B 到平面DEF 的距离为322【答案】BCD 【分析】利用异面直线的位置关系,线面平行的判定方法,利用空间直角坐标系异面直线所成角和点到面的距离,对各个选项逐一判断. 【详解】对选项A ,由图知1AC ⊂平面11ACC A ,EF 平面11ACC A E =,且1.E AC ∉由异面直线的定义可知1AC 与EF 异面,故A 错误;对于选项B ,在直三棱柱111ABC A B C -中,11B C //BC .D ,F 分别是AC ,AB 的中点, //∴FD BC ,11B C ∴ //FD .又11B C ⊄平面DEF ,DF ⊂平面DEF ,11B C ∴ //平面.DEF 故B 正确;对于选项C ,由题意,建立如图所示的空间直角坐标系,则(0C ,0,0),(2A ,0,0),(0B ,2,0),1(2A ,0,2),1(0B ,2,2),1(0C ,0,2),(1D ,0,0),(2E ,0,1),(1F ,1,0).(1EF ∴=-,1,1)-,1(2AC =-,0,2). 1·2020EF AC =+-=,1EF AC ∴⊥,1EF AC ∴⊥. EF 与1AC 所成的角为90︒,故C 正确;对于选项D ,设向量(n x =,y ,)z 是平面DEF 的一个法向量. (1DE =,0,1),(0DF =,1,0), ∴由n DE n DF ⎧⊥⎨⊥⎩,,,即·0·0n DE n DF ⎧=⎨=⎩,,,得00.x z y +=⎧⎨=⎩,取1x =,则1z =-,(1n ∴=,0,1)-, 设点1B 到平面DEF 的距离为d . 又1(1DB =-,2,2),1·102DB n d n-+∴===, ∴点1B 到平面DEF 的距离为2,故D 正确.故选:BCD 【点睛】本题主要考查异面直线的位置关系,线面平行的判定,异面直线所成角以及点到面的距离,还考查思维能力及综合分析能力,属难题.2.如图,正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2,则下列说法正确的是( )A .异面直线1AB 与1AD 所成的角是3πB .1BD ⊥平面11AC DC .平面1ACB 截正四面体11A BDC -所得截面面积为3D .正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ,利用正方体的结构特征找到异面直线所成的角;选项B ,根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证;选项C ,由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一;选项D ,分别求出正方体的体对角线长和正四面体11A BDC -的高,然后判断数量关系即可得解. 【详解】A :正方体1111ABCD ABCD -中,易知11//AD BC ,异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角,即11A BC ∠,11A BC 为等边三角形,113A BC π∠=,正确;B :连接11B D ,1B B ⊥平面1111DC B A ,11A C ⊂平面1111D C B A ,即111AC B B ⊥,又1111AC B D ⊥,1111B B B D B ⋂=,有11A C ⊥平面11BDD B ,1BD ⊂平面11BDD B ,所以111BD AC ⊥,同理可证:11BD A D ⊥,1111AC A D A ⋂=,所以1BD ⊥平面11AC D ,正确;C :易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=,错误;D :易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -22222262213⎛⎫--⨯ ⎪⎝⎭,故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23,正确. 故选:ABD. 【点睛】关键点点睛:利用正方体的性质,找异面直线所成角的平面角求其大小,根据线面垂直的判定证明1BD ⊥平面11AC D ,由正四面体的性质,结合几何图形确定截面的面积,并求高,即可判断C 、D 的正误.3.已知正方体1111ABCD A B C D -的棱长为2,点E ,F 在平面1111D C B A 内,若||5AE =,AC DF ⊥,则( )A .点E 的轨迹是一个圆B .点F 的轨迹是一个圆C .EF 21-D .AE 与平面1A BD 21530+【答案】ACD 【分析】对于A 、B 、C 、D 四个选项,需要对各个选项一一验证. 选项A :由2211||5AE AA A E =+=1||1A E =,分析得E 的轨迹为圆;选项B :由AC DBF ⊥,而点F 在11B D 上,即F 的轨迹为线段11B D ,; 选项C :由E 的轨迹为圆,F 的轨迹为线段11B D ,可分析得min ||EF d r =-; 选项D :建立空间直角坐标系,用向量法求最值. 【详解】 对于A:2211||5AE AA A E =+=221|25A E +=1||1A E =,即点E 为在面1111D C B A 内,以1A 为圆心、半径为1 的圆上;故A 正确;对于B: 正方体1111ABCD A B C D -中,AC ⊥BD ,又AC DF ⊥,且BD ∩DF=D ,所以AC DBF ⊥,所以点F 在11B D 上,即F 的轨迹为线段11B D ,故B 错误;对于C:在平面1111D C B A 内,1A 到直线11B D 的距离为2,d =当点E ,F 落在11A C 上时,min ||21EF =-;故C 正确; 对于D:建立如图示的坐标系,则()()()()10,0,0,2,0,0,0,0,2,0,2,0A B A D因为点E 为在面1111D C B A 内,以1A 为圆心、半径为1 的圆上,可设()cos ,sin ,2E θθ 所以()()()1cos ,sin ,2,2,0,2,2,2,0,AE A B BD θθ==-=-设平面1A BD 的法向量(),,n x y z =,则有1·220·220n BD x y n A B x z ⎧=-+=⎪⎨=-=⎪⎩不妨令x =1,则()1,1,1n =, 设AE 与平面1A BD 所成角为α,则:22|||sin |cos ,|||||5315n AE n AE n AE πθα⎛⎫++ ⎪⎝⎭====⨯⨯当且仅当4πθ=时,sin α有最大值222153015++=, 故D 正确 故选:CD 【点睛】多项选择题是2020年高考新题型,需要要对选项一一验证.4.在棱长为1的正方体1111ABCD A B C D -中,P 为底面ABCD 内(含边界)一点.( ) A .若13A P =,则满足条件的P 点有且只有一个 B .若12A P =,则点P 的轨迹是一段圆弧 C .若1//A P 平面11B D C ,则1A P 长的最小值为2D .若12A P =且1//A P 平面11B DC ,则平面11A PC 截正方体外接球所得截面的面积为23π【答案】ABD 【分析】选项A ,B 可利用球的截面小圆的半径来判断;由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD 上,1A P 长的最大值为2;结合以上条件点P 与B 或D 重合,利用12sin 60A P r =︒,求出63r =,进而求出面积. 【详解】对A 选项,如下图:由13A P =,知点P 在以1A 为球心,半径为3的球上,又因为P 在底面ABCD 内(含边界),底面截球可得一个小圆,由1A A ⊥底面ABCD ,知点P 的轨迹是在底面上以A 为圆心的小圆圆弧,半径为22112r A P A A =-=,则只有唯一一点C满足,故A 正确;对B 选项,同理可得点P 在以A 为圆心,半径为22111r A P A A =-=的小圆圆弧上,在底面ABCD 内(含边界)中,可得点P 轨迹为四分之一圆弧BD .故B 正确;对C 选项,移动点P 可得两相交的动直线与平面11B D C 平行,则点P 必在过1A 且与平面11B D C 平行的平面内,由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD上,则1A P 长的最大值为12A B =,则C 不正确; 对选项D ,由以上推理可知,点P 既在以A 为圆心,半径为1的小圆圆弧上,又在线段BD 上,即与B 或D 重合,不妨取点B ,则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆,利用2126622,,sin 60333A B r r S r ππ==∴=∴==︒.故D 正确.故选:ABD 【点睛】(1)平面截球所得截面为圆面,且满足222=R r d +(其中R 为球半径,r 为小圆半径,d 为球心到小圆距离);(2)过定点A 的动直线平行一平面α,则这些动直线都在过A 且与α平行的平面内.5.在三棱锥M ABC -中,下列命题正确的是( ) A .若1233AD AB AC =+,则3BC BD = B .若G 为ABC 的重心,则111333MG MA MB MC =++ C .若0MA BC ⋅=,0MC AB ⋅=,则0MB AC ⋅=D .若三棱锥M ABC -的棱长都为2,P ,Q 分别为MA ,BC 中点,则2PQ = 【答案】BC 【分析】作出三棱锥M ABC -直观图,在每个三角形中利用向量的线性运算可得.【详解】对于A ,由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-,即2CD DB =,则32BD BD DC BC =+=,故A 错误; 对于B ,由G 为ABC 的重心,得0GA GB GC ++=,又MG MA AG =+,MG MB BG =+,MG MC CG =+,3MA MB MC MG ∴++=,即111333MG MA MB MC =++,故B 正确;对于C ,若0MA BC ⋅=,0MC AB ⋅=,则0MC MA BC AB ⋅+⋅=,即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅,即0MB AC ⋅=,故C 正确;对于D ,111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-,又()2222222MB MC MA MB MC MA MB MC MB MA MC MA+-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=,1822PQ ∴==,故D 错误. 故选:BC 【点睛】关键点睛:本题考查向量的运算,用已知向量表示某一向量的三个关键点: (1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量. (3)在立体几何中三角形法则、平行四边形法则仍然成立.6.在长方体1111ABCD A B C D -中,AB =12AD AA ==,P 、Q 、R 分别是AB 、1BB 、1A C 上的动点,下列结论正确的是( )A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥C .当1AR A C ⊥时,1ARD R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABCD 【分析】本题先建立空间直角坐标系,再运用空间向量在立体几何中的应用逐一判断即可. 【详解】如图所示,建立空间直角坐标系,设(2,,0)P a,0a ⎡∈⎣,(2,)Q b ,[]0,2b ∈,设11A R AC λ=,得到(22,,22)R λλ--,[]0,1λ∈. 1(2,,2)D P a =-,(2,0,)CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;1(22,2)D R λλ=--,12(22)2D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确;1AR A C ⊥,则1(2,22)(2)412440AR AC λλλλλ⋅=--⋅--=+-+=,解得:15λ=,此时12282()()05555AR D R ---⋅=⋅=,1AR D R ⊥,C 正确;113AC A R =,则44()33R,142()33D R =-,设平面1BDC 的法向量为(,,)n x y z =,则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得(3,n =-,故10n D R ⋅=,故1//D R 平面1BDC ,D 正确.故选:ABCD.【点睛】本题考查了空间向量在立体几何中的应用,是偏难题.7.已知直三棱柱111ABC A B C -中,AB BC ⊥,1AB BC BB ==,D 是AC 的中点,O 为1A C 的中点.点P 是1BC 上的动点,则下列说法正确的是( )A .当点P 运动到1BC 中点时,直线1A P 与平面111ABC 5 B .无论点P 在1BC 上怎么运动,都有11A P OB ⊥C .当点P 运动到1BC 中点时,才有1A P 与1OB 相交于一点,记为Q ,且113PQ QA = D .无论点P 在1BC 上怎么运动,直线1A P 与AB 所成角都不可能是30° 【答案】ABD 【分析】构造线面角1PA E ∠,由已知线段的等量关系求1tan EPPA E AE∠=的值即可判断A 的正误;利用线面垂直的性质,可证明11A P OB ⊥即可知B 的正误;由中位线的性质有112PQ QA =可知C 的正误;由直线的平行关系构造线线角为11B A P ∠,结合动点P 分析角度范围即可知D 的正误 【详解】直三棱柱111ABC A B C -中,AB BC ⊥,1AB BC BB ==选项A 中,当点P 运动到1BC 中点时,有E 为11B C 的中点,连接1A E 、EP ,如下图示即有EP ⊥面111A B C∴直线1A P 与平面111A B C 所成的角的正切值:1tan EPPA E AE∠= ∵112EP BB =,22111152AE A B B E BB =+= ∴15tan PA E ∠=,故A 正确选项B 中,连接1B C ,与1BC 交于E ,并连接1A B ,如下图示由题意知,11B BCC 为正方形,即有11B C BC ⊥而AB BC ⊥且111ABC A B C -为直三棱柱,有11A B ⊥面11B BCC ,1BC ⊂面11B BCC ∴111A B BC ⊥,又1111A B B C B =∴1BC ⊥面11A B C ,1OB ⊂面11A B C ,故11BC OB ⊥ 同理可证:11A B OB ⊥,又11A B BC B ⋂=∴1OB ⊥面11A BC ,又1A P ⊂面11A BC ,即有11A P OB ⊥,故B 正确选项C 中,点P 运动到1BC 中点时,即在△11A B C 中1A P 、1OB 均为中位线∴Q为中位线的交点∴根据中位线的性质有:112PQQA=,故C错误选项D中,由于11//A B AB,直线1A P与AB所成角即为11A B与1A P所成角:11B A P∠结合下图分析知:点P在1BC上运动时当P在B或1C上时,11B A P∠最大为45°当P在1BC中点上时,11B A P∠最小为23arctan30>=︒∴11B A P∠不可能是30°,故D正确故选:ABD【点睛】本题考查了利用射影定理构造线面角,并计算其正弦值;利用线面垂直证明线线垂直;中位线的性质:中位线交点分中位线为1:2的数量关系;由动点分析线线角的大小8.如图,正方体1111ABCD A B C D-的棱长为1,线段11B D上有两个动点E,F,且2EF=则下列结论正确的是()A .三棱锥A BEF -的体积为定值B .当E 向1D 运动时,二面角A EF B --逐渐变小C .EF 在平面11ABB A 内的射影长为12D .当E 与1D 重合时,异面直线AE 与BF 所成的角为π4【答案】AC 【分析】对选项分别作图,研究计算可得. 【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形,1112212224BEF S EF BB ∆∴=⋅=⨯=连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以,AO 是点A 到平面11BDD B 的距离,即22AO =112213312A BEF BEF V S AO -∆∴=⨯==A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ,连接11,AD AB , 由正方体性质知11AD AB =,M 是11B D 中点,AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角,在直角三角形1AA M 中,12tan 2MAA ∠=为定值. 选项C:如图,作1111,,,FH A B EG A B ET EG ⊥⊥⊥ 在直角三角形EFT 中,221cos 452FT EF =⨯=⨯=12HG FT ∴== 选项D:当E 与1D 重合时,F 与M 重合,连接AC 与BD 交于点R ,连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角, 在三角形1AD R 中,22111132,2AD D R MB BB M B ===+=2AR =由余弦定理得13cos AD R ∠= 故选:AC 【点睛】本题考查空间几何体性质问题.求解思路:关键是弄清(1)点的变化,点与点的重合及点的位置变化;(2)线的变化,应注意其位置关系的变化;(3)长度、角度等几何度量的变化.求空间几何体体积的思路:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法;若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.9.如图所示,在长方体1111ABCD A B C D -中,11,2,AB BC AA P ===是1A B 上的一动点,则下列选项正确的是( )A .DP 35B .DP 5C .1AP PC +6D .1AP PC +170【答案】AD 【分析】DP 的最小值,即求1DA B △底边1A B 上的高即可;旋转11A BC 所在平面到平面11ABB A ,1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值,即求1DA B △底边1A B 上的高,易知115,2A B A D BD ===,所以1A B 边上的高为355h =111,AC BC ,得11A BC ,以1A B 所在直线为轴,将11A BC 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',则AC '即为所求的最小值,易知11122,2,cos AA AC AAC ''==∠=, 所以217042222()105AC '=+-⨯⨯⨯-=.故选:AD. 【点睛】本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否, (1)点的变化,点与点的重合及点的位置变化;(2)线的变化,翻折、旋转前后应注意其位置关系的变化;(3)长度、角度等几何度量的变化.10.半正多面体(semiregularsolid)亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形构成(如图所示),若它的所有棱长都为2,则()A.BF⊥平面EABB.该二十四等边体的体积为20 3C.该二十四等边体外接球的表面积为8πD.PN与平面EBFN所成角的正弦值为2 2【答案】BCD【分析】A用反证法判断;B先补齐八个角成正方体,再计算体积判断;C先找到球心与半径,再计算表面积判断;D先找到直线与平面所成角,再求正弦值判断.【详解】解:对于A,假设A对,即BF⊥平面EAB,于是BF AB⊥,90ABF∠=︒,但六边形ABFPQH为正六边形,120ABF∠=︒,矛盾,所以A错;对于B,补齐八个角构成棱长为2的正方体,则该二十四等边体的体积为3112028111323-⋅⋅⋅⋅⋅=,所以B对;对于C,取正方形ACPM对角线交点O,即为该二十四等边体外接球的球心, 其半径为2R =,其表面积为248R ππ=,所以C 对;对于D ,因为PN 在平面EBFN 内射影为NS , 所以PN 与平面EBFN 所成角即为PNS ∠, 其正弦值为22PS PN ==,所以D 对. 故选:BCD .【点睛】本题考查了正方体的性质,考查了直线与平面所成角问题,考查了球的体积与表面积计算问题.。
高三数学平面法向量的求法试题

高三数学平面法向量的求法试题1.已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.(1)证明:⊥平面(2)求平面与平面所成角的余弦值;【答案】(1)通过建系证明,.得到,.故⊥平面.(2)二面角C-NB1-C1的余弦值为.【解析】(1)证明:∵该几何体的正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形,∴两两垂直.以分别为轴建立空间直角坐标系如图.则.∴,.∴,.又与相交于,∴⊥平面. ………6分(2)∵⊥平面,∴是平面的一个法向量,设为平面的一个法向量,则,所以可取.则.∴所求二面角C-NB1-C1的余弦值为. 12分【考点】本题主要考查立体几何中的垂直关系,角的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离的计算。
证明过程中,往往需要将立体几何问题转化成平面几何问题加以解答。
本题解答,通过建立适当的空间直角坐标系,利用向量的坐标运算,简化了繁琐的证明过程,实现了“以算代证”,对计算能力要求较高。
2.如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC BD,垂足为H,PH是四棱锥的高,E为AD中点;(Ⅰ)证明:PE BC;(Ⅱ)若APB=ADB=60°,求直线PA与平面PEH所成角的正弦值。
【答案】(1)略(2)【解析】求解和证明立体几何问题一方面可以直接利用几何方法,通过证明或找到线面之间的关系,依据判定定理或性质进行证明求解.以为原点,分别为轴,线段的长为单位长,建立空间直角坐标系如图,则(Ⅰ)设则可得因为所以……………………5分(Ⅱ)由已知条件可得设为平面的法向量则即因此可以取,由,可得所以直线与平面所成角的正弦值为…………………12分3.如图,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB上一点(I) 当点E为AB的中点时,求证;BD1//平面A1DE(II)求点A1到平面BDD1的距离;(III) 当时,求二面角D1-EC-D的大小.【答案】(1)略(2)A1到面BDD1的距离为(3)D1-EC-D的大小为【解析】(I) 要证BD1//平面A1DE,只要证明BD1平行该面内的一条直线,取中点,由中位线可证得;(II)等积法求高;(III)可以用传统法找出平面角也可以向量法求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【关键字】高考用平面的法向量解高考立体几何试题张靖松平面的法向量在课本上有定义,考试大纲中有“理解”要求,但在课本和多数的教辅材料中都没有提及它的应用,其实平面的法向量是中学数学中的一颗明珠,是解立体几何题的锐利武器,开发平面法向量的解题功能,可以解决不少立体几何中有关角和距离的难题,也能顺利解决2005年全国高考试卷中的立体几何试题。
一、平面法向量的概念和求法向量与平面垂直如果表示向量a的有向线段所在的直线垂直于平面,则称这个向量垂直于平面,记作a。
平面的法向量如果a,那么向量a叫做平面的法向量。
一般根据平面法向量的定义推导出平面的法向量,进而就可以利用平面的法向量解决相关立体几何问题。
推导平面法向量的方法如下:在给定的空间直角坐标系中,设平面的法向量[或,或],在平面内任找两个不共线的向量。
由,得且,由此得到关于的方程组,解此方程组即可得到。
有时为了需要,也求法向量上的单位法向量,则。
例1 在棱长为1的正方体中,求平面的法向量和单位法向量。
解:建立空间直角坐标系,如图1,则,。
设平面的法向量。
得,。
又面,得,。
有,得。
,。
二、平面法向量的三个引理为了能方便地运用平面法向量解题,特介绍平面法向量的三个引理,以此为工具,可以顺利地解决立体几何问题。
引理1 设向量是平面的单位法向量,点B是平面外一定点,点A是内任意一点,则点B 到平面的距离。
证明:如图2,过B作BO垂直平面于O,在平面上任取一点A,则为与的夹角,设为。
在中,,得。
例2 在例1中,求点到平面的距离。
解析:由例1的解答知,平面的单位法向量,又,设点到平面的距离为,则。
所以,点到平面的距离为。
说明:利用引理1求点到平面的距离比用保守的几何方法求距离简单得多,它省去了作图、证明等推理论证,直接通过向量运算得到正确的结果。
引理2 设AB是平面的斜线,BO是平面的垂线,AB与平面所成的角,向量与的夹角(见图2),则。
(证略)例3 在例1中,求直线与平面所成的角。
解析:由例1知,,, ,即。
引理3 如图3,设向量与分别是二面角 中的两个半平面,的法向量, 则向量与的夹角的大小就是 所求二面角或其补角的大小。
(证略) 例4 在例1中,求二面角的大小。
解:由例1知,平面的法向量是,平面的法向量是, 设二面角的大小为,则 ,得。
说明:由于法向量的多样性,二面角的两个半平面的法向量与的夹角可能等于所求二面角的平面角,如本例;也可能等于二面角的平面角的补角,如若, 则, 于是。
如何来确定两法向量的夹角是二面角的平面角还是其补角呢?一靠经验:通过题目估计它是钝角还是锐角,同类相等,异类互补;二用半平面旋转法:把二面角的一个半平面绕棱 按照同一个方向旋转到与另一个半平面重合时,若两个半平面的法向量的方向相同,则相等, 若方向相反,则互补。
三、利用法向量解2005年高考立体几何试题 例5 (05江西 理)如图4,在长方体ABCD -1111A B C D 中,AD=1AA =1,AB=2,点E 在棱AB上移动。
(Ⅰ)证明:11D E A D ⊥;(Ⅱ)当E 为AB 的中点时,求点E 到面1ACD 的距离;(Ⅲ)AE 等于何值时,二面角1D EC D --的大小为4π。
分析 本题是立体几何试题的常见题型,考查的是传统内容。
证线线垂直,求点到平面的距离,求二面角的大小,可用传统的几何方法求解,也可利用向量法求解。
下面给出向量法求解。
解:建立如图所示的空间直角坐标系,设AE a =,则1(1,0,1)A ,1(0,0,1)D ,(1,,0)E a ,(1,0,0)A ,(0,2,0)C 。
(Ⅰ)证明:由1(1,0,1)DA =,1(1,1,1)D E a =--, 11(1,0,1)(1,1,1)110DA D E a ⋅=⋅--=-=,有11DA D E ⊥,于是11D E A D ⊥。
(Ⅱ)E 是AB 的中点,得(1,1,0)E 。
∴1(1,1,1)D E=-,(1,2,0)AC=-,1(1,0,1)AD=-。
设平面1ACD的法向量为(,,1)n x y=,单位法向量为n,由1n ACn AD⎧⋅=⎪⎨⋅=⎪⎩⇒(,,1)(1,2,0)0(,,1)(1,0,1)0x yx y⋅-=⎧⎨⋅-=⎩⇒2010x yx-+=⎧⎨-+=⎩,解得112xy=⎧⎪⎨=⎪⎩。
于是1(1,,1)2n=,有1(1,,1)212(,,)333n==。
设点E到平面1ACD的距离为d,则102121(1,1,1)(,,)3333d D E n=⋅=-⋅=。
所以点E到平面1ACD的距离为13。
(Ⅲ)平面DEC的法向量1(0,0,1)n=,设平面1D EC的法向量2(,,1)n x y=。
又(1,2,0)EC a=--,1(0,2,1)DC=-。
由221n ECn D C⎧⋅=⎪⎨⋅=⎪⎩,得(,,1)(1,2,0)0(,,1)(0,2,1)0x y ax y⋅--=⎧⎨⋅-=⎩(2)0210x y ay-+-=⎧⇒⎨-=⎩,解得1212axy⎧=-⎪⎪⎨⎪=⎪⎩,于是21(1,,1)22an=-。
设所求的二面角为θ,则4πθ=。
有121(0,0,1)(1,,1)cos cos,aDD nθ⋅-=<>==,得21(1)1224a-++=。
解得2a=-所以,当AE=2时,二面角1D EC D--例6(05全国卷Ⅱ)如图5,四棱锥P ABCD-中,底面ABCD 为矩形,PD ⊥底面ABCD ,AD=PD , E ,F 分别CD 、PB 的中点。
(Ⅰ)求证:EF ⊥平面PAB ;(Ⅱ)设,求AC 与平面AEF 所成角的大小。
分析:本题考查的是立体几何的重点内容:直线与平面 垂直和直线与平面所成的角,考查空间想像能力和推理 论证能力,本题也是一题两法。
(Ⅰ)证明:建立空间直角坐标系(如图5),设AD=PD=1,AB=2a (0a >),则E(a,0,0),C(2a,0,0),A(0,1,0),B(2a,1,0),P(0,0,1), 11(,,)22F a .得11(0,,)22EF =,(2,1,1)PB a =-,(2,0,0)AB a =。
由11(0,,)(2,0,0)022EF AB a ⋅=⋅=,得EF AB ⊥,即EF AB ⊥,同理EF PB ⊥,又AB PB B =, 所以,EF⊥平面PAB 。
(Ⅱ)解:由AB =,得2a =2a=。
得E ,11,)22F ,C 。
有(2,1,0)AC =-,2(,1,0)2AE =-,11(0,,)22EF =。
设平面AEF 的法向量为(,,1)n x y =,由00n EF n AE ⎧⋅=⎪⎨⋅=⎪⎩11(,,1)(0,,)022(,,1)(1,0)02x y x y ⎧⋅=⎪⎪⇒⎨⎪⋅-=⎪⎩1102202y x y ⎧+=⎪⎪⇒-=⎪⎩,解得1y x =-⎧⎪⎨=⎪⎩。
于是(1,1)n =-。
设AC 与面AEF 所成的角为θ,AC 与n 的夹角为,AC n <>。
则sin cos ,211AC n AC n AC nθ⋅=<>===++⋅。
得arcsinθ=。
ABCD MP图 6 所以,AC 与平面AEF所成角的大小为arcsin6。
说明:用传统的几何方法,在限定的时间内,很难找到AC 与平面AEF 所成的角。
而利用平面的法向量解题,可顺利地避开这一切麻烦,只要找到平面的法向量n ,利用向量间的代数运算,可方便简捷地解决此题。
利用法向量也可顺利求解2005全国卷Ⅰ第18题: 如图6 已知四棱锥P ABCD -的底面为直角梯 形,AB//DC ,090DAB ∠=,PA ⊥底面ABCD ,且PA=AD=DC=112AB =,M 是PB 的中点。
(Ⅰ)证明:面PAD ⊥面PCD ;(Ⅱ)求AC 与PB 所成的角;(Ⅲ)求面AMC 与面BMC 所成二面角的大小。
解:(略)说明:本题求二面角的大小,由于不易找到二面角的平面角,无论是用传统的几何方法还用一般的向量方法,都很不易解决,这也是造成立体几何解答题得分不高的原因之一,如果 采用平面的法向量解题,情况就大不相同了,请大家仔细体会。
以上介绍了平面的法向量及其几个引理,以此为工具,解决了立体几何中的部分难题。
利用平面法向量解题,方法简便,易于操作,可以避开传统几何中的作图、证明的麻烦,又可 弥补空间想像能力的不足,发挥代数运算的长处。
深入开发它的解题功能,平面法向题将在数学解题中起到越来越大的作用。
(摘自《试题与研究》2005/26 高考数学)此文档是由网络收集并进行重新排版整理.word 可编辑版本!。
