电子相关效应
有机化学中的电子效应
硝酰基-I效应 活性中间体不稳定 反应活化能高 反应速率小。
③.取代基的电子效应对化合物酸性大小的影响：
例：比较对硝基 苯酚、苯酚、对 甲基苯酚的酸性 大小？
（看质子离去后负离子的稳定性）
拉电子基使酸性增强
推电子基使酸性减弱
•对羧酸酸性的影响
羧酸的酸性主要取决于O-H键离解的倾向以及共轭碱 的稳定性，而诱导效应对两者均有影响。 凡是烃基上带吸电基时将增加羧酸的酸性，带供电基 时减小其酸性。
O H C C H C O C O H O
H H
O C C C C O O H O-
pKa1 1.92
-I, 场效应有利于 第一质子的离去
H
pKa2 6.59
+I, 场效应不有利于 第二质子的离去
⑷诱导效应对物质性质及反应的影响 ①对反应活性中间体稳定性的影响 •碳正离子稳定性：叔C+>仲C+>伯C+> +CH3
•烷基苯、烯烃α-氢卤代反应：
p-π 共轭的中间体比单独的离子或自由基稳定，反应更容易。 • p-π共轭体系使乙烯型卤代烃不易反应
双键碳、碳正离子、碳自由基中的碳都是sp2杂化。
• P-π共轭体系使醚键断裂有选择
•（醛）的加成反应
δ+ δ CH O +
δ+ δCH2 CH
R3C
I=0 标准
H
R3C
Z
(-I) Z:吸电基
R3C Y (+I)
Y:供电基
通常以H的电负性作为0。凡是比H电负性大的原 子或基团叫吸电子基，其诱导效应叫吸电子诱导效应 （-I），反之叫供电子基和供电子诱导效应（+I）。 基团的吸电子诱导效应（-I）的顺序为：
推电子效应和吸电子效应
推电子效应和吸电子效应电子效应是物理学中的一个重要概念，物质和能量之间的相互转换过程中发挥着重要作用。
电子效应可以分为推电子效应和吸电子效应这两大类。
推电子效应的特征是，在电场中，电子受到电场的作用而受力，产生偏转，或称电场作用力，使电子对电场有所反应。
当电场强度变化时，电子受到该变化影响而变化，会形成粒子推进力，产生前进力，使物质向前运动，从而将能量转换成动能。
吸电子效应是另一种电子效应，它的特征是，在物体表面形成的电荷可以吸引周围的电子，从而形成电荷层。
在电荷层中，空间电场对电子的作用是使其排列成等间距的结构，这也是吸电子效应的基本特征。
吸电子效应也可以将物质能量转换成动能，同时，它也有助于把存储在电荷层中的能量释放出来，实现能量的转换。
推电子效应和吸电子效应是电子效应的两大类，它们在物质和能量之间的相互转换中发挥着重要作用。
它们都是由电荷的存在而引起的，在实际的应用中，它们的作用也有着重要的实际意义。
推电子效应可以用于动力发动机的设计与应用，使船只和飞机能够进行长距离的航行，同时也可以被用于研究宇宙的运动规律。
在电子器件中，推电子效应也是一种重要的电子作用机制，它可以使电子在电子器件中更容易地流动，从而起到调节电子流动的作用。
吸电子效应主要被用于电子学中，它可以使电子在电路中更容易流动，也可以在无线电技术中被用于信号增强，而在生物学中，吸电子效应也可以非常有效地改变蛋白质的构象，从而实现分子调控。
由于推电子效应和吸电子效应的重要作用，它们在现代科学技术中的广泛应用，在航空航天技术、电子技术和生物技术等领域都发挥着重要的作用。
两种电子效应的研究和发展也使人们对能源转换有更深入的认识，促进了能源转换科学技术的发展。
因此可见，推电子效应和吸电子效应是至关重要的物理过程，在物质和能量转换中起着至关重要的作用，它们的研究和发展有及其重要的意义，将为现代科学技术的发展提供极大的帮助。
《电子相关效应》课件
电子相关效应在新能源、信息等领域的应用前景
新能源领域
电子相关效应在新能源领域中具有广泛 的应用前景，如太阳能电池中的光电转 换效应、燃料电池中的电化学反应等， 这些应用将有助于推动新能源技术的发 展和应用。
VS信息领域ຫໍສະໝຸດ 电子相关效应在信息领域中也有广泛的应 用前景，如电子存储器中的磁电阻效应、 集成电路中的热电效应等，这些应用将有 助于推动信息技术的发展和创新。
02
它通过将分子中的电子云分布和能量状态与分子轨道的波函数
和能量联系起来，能够描述分子的电子结构和性质。
分子轨道理论在化学反应机理、分子光谱学和材料科学等领域
03
有广泛应用。
哈特里-福克方程
01
哈特里-福克方程是一种求解多 电子系统薛定谔方程的数值方 法。
02
它通过将多电子波函数表示为 单电子波函数的线性组合，能 够更精确地描述多电子系统的 电子结构和性质。
紧束缚近似
用于描述固体中电子行为的物理模型 ，将电子看作被原子核强烈束缚的波 函数，适用于金属和半导体等材料。
03
电子相关效应的实验研究
实验方法与技术
实验原理
介绍实验的基本原理和理论基 础，说明实验的目的和意义。
实验设备
详细描述实验所需的设备和工 具，包括电子显微镜、光谱仪 、电导率测量仪等。
实验步骤
THANKS。
03
哈特里-福克方程在量子化学计 算、材料科学和物理等领域有 广泛应用。
理论计算的应用与展望
理论计算在材料科学、化学、物理和生物学等 领域有广泛应用，能够提供对实验现象的深入 理解和预测。
随着计算机技术和算法的发展，理论计算在精 度和规模上不断取得突破，为解决复杂系统问 题提供了有力工具。
电子效应
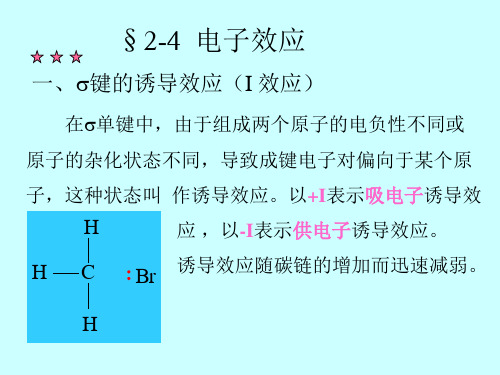
二、键诱导效应
当形成键的两端原子存在电负性差异时， 键电子云偏向于电负性强的一端。
R CO
R
R CO
R
Rδ C
Oδ
R
R CO
R
δδ C=O
:易亲核加成, 亲核试剂先进攻
Cδ+,
Cδ+活性 大于 Oδ - (O形成 八 e 稳定) 区别： C=C : 富电子体系, 烯烃易亲电加成
诱导效应的理论解释： 电负性差 ： C=C : SP2 杂化 （1/3 S + 2/3 P），离
核近，C 电负性：2.62 C : SP3杂化 (1/4S +3/4P), 离核远,
C 电负性 :2.50
静态诱导效应可以通过元素的电负性强弱给予判 断。而动态诱导效应（即在外电场作用下的瞬间极 化），不但与电负性有关，还与原子的极化率有关， 即在外电场下核外电子云的变形能力。
H
CH2
C
CC
H
H H
+
CH
CH2
2 ： 共轭效应----共轭体系中存在的特殊电子效应 ——共轭体系中分子内原子间的相互影响，引起
电子云密度分布“ 平均化” ，键长趋于“ 平均化” ，体 系能量降低的效应。
共轭效应的特点： ①：三个或三个以上共平面原子， P 轨道对称轴互相平行。 ②： 电子云密度 “ 平均化” ，导致键长 “ 平均化” ③：共轭体系受外界电场影响时， π 电子云发生转移，共
三. 共轭体系与共轭效应
例: 共轭二烯烃 (重要) : CH2=CH-CH=CH2
高考专题复习 高中化学电子效应应用
专题电子效应在共价键中，因成键原子的电负性不同，吸引电子的能力不同;或因分子的结构和成键方式的影响，电子云往往不是均匀地分布在成键原子周围，会出现电子云偏向某个原子，或发生电子云“离域”(绕多个原子核运动)。
这种电子的偏向或离域，称电子效应。
电子效应主要有诱导效应和共轭效应。
一、诱导电子效应:分子因成键原子的电负性不同，电子云偏向电负性大的元素，出现正负电荷中心不重合的现象，称诱导电子效应（I）。
电子云偏向电负性大的元素，为“吸电子”诱导效应(-I);电子云偏离的元素，为“给(推)电子”诱导效应(+I)。
如:效应基团推电子-R（烷基）吸电子-X、-OH、-OR、-NH2、-NO2、-SH、-SR、-CX3等原子的电负性越高，对应的基团吸电子诱导效应也会越强。
-C≡CH> -CH=CH> -CH2CH3对于不同杂化状态的碳原子来说，s成分越多，其吸电子能力越强诱导效应的特点:诱导效应可沿碳链的σ键依次传递，强度迅速减弱。
σ+表示部分正电荷，σσ+表示微弱的正电荷，一般超过3个σ键以后影响几乎消失。
因此通常只考虑与官能团直接相连的第一个碳原子所受的影响(即α-C的影响)。
形象地说，导效应是短程的，也是永恒的。
二、共轭电子效应:1、共轭体系及分类:分子中，多个相互连接的原子，各提供一条P轨道，两两间彼此平行重叠形成的π键称共轭π键(大π键)。
具有共轭π键的分子，其共轭部分又称共轭体系。
有共轭体系的分子，π电子云分布在参加共轭的原子上，称π电子的离域。
形成条件单双键交替或双键与苯环双键（苯环）相连的原子上的p轨道与π键的p轨道共轭效分类π-πp -πp -p例CH2=CH2稳定性顺序为π-π> p -π> p -p（1）π -π共轭：如:1,3-丁二烯。
实测分子在同一个平面上,4个碳原子都采取SP2杂化，每个C上未杂化的P轨道与该平面垂直，彼此间平行重叠成π键。
如图所示:共轭的结果：分子中4个碳原子提供4条P轨道，4个电子，形成共体系，表示为π44电子云围绕分子中的4个碳核运动(离域)，有平均化趋势:在分子中的C2和C3间有π键性质，碳碳键键长也趋于平均化。
电子效应论文——有机反应中的电子效应
有机反应中的电子效应——有机反应机理作业班级：应用化学101班姓名：祖广权学号：2010014032在有机化学中，分子间中原子间的相互影响一般可以用电子效应和立体效应来描述，其中电子效应主要包括诱导效应和共轭效应。
所谓的电子效应顾名思义，就是通过改变分子中电子云密度的分布来影响分子的理化性质的。
下面我们将对两种相应进行讨论。
一、诱导效应当两个原子形成共价键时，由于原子的电负性不同，使成键电子云偏向于电负性较大的一方，从而形成极性共价键。
而这种极性共价键产生的电场将引起临近价键电荷的偏移。
如：C—F键形成的电场使第二个碳原子也带上部分的正电荷(σσ+),而第三个碳原子带有更小的正电荷（σσσ+）。
在分子中引入一个原子或原子团后，可使分子中电子云密度发生变化，这种变化不仅发生在直接相连的部分，而且沿着分子链影响整个分子的电子云密度分布。
这种因某一原子或原子团的电负性，而引起分子中σ键电子云分布发生变化，进而引起分子性质发生变化的效应叫做诱导效应（inductive effect），通常用I来表示。
例如：溴乙酸的酸性比乙酸的酸性要强，我们可以利用溴原子的诱导效应来解释。
我们知道溴原子的电负性比氢原子的电负性大，吸电子能力比氢原子强，所以在溴乙酸分子中，Br—C键上σ电子向 Br原子方向“偏移”，使C2原子变得带正电性，C2原子再通过C2原子影响O原子，结果在溴乙酸分子中O—H键的σ电子“偏向”O原子，加大了O—H键的极化度，从而有利于氢原子的电离，使酸性较乙酸增强。
显然溴原子的诱导效应是吸电子的。
甲酸的酸性比乙酸强，说明甲基的诱导效应与溴原子是相反的，是推电子的。
我们现在知道，诱导效应有拉电子和推电子之分，那么我们该如何判断一个原子或原子团是拉电子诱导效应还是推电子诱导效应呢？在讨论原子或原子团的诱导效应方向时，我们都以H原子作为比较标准，我们将饱和的H—C键的诱导效应规定为零。
当一个原子或原子团X取代了H—Cabc分子中的H以后，若X—Cabc分子中的Cabc 部分带了部分正电荷（常用σ+来表示）或正电荷增大，则X的诱导效应就是吸电子诱导效应或拉电子诱导效应，用-I表示。
电子效应——精选推荐
电⼦效应电⼦效应：共轭效应、诱导效应、超共轭效应。
⼀、共轭效应共轭体系： π-π共轭：π键 + π键（双键/三键 + 单键 + 双键/三键）。
例： CH2=CH-CH=CH2（1,3-丁⼆烯）：C=C（碳碳双键） + C=C（碳碳双键）π-π共轭。
CH2=CH-CHO（丙烯醛）：C=C（碳碳双键） + C=O（碳氧双键）π-π共轭。
CH2=CH-CN（丙烯腈）：C=C（碳碳双键） + C≡N（碳氮三键）π-π共轭。
p-π共轭：p轨道 + π键。
多电⼦p-π共轭： 例：CH2=CH-Cl（氯⼄烯）：3原⼦4电⼦。
等电⼦p-π共轭： 例：CH2=CH-CH2·（烯丙基⾃由基）：3原⼦3电⼦。
缺电⼦p-π共轭： 例：CH2=CH-CH2+（烯丙基碳正离⼦）：3原⼦2电⼦。
p-p共轭：p轨道 + p轨道。
例：C=O（羰基）。
共轭效应： 正效应（推电⼦效应/+C效应）： 例：C=C（碳碳双键）、-CH3（甲基）。
负效应（吸电⼦效应/-C效应）： 例：C=O（碳氧双键）、-CN（氰基）、-NO2（硝基）。
性质： ①共平⾯（sp2）。
②体系能量降低（共轭能/离域能）。
③键长趋于平均化（单键变短，双键变长）。
④正负电荷交替出现。
⑤沿共轭链传递，⼤⼩不变。
⼆、诱导效应共价键：极性共价键（同种元素）、⾮极性共价键（不同种元素）。
元素电负性差越⼤，极性越⼤。
电负性：s > sp > sp2 > sp3。
偶极矩：键偶极矩（键矩）、分⼦偶极矩。
物理意义：描述共价键/分⼦极性⼤⼩的物理量。
定义：电荷中⼼的电荷量与电荷中⼼之间的距离之积。
标⽮性：⽮量。
⼤⼩：µ = qd。
µ：偶极矩。
q：电荷中⼼的电荷量。
d：电荷中⼼之间的距离。
分⼦偶极矩 = 键偶极矩（键矩）的⽮量和。
单位： 国际单位：库·⽶（C·m）。
常⽤单位：德拜（德，D）。
电子相关效应
各种能量值的关系
无限(完备)基组变分计算 有限基组变分计算 近似HF极限值
基组误差
HF极限值
相 关 能 理 论 值 近 似 相 关 能 实 验 值 近 似 相 关 能 计 算 值
近似非相对论极限值 精确非相对论极限值
相对论效应校正
基组误差
相对论效应校正(近似)
总能量实验值
相关能在化学问题中的重要性
大小一致性
• 对距离很远的两个体系, 有E(A+B) =E(A)+E(B) • 对有2个基函数的He原子, CID为
0 t A • 对两个He原子分别计算得到
2 A2 A 1A1A
2B2B A2 A (0 A t A 12A1 )( t 0B B 1B1B ) A 2B2B 2 A2 A2 B 2 B A2 A 0 t A 12A1 t t t B 1B1B A B 1A1A1B1B A • 两个He原子距离很远时, CID为 (没有包括四重激发态)
ˆ d / *d with respect tot minimizeE *H
• CIS – 包括所有单激发态
– 用于激发态计算, 不是用于基态相关能
• CISD – 包括所有单激发和双激发态
– 对计算基态的相关能非常有用 – O2V2 个行列式 (O= 占据轨道的数目, V=未占据轨道的数目)
正六角形H6分子 的相关函数
(a)r2在氢核上
(b)r2在氢核中间
HF的相关能 是精确的 (Exact)!!!
相关能的定义
• 由于HF方法主要未考虑Columb相关, 忽略 了电子之间的排斥作用(排斥使得能量升高), 因此, 相关能是负值, 将导致体系计算能量 更加负 • Lowdin的定义: 指定的一个Hamilton量的某 个本征态的电子相关能, 是指该Hamilton量 在该态的精确本征值与它的限制的HartreeFockFra bibliotek限期望值之差。
3.2 有机化学中的电子效应
3.2 有机化学中的电子效应诱导效应共轭效应超共轭效应3.2 有机化学中的电子效应电子效应: 有机分子中某个基团的存在, 使某种结构中的电子云发生了偏移的现象。
诱导效应（inductive effect ）共轭效应（conjugation ）超共轭效应（hypercongjugation ）场效应（field effect ）电子效应（详见“羧酸及其衍生物”)3.2 有机化学中的电子效应一、诱导效应诱导效应(inductive effect)( I ):因分子中原子或基团的极性(电负性)不同而引起成键电子云沿着原子链向某一方向移动的效应。
诱导效应特点：1）电子云沿原子链传递；2）诱导效应随着距离的增长迅速减弱，一般只考虑三根键的影响；3）诱导效应是一种永久效应。
一、诱导效应氯的电负性大于碳原子，导致α-C 带正电性，Cl 原子带负电性；同理, γ-碳原子带更少的部分正电性, 用“δδδ+”表示。
由于α-碳原子带部分正电性, 其电负性大于β-碳原子, 故α-碳原子与β-碳原子间的成键电子对略偏向α-碳原子, 以致β-碳原子带较少的部分正电性, 用“δδ+”表示；CH 3CH 2CH 2CH 2Cl δ+δ-δδ+δδδ+αβγ一、诱导效应诱导效应的方向：给电子的诱导效应+I electron-donating inductive effect吸电子的诱导效应-Ielectron-withdrawing inductive effect 标准诱导效应一般以乙酸的α 氢为比较标准。
H-CH2COOH取代基的电负性小于氢的, 叫给电子基, 用“+I ”表示; 反之叫吸电子基, 用“-I ”表示。
3.2 有机化学中的电子效应一、诱导效应诱导效应大小的一般规律：①与碳原子直接相连的原子，若为同一族，吸电子诱导效应随原子序数增加而降低；若为同一周期，则从右到左吸电子效应降低。
-F > -Cl > -Br > -I-OR > -SR-F > -OR > -NR2> -CR33.2 有机化学中的电子效应一、诱导效应诱导效应大小的一般规律：②碳原子与不同杂化状态的同一元素相连, s成份越多, 吸电子能力越强。
有机化学中个各种效应及其应用
向长波方向移动。随着共轭链增长，吸收光谱的波长移 向波长更长的区域，进入可见光区。
•
颜色
最大吸收峰波长（nm）
• 丁二烯
无
217
• 己三烯
无
258
• 二甲辛四烯 淡黄
298
• 蕃茄红素 红色
470
番茄红素与胡萝卜素
4/15/2021 11:26 AM
（2）-C效应
在同周期元素中，原子序数越大，电负性越强，-C 效应越强。
如： =O > =NH > =CH2
对于同族元素，随着原子序数的增加，原子半径变
大，能级升高，即与碳原子差别变大，使π键与π
键的重迭程度变小，故-C效应变弱。
如：
C=O > C=S
但共轭效应的影响因素是多方面、比较复杂的，不 仅取决于中心原子的电负性和 p轨道的相对大小，
共轭体系。 π-π 共轭体系的结构特征是：双键、单键、
双键交替连接。组成该体系的不饱和键可以是双
键，也可以是三键；组成该体系的原子也不是仅
限于碳原子，还可以是氧、氮等其它原子。如：
CH2 CH C CH 乙烯基乙炔
CH2 CH CH O 丙烯醛
CH2 CH C N 丙烯腈
在共轭体系中， π电子离域的表示方法：
• 以上各种效应可直接影响到化合物的结构和性质。 如它可影响化合物的物理性质，影响有机分子、 中间体和过渡态的稳定性，影响分子的酸碱性质， 影响化学反应活性和反应方向，还可影响反应的 立体化学等。
二.电子效应
•电子效应包括诱导效应、共轭效应和超共轭效应。
• 1.诱导效应： • 由于极性σ键存在，使分子中其他σ键电子
电子效应及位阻效应
电子效应及位阻效应电子效应和位阻效应是化学反应中两个非常重要的概念，它们都可以影响分子和原子之间的相互作用，从而改变反应的速率和产物选择性。
本文将详细解释电子效应和位阻效应的原理、影响和应用。
一、电子效应的定义和原理电子效应是指分子中电子密度的变化所引起的化学反应的影响。
在分子中，由于电子的带电性质和轨道的分布不同，不同位置的原子之间存在着不同的电子云分布和反应活性。
主要有取代基效应、缩合基效应和电子吸引/排斥效应等。
(a) 取代基效应取代基效应是指有机化合物中，取代基的性质会影响反应中的电荷分布和化学键强度。
如果取代基是电子供体，则它会增加邻位原子的电荷密度，促进反应的进行；如果取代基是电子受体，则它会减少邻位原子的电荷密度，抑制反应的进行。
例如，对于苯基的取代反应，在苯环上引入-NO2（硝基）基团可使其反应速率加快，而引入-CH3（甲基）基团则使其反应速率降低。
(b)缩合基效应缩合基效应是指大环化合物中，缩合基的存在会影响环上的电荷分布和反应活性。
一般来说，缩合基越大，环上电子密度越低，反应活性越弱，而缩合基越小，则环上电子密度越高，反应活性越强。
例如，有机合成中的Diels-Alder反应，对于环侧基为甲基的二烯体和苯乙烯缩合反应，反应活性要比环侧基为丁基的二烯体反应活性强得多。
(c) 电子吸引/排斥效应电子吸引/排斥效应是指分子中不同原子或基团之间的电子云分布不对称会引发的化学反应影响。
例如，在酸催化条件下的芳香化反应中，亚硝基（-NO2）和硝基（-NO3）等电子吸引基团会使反应活性得到增强，而甲基（-CH3）等电子排斥基团则会使反应活性下降。
二、位阻效应的定义和原理位阻效应是指分子中原子或基团之间的体积排斥效应所引起的化学反应的影响。
分子中原子和基团之间的体积大小不同，因此会使化学反应的难易程度和产物选择性发生变化。
一般来说，较大的原子和基团会受到更大的位阻效应，反应活性会降低，而较小的原子和基团则不受位阻效应的影响，反应活性和选择性较高。
有机化学中的电子效应
3. 带正电荷的基团具有吸电子诱导效应，带负电荷的基团具有给电子的诱导 效应 4. 烷基有给电子的诱导效应，同时又有给电子的超共轭效应吸电子基团：源自给电子基团：共轭效应
单双键交替出现的体系称为共轭体系。在共轭体系中，由于原子间的 相互影响而使体系内的π电子（或P电子）分布发生变化的一种电子 效应称为共轭效应
特点：电子云是沿原子链传递的；其作用随着距离的增加迅速 下降，一般只考虑三 根键的影响
诱导效应一般以氢为标准
1.与碳原子直接相连的原子，如同一族的随原子序数增加而吸电子诱导效应 降低，同一周期的自左到右吸电子诱导效应增强
-F>-Cl>-Br>-I -OR>-SR -F>-OR>-NR2>-CR3
2.与碳原子直接相连的基团不饱和程度越大，吸电子能力越强。
有机化学中的电子效应：诱导效应、共轭效应、超共轭效应
诱导效应：
分子中引入一个原子或基团后，使分子中的电子云密度分布发生 变化，而这种变化不但发生在直接部分部分，也可以影响到不相 连的部分，这种因某一原子或基团的极性，σ键的电子沿着原子 链向某一方向移动的效应称为诱导效应。 诱导效应是指σ电子的偏移。
超共轭效应：烷基的碳原子与极小的氢原子相结合，对于电子云的屏蔽效 应很小，烷基上C-H键的一对电子，受核的作用相互吸引，到一定的距离 时，烷基上的几个C-H键电子之间又互相排斥，如果邻近有π轨道或P轨 道可以容纳电子，这时电子偏离原来的轨道，而趋向于π轨道或P轨道， 使δ轨道与π轨道呈现部分的重叠，其结果使共轭的范围扩大，体系稳定。
与p轨道或π轨道相邻碳上的C－H键多少有关，C－H键愈多，超 共轭效应愈大。
凡共轭体系上的取代基能降低体系的π电子密度，则这些基团有吸电子的 共轭效应，用－C表示。
有机化学电子效应
一、 诱导效应——由于分子中电负性不同的原子或基团 的影响使整个分子中成键的电子云沿分子链(共价键)向一 个方向偏移，使分子发生极化的现象。(P314)
诱导效应
吸电子诱导效应(-I ) 供电子诱导效应(+I )
H
H
H
H
ddd+ dd+
d+
C
g
C
b
Ca
dHF
H
H
H
诱导效应中电子偏移的方向以C—H键中H作为比较标准.
特点
I 静电极性 沿碳链传递 +I 和-I
单向极化 短程作用
极性交替，远程作用
C 电子离域 沿共轭链传递 +C 和-C
键长平均化
内能降低
谢谢观赏
——C X
——C——H
—— C Y
-I 效应
比较标准
+I 效应
如果取代基X的电负性大于H,X具有吸电子性，故称为吸 电子基。由它引起的诱导效应叫做吸电子诱导效应, 用-I 表示。
如果取代基Y的电负性小于H,Y具有斥电子性，称为斥电 子基。由它引起的诱导效应叫做供电子诱导效应，用+I表 示。
常见原子或基团的诱导效应强弱次序 为： 吸电诱导效应（–I）：-NO2> -COOH > -F > -Cl > -Br > -I > -OH > RC≡C- > C6H5- > R’CH=CR-。
2.p-π共轭体系：
C H 2C H C H 2
δ
δ
C H 2C H C H 2
烯丙基正离子
C H 2C HC H 2 C H 2C HC l
有机化学 电子效应
电子效应电子效应分为：诱导效应、共轭效应、超共轭效应 一、诱导效应1概念：有机物分子中，由电负性不同的取代基的影响沿着键链传递，使分子中电子云密度而偏移的效应，用I 表示。
2分类：吸电子诱导效应：电负性大的原子或原子团使分子其余部分的电子云密度降低推电子诱导效应：电负性小的原子或原子团使分子其余部分的电子云密度升高3注意（1）与分子结构有关，永久性的（2）只能沿着σ键传递，随距离增加而迅速减小，一般超过3个σ键不再考虑 （3）只涉及电子云密度的改变，并不造成共用电子对单独属于某一原子的情况 （4）引起键极性的改变，键的极性改变一般是单一方向的，不会产生极性交替的现象 4相对强度（1）通过测定取代酸解离常数确定 （2）测定偶极矩确定 （3）NMR 化学位移确定（化学位移越大，电子云密度越低） ☆5影响取代基诱导效应相对强度的因素 （1）周期律→电负性①同一周期吸电子诱导效应从左向右增加 例 ―CR 3< ―NR 2< ―OR < ―F②同族吸电子诱导效应从上而下降低 例 ―F > ―Cl > ―Br > ―I （2）电荷带正电荷的基团比同类型的不带电荷的基团吸电子能力强得多X C δδδδδδYC C δδδδ带负电荷的基团比同类型的不带电荷的基团给电子能力强得多（3）价键饱和程度不饱和程度高的同种原子吸电子能力强（s 成分越多，碳的电负性越强） 吸电子诱导效应：二、共轭效应 1概念三个或三个以上相邻原子P 轨道相互平行重叠，形成一个大π键，称为共轭体系。
π电子围绕三个或更多的原子运动，称为离域。
电子通过共轭体系传递并引起体系性质改变的效应称为共轭效应，用C 表示。
2基本类型（1）π−π共轭体系 多个饱和键之间的共轭体系（单间与不饱和键相间）（2）p −π共轭体系 不饱和键与相邻原子p 轨道之间的共轭体系3注意（1）共轭效应起源于共轭体系中π电子的高度活动性 例 聚乙炔导电 （2）传到距离：从共轭体系的一端，沿共轭键传递到另一端（3）传递方式：沿着共轭键传递→共轭键电子云密度平均化（键长平均化） （4）极性交替 电子在共轭链中传递时，出现电荷密度高低不同的交替现象C CR CR CR CR CR >>222CH 2CH CH CH 2CH 2CH CHNH CH 2CHCHO CCCH CH 2CCCH CHCCH 2CHN CH 2CHCl 2CH CH 2CHCH 2CHCH 2COX O CO(R)（5）共轭体系中，电子的运动范围扩大，体系的能量降低；共轭体系越大，体系越稳定；共轭结构有利于分子整体结构的稳定。
电子效应
电子效应：诱导效应、共轭效应、场效应等一．诱导效应1．基础知识存在于不同的原子形成的极性共价键中如：X d- ←A d+在多原子分子中，这种极性还可以沿着分子链进行传递X d- ←A d+ ←B dd+ ←C ddd+Y d+→A d- →B dd- →C ddd-由于原子或原子团电负性的影响，引起分子中电子云沿σ键传递的效应称为诱导效应。
这种效应经过三个原子后其影响就很小诱导效应的方向，是以氢原子作为标准。
用－I表示Y d+ →d-CR3H—CR3 X d- ←d+CR3+I效应比较标准－I 效应+I诱导效应与-I诱导效应相反。
具有+I效应的原子或原子团与碳原子成键后，可使电子云偏向该碳原子。
正诱导效应用+I表示。
例：C H3C H3C CH H常见的具有+I 效应的基团有：―O―＞(CH3)3C―＞(CH3)2CH―＞CH3CH2―＞CH3―＞D―常见的具有－I效应的基团有：―CN，―NO2＞―F ＞―Cl ＞―Br ＞―I ＞RO―＞C6H5―＞CH2=CH―一般来说，诱导效应的强弱变化有以下规律：A．同一族的元素随着原子层的增加而吸电子诱导效应降低。
如：—F > —Cl > —Br > —I—OR > —SR—NR2 > —PR2B．同一周期的元素从左到右吸电子诱导效应增加。
如：—F > —OR > —NR2 > —CR3C．不同杂化状态的碳原子以s轨道成分多者吸电子能力强。
（sp>sp2>sp3）反映在基团方向时，如：D．带正电荷的基团具有吸电子诱导效应，带负电荷的基团具有给电子诱导效应。
与硫直接相连的原子，具有共价键，有强的吸电子诱导效应。
上面为静态分子中所表现出来的诱导效应，称静态诱导效应，它仅与键本身的极性有关。
另外，在化学反应中，由于分子受到许多外界条件的影响，例另一分子的影响，其它进攻试剂的影响，溶剂的影响等等。
在外界电场的作用下，分子会发生诱导极化，这种在外界电场影响下在化学反应时才表现出来的诱导效应称为动态诱导效应。
高中化学竞赛-电子效应
高中化学奥林匹克竞赛辅导元素电负性表电子效应电子效应分为诱导效应、共轭效应、超共轭效应、场效应。
一、诱导效应诱导效应是电子效应的一种，是由路易斯首先提出的。
诱导效应是指在有机化合物分子中由于原子的电负性差异，导致σ键电子的移动，使分子中的电子云密度分布发生变化。
这种因分子中原子或基团的极性（电负性）不同而引起成键电子对向电负性大的方向移动的现象称为诱导效应，其特点是能沿分子链传递且迅速减弱。
如氯丁烷分子中，取代在碳原子上的氯原子的电负性较强，C-Cl键产生偶极，使与氯原子连接的第一个碳原子(α–C)产生部分正电荷(δ+)，也使第二个碳原子(β-C)带有部分正电荷，第三个碳原子(γ-C)带有部分更少的正电荷，依次影响下去。
这种影响的特征是沿着碳链传递，随着碳链的增长而迅速减弱，一般传递到第三个碳原子这种影响就忽略不计了。
(其中δ表示微小，δδ表示更微小，依次类推)诱导效应是一种静电作用，共用电子并不能完全转移到另一原子上，只是电子云密度分布发生变化，即键的极性发生变化。
由极性键所表现出的诱导效应称作静态诱导效应( Is)，而在化学反应过程中由于外电场（如溶剂、试剂）的影响而产生键的极化称作动态诱导效应(Id)。
实验测得原子或基团的吸电子能力顺序为：1.吸电子诱导效应(–I)和给电子诱导效应(+I)静态诱导效应通常采用烷烃H-CR3上的氢作为比较标准，规定其为0。
如果用电负性较碳原子小的Y取代了H-CR3上的氢原子，化合物Y-CR3中-CR3部分的电子云密度比H-CR3中大，Y 叫做给电子基团。
由给电子基团引起的诱导效应叫做给电子诱导效应(+I)。
如果用电负性较碳原子大的X取代了H-CR3上的氢原子后，化合物X-CR3中-CR3部分的电子云密度比在H-CR3中的小，X叫做吸电子基团。
由吸电子基团引起的诱导效应叫做吸电子诱导效应(–I)。
2.吸电子诱导效应(–I)和给电子诱导效应(+I)的相对强度静态诱导效应的强弱与取代基或原子的电负性强弱相关。
电子效应
CH3CH =CH CH =CH2 + 2 H2
1,4 - 戊二烯 + H2
CH3CH2CH2CH2CH3
-1 氢化热 = 226 kj mol
28 kj mol -1
1,3 - 戊二烯 + H2
254 kj mol -1 E
226 kj mol -1
同是加2mol的H2， 的 同是加 但放出的氢化热却不 同，这只能归于反应 物的能量不同。 物的能量不同。
X
p-π之间没有共轭 之间没有共轭
CH R
X
H R
所以，烯丙位的卤素容易离去，形成 所以，烯丙位的卤素容易离去， 稳定的烯丙基正碳离子。 稳定的烯丙基正碳离子。
4.烯烃的稳定性 烯烃的稳定性
H H H
H
H
由于丙烯中σ-π的超共轭作 的超共轭作 由于丙烯中 使烯烃稳定。同样， 用，使烯烃稳定。同样，双键碳 上连接的烷基越多，这种σ-π的 的 H 上连接的烷基越多，这种 超共轭作用就越强， 超共轭作用就越强，烯烃就越稳 定。
共轭体系。 成 p ,π - 共轭体系。如：
CH2 = CH Cl
H Cl C C H H
CH3 O CH =CH2
能形成 p ,π - 共轭体系的除具有未共用电子 对的中性分子外，还可以是正、负离子或自由基。 对的中性分子外，还可以是正、负离子或自由基。
+ H H C C CH2 H CH2
+
H H C C
（二）共轭效应（Conjugative effect） 二 共轭效应（ ） 丁二烯分子那样，四个π电子不是分别固定在 象1,3 – 丁二烯分子那样，四个 电子不是分别固定在 两个双键碳原子之间， 两个双键碳原子之间，而是扩展到四个碳原子之间的 这种现象，称为电子的离域。 这种现象，称为电子的离域。 在共轭分子中，由于π电子的离域，任何一个原子受 电子的离域， 在共轭分子中，由于 电子的离域 到外界的影响，均会影响到分子的其余部分， 到外界的影响，均会影响到分子的其余部分，这种电 子通过共轭体系传递的现象，称为共轭效应。 子通过共轭体系传递的现象，称为共轭效应。 共轭效应也分为给电子的 共轭效应也分为给电子的（+C）和吸电子的（-C） 给电子 ） 吸电子的 ） 两种不同的作用。 两种不同的作用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ˆ ˆ H0 Fi
• 按照Hartree-Fock行列式, 单激发, 双激发和多重 激发行列式的方式展开微扰波函数
ab ab 1 aia ia aij ij ia ijab abc abc aijk ijk ijkabc
正六角形H6分子 的相关函数
(a)r2在氢核上
(b)r2在氢核中间
HF的相关能 是精确的 (Exact)!!!
相关能的定义
• 由于HF方法主要未考虑Columb相关, 忽略 了电子之间的排斥作用(排斥使得能量升高), 因此, 相关能是负值, 将导致体系计算能量 更加负 • Lowdin的定义: 指定的一个Hamilton量的某 个本征态的电子相关能, 是指该Hamilton量 在该态的精确本征值与它的限制的HartreeFock极限期望值之差。
• 把l幂次相同的项合并在一起 ˆ H E
0 0 0 0
ˆ ˆ H 0 1 V0 E0 1 E10
ˆ E1 0 V0 d ˆ E2 0 V1d
ˆ ˆ H 0 2 V1 E0 2 E11 E2 0
Mø ller-Plesset 微扰理论
HF方法是MBPT方法的一级近似
• HF方程的Hamilton量就是MBPT的零级表示
H 0 Fi ; E
i 1 N (0) 0
Occupied
i 1
ei
• HF方程中的交换作用, 就是MBPT的一级表 示
(1) V 1 ( J j K j ); E0 1 1 [(ii | jj ) (ij | ij )] 2 i1 j i1 rij i 1 j i 1 rij j 1 (0) (1) EHF E0 E0 N N N N N
组态相互作用方法的简化
• CI方法的实现就是降低行列式的个数 (2K!)/[N!(2K-N)!], 即减小K和N • 只允许低等级激发, 一级激发(CIS, N(2K-N)项), 二 级激发(CID, N(N-1)(2K-N)(2K-N-1)/[2!2!]项);一级 +二级激发(CISD) • 完全活性空间自洽场方法(CASSCF): 把所有自洽场分子轨道分为内层(永远双占据), 外 层(永远不占据)和活性轨道, 只对活性轨道进行 MCSCF计算, 这样, 同时减小了K和N。
• 理论和实验能量差值的比较
– – – – 实验误差: 1kcal/mol~0.002Hartree 体系总能量 101~5Hartree 体系相关能 10-1~1Hartree 总能量差值受相关能影响很大。
• 弱相互作用（比如分子间作用）
– 氢键键能～3－102 包含在波函数中
耦合簇理论
• CCSD 能量和波幅可以通过解下式得到
ˆ 0 (H ECC )CC d 0 ˆ (H ECC )CC d 0
a i ab ˆ ij (H ECC )CC d 0
耦合簇理论
• • • • • • • CC 方程在波幅上是二次的 必须用迭代法求解 每次迭代的计算成本类似于 MP4SDQ CC 是大小一致的 CCSD – 单和双激发态校正, 直到无穷大阶次 CCSD(T) – 把三重激发用微扰的方式加上 QCISD – 组态相互作用, 且添加足够的二次项以使 得其大小一致(等价于CCSD的截断形式)
组态相互作用方法
• HF方法把电子按从低到高填充, 是合理的, 但是, 有一定的人为性 • 从统计力学的角度来看, 任何填充方式都是可能的, 只不过其在真实体系中的几率不同, HF的填充方 式是几率最大的一种 • 因为把电子都限制在了HF的占据轨道上, 所以使 得不同自旋的电子过分接近, 导致排斥能升高 • 为了改进这种硬性限制, 允许电子在所有可能的轨 道上自由填充, 再确定出每种填充方式的几率。
– 不需要人为选择就可以应用于所有分子 – 可用于构建模型化学
• 效率
– 不能仅限于非常小的体系
• 变分性
– 是精确能量的上限
• 大小一致性(size extensive)
– E(A+B) = E(A) + E(B) – 需要对热化学进行正确描写
• 计算成本与精确性的等级性
– 这样计算才能被系统改进
计算化学及其应用
电子相关效应 Electron Correlation Effects
电子相关能
• 在Hartree-Fock近似下, 每个电子感受到的是 所有其它电子的平均密度 • 但是, 在某个瞬间, 两个电子不能出现在同一 地点 • 电子之间必然两两之间互相避免, 即它们的运 动是相关的 • 给定基组的情况下, 相关能就是精确能量与 Hartree-Fock能量之差 • 每个电子对的相关能大概是 20 kcal/mol
ˆ minimizeE *Hd / *d with respect tot
• CIS – 包括所有单激发态
– 用于激发态计算, 不是用于基态相关能
• CISD – 包括所有单激发和双激发态
– 对计算基态的相关能非常有用 – O2V2 个行列式 (O= 占据轨道的数目, V=未占据轨道的数目)
各种能量值的关系
无限(完备)基组变分计算 有限基组变分计算 近似HF极限值
基组误差
HF极限值
相 关 能 理 论 值 近 似 相 关 能 实 验 值 近 似 相 关 能 计 算 值
近似非相对论极限值 精确非相对论极限值
相对论效应校正
基组误差
相对论效应校正(近似)
总能量实验值
相关能在化学问题中的重要性
单激发态行列式(把占据轨道fi用未占据的轨道fa代替)
ab ij | f1 fi 1fafi 1 f j 1fbf j 1 fn | 双激发态行列式 (fi fa , f j fb )
等等
组态相互作用
• 用变分原理来确定CI系数
ab ab 0 tia ia tij ij ia ijab abc abc tijk ijk ijkabc
HF MP3 MP5 MP4 MP6
MP2
MBPT方法的说明
• MBPT可以有MP2, MP3, MP4等各级修正, 主要应用的是MP2, MP4, 而MP3给出的修正 往往很差 • MP2是从头算最经常使用的可承受包含相关 能的方法,最常用的组合就是MP2/6-31G*, 但是在基函数超过500后就很慢了 • MBPT方法有可能给出不体系能量低的值, 因为它 没有变分原理保证其高于体系真实 能量
电子相关的表现
• 对于闭壳层组态, 电子相关性分解为两个部 分: 自旋相同的电子之间和自旋相反的电子 之间 • f(r1,r2) =[fab(r1,r2)+ faa(r1,r2)]/2 • faa(r1,r2): Fermi孔; fab(r1,r2): Columb孔 • HF方法基本上反映了Fermi孔(由于波函数 的反对称性), 完全没有反映Columb孔!
Basis 6-31G*
Polarized 6-311G* Diffuse 6-311+G* High Ang. Mom. 6-311+G(3df,p) …
N2
N5
N6
N7
Schrö dinger Equation
Mø ller-Plesset 微扰理论
• 在每个阶次都是大小一致的 • MP2 – 二阶计算相对容易(只需要双激发态) • 在Hartree-Fock是一个相当好的起点时, 二阶将可以 得到很大一部分相关能 • 实际使用中可以到四阶(单, 双, 三和四重激发态) • MP4 能够得到大部分的相关能 • 整个系列有点振荡(偶数阶更低一些) • 如果出现了严重的自旋污染或者Hartree-Fock不是一 个好的起点, 相关能的收敛很困难
总结
• CI是最直接的方法 • MP是最常用的方法 • 耦合簇方法(CC)是最有效的计算相关能的 方法
计算化学及其应用
模型化学 Model Chemistries
模型图(Pople图)
Minimal STO-3G Split-Valence 3-21G HF MP2 MP3 MP4 QCISD(T) ... Full CI
组态相互作用
ab ab 0 tia ia tij ij ia ijab abc abc tijk ijk ijkabc
0 | f1 fn | 参考行列式(Hartree-Fock波函数) ia | f1 fi 1fafi 1 fn |
大小一致性
• 对距离很远的两个体系, 有E(A+B) =E(A)+E(B) • 对有2个基函数的He原子, CID为
0 t A • 对两个He原子分别计算得到
2 A2 A 1A1A
2 A (0 A t A 12A12 A )(0 B t B 12 B B B ) A B1 2 A A 0 t A 12A12 A t B 12 BB B t At B 12A121AB21BB2 B A B1 A • 两个He原子距离很远时, CID为 (没有包括四重激发态)
只有 价轨道
只有 HOMO+LUMO
0 活性空间 能 量
内 层
CAS-SCF
微扰方法
• 把Hamilton量分为精确可解的部分和微扰部分 ˆ ˆ ˆ ˆ ˆ H E H0i0 Ei0i0 H H0 V • 按l展开Hamilton量, 能量和波函数
ˆ ˆ ˆ H H0 lV E E0 lE1 l2 E2 0 l1 l22
– E=E(A)+E(B), = AB
0 t A
2 A2 A 1A1A