图像的频域滤波
数字图像处理中的频域滤波数学原理探索

数字图像处理中的频域滤波数学原理探索数字图像处理是一门涉及图像获取、图像处理和图像分析的学科,其中频域滤波是其中一个重要的技术。
频域滤波通过将图像从空域转换到频域,利用频域的特性对图像进行处理。
本文将探索数字图像处理中的频域滤波的数学原理。
一、傅里叶变换傅里叶变换是频域滤波的基础,它将一个函数表示为正弦和余弦函数的和。
对于一维信号,傅里叶变换可以表示为以下公式:F(u) = ∫[f(x)e^(-i2πux)]dx其中F(u)表示信号f(x)在频率域的表示,u表示频率,x表示空间位置。
对于二维图像,傅里叶变换可以表示为以下公式:F(u,v) = ∬[f(x,y)e^(-i2π(ux+vy))]dxdy其中F(u,v)表示图像f(x,y)在频率域的表示,u和v表示频率,x和y表示图像的空间位置。
二、频域滤波在频域中,对图像进行滤波意味着对图像的频率分量进行操作。
常见的频域滤波操作包括低通滤波和高通滤波。
1. 低通滤波低通滤波器允许通过低频分量,并抑制高频分量。
在图像中,低频分量通常表示图像的平滑部分,而高频分量则表示图像的细节部分。
低通滤波器可以用于去除图像中的噪声和细节,使图像变得更加平滑。
2. 高通滤波高通滤波器允许通过高频分量,并抑制低频分量。
在图像中,高频分量通常表示图像的边缘和纹理部分,而低频分量则表示图像的整体亮度分布。
高通滤波器可以用于增强图像的边缘和纹理特征。
三、频域滤波的步骤频域滤波的一般步骤包括图像的傅里叶变换、滤波器的设计、滤波器与图像的乘积、逆傅里叶变换。
1. 图像的傅里叶变换首先,将原始图像转换为频域表示。
通过对图像进行傅里叶变换,可以得到图像在频率域中的表示。
2. 滤波器的设计根据需要进行滤波器的设计。
滤波器可以是低通滤波器或高通滤波器,具体设计方法可以根据应用需求选择。
3. 滤波器与图像的乘积将滤波器与图像在频域中的表示进行乘积操作。
乘积的结果是滤波后的频域图像。
4. 逆傅里叶变换对滤波后的频域图像进行逆傅里叶变换,将其转换回空域表示。
频域滤波的基本原理

频域滤波的基本原理频域滤波的基本原理频域滤波是一种信号处理技术,它根据信号的频率特征对信号进行处理,从而达到去噪、滤波等目的。
频域滤波的基本原理就是将时域中的信号转化为频域中的信号,利用频域中的特征进行处理,最后再将处理后的信号转回时域。
一、时域和频域时域和频域是信号处理中常用的两个概念。
时域是指信号随时间变化的情况,它通常用时域波形来表示。
例如,我们平常看到的声音、图像等都是时域信号。
频域是指信号在频率上的特征,与时域不同,它通常用其频谱图表示。
频谱图是一种表示信号频率分布情况的图形,它能够显示信号中存在的各种频率成分。
例如,下图分别是一个声音信号的时域波形和频谱图:二、傅里叶变换频域处理的基础是傅里叶变换。
傅里叶变换是一种将时域信号转换为频域信号的方法,它可以将任意周期的连续信号分解成一系列正弦和余弦函数的和。
傅里叶变换的基本形式为:F_freq(x) = ∫_{-∞}^∞f_time(t)e^{-2πif t}dt其中,f_{time}是时域信号,F_{freq}是频域信号,i表示虚数单位。
需要注意的是,傅里叶变换通常是定义在连续信号上的,在实际应用中,离散信号也常常需要进行傅里叶变换,这时候可以使用离散傅里叶变换(DFT)。
三、频域滤波的基本原理频域滤波是指利用傅里叶变换将信号从时域转换到频域,然后在频域中对信号进行滤波,最后再将信号从频域转回时域的一种信号处理方法。
在频域中,我们可以通过观察信号的频谱图来判断信号中是否存在噪声或需要滤除的部分。
例如,下图中的频谱图显示了一个信号中存在高频噪声:为了去除这种噪声,我们可以在频域中将高频的部分过滤掉,实现去噪的效果。
具体而言,频域滤波通常包括以下几个步骤:1. 将时域信号x(t)进行傅里叶变换,得到频域信号X(f);2. 在频域中对X(f)进行滤波处理,得到滤波后的频域信号Y(f),过滤方式包括低通、高通、带通滤波等;3. 将Y(f)进行傅里叶反变换,得到处理后的时域信号。
实验四 图像频域高通滤波

数字图像处理实验报告姓名:田蕾 学号:20091202098 专业:信号与信息处理 年级:09实验四 图像频域高通滤波一、 实验目的掌握常用频域高通滤波器的设计。
进一步加深理解和掌握图像频谱的特点和频域高通滤波的原理。
理解图象高通滤波的处理过程和特点。
二、 实验内容设计程序,分别实现截止频率半径分别为15、30、80理想高通滤波器、二阶巴特沃斯高通滤波器、二阶高斯高通滤波器对图像的滤波处理。
观察处理前后图像效果,分析实验结果和算法特点。
三、 实验原理二维理想高通滤波器的传递函数为:000.(,)(,) 1.(,)D u v D H u v D u v D ≤⎧=⎨>⎩D0是从频率矩形中点测得的截止频率长度,它将以D0为半径的圆周内的所有频率置零,而毫不衰减地通过圆周外的任何频率。
但其物理上是不可实现的。
巴特沃斯高通滤波器的传递函数为:201(,)1[](,)n H u v D D u v =+ 式中D0为截止频率距远点距离。
与低通滤波器的情况一样,可认为巴特沃斯高通型滤波器比IHPF 更平滑。
高斯高通滤波器传递函数为:220(,)/2(,)1D u v D H u v e -=- 高通滤波器能够用高斯型低通滤波器的差构成。
这些不同的滤波器有更多的参数,因此能够对滤波器的形状进行更多的控制。
四、算法设计(含程序设计流程图)五、实验结果及分析(需要给出原始图像和处理后的图像)实验结果分析:(1)理想的高通滤波器把半径为D0的圆内的所有频率完全衰减掉,却使圆外的所有的频率无损的通过。
图像整体变得模糊,边缘和细节比较清晰。
(2)巴特沃思高通滤波器和高斯高通滤波器处理后的图像中只显现边缘,边缘的强度不同,而灰度平滑的区域都变暗了。
附:程序源代码(1)理想高通滤波器:(以D0=15为例):I1=imread('D:\Matlab\project\低通、高通滤波实验原图.jpg');figure(1); imshow(I1);title('原图');>> f=double(I1); % 转换数据为双精度型g=fft2(f); % 进行二维傅里叶变换g=fftshift(g); % 把快速傅里叶变换的DC组件移到光谱中心[M,N]=size(g);d0=15; %cutoff frequency以15为例m=fix(M/2); n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);if(d<=d0)h=0;else h=1;endresult(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));figure(2);imshow(J2);title('IHPF滤波(d0=15)') ;(2)巴特沃斯高通滤波器:(以D0=15为例):I1=imread('D:\Matlab\project\低通、高通滤波实验原图.jpg');figure(1); imshow(I1);title('原图');f=double(I1);g=fft2(f);g=fftshift(g);[M,N]=size(g);nn=2; % 2-grade Butterworth highpass filterd0=15; % 15,30,80其中以15为例m=fix(M/2); n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=1/(1+0.414*(d/d0)^(2*nn)); % filter transform function%h=1./(1+(d./d0).^(2*n))%h=exp(-(d.^2)./(2*(d0^2)));result(i,j)=(1-h)*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));figure(2);imshow(J2);title('BHPF滤波(d0=15)');(3)高斯高通滤波器:(以D0=15为例):I1=imread('D:\Matlab\project\低通、高通滤波实验原图.jpg'); figure(1); imshow(I1);title('原图');f=double(I1);g=fft2(f);g=fftshift(g);[M,N]=size(g);d0=15;m=fix(M/2); n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=exp(-(d.^2)./(2*(d0^2))); % gaussian filter transformresult(i,j)=(1-h)*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));>> figure(2);>> imshow(J2);title('GHPF滤波(d0=15)');。
透射电镜高分辨频域滤波优化

透射电镜高分辨频域滤波优化透射电镜高分辨频域滤波优化透射电镜高分辨频域滤波优化是一种常用的方法,用于提高透射电子显微镜(TEM)图像的分辨率。
在本文中,我们将逐步讨论如何进行这样的优化。
第一步是获取TEM图像。
首先,我们需要将待观察的样品放置在透射电镜中。
样品通常是非晶态或晶态的材料,它们会散射电子束。
这些散射的电子束将通过透射电子显微镜的透镜系统,最终形成图像。
第二步是进行图像的预处理。
在进行高分辨率滤波之前,通常需要对图像进行一些预处理操作,以去除噪音和伪影。
这可以通过应用空间域滤波器,如中值滤波器或高斯滤波器来实现。
接下来,我们将进入关键的步骤,即高分辨滤波。
高分辨率滤波是通过在频域中操作图像来实现的。
首先,我们需要进行傅里叶变换,将图像转换到频域。
这可以通过应用二维离散傅里叶变换(DFT)来实现。
DFT将图像从空间域转换到频域,并产生一个复数矩阵,其中每个元素表示不同频率的振幅和相位信息。
在频域中,我们可以应用滤波器来提高图像的分辨率。
常见的滤波器包括高通滤波器和带通滤波器。
高通滤波器有助于增强图像中的高频信息,从而提高图像的细节和分辨率。
带通滤波器允许通过特定的频率范围,从而保留所需的信息并滤除其他频率的干扰。
应用完滤波器后,我们需要进行反傅里叶变换,将图像从频域恢复到空间域。
这可以通过应用二维逆离散傅里叶变换(IDFT)来实现。
IDFT将频域的复数矩阵转换回空间域,并产生最终的滤波图像。
最后一步是对滤波图像进行后处理。
在高分辨滤波之后,我们可能需要对图像进行一些后处理,以进一步优化其质量。
这可能包括去噪、增强对比度或者应用其他图像增强技术。
总结起来,透射电镜高分辨频域滤波优化是一个多步骤的过程。
首先,我们需要获取原始TEM图像,并对其进行预处理。
接下来,我们将图像转换到频域,应用滤波器来提高图像的分辨率,并通过逆傅里叶变换将其恢复到空间域。
最后,我们可以对滤波图像进行后处理以进一步优化其质量。
频域滤波器设计(数字图像处理实验报告)

数字图像处理作业——频域滤波器设计摘要在图像处理的过程中,消除图像的噪声干扰是一个非常重要的问题。
本文利用matlab软件,采用频域滤波的方式,对图像进行低通和高通滤波处理。
低通滤波是要保留图像中的低频分量而除去高频分量,由于图像中的边缘和噪声都对应图像傅里叶频谱中的高频部分,所以低通滤波可以除去或消弱噪声的影响并模糊边缘轮廓;高通滤波是要保留图像中的高频分量而除去低频分量,所以高通滤波可以保留较多的边缘轮廓信息。
本文使用的低通滤波器有巴特沃斯滤波器和高斯滤波器,使用的高通滤波器有巴特沃斯滤波器、高斯滤波器、Laplacian高通滤波器以及Unmask高通滤波器。
实际应用中应该根据实际图像中包含的噪声情况灵活地选取适当的滤波算法。
1、频域低通滤波器:设计低通滤波器包括 butterworth and Gaussian (选择合适的半径,计算功率谱比),平滑测试图像test1和2。
实验原理分析根据卷积定理,两个空间函数的卷积可以通过计算两个傅立叶变换函数的乘积的逆变换得到,如果f(x, y)和h(x, y)分别代表图像与空间滤波器,F(u, v)和H(u, v)分别为响应的傅立叶变换(H(u, v)又称为传递函数),那么我们可以利用卷积定理来进行频域滤波。
在频域空间,图像的信息表现为不同频率分量的组合。
如果能让某个范围内的分量或某些频率的分量受到抑制,而让其他分量不受影响,就可以改变输出图的频率分布,达到不同的增强目的。
频域空间的增强方法的步骤:(1)将图像从图像空间转换到频域空间;(2)在频域空间对图像进行增强;(3)将增强后的图像再从频域空间转换到图像空间。
低通滤波是要保留图像中的低频分量而除去高频分量。
图像中的边缘和噪声都对应图像傅里叶频谱中的高频部分,所以低通滤波可以除去或消弱噪声的影响并模糊边缘轮廓。
理想低通滤波器具有传递函数:其中D0为制定的非负数,D(u,v)为点(u,v)到滤波器中心的距离。
频域滤波原理
cut-off=14, power=99.85%
cut-off=12, power=99.84%
cut-off=10, power=99.82%
用不同的功率百分比恢复的水田图像 Paddy (泗洪)
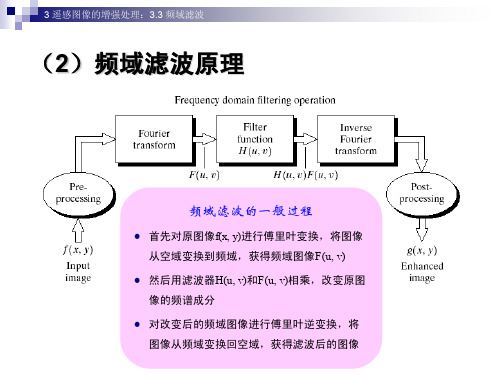
3 遥感图像的增强处理:3.3 频域滤波
power=100% cut-off=40, power=99.98% cut-off=38, power=99.98% cut-off=36, power=99.98% cut-off=34, power=99.98%
cut-off=49, power=99.18%
cut-off=45, power=99.04%
cut-off=41, power=98.88%
cut-off=37, power=98.67%
cut-off=33, power=98.41%
cut-off=29, power=98.06%
cut-off=25, power=97.6
Smoothing with a Gaussian
3 遥感图像的增强处理:3.3 频域滤波
The Gaussian pyramid
3 遥感图像的增强处理:3.3 频域滤波
Character recognition
using a GLPF with D0 80
• Although humans fill these gaps visually without difficulty, • A machine recognition system has real difficulties reading broken characters.
3 遥感图像的增强处理:3.3 频域滤波
the average value of the resulting image will be zero make prominent edges stand out pixels which have negative values will be produced
空域滤波和频域滤波的关系

空域滤波和频域滤波的关系空域滤波是指对图像的像素进行直接操作,通过改变像素的数值来达到滤波的目的。
常见的空域滤波方法包括均值滤波、中值滤波和高斯滤波等。
这些方法主要是通过对像素周围的邻域进行计算,然后用计算结果替代中心像素的值,从而达到平滑图像、去噪或者增强图像细节等效果。
空域滤波是一种直观简单的滤波方法,易于理解和实现。
频域滤波则是将图像从空域转换到频域进行滤波处理。
频域滤波基于图像的频谱特性,通过对图像的频率分量进行调整来实现滤波效果。
频域滤波的基本原理是将图像进行傅里叶变换,将图像从空间域转换到频率域,然后在频率域对图像进行滤波处理,最后再将图像进行傅里叶反变换,将图像从频率域转换回空间域。
常见的频域滤波方法包括低通滤波、高通滤波和带通滤波等。
频域滤波可以有效地去除图像中的噪声、增强图像的细节和边缘等。
空域滤波和频域滤波是两种不同的滤波方法,它们在滤波原理和实现方式上存在一定的差异。
空域滤波是直接对图像像素进行操作,易于理解和实现,但在处理复杂图像时会存在一定的局限性。
频域滤波则是将图像转换到频率域进行处理,可以更加灵活地调整图像的频率特性,适用于处理复杂图像和去除特定频率的噪声。
虽然空域滤波和频域滤波有着不同的原理和实现方式,但它们之间并不是相互独立的。
事实上,这两种滤波方法是可以相互转换和组合的。
在一些实际应用中,我们可以将频域滤波和空域滤波结合起来,通过先对图像进行傅里叶变换,然后在频率域对图像进行滤波处理,最后再将图像进行傅里叶反变换,将图像从频率域转换回空间域。
这种组合使用的方法可以充分发挥两种滤波方法的优势,既可以处理复杂图像,又能够简化计算和提高效率。
空域滤波和频域滤波是数字图像处理中常用的滤波方法。
空域滤波直接对图像像素进行操作,简单直观;频域滤波则是将图像转换到频率域进行处理,更加灵活精确。
虽然它们有着不同的原理和实现方式,但可以相互转换和组合使用,以提高图像处理的效果和质量。
数字图像处理-频域滤波-高通低通滤波

数字图像处理-频域滤波-⾼通低通滤波频域滤波频域滤波是在频率域对图像做处理的⼀种⽅法。
步骤如下:滤波器⼤⼩和频谱⼤⼩相同,相乘即可得到新的频谱。
滤波后结果显⽰,低通滤波去掉了⾼频信息,即细节信息,留下的低频信息代表了概貌。
常⽤的例⼦,⽐如美图秀秀的磨⽪,去掉了脸部细节信息(痘坑,痘印,暗斑等)。
⾼通滤波则相反。
⾼通/低通滤波1.理想的⾼/低通滤波顾名思义,⾼通滤波器为:让⾼频信息通过,过滤低频信息;低通滤波相反。
理想的低通滤波器模板为:其中,D0表⽰通带半径,D(u,v)是到频谱中⼼的距离(欧式距离),计算公式如下:M和N表⽰频谱图像的⼤⼩,(M/2,N/2)即为频谱中⼼理想的⾼通滤波器与此相反,1减去低通滤波模板即可。
部分代码:# 定义函数,显⽰滤波器模板def showTemplate(template):temp = np.uint8(template*255)cv2.imshow('Template', temp)return# 定义函数,显⽰滤波函数def showFunction(template):row, col = template.shaperow = np.uint16(row/2)col = np.uint16(col/2)y = template[row, col:]x = np.arange(len(y))plt.plot(x, y, 'b-', linewidth=2)plt.axis([0, len(x), -0.2, 1.2])plt.show()return# 定义函数,理想的低通/⾼通滤波模板def Ideal(src, d0, ftype):template = np.zeros(src.shape, dtype=np.float32) # 构建滤波器 r, c = src.shapefor i in range(r):for j in range(c):distance = np.sqrt((i - r/2)**2 + (j - c/2)**2)if distance < d0:template[i, j] = 1else:template[i, j] = 0if ftype == 'high':template = 1 - templatereturn templateIdeal2. Butterworth⾼/低通滤波Butterworth低通滤波器函数为:从函数图上看,更圆滑,⽤幂系数n可以改变滤波器的形状。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验六:图像的频域滤波姓名:朱永祥学号20171170238 得分:一、实验目的:1、掌握傅立叶变换及逆变换的基本原理方法。
2、理解频域滤波的基本原理及方法。
3、掌握进行图像的频域滤波的方法。
二、实验内容与要求:1、傅立叶变换(1)读出woman.tif这幅图像,对其进行快速傅立叶变换,分别显示其幅度图像和相位图像。
仅对相位部分进行傅立叶反变换后查看结果图像。
(2)仅对幅度部分进行傅立叶反变换后查看结果图像。
(3)将图像的傅立叶变换F置为其共轭后进行反变换,比较新生成图像与原始图像的差异。
2、平滑频域滤波(1)设计理想低通滤波器、巴特沃斯低通滤波器和高斯低通滤波器,截至频率自选,分别给出各种滤波器的透视图。
(2)读出test_pattern.tif这幅图像,分别采用理想低通滤波器、巴特沃斯低通滤波器和高斯低通滤波器对其进行滤波(截至频率自选),再做反变换,观察不同的截止频率下采用不同低通滤波器得到的图像与原图像的区别,特别注意振铃效应。
(提示:1)在频率域滤波同样要注意到填充问题;2)注意到(-1)x+y;)3、锐化频域滤波(1)设计理想高通滤波器、巴特沃斯高通滤波器和高斯高通滤波器,截至频率自选,分别给出各种滤波器的透视图。
(2)读出test_pattern.tif这幅图像,分别采用理想高通滤波器、巴特沃斯高通滤波器和高斯高通滤波器对其进行滤波(截至频率自选),再做反变换,观察不同的截止频率下采用不同高通滤波器得到的图像与原图像的区别。
三、实验代码及结果:1、(1)a、实验代码:>> img=imread('C:\Users\xxdn\Desktop\图片1.png');>> img=rgb2gray(img);>> f1=fft2(img);>> f2=log(1+abs(f1));>> f3=fftshift(f1);>> f4=angle(f1);>>figure,subplot(1,3,1),imshow(img),title('Original Image'); subplot(1,3,2),imshow(log(1+abs(f3)),[]),title('amplitude spectrum'); subplot(1,3,3),imshow(f4),title('phase spectrum');>> i=sqrt(-1);>> f5=ifft(exp(i*angle(f1)));>> imshow(real(f5),[]);>> imshow(real(f5),[]),title('Phasw-based Restoration Image');B、实验结果:(2)a、实验代码:>> f=ifft2(abs(f1));>> imshow(log(1+abs(f)),[]),title('absamplitude spectrum');b、实验结果:(3)a、实验代码:>> f6=conj(f1);>> f7=ifft2(f6);>> imshow(f7,[]),title('inverse fourier transform');b、实验结果:2、(1)a、实验代码:>> %%%%%%%%%%%%%%%%%%%理想低通滤波器的透视图%%%%%>> a=100;>> b=100;>> U=0:a;>> V=0:b;>> M=length(U);N=length(V);>> D0=10;>> x1=50;y1=50;>> x0=-50;y0=-50;>> m=fix(M/2); n=fix(N/2);>> H=zeros(M,N);>> n=2;>> for u=1:Mfor v=1:Na=sqrt((U(u) - 50) .* (U(u)-50) + (V(v) - 50) .* (V(v) - 50));if(a<=D0)%理想滤波器H(u,v)=1;elseH(u,v)=0;endendend>>surf(U,V,H),title('理想低通滤波透视图') ;>> %%%%%%%%%%%%2 阶巴特沃斯低通滤波透视图%%%%%%%%%%%%%%%%55>> a=100;>> b=100;>> U=0:a;>> V=0:b;>> M=length(U);N=length(V);>> D0=10;>> x1=50;>> y1=50;>> x0=-50;>> y0=-50;>> m=fix(M/2);>> n=fix(N/2);>> H=zeros(M,N);>> n=2;>> for u=1:Mfor v=1:Na=sqrt((U(u) - 50) .* (U(u)-50) + (V(v) - 50) .* (V(v) - 50));b=1+(a/D0)^2*n;H(u,v)=1/b;endend>>surf(U,V,H),title('n=2 Butterworth lowess filter');>> %%%%%%%%%%%%%%%%%%%%%%高斯低通滤波%%%%%%%%%%%%%%%%%%%%%>> a=100;>> b=100;>> U=0:a;>> V=0:b;>> M=length(U);N=length(V);>> D0=10;>> x1=50;>> y1=50;>> x0=-50;>> y0=-50;>> m=fix(M/2);>> n=fix(N/2);>> H=zeros(M,N);>> for u=1:Mfor v=1:ND1=((u-m-x0)^2+(v-n-y0).^2)^0.5;D2=((u-m+x0)^2+(v-n+y0).^2)^0.5;D11=((u-m-x1)^2+(v-n-y1).^2)^0.5;D21=((u-m+x1)^2+(v-n+y1).^2)^0.5;H(u,v) = (U(u) - 50) .* (U(u)-50) + (V(v) - 50) .* (V(v)- 50); endend>> S=50;>> H = -H/(2*S);>> H = exp(H) / (sqrt(2*pi) * sqrt(S));>> surf(U,V,H),title('Gaussian lowess filter');b、实验结果:(2)a、实验代码:%理想低通滤波>> img=imread('C:\Users\xxdn\Desktop\test_pattern.tif'); >> img=rgb2gray(img);>> f=double(img);>> g=fft2(f);>> g=fftshift(g);>> [M,N]=size(g);>> d0=15;>> m=fix(M/2);>> n=fix(N/2);>> for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);if(d<=d0)h=1;elseh=0;endresult(i,j)=h*g(i,j);endend>> result=ifftshift(result);>> J1=ifft2(result);>> J2=uint8(real(J1));>>figure,subplot(1,2,1),imshow(img),title('Original Image'); subplot(1,2,2),imshow(J2),title('d0=15 lowpss filter');>> d0=30;>> m=fix(M/2);>> n=fix(N/2);>> for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);if(d<=d0)h=1;elseh=0;endresult(i,j)=h*g(i,j);endend>> result=ifftshift(result);>> J1=ifft2(result);>> J2=uint8(real(J1));>> imshow(J2),title('d0=30 lowpss filter');>> d0=100;>> m=fix(M/2);n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);if(d<=d0)h=1;elseh=0;endresult(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));imshow(J2),title('d0=100 lowpss filter');>> %2 阶巴特沃斯低通滤波>> nn=2;>> d0=15;>> m=fix(M/2);>>n=fix(N/2);>> for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=1/(1+0.414*(d/d0)^(2*nn));result(i,j)=h*g(i,j);endend>> result=ifftshift(result);>> J1=ifft2(result);>> J2=uint8(real(J1));>> figure,subplot(1,2,1),imshow(img),title('Original Image'); subplot(1,2,2),imshow(J2),title('d0=15 Butterworth lowpss filter');>> %%%%%%%%d0=30 的巴特沃斯低通滤波%%%%%%%%%%%%%%% >> d0=30;>> m=fix(M/2);>>n=fix(N/2);>> for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=1/(1+0.414*(d/d0)^(2*nn));result(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));>> imshow(J2),title('d0=30 Butterworth lowpss filter');>> %%%%%%%%d0=100 的巴特沃斯低通滤波%%%%%%%%%%%%%%%d0=100;>> d0=100;>> m=fix(M/2);>>n=fix(N/2);>> for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=1/(1+0.414*(d/d0)^(2*nn));result(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));>> imshow(J2),title('d0=100 Butterworth lowpss filter');%高斯低通滤波d0=15;>> m=fix(M/2);>>n=fix(N/2);>> for i=1:M>> for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=exp(-(d.^2)./(2*(d0^2)));result(i,j)=h*g(i,j);endend>> result=ifftshift(result);>> J1=ifft2(result);>> J2=uint8(real(J1));subplot(1,2,1),imshow(img),title('Original Image'); subplot(1,2,2),imshow(J2),title('d0=15 Gaussian filter');>> %%%%%%%%d0=30 的高斯低通滤波%%%%%%%%%%%%%%% >> d0=30;>> m=fix(M/2);>>n=fix(N/2);>> for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=exp(-(d.^2)./(2*(d0^2)));result(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));imshow(J2),title('d0=30 Gaussian filter');>> %%%%%%%%d0=100 的高斯低通滤波%%%%%%%%%%%%%%% >> d0=100;>> m=fix(M/2);>>n=fix(N/2);>> for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=exp(-(d.^2)./(2*(d0^2)));result(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));imshow(J2),title('d0=100 Gaussian filter');3、(1)a、实验代码:>> %%%%%%%%%%%%%%%%理想高通滤波器%%%%%%%%%%%%%%%%%%%%%%%%%%%>> a=100;>> b=100;>> U=0:a;>> V=0:b;>> M=length(U);N=length(V);>> D0=15;>> H=zeros(M,N);>> n=2;>> for u=1:Mfor v=1:Na=sqrt((U(u)-50).*(U(u)-50)+(V(v)-50).*(V(v)-50));if(a>=D0)H(u,v)=1;elseH(u,v)=0;endendend>> surf(U,V,H),title('理想高通滤波透视图') ;>> %%%%%%%%%%%%%%%巴特沃斯高通滤波器%%%%%%%%%%%%%%%%%%%%%%%%>> a=100;b=100;U=0:a;V=0:b;M=length(U);N=length(V);D0=15;>> x1=50;>> y1=50;>> x0=-50;>> y0=-50;>> m=fix(M/2);>> n=fix(N/2);>> H=zeros(M,N);>> n=2;>> for u=1:Mfor v=1:Na=sqrt((U(u) - 50) .* (U(u)-50) + (V(v) - 50) .* (V(v) - 50));b=1+(a/D0)^2*n;H(u,v)=-1/b;endend>> surf(U,V,H),title('n=2 Butterworth high filter')>> %%%%%%%%%%%%%%高斯高通滤波>> a=100;b=100;U=0:a;V=0:b;M=length(U);N=length(V);D0=15;x1=50;y1=50;x0=-50;y0=-50;m=fix(M/2);n=fix(N/2);H=zeros(M,N);>> for u=1:Mfor v=1:ND1=((u-m-x0)^2+(v-n-y0).^2)^0.5;D2=((u-m+x0)^2+(v-n+y0).^2)^0.5;D11=((u-m-x1)^2+(v-n-y1).^2)^0.5;D21=((u-m+x1)^2+(v-n+y1).^2)^0.5;H(u,v) = (U(u) - 50) .* (U(u)-50) + (V(v) - 50) .* (V(v) - 50);endend>> S=50;>> H = -H/(2*S);>> H =- exp(H) / (sqrt(2*pi) * sqrt(S));>> surf(U,V,H),title('Gaussian high filter');(2)a、实验代码:>> img=imread('C:\Users\xxdn\Desktop\test_pattern.tif'); >> img=rgb2gray(img);>> f=double(img);>> g=fft2(f);>> g=fftshift(g);>> [M,N]=size(g);>> d0=15;>> m=fix(M/2);>> n=fix(N/2);>> for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);if(d>=d0)h=1;elseh=0;endresult(i,j)=h*g(i,j);endend>> result=ifftshift(result);>> J1=ifft2(result);>> J2=uint8(real(J1));>> subplot(1,2,1),imshow(img),title('Original Image'),subplot(1,2,2),imshow(J2),title('d0=15 high filter');>> d0=30;>> m=fix(M/2);n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);if(d>=d0)h=1;elseh=0;endresult(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));>> imshow(J2),title('d0=30 high filter');>> d0=80;>> m=fix(M/2);n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);if(d>=d0)h=1;elseh=0;endresult(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));>> imshow(J2),title('d0=80 high filter');>> %巴特沃斯高通滤波>> img=imread('C:\Users\xxdn\Desktop\test_pattern.tif'); img=rgb2gray(img);f=double(img);g=fft2(f);g=fftshift(g);[M,N]=size(g);>> img=imread('C:\Users\xxdn\Desktop\test_pattern.tif'); >> img=rgb2gray(img);>> f=double(img);>> g=fft2(f);>> g=fftshift(g);>> [M,N]=size(g);>> nn=2;>> d0=15;>> m=fix(M/2);>> n=fix(N/2);>> for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);if(d==0)h=0;elseh=1/(1+0.414*(d0/d)^(2*nn));endresult(i,j)=h*g(i,j);endend>> result=ifftshift(result);>> J1=ifft2(result);>> J2=uint8(real(J1));>> subplot(1,2,1),imshow(img),title('Original Image'),subplot(1,2,2),imshow(J2),title('d0=15 Butterworth high filter');>> d0=30;>> m=fix(M/2);n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);if(d==0)h=0;elseh=1/(1+0.414*(d0/d)^(2*nn));endresult(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));>> imshow(J2),title('d0=30 Butterworth high filter');>> d0=80;>> m=fix(M/2);n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);if(d==0)h=0;elseh=1/(1+0.414*(d0/d)^(2*nn));endresult(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));imshow(J2),title('d0=80 Butterworth high filter');>> %高斯高通滤波器>> img=imread('C:\Users\xxdn\Desktop\test_pattern.tif'); >> img=rgb2gray(img);>> f=double(img);>> g=fft2(f);>> g=fftshift(g);>> [M,N]=size(g);>> n=2;>> d0=15;>> m=fix(M/2);>> n=fix(N/2);>> for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=1-exp(-(d.^2)./(2*(d0^2)));result(i,j)=h*g(i,j);endend>> result=ifftshift(result);>> J1=ifft2(result);>> subplot(1,2,1),imshow(img),title('Original Image'), subplot(1,2,2),imshow(J2),title('d0=15 Gaussian filter');>>>> d0=30;>> m=fix(M/2);n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=1-exp(-(d.^2)./(2*(d0^2)));result(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));>> imshow(J2),title('d0=30 Gaussian filter');>> d0=80;>> m=fix(M/2);n=fix(N/2);for i=1:Mfor j=1:Nd=sqrt((i-m)^2+(j-n)^2);h=1-exp(-(d.^2)./(2*(d0^2)));result(i,j)=h*g(i,j);endendresult=ifftshift(result);J1=ifft2(result);J2=uint8(real(J1));imshow(J2),title('d0=80 Gaussian filter');三、实验结论:1、当频带中心宽度相同时,理想低通滤波器为圆柱形图像,二阶巴特沃斯低通滤波器的面线比较紧凑,高斯滤波图像最为平滑;2、理想低通滤波器截止频率d0=15 时,滤波后的图像比较模糊,振铃现象也很明显;当d0=30 时,图像模糊程度减弱,振铃现象仍存在。
