九年级数学相似相似三角形测试题

合集下载

人教版九年级下册数学 27.2相似三角形同步练习(含解析)

27.2相似三角形同步练习一．选择题1．如图，△ABC∽△DCA，∠B＝33°，∠D＝117°，则∠BAD的度数是（）A．150°B．147°C．135°D．120°2．两个相似三角形对应角平分线的比为4：3，那么这两个三角形的面积的比是（）A．2：3B．4：9C．16：36D．16：93．下列条件中，不能判断△ABC与△DEF相似的是（）A．∠A＝∠D，∠B＝∠F B．且∠B＝∠DC．D．且∠A＝∠D4．如图，在△ABC中，点D、E分别在边AB、AC上，下列条件中能判断△ABC∽△AED 的是（）①∠AED＝∠B；②∠ADE＝∠C；③＝；④＝．A．①②B．①②③C．①②④D．①②③④5．如图，在平行四边形ABCD中，点E在边DC上，DE：EC＝5：2，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（）A．5：7B．10：4C．25：4D．25：496．已知点E、F分别在△ABC的AB、AC边上，则下列判断正确的是（）A．若△AEF与△ABC相似，则EF∥BCB．若AE×BE＝AF×FC，则△AEF与△ABC相似C．若，则△AEF与△ABC相似D．若AF•BE＝AE•FC，则△AEF与△ABC相似7．如图，在△ABC，D是BC上一点，BD：CD＝1：2，E是AD上一点，DE：AE＝1：2，连接CE，CE的延长线交AB于F，则AF：AB为（）A．1：2B．2：3C．4：3D．4：78．如图，在▱ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则△DEF与四边形EFCO的面积比为（）A．1：4B．1：5C．1：6D．1：79．如图，AD∥BC，∠D＝90°，AD＝3，BC＝4，DC＝6，若在边DC上有点P，使△P AD 与△PBC相似，则这样的点P有（）A．1 个B．2 个C．3 个D．4 个10．如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于F，连接DF，若BF＝，BC ＝3，则DF＝（）A．4B．3C．2D．二．填空题11．已知△ABC∽△A′B′C′，且AB＝3cm，A′B′＝5cm，则相似比为．12．如图，△ABC中，CA＝CB，点E在BC边上，点D在AC边上，连接AE、DE，若AB ＝AE，2∠AEB+∠ADE＝180°，BE＝8，CD＝，则CE＝．13．如图，在△ABC中，若DE∥BC，EF∥CD，AE＝2EC，则AF：FD：DB＝．14．如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S△DOE：S△COA＝1：25，则的值是．15．如图，在矩形ABCD中，AD＝2，AB＝4，E、F分别是AB、CD边上的动点，EF⊥AC，则AF+CE的最小值为．三．解答题16．如图，点P是菱形ABCD的对角线AC上一点，连接DP并延长，交AB于点F，交CB 的延长线于点E．求证：（1）△APB≌△APD；（2）PD2＝PE•PF．17．如图，在△ABC中，点D、E分别在AB、AC上，DE、BC的延长线相交于点F，且EF•DF＝CF•BF．求证：△CAB∽△DAE．18．如图，AF，AG分别是△ABC和△ADE的高，∠BAF＝∠DAG．（1）求证：△ABC∽△ADE；（2）若DE＝3，，求BC的长．参考答案一．选择题1．解：∵△ABC∽△DCA，∴∠BAC＝∠D＝117°，∠DAC＝∠B＝33°，∴∠BAD＝∠BAC+∠DAC＝150°，故选：A．2．解：∵两个相似三角形对应角平分线的比为4：3，∴它们的相似比为4：3，∴它们的面积比为16：9．故选：D．3．解：A、∠A＝∠D，∠B＝∠F，可以得出△ABC∽△DFE，故此选项不合题意；B、＝且∠B＝∠D，不是两边成比例且夹角相等，故此选项符合题意；C、＝＝，可以得出△ABC∽△DEF，故此选项不合题意；D、＝且∠A＝∠D，可以得出△ABC∽△DEF，故此选项不合题意；故选：B．4．解：∵∠A＝∠A，∴∠AED＝∠B或∠ADE＝∠C时，△ABC∽△AED．∵＝，∴＝∵∠A＝∠A，∴△ABC∽△AED，故①②③可以判断三角形相似，故选：B．5．解：设DE＝5k，EC＝2k，则CD＝7k，∵四边形ABCD是平行四边形，∴AB＝CD＝7k，DE∥AB，∴△DEF∽△BAF，∴＝＝＝，故选：D．6．解：选项A错误，∵△AEF与△ABC相似，可能是∠AEF＝∠C，推不出EF∥BC．选项B错误，由AE×BE＝AF×FC，推不出△AEF与△ABC相似．选项C错误，由，推不出△AEF与△ABC相似．选项D正确．理由：∵AF•BE＝AE•FC，∴＝，∴EF∥BC，∴△AEF∽△ABC．故选：D．7．解：过D作DH∥AB交CF于H，如图，∵DH∥BF，∴＝，∵BD：CD＝1：2，∴CD：BC＝2：3，∴BF＝DH，∵DH∥AF，∴＝＝2，∴AF＝2DH，∴AF：BF＝2DH：DH＝4：3，∴AF：AB＝4：7．故选：D．8．解：∵四边形ABCD是平行四边形，∴BO＝DO，AB∥CD，∵E为OD的中点，∴DE＝EO＝DO，∴BO＝2EO，BE＝3DE，∵DF∥AB，∴△DFE∽△BAE，∴＝（）2＝，设S△DEF＝x，则S△BEA＝9x，∵BO＝2OE，∴S△AOB＝6x＝S△DOC，∴四边形EFCO的面积＝5x，∴△DEF与四边形EFCO的面积比＝1：5，故选：B．9．解：∵AB⊥BC，∴∠B＝90°．∵AD∥BC∴∠A＝180°﹣∠B＝90°，∴∠P AD＝∠PBC＝90°．设DP的长为x，则CP长为6﹣x．若AB边上存在P点，使△P AD与△PBC相似，那么分两种情况：①若△APD∽△BPC，则DP：CP＝AD：BC，即x：（6﹣x）＝3：4，解得：x＝②若△APD∽△BPC，则DP：PC＝AD：BC，即x：4＝3：（6﹣x），整理得：x2﹣6x+12＝0，∵△＜0，这种情形不存在，∴满足条件的点P的个数是1个，故选：A．10．解：如图，连接BD，∵∠AEF＝∠BEA，∠AFE＝∠BAE＝90°，∴△AEF∽△BEA，∴＝，∵AE＝ED，∴＝，又∵∠FED＝∠DEB，∴△FED∽△DEB，∴∠EFD＝∠EDB，∵∠EFD+∠DFC＝90°，∠EDB+∠ODC＝90°，∴∠DFC＝∠ODC，∵在矩形ABCD中，OC＝AC，OD＝BD，AC＝BD，∴OD＝OC，∴∠OCD＝∠ODC，∴∠DFC＝∠OCD，∴DF＝DC，在Rt△BCF中，FC＝＝＝2，∵AD∥BC，∴△AEF∽△CBF，∴＝＝，∴AF＝FC＝，∴AB＝＝＝3，∴DF＝3，故选：B．二．填空题11．解：由题意得，＝，∵△ABC∽△A′B′C′，∴△ABC与△A′B′C′的相似比为＝，故答案为：．12．解：如图，过点A作AM⊥BE于E，过点D作DN⊥EC于N，∵CA＝CB，AB＝AE，∴∠B＝∠CAB，∠B＝∠AEB，∴∠B＝∠CAB＝∠AEB，∵∠B+∠BAC+∠C＝180°，∠B+∠AEB+∠BAE＝180°，∴∠C＝∠BAE，∴2∠AEB+∠C＝180°，又∵2∠AEB+∠ADE＝180°，∴∠C＝∠ADE，又∵∠ADE＝∠C+∠DEC，∴∠C＝∠DEC，∴DE＝DC＝，∵AB＝AE，AM⊥BE，DE＝CC，DN⊥EC，∴BM＝ME＝BE＝4，EN＝NC＝EC，AM∥DN，∴△CDN∽△CAM，∴，∴，∴EC＝12，EC＝﹣5（不合题意舍去），故答案为：12．13．解：∵EF∥CD，AE＝2EC，∴＝＝2，∵DE∥BC，∴＝＝2，设DF＝m，则AF＝2m，AD＝3m，DB＝m，∴AF：DF：DB＝2m：m：m＝4：2：3．故答案为：4：2：3．14．解：∵DE∥AC，∴△DOE∽△COA，∴＝（）2＝，∴＝，∵DE∥AC，∴△BDE∽△BAC，∴＝，∴＝，故答案为：．15．解：如图所示：设DF＝x，则FC＝4﹣x；过点C作CG∥EF，且CG＝EF，连接FG，当点A、F、G三点共线时，AF+FG的最值小；∵CG∥EF，且CG＝EF，∴四边形CEFG是平行四边形；∴EC∥FG，EC＝FG，又∵点A、F、G三点共线，∴AF∥EC，又∵四边形ABCD是矩形，∴AE∥DC，∠D＝90°，∴四边形AECF是平行四边形，∴OA＝OC，OE＝OF，又∵EF⊥AC，AF＝CF＝4﹣x，在Rt△ADF中，由勾股定理得：AD2+DF2＝AF2，又∵AD＝2，DF＝x，则FC＝4﹣x，∴22+x2＝（4﹣x）2，解得：x＝，∴AF＝，在Rt△ADC中，由勾股定理得：AD2+DC2＝AC2，∴AC＝，∴AO＝，又∵OF∥CG，∴△AOF∽△ACG，∴＝，∴AG＝5，又∵AG＝AF+FG，FG＝EC，∴AF+EC＝5，故答案为5．三．解答题16．证明：（1）∵四边形ABCD是菱形，∴AB＝AD，∠BAC＝∠DAC，在△ABP和△ADP中，，∴△ABP≌△ADP（SAS）；（2）∵△ABP≌△ADP，∴PB＝PD，∠ADP＝∠ABP，∵AD∥BC，∴∠ADP＝∠E，∴∠E＝∠ABP，又∵∠FPB＝∠EPB，∴△EPB∽△BPF，∴，∴PB2＝PE•PF，∴PD2＝PE•PF．17．证明：∵EF•DF＝CF•BF．∴，∵∠EFC＝∠BFD，∴△EFC∽△BFD，∴∠CEF＝∠B，∴∠B＝∠AED，∵∠CAB＝∠DAE，∴△CAB∽△DAE．18．（1）证明：∵AF，AG分别是△ABC和△ADE的高，∴AF⊥BC，AG⊥DE，∴∠AFB＝90°，∠AGD＝90°，∴∠BAF+∠B＝90°，∠DAG+∠ADG＝90°，∵∠BAF＝∠DAG，∴∠B＝∠ADG，又∵∠EAD＝∠BAC，∴△ABC∽△ADE；（2）解：∵△ADE∽△ABC，∴，∵，BC＝3，∴，∴BC＝．。

人教版九年级数学下册第二十七章《相似——相似三角形》同步测试含答案

人教版九年级数学下册第二十七章《相似——相似三角形》同步测试题一．选择题（共10小题）1．（2013•自贡）如图，在平行四边形ABCD中，AB=6，AD=9，∠BAD的平分线交BC于E，交DC的延长线于F，BG⊥AE于G，BG=，则△EFC的周长为（）A．11 B．10 C．9D．82．（2013•重庆）如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE=2ED，CD=3cm，则AF的长为（）A．5cm B．6cm C．7cm D．8cm 3．（2013•孝感）如图，在△ABC中，AB=AC=a，BC=b（a＞b）．在△ABC内依次作∠CBD=∠A，∠DCE=∠CBD，∠EDF=∠DCE．则EF等于（）A．B．C．D．4．（2013•咸宁）如图，正方形ABCD是一块绿化带，其中阴影部分EOFB，GHMN都是正方形的花圃．已知自由飞翔的小鸟，将随机落在这块绿化带上，则小鸟在花圃上的概率为（）A．B．C．D．5．（2013•绥化）如图，点A，B，C，D为⊙O上的四个点，AC平分∠BAD，AC交BD于点E，CE=4，CD=6，则AE的长为（）A．4B．5C．6D．76．（2013•内江）如图，在▱ABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，S△DEF：S△ABF=4：25，则DE：EC=（）A．2：5 B．2：3 C．3：5 D．3：27．（2013•黑龙江）如图，在直角梯形ABCD中，AD∥BC，∠BCD=90°，∠ABC=45°，AD=CD，CE平分∠ACB交AB于点E，在BC上截取BF=AE，连接AF交CE于点G，连接DG交AC于点H，过点A作AN⊥BC，垂足为N，AN交CE于点M．则下列结论；①CM=AF；②CE⊥AF；③△ABF∽△DAH；④GD平分∠AGC，其中正确的个数是（）A．1B．2C．3D．48．（2013•恩施州）如图所示，在平行四边形ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则DF：FC=（）A．1：4 B．1：3 C．2：3 D．1：2 9．（2013•德阳）如图，在⊙O上有定点C和动点P，位于直径AB的异侧，过点C作CP 的垂线，与PB的延长线交于点Q，已知：⊙O半径为，tan∠ABC=，则CQ的最大值是（）A．5B．C．D．10．（2012•岳阳）如图，AB为半圆O的直径，AD、BC分别切⊙O于A、B两点，CD切⊙O于点E，AD与CD相交于D，BC与CD相交于C，连接OD、OC，对于下列结论：①OD2=DE•CD；②AD+BC=CD；③OD=OC；④S梯形ABCD=CD•OA；⑤∠DOC=90°，其中正确的是（）A．①②⑤B．②③④C．③④⑤D．①④⑤二．填空题（共10小题）11．（2013•昭通）如图，AB是⊙O的直径，弦BC=4cm，F是弦BC的中点，∠ABC=60°．若动点E以1cm/s的速度从A点出发在AB上沿着A→B→A运动，设运动时间为t（s）（0≤t ＜16），连接EF，当△BEF是直角三角形时，t（s）的值为_________．（填出一个正确的即可）12．（2013•南通）如图，在▱ABCD中，AB=6cm，AD=9cm，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=4cm，则EF+CF的长为_________ cm．13．（2013•菏泽）如图所示，在△ABC中，BC=6，E、F分别是AB、AC的中点，动点P 在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当CQ=CE时，EP+BP=_________．14．（2013•巴中）如图，小明在打网球时，使球恰好能打过网，而且落在离网4米的位置上，则球拍击球的高度h为_________．15．（2012•自贡）正方形ABCD的边长为1cm，M、N分别是BC、CD上两个动点，且始终保持AM⊥MN，当BM=_________cm时，四边形ABCN的面积最大，最大面积为_________cm2．16．（2012•宜宾）如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是的中点，弦CE⊥AB于点F，过点D的切线交EC的延长线于点G，连接AD，分别交CF、BC于点P、Q，连接AC．给出下列结论：①∠BAD=∠ABC；②GP=GD；③点P是△ACQ的外心；④AP•AD=CQ•CB．其中正确的是_________（写出所有正确结论的序号）．17．（2012•泉州）在△ABC中，P是AB上的动点（P异于A、B），过点P的直线截△ABC，使截得的三角形与△ABC相似，我们不妨称这种直线为过点P的△ABC的相似线，简记为P（l x）（x为自然数）．（1）如图①，∠A=90°，∠B=∠C，当BP=2PA时，P（l1）、P（l2）都是过点P的△ABC 的相似线（其中l1⊥BC，l2∥AC），此外，还有_________条；（2）如图②，∠C=90°，∠B=30°，当=_________时，P（l x）截得的三角形面积为△ABC面积的．18．（2012•嘉兴）如图，在Rt△ABC中，∠ABC=90°，BA=BC．点D是AB的中点，连接CD，过点B作BG丄CD，分别交CD、CA于点E、F，与过点A且垂直于AB的直线相交于点G，连接DF．给出以下四个结论：①；②点F是GE的中点；③AF=AB；④S△ABC=5S△BDF，其中正确的结论序号是_________．19．（2012•泸州）如图，n个边长为1的相邻正方形的一边均在同一直线上，点M1，M2，M3，…M n分别为边B1B2，B2B3，B3B4，…，B n B n+1的中点，△B1C1M1的面积为S1，△B2C2M2的面积为S2，…△B n C n M n的面积为S n，则S n=_________．（用含n的式子表示）20．（2013•荆州）如图，△ABC是斜边AB的长为3的等腰直角三角形，在△ABC内作第1个内接正方形A1B1D1E1（D1、E1在AB上，A1、B1分别在AC、BC上），再在△A1B1C 内接同样的方法作第2个内接正方形A2B2D2E2，…如此下去，操作n次，则第n个小正方形A n B n D n E n的边长是_________．三．解答题（共8小题）21．（2013•珠海）如图，在Rt△ABC中，∠C=90°，点P为AC边上的一点，将线段AP绕点A顺时针方向旋转（点P对应点P′），当AP旋转至AP′⊥AB时，点B、P、P′恰好在同一直线上，此时作P′E⊥AC于点E．（1）求证：∠CBP=∠ABP；（2）求证：AE=CP；（3）当，BP′=5时，求线段AB的长．22．（2013•湛江）如图，已知AB是⊙O的直径，P为⊙O外一点，且OP∥BC，∠P=∠BAC．（1）求证：PA为⊙O的切线；（2）若OB=5，OP=，求AC的长．23．（2013•宜宾）如图，AB是⊙O的直径，∠B=∠CAD．（1）求证：AC是⊙O的切线；（2）若点E是的中点，连接AE交BC于点F，当BD=5，CD=4时，求AF的值．24．（2013•襄阳）如图，△ABC内接于⊙O，且AB为⊙O的直径．∠ACB的平分线交⊙O 于点D，过点D作⊙O的切线PD交CA的延长线于点P，过点A作AE⊥CD于点E，过点B作BF⊥CD于点F．（1）求证：DP∥AB；（2）若AC=6，BC=8，求线段PD的长．25．（2013•绍兴）在△ABC中，∠CAB=90°，AD⊥BC于点D，点E为AB的中点，EC与AD交于点G，点F在BC上．（1）如图1，AC：AB=1：2，EF⊥CB，求证：EF=CD．（2）如图2，AC：AB=1：，EF⊥CE，求EF：EG的值．26．（2013•汕头）如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，AB=12，BC=5，BE⊥DC交DC的延长线于点E．（1）求证：∠BCA=∠BAD；（2）求DE的长；（3）求证：BE是⊙O的切线．27．（2013•朝阳）如图，直线AB与⊙O相切于点A，直径DC的延长线交AB于点B，AB=8，OB=10（1）求⊙O的半径．（2）点E在⊙O上，连接AE，AC，EC，并且AE=AC，判断直线EC与AB有怎样的位置关系？并证明你的结论．（3）求弦EC的长．28．（2013•成都）如图，点B在线段AC上，点D，E在AC同侧，∠A=∠C=90°，BD⊥BE，AD=BC．（1）求证：AC=AD+CE；（2）若AD=3，CE=5，点P为线段AB上的动点，连接DP，作PQ⊥DP，交直线BE于点Q；（i）当点P与A，B两点不重合时，求的值；（ii）当点P从A点运动到AC的中点时，求线段DQ的中点所经过的路径（线段）长．（直接写出结果，不必写出解答过程）参考答案与解析一．选择题（共10小题）1．（2013•自贡）如图，在平行四边形ABCD中，AB=6，AD=9，∠BAD的平分线交BC于E，交DC的延长线于F，BG⊥AE于G，BG=，则△EFC的周长为（）A．11 B．10 C．9D．8考点：相似三角形的判定与性质；勾股定理；平行四边形的性质．分析：判断出△ADF是等腰三角形，△ABE是等腰三角形，DF的长度，继而得到EC的长度，在Rt△BGE中求出GE，继而得到AE，求出△ABE的周长，根据相似三角形的周长之比等于相似比，可得出△EFC的周长．解答：解：∵在▱ABCD中，AB=CD=6，AD=BC=9，∠BAD的平分线交BC于点E，∴∠BAF=∠DAF，∵AB∥DF，AD∥BC，∴∠BAF=∠F=∠DAF，∠BAE=∠AEB，∴AB=BE=6，AD=DF=9，∴△ADF是等腰三角形，△ABE是等腰三角形，∵AD∥BC，∴△EFC是等腰三角形，且FC=CE，∴EC=FC=9﹣6=3，在△ABG中，BG⊥AE，AB=6，BG=4，∴AG==2，∴AE=2AG=4，∴△ABE的周长等于16，又∵△CEF∽△BEA，相似比为1：2，∴△CEF的周长为8．故选D．点评：本题主要考查了勾股定理、相似三角形、等腰三角形的性质，注意掌握相似三角形的周长之比等于相似比，此题难度较大．2．（2013•重庆）如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE=2ED，CD=3cm，则AF的长为（）A．5cm B．6cm C．7cm D．8cm考点：相似三角形的判定与性质；平行四边形的性质．分析：由边形ABCD是平行四边形，可得AB∥CD，即可证得△AFE∽△DEC，然后由相似三角形的对应边成比例，求得答案．解答：解：∵四边形ABCD是平行四边形，∴AB∥CD，∴△AFE∽△DEC，∴AE：DE=AF：CD，∵AE=2ED，CD=3cm，∴AF=2CD=6cm．故选B．点评：此题考查了相似三角形的判定与性质以及平行四边形的性质．此题难度不大，注意掌握数形结合思想的应用．3．（2013•孝感）如图，在△ABC中，AB=AC=a，BC=b（a＞b）．在△ABC内依次作∠CBD=∠A，∠DCE=∠CBD，∠EDF=∠DCE．则EF等于（）A．B．C．D．考点：相似三角形的判定与性质；等腰三角形的判定与性质．专题：压轴题．分析：依次判定△ABC∽△BDC∽△CDE∽△DFE，根据相似三角形的对应边成比例的知识，可得出EF的长度．解答：解：∵AB=AC，∴∠ABC=∠ACB，又∵∠CBD=∠A，∴△ABC∽△BDC，同理可得：△ABC∽△BDC∽△CDE∽△DFE，∴=，=，=，=，∵AB=AC，∴CD=CE，解得：CD=CE=，DE=，EF=．故选C．点评：本题考查了相似三角形的判定与性质，本题中相似三角形比较容易找到，难点在于根据对应边成比例求解线段的长度，注意仔细对应，不要出错．4．（2013•咸宁）如图，正方形ABCD是一块绿化带，其中阴影部分EOFB，GHMN都是正方形的花圃．已知自由飞翔的小鸟，将随机落在这块绿化带上，则小鸟在花圃上的概率为（）A．B．C．D．考点：相似三角形的应用；正方形的性质；几何概率．专题：压轴题．分析：求得阴影部分的面积与正方形ABCD的面积的比即可求得小鸟在花圃上的概率；解答：解：设正方形的ABCD的边长为a，则BF=BC=，AN=NM=MC=a，∴阴影部分的面积为（）2+（a）2=a2，∴小鸟在花圃上的概率为=故选C．点评：本题考查了正方形的性质及几何概率，关键是表示出大正方形的边长，从而表示出两个阴影正方形的边长，最后表示出面积．5．（2013•绥化）如图，点A，B，C，D为⊙O上的四个点，AC平分∠BAD，AC交BD于点E，CE=4，CD=6，则AE的长为（）A．4B．5C．6D．7考点：圆周角定理；圆心角、弧、弦的关系；相似三角形的判定与性质．分析：根据圆周角定理∠CAD=∠CDB，继而证明△ACD∽△DCE，设AE=x，则AC=x+4，利用对应边成比例，可求出x的值．解答：解：设AE=x，则AC=x+4，∵AC平分∠BAD，∴∠BAC=∠CAD，∵∠CDB=∠BAC（圆周角定理），∴∠CAD=∠CDB，∴△ACD∽△DCE，∴=，即=，解得：x=5．故选B．点评：本题考查了圆周角定理、相似三角形的判定与性质，解答本题的关键是得出∠CAD=∠CDB，证明△ACD∽△DCE．6．（2013•内江）如图，在▱ABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，S△DEF：S△ABF=4：25，则DE：EC=（）A．2：5 B．2：3 C．3：5 D．3：2考点：相似三角形的判定与性质；平行四边形的性质．分析：先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF，再根据S△DEF：S△ABF=4：25即可得出其相似比，由相似三角形的性质即可求出DE：AB 的值，由AB=CD即可得出结论．解答：解：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠EAB=∠DEF，∠AFB=∠DFE，∴△DEF∽△BAF，∵S△DEF：S△ABF=4：25，∴DE：AB=2：5，∵AB=CD，∴DE：EC=2：3．故选B．点评：本题考查的是相似三角形的判定与性质及平行四边形的性质，熟知相似三角形边长的比等于相似比，面积的比等于相似比的平方是解答此题的关键．7．（2013•黑龙江）如图，在直角梯形ABCD中，AD∥BC，∠BCD=90°，∠ABC=45°，AD=CD，CE平分∠ACB交AB于点E，在BC上截取BF=AE，连接AF交CE于点G，连接DG交AC于点H，过点A作AN⊥BC，垂足为N，AN交CE于点M．则下列结论；①CM=AF；②CE⊥AF；③△AB F∽△DAH；④GD平分∠AGC，其中正确的个数是（）A．1B．2C．3D．4考点：相似三角形的判定与性质；全等三角形的判定与性质；直角梯形．专题：压轴题．分析：如解答图所示：结论①正确：证明△ACM≌△ABF即可；结论②正确：由△ACM≌△ABF得∠2=∠4，进而得∠4+∠6=90°，即CE⊥AF；结论③正确：证法一：利用四点共圆；证法二：利用三角形全等；结论④正确：证法一：利用四点共圆；证法二：利用三角形全等．解答：解：（1）结论①正确．理由如下：∵∠1=∠2，∠1+∠CMN=90°，∠2+∠6=90°，∴∠6=∠CMN，又∵∠5=∠CMN，∴∠5=∠6，∴AM=AE=BF．易知ADCN为正方形，△ABC为等腰直角三角形，∴AB=AC．在△ACM与△ABF中，，∴△ACM≌△ABF（SAS），∴CM=AF；（2）结论②正确．理由如下：∵△ACM≌△ABF，∴∠2=∠4，∵∠2+∠6=90°，∴∠4+∠6=90°，∴CE⊥AF；（3）结论③正确．理由如下：证法一：∵CE⊥AF，∴∠ADC+∠AGC=180°，∴A、D、C、G四点共圆，∴∠7=∠2，∵∠2=∠4，∴∠7=∠4，又∵∠DAH=∠B=45°，∴△ABF∽△DAH；证法二：∵CE⊥AF，∠1=∠2，∴△ACF为等腰三角形，AC=CF，点G为AF中点．在Rt△ANF中，点G为斜边AF中点，∴NG=AG，∴∠MNG=∠3，∴∠DAG=∠CNG．在△ADG与△NCG中，，∴△ADG≌△NCG（SAS），∴∠7=∠1，又∵∠1=∠2=∠4，∴∠7=∠4，又∵∠DAH=∠B=45°，∴△ABF∽△DAH；（4）结论④正确．理由如下：证法一：∵A、D、C、G四点共圆，∴∠DGC=∠DAC=45°，∠DGA=∠DCA=45°，∴∠DGC=∠DGA，即GD平分∠AGC．证法二：∵AM=AE，CE⊥AF，∴∠3=∠4，又∠2=∠4，∴∠3=∠2则∠CGN=180°﹣∠1﹣90°﹣∠MNG=180°﹣∠1﹣90°﹣∠3=90°﹣∠1﹣∠2=45°．∵△ADG≌△NCG，∴∠DGA=∠CGN=45°=∠AGC，∴GD平分∠AGC．综上所述，正确的结论是：①②③④，共4个．故选D．点评：本题是几何综合题，考查了相似三角形的判定、全等三角形的判定与性质、正方形、等腰直角三角形、直角梯形、等腰三角形等知识点，有一定的难度．解答中四点共圆的证法，仅供同学们参考．8．（2013•恩施州）如图所示，在平行四边形ABCD中，AC与BD相交于点O，E为OD 的中点，连接AE并延长交DC于点F，则DF：FC=（）A．1：4 B．1：3 C．2：3 D．1：2考点：相似三角形的判定与性质；平行四边形的性质．分析：首先证明△DFE∽△BAE，然后利用对应变成比例，E为OD的中点，求出DF：AB 的值，又知AB=DC，即可得出DF：FC的值．解答：解：在平行四边形ABCD中，AB∥DC，则△DFE∽△BAE，∴=，∵O为对角线的交点，∴DO=BO，又∵E为OD的中点，∴DE=DB，则DE：EB=1：3，∴DF：AB=1：3，∵DC=AB，∴DF：DC=1：3，∴DF：FC=1：2．故选D．点评：本题考查了相似三角形的判定与性质以及平行四边形的性质，难度适中，解答本题的关键是根据平行证明△DFE∽△BAE，然后根据对应边成比例求值．9．（2013•德阳）如图，在⊙O上有定点C和动点P，位于直径AB的异侧，过点C作CP 的垂线，与PB的延长线交于点Q，已知：⊙O半径为，tan∠ABC=，则CQ的最大值是（）A．5B．C．D．考点：圆周角定理；圆内接四边形的性质；相似三角形的判定与性质．专题：计算题；压轴题．分析：根据圆周角定理的推论由AB为⊙O的直径得到∠ACB=90°，再根据正切的定义得到tan∠ABC==，然后根据圆周角定理得到∠A=∠P，则可证得△ACB∽△PCQ，利用相似比得CQ=•PC=PC，PC为直径时，PC最长，此时CQ最长，然后把PC=5代入计算即可．解答：解：∵AB为⊙O的直径，∴AB=5，∠ACB=90°，∵tan∠ABC=，∴=，∵CP⊥CQ，∴∠PCQ=90°，而∠A=∠P，∴△ACB∽△PCQ，∴=，∴CQ=•PC=PC，当PC最大时，CQ最大，即PC为⊙O的直径时，CQ最大，此时CQ=×5=．故选D．点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了三角形相似的判定与性质．10．（2012•岳阳）如图，AB为半圆O的直径，AD、BC分别切⊙O于A、B两点，CD切⊙O于点E，AD与CD相交于D，BC与CD相交于C，连接OD、OC，对于下列结论：①OD2=DE•CD；②AD+BC=CD；③OD=OC；④S梯形ABCD=CD•OA；⑤∠DOC=90°，其中正确的是（）A．①②⑤B．②③④C．③④⑤D．①④⑤考点：切线的性质；切线长定理；相似三角形的判定与性质．专题：计算题；压轴题．分析：连接OE，由AD，DC，BC都为圆的切线，根据切线的性质得到三个角为直角，且利用切线长定理得到DE=DA，CE=CB，由CD=DE+EC，等量代换可得出CD=AD+BC，选项②正确；由AD=ED，OD为公共边，利用HL可得出直角三角形ADO与直角三角形EDO全等，可得出∠AOD=∠EOD，同理得到∠EOC=∠BOC，而这四个角之和为平角，可得出∠DOC为直角，选项⑤正确；由∠DOC与∠DEO都为直角，再由一对公共角相等，利用两对对应角相等的两三角形相似，可得出三角形DEO与三角形DOC相似，由相似得比例可得出OD2=DE•CD，选项①正确；又ABCD为直角梯形，利用梯形的面积计算后得到梯形ABCD的面积为AB（AD+BC），将AD+BC化为CD，可得出梯形面积为AB•CD，选项④错误，而OD不一定等于OC，选项③错误，即可得到正确的选项．解答：解：连接OE，如图所示：∵AD与圆O相切，DC与圆O相切，BC与圆O相切，∴∠DAO=∠DEO=∠OBC=90°，∴DA=DE，CE=CB，AD∥BC，∴CD=DE+EC=AD+BC，选项②正确；在Rt△ADO和Rt△EDO中，，∴Rt△ADO≌Rt△EDO（HL），∴∠AOD=∠EOD，同理Rt△CEO≌Rt△CBO，∴∠EOC=∠BOC，又∠AOD+∠DOE+∠EOC+∠COB=180°，∴2（∠DOE+∠EOC）=180°，即∠DOC=90°，选项⑤正确；∴∠DOC=∠DEO=90°，又∠EDO=∠ODC，∴△EDO∽△ODC，∴=，即OD2=DC•DE，选项①正确；而S梯形ABCD=AB•（AD+BC）=AB•CD，选项④错误；由OD不一定等于OC，选项③错误，则正确的选项有①②⑤．故选A点评：此题考查了切线的性质，切线长定理，相似三角形的判定与性质，全等三角形的判定与性质，以及梯形面积的求法，利用了转化的数学思想，熟练掌握定理及性质是解本题的关键．二．填空题（共10小题）11．（2013•昭通）如图，AB是⊙O的直径，弦BC=4cm，F是弦BC的中点，∠ABC=60°．若动点E以1cm/s的速度从A点出发在AB上沿着A→B→A运动，设运动时间为t（s）（0≤t ＜16），连接EF，当△BEF是直角三角形时，t（s）的值为4s．（填出一个正确的即可）考点：圆周角定理；垂径定理；相似三角形的判定与性质．专题：压轴题；开放型．分析：根据圆周角定理得到∠C=90°，由于∠ABC=60°，BC=4cm，根据含30度的直角三角形三边的关系得到AB=2BC=8cm，而F是弦BC的中点，所以当EF∥AC时，△BEF 是直角三角形，此时E为AB的中点，易得t=4s；当从A点出发运动到B点名，再运动到O点时，此时t=12s；也可以过F点作AB的垂线，点E点运动到垂足时，△BEF 是直角三角形．解答：解：∵AB是⊙O的直径，∴∠C=90°，而∠ABC=60°，BC=4cm，∴AB=2BC=8cm，∵F是弦BC的中点，∴当EF∥AC时，△BEF是直角三角形，此时E为AB的中点，即AE=AO=4cm，∴t==4（s）．故答案为4s．点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了圆周角定理的推论以及含30度的直角三角形三边的关系．12．（2013•南通）如图，在▱ABCD中，AB=6cm，AD=9cm，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=4cm，则EF+CF的长为5cm．考点：相似三角形的判定与性质；等腰三角形的判定与性质；勾股定理；平行四边形的性质．专题：压轴题．分析：首先，由于AE平分∠BAD，那么∠BAE=∠DAE，由AD∥BC，可得内错角∠DAE=∠BEA，等量代换后可证得AB=BE，即△ABE是等腰三角形，根据等腰三角形“三线合一”的性质得出AE=2AG，而在Rt△ABG中，由勾股定理可求得AG的值，即可求得AE的长；然后，利用平行线分线段成比例的性质分别得出EF，FC的长，即可得出答案．解答：解：∵AE平分∠BAD，∴∠DAE=∠BAE；又∵AD∥BC，∴∠BEA=∠DAE=∠BAE，∴AB=BE=6cm，∴EC=9﹣6=3（cm），∵BG⊥AE，垂足为G，∴AE=2AG．在Rt△ABG中，∵∠AGB=90°，AB=6cm，BG=4cm，∴AG==2（cm），∴AE=2AG=4cm；∵EC∥AD，∴====，∴=，=，解得：EF=2（cm），FC=3（cm），∴EF+CF的长为5cm．故答案为：5．点评：本题考查了平行四边形的性质，相似三角形的判定与性质，勾股定理等知识的掌握程度和灵活运用能力，同时也体现了对数学中的数形结合思想的考查，难度适中．13．（2013•菏泽）如图所示，在△ABC中，BC=6，E、F分别是AB、AC的中点，动点P 在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当CQ=CE时，EP+BP=12．考点：相似三角形的判定与性质；等腰三角形的判定与性质；三角形中位线定理．专题：压轴题．分析：延长BQ交射线EF于M，根据三角形的中位线平行于第三边可得EF∥BC，根据两直线平行，内错角相等可得∠M=∠CBM，再根据角平分线的定义可得∠PBM=∠CBM，从而得到∠M=∠PBM，根据等角对等边可得BP=PM，求出EP+BP=EM，再根据CQ=CE求出EQ=2CQ，然后根据△MEQ和△BCQ相似，利用相似三角形对应边成比例列式求解即可．解答：解：如图，延长BQ交射线EF于M，∵E、F分别是AB、AC的中点，∴EF∥BC，∴∠M=∠CBM，∵BQ是∠CBP的平分线，∴∠PBM=∠CBM，∴∠M=∠PBM，∴BP=PM，∴EP+BP=EP+PM=EM，∵CQ=CE，∴EQ=2CQ，由EF∥BC得，△MEQ∽△BCQ，∴==2，∴EM=2BC=2×6=12，即EP+BP=12．故答案为：12．点评：本题考查了相似三角形的判定与性质，角平分线的定义，平行线的性质，延长BQ构造出相似三角形，求出EP+BP=EM并得到相似三角形是解题的关键，也是本题的难点．14．（2013•巴中）如图，小明在打网球时，使球恰好能打过网，而且落在离网4米的位置上，则球拍击球的高度h为 1.5米．考点：相似三角形的应用．分析：根据球网和击球时球拍的垂直线段平行即DE∥BC可知，△ADE∽△ACB，根据其相似比即可求解．解答：解：∵DE∥BC，∴△ADE∽△ACB，即=，则=，∴h=1.5m．故答案为：1.5米．点评：本题考查了相似三角形在测量高度时的应用，解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．15．（2012•自贡）正方形ABCD的边长为1cm，M、N分别是BC、CD上两个动点，且始终保持AM⊥MN，当BM=cm时，四边形ABCN的面积最大，最大面积为cm2．考点：相似三角形的判定与性质；二次函数的最值；正方形的性质．专题：压轴题．分析：设BM=xcm，则MC=1﹣xcm，当AM⊥MN时，利用互余关系可证△ABM∽△MCN，利用相似比求CN，根据梯形的面积公式表示四边形ABCN的面积，用二次函数的性质求面积的最大值．解答：解：设BM=xcm，则MC=1﹣xcm，∵∠AMN=90°，∴∠AMB+∠NMC=90°，∠NMC+∠MNC=90°，∴∠AMB=∠MNC，又∵∠B=∠C∴△ABM∽△MCN，则，即，解得CN==x（1﹣x），∴S四边形ABCN=×1×[1+x（1﹣x）]=﹣x2+x+，∵﹣＜0，∴当x=﹣=cm时，S四边形ABCN最大，最大值是﹣×（）2+×+=cm2．故答案是：，．点评：本题考查了二次函数的性质的运用．关键是根据已知条件判断相似三角形，利用相似比求函数关系式．16．（2012•宜宾）如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是的中点，弦CE⊥AB于点F，过点D的切线交EC的延长线于点G，连接AD，分别交CF、BC于点P、Q，连接AC．给出下列结论：①∠BAD=∠ABC；②GP=GD；③点P是△ACQ的外心；④AP•AD=CQ•CB．其中正确的是②③④（写出所有正确结论的序号）．考点：切线的性质；圆周角定理；三角形的外接圆与外心；相似三角形的判定与性质．专题：计算题；压轴题．分析：连接BD，由GD为圆O的切线，根据弦切角等于夹弧所对的圆周角得到∠GDP=∠ABD，再由AB为圆的直径，根据直径所对的圆周角为直角得到∠ACB为直角，由CE垂直于AB，得到∠AFP为直角，再由一对公共角，得到三角形APF与三角形ABD相似，根据相似三角形的对应角相等可得出∠APF等于∠ABD，根据等量代换及对顶角相等可得出∠GPD=∠GDP，利用等角对等边可得出GP=GD，选项②正确；由直径AB垂直于弦CE，利用垂径定理得到A为的中点，得到两条弧相等，再由C为的中点，得到两条弧相等，等量代换得到三条弧相等，根据等弧所对的圆周角相等可得出∠CAP=∠ACP，利用等角对等边可得出AP=CP，又AB为直径得到∠ACQ为直角，利用等角的余角相等可得出∠PCQ=∠PQC，得出CP=PQ，即P为直角三角形ACQ斜边上的中点，即为直角三角形ACQ的外心，选项③正确；利用等弧所对的圆周角相等得到一对角相等，再由一对公共角相等，得到三角形ACQ 与三角形ABC相似，根据相似得比例得到AC2=CQ•CB，连接CD，同理可得出三角形ACP与三角形ACD相似，根据相似三角形对应边成比例可得出AC2=AP•AD，等量代换可得出AP•AD=CQ•CB，选项④正确．解答：解：∠BAD与∠ABC不一定相等，选项①错误；连接BD，如图所示：∵GD为圆O的切线，∴∠GDP=∠ABD，又AB为圆O的直径，∴∠ADB=90°，∵CE⊥AB，∴∠AFP=90°，∴∠ADB=∠AFP，又∠PAF=∠BAD，∴△APF∽△ABD，∴∠ABD=∠APF，又∠APF=∠GPD，∴∠GDP=∠GPD，∴GP=GD，选项②正确；∵直径AB⊥CE，∴A为的中点，即=，又C为的中点，∴=，∴=，∴∠CAP=∠ACP，∴AP=CP，又AB为圆O的直径，∴∠ACQ=90°，∴∠PCQ=∠PQC，∴PC=PQ，∴AP=PQ，即P为Rt△ACQ斜边AQ的中点，∴P为Rt△ACQ的外心，选项③正确；连接CD，如图所示：∵=，∴∠B=∠CAD，又∠ACQ=∠BCA，∴△ACQ∽△BCA，∴=，即AC2=CQ•CB，∵=，∴∠ACP=∠ADC，又∠CAP=∠DAC，∴△ACP∽△ADC，∴=，即AC2=AP•AD，∴AP•AD=CQ•CB，选项④正确，则正确的选项序号有②③④．故答案为：②③④点评：此题考查了切线的性质，圆周角定理，相似三角形的判定与性质，以及三角形的外接圆与圆心，熟练掌握性质及定理是解本题的关键．17．（2012•泉州）在△ABC中，P是AB上的动点（P异于A、B），过点P的直线截△ABC，使截得的三角形与△ABC相似，我们不妨称这种直线为过点P的△ABC的相似线，简记为P（l x）（x为自然数）．（1）如图①，∠A=90°，∠B=∠C，当BP=2PA时，P（l1）、P（l2）都是过点P的△ABC 的相似线（其中l1⊥BC，l2∥AC），此外，还有1条；（2）如图②，∠C=90°，∠B=30°，当=或或时，P（l x）截得的三角形面积为△ABC面积的．考点：相似三角形的判定与性质．专题：压轴题．分析：（1）过点P作l3∥BC交AC于Q，则△APQ∽△ABC，l3是第3条相似线；（2）按照相似线的定义，找出所有符合条件的相似线．总共有4条，注意不要遗漏．解答：解：（1）存在另外 1 条相似线．如图1所示，过点P作l3∥BC交AC于Q，则△APQ∽△ABC；故答案为：1；（2）设P（l x）截得的三角形面积为S，S=S△ABC，则相似比为1：2．如图2所示，共有4条相似线：①第1条l1，此时P为斜边AB中点，l1∥AC，∴=；②第2条l2，此时P为斜边AB中点，l2∥BC，∴=；③第3条l3，此时BP与BC为对应边，且=，∴==；④第4条l4，此时AP与AC为对应边，且=，∴==，∴=．故答案为：或或．点评：本题引入“相似线”的新定义，考查相似三角形的判定与性质和解直角三角形的运算；难点在于找出所有的相似线，不要遗漏．18．（2012•嘉兴）如图，在Rt△ABC中，∠ABC=90°，BA=BC．点D是AB的中点，连接CD，过点B作BG丄CD，分别交CD、CA于点E、F，与过点A且垂直于AB的直线相交于点G，连接DF．给出以下四个结论：①；②点F是GE的中点；③AF=AB；④S△ABC=5S△BDF，其中正确的结论序号是①③．考点：相似三角形的判定与性质；勾股定理；等腰直角三角形．专题：压轴题．分析：首先根据题意易证得△AFG∽△CFB，根据相似三角形的对应边成比例与BA=BC，继而证得正确；由点D是AB的中点，易证得BC=2BD，由等角的余角相等，可得∠DBE=∠BCD，即可得AG=AB，继而可得FG=BF；即可得AF=AC，又由等腰直角三角形的性质，可得AC=AB，即可求得AF=AB；则可得S△ABC=6S△BDF．解答：解：∵在Rt△ABC中，∠ABC=90°，∴AB⊥BC，AG⊥AB，∴AG∥BC，∴△AFG∽△CFB，∴，∵BA=BC，∴，故①正确；∵∠ABC=90°，BG⊥CD，∴∠DBE+∠BDE=∠BDE+∠BCD=90°，∴∠DBE=∠BCD，∵AB=CB，点D是AB的中点，∴BD=AB=CB，∵tan∠BCD==，∴在Rt△ABG中，tan∠DBE==，∵=，∴FG=FB，∵GE≠BF，∴点F不是GE的中点．故②错误；∵△AFG∽△CFB，∴AF：CF=AG：BC=1：2，∴AF=AC，∵AC=AB，∴AF=AB，故③正确；∵BD=AB，AF=AC，∴S△ABC=6S△BDF，故④错误．故答案为：①③．点评：此题考查了相似三角形的判定与性质、直角三角形的性质以及三角函数等知识．此题难度适中，解题的关键是证得△AFG∽△CFB，注意掌握数形结合思想与转化思想的应用．19．（2012•泸州）如图，n个边长为1的相邻正方形的一边均在同一直线上，点M1，M2，M3，…M n分别为边B1B2，B2B3，B3B4，…，B n B n+1的中点，△B1C1M1的面积为S1，△B2C2M2的面积为S2，…△B n C n M n的面积为S n，则S n=．（用含n的式子表示）考点：相似三角形的判定与性质．专题：压轴题；规律型．分析：由n个边长为1的相邻正方形的一边均在同一直线上，点M1，M2，M3，…M n分别为边B1B2，B2B3，B3B4，…，B n B n+1的中点，即可求得△B1C1M n的面积，又由B n C n∥B1C1，即可得△B n C n M n∽△B1C1M n，然后利用相似三角形的面积比等于相似比的平方，求得答案．解答：解：∵n个边长为1的相邻正方形的一边均在同一直线上，点M1，M2，M3，…M n分别为边B1B2，B2B3，B3B4，…，B n B n+1的中点，∴S1=×B1C1×B1M1=×1×=，S△B1C1M2=×B1C1×B1M2=×1×=，S△B1C1M3=×B1C1×B1M3=×1×=，S△B1C1M4=×B1C1×B1M4=×1×=，S△B1C1Mn=×B1C1×B1M n=×1×=，∵B n C n∥B1C1，∴△B n C n M n∽△B1C1M n，∴S△BnCnMn：S△B1C1Mn=（）2=（）2，即S n：=，∴S n=．故答案为：．点评：此题考查了相似三角形的判定与性质、正方形的性质以及直角三角形面积的公式．此题难度较大，注意掌握相似三角形面积的比等于相似比的平方定理的应用是解此题的关键．20．（2013•荆州）如图，△ABC是斜边AB的长为3的等腰直角三角形，在△ABC内作第1个内接正方形A1B1D1E1（D1、E1在AB上，A1、B1分别在AC、BC上），再在△A1B1C 内接同样的方法作第2个内接正方形A2B2D2E2，…如此下去，操作n次，则第n个小正方形A n B n D n E n的边长是．考点：相似三角形的判定与性质；等腰直角三角形．专题：规律型．分析：求出第一个、第二个、第三个内接正方形的边长，总结规律可得出第n个小正方形A nB n D n E n的边长．解答：解：∵∠A=∠B=45°，∴AE1=A1E=A1B1=B1D1=D1B，∴第一个内接正方形的边长=AB=1；同理可得：第二个内接正方形的边长=A1B1=AB=；第三个内接正方形的边长=A2B2=AB=；故可推出第n个小正方形A n B n D n E n的边长=AB=．故答案为：．点评：本题考查了相似三角形的判定与性质、等腰直角三角形的性质，解答本题的关键是求出前几个内接正方形的边长，得出一般规律．三．解答题（共8小题）21．（2013•珠海）如图，在Rt△ABC中，∠C=90°，点P为AC边上的一点，将线段AP绕点A顺时针方向旋转（点P对应点P′），当AP旋转至AP′⊥AB时，点B、P、P′恰好在同一直线上，此时作P′E⊥AC于点E．（1）求证：∠CBP=∠ABP；（2）求证：AE=CP；（3）当，BP′=5时，求线段AB的长．考点：全等三角形的判定与性质；角平分线的性质；勾股定理；相似三角形的判定与性质．专题：几何综合题；压轴题．分析：（1）根据旋转的性质可得AP=AP′，根据等边对等角的性质可得∠APP′=∠AP′P，再根据等角的余角相等证明即可；（2）过点P作PD⊥AB于D，根据角平分线上的点到角的两边的距离相等可得CP=DP，然后求出∠PAD=∠AP′E，利用“角角边”证明△APD和△P′AE全等，根据全等三角形对应边相等可得AE=DP，从而得证；（3）设CP=3k，PE=2k，表示出AE=CP=3k，AP′=AP=5k，然后利用勾股定理列式求出P′E=4k，再求出△ABP′和△EPP′相似，根据相似三角形对应边成比例列式求出P′A=AB，然后在Rt△ABP′中，利用勾股定理列式求解即可．解答：（1）证明：∵AP′是AP旋转得到，∴AP=AP′，∴∠APP′=∠AP′P，∵∠C=90°，AP′⊥AB，∴∠CBP+∠BPC=90°，∠ABP+∠AP′P=90°，又∵∠BPC=∠APP′（对顶角相等），∴∠CBP=∠ABP；（2）证明：如图，过点P作PD⊥AB于D，∵∠CBP=∠ABP，∠C=90°，∴CP=DP，∵P′E⊥AC，。

初中数学相似三角形单元测试卷

相似三角形单元测试卷（满分120分，考试时间90分钟）一．选择题【本题共6题，每小题3分，共18分】1．在△ABC 中，点D 、E 分别在边AB 、AC 上，AD :BD =1：2，那么下列条件中能够判断DE//BC 的是……………………………………………………………………（） (A) 21=BCDE ； (B) 31=BC DE ； (C) 21=AC AE ； (D) 31=AC AE2．如图，123//// ，下列比例式中正确的是…………………………………（）（A ）AD CE BC DF =；（B ）AD DF BC CE =；（C ）AB CD CD EF =；（D ）AD BCBE AF =． 3．已知a ，b ，c 是非零向量，不能判定a ∥b的是……………………………（）（A ）a ∥c ，b ∥c ；（B ） a ＝3b ；（C ）a ＝b ；（D ）a ＝12c ,b ＝－2c． 4．如图，△ABC 中，DE //BC 交AB 于点D ，交AC 于点E ，如果ADE BCED S S ∆=四边形，那么下列等式成立的是 ……………………………………………………………（）（A ）:1:2DE BC =；（B ）:1:3DE BC =；（C ）:1:4DE BC =；（D ）:DE BC = 5．在Rt △ABC 和Rt △DEF 中，90C F ∠=∠=°，下列条件中不能判定这两个三角形相似的是…………………………………………………………………………………（）（A ）55,35A D ∠=°∠=°；（B ）9,12,6,8AC BC DF EF ====；（C ）3,4,6,8AC BC DF DE ====；（D ）10,8,15,9AB AC DE EF ====． 6．如图，在三角形纸片ABC 中，AB=AC ，∠A=36°。

初三数学相似三角形测试题及答案

初三数学相似三角形测试题及答案1、若b m m a 2,3==，则_____:=b a 。

2、已知653z y x ==，且623+=z y ，则__________,==y x 。

3、在等腰Rt △ABC 中，斜边长为c ,斜边上的中线长为m ，则______:=c m . 4、反向延长线段AB 至C ，使2AC ＝AB ，那么BC ：AB ＝。

5、△ABC ∽△A ′B ′C ′，相似比为3：2,它们周长的差为40厘米，则△A ′B ′C ′的周长为厘米。

7、如图，△ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，若∠A ＝30°,则BD ：BC ＝。

若BC ＝6，AB ＝10，则BD ＝，CD ＝。

8、如图，梯形ABCD 中，DC ∥AB ，DC ＝2cm ，AB ＝3。

5cm,且MN ∥PQ ∥AB ， DM ＝MP ＝PA,则MN ＝，PQ ＝。

9、如图，四边形ADEF 为菱形，且AB ＝14，BC ＝12，AC ＝10，那BE ＝。

10、梯形的上底长1.2厘米，下底长1.8厘米，高1厘米，延长两腰后与下底所成的三角形的高为厘米。

11、下面四组线段中，不能成比例的是（）A 、4,2,6,3====d c b aB 、3,6,2,1====d c b aC 、10,5,6,4====d c b aD 、32,15,5,2====d c b a12、等边三角形的中线与中位线长的比值是（ )A 、1:3B 、2:3C 、23:21 D 、1：3CB DAD C NPN QAB14、已知直角三角形三边分别为b a b a a 2,,++，()0,0>>b a ，则=b a :（ ) A 、1:3 B 、1：4 C 、2：1 D 、3:115、△ABC 中,AB ＝12，BC ＝18,CA ＝24，另一个和它相似的三角形最长的一边是36，则最短的一边是（） A 、27 B 、12 C 、18 D 、20 16、已知c b a ,,是△ABC 的三条边，对应高分别为cb a h h h ,,,且6:5:4::=c b a ，那么cb a h h h ::等于（）A 、4：5：6 B 、6：5：4 C 、15：12：10 D 、10：12：1517、一个三角形三边长之比为4：5：6，三边中点连线组成的三角形的周长为30cm ，则原三角形最大边长为（） A 、44厘米 B 、40厘米 C 、36厘米 D 、24厘米 18、下列判断正确的是（）A 、不全等的三角形一定不是相似三角形B 、不相似的三角形一定不是全等三角形C 、相似三角形一定不是全等三角形D 、全等三角形不一定是相似三角形19、如图，△ABC 中,AB ＝AC ，AD 是高，EF ∥BC ，则图中与△ADC 相似的三角形共有（） A 、1个 B 、2个 C 、3个 D 、多于3个20、如图，在平行四边形ABCD 中，E 为BC 边上的点，若BE ：EC ＝4:5，AE 交BD 于F ，则BF ：FD 等于（ ) A 、4:5 B 、3：5 C 、4：9 D 、3：821、已知()3:2:=-y y x ,求y x yx 2352-+的值。

九年级数学相似三角形经典题(含答案)

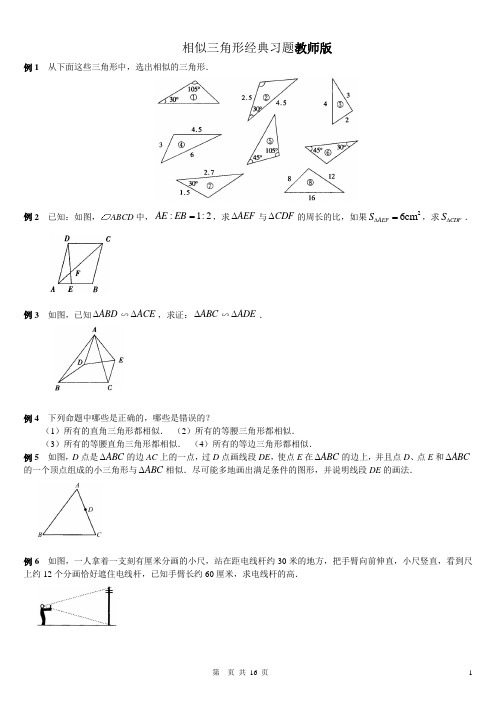
相似三角形经典习题教师版例1 从下面这些三角形中，选出相似的三角形．例2 已知：如图，ABCD 中，2:1:=EB AE ，求AEF ∆与CDF ∆的周长的比，如果2cm 6=∆AEF S ，求CDF S ∆．例3 如图，已知ABD ∆∽ACE ∆，求证：ABC ∆∽ADE ∆．例4 下列命题中哪些是正确的，哪些是错误的？（1）所有的直角三角形都相似．（2）所有的等腰三角形都相似．（3）所有的等腰直角三角形都相似．（4）所有的等边三角形都相似．例5 如图，D 点是ABC ∆的边AC 上的一点，过D 点画线段DE ，使点E 在ABC ∆的边上，并且点D 、点E 和ABC ∆的一个顶点组成的小三角形与ABC ∆相似．尽可能多地画出满足条件的图形，并说明线段DE 的画法．例6 如图，一人拿着一支刻有厘米分画的小尺，站在距电线杆约30米的地方，把手臂向前伸直，小尺竖直，看到尺上约12个分画恰好遮住电线杆，已知手臂长约60厘米，求电线杆的高．例7 如图，小明为了测量一高楼MN 的高，在离N 点20m 的A 处放了一个平面镜，小明沿NA 后退到C 点，正好从镜中看到楼顶M 点，若5.1=AC m ，小明的眼睛离地面的高度为1.6m ，请你帮助小明计算一下楼房的高度（精确到0.1m ）．例8 格点图中的两个三角形是否是相似三角形，说明理由．例9 根据下列各组条件，判定ABC ∆和C B A '''∆是否相似，并说明理由：（1）,cm 4,cm 5.2,cm 5.3===CA BC AB cm 28,cm 5.17,cm 5.24=''=''=''A C C B B A ．（2）︒='∠︒='∠︒=∠︒=∠35,44,104,35A C B A ．（3）︒='∠=''=''︒=∠==48,3.1,5.1,48,6.2,3B C B B A B BC AB ．例10 如图，下列每个图形中，存不存在相似的三角形，如果存在，把它们用字母表示出来，并简要说明识别的根据．例11 已知：如图，在ABC ∆中，BD A AC AB ,36,︒=∠=是角平分线，试利用三角形相似的关系说明AC DC AD ⋅=2．例12 已知ABC ∆的三边长分别为5、12、13，与其相似的C B A '''∆的最大边长为26，求C B A '''∆的面积S ．例13 在一次数学活动课上，老师让同学们到操场上测量旗杆的高度，然后回来交流各自的测量方法．小芳的测量方法是：拿一根高3.5米的竹竿直立在离旗杆27米的C 处（如图），然后沿BC 方向走到D 处，这时目测旗杆顶部A 与竹竿顶部E 恰好在同一直线上，又测得C 、D 两点的距离为3米，小芳的目高为1.5米，这样便可知道旗杆的高．你认为这种测量方法是否可行？请说明理由．例14．如图，为了估算河的宽度，我们可以在河对岸选定一个目标作为点A ，再在河的这一边选点B 和C ，使BC AB ⊥，然后再选点E ，使BC EC ⊥，确定BC 与AE 的交点为D ，测得120=BD 米，60=DC 米，50=EC 米，你能求出两岸之间AB 的大致距离吗？例15．如图，为了求出海岛上的山峰AB 的高度，在D 和F 处树立标杆DC 和FE ，标杆的高都是3丈，相隔1000步（1步等于5尺），并且AB 、CD 和EF 在同一平面内，从标杆DC 退后123步的G 处，可看到山峰A 和标杆顶端C 在一直线上，从标杆FE 退后127步的H 处，可看到山峰A 和标杆顶端E 在一直线上．求山峰的高度AB 及它和标杆CD 的水平距离BD 各是多少？（古代问题）例16 如图，已知△ABC 的边AB ＝32，AC ＝2，BC 边上的高AD ＝3．（1）求BC 的长；（2）如果有一个正方形的边在AB 上，另外两个顶点分别在AC ，BC 上，求这个正方形的面积．相似三角形经典习题答案例1．解 ①、⑤、⑥相似，②、⑦相似，③、④、⑧相似例2．解 ABCD 是平行四边形，∴CD AB CD AB =,//，∴AEF ∆∽CDF ∆，又2:1:=EB AE ，∴3:1:=CD AE ，∴AEF ∆与CDF ∆的周长的比是1：3．又)cm (6,)31(22==∆∆∆AEF CDF AEF S S S ，∴)cm (542=∆CD F S ．例3 分析由于ABD ∆∽ACE ∆，则CAE BAD ∠=∠，因此DAE BAC ∠=∠，如果再进一步证明AECAAD BA =，则问题得证．证明 ∵ABD ∆∽ACE ∆，∴CAE BAD ∠=∠．又DAC BAD BAC ∠+∠=∠ ，∴CAE DAC DAE ∠+∠=∠， ∴DAE BAC ∠=∠．∵ABD ∆∽ACE ∆，∴AEACAD AB =．在ABC ∆和ADE ∆中，∵AEACAD AB ADE BAC =∠=∠,，∴ABC ∆∽ADE ∆ 例4．分析（1）不正确，因为在直角三角形中，两个锐角的大小不确定，因此直角三角形的形状不同．（2）也不正确，等腰三角形的顶角大小不确定，因此等腰三角形的形状也不同．（3）正确．设有等腰直角三角形ABC 和C B A '''，其中︒='∠=∠90C C ，则︒='∠=∠︒='∠=∠45,45B B A A ，设ABC ∆的三边为a 、b 、c ，C B A '''∆的边为c b a '''、、，则a c b a a c b a '=''='==2,,2,，∴a ac c b b a a '=''=',，∴ABC ∆∽C B A '''∆．（4）也正确，如ABC ∆与C B A '''∆都是等边三角形，对应角相等，对应边都成比例，因此ABC ∆∽C B A '''∆．答：（1）、（2）不正确．（3）、（4）正确．例5．解：画法略．例6．分析本题所叙述的内容可以画出如下图那样的几何图形，即60=DF 厘米6.0=米，12=GF 厘米12.0=米，30=CE 米，求BC ．由于ADF ∆∽ACAF EC DF AEC =∆,，又ACF ∆∽ABC ∆，∴BC GFEC DF =，从而可以求出BC 的长．解 EC DF EC AE //,⊥ ，∴EAC DAF AEC ADF ∠=∠∠=∠,，∴ADF ∆∽AEC ∆．∴ACAFEC DF =．又EC BC EC GF ⊥⊥,，∴ABC AGF ACB AFG BC GF ∠=∠∠=∠,,//， ∴AGF ∆∽ABC ∆，∴BC GF AC AF =，∴BCGFEC DF =．又60=DF 厘米6.0=米，12=GF 厘米12.0=米，30=EC 米，∴6=BC 米．即电线杆的高为6米．例7．分析根据物理学定律：光线的入射角等于反射角，这样，BCA ∆与MNA ∆的相似关系就明确了．解因为MAN BAC AN MN CA BC ∠=∠⊥⊥,,，所以BCA ∆∽MNA ∆．所以AC AN BC MN ::=，即5.1:206.1:=MN ．所以3.215.1206.1≈÷⨯=MN （m ）．说明这是一个实际应用问题，方法看似简单，其实很巧妙，省却了使用仪器测量的麻烦．例8．分析这两个图如果不是画在格点中，那是无法判断的．实际上格点无形中给图形增添了条件——长度和角度．解在格点中BC AB EF DE ⊥⊥,，所以︒=∠=∠90B E ，又4,2,2,1====AB BC DE EF ．所以21==BC EF AB DE ．所以DEF ∆∽ABC ∆．说明遇到格点的题目一定要充分发现其中的各种条件，勿使遗漏．例9．解（1）因为7128cm 4cm ,7117.5cm 2.5cm ,7124.5cm 3.5cm ==''==''==''A C CA C B BC B A AB ，所以ABC ∆∽C B A '''∆；（2）因为︒=∠-∠-︒=∠41180B A C ，两个三角形中只有A A '∠=∠，另外两个角都不相等，所以ABC ∆与C B A '''∆不相似；（3）因为12,=''='''∠=∠C B BC B A AB B B ，所以ABC ∆相似于C B A '''∆．例10．解（1）ADE ∆∽ABC ∆ 两角相等；（2）ADE ∆∽ACB ∆ 两角相等；（3）CDE ∆∽CAB ∆ 两角相等；（4）EAB ∆∽ECD ∆ 两边成比例夹角相等；（5）ABD ∆∽ACB ∆ 两边成比例夹角相等；（6）ABD ∆∽ACB ∆ 两边成比例夹角相等．例11．分析有一个角是65°的等腰三角形，它的底角是72°，而BD 是底角的平分线，∴︒=∠36CBD ，则可推出ABC ∆∽BCD ∆，进而由相似三角形对应边成比例推出线段之间的比例关系．证明 AC AB A =︒=∠,36 ，∴︒=∠=∠72C ABC ．又BD 平分ABC ∠，∴︒=∠=∠36CBD ABD ．∴BC BD AD ==，且ABC ∆∽BCD ∆，∴BC CD AB BC ::=，∴CD AB BC ⋅=2，∴CD AC AD ⋅=2．说明（1）有两个角对应相等，那么这两个三角形相似，这是判断两个三角形相似最常用的方法，并且根据相等的角的位置，可以确定哪些边是对应边．（2）要说明线段的乘积式cd ab =，或平方式bc a =2，一般都是证明比例式，b dc a =，或caa b =，再根据比例的基本性质推出乘积式或平方式．例12分析由ABC ∆的三边长可以判断出ABC ∆为直角三角形，又因为ABC ∆∽C B A '''∆，所以C B A '''∆也是直角三角形，那么由C B A '''∆的最大边长为26，可以求出相似比，从而求出C B A '''∆的两条直角边长，再求得C B A '''∆的面积．解设ABC ∆的三边依次为，13,12,5===AB AC BC ，则222AC BC AB += ，∴︒=∠90C ．又∵ABC ∆∽C B A '''∆，∴︒=∠='∠90C C ．212613==''=''=''B A AB C A AC C B BC ，又12,5==AC BC ，∴24,10=''=''C A C B ． ∴12010242121=⨯⨯=''⨯''=C B C A S ．例13．分析判断方法是否可行，应考虑利用这种方法加之我们现有的知识能否求出旗杆的高．按这种测量方法，过F作AB FG ⊥于G ，交CE 于H ，可知AGF ∆∽EHF ∆，且GF 、HF 、EH 可求，这样可求得AG ，故旗杆AB 可求．解这种测量方法可行．理由如下：设旗杆高x AB =．过F 作AB FG ⊥于G ，交CE 于H （如图）．所以AGF ∆∽EHF ∆．因为3,30327,5.1==+==HF GF FD ，所以5.1,25.15.3-==-=x AG EH ．由AGF ∆∽EHF ∆，得HF GF EH AG =，即33025.1=-x ，所以205.1=-x ，解得5.21=x （米）所以旗杆的高为21.5米．说明在具体测量时，方法要现实、切实可行．例14. 解：︒=∠=∠∠=∠90,ECD ABC EDC ADB ，∴ABD ∆∽ECD ∆，1006050120,=⨯=⨯==CD EC BD AB CD BD EC AB （米），答：两岸间AB 大致相距100米．例15. 答案：1506=AB 米，30750=BD 步，（注意：AK FEFHKE AK CD DG KC ⋅=⋅=,．）例16. 分析：要求BC 的长，需画图来解，因AB 、AC 都大于高AD ，那么有两种情况存在，即点D 在BC 上或点D 在BC 的延长线上，所以求BC 的长时要分两种情况讨论．求正方形的面积，关键是求正方形的边长．解：（1）如上图，由AD ⊥BC ，由勾股定理得BD ＝3，DC ＝1，所以BC ＝BD ＋DC ＝3＋1＝4．如下图，同理可求BD ＝3，DC ＝1，所以BC ＝BD －CD ＝3－1＝2．（2）如下图，由题目中的图知BC ＝4，且162)32(2222=+=+AC AB ，162=BC ，∴222BC AC AB =+．所以△ABC 是直角三角形．由AE G F 是正方形，设G F ＝x ，则FC ＝2－x ， ∵G F ∥AB ，∴AC FC AB GF =，即2232xx -=． ∴33-=x ，∴3612)33(2-=-=AEG F S 正方形．如下图，当BC ＝2，AC ＝2，△ABC 是等腰三角形，作CP ⊥AB 于P ，∴AP ＝321=AB ，在Rt △APC 中，由勾股定理得CP ＝1， ∵GH ∥AB ，∴△C GH ∽△CBA ，∵x x x -=132，32132+=x ∴121348156)32132(2-=+=GFEH S 正方形因此，正方形的面积为3612-或121348156-．相似三角形一，比例线段 1，成比例线段对于四条线段a ，b ，c ，d ，如果其中两条线段的长度的比等于另外两条线段的比，如b a =dc（或a ：b=c ：d ），那么，这四条线段叫做成比例线段，简称比例线段。

数学九年级上册相似试卷【含答案】

数学九年级上册相似试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 若两个三角形的对应角相等，则它们是相似的，这句话是否正确？A. 正确B. 错误2. 在ΔABC和ΔDEF中，若AB/DE = BC/EF = AC/DF，则这两个三角形是否相似？A. 相似B. 不相似3. 两个相似三角形的面积比是9:1，它们的边长比是：A. 3:1B. 1:3C. 9:1D. 1:94. 若ΔABC ∽ ΔA'B'C'，则以下哪个比例是错误的？A. AB/A'B' = BC/B'C'B. AB/A'B' = AC/A'C'C. AB/A'B' = (BCAC)/(B'C'A'C')D. AB/A'B' = (BC+AC)/(B'C'+A'C')5. 在ΔABC中，AB = 6cm, BC = 8cm, ∠B = 90°，若ΔDEF ∽ ΔABC，且EF = 4cm，则DE的长度是：A. 3cmB. 4cmC. 5cmD. 6cm二、判断题（每题1分，共5分）6. 相似三角形的对应边长之比相等。

（）7. 相似三角形的面积比等于对应边长比的平方。

（）8. 若两个三角形的对应边成比例，则这两个三角形一定相似。

（）9. 在ΔABC中，若AB = AC，则ΔABC是等腰三角形。

（）10. 两个全等三角形的面积比一定是1:1。

（）三、填空题（每题1分，共5分）11. 在ΔABC和ΔDEF中，若AB/DE = BC/EF = AC/DF = 2/3，则ΔABC与ΔDEF______。

12. 若ΔABC ∽ ΔA'B'C'，且AB = 6cm, A'B' = 9cm，则BC与B'C'的长度之比是______。

初三数学13 相似三角形-2024年中考数学真题分项汇编(全国通用)(解析版)

专题13 相似三角形一．选择题1．（2022·黑龙江哈尔滨）如图，,,AB CD AC BD ∥相交于点E ，1,2,3AE EC DE ===，则BD 的长为（）A ．32B ．4C ．92D ．6【答案】C【分析】根据相似三角形对应边长成比例可求得BE 的长，即可求得BD 的长．【详解】∵//AB CD ∴ABE CDE ∽ ∴AE BE EC DE= ∵1,2,3AE EC DE ===，∴32BE =∵BD BE ED =+ ∴92BD = 故选：C ．【点睛】本题考查了相似三角形的对应边长成比例，解题的关键在于找到对应边长．2．（2022·广西贺州）如图，在ABC 中，25DE BC DE BC ==∥，，，则:ADE ABC S S 的值是（）A ．325B ．425C ．25D ．35【答案】B【分析】根据相似三角形的判定定理得到ADE ABC ，根据相似三角形的面积比等于相似比的平方计算，得到答案．【详解】解：25DE BC DE BC ==∥，，∴ADE ABC ，∴2224525ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ，故选：B ．【点睛】此题考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．3．（2022·广西梧州）如图，以点O 为位似中心，作四边形ABCD 的位似图形''''A B C D ﹐已知'13OA OA =，若四边形ABCD 的面积是2，则四边形''''A B C D 的面积是（）A ．4B ．6C ．16D ．18【答案】D 【分析】两图形位似必相似，再由相似的图形面积比等于相似比的平方即可求解．【详解】解：由题意可知，四边形ABCD 与四边形''''A B C D 相似，由两图形相似面积比等于相似比的平方可知：''''22'1139ABCD A B C D S OA S OA ⎛⎫⎛⎫= ⎪= ⎪= ⎪ ⎪⎝⎭⎝⎭，又四边形ABCD 的面积是2，∴四边形''''A B C D 的面积为18，故选：D ．【点睛】本题考察相似多边形的性质，属于基础题，熟练掌握相似图形的性质是解决本题的关键．4．（2022·四川雅安）如图，在△ABC 中，D ，E 分别是AB 和AC 上的点，DE ∥BC ，若AD BD ＝21，那么DE BC ＝（）A ．49B ．12C ．13D ．23【答案】D【分析】先求解2,3AD AB =再证明,ADE ABC ∽可得2.3DE AD BC AB ==【详解】解： AD BD ＝21，2,3AD AB ∴= DE ∥BC ，,ADE ABC ∴ ∽ 2,3DE AD BC AB ∴== 故选D 【点睛】本题考查的是相似三角形的判定与性质，证明ADE ABC △△∽是解本题的关键．5．（2022·内蒙古包头）如图，在边长为1的小正方形组成的网格中，A ，B ，C ，D 四个点均在格点上，AC 与BD 相交于点E ，连接,AB CD ，则ABE △与CDE △的周长比为（）A ．1：4B ．4：1C ．1：2D ．2：1【答案】D 【分析】运用网格图中隐藏的条件证明四边形DCBM 为平行四边形，接着证明ABE CDE ∽，最后利相似三角形周长的比等于相似比即可求出．【详解】如图：由题意可知，3DM =，3BC =， ∴DM BC =，而DM BC ∥，∴四边形DCBM 为平行四边形，∴AB DC ∥，∴BAE DCE ∠=∠，ABE CDE ∠=∠，∴ABE CDE ∽，∴21ABE CDE C AB C CD ===△△．故选：D ．【点睛】本题考查了平行四边形的判定与性质、相似三角形的判定与性质及勾股定理，熟练掌握相关知识并正确计算是解题关键．6．（2022·黑龙江绥化）如图，在矩形ABCD 中，P 是边AD 上的一个动点，连接BP ，CP ，过点B 作射线，交线段CP 的延长线于点E ，交边AD 于点M ，且使得ABE CBP =∠∠，如果2AB =，5BC =，AP x =，PM y =，其中25x < ．则下列结论中，正确的个数为（）（1）y 与x 的关系式为4y x x =-；（2）当4AP =时，ABP DPC ∽；（3）当4AP =时，3tan 5EBP ∠=．A ．0个B ．1个C ．2个D ．3个【答案】C 【分析】（1）证明ABM APB ∽，得AB AM AP AB=，将2AB =，AP x =，PM y =代入，即可得y 与x 的关系式；（2）利用两组对应边成比例且夹角相等，判定ABP DPC ∽；（3）过点M 作MF BP ⊥垂足为F ，在Rt APB △中，由勾股定理得BP 的长，证明FPM APB ∽，求出MF ，PF ，BF 的长，在Rt BMF △中，求出tan EBP ∠的值即可．【详解】解：（1）∵在矩形ABCD 中，∴AD BC ∥，90A D ∠=∠=︒，5BC AD ==，2AB DC ==，∴APB CBP ∠=∠，∵ABE CBP =∠∠，∴ABE APB ∠=∠，∴ABM APB ∽，∴AB AM AP AB=，∵2AB =，AP x =，PM y =，∴22x y x -=，解得：4y x x=-，故（1）正确；（2）当4AP =时，541DP AD AP =-=-=，∴12DC DP AP AB ==，又∵90A D ∠=∠=︒，∴ABP DPC ∽，故（2）正确；（3）过点M 作MF BP ⊥垂足为F ，∴90A MFP MFB ∠=∠=∠=︒，∵当4AP =时，此时4x =，4413y x x =-=-=，∴3PM =，在Rt APB 中，由勾股定理得：222BP AP AB =+，∴BP ===，∵FPM APB ∠=∠，∴FPM APB ∽，∴MF PF PM AB AP PB ==，∴24MF PF ==∴MF =PF =∴BF BP PF =-=∴3tan 4MF EBP BF ∠===故（3）不正确；故选：C ．【点睛】本题主要考查相似三角形的判定和性质，勾股定理的应用，矩形的性质，正确找出相似三角形是解答本题的关键．7．（2022·湖北鄂州）如图，定直线MN ∥PQ ，点B 、C 分别为MN 、PQ 上的动点，且BC =12，BC 在两直线间运动过程中始终有∠BCQ =60°．点A 是MN 上方一定点，点D 是PQ 下方一定点，且AE ∥BC ∥DF ，AE =4，DF =8，ADBC 在平移过程中，AB +CD 的最小值为（）A ．B ．C ．D ．【答案】C 【分析】如图所示，过点F 作FH CD ∥交BC 于H ，连接EH ，可证明四边形CDFH 是平行四边形，得到CH =DF =8，CD =FH ，则BH =4，从而可证四边形ABHE 是平行四边形，得到AB =HE ，即可推出当E 、F 、H 三点共线时，EH +HF 有最小值EF 即AB +CD 有最小值EF ，延长AE 交PQ 于G ，过点E 作ET ⊥PQ 于T ，过点A 作AL ⊥PQ 于L ，过点D 作DK ⊥PQ 于K ，证明四边形BEGC 是平行四边形，∠EGT =∠BCQ =60°，得到EG =BC =12，然后通过勾股定理和解直角三角形求出ET 和TF 的长即可得到答案．【详解】解：如图所示，过点F 作FH CD ∥交BC 于H ，连接EH ，∵BC DF FH CD ∥∥，，∴四边形CDFH 是平行四边形，∴CH =DF =8，CD =FH ，∴BH =4，∴BH =AE =4，又∵AE BC ∥，∴四边形ABHE 是平行四边形，∴AB =HE ，∵EH FH EF +≥，∴当E 、F 、H 三点共线时，EH +HF 有最小值EF 即AB +CD 有最小值EF ，延长AE 交PQ 于G ，过点E 作ET ⊥PQ 于T ，过点A 作AL ⊥PQ 于L ，过点D 作DK ⊥PQ 于K ，∵MN PQ BC AE ∥∥，，∴四边形BEGC 是平行四边形，∠EGT =∠BCQ =60°，∴EG =BC =12，∴=cos =6=sin GT GE EGT ET GE EGT ⋅⋅∠，∠，同理可求得8GL AL ==，，4KF DK ==，，∴2TL =，∵AL ⊥PQ ，DK ⊥PQ ，∴AL DK ∥，∴△ALO ∽△DKO ，∴2AL AO DK DO==，∴2133AO AD DO AD ====∴24OL OK ===，，∴42TF TL OL OK KF =+++=，∴EF ==故选C ．【点睛】本题主要考查了平行四边形的性质与判定，相似三角形的性质与判定，勾股定理，解直角三角形，正确作出辅助线推出当E 、F 、H 三点共线时，EH +HF 有最小值EF 即AB +CD 有最小值EF 是解题的关键．8．（2022·广西贵港）如图，在边长为1的菱形ABCD 中，60ABC ∠=︒，动点E 在AB 边上（与点A 、B 均不重合），点F 在对角线AC 上，CE 与BF 相交于点G ，连接,AG DF ，若AF BE =，则下列结论错误的是（）A ．DF CE =B ．120BGC ∠=︒C ．2AF EG EC =⋅D ．AG【答案】D【分析】先证明△BAF ≌△DAF ≌CBE ，△ABC 是等边三角形，得DF =CE ，判断A 项答案正确，由∠GCB +∠GBC =60゜，得∠BGC =120゜，判断B 项答案正确，证△BEG ∽△CEB 得BE CE GE BE= ，即可判断C 项答案正确，由120BGC ∠=︒，BC =1，得点G 在以线段BC 为弦的弧BC 上，易得当点G 在等边△ABC 的内心处时，AG 取最小值，由勾股定理求得AG D 项错误．【详解】解：∵四边形ABCD 是菱形，60ABC ∠=︒，∴AB =AD =BC =CD ，∠BAC =∠DAC =12∠BAD =12(180)ABC ⨯︒-∠=60ABC ︒=∠，∴△BAF ≌△DAF ≌CBE ，△ABC 是等边三角形，∴DF =CE ，故A 项答案正确，∠ABF =∠BCE ，∵∠ABC =∠ABF +∠CBF =60゜，∴∠GCB +∠GBC =60゜，∴∠BGC =180゜-60゜=180゜-（∠GCB +∠GBC ）=120゜，故B 项答案正确，∵∠ABF =∠BCE ，∠BEG =∠CEB ，∴△BEG ∽△CEB ，∴BE CE GE BE = ，∴2BE GE CE = ，∵AF BE =，∴2AF GE CE = ，故C 项答案正确，∵120BGC ∠=︒，BC =1，点G 在以线段BC 为弦的弧BC 上，∴当点G 在等边△ABC 的内心处时，AG 取最小值，如下图，∵△ABC 是等边三角形，BC =1，∴BF AC ⊥，AF =12AC =12，∠GAF =30゜，∴AG =2GF ，AG 2=GF 2+AF 2，∴2221122AG AG ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，解得AG D 项错误，故应选：D【点睛】本题主要考查了菱形的基本性质、等边三角形的判定及性质、圆周角定理，熟练掌握菱形的性质是解题的关键．9．（2022·贵州贵阳）如图，在ABC 中，D 是AB 边上的点，B ACD ∠=∠，:1:2AC AB =，则ADC 与ACB △的周长比是（）A ．B ．1:2C ．1:3D ．1:4【答案】B 【分析】先证明△ACD ∽△ABC ，即有12AC AD CD AB AC BC ===，则可得12AC AD CD AB AC BC ++=++，问题得解．【详解】∵∠B =∠ACD ，∠A =∠A ，∴△ACD ∽△ABC ，∴AC AD CD AB AC BC ==，∵12AC AB =，∴12AC AD CD AB AC BC ===，∴12AC AD CD AC AD CD AB AC BC AB AC BC ++====++，∴△ADC 与△ACB 的周长比1:2，故选：B ．【点睛】本题主要考查了相似三角形的判定与性质，证明△ACD ∽△ABC 是解答本题的关键．10．（2022·广西）已知△ABC 与△A 1B 1C 1是位似图形，位似比是1：3，则△ABC 与△A 1B 1C 1的面积比（）A ．1 ：3B ．1：6C ．1：9D ．3：1【答案】C【分析】根据位似图形的面积比等于位似比的平方，即可得到答案．【详解】∵△ABC 与△A 1B 1C 1是位似图形，位似比是1：3，∴△ABC 与△A 1B 1C 1的面积比为1：9，故选：C ．【点睛】本题考查位似图形的性质，熟练掌握位似图形的面积比等于位似比的平方是解题的关键．11．（2022·山东临沂）如图，在ABC 中，∥DE BC ，23AD DB =，若6AC =，则EC =（）A ．65B ．125C ．185D ．245【答案】C【分析】由∥DE BC ，23AD DB =，可得2,3AD AE DB EC ==再建立方程即可．【详解】解： ∥DE BC ，23AD DB =，2,3AD AE DB EC ∴== 6AC =，62,3CE CE -∴= 解得：18.5CE =经检验符合题意故选C 【点睛】本题考查的是平行线分线段成比例，证明“23AD AE DB EC ==”是解本题的关键．12．（2022·山东威海）由12个有公共顶点O 的直角三角形拼成如图所示的图形，∠AOB ＝∠BOC ＝∠COD ＝…＝∠LOM ＝30°．若S △AOB ＝1，则图中与△AOB 位似的三角形的面积为( )A ．（43）3B ．（43）7C ．（43）6D ．（34）6【答案】C【分析】根据题意得出A 、O 、G 在同一直线上，B 、O 、H 在同一直线上，确定与△AOB 位似的三角形为△GOH ，利用锐角三角函数找出相应规律得出OG=6x ，再由相似三角形的性质求解即可．【详解】解：∵∠AOB ＝∠BOC ＝∠COD ＝…＝∠LOM ＝30°∴∠AOG ＝180°，∠BOH ＝180°，∴A 、O 、G 在同一直线上，B 、O 、H 在同一直线上，∴与△AOB 位似的三角形为△GOH ，设OA =x ，则OB=1cos30OA x ==︒，∴OC=24cos303OB x x ==︒，∴OD=3cos30OC x ==︒，…∴OG=6x ，∴6OG OA =，∴12643GOH AOB S S ⎛⎫== ⎪⎝⎭ ，∵1AOB S = ，∴643GOH S ⎛⎫= ⎪⎝⎭ ，故选：C ．【点睛】题目主要考查利用锐角三角函数解三角形，找规律问题，相似三角形的性质等，理解题意，找出相应边的比值规律是解题关键．二．填空题13．（2022·贵州黔东南）如图，折叠边长为4cm 的正方形纸片ABCD ，折痕是DM ，点C 落在点E 处，分别延长ME 、DE 交AB 于点F 、G ，若点M 是BC 边的中点，则FG =______cm．【答案】53【分析】根据折叠的性质可得DE =DC =4，EM =CM =2，连接DF ，设FE =x ，由勾股定理得BF ，DF ，从而求出x 的值，得出FB ，再证明FEG FBM ∆∆ ，利用相似三角形对应边成比例可求出FG ．【详解】解：连接,DF 如图，∵四边形ABCD 是正方形，∴4,90.AB BC CD DA A B C CDA ︒====∠=∠=∠=∠=∵点M 为BC 的中点，∴114222BM CM BC ===⨯=由折叠得，2,4,ME CM DE DC ====∠90,DEM C ︒=∠=∴∠90DEF ︒=，90,FEG ∠=︒设,FE x =则有222DF DE EF =+∴2224DF x =+又在Rt FMB ∆中，2,2FM x BM =+=，∵222FM FB BM =+∴FB ==∴4AF AB FB =-=在Rt DAF ∆中，222,DA AF DF +=∴2224(44,x +=+解得，124,83x x ==-（舍去）∴4,3FE =∴410233FM FE ME =+=+=∴83FB ==∵∠90DEM ︒=∴∠90FEG ︒=∴∠,FEG B =∠又∠.GFE MFB =∠∴△FEG FBM∆ ∴,FG FE FM FB=即4310833FG =∴5,3FG =故答案为：53【点睛】本题主要考查了正方形的性质，折叠的性质，勾股定理，相似三角形的判定与性质，正确作出辅助线是解答本题的关键．14．（2022·上海）如图，在△ABC 中，∠A =30°，∠B =90°，D 为AB 中点，E 在线段AC 上，AD DE AB BC=，则AE AC =_____．【答案】12或14【分析】由题意可求出12DE BC =，取AC 中点E 1，连接DE 1，则DE 1是△ABC 的中位线，满足112DE BC =，进而可求此时112AE AC =，然后在AC 上取一点E 2，使得DE 1＝DE 2，则212DE BC =，证明△DE1E2是等边三角形，求出E1E2＝14AC ，即可得到214AE AC =，问题得解．【详解】解：∵D 为AB中点，∴12AD DE AB BC ==，即12DE BC =，取AC 中点E 1，连接DE 1，则DE 1是△ABC 的中位线，此时DE 1∥BC ，112DE BC =，∴112AE AD AC AB ==，在AC 上取一点E 2，使得DE 1＝DE 2，则212DE BC =，∵∠A =30°，∠B =90°，∴∠C =60°，BC ＝12AC ，∵DE 1∥BC ，∴∠DE1E2=60°，∴△DE1E2是等边三角形，∴DE 1＝DE 2＝E1E2＝12BC ，∴E1E2＝14AC ，∵112AE AC =，∴214AE AC =，即214AE AC =，综上，AE AC 的值为：12或14，故答案为：12或14．【点睛】本题考查了三角形中位线的性质，平行线分线段成比例，等边三角形的判定和性质以及含30°角的直角三角形的性质等，根据12DE BC =进行分情况求解是解题的关键．15．（2022·北京）如图，在矩形ABCD 中，若13,5,4AF AB AC FC ===，则AE 的长为_______．【答案】1【分析】根据勾股定理求出BC ，以及平行线分线段成比例进行解答即可．【详解】解：在矩形ABCD 中：AD BC ∥，90ABC ∠=︒，∴14AE AF BC FC ==，4BC =，∴144AE =，∴1AE =，故答案为：1．【点睛】此题考查了勾股定理以及平行线分线段成比例，掌握平行线分线段成比例是解题的关键．16．（2022·江苏常州）如图，在Rt ABC △中，90C ∠=︒，9AC =，12BC =．在Rt DEF 中，90F ∠=︒，3DF =，4EF =．用一条始终绷直的弹性染色线连接CF ，Rt DEF 从起始位置（点D 与点B 重合）平移至终止位置（点E 与点A 重合），且斜边DE 始终在线段AB 上，则Rt ABC △的外部被染色的区域面积是______．【答案】28【分析】过点F 作AB 的垂线交于G ，同时在图上标出,,M N F '如图，需要知道的是Rt ABC 的被染色的区域面积是MNF F S '梯形，所以需要利用勾股定理，相似三角形、平行四边形的判定及性质，求出相应边长，即可求解．【详解】解：过点F 作AB 的垂线交于G ，同时在图上标出,,M N F '如下图：90C ∠=︒ ，9AC =，12BC =，15AB ∴==，在Rt DEF 中，90F ∠=︒，3DF =，4EF =．5DE ∴==，15510AE AB DE =-=-= ，//,EF AF EF AF ''= ，∴四边形AEFF '为平行四边形，10AE FF '∴==，11622DEF S DF EF DE GF =⋅=⋅= ，解得：125GF =， //DF AC ，,DFM ACM FDM CAM ∴∠=∠∠=∠，DFM ACM ∴ ∽，13DM DF AM AC ∴==，1115344DM AM AB ∴===，//BC AF ' ，同理可证：ANF DNC ' ∽，13AF AN BC DN '∴==，345344DN AN AB ∴===，451530444MN DN DM ∴=-=-=，Rt ABC 的外部被染色的区域面积为130121028245MNF F S '⎛⎫=⨯+⨯= ⎪⎝⎭梯形，故答案为：28．【点睛】本题考查了直角三角形，相似三角形的判定及性质、勾股定理、平行四边形的判定及性质，解题的关键是把问题转化为求梯形的面积．17．（2022·广西）数学兴趣小组通过测量旗杆的影长来求旗杆的高度，他们在某一时刻测得高为2米的标杆影长为1.2米，此时旗杆影长为7.2米，则旗杆的高度为______米．【答案】12【分析】根据同时、同地物高和影长的比不变，构造相似三角形，然后根据相似三角形的性质解答．【详解】解：设旗杆为AB ，如图所示：根据题意得：ABC DEF ∆∆ ，∴DE EF AB BC= ∵2DE =米， 1.2EF =米，7.2BC =米，∴2 1.2=7.2AB 解得：AB =12米．故答案为：12．【点睛】本题考查了中心投影、相似三角形性质的应用，解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．18．（2022·广东深圳）已知ABC 是直角三角形，90,3,5,B AB BC AE ∠=︒===连接CE 以CE 为底作直角三角形CDE 且,CD DE =F 是AE 边上的一点，连接BD 和,BF BD 且45,FBD ∠=︒则AF 长为______．【分析】将线段BD 绕点D 顺时针旋转90︒，得到线段HD ，连接BH ，HE ，利用SAS 证明EDH CDB ∆≅∆，得5EH CB ==，90HED BCD ∠=∠=︒，从而得出////HE DC AB ，则ABF EHF ∆∆∽，即可解决问题．【详解】解：将线段BD 绕点D 顺时针旋转90︒，得到线段HD ，连接BH ，HE ，BDH ∴∆是等腰直角三角形，又EDC ∆ 是等腰直角三角形，HD BD ∴=，EDH CDB ∠=∠，ED CD =，()EDH CDB SAS ∴∆≅∆，5EH CB ∴==，90HED BCD ∠=∠=︒，90EDC ∠=︒ ，90ABC ∠=︒，////HE DC AB ∴，,ABF EHF BAF HEF ∴∠=∠∠=∠，ABF EHF ∴∆∆∽，∴==-AB AF AF EH EF AE AF ，AE =∴35=AF ∴=，【点睛】本题主要考查了等腰直角三角形的性质，全等三角形的判定与性质，相似三角形的判定与性质等知识，解题的关键是作辅助线构造全等三角形．19．（2022·广西河池）如图，把边长为1：2的矩形ABCD 沿长边BC ，AD 的中点E ，F 对折，得到四边形ABEF ，点G ，H 分别在BE ，EF 上，且BG ＝EH ＝25BE ＝2，AG 与BH 交于点O ，N 为AF 的中点，连接ON ，作OM ⊥ON 交AB 于点M ，连接MN ，则tan ∠AMN ＝_____．【答案】58##0.625【分析】先判断出四边形ABEF 是正方形，进而判断出△ABG ≌△BEH ，得出∠BAG =∠EBH ，进而求出∠AOB =90°，再判断出△AOB ~△ABG ，求出OA OB ==△OBM ～△OAN ，求出BM =1，即可求出答案．【详解】解：∵点E ，F 分别是BC ，AD 的中点，∴11,22AF AD BE BC ==，∵四边形ABCD 是矩形，∴∠A =90°，AD ∥BC ，AD =BC ，∴12AF BE AD ==，∴四边形ABEF 是矩形，由题意知，AD =2AB ，∴AF =AB ，∴矩形ABEF 是正方形，∴AB =BE ，∠ABE =∠BEF =90°，∵BG =EH ，∴△ABG≌△BEH（SAS），∴∠BAG=∠EBH，∴∠BAG+∠ABO=∠EBH+∠ABO=∠ABG=90°，∴∠AOB=90°，∵BG＝EH＝25BE＝2，∴BE=5，∴AF=5，∴AG==∵∠OAB=∠BAG，∠AOB=∠ABG，∴△AOB∽△ABG，∴OA OB ABAB BG AG==，即52OA OB==∴OA OB==∵OM⊥ON，∴∠MON=90°=∠AOB，∴∠BOM=∠AON，∵∠BAG+∠FAG=90°，∠ABO+∠EBH=90°，∠BAG=∠EBH，∴∠OBM=∠OAN，∴△OBM～△OAN，∴OB BM OA AN=，∵点N是AF的中点，∴1522AN AF==，52BM=，解得：BM=1，∴AM=AB-BM=4，∴552tan48ANAMNAM∠===．故答案为：5 8【点睛】此题主要考查了矩形性质，正方形性质和判定，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，求出BM 是解本题的关键．20．（2022·内蒙古赤峰）如图，为了测量校园内旗杆AB 的高度，九年级数学应用实践小组，根据光的反射定律，利用镜子、皮尺和测角仪等工具，按以下方式进行测量：把镜子放在点O 处，然后观测者沿着水平直线BO 后退到点D ，这时恰好能在镜子里看到旗杆顶点A ，此时测得观测者观看镜子的俯角α=60°，观测者眼睛与地面距离CD =1.7m ，BD =11m ，则旗杆AB 的高度约为_________m ． 1.7≈）【答案】17【分析】如图容易知道CD ⊥BD ，AB ⊥BD ，即∠CDO =∠ABO =90°．由光的反射原理可知∠COD =∠AOB =60°，这样可以得到△COD ∽△AOB ，然后利用对应边成比例就可以求出AB ．【详解】解：由题意知∠COD =∠AOB =60°，∠CDE =∠ABE =90°，∵CD =1.7m ，∴OD =60CD tan =︒≈1(m)，∴OB =11-1=10(m)，∴△COD ∽△AOB ．∴CD OD AB OB =，即1.7110AB =，∴AB =17(m)，答：旗杆AB 的高度约为17m ．故答案为：17．【点睛】本题考查了解直角三角形的应用，相似三角形的应用，本题只要是把实际问题抽象到相似三角形中，利用相似三角形的性质就可以求出结果．21．（2022·湖北鄂州）如图，在边长为6的等边△ABC 中，D 、E 分别为边BC 、AC 上的点，AD 与BE 相交于点P ，若BD =CE =2，则△ABP 的周长为 _____．【答案】6+【分析】如图所示，过点E 作EF ⊥AB 于F ，先解直角三角形求出AF ，EF ，从而求出BF ，利用勾股定理求出BE 的长，证明△ABD ≌△BCE 得到∠BAD =∠CBE ，AD =BE ，再证明△BDP ∽△ADB ，得到62BP PD==，即可求出BP ，PD ，从而求出AP ，由此即可得到答案．【详解】解：如图所示，过点E 作EF ⊥AB 于F ，∵△ABC 是等边三角形，∴AB =BC ，∠ABD =∠BAC =∠BCE =60°，∵CE =BD =2，AB =AC =6，∴AE =4，∴cos 2sin AF AE EAF EF AE EAF =⋅∠==⋅∠=，，∴BF =4，∴BE =又∵BD =CE ，∴△ABD ≌△BCE （SAS ），∴∠BAD =∠CBE ，AD =BE ，又∵∠BDP =∠ADB ，∴△BDP ∽△ADB ，∴BD BP DP AD AB BD==，62BP PD==，∴BP PD =∴AP AD AP =-=，∴△ABP 的周长=6AB BP AP ++=故答案为：6+【点睛】本题主要考查了等边三角形的性质，解直角三角形，勾股定理，相似三角形的性质与判定，全等三角形的性质与判定，正确作出辅助线是解题的关键．22．（2022·山东潍坊）《墨子·天文志》记载：“执规矩，以度天下之方圆．”度方知圆，感悟数学之美．如图，正方形ABCD 的面积为4，以它的对角线的交点为位似中心，作它的位似图形A B C D ''''，若:2:1A B AB =''，则四边形A B C D ''''的外接圆的周长为___________．【答案】【分析】根据正方形ABCD 的面积为4，求出2AB =，根据位似比求出4A B ''=，周长即可得出；【详解】解：正方形ABCD 的面积为4，∴2AB =，:2:1A B AB ''=，∴4A B ''=，∴A C ''==所求周长=；故答案为：．【点睛】本题考查位似图形，涉及知识点：正方形的面积，正方形的对角线，圆的周长，解题关键求出正方形ABCD 的边长．23．（2022·内蒙古包头）如图，在Rt ABC 中，90ACB ∠=︒，3AC BC ==，D 为AB 边上一点，且BD BC =，连接CD ，以点D 为圆心，DC 的长为半径作弧，交BC 于点E （异于点C ），连接DE ，则BE的长为___________．【答案】3##3-+【分析】过点D 作DF ⊥BC 于点F ，根据题意得出DC DE =，根据等腰三角形性质得出CF EF =，根据90ACB ∠=︒，3AC BC ==，得出AB =CF x =，则3BF x =-，证明DF AC ，得出BF BDCF AD=，列出关于x 的方程，解方程得出x 的值，即可得出3BE =．【详解】解：过点D 作DF ⊥BC 于点F ，如图所示：根据作图可知，DC DE =，∵DF ⊥BC ，∴CF EF =，∵90ACB ∠=︒，3AC BC ==，∴AB ===∵3BD BC ==，∴3AD =，设CF x =，则3BF x =-，∵90ACB ∠=︒，∴AC BC ⊥，∵DF BC ⊥，∴DF AC ，∴BF BDCF AD =，即3x x -=，解得：x =，∴226CE x ===-，∴3363BE CE =-=-+=．故答案为：3．【点睛】本题主要考查了等腰三角形的性质和判定，勾股定理，平行线分线段成比例定理，平行线的判定，作出辅助线，根据题意求出CF 的长，是解题的关键．24．（2022·江苏泰州）如图上，Δ,90,8,6,ABC C AC BC ∠=== 中O 为内心，过点O 的直线分别与AC 、AB 相交于D 、E ，若DE=CD+BE ，则线段CD 的长为__________.【答案】2或12##12或2【分析】分析判断出符合题意的DE 的情况，并求解即可；【详解】解：①如图，作//DE BC ，OF BC OG AB ⊥⊥，，连接OB ，则OD ⊥AC ，∵//DE BC ，∴OBF BOE ∠=∠∵O 为ABC ∆的内心，∴OBF OBE ∠=∠，∴BOE OBE ∠=∠∴BE OE =，同理，CD OD =，∴DE=CD+BE ，10AB ===∵O 为ABC ∆的内心，∴OF OD OG CD ===，∴BF BG AD AG==，∴6810AB BG AG BC CD AC CD CD CD =+=-+-=-+-=∴2CD =②如图，作DE AB ⊥，由①知，4BE =，6AE =，∵ACB AED CAB EAD ∠=∠∠=∠，∴ABC ADE ∆∆ ∴AB ADAC AE=∴1061582AB AE AD AC ⋅⨯===∴151822CD AC AD =-=-=∵92DE ===∴19422DE BE CD =+=+=∴12CD =故答案为：2或12．【点睛】本题主要考查三角形内心的性质、勾股定理、三角形的相似，根据题意正确分析出符合题意的情况并应用性质定理进行求解是解题的关键．25．（2022·黑龙江绥化）如图，60AOB ∠=︒，点1P 在射线OA 上，且11OP =，过点1P 作11PK OA ⊥交射线OB 于1K ，在射线OA 上截取12PP ，使1211PPPK =；过点2P 作22P K OA ⊥交射线OB 于2K ，在射线OA 上截取23P P ，使2322P P P K =.按照此规律，线段20232023P K 的长为________．20221【分析】解直角三角形分别求得11PK ，22P K ，33P K ，……，探究出规律，利用规律即可解决问题．【详解】解：11PK OA ⊥ ，11OPK ∴△是直角三角形，在11Rt OPK 中，60AOB ∠=︒，11OP =，12111tan 60PP PK OP ∴==⋅︒=11PK OA ⊥ ，22P K OA ⊥，1122PK P K ∴∥，2211OP K OPK ∴△∽△，222111P K OP PK OP ∴=，=221P K ∴，同理可得：2331P K =+，3441P K =，……，11n n n P K -∴=，2022202320231P K ∴=，20221．【点睛】本题考查了图形的规律，解直角三角形，平行线的判定，相似三角形的判定与性质，解题的关键是学会探究规律的方法．26．（2022·黑龙江）如图，在平面直角坐标系中，点1A ，2A ，3A ，4A ……在x 轴上且11OA =，212OA OA =，322OA OA =，432OA OA =……按此规律，过点1A ，2A ，3A ，4A ……作x轴的垂线分别与直线y =交于点1B ，2B ，3B ，4B ……记11OA B ，22OA B △，33 OA B ，44 OA B ……的面积分别为1S ，2S ，3S ，4S ……，则2022S =______．【答案】2【分析】先求出11A B =，可得11OA B S =112233n n A B A B A B A B ⋯⋯∥∥∥∥，从而得到11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △，再利用相似三角形的性质，可得11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231:2:2:2::2n ，即可求解．【详解】解：当x =1时，y =，∴点(1B ，∴11A B =∴11112OA B S =⨯= ，∵根据题意得：112233n n A B A B A B A B ⋯⋯∥∥∥∥，∴11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △，∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ：……∶n n OA B S = OA 12∶OA 22∶OA 32∶……∶OAn 2，∵11OA =，212OA OA =，322OA OA =，432OA OA =，……，∴22OA =，2342OA ==，3482OA ==，……，12n n OA -=，∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231246221:2:2:2::21:2:2:2::2n n --= ，∴11222n n n OA B OA B S S -= ，∴220222202222S ⨯-==故答案为：2【点睛】本题主要考查了图形与坐标的规律题，相似三角形的判定和性质，明确题意，准确得到规律，是解题的关键．27．（2022·广西）如图，在正方形ABCD 中，AB =，对角线,AC BD 相交于点O ．点E 是对角线AC 上一点，连接BE ，过点E 作EF BE ⊥，分别交,CD BD 于点F 、G ，连接BF ，交AC 于点H ，将EFH △沿EF 翻折，点H 的对应点H '恰好落在BD 上，得到EFH '△若点F 为CD 的中点，则EGH '△的周长是_________．【答案】5+【分析】过点E 作PQ //AD 交AB 于点P ，交DC 于点Q ，得到BP =CQ ，从而证得BPE ≌EQF △，得到BE =EF ，再利用BC =F 为中点，求得BF ==BE EF ===，再求出2EO ==，再利用AB //FC ，求出ABH CFH △∽△21AH CH ==，求得216833AH =⨯=，18833CH =⨯=，从而得到EH =AH -AE =1610233-=，再求得EOB GOE △∽△得到21242OG ===，求得EG OG =1，过点F 作FM ⊥AC 于点M ，作FN ⊥OD 于点N ，求得FM =2，MH =23，FN =2，证得Rt FH N '△≌Rt FMH 得到23H N MH '==，从而得到ON =2，NG =1，25133GH '=+=，从而得到答案．【详解】解：过点E 作PQ //AD 交AB 于点P ，交DC 于点Q ，∵AD //PQ ，∴AP =DQ ，BPQ CQE ∠=∠，∴BP =CQ ，∵45ACD ∠=︒，∴BP =CQ =EQ ，∵EF ⊥BE ，∴90PEB FEQ ∠+∠=︒∵90PBE PEB ∠+∠=︒∴PBE FEQ ∠=∠，在BPE 与EQF △中BPQ FQE PB EQPBE FEQ ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BPE ≌EQF △，∴BE =EF ，又∵BC AB ==F 为中点，∴CF =∴BF ==∴BE EF ===，又∵4BO ==，∴2EO ==，∴AE =AO -EO =4-2=2，∵AB //FC ，∴ABH CFH △∽△，∴AB AH CF CH=，21AH CH ==，∵8AC ==， ∴216833AH =⨯=，18833CH =⨯=，∴EH =AH -AE =1610233-=，∵90BEO FEO ∠+∠=︒，+90BEO EBO ∠∠=︒，∴FEO EBO ∠=∠，又∵90EOB EOG ∠=∠=︒，∴EOB GOE△∽△∴EG OG OE BE OE OB==，21242OG ===，∴EG OG =1，过点F 作FM ⊥AC 于点M ，∴FM=MC 2=，∴MH =CH -MC =82233-=，作FN ⊥OD 于点N ，2,FN ==，在Rt FH N '△与Rt FMH 中FH FH FN FM'=⎧⎨=⎩∴Rt FH N '△≌Rt FHM∴23H N MH '==，∴ON =2，NG =1，∴25133GH '=+=，∴10533EGH C EH EG GH EH EG GH '''=++=++=△，故答案为：【点睛】本题考查了正方形的性质应用，重点是与三角形相似和三角形全等的结合，熟练掌握做辅助线是解题的关键．28．（2022·辽宁）如图，在正方形ABCD 中，E 为AD 的中点，连接BE 交AC 于点F ．若6AB =，则AEF 的面积为___________．【答案】3【分析】由正方形的性质可知1113222AE AD AB BC ====，//AD BC ，则有AEF CBF ∽△△，然后可得12EF AE BF BC ==，进而问题可求解．【详解】解：∵四边形ABCD 是正方形，6AB =，∴6AD BC AB ===，//AD BC ，∴AEF CBF ∽△△，∴EF AE BF BC=，∵E 为AD 的中点，∴1113222AE AD AB BC ====，∴12EF AE BF BC ==，192ABE S AE AB =⋅= ，∴13EF BE =，∴133AEF ABE S S == ；故答案为3．【点睛】本题主要考查正方形的性质及相似三角形的性质与判定，熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键．29．（2022·贵州贵阳）如图，在四边形ABCD 中，对角线AC ，BD 相交于点E ，6cm AC BC ==，90ACB ADB ∠=∠=︒．若2BE AD =，则ABE △的面积是_______2cm ，AEB ∠=_______度．【答案】 36-36- 112.5【分析】通过证明ADE BCE ，利用相似三角形的性质求出23m AE =，263m CE =-，再利用勾股定理求出其长度，即可求三角形ABE 的面积，过点E 作EF ⊥AB ，垂足为F ，证明AEF 是等腰直角三角形，再求出AE CE =，继而证明()Rt BCE Rt BFE HL ≅ ，可知122.52EBF EBC ABC ∠=∠=∠=︒，利用外角的性质即可求解．【详解】90,ACB ADB AED BEC ∠=∠=︒∠=∠ ，ADE BCE ∴ ，AD AE BC BE∴=，6,2BC AC BE AD === ，设,2AD m BE m ==，62m AE m∴=，23m AE ∴=，263m CE ∴=-，在Rt BCE 中，由勾股定理得222BC CE BE +=，22226(6)(2)2m m ∴+-=，解得236m =-或236m =+ 对角线AC ，BD 相交于点E ，236m ∴=-，12AE ∴=-，6CE ∴=，∴(2111263622ABE S AE BC =⋅⋅=⨯-⨯=- ，过点E 作EF ⊥AB ，垂足为F ，90,ACB AC BC ∠=︒= ，45BAC ABC AEF ∴∠=∠=︒=∠，6AE AF AE CE ∴====，BE BE = ，()Rt BCE Rt BFE HL ∴≅ ，122.52EBF EBC ABC ∴∠=∠=∠=︒，112.5AEB ACB EBC ∴∠=∠+∠=︒，故答案为：36-，112.5．【点睛】本题考查了相似三角形的判定和性质，勾股定理，等腰直角三角形的判定和性质，全等三角形的判定和性质及三角形外角的性质，熟练掌握知识点是解题的关键．三．解答题30．（2022·河北）如图，某水渠的横断面是以AB 为直径的半圆O ，其中水面截线MN AB ∥．嘉琪在A 处测得垂直站立于B 处的爸爸头顶C 的仰角为14°，点M 的俯角为7°．已知爸爸的身高为1.7m ．(1)求∠C 的大小及AB 的长；(2)请在图中画出线段DH ，用其长度表示最大水深（不说理由），并求最大水深约为多少米（结果保留小数点后一位）．（参考数据：tan 76︒取4 4.1）【答案】(1)=76C ∠︒， 6.8(m)AB =(2)见详解，约6.0米【分析】（1）由水面截线MN AB ∥可得BC AB ⊥，从而可求得76C ∠=︒，利用锐角三角形的正切值即可求解．（2）过点O 作O H M N ⊥，交MN 于D 点，交半圆于H 点，连接OM ，过点M 作MG ⊥OB 于G ，水面截线MN AB ∥，即可得DH 即为所求，由圆周角定理可得14BOM ∠=︒，进而可得ABC OGM ，利用相似三角形的性质可得4OG GM =，利用勾股定理即可求得GM 的值，从而可求解．(1)解：∵水面截线MN AB∥BC AB ∴⊥，90ABC ∴∠=︒，90=76C CAB ∴∠=︒-∠︒，在t R ABC 中，90ABC ∠=︒， 1.7BC =，tan 76 1.7AB AB BC ∴︒==，解得 6.8(m)AB ≈．(2)过点O 作O H M N ⊥，交MN 于D 点，交半圆于H 点，连接OM ，过点M 作MG ⊥OB 于G ，如图所示：水面截线MN AB ∥，OH AB ⊥，DH MN ∴⊥，GM OD =，DH ∴为最大水深，7BAM ∠=︒ ，214BOM BAM ∴∠=∠=︒，90ABC OGM ∠=∠=︒ ，且14BAC ∠=︒，ABC OGM ∴ ，OG MG AB CB ∴=，即6.8 1.7OG MG =，即4OG GM =，在Rt OGM △中，90OGM ∠=︒， 3.42AB OM =≈，222OG GM OM ∴+=，即2224(3.4)GM GM +=（），解得0.8GM ≈，= 6.80.86DH OH OD ∴-=-≈，∴最大水深约为6.0米．【点睛】本题考查了解直角三角形，主要考查了锐角三角函数的正切值、圆周角定理、相似三角形的判定及性质、平行线的性质和勾股定理，熟练掌握解直角三角形的相关知识是解题的关键．31．（2022·吉林）下面是王倩同学的作业及自主探究笔记，请认真阅读并补充完整．【作业】如图①，直线12l l ∥，ABC 与DBC △的面积相等吗？为什么？解：相等．理由如下：设1l 与2l 之间的距离为h ，则12ABC S BC h =⋅ ，12DBC S BC h =⋅△．∴ABC DBC S S = ．【探究】(1)如图②，当点D 在1l ，2l 之间时，设点A ，D 到直线2l 的距离分别为h ，h '，则ABC DBC S h S h ='△△．证明：∵ABC S(2)如图③，当点D 在1l ，2l 之间时，连接AD 并延长交2l 于点M ，则ABC DBC S AM S DM =△△．证明：过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，则90AEM DFM ∠=∠=︒，∴AE ∥ ．∴AEM △∽ ．∴AE AM DF DM =．由【探究】（1）可知ABC DBC S S =△△ ，∴ABC DBC S AM S DM =△△．(3)如图④，当点D 在2l 下方时，连接AD 交2l 于点E ．若点A ，E ，D 所对应的刻度值分别为5，1.5，0，ABC DBC S S △△的值为．【答案】(1)证明见解析(2)证明见解析(3)73【分析】（1）根据三角形的面积公式可得11,22ABC DBC S S BC h BC h '=⋅=⋅ ，由此即可得证；（2）过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，先根据平行线的判定可得AE DF ，再根据相似三角形的判定可证AEM DFM ~ ，根据相似三角形的性质可得AE AM DF DM=，然后结合【探究】（1）的结论即可得证；（3）过点A 作AM BC ⊥于点M ，过点D 作DN BC ⊥于点N ，先根据相似三角形的判定证出AME DNE ~ ，再根据相似三角形的性质可得73AM AE DN DE ==，然后根据三角形的面积公式可得12ABC S BC AM =⋅ ，12DBC S BC DN =⋅ ，由此即可得出答案．(1)证明：12ABC S BC h =⋅ ，12DBC BC h S '=⋅ ，ABC DBC S h S h ∴='．(2)证明：过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，则90AEM DFM ∠=∠=︒，AE DF ∴∥．AEM DFM ~∴ ．AE AM DF DM∴=．由【探究】（1）可知ABC DBC S AE S DF= ，ABC DBC S AM S DM ∴= ．(3)解：过点A 作AM BC ⊥于点M ，过点D 作DN BC ⊥于点N ，则90AME DNE ∠=∠=︒，AM DN ∴ ，AME DNE ∴~ ，AM AE DN DE∴=，点,,A E D 所对应的刻度值分别为5，1.5，0，5 1.5 3.5AE ∴=-=， 1.5DE =，3.571.53AM DN ∴==，又12ABC S BC AM =⋅ ，12DBC S BC DN =⋅ ，73ABCDBC S AM S DN =∴= ，故答案为：73．【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点，熟练掌握相似三角形的判定与性质是解题关键．32．（2022·山东青岛）如图，在Rt ABC △中，90,5cm,3cm ACB AB BC ∠=︒==，将ABC 绕点A 按逆时针方向旋转90︒得到ADE ，连接CD ．点P 从点B 出发，沿BA 方向匀速运动，速度为1cm/s ；同时，点Q 从点A 出发，沿AD 方向匀速运动，速度为1cm/s ．PQ 交AC 于点F ，连接,CP EQ ．设运动时间为(s)(05)t t <<．解答下列问题：(1)当EQ AD ⊥时，求t 的值；(2)设四边形PCDQ 的面积为()2cm S ，求S 与t 之间的函数关系式；(3)是否存在某一时刻t ，使PQ CD ∥？若存在，求出t 的值；若不存在，请说明理由．【答案】(1)16s 5(2)213714210S t t =-+(3)存在，65s 29t =【分析】（1）利用AQE AED △∽△得AQ AE AE AD =，即445t =，进而求解；（2）分别过点C ，P 作,CM AD PN BC ⊥⊥，垂足分别为M ，N ，证ABC CAM △∽△得，AB BC AC CA AM CM ==，求得121655AM CM ==，再证BPN BAC △∽△得BP PN BA AC=，得出45PN t =，根据ABC ACD APQ BPC PCDQ S S S S S S ==+-- 四边形即可求出表达式；（3）当PQ CD ∥时AQP ADC ∠=∠，易证APQ MCD △∽△，得出AP AQ MC MD =，则5161355t t -=，进而求出t 值．(1)解：在Rt ABC △中，由勾股定理得，4AC ===∵ABC 绕点A 按逆时针方向旋转90︒得到ADE。

初三数学相似三角形试题答案及解析

初三数学相似三角形试题答案及解析1.（2013山东济宁）如图，放映幻灯片时，通过光源，把幻灯片上的图形放大到屏幕上，若光源到幻灯片的距离为20cm，到屏幕的距离为60cm，且幻灯片中的图形的高度为6cm，则屏幕上图形的高度为________cm．【答案】18【解析】如图，过A作AN⊥BC，交DE于M．∵DE∥BC，∴△ADE∽△ABC，AM⊥DE，∴．设屏幕上图形的高度是xcm，则，解得x＝18．故答案为18．2.阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不可到达），他们带了以下测量工具：皮尺、标杆、一副三角尺、小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是________；（2）请在图中画出测量示意图；（3）设树AB的高度为x，请用所测数据（用小写字母表示）求出x．【答案】见解析【解析】（1）皮尺、标杆．（2）测量示意图如图所示．（3）如图，测得标杆DE＝a，树和标杆的影长分别为AC＝b，EF＝c．∵DF、BC是同一时刻的太阳光线，∴∠DFE＝∠BCA．又∵DE⊥AF，BA⊥AF，∴△DEF∽△BAC，∴，∴，∴．3.（2014山东潍坊）如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的标杆CD和EF，两标杆相隔52米，并且建筑物AB、标杆CD和EF在同一竖直平面内．从标杆CD后退2米到点G处，在G处测得建筑物顶端A和标杆顶端C在同一条直线上；从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，则建筑物的高是________米．【答案】54【解析】设建筑物的高为x米，根据题意易得△CDG∽△ABG，∴，∵CD＝DG＝2，∴BG＝AB＝x，再由△EFH∽△ABH可得，即，∴BH＝2x，即BD＋DF＋FH ＝2x，亦即x－2＋52＋4＝2x，解得x＝54，即建筑物的高是54米．4.已知：△ABC∽△A′B′C′，AB＝4cm，A′B′＝10cm，AE是△ABC的一条高，AE＝4.8cm．求△A′B′C′中对应高线A′E′的长．【答案】12cm【解析】∵△ABC∽△A′B′C′．∴．∴．∴A′E′＝12cm．5.两个相似三角形的相似比为2︰5，它们周长的差为9，则较大三角形的周长为________．【答案】15【解析】设较大三角形的周长为x，则较小三角形的周长为x－9，根据周长的比等于相似比可得（x－9）︰x＝2︰5，解得x＝15，即较大三角形的周长为15．6.（2013重庆）已知△ABC∽△DEF，若△ABC与△DEF的相似比为3︰4，则△ABC与△DEF的面积之比为（）A．4︰3B．3︰4C．16︰9D．9︰16【答案】D【解析】相似三角形面积的比等于相似比的平方．7.如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若AD︰AB＝3︰4，AE＝6，则AC等于（）A．3B．4C．6D．8【答案】D【解析】∵DE∥BC，∴，即，∴AC＝8．故选D．8.如图，△ABC∽△DEF，相似比为1︰2，若BC＝1，则EF的长是（）A．1B．2C．3D．4【答案】B【解析】∵△ABC∽△DEF，相似比为1︰2，∴BC︰EF＝1︰2．∵BC＝1，∴EF＝2．故选B．9.（2014浙江宁波）如图，梯形ABCD中，AD∥BC，∠B＝∠ACD＝90°，AB＝2，DC＝3，则△ABC与△DCA的面积比为（）A．2︰3B．2︰5C．4︰9D．【答案】C【解析】∵AD∥BC，∴∠ACB＝∠DAC．又∵∠B＝∠ACD＝90°，∴△CBA∽△ACD，∴．又∵AB ＝2，DC ＝3，∴，∴．故选C ．10. （2014江苏宿迁）如图，在直角梯形ABCD 中，AD ∥BC ，∠ABC ＝90°，AB ＝8，AD ＝3，BC ＝4，点P 为AB 边上一动点，若△PAD 与△PBC 是相似三角形，则满足条件的点P 个数是（）A ．1个B ．2个C ．3个D ．4个【答案】C【解析】∵AD ∥BC ，∠ABC ＝90°，∴∠A ＝90°．设AP 的长为x ，则BP 的长为8－x ．若AB 边上存在P 点，使△PAD 与△PBC 相似，那么分两种情况：①若△PAD ∽△PBC ，则AP ︰BP ＝AD ︰BC ，即x ︰（8－x ）＝3︰4，解得，经检验，其是原方程的解；②若△PAD ∽△CBP ，则AP ︰BC ＝AD ︰BP ，即x ︰4＝3︰（8－x ），解得x ＝2或x ＝6，经检验，它们都是原方程的解．故满足条件的点P 有3个，故选C ．11. （2013安徽）如图，P 为平行四边形ABCD 边AD 上一点，E 、F 分别为PB 、PC 的中点，△PEF ，△PDC ，△PAB 的面积分别为S ，S 1，S 2，若S ＝2，则S 1＋S 2＝________．【答案】8【解析】∵E 、F 分别为PB 、PC 的中点，∴EF 是△PBC 的中位线．∴EF ∥BC ，，∴△PEF ∽△PBC ，∴．∵S ＝2，∴S △PBC ＝8．∴S 1＋S 2＝S △PBC ＝8．12. 若△ABC 与△A′B′C′相似，一组对应边的长为AB ＝6cm ，A′B′＝8cm ，那么△ABC 与△A′B′C′的相似比为________．【答案】【解析】相似三角形的对应边的比叫做相似比，即相似比为．13. 如图，已知直线a ∥b ∥c ，直线m 、n 与a 、b 、c 分别交于点A 、C 、E 、B 、D 、F ，AC ＝4，CE＝6，BD＝3，则BF＝（）A．7B．7.5C．8D．8.5【答案】B【解析】∵a∥b∥c，∴，即．∴．∴BF＝BD＋DF＝3＋4.5＝7.5．14.如图，已知在等腰△ABC中，顶角∠A＝36°，BD为∠ABC的平分线，则一定相似的三角形是（）A．△ABC和△BADB．△ABD和△BDCC．△BDC和△ABCD．△ABD和△BDC和△ABC【答案】C【解析】∵∠A＝36°，AB＝AC，∴．又∵BD平分∠ABC，∴∠DBC＝36°．在△BDC和△ABC中，∠DBC＝∠A＝36°，∠C＝∠C，∴△BDC∽△ABC．故选C．15.在△ABC与△A′B′C′中，AB︰AC＝A′B′︰A′C′，∠B＝∠B′，则这两个三角形（）A．相似，但不全等B．全等或相似C．不相似D．无法判定是否相似【答案】D【解析】因为AB︰AC＝A′B′︰A′C′，∠B＝∠B′，条件中相等的角不是成比例的两边的夹角，所以无法判定是否相似，故选D．16.如图，已知∠1＝∠2，那么添加下列一个条件后，仍无法判定△ABC∽△ADE的是（）A．B．∠C＝∠AEDC．∠B＝∠DD．【答案】D【解析】由∠1＝∠2可得∠DAE＝∠BAC，但条件与∠DAE＝∠BAC不是成比例的两边与夹角的关系，故不能判定三角形相似．17.如图，点P是△ABC的边AC上一点，连接BP，以下条件中，不能判定△ABP∽△ACB的是（）A．B．C．∠ABP＝∠CD．∠APB＝∠ABC【答案】B【解析】△ABP和△ACB有公共角∠A，故添加，由“两边成比例且夹角相等的两个三角形相似”可得△ABP∽△ACB；添加∠ABP＝∠C或∠APB＝∠ABC，由“两角分别相等的两个三角形相似”可得△ABP∽△ACB；只有添加不能得出△ABP∽△ACB．故选B．18.（2014河北）在研究相似问题时，甲、乙同学的观点如下：对于两人的观点，下列说法正确的是（）A．两人都对B．两人都不对C．甲对，乙不对D．甲不对，乙对【答案】A【解析】由题意知新三角形与原三角形的对应角相等，对应边的比也相等，所以两个三角形相似，甲的观点正确；新矩形与原矩形的对应角相等，但对应边的比并不相等，所以新矩形与原矩形不相似，乙的观点也正确．故选A．19.如图，已知△ABC中，D为边AC上一点，P为边AB上一点，AB＝12，AC＝8，AD＝6，当AP的长为________时，△ADP和△ABC相似．【答案】4或9【解析】当△ADP∽△ACB时，需有，∴，解得AP＝9．当△ADP∽△ABC时，需有，∴，解得AP＝4．∴当AP的长为4或9时，△ADP和△ABC相似．20.如图，点A，B的坐标分别是（0，8），（6，0），过边OA上的点P（0，4）作直线PQ与△OAB的另一边相交于点Q，当点Q的坐标为________时，形成的新三角形与△OAB相似．【答案】（3，4）或（3，0）或（1.92，5.44）或（，0）【解析】由已知得OA＝8，OB＝6，OP＝4，由勾股定理可得AB＝10．①当PQ∥x轴时，△APQ∽△AOB，此时Q是AB的中点，可得Q（3，4）．②当PQ∥AB时，△OPQ∽△OAB，此时点Q是OB的中点，可得Q（3，0）．③当PQ⊥AB于Q时，由，可得△APQ∽△ABO，则，解得AQ＝3.2．此时，作QC⊥OA于C，可得△AQC∽△ABO，，即，解得AC＝2.56，QC＝1.92，∴OC＝8－2.56＝5.44，∴点Q（1.92，5.44）．④当时，△OPQ∽△OBA，则，解得，∴Q（，0）．故点Q的坐标为（3，4）或（3，0）或（1.92，5.44）或（，0）．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

相似三角形测试题
一选择题：
1.下列说法中正确的是（）
A.两个平行四边形一定相似
B.两个菱形一定相似
C.两个矩形一定相似
D.两个等腰直角三角形一定相似
2.在相同时刻的物高与影长成比例，如果高为1.5米的测竿的影长为2.5米，那么影长为30米的旗杆的高是（）
A.20米
B.18米
C.16米
D.15米
3.如图,DE∥BC,分别交△ABC的边AB,AC于点D,E,=，若AE=5,则EC长度为（）
A．10 B．15 C．20 D．25
4.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为
1:2,∠OCD=90°,CO=CD．若B（1，0），则点C的坐标为（）
A.(1,2)
B.(1,1)
C.(，)
D.(2,1)
5.△ABC的三边长分别为2，△DEF的两边长分别为1和，如果△ABC∽△DEF，那么△DEF的第三边长为（）
6.如图，Rt△ABC中，∠ACB=90°，AC=4，BC=6，以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E，则AD为（）
A.2.5
B.1.6
C.1.5
D.1
7.如图，点F在平行四边形ABCD的边AB上，射线CF交DA的延长线于点E，在不添加辅助线的情况下，与△AEF相似的三角形有（）
A．0个B．1个C．2个D．3个
8.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为（）
A. B. C. D.
9.如图，△ABC中，D、E两点分别在BC、AD上，且AD平分∠BAC，若∠ABE=∠C，AD：ED=3:1，则△BDE与△ADC的面积比为（）
A.16:45
B.2:9
C.1:9
D.1:3
10..如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴，y轴的正半轴上,正方形
A/B/C/D/与正方形ABCD是以AC的中点O/为中心的位似图形,已知AC=3,若点A/的坐标为(1,2),则正方形A/B/C/D/与正方形ABCD的相似比是( )
A. B. C. D.
11.如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,B上的两个动点,则BM+MN 最小值为（）
A．10 B．8 C．5D．6
12.将一副三角尺（在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中，∠EDF=90°,∠E=45°)如图摆放，点D为AB的中点，DE交AC于点P，DF经过点C，将△EDF绕点D顺时针方向旋转α（0°<α<60°），DE′交AC于点M，DF′交BC于点N，则的值为（）
A. B. C. D.
二填空题：
13.下面各组中的两个图形，是形状相同的图形，是形状不同的图形.
14.如图,在平行四边形ABCD中,对角线AC，BD相交于点O,点E，F分别是边AD,AB的中点,EF 交AC于点H,则AH:CH的值为．
15.如图，线段AB的两个端点坐标分别为A（1，1），B（2，1），以原点O为位似中心，将线
段AB放大后得到线段CD，若CD=2，则端点C的坐标为．
16.如图，在正方形ABCD中，E为AB边的中点，G、F分别为AD、BC边上的点．若AG=1，BF=2，∠GEF=90°，则GF的长为．
17.如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知折痕AE=5cm，且tan∠EFC=0.75，则矩形ABCD的周长为
18.如图,在△ABC中,AB=AC=10,点D是BC边上的一动点（不与B、C重
合）,∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=0.75,有以下的结论：
①△DBE∽△ACD；②△ADE∽△ACD；③△BDE为直角三角形时,BD为8或3.5；
④0＜BE≤5.其中正确的结论是（填入正确结论的序号）
三解答题：
19.如图,在平面直角坐标系中,已知△ABC 三个顶点的坐标分别为A （-1,2）,B （-3,4）C （-2,6）
（1）画出△ABC 绕点A 顺时针旋转90°后得到的△A 1B 1C 1
（2）以原点O 为位似中心，画出将△A 1B 1C 1三条边放大为原来的2倍后的△A 2B 2C 2．
20.如图,在△ABC 中,D 为AC 边上一点,∠DBC=∠A ．
（1）求证：△BCD ∽△ACB ；
（2）如果BC=,AC=3,求CD 的长．
21.已知在直角梯形ABCD中，AD∥BC，∠C=90°，AB=AD=25，BC=32．连接BD，AE⊥BD 垂足为E．
（1）求证：△ABE∽△DBC；
（2）求线段AE的长．
22.如图，已知△ABC中,AB＞AC,BC=6,BC边上的高AN=4.直角梯形DEFG的底EF在BC 边上,EF=4,点D、G分别在边AB、AC上,且DG∥EF,GF⊥EF,垂足为F.设GF的长为x,直角梯形DEFG的面积为y,求y关于x的函数关系式，并写出x的取值围．
23.如图F为平行四边形ABCD的AD延长线上一点,BF分别交CD、AC于G、E,若EF=32,GE=8,求BE.
24.（1）问题：
如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°，求证：AD•BC=AP•BP．
（2）探究：
如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．
（3）应用：请利用（1）（2）获得的经验解决问题：
如图3，在△ABD中，AB=6，AD=BD=5，点P以每秒1个单位长度的速度，由点A出了，沿边AB向点B运动，且满足∠DPC=∠A，设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB相切时，求t的值．
参考答案
1.D
2.B
3.A
4.B
5.C
6.B
7.C
8.B
9.B
10.B
11.B【解答】解：过B点作AC的垂线，使AC两边的线段相等，到E点，过E作EF垂直AB 交AB于F点，
AC=5，AC边上的高为2，所以BE=4．∵△ABC∽△EFB，∴=，即=,EF=8．故选B．
12.C
13.略
14.答案为：．
15.（2，1）
16.答案为：3．
17.答案为：36；
18.解：①∵AB=AC ，∴∠B=∠C ，又∵∠ADE=∠B ∴∠ADC=180°﹣α﹣∠BDE ， ∵∠BED=180°﹣α﹣∠BDE ，∴∠BED=∠ADC ∴△DBE ∽△ACD ，故①正确；
②∵∠B=∠C ，∴∠C=∠ADE ，不能得到△ADE ∽△ACD ；故②错误，
③当∠AED=90°时，由①可知：△ADE ∽△ABD ，∴∠ADB=∠AED ，
∵∠AED=90°，∴∠ADB=90°，即AD ⊥BC ，
∵AB=AC ，∴BD=CD ，∴∠ADE=∠B=α且cos α=0.8，AB=10，BD=8．
当∠BDE=90°时，易△BDE ∽△CAD ，∵∠BDE=90°，∴∠CAD=90°，
∵∠B=α且cos α=0.8．AB=10，∴cosC=0.8，∴CD=12.5，∴BD=BC ﹣CD=3.5；故③正确．
④过A 作AG ⊥BC 于G ，∵cos α=0.8，∴BG=8，∴BC=16，易证得△BDE ∽△CAD ，设BD=y ，BE=x ，∴=，∴=，整理得：y 2﹣16y+64=64﹣10x ，
即（y ﹣8）2=64﹣10x ，∴0＜x ≤6.4．故④错误．故答案为：①③．
19.【解答】解：如图：（1）△A 1B 1C 1 即为所求；
（2）△A 2B 2C 2 即为所求．
20.【解答】（1）证明：∵∠DBC=∠A，∠C=∠C，∴△BCD∽△ACB；
（2）解：∵△BCD∽△ACB，∴=，∴=，∴CD=2．
21.【解答】（1）证明：∵AB=AD=25，∴∠ABD=∠ADB，∵AD∥BC，∴∠ADB=∠DBC，∴∠ABD=∠DBC，∵AE⊥BD，∴∠AEB=∠C=90°，∴△ABE∽△DBC；（2）解：∵AB=AD，又AE⊥BD，∴BE=DE，∴BD=2BE，
由△ABE∽△DBC，得，∵AB=AD=25，BC=32，∴，∴BE=20，∴AE=25．
22.y关于x的函数关系式为：y═﹣3/4x2+5x（0＜x＜4）．
23.
24.。