江苏省苏州市2020～2021学年第一学期高三期初调研试卷数学(word版含答案)

合集下载

2020-2021学年江苏省南京市高二上学期期中调研测试数学试题 Word版

南京市2020－2021学年度第一学期期中调研测试高二数学2020.11注意事项：1．本试卷共6页，包括单项选择题（第1题~第8题）、多项选择题（第9题~第12题）、填空题（第13题~第16题）、解答题（第17题~第22题）四部分．本试卷满分为150分，考试时间为120分钟．2．答卷前，考生务必将自己的学校、姓名、考生号填涂在答题卡上指定的位置． 3．作答选择题时，选出每小题的答案后，用2B 铅笔在答题卡上将对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案．答案不能答在试卷上． 4．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内，在其他位置作答一律无效．一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的，请把答案填涂在答题卡相应位置上．1．在平面直角坐标系xOy 中，已知抛物线x 2＝2y 的焦点为F ，准线为l ，则点F 到直线l 的距离为A ．12B ．1C ．2D ．42．已知向量a ＝(－2，3，－1)，b ＝(4，m ，n )，且a ∥b ，其中m ，n ∈R ，则m ＋n ＝ A ．4 B ．－4 C ．2 D ．－2 3．若sin θ＝2cos(π－θ)，则tan(θ＋π4)的值为 A ．3 B ．13C ．－3D ．－134．在平面直角坐标系xOy 中，若椭圆C ：x 29＋y 2m ＝1与双曲线T ：x 2－y 2m ＝1有相同的焦点，则双曲线T 的渐近线方程为 A ．y ＝±14x B ．y ＝±12xC ．y ＝±4xD ．y ＝±2x5．在平面直角坐标系xOy 中，直线x ＋2y －4＝0与两坐标轴分别交于点A ，B ，圆C 经过A ，B ，且圆心在y 轴上，则圆C 的方程为A ．x 2＋y 2＋6y －16＝0B ．x 2＋y 2－6y －16＝0C ．x 2＋y 2＋8y －9＝0D ．x 2＋y 2－8y －9＝06．如图，已知圆柱的底面半径为2，与圆柱底面成60°角的平面截这个圆柱得到一个椭圆，则该椭圆的焦距为A ．2 2B ．2 3C ．42D ．437．如图，在三棱柱ABC －A 1B 1C 1中，BC 1与B 1C 相交于点O ，∠A 1AB ＝∠A 1AC ＝60°， ∠BAC ＝90°，A 1A ＝3，AB ＝AC ＝2，则线段AO 的长度为 A ．292B ．29C ．232D ．23 8．在平面直角坐标系xOy 中，已知双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左焦点为F ，点M ，N 在双曲线C 上．若四边形OFMN 为菱形，则双曲线C 的离心率为 A ．3－1 B ．5－1 C ．3＋1 D ．5＋1二、多项选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求，请把答案填涂在答题卡相应位置上．全部选对得5分，部分选对得3分，不选或有错选的得0分．9．已知两个不重合的平面α，β及直线m ，下列说法正确的是A ．若α⊥β，m ⊥α，则m ∥βB ．若α∥β，m ⊥α，则m ⊥βC ．若m ∥α，m ⊥β，则α⊥βD ．若m ∥α，m ∥β，则α∥β10．在平面直角坐标系xOy 中，F 1，F 2分别为椭圆 x 24＋y 22＝1的左、右焦点，点A 在椭圆上．若△AF 1F 2为直角三角形，则AF 1的长度可以为 A ．1B ．2C ．3D ．411．如图，直线l 1，l 2相交于点O ，点P 是平面内的任意一点，若x ，y 分别表示点P 到l 1，l 2的距离，则称(x ，y )为点P 的“距离坐标”．下列说法正确的是 A ．距离坐标为(0，0)的点有1个 B ．距离坐标为(0，1)的点有2个NP l 1（第6题）C 1（第7题）ABCB 1OC ．距离坐标为(1，2)的点有4个D ．距离坐标为(x ，x )的点在一条直线上12．20世纪50年代，人们发现利用静态超高压和高温技术，通过石墨等碳质原料和某些金属反应可以人工合成金刚石．人工合成金刚石的典型晶态为立方体（六面体）、八面体和立方八面体以及它们的过渡形态．其中立方八面体（如图所示）有24条棱、12个顶点、14个面（6个正方形、8个正三角形），它是将立方体“切”去8个“角”后得到的几何体．已知一个立方八面体的棱长为1，则A ．它的所有顶点均在同一个球面上，且该球的直径为2B ．它的任意两条不共面的棱所在直线都相互垂直C ．它的体积为523D ．它的任意两个共棱的面所成的二面角都相等三、填空题：本大题共4小题，每小题5分，共20分．请把答案填写在答题卡相应位置上． 13．在平面直角坐标系xOy 中，已知直线l 1：x ＋ay ＝0和直线l 2：2x －(a －3)y －4＝0，a ∈R ．若l 1与 l 2平行，则l 1与 l 2之间的距离为▲________．14．在空间直角坐标系中，若三点A (1，－1，a )，B (2，a ，0)，C (1，a ，－2)满足(AB →－2AC →)⊥BC →，则实数a 的值为▲________．15．词语“堑堵”、“阳马”、“鳖臑”等出自中国数学名著《九章算术·商功》，是古代人对一些特殊锥体的称呼．在《九章算术·商功》中，把四个面都是直角三角形的四面体称为“鳖臑”．现有如图所示的“鳖臑”四面体P ABC ，其中P A ⊥平面ABC ，P A ＝AC ＝1，BC ＝2，则四面体P ABC 的外接球的表面积为▲________．16．早在一千多年之前，我国已经把溢流孔技术用于造桥，以减轻桥身重量和水流对桥身的冲击．现设桥拱上有如图所示的4个溢流孔，桥拱和溢流孔轮廓线均为抛物线的一部分，且四个溢流孔轮廓线相同．建立如图所示的平面直角坐标系xOy ，根据图上尺寸，溢流孔ABC 所在抛物线的方程为▲________，溢流孔与桥拱交点A 的横坐标．．．为▲________．（第12题）ABC P（第15题）第16题四、解答题：本大题共6小题，共70分．请在答题卡指定区域内作答，解答时应写出必要的文字说明，证明过程或演算步骤． 17．（本小题满分10分）在 ①sin(A －B )＝sin B ＋sin C ；②2a cos C ＝2b ＋c ；③△ABC 的面积S ＝34(a 2－b 2－c 2) 三个条件中任选一个，补充在下面的问题中，并解答该问题．已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，__________，D 是边BC 上的一点，∠BAD ＝π2，且b ＝4，c ＝2，求线段AD 的长．注：如果选择多个条件分别解答，按第一个解答计分．18．（本小题满分12分）在平面直角坐标系xOy 中，已知圆F ：(x －2)2＋y 2＝1，动圆M 与直线l ：x ＝－1相切且与圆F 外切．（1）记圆心M 的轨迹为曲线C ，求曲线C 的方程；（2）已知A (－2，0)，曲线C 上一点P 满足P A ＝2PF ，求∠P AF 的大小．19．（本小题满分12分）如图，在直三棱柱ABC －A 1B 1C 1中，D 为AC 中点．（1）求证：B 1A ∥平面C 1BD ；（2）若AA 1＝AB ＝3，BC ＝4，且AB ⊥BC ，求三棱锥B －B 1C 1D 的体积．20．（本小题满分12分）在平面直角坐标系xOy 中，已知圆O ：x 2＋y 2＝1，点A ，B 是直线x －y ＋m ＝0(m ∈R )与圆O 的两个公共点，点C 在圆O 上．（1）若△ABC 为正三角形，求直线AB 的方程；（2）若直线x －y －3＝0上存在点P 满足AP →·BP →＝0，求实数m 的取值范围．DBB 1A 1（第19题）C 1AC21．（本小题满分12分）如图，在四棱锥P -ABCD 中，平面P AB ⊥平面ABCD ，P A ⊥AB ，P A ＝AD ＝4， BC ∥AD ，AB ⊥AD ，AB ＝BC ＝2，→PE ＝λ→PC (0≤λ＜1)．（1）若λ＝12，求直线DE 与平面ABE 所成角的正弦值；（2）设二面角B -AE -C 的大小为θ，若|cos θ|＝23417，求λ的值．22．（本小题满分12分）在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0) 的左顶点与上顶点的距离为23，且经过点(2，2)．（1）求椭圆C 的方程；（2）直线l 与椭圆C 相交于P ，Q 两点，M 是PQ 的中点．若椭圆上存在点N 满足 ON →＝3MO →，求证：△PQN 的面积S 为定值．（第21题）PABCDE（第22题图）南京市2020－2021学年度第一学期期中调研测试高二数学参考答案 2020.11一、单项选择题：本大题共8小题，每小题5分，共40分．1．B 2．B 3．D 4．D 5．A 6．D 7．A 8．C 二、多项选择题：本大题共4小题，每小题5分，共20分． 9．BC 10．ABC 11．ABC 12．ACD三、填空题：本大题共4小题，每小题5分，共20分． 13． 2 14．－92 15．4π 16．y ＝－536(x －14)2，14013四、解答题：本大题共6小题，共70分． 17．（本小题满分10分）解：选①．由条件① sin(A －B )＝sin B ＋sin C ，在△ABC 中，A ＋B ＋C ＝π，所以sin(A －B )＝sin B ＋sin(A ＋B )，即 sin A cos B －cos A sin B ＝sin B ＋sin A cos B ＋cos A sin B ， ……………… 2分从而sin B ＝－2cos A sin B ．因为B 为三角形内角，所以sin B ≠0，所以cos A ＝－12．因为A 为三角形内角，所以A ＝2π3． ……………… 4分在△ABC 中，因为b ＝4，c ＝2，故由正弦定理b sin B ＝c sin C得4sin C ＝2sin B ，即2sin C ＝sin B ，所以sin B ＝2sin C ＝2sin(π3－B )＝3cos B －sin B ，即2sin B ＝3cos B ．由sin B ≠0知cos B ≠0，因此tan B ＝sin B cos B ＝32． ……………… 8分因为∠BAD ＝π2，所以AD ＝AB ·tan B ＝3． ……………… 10分选②．由条件②2a cos C ＝2b ＋c ，结合余弦定理得2a ×b 2＋a 2－c 22ab＝2b ＋c ，即 a 2＝b 2＋c 2＋bc ， ……………… 2分所以cos A ＝b 2＋c 2－a 2 2bc ＝－12，因为A 为三角形内角，所以A ＝2π3． ……………… 4分在△ABC 中，因为b ＝4，c ＝2，故由正弦定理b sin B ＝c sin C得4sin C ＝2sin B ，即2sin C ＝sin B ，所以sin B ＝2sin C ＝2sin(π3－B )＝3cos B －sin B ，即2sin B ＝3cos B ．由sin B ≠0知cos B ≠0，因此tan B ＝sin B cos B ＝32． ……………… 8分因为∠BAD ＝π2，所以AD ＝AB ·tan B ＝3． ……………… 10分选③．由条件③，△ABC 的面积S ＝34(a 2－b 2－c 2)，得12bc sin A ＝34(－2bc cos A )，即sin A ＝－3cos A ， ……………… 2分因为A 为三角形内角，所以sin A ≠0，从而cos A ≠0，所以tan A ＝sin A cos A ＝－3，所以A ＝2π3． ……………… 4分在△ABC 中，因为b ＝4，c ＝2，故由正弦定理b sin B ＝csin C得4sin C ＝2sin B ，即2sin C ＝sin B ，所以sin B ＝2sin C ＝2sin(π3－B )＝3cos B －sin B ，即2sin B ＝3cos B ．由sin B ≠0知cos B ≠0，因此tan B ＝sin B cos B ＝32． ……………… 8分因为∠BAD ＝π2，所以AD ＝AB ·tan B ＝3． ……………… 10分另解：A ＝2π3（略）……………… 4分在△ABC 中，因为b ＝4，c ＝2，由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝42＋22－2×4×2×cos 2π3＝28，所以a ＝27．……………… 6分由正弦定理得a sin A ＝bsin B ，则sin B ＝b sin A a ＝4×sin2π327＝217，又B 为锐角，所以cos B ＝1－sin 2B ＝277，则tan B ＝sin B cos B ＝32．……… 8分在△ABD 中，因为∠BAD ＝π2，所以AD ＝AB ·tan B ＝3． ……………… 10分18．（本小题满分12分）解：（1）设M (x ，y )，圆M 的半径为r ．由题意知，MF ＝r ＋1，M 到直线l 的距离为r ．方法一：点M 到点F (2，0)的距离等于M 到定直线x ＝－2的距离，根据抛物线的定义知，曲线C 是以F (2，0)为焦点，x ＝－2为准线的抛物线．故曲线C 的方程为y 2＝8x ． ……………………6分方法二：因为MF ＝(x －2)2＋y 2＝r ＋1，|x ＋1|＝r ，x ＞－1，所以(x －2)2＋y 2＝x ＋2，化简得y 2＝8x ，故曲线C 的方程为y 2＝8x ． ……………………6分（2）方法一：设P (x 0，y 0)，由P A ＝2PF ，得(x 0＋2)2＋y 02＝2[(x 0－2)2＋y 02]， ……………………8分又y 02＝8x 0，解得x 0＝2，故P (2，±4)， ……………………10分所以k P A ＝±1，从而∠P AF ＝π4． …………………12分方法二：过点P 向直线x ＝－2作垂线，垂足为Q ．由抛物线定义知，PQ ＝PF ，所以P A ＝2PQ ， ……………………8分在△APQ 中，因为∠PQA ＝π2，所以sin ∠QAP ＝PQ P A ＝ 22， ……………………10分从而∠QAP ＝π4，故∠P AF ＝π4． …………………12分19．（本小题满分12分）（1）证明：连结B 1C 交BC 1于点O ，连结OD ．在三棱柱ABC －A 1B 1C 1中，BC ＝B 1C 1，BC ∥B 1C 1，所以四边形B 1BCC 1为平行四边形，所以O 为B 1C 中点．又因为D 为AC 中点，所以OD 为△CB 1A 的中位线，所以B 1A ∥OD ． …………………3分又因为B 1A ⊄平面C 1BD ，OD ⊂平面C 1BD ，所以B 1A ∥平面C 1BD ． …………………5分（2）解：方法一：三棱锥B －B 1C 1D 的体积就是三棱锥D －BB 1C 1的体积． …7分过点D 作DE ⊥BC ，垂足为E ．在直三棱柱ABC －A 1B 1C 1中，B 1B ⊥平面ABC ．B 1（第19题）A 1C 1BDAC OE因为DE ⊂平面ABC ，所以B 1B ⊥DE ．又因为DE ⊥BC ，且B 1B ，BC ⊂平面B 1BCC 1，B 1B ∩BC ＝B ，所以DE ⊥平面B 1BCC 1，即DE 为三棱锥D －BB 1C 1的高． ………9分在△ABC 中，AB ＝3，BC ＝4，且AB ⊥BC ，所以AC ＝32＋42＝5，sin C ＝35，在Rt △DEC 中，DC ＝12AC ＝52，所以DE ＝DC ×sin C ＝32．又△BB 1C 1的面积S ＝12×BB 1×B 1C 1＝12×3×4＝6，所以三棱锥D －BB 1C 1的体积V ＝13×S ×DE ＝3，故三棱锥B －B 1C 1D 的体积等于3．………12分方法二：三棱锥B －B 1C 1D 的体积就是三棱锥B 1－BDC 1的体积． ………7分因为（1）中已证B 1A ∥平面C 1BD ，所以B 1到平面BDC 1的距离等于A 到平面BDC 1的距离．因此三棱锥B 1－BDC 1的体积等于三棱锥A －BDC 1的体积，即等于三棱锥C 1－ABD 的体积．在直三棱柱ABC －A 1B 1C 1中，C 1C ⊥平面ABC ，所以C 1C 为三棱锥C 1－ABD 的高．………10分因为AB ＝3，BC ＝4，且AB ⊥BC ，S △ABC ＝12×AB ×BC ＝6．因为D 是AC 的中点，所以△ABD 的面积S ＝12S △ABC ＝3．故三棱锥C 1－ABD 的体积V ＝13×S ×C 1C ＝3，即三棱锥B －B 1C 1D 的体积等于3．………12分20．（本小题满分12分）解：（1）由△ABC 为正三角形，得∠AOB ＝2∠ACB ＝2π3，所以∠ABO ＝∠BAO ＝π6，所以原点O 到直线AB 的距离d ＝1×sin π6＝12． ………3分由点到直线的距离公式得|m |2＝12，解得m ＝22或－22．所以直线AB 的方程为2x －2y ＋2＝0或2x －2y －2＝0． ………5分（2）方法一：设A (x 1，y 1)，B (x 2，y 2)，P (x ，y )．因为AP →·BP →＝0，所以点P 在以AB 为直径的圆上．记该圆圆心为(x 0，y 0)，则⎩⎨⎧x ＝x 0，y ＝y 0是方程组⎩⎨⎧x ＋y ＝0，x －y ＋m ＝0的解，解得⎩⎨⎧x 0＝－m 2，y 0＝m 2．故以AB 为直径的圆的方程为(x ＋m 2)2＋(y －m 2)2＝1－m 22，其中－2＜m ＜2． …9分又点P 在直线x －y － 3 ＝0上，即直线与圆有公共点，所以|m ＋3|2≤1－m 22，即2m 2＋23m ＋1≤0．解得－3＋12≤m ≤1－32．综上，实数m 的取值范围是[－3＋12，1－32]． ………12分方法二：设A (x 1，y 1)，B (x 2，y 2)．联立直线AB 与圆O 方程，得⎩⎨⎧x 2＋y 2＝1，x －y ＋m ＝0，消去y 得2x 2＋2mx ＋m 2－1＝0． ①所以x 1，x 2是①的两个解，判别式△＝(2m )2－4×2×(m 2－1)＞0，即－2＜m ＜2，且x 1＋x 2＝－m ，x 1x 2＝m 2－12．………7分设点P (x ，y )，则AP →＝(x －x 1，y －y 1)，BP →＝(x －x 2，y －y 2)．由AP →·BP →＝0，得(x －x 1) (x －x 2)＋(y －y 1) (y －y 2)＝0， ②将y ＝x －3，y 1＝x 1＋m ，y 2＝x 2＋m 代入②，整理得2x 2－2(x 1＋x 2＋m ＋3)x ＋2x 1x 2＋(m ＋3)(x 1＋x 2)＋(m ＋3)2＝0．又x 1＋x 2＝－m ，x 1x 2＝m 2－12，所以2x 2－23x ＋m 2＋3m ＋2＝0，关于x 的方程2x 2－23x ＋m 2＋3m ＋2＝0有实数解， ………10分因此(－23)2－4×2×(m 2＋3m ＋2)≥0，即2m 2＋23m ＋1≤0，解得－3＋12≤m ≤1－32．综上，实数m 的取值范围是[－3＋12，1－32]． ………12分 21．（本小题满分12分）解：因为平面P AB ⊥平面ABCD ，P A ⊥AB ，平面P AB ∩平面ABCD ＝AB ，P A ⊂平面P AB ，所以P A ⊥平面ABCD ．因为AD ⊂平面ABCD ，所以P A ⊥AD ．又AB ⊥AD ，所以P A ，AB ，AD 两两互相垂直．以{AB →，AD →，AP →}为正交基底，建立如图所示的空间直角坐标系A -xyz ．…………2分因为P A ＝AD ＝4，AB ＝BC ＝2，所以A (0，0，0)，B (2，0，0)，C (2，2，0)，D (0，4，0)，P (0，0，4)．（1）若λ＝12，即E 为PC 中点，则E ()1，1，2，所以DE →＝()1，－3，2，AB →＝()2，0，0，AE →＝()1，1，2．设平面ABE 的一个法向量为m ＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧m ·AB →＝0，m ·AE →＝0，即⎩⎪⎨⎪⎧2x 1＝0，x 1＋y 1＋2z 1＝0．令z 1＝1，得y 1＝－2，所以平面ABE 的一个法向量为m ＝(0，－2，1)． …………………4分设直线DE 与平面ABE 所成角为α，则sin α＝|cos ＜DE →，m ＞|＝|6＋214×5|＝47035． …………………6分（2）因为PE →＝λPC →(0≤λ＜1)，则E (2λ，2λ，4－4λ)．设平面ABE 的一个法向量为n ＝(x 2，y 2，z 2)，则⎩⎪⎨⎪⎧n ·AB →＝0，n ·AE →＝0，即⎩⎪⎨⎪⎧2x 2＝0，2λx 2+2λy 2+(4－4λ)z 2＝0．令y 2＝2，得z 2＝λλ－1，所以平面ABE 的一个法向量为n ＝(0，2，λλ－1)．设平面AEC 的一个法向量为l ＝(x 3，y 3，z 3)，则⎩⎪⎨⎪⎧l ·AC →＝0，l ·AP →＝0，即⎩⎪⎨⎪⎧2x 3＋2y 3＝0，4z 3＝0．令x 3＝1，得y 3＝－1，所以平面AEC 的一个向量为l ＝(1，－1，0)． ……………………9分（或证明CD ⊥平面P AC ，从而CD →为平面P AC 的一个法向量）因为二面角B -AE -C 的大小为θ，且|cos θ|＝23417，得|cos ＜n ，l ＞|＝|－24＋(λλ－1)2×2|＝23417，整理得3λ2＋2λ－1＝0，解得λ＝13，或λ＝－1(舍)．所以λ＝13． ……………12分22．（本小题满分12分）解：（1）椭圆C 的左顶点(－a ，0)，上顶点(0，b )．因为左顶点与上顶点的距离为23，所以a 2＋b 2＝23，化简得a 2＋b 2＝12． ① 因为椭圆经过点(2，2)，所以4a 2＋2b 2＝1，② …………2分由①②解得a 2＝8，b 2＝4或a 2＝6，b 2＝6（舍去），所以椭圆C 的方程为x 28＋y 24＝1． …………4分（2）当PQ 斜率不存在时，N 为(±22，0)，PQ 方程为x ＝±223，易得PQ ＝823，此时S ＝12×MN ×PQ ＝12×823×823＝649． …………5分当PQ 斜率存在时，设PQ 的方程为y ＝kx ＋m (m ≠0)，联立⎩⎪⎨⎪⎧y ＝kx ＋m ，x 28＋y 24＝1得(1＋2k 2)x 2＋4kmx ＋2(m 2－4)＝0，由△＝(4km )2－8(1＋2k 2)(m 2－4)＞0，得0＜m 2＜8k 2＋4．（*）设P (x 1，y 1)，Q (x 2，y 2)，则x 1＋x 2＝－4km 1＋2k 2，x 1x 2＝2(m 2－4)1＋2k 2，因此PQ 的中点M 为(－2km 1＋2k 2，m1＋2k 2)．又因为ON →＝3MO →，所以N (6km 1＋2k 2，－3m 1＋2k 2)，将点M 代入椭圆方程，得18k 2m 24(1＋2k 2)2＋9m 24(1＋2k 2)2＝1，化简得2k 2＋1＝94m 2，符合（*）式． ……………9分记点O 到直线l 的距离为d ，则S ＝4S △OPQ ＝2PQ ×d ＝21＋k 2|x 1－x 2|×d＝21＋k 2×22×8k 2＋4－m 21＋2k 2×|m |1＋k2＝42|m |×8k 2＋4－m 21＋2k 2，将2k 2＋1＝94m 2代入，得S ＝42|m |×9m 2－m 294m 2＝649．综上，△PQN 的面积S 为定值649． …………12分。

2021年江苏省苏州市中考数学真题试卷(word版,含解析)

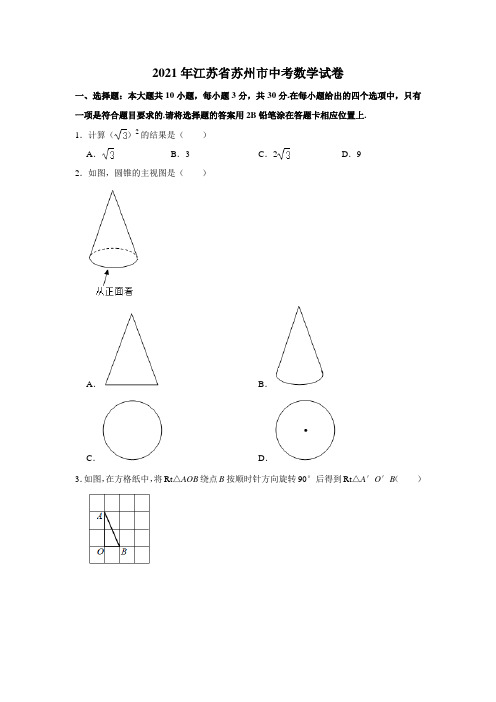
2021年江苏省苏州市中考数学试卷一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.请将选择题的答案用2B铅笔涂在答题卡相应位置上.1．计算（）2的结果是（）A．B．3C．2D．92．如图，圆锥的主视图是（）A．B．C．D．3．如图，在方格纸中，将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B（）A ．B ．C ．D ．4．已知两个不等于0的实数a、b满足a+b＝0，则+等于（）A．﹣2B．﹣1C．1D．25．为增强学生的环保意识，共建绿色文明校园，某学校组织“废纸宝宝旅行记”活动．经统计班级一班二班三班四班五班4.5 4.45.1 3.3 5.7废纸重量（kg）则每个班级回收废纸的平均重量为（）A．5kg B．4.8kg C．4.6kg D．4.5kg6．已知点A （，m），B （，n）在一次函数y＝2x+1的图象上，则m与n的大小关系是（）A．m＞n B．m＝n C．m＜n D．无法确定7．某公司上半年生产甲、乙两种型号的无人机若干架，已知甲种型号无人机架数比总架数的一半多11架，乙种型号无人机架数比总架数的三分之一少2架．设甲种型号无人机x 架，根据题意可列出的方程组是（）A ．B ．C．D．8．已知抛物线y＝x2+kx﹣k2的对称轴在y轴右侧，现将该抛物线先向右平移3个单位长度，再向上平移1个单位长度后，则k的值是（）A．﹣5或2B．﹣5C．2D．﹣29．如图，在平行四边形ABCD中，将△ABC沿着AC所在的直线得到△AB′C，连接B′D，若∠B＝60°，AC＝，则B′D的长是（）A．1B．C．D．10．如图，线段AB＝10，点C、D在AB上，以每秒1个单位长度的速度沿着AB向点D移动，到达点D后停止移动．在点P移动过程中作如下操作：先以点P为圆心，再将两个扇形分别围成两个圆锥的侧面，设点P的移动时间为t（秒），则S关于t的函数图象大致是（）A．B．C．D．二、填空题：本大题共8小题，每小题3分，共24分.把答案直接填在答题卡相应位置上。

江苏省苏州市2023-2024学年高三上学期期初调研测试生物

2023~2024学年第一学期高三期初调研测试生物学2023. 09一、单项选择题:共14 题,每题2分,共28分。

每题只有一个选项最符合题意。

1.下列关于细胞生命历程的叙述,正确的是A.多细胞生物的生长是细胞增殖的结果B.高度分化的细胞中不存在DNA复制C.衰老细胞的染色质固缩,细胞核缩小D.细胞凋亡时，基因发生了选择性表达2.高尔基体是有“极性”的,其顺面接受由内质网合成的物质并转入中间膜囊进一步修饰加工，反面参与溶酶体酶等蛋白质的分类和包装。

如图是发信号生在反面的3条分选途径。

下列叙述错误的是A.在高尔基体中间膜囊中会形成具有一定功能的蛋白质B.胰岛B细胞分泌胰岛素的过程属于是调节型分泌.C.若反面上的M6P受体数量减少会影响衰老细胞器的水解D.膜的流动性使顺面和反面的蛋白质种类和数量相同3.线粒体内膜是有氧呼吸第三阶段的场所,其上存在两条呼吸途径。

主呼吸链途径发生时，电子传递链释放的能量使H+通过蛋白复合体从基质移至内外膜间隙，然后H+驱动ATP合酶合成ATP;交替呼吸途径发生时，不发生H+的跨膜运输。

下列叙述的错误是A.合成ATP时H+顺浓度梯度由内外膜间隙进人基质B.主呼吸链途径中的蛋白复合体起载体蛋白的作用C.交替呼吸途径比主呼吸链途径产生更多的ATPD.乳酸菌细胞内不存在主呼吸链和交替呼吸途径4.下列关于构成细胞的元素和化合物的叙述,正确的是A.Mg是叶绿素的重要组分,缺Mg叶脉周围通常呈现黄色B.缺乏P时细胞中磷脂、核酸和A TP等物质的合成会受影响C.果糖是光合作用植物特有的，而半乳糖是动物特有的D.真核生物遗传信息的载体主要是由蛋白质和DNA组成的5.某家族患有甲、乙两种单基因遗传病,其中一种病的致病基因位于X染色体上。

研究人员通过调查得到了该家族的遗传系谱图(图1) ,然后对I1、II2、II3及III2的两对基因进行电泳分离,得到了不同的条带(图2)。

下列叙述正确的是A.甲病是伴X染色体显性遗传病，乙病是常染色体隐性遗传病B.条带①代表甲病的致病基因,条带③代表乙病的致病基因C.对II的两对基因进行电泳分离，所得的条带应该是①和③D.只考虑甲、乙两种遗传病，I4和II1基因型相同的概率是1/26.为研究DNA复制机制,科学家用荧光染料给Rep(解旋酶中驱动复制叉移动的结构)加上标记，以获知Rep相对于DNA分子的运动轨迹(如图)。

江苏省南京市2020-2021学年七年级下学期期中考试数学试卷(word版含答案)

2020~2021学年度第二学期期中学情分析样题七年级数学注意事项：1．本试卷共6页．全卷满分100分．考试时间为100分钟．考生答题全部答在答题卷上，答在本试卷上无效．2．请认真核对监考教师在答题卷上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卷及本试卷上．3．答选择题必须用2B 铅笔将答题卷上对应的答案标号涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案．答非选择题必须用0.5毫米黑色墨水签字笔写在答题卷上的指定位置，在其他位置答题一律无效．4．作图必须用2B 铅笔作答，并请加黑加粗，描写清楚．一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡．．．相应位置．．．．上） 1．在下列图形中，∠1与∠2是同位角的是A ．B ．C ．D ．2．计算（－a 2）3的结果是 A ．a 5B ．－a 5C ．a 6D ．－a 63．下列各式能用平方差公式计算的是 A ．（a ＋b ）（b ＋a ）B ．（2a ＋b ）（2b －a ）C ．（a ＋1）（－a －1）D ．（2a －1）（2a ＋1）4．如图，点E 在AC 的延长线上，下列条件中不能判断．．．．BD ∥AC 的是 A ．∠1＝∠2B ．∠3＝∠4C ．∠D ＝∠DCE D ．∠D ＋∠ACD ＝180°5．能说明命题“如果|a |＝|b |，那么a ＝b ”是假命题的反例是A ．a ＝2，b ＝2B ．a ＝－2，b ＝3C ．a ＝－3，b ＝3D ．a ＝－3，b ＝－3 6．如图，两个正方形的边长分别为a 和b ，如果a ＋b ＝10,a b ＝22，那么阴影部分的面积是 A ．15B ．17C ．20B 31 4 2（第4题）ACDE121 21221（第6题）二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置．．．．．．．上） 7．计算：20＝ ▲ ，2－1＝ ▲ ． 8．多项式3a 2b －6a 3b 各项的公因式是 ▲ ．9．新型冠状病毒的直径大约是0.000 000 7米，将0.000 000 7用科学记数法表示为 ▲ ．10．已知⎩⎨⎧x =2，y =3是二元一次方程x ＋ky ＝－1的一个解，那么k 的值是 ▲ ．11．若 2m ＝3，2n ＝2，则2m －2n的值为 ▲ ．12．已知x 、y 满足方程组⎩⎪⎨⎪⎧x ＋3y ＝－1x －y ＝3 则x ＋y 的值为 ▲ ．13．命题“垂直于同一条直线的两条直线平行”写成“如果…，那么…”的形式为：如果 ▲ ，那么14．公式（a －b ）2＝a 2a ＋b ）2＝a 2＋2ab ＋b 2推导得出，已知（a ＋b ）3＝a 3＋3a 2b ＋3ab 2＋b 3，则（a －b ）3＝ ▲ ．15．如图，将一张长方形纸片沿EF 折叠后，点D 落在BC 上的点D'处，点C 落在点C'处．若∠DEF ＝62°，则∠C'F D'＝ ▲ °．16．如图，AB //DE ，∠C ＝30°，∠CDE －∠B ＝110°，则∠CDE ＝ ▲ °．三、解答题（本大题共10小题，共68分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤） 17．（6分）计算：（1）a 6÷a 2－2a 3·a ；（2）2x （x －2y ）－（x －y ）2．18．（6分）因式分解：（1）3ab 2＋6ab ＋3a ；（2）a 2（a －b ）－4（a －b ）．（第15题）ABCDEFD ´C ´AB（第16题）ED，，19．（7分）先化简，再求值：（m －2n ）（m ＋2n ）－（m －2n ）2＋4n 2，其中m ＝－2，n ＝12．20．（7分）解二元一次方程组⎩⎪⎨⎪⎧3x ＋y ＝1， ①x －2y ＝12．②（1）有同学这么做：由②，得x ＝2y ＋12．③将③代入①，得3（2y ＋12）＋y ＝1，解得y ＝－5，将y ＝－5代入③，得x ＝2，所以这个方程组的解为⎩⎨⎧x ＝2y ＝－5．该同学解这个方程组的过程中使用了代入消元法，目的是把二元一次方程组转化为 ▲ ．（2）请你用加减消元法解该二元一次方程组．21．（5分）如图，点A 、B 、C 、D 在同一条直线上，EC //FD ，∠F ＝∠E ，求证：AE //BF ．将证明过程补充完整，并在括号内填写推理依据．证明：∵EC //FD ，（已知）∴∠F ＝∠ ▲ ．( ▲ ) ∵∠F ＝∠E ，（已知）∴∠ ▲ ＝∠E ，( ▲ ) ∴AE //BF ．( ▲ )CDEABF(第21题)1222．（6分）如图，在每个小正方形边长为1的方格纸中，点A 、B 、A 1都在方格纸的格点上．（1）平移线段AB ，使点A 与点A 1重合，点B 与点B 1重合，画出线段A 1B 1；（2）连接AA 1、BB 1，AA 1与BB 1的关系是 ▲ ；（3）四边形ABB 1A 1的面积是 ▲ ．23．（6分）同底数幂的乘法公式为：a m ·a n ＝ ▲ （m 、n 是正整数）.请写出这一公式的推导过程.24．（6分）观察下列各式：①32－12＝4×2； ②42－22＝4×3； ③52－32＝4×4；……（1）探索以上式子的规律，写出第n 个等式 ▲ （用含n 的字母表示）；（2）若式子a 2－b 2＝2020满足以上规律，则a ＝ ▲ ，b ＝ ▲ ；（3）计算：20＋24＋28＋ (100)（第22题）A。

2024-2025学年江苏省苏州市高三上学期开学调研化学试题及答案

2025届高三年级期初阳光调研试卷化学注意事项：1．本试卷分为单项选择题和非选择题两部分，试卷满分100分。

考试时间75分钟。

2．将选择题答案填涂在答题卡的对应位置上，非选择題的答案写在答题卡的指定栏目内。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 S 32 Fe 56 Mo 96一、单项选择题：共13题，每题3分，共39分。

每题只有一个选项最符合题意。

1．第19届杭州亚运会采用石墨烯纳米防滑涂层以增加地面防滑性。

石墨烯属于（）A ．有机材料B ．无机非金属材料C ．金属材料D ．复合材料2．草酸易被NaClO 氧化：22422H C O +NaClO=NaCl+2CO +H O ↑，下列说法不．正确的是（）A ．2CO 的空间构型为直线形B ．NaClO 属于离子化合物C ．2H O 的电子式为+2-+H [O ]H ∶∶D ．Cl 的结构示意图为3．实验室模拟侯氏制碱法制备23Na CO ，下列装置与原理均正确的是（）A ．制取2COB ．制取3NHC ．制取3NaHCOD ．制取23Na CO 4．()344Cu NH SO ⎡⎤⎣⎦常用作杀虫剂、媒染剂。

下列说法正确的是（）A ．原子半径：r(N)>r(O)>r(S)B ．沸点：223H S>H O>NHC ．第一电离能：111I (N)>I (O)>I (S)D ．电负性：χ(N)>χ(O)>χ(Cu)阅读下列材料，完成5~7题：VA 族元素及其化合物应用广泛。

3NH 催化氧化生成NO ，NO 继续被氧化为2NO ，将2NO 通入水中可制得3HNO ；肼（24N H ）常温下为液态，燃烧热大（-1642kJ mol ⋅），产物无污染，常用作火箭燃料：白磷（4P ）为正四面体结构，常用来制烟雾弹、燃烧弹；雄黄（44As S ）具有解毒、杀虫功效，燃烧后生成砒霜（23As O ）和一种具有刺激性气味的气体；锑是一种银白色金属，其氧化物23Sb O 可用于制造颜料，铅锑合金可用作铅蓄电池的电极材料。

江苏省苏州市2021届高三第一学期开学调研数学试卷

江苏省苏州市2020～2021学年第一学期高三期初调研试卷数学试题2020．9一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上） 1．集合A ＝{}2230x x x --≤，B ＝{}1x x >，A B ＝A ．(1，3)B ．(1，3]C ．[﹣1，+∞)D ．(1，+∞)2．复数z 满足(1＋i)z ＝2＋3i ，则z 在复平面表示的点所在的象限为 A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3．421(2)x x-的展开式中x 的系数为 A ．﹣32B ．32C ．﹣8D ．84．已知随机变量ξ服从正态分布N(1，2σ)，若P(ξ＜4)＝0.9，则P(﹣2＜ξ＜1)为 A ．0.2 B ．0.3 C ．0.4 D ．0.65．在△ABC 中，AB+AC=2AD ，AE+2DE=0，若EB=XAB+YAC ，则 A ．y ＝2x B ．y ＝﹣2x C ．x ＝2y D ．x ＝﹣2y6．大西洋鲑鱼每年都要逆流而上，游回到自己出生的淡水流域产卵，记鲑鱼的游速为v (单位：m /s )，鲑鱼的耗氧量的单位数为Q ．科学研究发现v 与3Qlog 100成正比，当v ＝1m /s 时，鲑的耗氧量的单位数为900．当v ＝2m /s 时，其耗氧量的单位数为 A ．1800 B ．2700 C ．7290 D ．81007．如图，正方体ABCD —A 1B 1C 1D 1的棱长为1，则下列四个命题不正确的是 A ．直线BC 与平面ABC 1D 1所成的角等于4πB ．点C 到面ABC 1D 1 C ．两条异面直线D 1C 和BC 1所成的角为4πD ．三棱柱AA 1D 1—BB 1C 1外接球半径为3 8．设a ＞0，b ＞0，且2a ＋b ＝1，则12a a a b++ A ．有最小值为4B ．有最小值为221+ C ．有最小值为143D ．无最小值二、多项选择题（本大题共4小题，每小题5分，共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上） 9．A ，B 是不在平面α内的任意两点，则A ．在α内存在直线与直线AB 异面B ．在α内存在直线与直线AB 相交C ．存在过直线AB 的平面与α垂直D ．在α内存在直线与直线AB 平行10．水车在古代是进行灌溉引水的工具，亦称“水转简车”，是一种以水流作动力，取水灌田的工具．据史料记载，水车发明于隋而盛于唐，距今已有1000多年的历史，是人类的一项古老的发明，也是人类利用自然和改造自然的象征，如图是一个半径为R 的水车，一个水斗从点A(3，33-)出发，沿圆周按逆时针方向匀速旋转，且旋转一周用时120秒．经过t 秒后，水斗旋转到P 点，设点P 的坐标为(x ，y )，其纵坐标满足()Ry f t ==sin()t ωϕ+(t ≥0，ω＞0，2πϕ<)，则下列叙述正确的是 A ．3πϕ=-B ．当t ∈(0，60]时，函数()y f t =单调递增C ．当t ∈(0，60]时，()f t 的最大值为33D ．当t ＝100时，PA 6=11．把方程1x x y y +=表示的曲线作为函数()y f x =的图象，则下列结论正确的有 A ．()y f x =的图象不经过第三象限 B ．()f x 在R 上单调递增C ．()y f x =的图象上的点到坐标原点的距离的最小值为1D ．函数()()g x f x x =+不存在零点 12．数列{}n a 为等比数列 A ．{}1n n a a ++为等比数列 B ．{}1n n a a +为等比数列 C ．{}221n n a a ++为等比数列D ．{}n S 不为等比数列(n S 为数列{}n a 的前n 项和三、填空题（本大题共4小题，每小题5分，共计20分．请把答案填写在答题卡相应位置上）13．已知tan 2α=，则cos(2)2πα+＝．14．已知正方体棱长为2，以正方体的一个顶点为球心，以为半径作球面，则该球面被正方体表面所截得的所有的弧长和为．15．直线40kx y ++=将圆C ：2220x y y +-=分割成两段圆弧之比为3：1，则k ＝． 16．已知各项均为正数的等比数列{}n a ，若4321228a a a a +--=，则872a a +的最小值为．四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤） 17．（本小题满分10分）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，△ABC 的面积为S ．现在以下三个条件：①(2c ＋b)cosA ＋acosB ＝0；②sin 2B ＋sin 2C ﹣sin 2A ＋sinBsinC ＝0；③a 2﹣b 2﹣c 2＝3S ．请从以上三个条件中选择一个填到下面问题中的横线上，并求解．已知向量m ＝(4sin x ，，n ＝(cos x ，sin 2x )，函数()23f x m n =⋅-，在△ABC 中，a ＝()3f π，且，求2b ＋c 的取值范围． 18．（本小题满分12分）已知各项均不相等的等差数列{}n a 的前4项和为10，且1a ，2a ，4a 是等比数列{}n b 的前 3项．（1）求{}n a ，{}n b ；（2）设1(1)n n n n c b a a =++，求{}n c 的前n 项和n S ．19．（本小题满分12分）如图，在四棱锥S —ABCD 中，ABCD 是边长为4的正方形，SD ⊥平面ABCD ，E ，F 分别为AB ，SC 的中点．（1）证明：EF ∥平面SAD ；（2）若SD ＝8，求二面角D —EF —S 的正弦值．20．（本小题满分12分）某省2021年开始将全面实施新高考方案，在6门选择性考试科目中，物理、历史这两门科目采用原始分计分：思想政治、地理、化学、生物这4门科目采用等级转换赋分，将每科考生的原始分从高到低划分为A ，B ，C ，D ，E 共5个等级，各等级人数所占比例分别为15%、35%、35%、13%和2%，并按给定的公式进行转换赋分．该省组织了一次高一年级统一考试，并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分．（1）某校生物学科获得A 等级的共有10名学生，其原始分及转换分如表：现从这10名学生中随机抽取3人，设这3人中生物转换分不低于95分的人数为X ，求X 的分布列和数学期望；（2）假设该省此次高一学生生物学科原始分Y 服从正态分布N(75.8，36)．若Y~N(μ，2σ)，令Y μησ-=，则η~N(0，1)，请解决下列问题：①若以此次高一学生生物学科原始分C 等级的最低分为实施分层教学的划线分，试估计该划线分大约为多少分？（结果保留整数）②现随机抽取了该省800名高一学生的此次生物学科的原始分，若这些学生的原始分相互独立，记ξ为被抽到的原始分不低于71分的学生人数，求P(ξ＝k )取得最大值时k 的值．附：若η~N(0，1)，则P(η≤0.8)≈0.788，P(η≤1.04)≈0.85． 21．（本小题满分12分）如图，已知椭圆22221x y a b+=(a ＞b ＞0)的长轴两个端点分别为A ，B ，P(0x ，0y )(0y ＞0)是椭圆上的动点，以AB 为一边在x 轴下方作矩形ABCD ，使AD ＝kb (k ＞0)，PD 交AB 于 E ，PC 交AB 于F ．（1）若k ＝1，△PCD 的最大面积为12，离心率为3，求椭圆方程；（2）若AE ，EF ，FB 成等比数列，求k 的值．22．（本小题满分12分）已知函数()ln sin 1f x x x x =-++．（1）求证：()f x 的导函数()f x '在(0，π)上存在一零点；（2）求证：()f x 有且仅有两个不同的零点．。

江苏省苏州市2024届高三上学期期初调研测试英语答案解析

2024届苏州四市五区高三期初考试解析（附原创作文2篇）答案汇总：听力1-5 CABAB6-10 ACCBA11-15 BCABC16-20 ACCBB传统阅读21-23 BCB24-27 CADC28-31 ABDA32-35 ACDB7选5阅读36-40 BDCFG完形填空41-45 CADBA46-50 BBCBA51-55 DBCDA语法填空56. that / which57. expected58. what59. a60. is scheduled61. With62. reveals63. generals64. adding65. valuable / invaluable01阅读答案：21-23 BCB24-27 CADC28-31 ABDA32-35 ACDBA篇主要向读者介绍了一些形式不一但都别具特色的艺术项目。

B篇主要向我们介绍了世界第一个自然河流公园的相关事项，主要包括其所在地区的自然环境、河流公园的成形过程以及其成就、特色。

C篇主要打破了普遍认知，通过一位心理学家的实验介绍了被打断的好处，也介绍了蔡格尼克记忆效应的应用，呼吁我们享受并利用好被打断。

D篇是科学研究类题目，介绍了科学家通过改变蚊子基因来控制疟疾，并从实验原理、实验过程、实验评价多方面进行介绍。

详细解析：A篇第21题B 根据本篇文章的小标题kinship和Family Memory Box都与家人、亲属有关，而两场展览也都是围绕着家人与亲属进行展开，故二者属于同一个主题。

第22题C 定位到文章A Tour in ASL这个部分，由该段标题可知本次展览是Virtual Portrait Signs，故是虚拟而不是实地展览，A选项错误；定位该段第一、二行which is first major Smithsonian museum to examine the War, 而D选项少了限定条件，故错误；由这一部分的第二段The Zoom link will be emailed on the morning of the program...可知，参观者可以通过Zoom进行展览的参观而不是以邮件的形式，邮件的形式主要是用于解决参观者的疑问，故B错误。

江苏省苏州市2024-2025学年高三上学期期初阳光调研语文试题及答案

2024～2025学年第一学期高三期初调研测试语文2024.09一、现代文阅读（35分）（一）现代文阅读I（本题共5小题，19分）阅读下面的文字，完成1～5题。

材料一：艺术创造不能完全脱离以往的传统基础而独立。

这在注重画学的中国应该用不着解释。

能发挥新创都是受过传统熏陶的，即使突然接受一种崭新的形式，有外来思想的影响，也仍能表现本国精神。

如南北朝的佛教雕刻，或唐宋的寺塔，都起源于印度，非中国本有的观念，但结果仍以中国风格造成成熟的中国特有艺术，驰名世界。

艺术的进境是基于丰富的遗产上，今后的中国建筑自亦不能例外。

将来中国将大量采用西洋现代建筑材料与技术。

如何发扬光大我民族建筑技艺之特点，在以往都是无名匠师不自觉的贡献，今后却要成近代建筑师的责任了。

如何接受新科学的材料方法而仍能表现中国特有的作风及意义，老树上发出新枝，则真是问题了。

中国建筑既是延续了两千余年的一种工程技术，本身已造成一个艺术系统，许多建筑物便是我们文化的表现。

除非我们不知尊重这古国灿烂的文化，如果我们有复兴国家民族的决心，便不能忽略中国建筑的研究。

东方古国的城市在建筑上若失掉艺术特性，于文化表现和观瞻方面令人痛心，代表着文化衰落。

四十年来，上海等通商大埠模仿欧美次等商业城市，多为租界外国人建设，中国市民只是附和而已。

此类建筑无中国复兴精神迹象。

今后虽仍需采用西洋方法建设，但应是自觉的，由专业建筑师指导，在科学结构上有艺术表现，为中国精神复兴而努力。

这种创造的火炬已曾在抗战前燃起，所谓“宫殿式”新建筑就是一例。

但以最清醒建筑理论来看，其不合近代科学及艺术理想。

它的产生是由于欣赏中国建筑的外貌。

在形式上它模仿清代宫衙，在结构及平面上它又仿西洋古典派的普通组织。

细项上东西凑合且多属过去时代，不适应中国经济情形也不能普遍。

这些尝试如同堆砌文字，抄袭章句，整篇结构不出于自然，辞藻也欠雅驯的文章，但这种努力是中国精神的抬头，实有无穷意义。

要能提炼旧建筑中所包含的中国质素，我们需增加对旧建筑结构系统及平面部署的认识。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。