编译原理第二章(1)
编译原理课后习题答案+清华大学出版社第二版

用以引用非局部(包围它的过程)变量时,寻找该变量的地址。 DL: 动态链,指向调用该过程前正在运行过程的数据段基地址,用以过程执行结束释放
数据空间时,恢复调用该过程前运行栈的状态。 RA: 返回地址,记录调用该过程时目标程序的断点,即调用过程指令的下一条指令的地
编译程序大致有哪几种开发技术?
答案:
(1)自编译:用某一高级语言书写其本身的编译程序。 (2)交叉编译:A 机器上的编译程序能产生 B 机器上的目标代码。 (3)自展:首先确定一个非常简单的核心语言 L0,用机器语言或汇编语言书写出它的编
译程序 T0,再把语言 L0 扩充到 L1,此时 L0⊂ L1 ,并用 L0 编写 L1 的编译程序 T1,再把语 言 L1 扩充为 L2,有 L1 ⊂ L2 ,并用 L1 编写 L2 的编译程序 T2,……,如此逐步扩展下 去, 好似滚雪球一样,直到我们所要求的编译程序。 (4)移植:将 A 机器上的某高级语言的编译程序搬到 B 机器上运行。
(main).
答案: 程序执行到赋值语句 b∶=10 时运行栈的布局示意图为:
1
《编译原理》课后习题答案第二章
第 3题 写出题 2 中当程序编译到 r 的过程体时的名字表 table 的内 容。
name
kind
level/val
adr
size
答案:
题 2 中当程序编译到 r 的过程体时的名字表 table 的内容为:
盛威网()专业的计算机学习网站
2
《编译原理》课后习题答案第一章
合实现方案,即先把源程序翻译成较容易解释执行的某种中间代码程序,然后集中解释执行 中间代码程序,最后得到运行结果。
编译原理第二章

上一页
下一页
11
▪ 符号串的术语
设s是符号串 前缀:移走s的尾部的零个或多于零个符号 后缀:删去s的头部的零个或多于零个符号 子串:从s中删去一个前缀和一个后缀 子序列:从s中删去零个或多于零个符号(这些符号不要求是连续的) 逆转:将S中的符号按相反次序写出而得到的符号串。 长度:是该符号串中的符号的数目。例如|aab|=3,|ε|=0。 真前缀,真后缀,真子串: x≠sx ≠ 例子:符号串s=banana 前缀:,b,ba,ban,bana,banan,banana 后缀:banana,anana,nana,ana,na,a, 子串:banana,anana,banan,anan,…, 子序列: baa(这些符号不要求是连续的) 逆转(用SR表示):ananab 长度:banana=6
β ε +T +T +T
ε ε
上一页
下一页
23
3.3 最左推导与最右推导
对于推导αβ,如果每一步都是对α中的最左非终结符进行替换 的,则我们称这种推导为最左推导,如果每一步都是对α中的最 右非终结符进行替换的,则我们称这种替换为最右推导。
例2-2:对于文法:E→E+ E|E*E|(E)|i 我们看对于(i*i+i)的推导 最左推导:E (E) (E+E) (E*E+E) (i*E+E) (i*i+E) (i*i+i) 最右推导:E (E) (E+E) (E+i) (E*E+i) (E*i+i) (i*i+i)
编译原理教程课后习题答案第二章
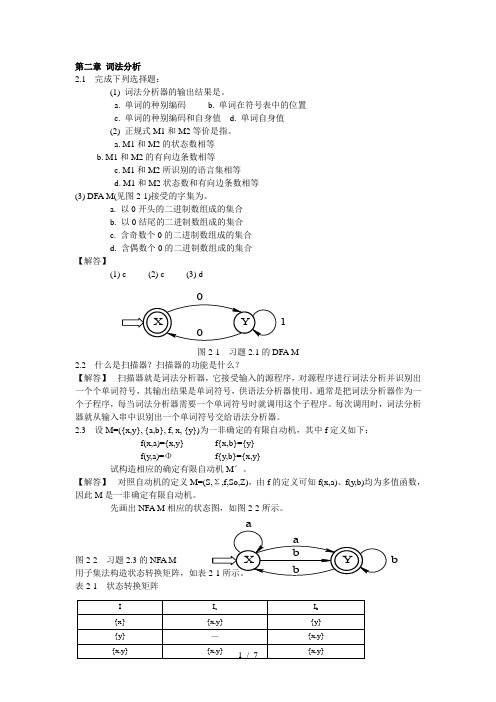
第二章 词法分析2.1 完成下列选择题:(1) 词法分析器的输出结果是。
a. 单词的种别编码b. 单词在符号表中的位置c. 单词的种别编码和自身值d. 单词自身值(2) 正规式M1和M2等价是指。
a. M1和M2的状态数相等b. M1和M2的有向边条数相等c. M1和M2所识别的语言集相等d. M1和M2状态数和有向边条数相等(3) DFA M(见图2-1)接受的字集为。
a. 以0开头的二进制数组成的集合b. 以0结尾的二进制数组成的集合c. 含奇数个0的二进制数组成的集合d. 含偶数个0的二进制数组成的集合【解答】(1) c (2) c (3) d图2-1 习题2.1的DFA M2.2 什么是扫描器?扫描器的功能是什么?【解答】 扫描器就是词法分析器,它接受输入的源程序,对源程序进行词法分析并识别出一个个单词符号,其输出结果是单词符号,供语法分析器使用。
通常是把词法分析器作为一个子程序,每当词法分析器需要一个单词符号时就调用这个子程序。
每次调用时,词法分析器就从输入串中识别出一个单词符号交给语法分析器。
2.3 设M=({x,y}, {a,b}, f, x, {y})为一非确定的有限自动机,其中f 定义如下:f(x,a)={x,y} f {x,b}={y}f(y,a)=Φ f{y,b}={x,y}试构造相应的确定有限自动机M ′。
【解答】 对照自动机的定义M=(S,Σ,f,So,Z),由f 的定义可知f(x,a)、f(y,b)均为多值函数,因此M 是一非确定有限自动机。
先画出NFA M 相应的状态图,如图2-2所示。
图2-2 习题2.3的NFA M 用子集法构造状态转换矩阵,如表表2-1 状态转换矩阵1b将转换矩阵中的所有子集重新命名,形成表2-2所示的状态转换矩阵,即得到 M ′=({0,1,2},{a,b},f,0,{1,2}),其状态转换图如图2-3所示。
表2-2 状态转换矩阵将图2-3所示的DFA M ′最小化。
《编译原理》课后习题答案第二章

有代表性的符号串:a,a0,aa,a00,a0a,aa0
习题2
3.(1)E T T/F F/F (E)/F (E+T)/F (T+T)/F (F+F)/F (i+i)/i
(2)E E+T E+T+T E+T*F+F E+T*F+i E+T*T*F+i
M:M(0,a)=1 M(0,b)=2
M(1,a)=1 M(1,b)=4
M(2,a)=1 M(2,b)=3
M(3,a)=3 M(3,b)=2
M(4,a)=0 M(4,b)=5
M(5,a)=5 M(5,b)=1
化简:
1.分化
① {0,1} {2,3,4,5}
② {0,1} {2,4} {3,5}
2.合并
=M(M(D,1),1011)
=M(M(C,1),011)
=M(M(F,0),11)
=M(M(E,1),1)
=M(C,1)
=F
∴DFA D能接受字符串0011011
8.解:将状态转换图列表,即:
由左图可知,该状态转换图直接对应的是确定有穷状态自动机DFA
DFA D=({0,1,2,3,4,5},{a,b},M,0,{0,1})
A::=bc|bAc
(2)Z::=AB
A::=ab|aAb
B::=b|Bb
7. 解:题中要求文法是:
Z::=1|3|5|7|9|Z1|Z3|Z5|Z7|Z9|A1|A3|A5|A7|A9
A::=2|4|6|8|A0|A2|A4|A6|A8|Z0|Z2|Z4|Z6|Z8
编译原理_第二章 词法分析(1)

第二章 词法分析
3,词法分析器输出单词的形式 ,
词法分析程序的输入是源程序字符串, 而输出是与源程序等价的单词符号序列, 词法分析器输出单词的形式 并且所输出的单词符号通常表示成如下 的二元式: 单词种别,单词自身的值) (单词种别,单词自身的值)
2010-7-22
2010-7-22
编译原理
11
第二章 词法分析
二,模式的形式化描述-正规式与正规集 模式的形式化描述-
1,字符串与语言 , 从词法分析的角度看,程序设计语言 是由记号组成的集合,每个记号又是由 若干字母按照一定规则组成的字符串.
2010-7-22
编译原理
12
第二章 词法分析
定义2.1 语言 是有限字母表 上有限长度字 语言L是有限字母表 是有限字母表∑上有限长度字 定义 符串的集合. 符串的集合. 定义2.1明确指出,语言是一个集合,集 明确指出, 定义 明确指出 语言是一个集合, 合中的元素是字符串,并且强调了两个有限: 合中的元素是字符串,并且强调了两个有限 字母表是有限的, ① 字母表是有限的,即字母表中元素是 有限多个; 有限多个; 字符串的长度是有限的, ② 字符串的长度是有限的,即字符串中 字符个数是有限多个. 字符个数是有限多个. 这是由于计算机所能表示的字符个数和 字符串的长度都是有限的. 字符串的长度都是有限的.
第二章 词Hale Waihona Puke 分析第二章词法分析
主要内容: 主要内容: 词法分析过程涉及的几个问题 模式的形式化描述模式的形式化描述-正规式与正规集 记号的识别记号的识别-有限自动机 从正规式到词法分析器 词法分析器生成器简介
2010-7-22
编译原理
编译原理课后答案

第二章 高级语言及其语法描述4.令+、*和↑代表加,乘和乘幂,按如下的非标准优先级和结合性质的约定,计算1+1*2↑2*1↑2的值:(1) 优先顺序(从高至低)为+,*和↑,同级优先采用左结合。
(2) 优先顺序为↑,+,*,同级优先采用右结合。
解:(1)1+1*2↑2*1↑2=2*2↑1*1↑2=4↑1↑2=4↑2=16 (2)1+1*2↑2*1↑2=1+1*2*1=2*2*1=2*2=46.令文法G6为 N →D|NDD →0|1|2|3|4|5|6|7|8|9 (1) G6 的语言L (G6)是什么?(2) 给出句子0127、34和568的最左推导和最右推导。
解:(1)L (G6)={a|a ∈∑+,∑=﹛0,1,2,3,4,5,6,7,8,9}}(2)N =>ND => NDD => NDDD => DDDD => 0DDD => 01DD => 012D => 0127 N => ND => N7=> ND7=> N27=> ND27=> N127=> D127=> 0127 N => ND => DD => 3D => 34 N => ND => N4=> D4 =>34N => ND => NDD => DDD => 5DD => 56D => 568 N => ND => N8=> ND8=> N68=> D68=> 5687.写一个文法,使其语言是奇数集,且每个奇数不以0开头。
解:A →SN, S →+|-|∑, N →D|MDD →1|3|5|7|9, M →MB|1|2|3|4|5|6|7|8|9 B →0|1|2|3|4|5|6|7|8|9 8. 文法:E T E T E T TF T F T F F E i→+-→→|||*|/()| 最左推导:E E T T TF T i T i T F i F F i i F i i i E T T F F F i F i E i E T i T T i F T i i T i i F i i i ⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒⇒⇒⇒⇒⇒+⇒+⇒+⇒+⇒+⇒+********()*()*()*()*()*()*()最右推导:E E T E TF E T i E F i E i i T i i F i i i i i E T F T F F F E F E T F E F F E i F T i F F i F i i i i i ⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒⇒⇒⇒⇒+⇒+⇒+⇒+⇒+⇒+⇒+**********()*()*()*()*()*()*()*()语法树:/********************************EE FTE +T F F T +iiiEEFTE-T F F T -iiiE EFT+T F FTiii*i+i+ii-i-ii+i*i*****************/9.证明下面的文法是二义的:S → iSeS|iS|I解:因为iiiiei 有两种最左推导,所以此文法是二义的。
编译原理第二章习题答案
第2章习题解答1.文法G[S]为:S->Ac|aBA->abB->bc写出L(G[S])的全部元素[答案]S=>Ac=>abc或S=>aB=>abc所以L(G[S])={abc}2.文法G[N]为:N->D|NDD->0|1|2|3|4|5|6|7|8|9G[N]的语言是什么?[答案]G[N]的语言是V。
V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD.... =>NDDDD...D=>D……D3.已知文法G[S]:Sf dAB Af aA|a B|bB问:相应的正规式是什么?G[S]能否改写成为等价的正规文法? [答案]正规式是daa*b* ;相应的正规文法为(由自动机化简来):G[S]:S —dA A —a|aB B —aB|a|b|bC C —bC|b也可为(观察得来):G[S]:S —dA A —a|aA|aB B —bB| &4.已知文法G[Z]:Z->aZb|ab写出L(G[Z])的全部元素。
[答案]Z=>aZb=>aaZbb=>aaa..Z...bbb=> aaa..ab...bbbL(G[Z])={a n b n|n>=1}5.给出语言{a n b n c1 n>=1,m>=0}的上下文无关文法。
[分析]本题难度不大,主要是考上下文无关文法的基本概念。
上下文无关文法的基本定义是:A-> B ,A € Vn ,B€( VnU Vt) *,注意关键问题是保证a n b n的成立,即“ a与b的个数要相等”,为此,可以用一条形如A->aAb|ab的产生式即可解决。
[答案]构造上下文无关文法如下:S->AB|AA->aAb|abB->Bc|c[扩展]凡是诸如此类的题都应按此思路进行,本题可做为一个基本代表。
基本思路是这样的:要求符合a n b n c m,因为a与b要求个数相等,所以把它们应看作一个整体单元进行,而c m做为另一个单位,初步产生式就应写为S->AB,其中A推出a n b n,B推出c m。
《编译原理》第2章 编译基础-形式语言与有穷自动机
句型、推导
G[E]: E→E+T|T T→T*F|F F→(E)|a
对于句子a+a*a 有不同 的推导
EE+T T+T F+T a+T a+T*F a+F*F a+a*F a+a*a
EE+T E+T*F E+T*a E+F*a E+a*a T+a*a F+a*a a+a*a
整理课件
例:奇偶测试器
0
0
1
q0
q1
∈
1
自动机:M=(Q,∑ ,δ ,q0,Z)
Q={ q0, q1}
∑ ={0,1}
q0=q0 Z={q1}
整理课件
映射函数:
δ( q0,0)= q0 0
0
δ( q0,1)= q1
1
δ( q1,0)= q1 q0
q1
δ( q1,1)= q0
1
例:000110001
整理课件
第四节 正规文法与有穷自动机 1、正规文法 产生的语言的推导 例:文法 G=(VN,VT,P,S) 其中: VN={A,B,C}
VT={a,b,c} S=A P:A →aB A →aA
B →bB B →bC C →cC C →c
整理课件
A=>aA=>aaA=>…..=>aa…aB =>aa…abB=>aa…abb…bC =>aa…abb…bcC=> aa…abb…bccC => aa…abb…bcc…c
D→ε
Aa→bD
自然语言属于上下文有关文法
整理课件
文法的类型
编译原理第二章-课后题答案
第二章3.何谓“标志符”,何谓“名字”,两者的区别是什么答:标志符是一个没有意义的字符序列,而名字却有明确的意义和属性。
4.令+、*和↑代表加、乘和乘幂,按如下的非标准优先级和结合性质的约定,计算1+1*2↑2*1↑2的值。
(1)优先顺序(从高到低)为+、*和↑,同级优先采用左结合。
(2)优先顺序为↑、+、*,同级优先采用右结合。
答:(1)1+1*2↑2*1↑2=2*2↑2*1↑2=4↑2*1↑2=4↑2↑2=16↑2=256(2)1+1*2↑2*1↑2=1+1*2↑2*1=1+1*4*1=2*4*1=2*4=86.令文法G6为N-〉D|NDD-〉0|1|2|3|4|5|6|7|8|9(1)G6的语言L(G6)是什么(2)给出句子0127、34、568的最左推导和最右推导。
答:(1)由0到9的数字所组成的长度至少为1的字符串。
即:L(G6)={d n|n≧1,d∈{0,1,…,9}}(2)0127的最左推导:N=>ND=>NDD=>NDDD=>DDDD=>0DDD=>01DD=>012D=>0127 0127的最右推导:N=>ND=>N7=>ND7=>N27=>ND27=>N127=>D127=>0127(其他略)7.写一个文法,使其语言是奇数集,且每个奇数不以0开头。
答:G(S):S->+N|-NN->ABC|CC->1|3|5|7|9A->C|2|4|6|8B->BB|0|A|ε[注]:可以有其他答案。
[常见的错误]:N->2N+1原因在于没有理解形式语言的表示法,而使用了数学表达式。
8.令文法为E->T|E+T|E-TT->F|T*F|T/FF->(E)|i(1)给出i+i*i、i*(i+i)的最左推导和最右推导。
(2)给出i+i+i、i+i*i和i-i-i的语法树,并给出短语,简单短语和句柄。
编译原理课件第二章
2
LL文法
从左到右扫描符号串,从左到右构建左推导,是递归下降式语法分析的基础。
3
LR文法
从左到右扫描符号串,从右到左构建右推导,是LR分析器(最常用的语法分析器) 的基础。
语义分析
符号表
类型检查
存储程序中所有标识符的信 息,如名字、值、数据类型、 作用域等。
对程序中的表达式进行类型 检查,检查其数据类型是否 匹配,发现类型错误,报告 错误信息。
目标代码生成
静态链接
所有和程序相关的代码和库都被合并到单一 静态程序中,生成的目标代码提供给编译器 后期处理和执行。
动态链接
当程序执行时,操作系统将共享库动态链接 到程序中。生成更小的目标程序,提高内存 效率。
中间代码生成
生成高级语言与目标代码之 间的中间代码。
优化器和中间代码
1 控制流分析
构建控制流图表示各 代码块的控制流程, 用于优化控制流程。
2 数据流分析
分析程序中信息的传 播和使用,用于优化 算法、寄存器分配和 内存使用。
3 中间代码
支持优化器的三元式、 四元式或间接三元式 形式,可以做优化、 可移植性更好。
编译原理第二章
编译器将源代码转换为目标代码的工具。编译过程分为三个部分:前端,优 化器和后端。本章介绍编译器的概述和基本部件。
编译器
前端
将源程序转换为内部表示, 检查其语法和语义。
优化器
将生成的代码优化,减少目 标代码的大小和时间成本。
后端
生成目标代码,包括中间代 码生成,寄存器分配和指令 生成。
词法分析
To ken
基本的词义单元是记号(Token),个记号表示源语言中的一个词、一个操作符、一个标点 符号或其他语法单元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2 字母表和符号串的基本概念
2. 符号(字符) 字母表中的元素称为符号或称为 字符。 例如,前述例子中 a、b、c 是字母表Σ中的符号; 0、1 是字母表Σ'中的符号。
2.2 字母表和符号串的基本概念
3. 符号串(字) 符号的有穷序列称为符号串。 例如,设有字母表∑={ a, b, c } 则有符号串 a,b,ab,ba, cba, abc… 符号串总是建立在某个特定字 母表上的且只由字母表上的有穷多 个符号组成。
若将定义标识符的文法设计成: G=(VN,VT,P,S )
其中 VN,VT ,S 同上
P={ I→L | I D L→a | b | c | …|x|y|z D→0 | 1 | 2 | 3 | …|9 }
缩小了所定义语言的范围
2.3.2 文法的形式定义
例3 设字母表 Σ={ a, b } , 试设计一个 文法,描述语言 L={ abna | n≥0 }
2.2 字母表和符号串的基本概念 2. 集合的乘积 设A和B是符号串的集合, 则A和B 的乘积定义为:
AB={xy | x∈A, y∈B}
集合的乘积是满足于 x∈A, y∈B 的所有符号串 xy 所构成的集合。
2.2 字母表和符号串的基本概念
例如:设A={ a, b }, B={ c, d }
则AB={ ac, ad, bc, bd }
2.3.2 文法的形式定义
当n=1 L={aa, bb}
L={a2n, b2n | n≥1}
当n=2 L={aaaa, bbbb} 当n=3 L={aaaaaa, bbbbbb}
……
即语言L是由偶数个a,偶数个b这样 的符号串组成的集合。
2.3.2 文法的形式定义
因此,定义语言L的文法 G=( VN,VT,P,S ) 注意: V 其中: N={A, B, D} VT≠{aa,bb} VT={a, b} P={ A→aa | aaB | bb | bbD B→aa | aaB D→bb | bbD } S=A
={ 0, 1, 00, 10, 11, 01, 000, 100, …}
当语言为无穷集合时,用文法来描述 语言。
2.3 文法和语言的形式定义
∑+=∑1∪∑2∪∑3∪… ={ 0, 1, 00, 10, 11, 01, 000, 100, …}
下面用A表示∑ + , 用式子A→0表示符 号串0∈A或A生成 符号串0,符号 “”读作“生成” 或“由…组成”。 则集合A可表示成:
L1={ a, b, c } L2={ a, aa, ab, ac } L3={ c, cc } 均表示字母表A上的一个形式语言。由于 这三个语言均是有限符号串的集合,因此, 可枚举出其全部句子来表示该语言。
2.3 文法和语言的形式定义
例如,设字母表∑={ 0, 1 }, 则
∑+=∑1∪∑2∪∑3∪…
使用规则 S0S1 此时 x=00 , y=11 000S11100001111 使用规则 S01 此时 x=000 y=111
2.3.2 文法的形式定义
G=(VN,VT,P,S) VN={I, L, D} 其中:
VT={a,b,c, … x,y,z,0,1,2,… ,9}
P={ I→L | I L| I D L→a | b | c | … | x | y | z D→0 | 1 | 2 | 3 | … | 9 }
S=I
2.3.2 文法的形式定义
G: A→aBa B→Bb | ε
2.3.2 文法的形式定义
例4 设字母表∑={ (, ) } ,试设计 一个文法描述语言 L={ (n )n | n≥0}
G: S→ ε | ( S )
2.3.3 语言的形式定义
1. 直接推导
令G是一文法,我们称 xAy直接 推导出 xαy ,即 xAyxαy 仅 A→α 是 G 的一条规则, 且 x, y(VN∪VT)*。也就是说从符号串 xAy 直接推导出 xαy 仅使用一次规 则。
2.2 字母表和符号串的基本概念 例如, 设 x=abc 则 x0= x1=abc
x2=xx=abcabc …
2.2 字母表和符号串的基本概念
4. 集合的幂运算 设A是符号串的集合,则集合A的 幂运算定义为: A0={} A1=A A2=AA … An= AA … A=AAn-1(n>0) n
2.3.2 文法的形式定义
终结符号是不属于非终结符号 的那些符号, 它是组成语言的基本符 号,是一个语言的不可再分的基本 符号,通常用小写字母表示。 例如,上例中的0和1。
2.3.2 文法的形式定义
2. 文法
规则的非空有穷集合,通常表示 成四元组 G={VN,VT, P, S } VN是规则中非终结符号的集合。 VT是规则中终结符号的集合。
2.2 字母表和符号串的基本概念 例如,设A={ a, b },则 A0={} A1=A={ a, b } A2=AA={ aa, ab, ba, bb } A3=AAA=A2A
={ aaa, aab, aba, abb, baa, bab, bba, bbb }
…
2.2 字母表和符号串的基本概念
2.3.2 文法的形式定义
描述该语言的文法G“是否与前面文 法等价?
G"=( {A}, {a, b}, P", A ) P"={ A→aa | bb | Aaa | Abb }
此文法超出了所定义语言的范围。
2.3.2 文法的形式定义
例2 试设计一个表示所有标识符 的文法
字母 字母或数字串
用I代表标识符;L代表字母; D代表数字; 则定义标识符的文法 为:
可见,集合A的正闭包表示A上元素 a,b构成的所有符号串的集合,集合A 的闭包比集合A的正闭包多含一个空 符号串。
2.3 文法和语言的形式定义
2.3.1形式语言
序列的集合称为形式语言。
每个形式语言都是某个字母表上按 某种规则构成的所有符号串的集合。 反之,任何一个字母表上符号串的集 合均可定义为一个形式语言。
2.3.2 文法的形式定义
提出问题: 描述该语言的文法是 否唯一呢? P' : A→B | D B→aa | aBa D→bb | bDb
显然,G不同于G'。由此可见, 对于一个给定的语言,描述该语言 的文法是不唯一的。
2.3.2 文法的形式定义
若G和G'是两个不同的文法,如 果它们描述的语言相同,那么,称G 和G' 为等价文法。
A→0 A→1 A→A0 A→A1
2.3.2 文法的形式定义
1. 规则 也称产生式
规则是一个符号与一个符号串的 有序对(A,β),通常写作:
A→β(或A∷= β)
规则的作用是告诉我们如何用规 则中的符号串生成语言中的序列。
2.3.2 文法的形式定义
例如,前述例中一组规则
A→0 A→1 A→A0 A→A1
P 是文法规则的集合。
2.3.2 文法的形式定义
S 是一个非终结符号,称为文法 的开始符号或文法的识别符号,它至 少要在一条规则中作为左部出现。由 它开始,识别出我们所定义的语言。 由文法定义可知,文法是对语言 结构的定义和描述,文法四大要素中 关键是规则的集合。
2.3.2 文法的形式定义
为了书写方便,对于若干个左 部相同的规则,如 A→1 A→2 … A→n 将它们缩写为:A→1 | 2 | … | n
2.3.3 语言的形式定义
例如,设有文法G[S]: P为:S→ 0 1 | 0 S 1 有如下直接推导: S01 使用规则 S01 此时 x=, y= S0S1 使用规则 S0S1 此时 x=, y=
2.3.3 语言的形式定义
S→ 0 1 | 0 S 1
0S10011 00S11000S111 使用规则 S01 此时 x=0, y=1
第二章 文法和语言的基本知识
形式语言理论是编译的重要理论 基础。本章主要介绍编译理论中用到 的有关形式语言理论的最基本概念, 重点介绍如何采用形式化的方法描述 程序设计语言。
第二章 文法和语言的基本知识 字母表和符号串 文法和语言的形式定义 文法和语言的分类 短语、直接短语和句柄 语法树和文法的二义性
2.2 字母表和符号串的基本概念
一、基本概念
1. 字母表 元素的非空有穷集合。 例如,∑={ a, b, c } 根据字母表的定义,Σ是字母表, 它由a、b、c三个元素组成。
2.2 字母表和符号串的基本概念 注意: (1) 字母表中至少包含一个元素。 (2) 字母表中的元素, 可以是字母、 数字或其他符号。 例如,∑' ={0, 1} 是一个字母表,由0、1两个元素 组成。
其中每个i有时也称为是A的一个候选式。
2.3.2 文法的形式定义
前例中描述∑+的文法是: G=(VN,VT,P,S ) VN={A}
VT={0,1} P: A→ 0 | 1 | A0 | A1
S=A
2.3.2 文法的形式定义
我们约定:
第一条规则的左部是识别符号。 对文法G不用四元式显示表示, 仅 只将规则写出。 G: A→ 0 | 1 | A0 | A1
由于对任意的符号串x,总有 x=x=x 所以, 对任意集合A, 我们有: {}A=A{}=A
2.2 字母表和符号串的基本概念 特别指出的是, 是符号串, 不是 集合,而{}表示由空符号串 所组 成的集合, 但这样的集合不是空集合 Φ={} 。
2.2 字母表和符号串的基本概念
3. 符号串的幂运算 设x是符号串, 则x的幂运算定义为: x 0= 注意:x0≠ 1 x 1= x x2= xx x3= xxx … xn= xx … x=x xn-1(n>0) n
2.3.2 文法的形式定义
