自动控制原理(梅晓榕)习题答案第八章
自动控制原理 课后习题答案(2020年7月整理).pdf

第1章控制系统概述【课后自测】1-1 试列举几个日常生活中的开环控制和闭环控制系统,说明它们的工作原理并比较开环控制和闭环控制的优缺点。
解:开环控制——半自动、全自动洗衣机的洗衣过程。
工作原理:被控制量为衣服的干净度。
洗衣人先观察衣服的脏污程度,根据自己的经验,设定洗涤、漂洗时间,洗衣机按照设定程序完成洗涤漂洗任务。
系统输出量(即衣服的干净度)的信息没有通过任何装置反馈到输入端,对系统的控制不起作用,因此为开环控制。
闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。
工作原理:以卫生间蓄水箱蓄水量控制为例,系统的被控制量(输出量)为蓄水箱水位(反应蓄水量)。
水位由浮子测量,并通过杠杆作用于供水阀门(即反馈至输入端),控制供水量,形成闭环控制。
当水位达到蓄水量上限高度时,阀门全关(按要求事先设计好杠杆比例),系统处于平衡状态。
一旦用水,水位降低,浮子随之下沉,通过杠杆打开供水阀门,下沉越深,阀门开度越大,供水量越大,直到水位升至蓄水量上限高度,阀门全关,系统再次处于平衡状态。
开环控制和闭环控制的优缺点如下表1-2 自动控制系统通常有哪些环节组成?各个环节分别的作用是什么?解:自动控制系统包括被控对象、给定元件、检测反馈元件、比较元件、放大元件和执行元件。
各个基本单元的功能如下:(1)被控对象—又称受控对象或对象,指在控制过程中受到操纵控制的机器设备或过程。
(2)给定元件—可以设置系统控制指令的装置,可用于给出与期望输出量相对应的系统输入量。
(3)检测反馈元件—测量被控量的实际值并将其转换为与输入信号同类的物理量,再反馈到系统输入端作比较,一般为各类传感器。
(4)比较元件—把测量元件检测的被控量实际值与给定元件给出的给定值进行比较,分析计算并产生反应两者差值的偏差信号。
常用的比较元件有差动放大器、机械差动装置和电桥等。
(5)放大元件—当比较元件产生的偏差信号比较微弱不足以驱动执行元件动作时,可通过放大元件将微弱信号作线性放大。
自动控制原理梅晓榕习题答案

习题参考答案1-1工作原理当水位达到规定值时,浮子使电位器活动端处于零电位,放大器输出电压和电机电枢电压是零,电机停转,进水阀门开度不变。
水位高于规定值时,浮子使电位器活动端电位为正,放大器输出电压和电机电枢电压是正,电机正转,阀门开度减小,进水量减小,水位下降。
而水位低于规定值时,浮子使电位器活动端电位为负,电机反转,阀门开度变大,水位上升。
参考输入是电位器中的零电位,扰动量包括出水量和进水管压力的变化等,被控变量是水位,控制器是放大器,控制对象是水箱。
1- 2 当水位处于规定值时,阀门开度正好使进水量和出水量相等,水位不变。
当水位高于规定值,浮子通过杠杆使阀门开度减小,进水减小,水位下降。
当水位低于规定值,浮子通过杠杆使阀门开度变大,进水增加,水位上升。
1-3系统的目的是使发射架转到希望的角度。
电压 5代表希望的角度,电位器输出电压U2表示发射架的实际转角。
它们的差值称为偏差电压,放大后加到电机电枢绕组上成为电压U a。
当发射架没有转到希望的角度时,偏差电压和电机电枢电压不是零,它们使电机转动,转动方向是使偏差角减小至零。
该系统是伺服系统。
参考输入信号是电压比,被控变量是发射架转角。
反馈信号是电位器活动端电压U2,控制变量是放大和补偿环节的输出电压U3。
测量元件是电位器,执行元件是直流电动机。
1-4 程序控制系统,控制器是计算机,执行元件是步进电动机,被控变量是刀具位移x。
1-5 (1)线性定常系统;(2)线性时变系统;(3)非线性系统;(4)线性时变系统;(5)线性定常系统;(6)线性时变系统c )对X o 的引出点列方程。
k 1 (X iX o ) k 2X o f (X iX o )0 fX o(k 1k 2)x °权 KxX o (s) fs K2-1 a) m3 kx(t)dtF(t)X(s) F(s)1 ms2 kb )取m 的平衡点为位移零点,列微分方程。
2d x(t) m A dt 2f 警kX (t )卡⑴X(s) F(s)I 1/I 2ms 2 fs k2-2 设A B 点及位移X 见图中(b ),(d )-AA图机械系统a )对质量m 列方程。
自动控制原理(孟华)第8章习题答案070520

第八章 非线性控制系统习题答案8-1 解:由原方程得:2225.03)5.03(),(x x x x x x x x x x f x--+-=----== ,令0==x x,得:0)1(2=+=+x x x x ,解出奇点为:1,0-=x 。
在0=x 处,特征根为:984.025.02,1j s ±=,显然为不稳定的焦点。
在1-=x 处,特征根为:225.45.02,1±=s ,显然为鞍点。
概略画出奇点附近的相轨迹如下:-1习题8-1相轨迹图8-2解:原方程可改写为:⎩⎨⎧=-+≥=++0II 0Ix x x x x x x x 0,:0,:系统的特征方程及特征根为:⎪⎩⎪⎨⎧+-==+±-==++)(618.0,618.1,01II )(2321,01I 2,122,12鞍点-:稳定焦点:s s s js s s 推导等倾线方程:xx dx xd --==1α,则有:x x xβα=+-=11 ,即: ⎪⎪⎩⎪⎪⎨⎧-=≥--=0,11II 0,11I x x βαβα::,画出系统相平面如下:习题8-2相平面图8-3 (1)解:相平面上任一点的相轨迹斜率为:x xxdxx dsin+-=,由=dxx d,得:),2,1,0(±±==kkxπ,因此在相平面的x轴上,),2,1,0(±±==kkxπ的点均为奇点。
在x轴上满足),2,1,0(2±±==kkxπ的所有奇点附近,由泰勒级数展开来验证这类奇点为稳定焦点。
在x轴上满足),2,1,0()12(±±=+=kkxπ的所有奇点附近,由泰勒级数展开来验证这类奇点为鞍点。
绘制相轨迹如下图所示:习题8-3(1)相轨迹图(2)解:原方程可改写为:⎩⎨⎧=-≥=+IIIxxxxxx0,:0,:系统的特征方程及特征根为:⎪⎩⎪⎨⎧±==±==+)(1,01II)(,01I2,122,12鞍点-:中心点:ssjss推导等倾线方程:⎪⎪⎩⎪⎪⎨⎧≥11xxxxxx,=,-=αα,画出系统相平面如下:习题8-3(2)相轨迹图(3)解:令0==xx,得0sin=x,得出系统的奇点:,2,,0ππ±±=x当,2,1,02±±==kx,κπ时,令2xx+=κπ,可以验证奇点,2,1,02±±==kx,κπ为中心点。
自动控制原理(梅晓榕)习题答案
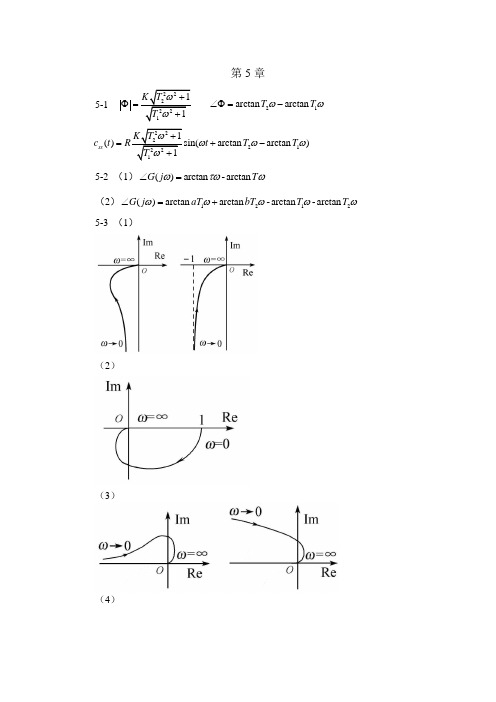
第5章5-1 222212211 arctan arctan 1K T T T T ωωωω+Φ=∠Φ=-+222212211()sin(arctan arctan )1ss K T c t Rt T T T ωωωωω+=+-+5-2 (1)()arctan -arctan G j T ωτωω∠=(2)1212()arctan arctan -arctan -arctan G j aT bT T T ωωωωω∠=+ 5-3 (1)(2)(3)(4)(5)(6)(7)(8)5-4(1)(3)(4)(6)(7)(8)(1)(2)(3)(4)(6)(7)(8)(10)5-6 (a )12100()11(1)(1)G s s s ωω=++ (b )231221(1)()1(1)s G s s s ωωω+=+(c )112211()11c s G s s s ωωωω⎛⎫+⎪⎝⎭=⎛⎫+ ⎪⎝⎭(d )123()11(1)(1)s G s s s ωωω=++ 5-7 (a )稳定 (b )稳定 (c )稳定 (d )不稳定(e )不稳定 (f )不稳定 (g )不稳定 (h )稳定5-8 (a )不稳定 (b )稳定 (c )稳定 (d )稳定 (e )稳定 5-9 (a )不稳定 (b )稳定 (c )稳定 5-10 稳定5-11 1:稳定 2:不稳定 3:稳定 4:不稳定 5-12 不稳定5-13 o 73γ= 此题传递函数改为(0.561)()(1)(0.11)(0.0281)K s G s s s s s +=+++或 幅值穿越频率 5.13rad/s c ω=,o 46.5γ=。
5-14(1)(j )48.2c G ω∠=-,o 131.8γ=(2)(j )155.4c G ω∠=-,o 24.6γ=5-15 o o o (1)55 20dB/dec (2)-15.840dB/dec (3)-52.860dB/dec --- ,,, 5-16s 2s1s3p1p 2p3t t t σσσ<<=< ,5-17 (1)o 54.9 20lg g K γ==∞,,系统稳定。
自动控制原理梅晓榕习题答案
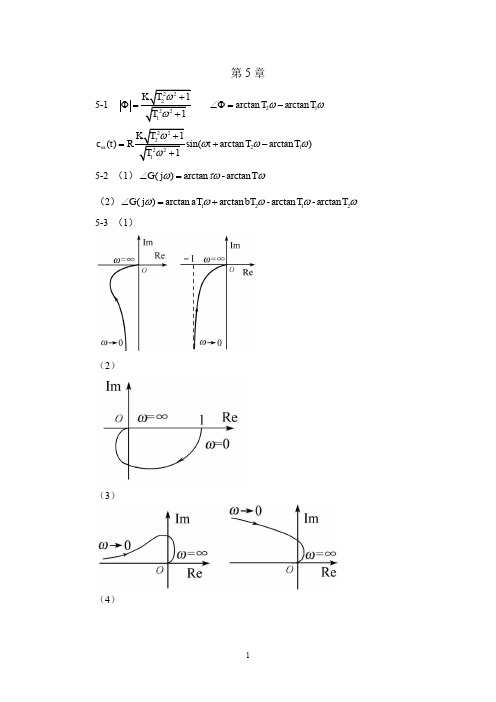
第5章5-121arctan arctan T T ωωΦ=∠Φ=-21()arctan arctan )ss c t t T T ωωω=+-5-2 (1)()arctan -arctan G j T ωτωω∠=(2)1212()arctan arctan -arctan -arctan G j aT bT T T ωωωωω∠=+ 5-3 (1)(2)(3)(4)(5)(6)(7)(8)5-4(1)(3)(4)(6)(7)(8)(1)(2)(3)(4)(6)(7)(8)(10)5-6 (a )12100()11(1)(1)G s s s ωω=++ (b )231221(1)()1(1)s G s s s ωωω+=+(c )112211()11c s G s s s ωωωω⎛⎫+⎪⎝⎭=⎛⎫+ ⎪⎝⎭(d )123()11(1)(1)s G s s s ωωω=++ 5-7 (a )稳定 (b )稳定 (c )稳定 (d )不稳定 (e )不稳定 (f )不稳定 (g )不稳定 (h )稳定5-8 (a )不稳定 (b )稳定 (c )稳定 (d )稳定 (e )稳定 5-9 (a )不稳定 (b )稳定 (c )稳定 5-10 稳定5-11 1:稳定 2:不稳定 3:稳定 4:不稳定 5-12 不稳定5-13 o 73γ= 此题传递函数改为(0.561)()(1)(0.11)(0.0281)K s G s s s s s +=+++或 幅值穿越频率 5.13rad/s c ω=,o 46.5γ=。
5-14(1)(j )48.2c G ω∠=-,o 131.8γ=(2)(j )155.4c G ω∠=-,o 24.6γ=5-15 o o o (1)55 20dB/dec (2)-15.840dB/dec (3)-52.860dB/dec --- ,,, 5-16s2s1s3p1p2p3t t t σσσ<<=< ,5-17 (1)o 54.9 20lg g K γ==∞,,系统稳定。
自动控制原理答案(第八章)

o o
− 90
o
o
− 45
o
= −180
(d) Angle of departure
K > 0:
−θ 1 − θ 2 − θ 3 − θ 4 = −180 −θ 1 − 135
o
o o
− 135
o
o
− 90
o
= −180
θ 1 = −180
121
(e) Angle of arrival
K < 0:
Asymptotes:
K > 0:
,
270
o
K < 0:
0 ,
o
180
o
Intesect of Asymptotes:
σ1 =
Breakaway-point Equation: Breakaway Points:
0, s
5
0
+ 0 − 8 − 8 − ( −4 ) − ( −4 )
4 s
4
−2
3
+ 20
90
and
K < 0:
0
o
and
180
o
σ1 =
Breakaway-point Equation:
2s
3
0
− 5 − 6 − ( −8 )
3 s ,
2
−1
s
= − 1.5
+ 35
+ 176
+ 240 = 0 − 9 . 7098
Breakaway Points: Root Locus Diagram:
− 1, − 2 . 5
6
(c) Breakaway-point Equation: 3 s + 54
自动控制原理_清华大学出版社课后习题答案

第一章习题答案1.自动控制:就是在人不直接参与的情况下,依靠外加装置或设备(称为控制装置或控制器),使机械、设备或生产过程(称为被控对象)的某个工作状态或参数(称为被控量)自动地按照预定的规律运行,或使某个被控制的参数按预定要求变化。
给定量:它是人们期望系统输出按照这种输入的要求而变化的控制量。
故一般又称给定输入或简称输入。
上例中的调节器的给定值u g 即是给定输入。
扰动量:它是一种人们所不希望的﹑影响系统输出使之偏离了给定作用的控制量。
上例中给水压力变化或蒸汽负荷变化都属于扰动。
开环控制:指控制装置与被控对象之间只有顺向作用而没有反向联系的控制过程,按这种方式组成的系统称为开环控制系统,其特点是系统的输出量不会对系统的输入量产生影响。
闭环控制:按照偏差进行控制的,其特点是不论什么原因使被控量偏离期望而出现偏差时,必定会产生一个相应的控制作用去减小或消除这个偏差,使被控量与期望值趋于一致。
复合控制:将闭环控制系统和开环控制系统结合在一起构成的开环-闭环相结合的控制系统,称为复合控制恒值控制:给定量是一定的,控制任务是保持被控量为一不变常数,在发生扰动时尽快地使被控量恢复为给定值。
随动控制:给定量是按照事先不知道的时间函数变化的,要求输出跟随给定量变化。
2.7. 自动控制系统的性能的要求:稳定性、快速性、准确性。
自动控制系统的性能的最基本要求:稳定性 第二章习题答案1. (a) 22()()1()()d y t f dy t k y t t dt m dt m m++=F (b )1211212()()()()k k k dy t y t t dt f k k k k +=++F (c )42422()2()()dy t k dy t kt dt m dt m+=F2. (a) 22211221122122112()d u du dvR C R C R C R C R C u R C v dt dt dt ++++=+(b )233112*********()d u duR C R C R C R C R C u dt dt++++2112211222()d v dvR C R C R C R C v dt dt=+++(c )222220.25 1.5d u du dv u v dt dt dt++=+ 3. (a)2111212()(1)()c r U s R R C s U s R R CR R s+=++ (b )222222()21()31c r U s C R s RCs U s C R s RCs ++=++ (c )2211212()()()c r U s R U s R LCs L R R C s R R =++++ 4. (a) 21212121221212212121()1()()()1f f f fs s k k k k Y s f f f f f X s s s k k k k k +++=++++ (b )21212112221212112212()()1()()1c r U s R R C C s R C R C s U s R R C C s R C R C R C s +++=++++ 5. 0.085d d i u ∆= 6. r d h Sh Q dt ∆+=∆ 7.2232(),()432t t s G s g t e e s s --+==-++ 8. 2()142tty t ee e --=-+9.(a )21()()c r U s RU s R =- (b )112212()(1)(1)()c r U s R C s R C s U s R C s++=- (c )212()()(1)c r U s R U s R R Cs =-+ 10.(1) 012180,3,211k k k π︒==-=-; (2) 略;(3)系统的闭环传递函数22301230123()11()1c M t M r M MQ s k k k k T Q s s s k k k k k k k k k k =+++11.闭环传递函数32()0.7(6)()(0.90.7)(1.180.42)0.68c r Q s s Q s s K s K s +=+++++ 12.闭环传递函数12342363451234712348()()1G G G G C s R s G G G G G G G G G G G G G G G G =+++- 13.传递函数21221)()(T s T s s K K s R s C +++=,2121)1()()(T s T s T s s s N s C ++-+= 14.传递函数333222()1()561c r U s U s R C s R C s RCs =+++。
自动控制原理课后参考答案

第一章1-1图1-2是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c维持不变, 试说明系统工作原理并画岀系统方块图。
图1-2 液位自动控制系统解:被控对象:水箱;被控量:水箱的实际水位;给定量电位器设定水位U r(表征液位的希望值C r);比较元件:电位器;执行元件:电动机;控制任务:保持水箱液位高度不变。
工作原理:当电位电刷位于中点(对应U r)时,电动机静止不动,控制阀门有一定的开度,流入水量与流出水量相等,从而使液面保持给定高度C r,一旦流入水量或流出水量发生变化时,液面高度就会偏离给定高度C r。
当液面升高时,浮子也相应升高,通过杠杆作用,使电位器电刷由中点位置下移,从而给电动机提供一定的控制电压,驱动电动机,通过减速器带动进水阀门向减小开度的方向转动,从而减少流入的水量,使液面逐渐降低,浮子位置也相应下降,直到电位器电刷回到中点位置,电动机的控制电压为零,系统重新处于平衡状态,液面恢复给定高度r。
反之,若液面降低,则通过自动控制作用,增大进水阀门开度,加大流入水量,使液面升高到给定高度C r。
系统方块图如图所示:1-10 下列各式是描述系统的微分方程,其中c(t)为输岀量,r (t)为输入量,试判断哪些是线性定常或时变系统,哪些是非线性系统?2c(t) =5 r2(t) t d2(^(1) dt ;3 2d c(t) 3d c(t) 6dc(t) --- 3 3 ---- 2 6 — dt dt dt xdc(t) dr(t)t c(t) =r(t) 3 dt dtc(t) = r(t)cos t 5 ;dr (t) tc(t) =3r(t)6 5 r(.)d. (5) dt =;(6)c(t)訂 2 ⑴;0, t ::: 6c(t)= “r(t), t 畠 6.(7) -解:(1)因为c(t)的表达式中包含变量的二次项 『(t),所以该系统为非线性系统。
(2) 因为该微分方程不含变量及其导数的高次幕或乘积项,且各项系数均为常数,所以该 系统为线性定常系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题答案88-1 1)二阶系统,2个状态变量。
设 2121212)(2)()( )()(x x t y t y t yx t y x x t y x --=--==⇒=== , []⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡--==00 01 2110 B y A A ,,,x x x 2)[]x x x 001 100322100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=y u 3)[]x x x 121 100321100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=y u 提示:本题利用了可控规范型与微分方程系数的关系。
8-2 1)23101)()(ss s U s Y += []x x x 001 1001000100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=y u 2)815611171181891)()(23+⋅++⋅-⋅=++=s s s s s s s U s Y []x x x 001 100980100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=y u 或 x x x ⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=5617181111800010000y u 3) []x x x 145 1006116100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=y u 提示:本题利用了状态空间的规范型与传递函数系数的关系。
8-38659122+++s s s8-4 ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡+-+---==⎥⎦⎤⎢⎣⎡----------t t t t tt t t t t Att x t x e e 11e 2e e2e 2e e e e 2)0(e )()(222221x 8-5 ⎥⎦⎤⎢⎣⎡-+-+-=-==------t t t t s BU A sI t 3232113e 4e 1e e 21)]()[(L )()0(x 0x , 8-6 [])(120)( )(100)(321100010)1(k k y k u k k x x x =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=+ 或 [])(100)( )(120)(310201100)1(k k y k u k k x x x =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=+ 或 [])(001)( )(111)(321100010)1(k k y k u k k x x x =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=+ 提示:利用状态空间的规范型与差分方程系数的关系。
8-7 []0110 3210=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--= C B A 下面是对该状态方程的求解过程。
设初始条件为零。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++-+++++=⎥⎦⎤⎢⎣⎡+-=---23232231233321)(222211z z zz z z z z z z z z A zI⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-++++--++-+=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-++-++=⎥⎥⎦⎤⎢⎢⎣⎡--=-⎥⎦⎤⎢⎣⎡-=-=---)1(6)1(2)2(32)1(6)1(2)2(3)1)(23()1)(23( 10)(110()(222111z z z z z z z z z z z z z z z z z z z z z z A zI z z A)(zI BU(z)A)zI z X⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+--+---==-61)1(21)2(3261)1(21)2(31)]([Z )(1kk kk z X k x 8-8 1) ⇒⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡= 10 0010B A 101])[(L e 11⎥⎦⎤⎢⎣⎡=-=--t A sI At)(21)(101)()d e ()(e )1(21d e 110101e 101e 2020k u T T k T k u t B k k T T t B t t B T T AtAT T AtAt AT⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+=+⎥⎥⎦⎤⎢⎢⎣⎡=⇒⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⇒⎰⎰x x x ,2) ⇒⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-= 10 2010B A e 0)e 1(211])[(L e 2211⎥⎥⎦⎤⎢⎢⎣⎡-=-=----t t At A sI )()e 1(21)21e (21)(e 0)e 1(211)()d e ()(e)1()e 1(21)21e (21d e e )e 1(21e 2222022022k u T k k u t B k k T t B B T TT T TAtATT TT At t t At ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--++⎥⎥⎦⎤⎢⎢⎣⎡-=+=+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--+=⇒⎥⎥⎦⎤⎢⎢⎣⎡-=--------⎰⎰x x x8-9 1) 322123222126410)(x x x x x x x x V --++=-[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=3213214101103031x x x x x x 0361404101103031091010331 01>--=---->-=-->,,-V (x )正定,V (x )负定。
2) 3132212322212624)(x x x x x x x x x x V ++---=-0194334131341111 0144111 01 131341111<+-+--=----<--=--->⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=,,,P故V (x )不定。
8-10 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡---=1001 4121Q A 取 解方程 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⇒-=+60116076076023T P Q PA P A 渐近稳定。
正定,平衡状态大范围。
,P P 0 06023>> 提示:求P 的方法如下 1) 求P 的MATLAB 程序a =[-1 -2;1 -4] ;q =[1 0; 0 1];p =lyap (a ’,q )2) 设 ⎥⎦⎤⎢⎣⎡=22121211p p p p P ⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡---⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡---1001412142112212121122121211p p p p p p p p 6011 607 6023 184052122 22121122122212111211=-==⇒⎪⎩⎪⎨⎧-=--=+---=+-⇒p p p p p p p p p p8-11 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=1001 3211Q A 取 解方程 ⎥⎦⎤⎢⎣⎡---=⇒-=+15.005.005.04.0T P Q PA P A 。
, 00625.0 04.0<-=>P 系统不稳定。
8-12 解法1 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=001323031A ,求A 的特征根的MATLAB 程序为: a =[1 3 0 ; -3 -2 -3 ; 1 0 0],eig (a )特征根为 0.1173±j2.6974,-1.2346。
特征根在z 平面单位圆外,系统不稳定。
解法2 取 Q=I ,P 是对称阵,解方程 Q P PA A -=-T⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---------=⇒6538.44615.15.04615.16282.02564.05.02564.02463.0 P -0.2463<0,P 不是正定的,故系统不稳定。
求P 的MATLAB 程序: a =[1 3 0 ; -3 -2 -3 ;1 0 0] ; a 1=inv (a ), c = a 1, p =lyap (a ’,-a 1,c ) 8-13 解法13212,31001()0022021 02zK K zI A z z z z z z z K zK --=-=-=-=⇒==-⇒<<,令解法2取 ⇒-=-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡== T332313232212131211Q P PA A p p p p p p p p p I ,, Q 解方程 22210024 0014300114K P K K⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥=⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦欲使P 为正定,只要04112>-K ,即 K <2。
8-14 可控性矩阵设为k Q 。
1)32)rank(0 210111210<==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=k k k Q Q Q ,,,不可控。
2) 3)rank(001111442211672312=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=k k Q Q ,,可控。
3) 32)rank(0 222000111<==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=k k k Q Q Q ,,,不可控。
4) 3)rank(020202040201442110=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=k k Q Q ,,可控。
或,对角线标准型,输入矩阵任一行不全为零,可控。
5) 32)rank(0270903000000844221<=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=k k Q Q ,,不可控。
或,对角线标准型,输入矩阵第二行全为零,不可控。
6) 32)rank(442211442211452312<=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=k k Q Q ,,不可控。
8-15 1)[]110rank ) rank(=-=CAB CB ,可控,1个输出量。
2)21113rank )rank(=⎥⎦⎤⎢⎣⎡--=CB ,可控(2个输出变量)。
2)rank(] rank[2==CB B CA CAB CB 8-16 可观性矩阵为g Q1),可观。
3)(rank 8111231001=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=g g Q Q 2),不可观。
1)(rank 0180090060030020010=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--=g g Q Q 3),可观。
3)(rank 014404012202011101=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---=g g Q Q4)230010000 rank()1 3 000000g g c Q Q c c ⎡⎤⎢⎥⎢⎥==<⎢⎥⎢⎥⎣⎦,不可。
当a 、b 、c 、d 互不相等时,由于A 是对角线标准型,c 中有全零的列,故不可观。
8-17 的充要条件是 2)rank( 111=⎥⎦⎤⎢⎣⎡+=k k Q b a Q 1 01-≠-≠--b a a b ,即时,既可控,又可观。
