第九节 各种积分间的关系2
格林公式
E
F
积分中L的方向.
oA
Bx
D
Q x
P y
dxdy
L
Pdx
Qdy
44
(2)求曲线积分时, 可利用格林公式简化计算, 若积分路径不是闭曲线, 可添加辅助线;
(3) 可用积分法求 d u P d x Q d y
在域D内的原函数:
思考题
1. 若区域 如图
为复连通域，试描
y
D
C
G
述格林公式中曲线
E
F
积分中L的方向.
oA
Bx
D
Q x
P y
dxdy
L
Pdx
Qdy
37
设区域D既是X-型 d
又是Y-型,
x
即平行于
1
(
y)
E y 2(x)
D
B
坐标轴的直线和 L 至多交于两点.
A c
oa
x 2( y) Cy 1(x)
bx
D {( x, y)1( x) y 2( x),a x b}
D {( x, y)1( y) x 2( y),c y d }
7
证明
Ñ L 2xydx x2dy 0.
14
证明 Ñ L 2xydx x2dy 0.
证: 因 P 2x y, Q x2, 则
利用格林公式
Q P
(
D
x
y
)dxdy
Ñ L Pdx
Qdy
得 Ñ L 2x y d x x2 d y 0d x d y 0 D 15
例3 计算
xdy ydx L x2 y2
Q P
Q P
( )dxdy
( )dxdy
高等数学中五类积分之间的关联
(通联：郑州科技学院基础部)
26 2019 第 3 期 下 （总 第 295 期 ）
Z HONG GUO NONG CUN JIAO YU
高等数学中五类积分之间的关联
王 涛 席祥祥
本文针对高等数学教学过程中的定积 分概念，利用密度函数与求不同几何物体的 质量，引入五类不同类型的积分定义与概 念，力求学生易于理解和掌握定积分概念。
一、引言 定积分是高等数学在最重要的基本内 容，但冗长的定义和难以理解的内涵往往 使学生望而生畏。本通过求不同几何物体 的质量，对高等数学中的五类积分的概念 进行分析和阐述，以期使学生易于理解和 掌握五类积分的基本概念和内涵。 二、五类抽象的积分 在高等数学教材中，分别有定积分、重 积分、线积分和面积分。我们通过对不同几 何形状和不同维数的物体求质量的问题， 引入如下问题： 问题 1：设有一直线型构件 ，其 放 在平 面 直 角坐 标 系 的 轴 上 所 占 区 间 为 [a，b]，且 其 线 密 度 ρ（x）在 [a，b]上 连 续 ，问 该 构 件 的 质量为多少？ 问题 2:（平 面 型构 件 的 质量 ）已 知 某平 面型构件在 xoy 面所占区域为 D，且 面 密 度 ρ（x，y）在 D 上连续，问如何求该构件的质量？ 问题 3:（空 间 型构 件 的 质量 ）已 知 某物 体 在 o-xyz 直 角 坐 标 系 中 所 占 空 间 区 域 为 Ω，且体 密 度 ρ（x，y，z）在 Ω 上 连 续，问 如 何 求该物体的质量？ 问题 4:（曲 线 型构 件 的 质量 ）已 知 某曲 线型构件在空间直角坐标系中所占空间曲 线为 Γ，且 线 密度 ρ（x，y，z）在 Γ 上 连 续 ，问 如何求该构件的质量？ 问题 5: （曲 面 型构 件 的 质量 ）已 知 某 曲面型构件在空间直角坐标系中所占空间 曲面为 Σ，且 面 密度 ρ（x，y，z）在 Σ 上 连续 ， 问如何求该构件的质量？ 分析上述五个问题会发现它们有一个 共同点，均为求物体质量的问题，不同点只 在于物体的形态以及涉及到的密度形式不 同，但质量计算的思想都是一样的（以下三 种形式之一）： 质量 = 线密度×长度；质量 = 面密 度×面积；质量 = 体密度×体积。 关于问题 1，学生已知的物理知识是密 度恒定来求质量，如：已知线密度 ρ，则质量 m= ρx（其中代表长度），引导学生如何 用已 知的思想来解决未知的事物。于是提出如 下的四部曲： ① 分 割 [a，b]：a=x0 ＜x1 ＜···xn=b，记 Δxi=xi-xi-1 ②近似：（由于 ρ（x）在[a，b]上连续，当 小区间[xi-1，xi]充分小的时候，ρ（x）在该区间
二阶变系数线性微分方程的一些解法
第九节 二阶变系数线性微分方程的一些解法常系数线性齐次方程和某些特殊自由项的常系数线性非齐次方程的解法已在第七节中介绍，而对于变系数线性方程，要求其解一般是很困难的。
本节介绍处理这类方程的二种方法§9.1 降阶法在第五节中我们利用变量替换法使方程降阶，从而求得方程的解，这种方法也可用于二阶变系数线性方程的求解。
考虑二阶线性齐次方程22dx y d ＋p(x) dxdy ＋q(x)y ＝0 (9.1)设已知其一个非零特解y １，作变量替换，令 y ＝uy 1 (9.2)其中u ＝u(x)为未知函数，求导数有dx dy ＝y 1dx du ＋u dxdy 1求二阶导数有22dx y d ＝y 122dx u d ＋2dx du dxdy 1＋u 212dx y d代入(9.1)式得y 122dx u d ＋（2dx dy 1＋p(x)y 1）dx du ＋(212dx y d ＋p(x)dx dy 1＋q(x)y 1)u ＝0 (9.3)这是一个关于u 的二阶线性齐次方程，各项系数是x 的已知函数，因为y 1是(9.1)的解，所以其中212dx y d ＋p(x) dx dy 1＋q(x)y 1≡0故(9.3)式化为 y 122dx u d ＋(2dx dy 1＋p(x)y 1) dxdu ＝0再作变量替换，令dxdy＝z 得y 1dx dz ＋(2dxdy 1＋p(x)y 1)z ＝0分离变量 z1dz ＝－[1y 2＋p(x)］dx两边积分，得其通解z ＝212y C e－∫p(x)dx其中C 2为任意常数积分得u ＝C 2∫21y 1e －∫p(x)dxdx ＋C 1代回原变量得(9.1)的通解y ＝y 1［C １＋C 2∫21y 1e －∫p(x)dxdx ］此式称为二阶线性方程的刘维尔(Liouville )公式。
综上所述，对于二阶线性齐次方程，若已知其一个非零特解，作二次变换，即作变换y ＝y 1∫zdx可将其降为一阶线性齐次方程，从而求得通解。
高等数学教学中各种积分之间关系的研究
高等数学教学中各种积分之间关系的研究在高等数学教学中，各种积分之间存在着密切的关系。
通常来讲，各种积分之间可以互相转化，即通过不同的转化方法，可以将一种积分表示为另一种积分。
因此，研究各种积分之间的关系，对于高等数学教学具有重要意义。
常见的各种积分包括定积分、不定积分、微积分、向量积分等。
定积分是指在一个定义域内，通过求解下限和上限之间的积分，来确定函数的积分。
不定积分是指对于一个定义域内的函数，求解其积分的过程，而不需要确定下限和上限。
微积分是指研究函数的微小变化，包括导数、二阶导数等。
向量积分是指在空间中，对于一个函数或一个向量场，求解其积分的过程。
研究各种积分之间的关系，可以帮助学生更好地理解这些积分的定义和性质，并运用不同的积分方法来解决问题。
在继续研究各种积分之间的关系时，还可以关注以下几点：1.各种积分的定义域和求解范围：每种积分都有自己的定义域和求解范围，在研究这些积分之间的关系时，要注意这些积分在何种情况下可以使用。
2.各种积分的转化方法：各种积分之间可以互相转化，在研究这些积分之间的关系时，要注意这些积分之间的转化方法。
3.各种积分的应用场景：各种积分都有自己的应用场景，在研究这些积分之间的关系时，要注意这些积分在何种情况下可以使用。
各在继续研究各种积分之间的关系时，还可以关注以下几点：1.各种积分的解题方法：各种积分都有自己的解题方法，在研究这些积分之间的关系时，要注意这些积分的解题方法。
2.各种积分的性质：各种积分都有自己的性质，在研究这些积分之间的关系时，要注意这些积分的性质。
3.各种积分的实际应用：各种积分都有自己的实际应用，在研究这些积分之间的关系时，要注意这些积分的实际应用。
通过对各种积分之间的关系的研究，学生可以更好地理解这些积分的定义和性质，并运用不同的积分方法来解决问题。
各类积分之间的联系与计算(朱静)
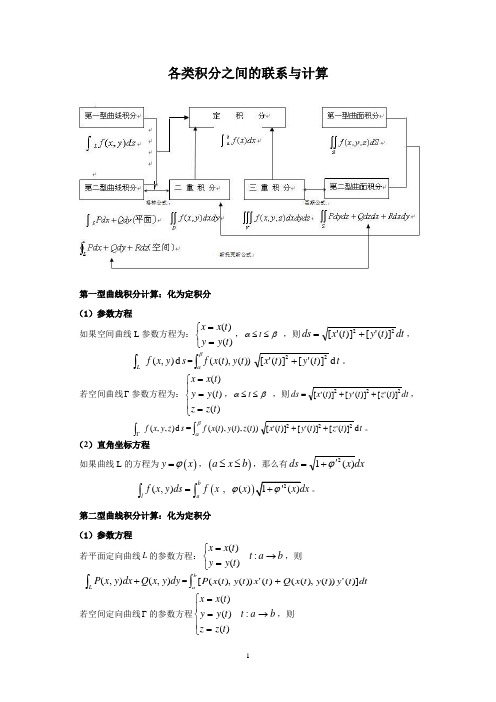
各类积分之间的联系与计算第一型曲线积分计算：化为定积分 （1）参数方程如果空间曲线L 参数方程为：⎩⎨⎧==)()(t y y t x x ，βα≤≤t ，则dt t y t x ds 22)]('[)]('[+=，s y x f Ld ),(⎰=⎰βα))(),((t y t x f t t y t x d )]('[)]('[22+。
若空间曲线Γ参数方程为：⎪⎩⎪⎨⎧===)()()(t z z t y y t x x ，βα≤≤t ，则dt t z t y t x ds 222)]('[)]('[)]('[++=，s z y x f d ),,(⎰Γ=⎰βα))(),(),((t z t y t x f t t z t y t x d )]('[)]('[)]('[222++。
（2）直角坐标方程如果曲线L 的方程为()y x ϕ=，()a x b ≤≤，那么有dx x ds )(12ϕ'+=((,) , ()blaf x y ds f x x ϕ=⎰⎰。
第二型曲线积分计算：化为定积分（1）参数方程若平面定向曲线L 的参数方程：b a t t y y t x x →⎩⎨⎧==:)()(，则⎰+L dy y x Q dx y x P ),(),(=⎰+badt t y t y t x Q t x t y t x P )]('))(),(()('))(),(([若空间定向曲线Γ的参数方程b a t t z z t y y t x x →⎪⎩⎪⎨⎧===:)()()(，则⎰Γ++dzz y x R dy z y x Q dx z y x P ),,(),,(),,(=⎰++b adt t z t z t y t x R t y t z t y t x Q t x t z t y t x P )]('))(),(),(()('))(),(),(()('))(),(),(([（2）直角坐标方程若曲线L 的方程为()y x ϕ=，b a x →: 则[]dx x y x y x Q x y x P dy y x Q dx y x P bal⎰⎰'+=+)()(,())(,(),(),(二重积分的计算：化为二次积分（1）直角坐标系若),(y x f 在x 型区域}),()(|),{(21b x a x y y x y y x D ≤≤≤≤=上连续 则σd y x f D⎰⎰),(=11()()(,)by x ay x dx f x y dy ⎰⎰.若),(y x f 在y 型区域}),()(|),{(21d y c y x x y x y x D ≤≤≤≤=上连续，则σd y x f D⎰⎰),(=⎰⎰)()(21),(y x y x dcdx y x f dy .（2）极坐标变换极坐标变换：⎩⎨⎧==θθsin cos r y r x , πθ20,0,≤≤+∞<≤r⎰⎰⎰⎰=DDrdrd r r f dxdy y x f θθθ)sin ,cos (),(情形1 原点D O ∉1）∆为θ型区域，即}),()(|),{(21βθαθθθ≤≤≤≤=∆r r r r ，此时.)sin ,cos (),()()(21dr r r r f d dxdy y x f r r D⎰⎰⎰⎰=θθβαθθθ2）∆为r 型区域，即}),()(|),{(2121r r r r r r ≤≤≤≤=∆θθθθ，此时.)sin ,cos (),()()(2121θθθθθd r r f rdr dxdy y x f r r r r D⎰⎰⎰⎰=情形2 原点O 是积分区域D 的内点，D 的边界极坐标方程为)(θr r =，则变换后的区域}20),(0|),{(πθθθ≤≤≤≤=∆r r r ，此时.)sin ,cos (),()(020dr r r r f d dxdy y x f r D⎰⎰⎰⎰=θπθθθ情形3 原点O 在积分区域的边界曲线)(θr r =上，}),(0|),{(βθαθθ≤≤≤≤=∆r r r ，此时有.)sin ,cos (),()(0dr r r r f d dxdy y x f r D⎰⎰⎰⎰=θβαθθθ广义极坐标变换:⎩⎨⎧==θθsin cos br y ar x πθ20,0,≤≤+∞<≤r⎰⎰⎰⎰=DDabrdrd br ar f dxdy y x f θθθ)sin ,cos (),(三重积分的计算：化为三次积分 （1）直角坐标系投影法（以投影到xy 平面为例）我们先在z 轴上做积分，暂时将y x ,看成是常数．把函数()z y x f ,,看作是z 的函数，将它在区间()()],,,[21y x z y x z 上积分得到“线”的质量()()()⎰y x z y x z dz z y x f ,,21,,．显然这个结果是y x ,的函数，再把这个结果在平面区域xy D 上做二重积分“体”的质量()()()d x d y dz z y x f y x z y x z D xy⎪⎭⎫ ⎝⎛⎰⎰⎰,,21,,，即 ⎰⎰⎰⎰⎰⎰=),(),(V21),,(V ),,(y x z y x z D dz z y x f dxdy d z y x f xy若}),()(),,(),(|),,{(2121b x a x y y x y y x z z y x z z y x V ≤≤≤≤≤≤=，⎰⎰⎰⎰⎰⎰=),(),()()(V2121),,(d V ),,(y x z y x z x y x y badz z y x f y dx d z y x f ；若}),()(),,(),(|),,{(2121d y c y x x y x y x z z y x z z y x V ≤≤≤≤≤≤=，⎰⎰⎰⎰⎰⎰=),(),()()(V2121),,(d V ),,(y x z y x z y x y x dcdz z y x f x dy d z y x f ；截面法（以截面平行于xy 平面为例）确定V 位于平面21c z c z ==与之间，即],[21c c z ∈，过z 作平行于xoy 面的平面截V ，得截面z D ，不难得到： “面”的质量(),,zD f x y z dxdy ⎰⎰，“体”的质量 dzdv z y x f Vc c ⎰⎰⎰⎰=21),,(⎰⎰zD dxdy z y x f ),,(（2）柱面坐标变换,,20,0,,sin ,cos :+∞<<-∞≤≤+∞<≤===z r z z r y r x T πθθθdz rdrd dV θ=⎰⎰⎰Vdxdydz z y x f ),,(=.),sin ,cos (⎰⎰⎰'V dz rdrd z r r f θθθ{}212121/),()(),,(),(),,(θθθθθθθθ≤≤≤≤≤=r r r z z r z z r V⎰⎰⎰Vdxdydz z y x f ),,(=rdz z r r f dr d r z r z r r ),sin ,cos (),(),()()(212121⎰⎰⎰θθθθθθθθθ（3）球坐标变换,0,20,0,rcos ,sin sin ,cos sin :πϕπθϕθϕθϕ≤≤≤≤+∞<≤===r z r y r x T θϕϕd drd r dV sin 2=⎰⎰⎰Vdxdydz z y x f ),,(.sin )cos ,sin sin ,cos sin (2⎰⎰⎰'=V d drd rr r r f θϕϕϕθϕθϕ{}212121/),()(),,(),(),,(θθθθϕθϕθϕθϕθϕ≤≤≤≤≤=r r r r V⎰⎰⎰Vdxdydz z y x f ),,(=dr r r r f d d r r ϕϕθϕθϕϕθθϕθϕθϕθϕθθsin )rcos ,sin sin ,cos sin (2),(),()()(212121⎰⎰⎰广义球坐标变换,0,20,0,rcos ,sin sin ,cos sin :πϕπθϕθϕθϕ≤≤≤≤+∞<≤===r c z br y ar x T⎰⎰⎰Vdxdydz z y x f ),,(.sin )cos ,sin sin ,cos sin (2⎰⎰⎰'=V d drd abcr cr br ar f θϕϕϕθϕθϕ第一型曲面积分：化为二重积分（1）直角坐标方程若光滑曲面S ：()y x z z ,=，()D y x ∈,， ),,(z y x f 为定义在S 上的连续函数，则()⎰⎰SdS z y x f ,,=()⎰⎰++Dy x dxdy z z y x z y x f 221),(,,（2）参数方程第二型曲面积分：化为二重积分 （1）直角坐标方程设函数),,(z y x R 在有向光滑曲面∑：),(y x z z =，xy D y x ∈),(上连续，则有⎰⎰⎰⎰±=∧∑xyD dxdy y x z y x R dy dx z y x R )),(,,(),,(（上侧取正，下侧取负）若曲面为∑：),(z y x x =，则有⎰⎰⎰⎰±=∧∑yzD dydz z y z y x P dz dy z y x P ),),,((),,( （前侧取正，后侧取负）若曲面为∑：),(z x y y =，则有⎰⎰⎰⎰±=∧∑xzD dxdz z z x y x Q dz dx z y x Q )),,(,(),,(（右侧取正，左侧取负）注：如果S 的法线方向与相应坐标轴的正向成钝角的那一侧为正侧，则相应的公式右端要加“-”号（2）参数方程格林公式： 若函数),(),,(y x Q y x P 在闭区域D 上连续，且有连续的一阶偏导数，则有,)(⎰⎰⎰+=∂∂-∂∂L DQdy Pdx d yPx Q σL 为区域D 的边界曲线，并取正方向.设区域D 的边界L 由一条光滑曲线或几条光滑曲线组成，规定边界曲线的正方向为：当人沿边界行走时，区域D 总在他的左边；与上述方向相反的方向称为负方向，记为L -.为便于记忆，格林公式可写成下述形式=∂∂∂∂⎰⎰σd QP x Dy ⎰+LQdy Pdx .格林公式沟通了平面区域上的二重积分与其边界曲线上的曲线积分之间的联系.高斯公式：设空间闭区域Ω是由分片光滑的闭曲面2所围成，P （x,y,z ）,Q(x,y,z),R(x,y,z)在Ω上具有一阶连续偏导数，则有公式：⎰⎰⎰⎰⎰Ω∑++=∂∂+∂∂+∂∂Rdxdy Qdzdx Pdydz dxdydz z R y Q x P )(这里∑是由Ω的整个边界曲面的外侧构成。
几种积分之间的关系
⑤
设有向曲线弧
L
的参数方程为
x
y
x(t) y(t)
，且当参数 t
单调地从
变到
时，点
M (x, y) 从的起点 A 沿 L 运动到终点 B ，则
2
L
P(
x,
y)dx
Q(
x,
y)dy
P
Байду номын сангаасx(t
),
y(t
)
x(t
)
Q
x(t
),
y(t
)
y(t
)
dt
（积分下限 对应起点 A ，积分上限 对应终点 B ）．
情形 1：设曲面 : z z(x, y) ，(x, y) Dxy ，则曲面 的面积微元 dS
1
zx2
z
2 y
dxdy
，
f (x, y, z)dS f x, y, z(x, y)
1
zx2
z
2 y
dxdy
．
Dxy
情形 2：设曲面 : x x( y, z) ，( y, z) Dyz ，则曲面 的面积微元 dS 1 xy2 xz2 dydz ，
所以 Pdydz Qdzdx Rdxdy P cos Q cos R cos dS ，即第二类曲面积分
是第一类曲面积分的特殊情形．
⑧ 第二类曲面积分的计算
情形 1：设曲面 : x x( y, z) ， ( y, z) Dyz ，则
当 时， P(x, y, z)dydz Px(y ,z ),y ,zdydz ，上式右端取“+”号或“−”
．
z r cos
1
③ 第一类曲线积分 f (x, y)ds ，其中 L 是 xOy 面上的光滑曲线段，弧长微元 L ds (dx)2 (dy)2 ．
各类积分间关系工科
各类积分间的关系0、重积分的计算关键在于将积分区域分解X-型域或Y-型域；投影法（先一后二！）或截面法有时要先选择恰当的坐标系1、对弧长的曲线积分（第一类）算法：⎰⎰'+'=βαψϕψϕt t t t t f s y x f L d )()()](,)([d ),(22 （βα<） 关键在于给出曲线的方程（参数方程、普通方程或极坐标方程）； 曲线弧长元素：t t t ds d )()(22ψϕ'+'=2、对坐标的曲线积分（第二类）算法：{dt t t t Q t t t P y y x Q x y x P L })( )](),([)()](),([d ),(d ),(⎰⎰'+'=+βαψψϕϕψϕ 关键在于给出曲线的方程，并确定起止点对应的参数。
定积分是第二类曲线积分的特例！3、两类曲线积分之间的联系：()(){}ds y x Q y x P y y x Q x y x P LL ⎰⎰+=+βαcos ,cos ,d ),(d ),(βαcos ,cos 为L 的切向量之方向余弦{}s R Q P Rdz Qdy Pdx d cos cos cos γβα++=++⎰⎰ΓΓ 4、对面积的曲面积分算法： ()()dxdy y x z y x z y x z y x f S z y x f y xD y x ,,1)),(,,(d ),,(22++=⎰⎰⎰⎰∑ 其中：()==∑dS y x z z ；方程为,()()dxdy y x z y x z y x,,122++ （dS 曲面面积元素）5、对坐标的曲面积分算法：()dxdy y x z y x R dxdy z y x R y x D )),( ,,(,,⎰⎰⎰⎰±=∑（面上的投影在为XOY D xy ∑）其中：()()；方程为xy D y x y x z z ∈=∑,,, 上（侧）正、下（侧）负6、两类曲面积分之间的联系：()dS R Q P Rdxdy Qdzdx Pdydz ⎰⎰⎰⎰∑∑++=++γβαcos cos cos 7、格林公式：⎰⎰⎰+=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂LD y Q x P y x y P x Q d d d d 一般由右向左使用，的正向边界为区域D L ；注意例3及第二类曲线积分的路径无关。
各种积分间的关系
13
(2) 简化二重积分的计算
例 2 计算 e y2dxdy ,其中D 是
D
以O(0,0), A(1,1), B(0,1)为顶点
的三角形闭区域.
14
解 令 P 0, Q xe y2 ,
y
则 Q P e y2 , x y
B
A
1
D
应用格林公式,有
o
e y2dxdy
xe y2 dy
D
OA AB BO
计算 (1,1) xy2dx y ( x)dy. (0,0)
34
解 P( x, y) xy2, Q( x, y) y( x),
P ( xy2 ) 2xy, y y
Q [ y( x)] y( x), x x
积分与路无关 P Q ， y x
35
由 y( x) 2 xy ( x) x2 c
对 D 内任意闭曲线 L
有 在
D
内有
Q
P
x y
L Pd x Qd y 0
在 D 内有 d u P d x Q d y
41
根据定理2 , 若在某区域内 P Q , 则 y x
1) 计算曲线积分时, 可选择方便的积分路径; 2) 求曲线积分时, 可利用格林公式简化计算,
若积分路径不是闭曲线, 可添加辅助线;
y sin x .
2
32
解 P ( x2 2xy) 2x
y y Q ( x2 y4 ) 2x x x
P Q ， y x
原积分与路径无关
故原式
1 x2dx
1
(1
y4 )dy
23 .
0
0
15
33
例7 设曲线积分 xy2dx y ( x)dy L
一格林公式及其应用
2
利用格林公式 , 得
2x y d x x
L
2
d y 0 d x d y 0
D
13
(2) 简化二重积分的计算
例 2 计算 e
D
y2
D 是 dxdy ,其中
以O ( 0,0), A(1,1), B( 0,1) 为顶点 的三角形闭区域.
14
解
令 P 0, Q xe Q P y2 e , 则 x y
无重点,分段光滑且不经过原点的连续 闭曲线, L的方向为逆时针方向.
16
xdy ydx L x 2 y 2
解 记 L所围成的闭区域为 D ,
y x , Q 2 令P 2 , 2 2 x y x y
则当 x 2 y 2 0时,
Q y x P 有 2 . 2 2 x ( x y ) y
( L1, L2 , L3对D来说 为正方向 )
10
L3
D3D2ຫໍສະໝຸດ L2D1L1
L
格林公式的实质:
揭示了平面闭区域上二重积分与区域 边界上的曲线积分之间的联系.
11
3. 简单应用
(1) 简化曲线积分的计算
例1 设L是一条分段光滑的闭曲线， 证明
2 xydx x dy 0.
2 L
12
证: 令 P 2 x y , Q x , 则
y E
y 2 ( x)
d 型x 1 ( y) A c o a
D
B
x 2 ( y) Cy 1 ( x ) x b
D {( x , y ) 1 ( x ) y 2 ( x ), a x b}
D {( x , y ) 1 ( y ) x 2 ( y ), c y d }
各种积分间的关系
合并以上三式得：
P Q R ( x y z )dv Pdydz Qdzdx Rdxdy
这里是的整个边界曲面的外侧.
2. 简单应用
简化计算曲面积分
例1 计算曲面积分
z
3
( x y )dxdy ( y z ) xdydz，
4
R 证明 仅证 dv R( x , y , z )dxdy. z
设闭区域 在面xoy上的投影区域为 Dxy
由 1 , 2 和 3 三部分组成,
z
Dx y
1
:
z z1 ( x , y ) 下侧
2 1 3
2 : z z2 ( x , y )上侧
{ R[ x , y , z2 ( x , y )] R[ x , y , z1 ( x , y )]}dxdy,
Dxy
R dv R( x , y , z )dxdy . z
同理
P x dv P ( x , y, z )dydz, Q y dv Q( x , y, z )dzdx,
2 2 3 2
： z a x y 0
2
原式
2 0
( x y z )d v
2 2
2 2
r r sin drd d
d sin d
2 0
a
0
2 5 r dz a 5
4
例3 计算曲面积分
( x
2
cos y cos z cos )dS，
[ R( x , y , z )]
各类积分的关系
学院：统计与数学学院班级：信息与计算科学学号：902094135导师；毕远宏姓名：贾建慧各类积分之间的关系积分有不定积分、定积分以及二重积分，三重积分，第一类线积分，第二类线积分，第一类面积分，第二类面积分等。
我在这里只介绍我们在大学的时候学习过的几类常用积分的关系。
一、不定积分：即已知导数求原函数。
定义1:设函数f与F在区间I上都有定义。
若F′（x）=f(x),x ∈I,则称F为f在区间I上的一个原函数。
例如，13x3是x2在（—∞，＋∞）上的一个原函数，因为（13x3）＇=x2；又如-12cos2x与-12cos2x+1都是sin2x在（−∞,+∞）上的原函数，因为（-12cos2x）＇=（-12cos2x+1）＇=sin2x.定理8.1可知由于初等函数为连续函数，因此每个初等函数都有原函数（只是初等函数的原函数不一定是初等函数）当然如果一个函数存在间断点，那么此函数在其间断点所在的区间上就不一定存在原函数。
定义2:函数f在区间I上的全体原函数称为f在I上的不定积分，记作f x dx其中∫称为积分号,f x被积函数，f(x)dx为被积表达式，x为积分变量。
由定义2可知不定积分与原函数是总体与个体的关系，即若F′(x)=f(x)，那么[F(x)+C]′=f(x).(C∈R).也就是说，把f(x)积分，不一定能得到F(x)，因为F(x)+C的导数也是f(x)（C是任意常数）。
所以f(x)积分的结果有无数个，是不确定的。
我们一律用F(x)+C代替，这就称为不定积分。
即如果一个导数有原函数，那么它就有无限多个原函数。
f x dx=f x或d f x dx=f x dx；性质1：ddx性质2：F＇x dx=F x+C或dF x+C；性质3：αf x±βg x dx=αf x dx±βg x dx，α,β为非零常数。
二、定积分:定积分就是求函数f x在区间a,b中图线下包围的面积。
即由 y=0, x=a ,x=b, y=f x所围成图形的面积。
毕业论文-各类积分之间的关系【范本模板】
目录1。
引言 (2)2.积分的概念 (2)2.1 定积分的概念 (2)2。
2 曲线积分的概念 (3)2.3 二重积分的概念 (4)2.4 曲面积分的概念 (4)2.5 三重积分的概念 (6)3。
各类积分的关系 (6)3.1各类积分的共同属性 (7)3。
2各类积分计算的一致性 (7)3。
3几个积分公式 (9)4.几个积分公式之间的联系 (9)4。
1积分公式的介绍 (9)4。
2牛顿—莱布尼兹公式与格林公式的关系 (10)4。
3格林公式与高斯公式的关系 (10)4.4格林公式与斯托克斯公式的关系 (10)4.5小结 (11)4。
6积分公式在积分计算中的应用 (11)结论 (13)参考文献 (14)致谢 (15)各类积分之间关系的研究某某,某某学院摘要：本文从积分的本质属性和积分计算的一致性两个方面探讨了重积分、曲线积分、曲面积分与定积分之间的关系,进而讨论了几个重要的积分公式，即牛顿—莱布尼茨公式、格林公式、高斯公式、斯托克斯公式以及它们之间的联系,最后通过举例说明了这几个积分公式在积分计算中的重要作用。
关键词:定积分；重积分; 曲线积分；曲面积分;牛顿—莱布尼茨公式;格林公式；高斯公式；斯托克斯公式On the relationship between various types of integralSiting Liang，School of mathematics and computer science Abstract: This paper discusses the relationship between the triple integral，curve integral, surface integral and definite integral from the perspective of the essence of integral and the consistency of the integral calculation。
数学分析课件22.1各种积分间的联系334.00KB
l
Q ( x, y ) l 定理(格林公式) P ( x , y是以光滑曲线 D 为边界的 设 ) y x 平面单连通区域,函数 和 在 及 上连 P 续并具有对 和 Q 的连续偏导数,则有 ( ) dxdy Pdx Qdy . 【数学分析课件】
D
x
y
l
这里右端为沿有向闭路的积分,积分路径的方向是和区 域正向联系的,即当一个人沿着曲线 l 行走时区域 D 恒 在他的左边(亦即服从右手法则的联系). 这个公式称为格林公式.
我们再讨论复连通区域的格林公式.若 D 是复连通 区域,它的边界由两条曲线 l 和 L 组成,用一条曲线 c 把 区域 D 的边界曲线 L 和
c
l
联结起来,那么以曲线
Qdy
L,l
及
为边界的区域就成了一个单连通区域,应用格林公式
D
(
Q x
P y
) dxdy
Pdx
L
[( y
S
R
Q z
) cos( n , x ) (
P z
R x
) cos( n , y )
(
Q x
(
P y
) cos( n , z )] dS
) dydz ( P z R x ) dzdx ( Q x P y
S
cos( n , z ) z R
dS
S
x P
.
【数学分析课件】
例4
x y
2 2
计算
2
( y z ) dx ( z x ) dy ( x y ) dz
第二章 第九节 导数概念及其运算、定积分
题型突破·重点探究
课时作业·巩固提升
一轮 ·数学（理）
4．导数的运算法则 若 f′(x)，g′(x)存在，则有 (1)[f(x)±g(x)]′＝__f′_(x_)_±_g_′(_x_)_____； (2)[f(x)·g(x)]′＝__f′_(x_)_g_(x_)_＋__f(_x_)g_′_(_x)____；
(3)gf（（xx））′＝_f′_（__x_）__g_（__x[g）_（_－_x_）f_（_]_2x_）__g_′（__x_）___(g(x)≠0)． 5．复合函数的导数 复合函数 y＝f(g(x))的导数和函数 y＝f(u)，u＝g(x)的导数间的关系为 yx′ ＝__y_u_′·_u_x′___，即 y 对 x 的导数等于__y_对__u____的导数与___u_对___x__的导数 的乘积．
7
必备知识·自主梳理
题型突破·重点探究
课时作业·巩固提升
一轮 ·数学（理）
二级结论 1．奇函数的导数是偶函数，偶函数的导数是奇函数，周期函数的导数还 是周期函数． 2．函数y＝f(x)的导数f′(x)反映了函数f(x)的瞬时变化趋势，其正负号反映 了变化的方向，其大小|f′(x)|反映了变化的快慢，|f′(x)|越大，曲线在这点 处的切线越“陡”．
12
必备知识·自主梳理
题型突破·重点探究
课时作业·巩固提升
一轮 ·数学（理）
4．(易错题)已知直线 y＝－x＋1 是函数 f(x)＝－1a·ex 图像的切线，则实数 a＝__________． 解析：设切点为(x0，y0)，则 f′(x0)＝－1a·ex0＝－1，∴ex0＝a，又－1a·ex0＝ －x0＋1，∴x0＝2，a＝e2． 答案：e2
3
必备知识·自主梳理
积分学中各种积分之间的关系研究与例解
积分学中各种积分之间的关系研究与例解作者：杨元启来源：《科技风》2017年第01期摘要：本文讨论了高等数学中几种类型的积分之间的联系与转化技巧，并用适当例子说明这些转化技巧的具体应用。
这对各类积分思想的理解和计算都有很重要的意义。
关键词：定积分；重积分；累次积分；线积分；面积分高等数学中的积分学包含的积分类型很多，积分计算也经常走入死胡同，无法求解。
如果能深刻地领会不同积分之间的内在关系，掌握不同类型积分互相转化的技巧，一般都能顺利解答。
各种积分之间的关系及转化技巧，在国内众多文献中能找到一些零星的讨论，但都不够细致深入。
本文着重对定积分、重积分、线积分、面积分这几个常见常用的积分，用实例来详细讨论积分转换技巧的应用。
一、定积分与重积分重积分的计算问题除了用定义外，几乎都是化成两个或多个定积分（累次积分）来计算的。
对一些较复杂的定积分，也可能无法求出其原函数，必须借助重积分的思想才能求解。
以下通过几个例子来说明这些积分的转化技巧。
例1 计算∬D dxdy，其中D 是直线x=π，y=x，y=0所围成的闭区域。
解：如果将二重积分化成如下累次积分：∬D dxdy=dydx由被积函数的特点知这样的积分无法计算，为此交换积分次序：∬D dxdy=dxdy=sinxdx=[-cosx]π=2例2 计算dx解：用求原函数的方法几乎没法解答，注意到=xydy，为此，可以将定积分化成累次积分再来讨论。
原式=dxxydy，交换积分次序得：原式=dyxydx=dxxydy=dx=ln（）例3 设f（x），g（x）在[a，b]上连续，满足∀x∈[a，b），f（t）dt⩾g（t）dt，以及f （x）dx=g（x）dx，证明：xf（x）dx⩽xg（x）dx证：这样的题一般也需要借助累次积分以及换序技巧。
由题意，∀x∈[a，b），f（t）dt-g（t）dt⩾0，（f（t）-g（t））dt作为[a，b）上的非负连续函数，有：（f（t）-g（t））dtdx⩾0，交换积分次序，dt（f（t）-g（t））dx=b（f（t）-g（t））dt-（tf（t）-tg（t））dt⩾0，仍由题意有，tf（t）dt⩽tg（t）dt。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.是否满足高斯公式的条件; 2.是否满足高斯公式的条件; 是否满足高斯公式的条件
3.Σ 是取闭曲面的外侧. 3.Σ 是取闭曲面的外侧.
例2 计算曲面积分
∫∫ xz dydz + ( x
2 Σ
2
y z )dzdx + (2xy + y z )dxdy，
=
∫∫ { R[ x , y , z2 ( x , y )] R[ x , y , z1 ( x , y )]}dxdy, D
xy
R ∴ ∫∫∫ dv =∫∫ R( x, y, z)dxdy. z Σ
同理
P ∫∫∫ x dv =∫∫ P( x, y, z)dydz, Σ Q ∫∫∫ y dv =∫∫ Q( x, y, z)dzdx, Σ
3 2
其 中 Σ为 半 球 体
0≤ z≤ a x y
2 2
2
的 整 个 表 面 曲 面 的 外 侧.
解
P = xz , Q = x y z , R = 2 xy + y z
2 2 3 2
P Q R 2 2 2 + + =z +x +y x y z 2
0 ： ≤ z ≤ a x 2 y 2
Σ3为柱面上的一部分 外侧
x
Dxy y
: z1 ( x , y ) ≤ z ≤ z2 ( x , y ),( x , y ) ∈ Dxy
根据三重积分的计算法
: z1 ( x , y ) ≤ z ≤ z2 ( x , y ),( x , y ) ∈ Dxy
z 2 ( x , y ) R R ∫∫∫ z dv = D [∫z1 ( x , y ) z dz ]dxdy ∫∫ xy
1 4 = πh 2
Σ
Dxy
o
y
x
∫∫ x dydz + y dzdx + z dxdy (∵ Σ1在yoz和zox面上投影面积为零 )
2 2 2 Σ1
= ∫∫ z dxdy =
2 Σ1
∫∫ h dxdy = πh . D
2
4
xy
故所求积分为
原式 =
Σ+Σ1
∫∫ ∫∫ x dydz + y dzdx + z dxdy
立体与其表面曲面上积分间的关系？ 立体与其表面曲面上积分间的关系？
1.高斯（ 1.高斯（Gauss)公式 高斯 ) 定理3 定理 设空间闭区域是由光滑(或分片光滑) 曲面Σ所围成，函数P( x, y, z)、Q( x, y, z)、 R( x, y, z)在上具有一阶连续偏导数,则有
P Q R ∫∫∫( x + y + z )dv=
∫∫
Σ
Pd yd z + Qd z d x + Rd xd y = 0
的充要条件是: 的充要条件是 P Q R + + = 0, ( x, y, z)∈G x y z
三、通量与散度 设稳定流动的不可压缩流体的密度为1, 设稳定流动的不可压缩流体的密度为1, 速度场为 v( x, y, z) = P( x, y, z)i + Q( x, y, z) j + R( x, y, z)k 设Σ 为场中任一有向曲面, 则由对坐标的 为场中任一有向曲面, 曲面积分的物理意义可知 曲面积分的物理意义可知, 理意义可知 单位时间通过曲面Σ 单位时间通过曲面Σ 的流量为
2 2 2 Σ
曲面Σ不是封闭曲面, 曲面Σ不是封闭曲面, 为利用高斯公式
补充Σ1 : z = h ,( x + y ≤ h )
2 2 2
z
Σ1
Σ1取上侧，
Σ + Σ 1构 成 封 闭 曲 面 外 侧 ，
h
Σ
Σ + Σ1围成空间区域 ，
x
o
y
在上使 用高斯 公式 , 得 2 2 2 原式 = ∫∫ = ∫∫ ∫∫ x dydz + y dzdx + z dxdy
2
原式 = ∫∫∫ ( x + y + z )dv
2 2
= ∫∫∫ r r sindrddθ
2 2
= ∫ dθ ∫ sin d ∫
0 2 0
2π
π
a
0
2 5 r dz = πa 5
4
例3 计算曲面积分
∫∫ ( x
Σ
2
cos α + y cos β + z cos γ )dS，
2 2 2 2 2
div A= 0 =
表明该点处无源, 表明该点处无源,
散度绝对值的大小反映了源的强度. 散度绝对值的大小反映了源的强度.
处处有 若向量场 A 处处有 div A= 0 = 为无源场. 则称 A 为无源场. 例如, 例如, 匀速场
v = (vx , vy , vz )(其中vx , vy , vz 为常数),
Σ
o
y
x
Σ+Σ1
∫∫
x dydz + y dzdx + z dxdy = 2 ∫∫∫ zdv
2 2 2
= 2 ∫∫ dxdy ∫
Dxy
h x +y
2 2
zdz
2 2 2
= ∫∫
Dxy
Dxy = {( x , y ) | x + y ≤ h } z 2 2 2 ( h x y )dxdy
Σ1
h
∫∫ Pdydz + Qdzdx + Rdxdy
Σ
. 这里Σ是的整个边界曲面的外侧
3
由两类曲面积分之间的关系知
P Q R ∫∫∫ ( x + y + z )dv = ∫∫ ( P cosα + Qcos β + Rcosγ )dS.
Σ
Gauss公式的实质 Gauss公式的实质 揭示了空间闭区域上的三重积分与 其边界曲面上的曲面积分之间的关系. 其边界曲面上的曲面积分之间的关系.
原式 = ∫∫∫ ( y z )dxdydz
z
3
= ∫∫∫ ( ρ sinθ z ) ρ d ρ dθ dz
o x
= ∫ dθ ∫ ρdρ ∫ ( ρ sin θ z )dz
0 0 0
2π
1
1
y
1
3
9π π = . 2
(利用柱面坐标 利用柱面坐标) 利用柱面坐标
11
使用Guass公式时应该注意 公式时应该注意: 使用 公式时应该注意
定义: 定义: 设有向量场
A( x, y, z) = P( x, y, z)i + Q( x, y, z) j + R( x, y, z)k
其中P, 具有连续一阶偏导数, 其中 Q, R 具有连续一阶偏导数 Σ 是场内 的一片有向曲面，其单位法向量 n, 则称 的一片有向曲面， 曲面
∫∫
Σ
A nd S
根据高斯公式, 根据高斯公式, 流量也可表为
场内任意点M 场内任意点 处的特性
Φ lim →M V
P Q R =( + + )M x y z
Φ P Q R lim = ( + + →M V x y z
)M
散度 此式反应了流速场在点M 的特点: 此式反应了流速场在点 的特点: 其值为正,负或 0, 其值为正, , 分别反映在该点有流体涌出, 吸入, 分别反映在该点有流体涌出, 吸入, 或没有任何变化. 或没有任何变化.
第九节 各种积分间的关系
二、高斯(Gauss)公式及其应用 高斯( )
（第十章 第六节） 第六节）
二、高斯（Gauss)公式及其应用 高斯（ )
牛顿— 牛顿—莱布尼兹公式
∫ f ( x ) dx = F ( b ) F ( a )
b a
格林公式
Q P ∫∫ ( x y )dxdy = D
∫
L
Pdx + Qdy
1 xy
∫∫ R( x , y, z )dxdy = D R[ x , y , z2 ( x , y )]dxdy , ∫∫ Σ
2 xy
∫∫ R( x , y , z )dxdy = 0. 三项相加
Σ3
z
∑2
∫∫ R( x , y, z )dxdy
Σ
= ∫∫ + ∫∫ + ∫∫ R( x , y , z )dxdy
Σ1 Σ2 Σ3
x
∑3 ∑1 Dxy y
∫∫ R( x , y, z )dxdy
Σ
= ∫∫ + ∫∫ + ∫∫ R( x , y , z )dxdy
Σ1 Σ2 Σ3
= ∫∫ R[ x, y, z1 ( x, y)]dxdy + ∫∫ R[ x, y, z2 ( x, y)]dxdy + 0
Dxy Dxy
2 2
o
1
1
y
其 中 Σ 为 柱 面 x + y = 1及 平 面 z = 0， z = 3 所 围 成 的 空 间 闭 区 域 的 整 个 边 界 曲 面 的 外侧.
10
解 P = ( y z ) x , Q = 0, R = x y , P Q R = y z, = 0, = 0, x y z
Σ
Σ+Σ1
∫∫
x dydz + y dzdx + z dxdy = 2 ∫∫∫ ( x + y + z )dv
2 2 2
Σ+Σ1
Σ1
xoz 关于yoz面对称 面对称， 关于 面对称， 被积函数关于x是奇函数 被积函数关于 是奇函数 y= 2 Leabharlann ∫∫ zdv zΣ1h