断面法水库库容计算的算法细节
水库调洪演算的原理和方法

第三章 洪水调节
第二节 水库调洪计算的原理和方法
精选ppt
1
水利水能规划
水库调洪计算是确定入库洪水、泄洪建筑物的型式与尺寸、 调洪方式和调洪库容之间的定量关系。
一、水库调洪计算的任务
在水工建筑物或下游防护对象的防洪标准一定的情况下, 根据水文分析计算提供的各种标准的设计洪水或已知的设 计入库洪水过程线、水库特性曲线、拟定的泄洪建筑物的 型式与尺寸、调洪方式等,通过计算,推求水库出流过程、 最大下泄流量、特征库容和水库相应的特征水位。
(1)由Z~V曲线、泄流计算公式推求q~V曲线。
(2)推求水库下泄流量过程线q~t。
(a)分析确定起调水位Z1和计算时段。
无闸: Z1=Z堰顶
有闸: Z1=Z限
(b)由起始条件确定Q1、Q2 、V1和q1。
(c)试算(q2~V2~q'2)。
(d)将精q选2p、pVt 2作为下时段的起始条件,推求q~t5。
精选ppt
33
第十四章 水库防洪计算
水利水能规划
• 三、有闸溢洪道水库的防洪计算
精选ppt
34
水利水能规划
精选ppt
35
水利水能规划
• 四、具有非常泄洪设施水库的防洪计算
• (一)非常泄洪设施
• 有的水库校核洪水比设计洪水大得多,尤其当校核 洪水采用可能最大洪水时,二者相差更为悬殊。如 只设有正常泄洪建筑物,必将增加工程造价。因此, 为了安全又不致使造价过高,若条件许可,应尽量 修建位置适当、工程比较简易的非常泄洪建筑物, 帮助正常泄洪设置宣泄比设计洪水大得多的洪水。
精选ppt
37
水利水能规划
入库洪水:从水库周边汇入水库(包括入库断面)的 洪水。
断面法水库库容计算的算法细节

断面法水库库容计算的算法细节刘炜(黄河水利委员会水文局,河南郑州450004)摘要:本文论述了断面法水库库容计算的基本算法模型及间距采用、底部锥体和回水末端处理等细节问题。
关键词:断面法库容计算算法断面法是水库库容及冲淤量测算的常规方法之一,断面法分为加密断面法和基本断面法。
前者是通过在水库水系各干支流上布设足够密集的测量断面(称为加密断面),实现对水库库容接近于地形法测图精度的精确测算。
通过减少参与计算的断面数量,经过反复对比计算,并依照水库河道测量的有关规范要求,从加密断面中选取出一定数量和足够代表性的断面,固定下来进行历年的常规测量和库容计算,就构成了基本断面法,基本断面法又称为固定断面法,“断面法”在一般情况下所指的也就是基本断面法。
基本断面是在对比计算基础上确定的,数量少且对于库区地形变动的代表性强。
因此,基本断面法可以在相当长的时期(基本断面代表期)内,以较低的成本和较短的测量周期实现对水库库容的准确测算。
直到水库经过多年运行,河床形态和冲淤规律发生了显著变迁时,基本断面需要从新确定。
在基本断面代表期内,影响库容及冲淤量成果准确性的主要因素有两方面,一是外业测量的质量控制,二是数据处理与计算方法。
本文就后者的若干细节问题进行讨论。
1.基本算法模型及公式水库断面法计算通常采用截锥体概化,即假设将上下两个断面间的河道按概化间距拉直后,其容积立体构成一个截锥体:上下断面分别对应该截锥的两个底面,概化间距对应截锥的高。
在截锥体假设的情况下,计算区段内的任意河道横断面在宽和深两个方向上都被认为是沿河长线性变化的。
因而其面积在上下断面间以2次关系变化。
bb+aA 2A 1图1断面间容积立体的截锥体假设如图1所示,断间容积立体按照截锥体假设,其体积为两个锥体体积之差:(1)1231)(31aA A b a V -+=根据锥体的性质,有比例关系:解出2122)(A A b a a =+12211A A A A b bA a -⋅+=代入(1)式简化后得到:(2))(312211A A A A b V +⋅+=上式即为水库库容计算的基本公式,一般称为截锥(体体积)公式。
水库库容计算公式

水库库容计算公式1.水库角形面积计算公式:水库角形面积指的是水库在不同水位下的横截面积。
对于直角坐标系下的水库,可以通过连接水库两端边界上的点,形成一个多边形,然后使用多边形面积计算公式来计算。
多边形面积计算公式有多种,其中一种常用的计算公式是利用水库两端边界上点的坐标,按顺时针或逆时针方向计算如下:S = 0.5 * [(x1*y2 + x2*y3 + ... + xn-1*yn + xn*y1) - (x2*y1 + x3*y2 + ... + xn*y1 + x1*yn)]其中,S表示多边形的面积,n表示多边形的边数,(x1, y1) ~ (xn, yn)表示多边形边界上的点的坐标。
2.坝体造型计算公式:坝体造型计算公式指的是根据水库的几何形状参数,来计算水库不同水位下的横截面积。
常见的坝体造型有三角形坝、矩形坝、梯形坝等,这些形状的库容计算公式是不同的。
-三角形坝库容计算公式:三角形坝库容计算公式是根据坝顶高程、坝底高程和坝宽计算的。
V=0.5*h*b*l其中,V表示库容,h表示水位高程,b表示坝宽,l表示坝长。
-矩形坝库容计算公式:矩形坝库容计算公式是根据坝顶高程、坝底高程和坝宽计算的。
V=h*b*l其中,V表示库容,h表示水位高程,b表示坝宽,l表示坝长。
-梯形坝库容计算公式:梯形坝库容计算公式是根据坝顶高程、坝底高程、坝宽和坝高计算的。
V=(h1+h2)/2*b*l其中,V表示库容,h1表示坝顶高程,h2表示坝底高程,b表示坝宽,l表示坝长。
总结:以上是常见的水库库容计算公式,不同形状的水库可以选择相应的公式进行计算。
通过计算水库的库容,可以评估水库的蓄水能力,为水库的设计和管理提供重要依据。
水库库容

1. 断面法: 断面法是一种常规的计算方法,应用比较广泛,但有一定的局限性。主要适 用于典型的河槽式河流, 断面法计算模型建立在把水体沿水流流程分割成 n 个梯 形,整体库容由 n 个梯形体体积积分所得。考虑梯形体的不规则性,其数学模型 为: V=
n 1 i=0 3
A������ + A������ +1 + A������ ∗ A������ +1 ∗ ∆L������
n i=1 PS [H-(h������
+ h������ +1 + h������ +2 + h������ +3 )/4]
式中:V——库容,m3 ; PS ——单个 DEM 格网的面积值,m2 ; H——指定水位的高程面 ,m; h������ ——格网角点高程面,m;
n ——( h������ + h������ +1 + h������ +2 + h������ +3 ) /4 小于 H 的 DEM 格网个数,当 (h������ + h������ +1 + h������ +2 + h������ +3 )/4 大于 H 时,该格网不参与计算
式中:V——库容,m3 ; A������ ——第 i 个横断面面积,m2 ; ∆L������ ——第 i ~ i+1 个横断面之间间距,m
2. 等高线容积法 等高线容积法计算水库库容是一种计算精度较高的方法之一, 该计算模型建 立在把水体按不同高程面微分成 n 层梯形体, 整体库容由 n 层梯形体体积积分求 得。考虑梯形体的不规则性,其等高线容积法计算水库库容数学模型为: V=
谈水库库容的计算方法

随着社会经济的发展和人民生活水平的不断提高,对饮水水质的要求越来越高。
上海作为典型的水质型缺水的城市,目前供水水源地主要由黄浦江上游、长江口陈行水库以及部分内河和地下水组成。
地下水蕴藏量有限,开采量受到严格控制;黄浦江的水量、水质均不能满足本市发展的需要;长江口陈行水源地库容偏小,避咸蓄淡能力不足。
为此,上海将加快实施长江口青草沙和崇明岛东风西沙新水源地建设,提高避咸蓄淡能力,打造“两江并举、多源互补”水源地新格局,确保城市居民的饮用水安全。
水库的建设规模是水库前期论证的主要工作成果,也是水库调度运行的重要参数,其精度直接影响工程的蓄水效果、调度运行及工程投资等。
在受潮汐影响较大的式估算水库库容。
1、咸潮入侵规律淡水来源和淡水量是影响水库库容设计的关键因素之一,位于潮汐河口的供水水库在枯水期受海水咸潮入侵威胁严重,淡水量与所处水域内盐水倒灌的强弱程度及规律、特性直接相关。
因此,咸潮入侵规律是研究潮汐河口供水水库库容的前提条件,是河口水源地水资源开发利用的最大制约因素。
以长江口为例,长江河口系三级分叉四口入海的分潮汐河口。
从整体上说,长江口的咸潮入侵源只有一个,即外海海水。
但由于长江口呈多级分叉多口入海的形势,各叉道的过水断面、分流比、潮波传播速度不同,出现咸潮入侵源的派生现象,使得长江口的盐度分布非常复杂。
长江口盐水入侵有四条途径:南槽、北槽、北港和北支。
一般而言,北支的进潮量约占整个长江口进潮量的25%,但是进入北支的径流量目前只有不到5%,所以,北支口门连兴港断面处的盐度几乎与正常海水盐度相当,到北支上段青龙港处,枯季盐度仍然较高,这股高盐水随北支涨潮流上溯至崇头后被推出北支上口,然后绕过崇头倒灌侵入南支,使得南支水域出现盐度超标的现象。
如东风西沙水库工程水域咸潮主要来源于北支盐水倒灌,集中发生在大潮前后,最严重的时期为每年枯季的2-3月份,特点是咸潮超标次数多、持续时间长。
因此,咸潮入侵规律直接影响了淡水取水时间和淡水取水时机。
水库库容计算.
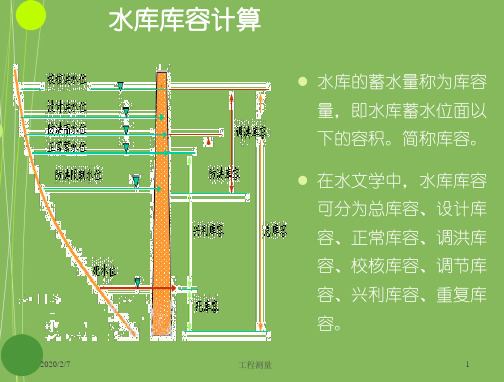
图4.3.8 水库的淹没面积
2020/2/7
工程测量
3
计算库容一般用等高线法。
先求出图4.3.8中阴影部分各条等 高线所围成的面积,然后计算各 相邻两等高线之间的体积,其总 和即为库容。
图4.3.8 水库的淹没面积
2020/2/7
工程测量
4
图4.3.8 水库的淹没面积
2020/2/7
设S1为淹没线高程的等高线 所围成的面积,S2、 S3、……Sn、Sn+1 为淹没线
以下各等高线所围成的面积,
1 V1 2 (S1 S2 ) h
V2
1 2
(
S
2
S3) h
…V…n …12…(S…n …S…n…1) …h …
Vn
1 2
Sn 1
h
V V1 V2 ...... V(n 库V底n 体积)
S1 2
S水库淹没线与
其下的第一根等高线之间
的高差不等于等高距。
工程测量
6
S n 1 2
h
1 3
S n 1h
工程测量
5
图4.3.8 水库的淹没面积
2020/2/7
其中Sn+1为最低一根等高 线所围成的面积,h为等高 距,h′为最低一根等高线 与库底的高差。
如果溢洪道高程不等于地 形图某一等高线高程时, 就要根据溢洪道高程用内 插法求出水库淹没线,然 后计算库容。
水库库容计算
水库的蓄水量称为库容 量,即水库蓄水位面以 下的容积。简称库容。
在水文学中,水库库容 可分为总库容、设计库 容、正常库容、调洪库 容、校核库容、调节库 容、兴利库容、重复库 容。
水库库容测量与计算
水库库容测量与计算水库库容是水库调度的重要参数,其精度直接影响到水库的防洪安全与蓄水兴利。
本文介绍了大中型水库容测量与库容计算的方法,论述了水库库容测量合理测图比例尺的选取、具体作业方法;采用ArcGIS建立数字高程模型方式,利用Python脚本文件建立循环,更加快速准确地实现分层库容自动计算和统计。
文中给出了Python脚本文件建立循环的实例,对大中型水库库容测量及库容计算有较好的借鉴意义。
标签:库容测量;库容计算;数字高程模型1、概述水库库容作为当今水利工程施工建设和运行管理中不可忽略的重要参数之一,它是确定装机容量、工程施工量、泄洪量以及水利功能的重要指导依据。
在目前的工程项目中,库容计算结果的精确度、可靠度的提高是水利工程事业发展的重要指导,更是对水利工程、水库运行管理决策与整合的技术指导。
因此定期对库容进行测量和计算,以了解水库淤积情况和水库实际有效库容,已成为当今水库工程中最受重视和关注的问题之一。
2、库容测量测图比例尺选取2.1 测图比例尺的选取大中型水库一般多建设在山区,库区的地形主要有河谷和山坡为主。
根据本单位几十年水库测量经验,水库在正常蓄水运行十年后,库区地形横断面近似为“U”字型,且非汛期兴利库容最高蓄水位以上部分地形较陡,平面投影面积较小,库区地形淤积变化主要发生在死水库容以下部分以及原河床部位。
因此,库容测量的重点在正常蓄水位以下部分,通常大中型水库测量测图比例尺为1:5000和1:10000,根据多年的资料进行库容计算分析对比,1:10000测图比例过小,1:5000测图通过适当加密水下测点密度可以确保库容计算精度。
测图比例尺过大对提高库容精度没有明显提高,且会大大提高生产成本和外业工作量。
建议选取测图比例为1:5000为宜。
2.2 基本等高距的选择水库库区地形图的基本等高距,应根据水库库区地形特征及满足设计精度的要求来确定。
一般来说,库区底部比较平缓,两侧山坡高度变化较大,同时为了提高库容计算精度,基本等高局应为1m,如库区高差变化较小基本等高距可定位0.5m。
百图断面CAD-第十三章 水库库容计算(一)
第十三章水库库容计算传统计算水库库容的方法是算等高线面积法,但实际中,常常一个水库有不止一个盆地,因而同一高程有多条等高线;有时,由于绘图的原因,每条等高线并不完整。
因此,等高线面积法计算库容,工作量大,容易出错,现介绍另外二种计算水库库容的方式,这两种方法均符合积分原理,因而结果正确,达到精度要求。
第一节断面法水库库容计算一、利用扫描地形图进行库容计算步骤1、利用image命令把扫描地形图贴到CAD中。
2、对扫描地形图进行放缩处理,使图中1个单位长度代表实际的1米。
3、在地形图上用多段线(pline)画出库区(若水库上游库区不确定,库区范围可以扩大),构成一封闭多边形,在封闭多边形的大致中间部位绘制一条直轴线,line或pline均可。
4、地形图批量切剖面点选菜单“平面”-->“平面图批量切剖面”-->“三角网法封闭区域批量切剖面”,出现对话框,一般设剖面间距为10米或20米,核选处理autoCAD 高程点和处理南方CASS高程点选项,点确定按钮后,软件会在地形图上绘制出断面位置线。
原来的扫描地形图相当于底图,用户用肉眼可看出底图上断面位置线附近的等高线或高程点的标高,需用户在断面位置线上补充绘制(编造)若干平面高程点(有绘制编造平面高程点菜单),补充编造高程点完毕,再一次在地形图批量切剖面,核选处理autoCAD 高程点和处理南方CASS 高程点选项,生成横断面数据文件。
5、用记事本打开横断面数据文件,可以对每个断面的左右两端进行加高延长(代表水库大坝加高),也可用断面工具下的“横断成果左右加点延长”批量处理。
6、点菜单“断面法水库库容计算”,选择第5步处理过的横断面数据文件,该步操作结束,生成水库库容成果文件和断面面积校核表。
其中水库库容成果文件的内容大致如下:7、点选菜单“横断模板” “绘制库容曲线或任意二维曲线”,在对话框中选择第6步生成水库库容成果文件,绘制库容图。
二、利用数字化三维地形图进行库容计算1、打开测量地形图,在地形图上用多段线(pline)画出库区(若水库上游库区不确定,库区范围可以扩大),构成一封闭多边形,在封闭多边形的大致中间部位绘制一条直轴线,line或pline均可。
断面法计算方法!
断面法计算方法!断面法定义:矿体被一系列勘探断面分为若干个矿段或称块段,先计算各断面上矿体面积,再计算各个矿段的体积和储量,然后将各个块段储量相加即得矿体的总储量,这种储量计算方法称为断面法或剖面法。
根据断面间的空间位置关系分为水平断面法和垂直断面法,凡是用勘探(线)网法进行勘探的矿床,都可采用垂直断面法;对于按一定间距,以穿脉、沿脉坑道及坑内水平钻孔为主勘探的矿床,一般采用水平断面法计算矿床资源量和储量。
根据断面间的关系分为平行断面法和不平行断面法。
1平行断面法无论是垂直平行断面法还是水平平行断面法,均是把相邻两平行断面间的矿段,作为基本储量计算单元。
首先在两断面图上分别测定矿体面积,然后计算块段的体积和储量。
体积(V)的计算有下述几种情况:1)设两断面上矿体面积为S1、S2,两断面间距为L(图4-7-4)则:图4-7-4 平行断面间的矿段图4-7-5 断面间内插断面(Sm)的三种求法示意图2)矿体边缘矿块只有一个矿体断面控制那么根据矿体形态及尖灭特点,用下述体积(V)计算公式:图4-7-6 矿体端部块段形态(a)锥形体;(b)楔形体断面法,在平均品位计算时,若需使用加权平均法计算,则单工程内线平均品图4-7-7 不平行断面间矿块(a)锥形体;(b)楔形体其他参数和块段矿石储量与金属储量计算同于平行断面法。
适用条件:断面法在地质勘探和矿山地质工作中应用极为广泛。
它原则上适用于各种形状、产状的矿体。
优点是能保持矿体断面的真实形状和地质构造特点,反映矿体在三维地质空间沿走向及倾向的变化规律;能在断面上划分矿石工业品级、类型和储量类别块段;不需另作图件,计算过程也不算复杂;计算结果具有足够的准确性。
缺点是,当工程未形成一定的剖面系统时或矿体太薄、地质构造变化太复杂时,编制可靠的断面图较困难,品位的“外延”也会造成一定误差。
地形图上水库库容的计算讲解
为65m,上下游的设计坝坡为1:3与1:2,等高距
h=5m,则坝坡面上各条等高线间的平距为 上游5×3=15m,下游5×2=10m,由坝顶边缘开始,
分别按15m和10m的图上距离绘出坝坡面等高线
(图8-15中的平行虚线)。 (3)将坝面等高线与同高程的地面等高线的交点 连成光滑的曲线,即为土坝坡脚线(图8-15所示)
1 h An h 3
An
h〃
四、在地形图上确定土坝坡脚线
土坝坡脚线就是土坝坡脚面与地面的交线。标定坡脚线,可确定清基范围。具 体方法如下: (1)在地形图上,先确定坝轴线的位置,根据坝顶设计高程和坝顶宽度,绘出 坝顶边线。 (2)根据坝顶高程及上、下游坝坡面的设计坡度,画出与地面等高线相应的坝 面等高线。例如在图8-12中,坝顶设计高程
8-15 在地形图上确定土坝坡脚线
9b的长度在横轴上截取相应的点并作垂线使垂线之长等于各点相应的高程值垂线的端点即是断面点连接各相邻断面点即得ab线路的纵断面二在地形图上确定汇水面积确定汇水面积先绘出分水线
一、根据等高线绘制线路的断面图 绘制AB方向断面图的方法: 1 、首先确定断面图的水平比例尺和高 程比例尺。断面图上的水平比例尺与地形 图的比例尺一致,高程比例尺比水平比例 尺大 10~15倍,可明显地反映地面起伏变 化情况。 2 、绘出直角坐标轴线,横轴表示水平 坐标线,纵轴表示高程坐标线,并在高程 坐标线上依高程比例尺标出各等高线的高 程。 3、以AB被等高线所截各线段之长A1, 12,23,…,9B的长度在横轴上截取相 应的点并作垂线,使垂线之长等于各点相 应的高程值,垂线的端点即是断面点,连 接各相邻断面点,即得AB线路的纵断面 图。
二、在地形图上确定汇水面积
确定汇水面积,先绘出分水线。 勾绘分水线应注意以下几点: 1、分水线应通过山顶和鞍部,与 山脊线相连。 2、分水线应与等高线正交。 3、汇水面积的边界线为一条闭合 环线。 汇水面积范围线确定后,可用面积 量算的方法求出以平方公里为单位的汇 水面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)
上式即为水库库容计算的基本公式,一般称为截锥(体体积)公 式。给定一个高程,计算出水库所有基本断面的断面面积,对相邻断 面采用(2)式计算断间库容,加起来即可实现该高程下水库库容的 粗略计算。 2.体积的分层计算 截锥体概化假设计算区段上下断面形状是概化相似的, 在河道原
2
型中,这种条件不可能准确达到。另一方面,由于实际的断面间河长 是与高程有关的, 用等高线法确定的断面间距也是一个随高程变化的 量。因而,在实际的库容计算中,通常不是直接采用(2)式,而是 通过分层——累加的方法来计算逐级的断间库容。
300 280 260 240 220 高程(m) 200 180 160 140 120 100 800 连续函数间距 分段函数间距
900
1000
1100
1200 间距(m)
1300
1400
1500
1600
图 3 断面间距高程函数
3.2 回水末端及底部锥体 在水库支流上游的最后一个实设断面以上, 河底高程到达水库设 计水位的位置虚设一个断面,称为回水末端断面。回水末端断面纯粹
8
表1
第一层截 锥的处理 (1) (2) (2)-(1) 补充锥体 (3) (4) (3)-(1) (4)-(1) 计算层 补充四面体 最高间距 最高间距 不处理 不处理 底部锥体 间距采用 最高间距 相应间距
黄河小浪底水库历年总库容算法结果对比
1999 127.5056 127.5088 0.0032 2000 126.9526 126.9559 0.0033 2001 123.1006 123.1036 0.0029 2002 119.6482 119.6503 0.0021 2003 118.0366 118.0383 0.0017 2004 113.2113 113.2128 0.0015
j
Vzj
3b ( A
i i 1
1
1i
j j 1 A1 i A2 i A2 i ) bi A1i bi ( A1 i A2 i ) i 1 i 1 2
(8)
j=1,2,3……
也就是说,支流河口区段的容积立体可以按照分层柱体来认定。 同理, 干流坝前区段的容积也是通过在大坝位置虚设断面按照分 层柱体来对待,同样采用(8)式来计算。 4 实际算例 针对底部截锥的间距采用和第一截锥的体积计算这两个细节问 题, 对黄河小浪底水库从 1999 年到 2004 年的 6 个汛前测次数据采用 不同的处理方法进行了库容实例计算,对比结果见表 1。
上断面
河底倾角θ
Z2
底部锥体 底部锥体顶面面积A2 z2
下断 面
Z1
下断面
上断面
下断面
上断面
间距bz2 Z2 Z2
间距 bz3
间距bz2
θ
Z1
Z3 Z1
(a)
(b)
图 5 底部锥体模型
回水末端锥体和底部锥体的情况很类似, 本文仅以后者为例进行 叙述。 当底部柱体完全处在一个间距 ——高程分段区间内时,例如
z1 , z2 175,200 ,见图 5(a) ,间距值是唯一的,其整体体积为:
1 V底锥 bz 2 A2 z 2 3
5
任意高程 z z1 , z 2 下的体积也直接按锥体计算
1 1 bz2 V底锥 , z ctg z A2 z z A2 z 3 3 z2
zi zi-1 zi-2
断面间距 bi
面积A2i
面积A 1i 一个截锥计算层,对应于( 3 )式中的一个求和项
图 2 断间库容的分层计算模型
如图 2 所示,以等间距的水平面将容积立体分成若干层,对每层 的体积应用截锥公式计算,再累计求和得到各个高程下的断间库容。 设 A1i , A2i ,b i 分别为上下断面在第 i 层边界内的面积和概化间距, 则第 j 层层顶高程对应的断间库容为:
如图 1 所示,断间容积立体按照截锥体假设,其体积为两个锥体 体积之差:
1 1 V ( a b) A2 aA1 3 3
(1)
根据锥体的性质,有比例关系:
a2 A 1 2 ( a b) A2
解出
a
bA1 b A1 A2 A2 A1
代入(1)式简化后得到:
1 V b( A1 A1 A2 A2 ) 3
3.3 第一层截锥的体积计算
6
底部锥体以上的计算层是按照分层截锥来计算的, 但是从下面数 的第一层形状比较特殊。见图 6,构成第一个计算层的两个底面中有 一个(对应于上断面)只有一条直线上边,下边则是由断面的最低河 底高程附近的部分河底曲线围成的。 如果上断面的最低河底高程不是 恰好等于某个分层高程时,在图 6 中就是 z 2 不等于 z j-1 时,如果对该 层采用截锥公式计算体积, 则其与以底部锥体计算的部分之间就会有 一块儿体积需要另外考虑。
上断面
下断面
Zj Z2 Zj- 1
四面体
Zj Z j- 1
Zj
截锥计算层
Zj
Z2
四面体
截锥计算层 锥体计算层
Z2
Zj-1
Zj-1
(a)
图 6 第一层截锥ຫໍສະໝຸດ 体积分划(b)一种处理方法是按照其确定的边界,直接补充一个四面体体积, 见图 6(a) 。 第二种方法见图 6(b), 以高程 z 2 增加一个水平分层, 把 z j-1,z j 之间认定的体积分成上下两部分,下面按照一个底部锥体层计算, 上 面按照一个截锥层计算,求和得到整层体积。 通常情况下断面面积是按照 1 米分层事先计算的, 第二种方法涉 及到一个额外的非整米处的断面面积(即 A 2z2 )计算,相对来说略为 复杂一些。 3.4 支流河口和干流坝前
V j
1 bz j ( z j A2 z j z j 1 A2 z j 1 ) 3 z2
(7)
其中 bzj 的取值,显然有: 当 z j1 , z j z1 , z 3 时 bzj =b(z3), z j1 , z j z 3 , z2 时 bzj =b(z2) 对 V j 进行累加后得到的体积对应于图 5(b)中实线所代表的部分。
7
支流河口
干流坝前
图 7 支流河口区段及 干流坝前区段位置示意图
对于某些支流,由于地形条件及其他因素的限制,无法恰好在河 口位置设置基本断面。于是,支流最下游的实设断面与河口之间的一 块儿容积就需要另做考虑。目前的做法是在河口位置虚设河口断面, 计算时完全借用上游实设断面的数据。因而在计算公式上有如下关 系:
断面法水库库容计算的算法细节
刘炜
(黄河水利委员会 水文局,河南 郑州 450004 )
摘要:本文论述了断面法水库库容计算的基本算法模型及间距采用、底部锥体和 回水末端处理等细节问题。 关键词:断面法 库容计算 算法
断面法是水库库容及冲淤量测算的常规方法之一, 断面法分为加 密断面法和基本断面法。 前者是通过在水库水系各干支流上布设足够 密集的测量断面(称为加密断面) ,实现对水库库容接近于地形法测 图精度的精确测算。通过减少参与计算的断面数量,经过反复对比计 算,并依照水库河道测量的有关规范要求,从加密断面中选取出一定 数量和足够代表性的断面,固定下来进行历年的常规测量和库容计 算,就构成了基本断面法,基本断面法又称为固定断面法, “断面法” 在一般情况下所指的也就是基本断面法。 基本断面是在对比计算基础 上确定的,数量少且对于库区地形变动的代表性强。因此,基本断面 法可以在相当长的时期(基本断面代表期)内,以较低的成本和较短 的测量周期实现对水库库容的准确测算。直到水库经过多年运行, 河 床形态和冲淤规律发生了显著变迁时,基本断面需要从新确定。 在基本断面代表期内, 影响库容及冲淤量成果准确性的主要因素 有两方面,一是外业测量的质量控制,二是数据处理与计算方法。本 文就后者的若干细节问题进行讨论。 1.基本算法模型及公式 水库断面法计算通常采用截锥体概化, 即假设将上下两个断面间
3
长事先作出规定,以该规定值的计算结果为准。例如对于百米级高差 的峡谷型水库(如黄河小浪底水库)规定标准计算流程中采用的分层 高程步长为 1 米。 3.算法细节 3.1 断面间距的采用 依据等高线量算得到的断面间距构成一张表格, 其内容是若干个 高程上的相邻断面间距值。 通过构造一个间距——高程的连续插值函 数, 就可以求出任意高程上的断面间距, 这相当于图 3 中的连续曲线 。 但工程上通常采用更简单的做法: 以上下两条等高线高程上的间距平 均值作为这两个高程范围内的间距来使用。例如,当计算中需要使用 175m ~200m 米之间任一高程(>175,<=200)的间距值时,都采用高 程 175m 和 200m 的实际量算间距 1270 和 1136 的平均值 1203 。这实 际上是把间距——高程作为一个分段常数函数来处理的办法。 相当于 图 3 中的分段曲线,下文中用 b(z) 或 bz 表示这个函数。
1
的河道按概化间距拉直后,其容积立体构成一个截锥体:上下断面分 别对应该截锥的两个底面,概化间距对应截锥的高。在截锥体假设的 情况下, 计算区段内的任意河道横断面在宽和深两个方向上都被认为 是沿河长线性变化的。因而其面积在上下断面间以 2 次关系变化。
A2 b
A1
b+a
图 1 断面间容积立体的截锥体假设
127.5531 127.5520 0.0474 0.0464
127.0058 126.9946 0.0532 0.0420
123.1561 123.1569 0.0555 0.0563
119.6931 119.7028 0.0449 0.0546
118.0917 118.0896 0.0552 0.0530
113.2614 113.2715 0.0501 0.0603
