合肥工业大学机械原理本科课件-4平面机构的力分析
合集下载
机械原理课件——平面机构的运动分析和力分析
第三章 平面机构的运动分析和力分析
(Chapter 3: Kinematics and Forces Analysis of Planar mechanisms)
机构运动分析的目的和方法
解决的问题： 轨迹（角位移） 速度（角速度） 加速度（角加速度）
目的： 了解现有机构的运动性能， 为受力分析打基础。
3
方向:C DCDB A C B CB
大小：lCD 32 ?
lAB12 lCB 22 ?
选 a ，任找 p’（绝对加速度为
A
1
4
零的点）。
D al l 2 =
c'" c'
CB =
CB
CB
a
c’ e’
p’ a c”
la l 3 =
c" c'
C=
CD
CD
a
b’
a E点加速度由影像得： E p'e' a
证得：P12、P23和P13必在一条线上。
例1：如图示机构，找出其全部瞬心。
解：N 41 2
P24
2 P23
{P14, P34
P13
P12, P23
P12
1
P14
P13
4
{ 3
P12, P14
P24
P34
P23, P34
框图法(瞬心多边形)
各机构的瞬心求法用多边形表示，其中各 顶点代表构件，各顶点间的连线代表瞬心，连 线组成的三角形代表瞬心线。
方法：1. 瞬心法（求机构的速度和角速度） 2. 矢量方程图解法 3. 解析法（上机计算）
§ 3-1 速度瞬心
(Instant center of velocity )
(Chapter 3: Kinematics and Forces Analysis of Planar mechanisms)
机构运动分析的目的和方法
解决的问题： 轨迹（角位移） 速度（角速度） 加速度（角加速度）
目的： 了解现有机构的运动性能， 为受力分析打基础。
3
方向:C DCDB A C B CB
大小：lCD 32 ?
lAB12 lCB 22 ?
选 a ，任找 p’（绝对加速度为
A
1
4
零的点）。
D al l 2 =
c'" c'
CB =
CB
CB
a
c’ e’
p’ a c”
la l 3 =
c" c'
C=
CD
CD
a
b’
a E点加速度由影像得： E p'e' a
证得：P12、P23和P13必在一条线上。
例1：如图示机构，找出其全部瞬心。
解：N 41 2
P24
2 P23
{P14, P34
P13
P12, P23
P12
1
P14
P13
4
{ 3
P12, P14
P24
P34
P23, P34
框图法(瞬心多边形)
各机构的瞬心求法用多边形表示，其中各 顶点代表构件，各顶点间的连线代表瞬心，连 线组成的三角形代表瞬心线。
方法：1. 瞬心法（求机构的速度和角速度） 2. 矢量方程图解法 3. 解析法（上机计算）
§ 3-1 速度瞬心
(Instant center of velocity )
合工大机械原理课件
第一章平面机构的结构分析一. 基本概念1. 机械: 机器与机构的总称。
机器: 具有三个共性。
机构: 只具有机器的前两个共性。
2. 构件与零件零件——制造单元构件——运动单元构件可以由一个零件或多个零件刚接而成3. 运动副: 两构件通过表面直接接触而形成的可动联接。
运动副元素: 两构件表面直接接触的点、线、面。
4. 运动副的分类：平面运动副：两构件在同一平面内作相对运动平面低副—两构件以面接触构成的可动联接平面高副—两构件以点或线接触构成的可动联接平面低副：转动副—联接的两构件只能作相对转动移动副—联接的两构件只能作相对移动空间运动副：两构件在不同平面内作相对运动5. 运动链: 多个构件以运动副联接而成的系统分类：空间运动链、平面运动链闭式运动链、开式运动链6. 机构：有机架并有确定运动的运动链分类：平面机构、空间机构二. 基本知识和技能1. 机构运动简图的绘制与识别图在机构运动简图中：运动副—按国家标准所规定的代表符号画出构件—用线段、小方块等简单图形画出尺寸—按选定的比例画出2.平面机构的自由度的计算及机构运动确定性的判别F = 3n - 2P L- P Hn —活动构件数P L —低副数P H —高副数自由度计算时须注意:(1) K个构件在同一处构成的复合铰链中有( K - 1 )个转动副(2) 局部自由度应去除（通常每个滚子有一局部自由度）(3) 虚约束应去除。
（注意虚约束出现的场合）机构具有确定运动的条件F > 0 能动原动件数< F 机构运动不确定原动件数= F 机构运动确定原动件数> F 机构运动相互干涉F ≤0 不能动，为刚性构架3. 机构的结构分析（1）高副低代：用一个构件，两个低副代替一个高副须满足：代替前后机构的自由度不变代替前后机构的瞬时运动不变高副低代必须遵循一定的方法：曲线对曲线的高副低代点对曲线的高副低代曲线对直线的高副低代点对直线的高副低代2. 机构的结构分析（1）基本杆组及杆组的级别自由度为零的，不能再拆分的构件组Ⅱ级杆组：二杆三低副组Ⅲ级杆组：四杆六低副组含有一个带三低副的中心构件（2）机构的拆组及机构的级别从远离原动件的构件开始拆分杆组机构的级别由机构中杆组的最高级别所决定（3）机构的组成原理把杆组依次与机架和原动件相联得到机构第二章平面机构的运动分析一. 基本概念:（一）瞬心1. 瞬心的定义瞬心是两构件的瞬时等速重合点2. 机构中的瞬心数目机构中，每两个构件有一个瞬心。
chap4平面机构的力分析
机械基础及工程力学系 王震国
Mechanical Design
第四章 平面机构的力分析 1概 述
作用在机构上的力
在外加力中，包括驱动力、阻抗力和重力： 在外加力中，包括驱动力、阻抗力和重力： 阻力（ 阻力（矩）又可分为工作阻力（矩）和有害阻力（矩）。 又可分为工作阻力（ 和有害阻力（
克服工作阻力所完成的功称为输出功或有益功。 克服工作阻力所完成的功称为输出功或有益功。
机械基础及工程力学系 王震国
Mechanical Design
第四章 平面机构的力分析 1概 述
机构力分析原理和方法
对低速机械，由于惯性力的影响不大，可忽略不计。 对低速机械，由于惯性力的影响不大，可忽略不计。在不计 惯性力的条件下， 惯性力的条件下，对机械进行的力分析称为机构的静力分析 对高速及重型机械，由于某些构件的惯性力往往很大， 对高速及重型机械，由于某些构件的惯性力往往很大，有时 甚至比机械所受的外力还大得多，所以， 甚至比机械所受的外力还大得多，所以，在进行力分析时就 必须考虑惯性力的影响。根据达朗伯原理， 必须考虑惯性力的影响。根据达朗伯原理，如将惯性力视作 一般外力加于产生该惯性力的构件上， 一般外力加于产生该惯性力的构件上，就可将该机械视为处 于静力平衡状态，这样的力分析称为动态静力分析。 于静力平衡状态，这样的力分析称为动态静力分析。
F`I1 MI1 FI1
B 1 S1 as1
α1 A
第四章 平面机构的力分析 2 不考虑摩擦时平面机构的动态静力分析
构件组的静定条件
在不考虑摩擦时，平面运动副中的反力FR的作用线、方向 在不考虑摩擦时，平面运动副中的反力 的作用线、 及大小未知要素如下： 及大小未知要素如下： 转动副：FR通过转动副中心，大小和方向未知。 转动副： 通过转动副中心，大小和方向未知。 移动副：FR沿导路法线方向，作用点位置和大小未知。 移动副： 沿导路法线方向，作用点位置和大小未知。 平面高副： 作用在高副两元素接触点的公法线上，仅大小未知。 平面高副：FR作用在高副两元素接触点的公法线上，仅大小未知。 n FR FR FR n
《机械原理》课件_第4章_平面机构的力分析(
对于三角带：θ ＝18°
fv＝3.24 f
θ
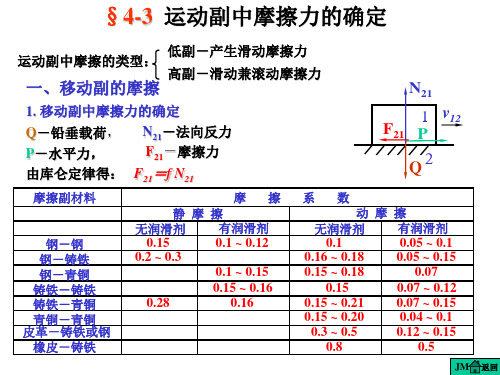
2.移动副中总反力的确定 总反力为法向反力与摩擦力的合成：
θ R21 N21 1 v12 P Q 2
φ
F21
R21=N21+F21
tgφ= F21 / N21 = fN21 / N21 =f
φ－摩擦角，
方向:∠R21V12 ＝(90°+φ)
阻碍相对运动
JM
Q
△N
△N
β
Q
β △N ∑△N＝Q
矩形螺纹――忽略升角影响时，△N近似垂直向上,
――∑△N△cosβ＝Q， β－牙形半角 ∑△N△＝∑△N /cosβ fv = f / cosβ φv＝ arctg fv
d2 拧松： M ' Qtg ( v ) 2
JM
返回
比较可得：∑△N△cosβ＝Q＝∑△N 引入当量摩擦系数: 当量摩擦角:
R r
f
JM
返回
§4-4 不考虑摩擦的平面机构力分析
一、构件组的静定条件 假设已对机构作过运动分析，得出 了惯性力，因为运动副中的反力对整个 机构是内力，因此必须把机构拆成若干 构件组分析，所拆得的杆组必须是静定 的才可解。
对构件列出的独立的平衡方程数目等于所有力 的未知要素数目。显然构件组的静定特性与构 件的数目、运动副的类型和数目有关。 ①转动副：反力大小和方向未知，作用点已知，两个未知数
槽面接触： N’21 +N”21= -Q
柱面接触：
N’21 = N”21 = Q / (2sinθ) F21=f N’21 + f N”21 = ( f / sinθ)• Q = fv Q
Q N”21 θ N’21 θ θ N’21 N”21 1
4 《机械原理》平面机构的力分析
I
C ε
FI′
FI
ε
可以用总惯性力FI’来代替FI和MI ，FI’ = FI，作用线由质心
S 偏移 lh
MI lh = F I
在确定构件惯性力时，如用一般的力学方法， 在确定构件惯性力时 ， 如用一般的力学方法 ， 就需先求出 构件质心的加速度和角加速度，如对一系列位置分析非常繁琐， 构件质心的加速度和角加速度，如对一系列位置分析非常繁琐， 为简化，可采用质量代换法。 为简化，可采用质量代换法。
ƒv ------当量擦系数 当量擦系数
5）槽面接触效应 所以在其它条件相同的情况下 槽面、 其它条件相同的情况下，槽面 因为 f v > f ，所以在其它条件相同的情况下 槽面、圆柱 面的摩擦力大于平面摩擦力。 面的摩擦力大于平面摩擦力
2. 移动副中总反力方向的确定
1）总反力和摩擦角 总反力FR21 ：法向反力 N21和摩擦力 f21的合力。 法向反力F 和摩擦力F 的合力。 总反力 总反力和法向反力之间的夹角。 摩擦角ϕ ：总反力和法向反力之间的夹角。
绕质心的转动惯量 用一个力简化之
v FI
v FIlhS源自εv MIv aS v v FI = − ma S v J Sε MI v lh = F = ma I S
2. 作平面移动的构件
v v 等速运动： 等速运动： FI = 0; M I = 0 v v v 变速运动： 变速运动： FI = − m a S ; M I = 0
mB + mK = m mBb = mkk mBb2 + mKk2 = Js
优点：代换精确。 优点：代换精确。
S B
b c
C
S B
m
B
C ε
FI′
FI
ε
可以用总惯性力FI’来代替FI和MI ，FI’ = FI，作用线由质心
S 偏移 lh
MI lh = F I
在确定构件惯性力时，如用一般的力学方法， 在确定构件惯性力时 ， 如用一般的力学方法 ， 就需先求出 构件质心的加速度和角加速度，如对一系列位置分析非常繁琐， 构件质心的加速度和角加速度，如对一系列位置分析非常繁琐， 为简化，可采用质量代换法。 为简化，可采用质量代换法。
ƒv ------当量擦系数 当量擦系数
5）槽面接触效应 所以在其它条件相同的情况下 槽面、 其它条件相同的情况下，槽面 因为 f v > f ，所以在其它条件相同的情况下 槽面、圆柱 面的摩擦力大于平面摩擦力。 面的摩擦力大于平面摩擦力
2. 移动副中总反力方向的确定
1）总反力和摩擦角 总反力FR21 ：法向反力 N21和摩擦力 f21的合力。 法向反力F 和摩擦力F 的合力。 总反力 总反力和法向反力之间的夹角。 摩擦角ϕ ：总反力和法向反力之间的夹角。
绕质心的转动惯量 用一个力简化之
v FI
v FIlhS源自εv MIv aS v v FI = − ma S v J Sε MI v lh = F = ma I S
2. 作平面移动的构件
v v 等速运动： 等速运动： FI = 0; M I = 0 v v v 变速运动： 变速运动： FI = − m a S ; M I = 0
mB + mK = m mBb = mkk mBb2 + mKk2 = Js
优点：代换精确。 优点：代换精确。
S B
b c
C
S B
m
B
机械原理-平面机构的力分析
完全组合、收摺组合、曲柄滑块组合
传动条件
曲柄摇杆机构、齿轮传动机构
存储条件
转动机构、滑动机构
力的基本概念
1 力的作用点
力作用的位置或接触点。
2 力的方向
力作用的方向或施力线。
3 力的大小
力作用的大小或强弱。
平面机构的受力分析
1
受力分析
2
根据力的分解结果，分析各构件的受力情况。
3
力的分解
将力分解为平行于连接构件的分力和垂直于 连接构件的分力。
交叉槽的弯曲影响
交叉槽是指曲柄和滑块之间存在的交叉形状，它会导致机构的弯曲失效和运 动不稳定。
非正交曲柄机构的分析
1 自由度分析
根据曲柄滑块机构的结构，确定其自由度以及运动学约束。
2 力分析
通过力的平衡分析，确定机构各处的力大小和方向。
3 运动模拟
使用模拟软件或物理实验，验证机构设计的正确性和稳定性。
摆线和椭圆曲柄机构的分析
摆线曲柄机构
利用摆线曲线的特性，实现更平稳的运动传动。
椭圆曲柄机构
利用椭圆曲线的特性，实现更精确的运动传动。
内嵌框架的应用
机构设计
通过内嵌框架的布局，实现机构零 件的紧凑排列和高效传动。
机器人技术
内嵌框架在机器人领域的应用，提 高了机器人的稳定性和工作效率。
汽车工程
通过内嵌框架的结构布局，实现汽 车发动机和悬挂系统的高性能和节 能效果。
力的平衡
通过分析和计算，判断平面机构是否处于力 的平衡状态。
计算机构的自由度
自由度是指机构中独立变量的个数，它决定了机构的运动和约束情况。
平面机构的结构形式
齿轮传动
通过齿轮的啮合来实现转动传动功 能。
传动条件
曲柄摇杆机构、齿轮传动机构
存储条件
转动机构、滑动机构
力的基本概念
1 力的作用点
力作用的位置或接触点。
2 力的方向
力作用的方向或施力线。
3 力的大小
力作用的大小或强弱。
平面机构的受力分析
1
受力分析
2
根据力的分解结果，分析各构件的受力情况。
3
力的分解
将力分解为平行于连接构件的分力和垂直于 连接构件的分力。
交叉槽的弯曲影响
交叉槽是指曲柄和滑块之间存在的交叉形状，它会导致机构的弯曲失效和运 动不稳定。
非正交曲柄机构的分析
1 自由度分析
根据曲柄滑块机构的结构，确定其自由度以及运动学约束。
2 力分析
通过力的平衡分析，确定机构各处的力大小和方向。
3 运动模拟
使用模拟软件或物理实验，验证机构设计的正确性和稳定性。
摆线和椭圆曲柄机构的分析
摆线曲柄机构
利用摆线曲线的特性，实现更平稳的运动传动。
椭圆曲柄机构
利用椭圆曲线的特性，实现更精确的运动传动。
内嵌框架的应用
机构设计
通过内嵌框架的布局，实现机构零 件的紧凑排列和高效传动。
机器人技术
内嵌框架在机器人领域的应用，提 高了机器人的稳定性和工作效率。
汽车工程
通过内嵌框架的结构布局，实现汽 车发动机和悬挂系统的高性能和节 能效果。
力的平衡
通过分析和计算，判断平面机构是否处于力 的平衡状态。
计算机构的自由度
自由度是指机构中独立变量的个数，它决定了机构的运动和约束情况。
平面机构的结构形式
齿轮传动
通过齿轮的啮合来实现转动传动功 能。
机械原理第4章 平面机构的力分析
Fig.4-7 Friction in a journal bearing(径向轴承中的摩擦)
2) 推力轴承的摩擦。 图4-8a为推力轴承示意图，G为轴向载荷。未经跑合时，接 触面压强p为常数，p=c。经过跑合时，压强与半径的乘积为 常数，pρ=c。
Fig.4-8 Friction in a thrust bearing(推力轴承的摩擦)
例4-4 图4-12a所示的摆动从动件盘形凸轮机构中，已知凸轮机构的尺 寸、轴径尺寸、运动副处的摩擦因数f以及作用在从动件F点的阻力Fr， 在不计构件质量和惯性力时，求各运动副处的反作用力及作用在凸轮上 的平衡力矩Mb。
2.计入摩擦力的力分析
例4-3 图4-11所示的曲柄滑块机构中，已知各构件尺寸和曲柄的位置和 作用在滑块4上的阻力Fr以及各运动副中的摩擦因数f，忽略各构件质量和 惯性力。在图4-11上标注出各运动副的反力以及加在曲柄上的平衡力矩Mb。
Fig.4-11 Force analysis considering the friction in a slider-crank linkage (考虑摩擦的曲柄滑块机构力分析)
Байду номын сангаас
(3)螺旋副中的摩擦 根据螺纹牙型可将螺纹分为矩形螺纹 和三角形螺纹。 图4-9a所示为一矩形螺纹，将螺母2简化为图4-9b所示的滑 块，承受轴向载荷[WTBX]G，由于螺纹可以看成是斜面缠 绕在圆柱体上形成的，故将矩形螺纹沿螺纹中径[WTBX]d展 开，该螺纹成为图4-9b所示的斜面，斜面底长为螺纹中径 处圆周长，高度为螺纹的导程l。驱动力F等于拧紧力矩M除 以螺纹半径d/2，方向一般垂直于螺纹轴线。
3) 槽面摩擦。如果将图4-6a所示滑块作成图4-6b所示夹角为 2θ的楔形滑块，并置于相应的槽面中，楔形滑块1在外力F 的作用下沿槽面等速运动。设两侧法向反力分别为N21 ， 铅直载荷为G，总摩擦力为Ff。
机械原理04机构的力分析
与构件2相对于构件1的角速度w12方向相反。
三、螺旋副中的摩擦
1. 矩形螺纹螺旋副中的摩擦 1）矩形螺纹螺旋副的简化
将螺纹沿中径d2 圆柱面展开，其螺纹将展成为一个斜 面，该斜面的升角a等于螺旋在其中径d2上的螺纹升角。 tg l zp
d2 d2 l--导程， z--螺纹头数， p--螺距
螺旋副可以化为斜面机构进行力分析。
由 Fx 0
2
由 MC 0
2
得：R12 (F2x F23x ) / sin1
得：T12 ( yC ys2 )F2x ( xS 2 xC )F2 y T2
就可以将所有解求出。
关于可变杆长二杆组的副反力的求解
由 MA 0 和 M3 0 得：
1、2
3
yC yA
yB
yC
2
进行整理得到
yC yB
yD
yC
xB xC
xC xD
R23x
R23
y
( (
yB yD
yS 2 )F2 x yS 3 )F3 x
( xS 2 ( xS 3
xB )F2 y xD )F3 y
T2 T3
求出内副C的反力后，可分别取BC、CD杆作力平衡方程 式，求得B、D两点的反力。
力开始，逐副进行，最后对含平衡力得杆件进行力分析。
一般是力矩平衡方程和导路方向的力平衡方程两种交替使用。
4.2 机构的传动角
衡量一个机构传力效果的指标： （1）输出功相同时，输入功最少。 （摩擦损失最小） （2）构件受力最小。（构件截面积小，重量轻） （3）运动副摩擦少。（运动精度高，动载荷和噪声小）
0
1、2
3
移动副的反力R12D可以由构件2对E取矩和构件1 对E 取矩求得。
三、螺旋副中的摩擦
1. 矩形螺纹螺旋副中的摩擦 1）矩形螺纹螺旋副的简化
将螺纹沿中径d2 圆柱面展开，其螺纹将展成为一个斜 面，该斜面的升角a等于螺旋在其中径d2上的螺纹升角。 tg l zp
d2 d2 l--导程， z--螺纹头数， p--螺距
螺旋副可以化为斜面机构进行力分析。
由 Fx 0
2
由 MC 0
2
得：R12 (F2x F23x ) / sin1
得：T12 ( yC ys2 )F2x ( xS 2 xC )F2 y T2
就可以将所有解求出。
关于可变杆长二杆组的副反力的求解
由 MA 0 和 M3 0 得：
1、2
3
yC yA
yB
yC
2
进行整理得到
yC yB
yD
yC
xB xC
xC xD
R23x
R23
y
( (
yB yD
yS 2 )F2 x yS 3 )F3 x
( xS 2 ( xS 3
xB )F2 y xD )F3 y
T2 T3
求出内副C的反力后，可分别取BC、CD杆作力平衡方程 式，求得B、D两点的反力。
力开始，逐副进行，最后对含平衡力得杆件进行力分析。
一般是力矩平衡方程和导路方向的力平衡方程两种交替使用。
4.2 机构的传动角
衡量一个机构传力效果的指标： （1）输出功相同时，输入功最少。 （摩擦损失最小） （2）构件受力最小。（构件截面积小，重量轻） （3）运动副摩擦少。（运动精度高，动载荷和噪声小）
0
1、2
3
移动副的反力R12D可以由构件2对E取矩和构件1 对E 取矩求得。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
h
H2
l
0.317 0.03
10.56mmM
MI2
F
A
B
B 1
FI 2
2
2
3
A φ S2
S2
C
FI2
B 1
A φ S2
2 S2
3 C
FI 3
2 质量代换法
质量代换法的目的 质量代换法的实质是为了简化构件惯性力的计算。
用一般力学方法须同时求得构件的惯性力FI和惯性力矩MI 。而 采用质量代换法可省去惯性力矩MI的计算，使问题得到简化。 质量代换法的方法
件的外形、位置或状态时所受到的阻力，克服这些阻力 就完成了工作。如机床中作用在刀具上的切削阻力，起 重机提升重物的重力等都是有效阻力。
有害阻力―为非工作阻力，克服这些阻力所做的功纯粹
是一种浪费，故称为损失功。摩擦力、介质阻力等 一般为有害阻力。
§4—2 构件惯性力的确定
1 构件惯性力的确定 1) 直线移动构件惯性力的确定
平衡力
驱动力―根据机构的阻力大小选择适当的驱动力来平衡 生产阻力―根据机构的驱动力大小选择适当的阻力来平衡
平衡力即可以是驱动力又可以是阻力
机构力分析的目的
1） 为现有机械工作性能的评价、鉴定提供参数； 2） 为新机械的强度计算、结构设计提供重要依据。
机构力分析的方法
图解法 解析法
驱动力
作用在机械上的力
应用质量代换法应满足的条件
1） 代换前后构件的质量不变； 2） 代换前后构件的质心位置不变；
同时满足三个条件 的叫做动质量代换
3） 代换前后构件对质心轴的转动惯量不变；
例2 在图示的摆动导杆机构中，已知LAC=200mm， LAB=100mm，
φ=90°,导杆的重心在C点，导杆对重心C的转动惯量J3=0.2kg·m2 曲柄的等角速度ω1=20rad/s。求导杆3的惯性力矩。
解：1 运动分析（过程略）
3
aB3 lBC
pb3 a BC l
231rad / s2
S2
2
2
aCt B
3 C
58 5 290m / s2
2
aCt B lBC
cc BC
a l
p
48.6 5 103.4rad / s2 2.35
c c
p
aCt B aS 2
b s2
c b
3 求惯性力和惯性力矩
（1）活塞 3 的惯性力
FI 3 m3 aC
m3 pc a
6 495 1470N
c aC
p
aS 2
s2
（2）连杆 2 上的惯性力和惯性力矩 c b
FI 2 m2aS 2 19 290 5510N
M I 2 JS 2 2 16.9 103.4 1768N m
B 1 Aφ
MI2
S2
aS 2
FI 2
2 2
3 C
FI 3
（3）连杆 2 的总惯性力和作用线的位置：
H M I 2 1748 0.317m FI 2 5510
匀速直线移动构件的惯性力： FI ma s 0
加速直线移动构件的惯性力： FI ma s 0
aS ―质心的加速度
V=
FI 0
C
S
aS
FI
S
2) 定轴转动构件惯性力的确定
① 构件的质心在转轴
匀角速度ω转动 FI maS 0
MI JS 0 角加速度ε转动 FI maS 0
MI JS 0
阻抗力
有效阻力 有害阻力
驱动力―驱使机械运动的力。驱动力与其作用点的速度
方向相同或成锐角，其所作的功为正功。
阻抗力―阻止机械运动的力。阻抗力与其作用点的速度方向相
反或成钝角，其所作的功为负功。
驱动力
F
1
V12
＜90
2 2
阻抗力
F
1
V12
＞90
阻抗力又可分为
有效阻力―即工作阻力，它是机械在生产过程中为了改变工
第四章 平面机构的力分析
§4—1机构力分析的任务、目的和方法 §4—2 构件惯性力的确定 §4—3 机构力分析的任务、目的和方法 §4—4 不考虑摩擦时机构的力分析
§4—1机构力分析的任务、目的和方法
机构力分析的任务 1）确定运动副中的反力 运动副反力指运动副处作用的正压力和摩擦力的合力 2）确定机械中的平衡力 平衡力是指机械在已知外力的作用下，为了使该机械能按 给定运动规律运动，还须加于机械上的未知外力
2.受力分析
M I 3 J33
b1(b2 )
b2 (b3)
0.2231
46N m
p(b3 )
A
4
C p
1 1aB3
2
B
3 MI3
3
例3 在图示发动机曲柄滑块机构中，已知曲柄长度 l AB 0.35m ,
连杆长度 lBC 2.35m , 连杆重心 S2 至曲柄销轴B的m2 19kg ， 6kg , 连杆对其重心的转动惯量 J
活塞及其附件的质量 S 2 16.9kgm 2 ，曲柄转
速 n1 300r / min ， 45, 求图示位置时活塞3的的惯性力和
连杆2的总惯性力。
解：1.运动分析
B
aS 2 ps2 a
1 Aφ
aS 2
把构件的质量用集中作用在构件的几个选定点的假想集中
质量来代替。 B
FI ε
1
2
A aS
S2 m2
MI C3
质量代换法的方法
把构件的质量用集中作用在构件的几个选定点的假想集中 质量来代替，这些假想的集中质量被称作代换质量。 B、K为所选定的代换点 mB 、 mk为代换质量
mB B
1
2
A
mk
S2
k
C3
0
VS 0 aS 0
0
VS 0 aS 0
ω S
ε
MI
S
构件的质心不在转轴
匀角速度ω转动 FI maSn 0 MI JS 0
角加速度ε转动 FI maS 0
MI JS 0
FI
S
aSn lAS 2 0
aS lAS 0
aSn lAS 2 0 aS lAS 0
FI
aS
aS
S
a
n S
A ω=C
ε
a
n S
MI
A
3) 作平面运动构件惯性力的确定
FI maS 0
MI JS 0
也可将上述 惯性力。
aS
FI , M合成I 为距质心S为距离h的总
h MI
FI
FI
ε
MI S
aS
， FI ε S
例 1 在图示的凸轮机构中，已知凸轮的半径R=200mm，LOA=100mm
从动件的质量为m2=20kg，凸轮的角速度ω1=20rad/s。当OA线 在水平的位置时，求从动件2的惯性力。
解：1. 高副低代
2.运动分析（过程略）
aB2
o(b)
C
3
b
C
3
2
B R
FI 2 2
B
aB2
p
p o
oA
1
1
O
A
aB2 pb a
1
3.受力分析 FI 2 m2aB2 m2 pb a 2023.4 468N