实验四用EXCEL实现方差分析
实验四 用EXCEL进行方差分析
实验四用EXCEL进行方差分析一、单因素方差分析例题1:某鞋厂为了比较几种不同材质的鞋跟耐磨程度，随机选取了十个人试穿一双鞋跟厚度相同的新鞋，分别用A、B、C三种不同的材质做成，试穿一个月后测量每个人所穿的两只鞋的鞋跟厚度，测得如下数据：试分析，在0.05的显著性水平下，三种材质的鞋跟质量有无显著性差别。
提出原假设：不同材料的鞋跟没有显著性差异表1.1单因素方差分析的汇总表组观测数求和平均方差材料A 10 38.5 3.85 0.196111材料B 10 36.4 3.64 0.202667材料C 10 38.3 3.83 0.189从各组的均值看，最低为3.64cm，最高为3.85cm。
从各组的方差看最小的为0.189，最大的等于0.202667。
表1.2单因素方差分析的方差分析表差异源SS df MS F P-value F crit组间0.268667 2 0.134333 0.685633 0.512328 3.354131组内 5.29 27 0.195926总计 5.558667 29由结果可知P值为0.512328，大于显著性水平0.05，因此接受原假设，即材料的不同并没有导致鞋跟质量有显著性差异。
二、用Excel进行无重复双因素方差分析例题2：假设四名工人操作机器A、B、C各一天，其日产量，分析在0.05的显著性水平下，机器或不同工人对日产量是否有显著影响。
原假设1：机器对日产量没有显著影响；原假设2：不同工人对日产量没有显著影响。
在数据分析中选择：无重复双因素分析得到如下所示结由分析结果可知：行因素的P值为0.014445，小于显著性水平0.05,即应拒绝原假设，可以认为机器对日产量有显著影响；列因素的P值为0.230838，大于显著性水平0.05，即应接受原假设，认为不同工人对日产量没有显著影响。
三、用Excel进行有重复双因素方差分析例题3：为考察通电方法和液温对某零件质量的影响，通电方法有3种A、B、C,液温选取两种水平（现行温度或增加10度）。
实验四用EXCEL实现方差分析
实验四用EXCEL实现方差分析方差分析（Analysis of Variance, ANOVA）是一种用于比较两个或更多个样本均值是否显著不同的统计方法。
它通过比较各样本的方差是否相等来推断样本均值是否有显著差异。
本实验将使用EXCEL软件来实现方差分析。
1.实验目的掌握用EXCEL实现方差分析的方法，能够对不同样本的均值进行比较，并判断是否有显著差异。
2.实验原理方差分析是通过计算组间与组内的均方差（mean square）与自由度（degree of freedom）来推断是否存在差异显著的方法。
在EXCEL中使用方差分析的步骤主要包括数据录入、数据分析工具的使用、方差分析表的解读和结果的判断。
3.实验步骤Step 1: 数据录入首先将要分析的数据录入到EXCEL的工作表中，每组数据占用一列或一行，例如：组1：67,75,62,71,73组2：82,79,85,80,87组3：91,85,89,95,93Step 2: 数据分析工具的使用选择数据分析工具，依次点击"数据"-"数据分析"，弹出数据分析对话框，选择"方差分析"，点击"确定"。
Step 3: 填写方差分析对话框参数Step 4: 方差分析结果解读与判断EXCEL会生成方差分析表，其中包括组间均方（MSb），组内均方（MSw），总均方（MSt），标准误差（Sb），F值，自由度（df），P值等数据。
根据F值和P值来判断是否有显著差异。
通常，如果P值小于显著性水平（0.05），则拒绝原假设，即表示组间均值有显著差异。
4.实验注意事项（1）确保数据录入准确无误，符合方差分析的前提条件。
（2）需事先安装加载数据分析工具，具体操作方法可参考EXCEL软件帮助手册。
（3）在解读结果时，除了判断P值是否小于显著性水平之外，还要注意观察各组的均值和方差大小关系。
5.结论通过上述步骤，在EXCEL中可以快速实现方差分析，并得到方差分析表。
试验四 利用EXCEL软件进行方差分析
试验四利用EXCEL软件进行方差分析一、试验目的：学会在计算机上利用EXCEL进行单因素（单向分组资料）、无重复双因素、组合内有重复观察值的两向分组资料以及组内又分亚组的单向分组资料的方差分析。
二、试验器具：计算机三、试验要求：每位同学一台计算机独立完成操作，并结合习题按照操作情况写出试验报告。
四、操作的方法步骤：（一）单因素方差分析1.打开计算机，点击开始，程序，附件，进入EXCEL 界面2.输入试验数据，例如教材101页表6.2。
3.点击工具，数据分析，单因素方差分析，确定4.将光标置于输入区域，用鼠标将数据所在的区域选定5.分组方式点中“行”，点输出区域，光标移入后面框内，用鼠标点任意区域，然后点确定，即可得到结果。
（二）无重复双因素试验结果的方差分析1.打开计算机，点击开始，程序，附件，进入EXCEL 界面2.输入试验数据，例如教材228页表12.3。
3.点击工具，数据分析，无重复双因素方差分析，确定4.将光标置于输入区域，用鼠标将数据所在的区域选定5.点输出区域，光标移入后面框内，用鼠标点任意区域，然后点确定，即可得到结果。
（三）有重复观察值的两向分组资料的方差分析1.打开计算机，点击开始，程序，附件，进入EXCEL 界面2.输入试验数据，例如教材122页表6.31。
应该将A1、A2、A3、B1、B2、B3输入3.点击工具，数据分析，可重复双因素方差分析，确定4.将光标置于输入区域，用鼠标将数据及A1、A2、A3、B1、B2、B3所在的区域选定，每一样本的行数是35.点输出区域，光标移入后面框内，用鼠标点任意区域，然后点确定，即可得到结果。
（四）组内又分亚组的单向分组资料的方差分析1.打开计算机，点击开始，程序，附件，进入EXCEL 界面2.输入试验数据，例如教材116页表6.19。
将组间即培养液间代号输入第一列，将组内亚组间即盆号输入第一行3.点击工具，数据分析，无重复双因素方差分析，确定4.将光标置于输入区域，用鼠标将数据及代码所在区域选定，每一样本的行数是45.点输出区域，光标移入后面框内，用鼠标点任意区域，然后点确定，即可得到结果。
实验四用EXCEL实现方差分析
实验四用EXCEL实现方差分析方差分析（Analysis of Variance，简称ANOVA）是一种用于比较两个或多个组之间均值差异是否显著的统计方法。
在统计学中，方差分析被广泛应用于各个领域，如医学、社会科学、经济学等。
方差分析的基本原理是通过比较组间方差与组内方差的大小来推断均值之间的差异是否显著。
在进行方差分析之前，我们首先要明确研究对象和目的。
假设我们要分析一个实验的结果，该实验包含三个组，每个组有若干个样本。
我们的目标是确定这三个组的均值是否有显著差异。
在EXCEL中进行方差分析，首先需要收集所需的数据，并将其整理成适合进行分析的形式。
我们将每个组的数据放在一个列中，列的顶部标有组的名称。
接下来，我们将这些数据输入到EXCEL的数据分析工具中。
1.打开EXCEL，并选中数据分析工具。
在EXCEL的菜单栏中，选择“数据”选项卡，然后选择“数据分析”。
如果未能找到“数据分析”选项，则需要先启用此选项。
点击“文件”选项卡，在“选项”中选择“增益”选项，然后勾选“数据分析”选项。
2.选择方差分析工具。
在数据分析工具中，选择“方差分析”选项，然后点击“确定”。
3.输入数据范围。
在方差分析工具的对话框中，输入数据范围，即每个组的数据所在的列。
确认输入范围后，点击“确定”。
4.设置其它参数。
方差分析工具还提供了一些可选参数，如方差齐性检验、置信水平等。
如果不需要使用这些参数，可以直接点击“确定”。
5.分析结果。
EXCEL将自动生成方差分析报告，报告包含了各个组的均值、方差、自由度、F值、P值等统计指标。
通过分析这些指标，我们可以判断各个组之间的均值差异是否显著。
方差分析的结论要根据P值的显著性确定。
如果P值小于设定的显著性水平（通常为0.05），则说明各个组之间的均值差异是显著的；反之，如果P值大于显著性水平，则说明各组之间的均值差异不显著。
需要注意的是，方差分析只能用于比较两个或多个组之间的均值差异，不能确定具体是哪个组之间存在差异。
EXCEL中方差分析
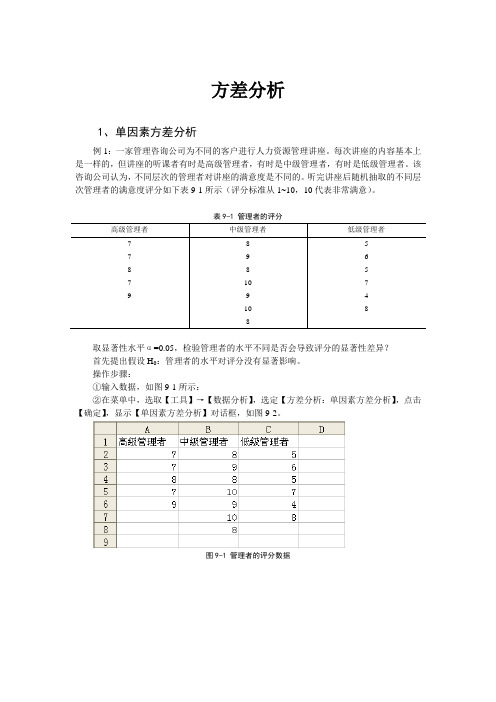
方差分析1、单因素方差分析例1：一家管理咨询公司为不同的客户进行人力资源管理讲座。
每次讲座的内容基本上是一样的，但讲座的听课者有时是高级管理者，有时是中级管理者，有时是低级管理者。
该咨询公司认为，不同层次的管理者对讲座的满意度是不同的。
听完讲座后随机抽取的不同层次管理者的满意度评分如下表9-1所示（评分标准从1~10，10代表非常满意）。
表9-1 管理者的评分高级管理者中级管理者低级管理者7 8 57 9 68 8 57 10 79 9 410 88取显著性水平α=0.05，检验管理者的水平不同是否会导致评分的显著性差异？首先提出假设H0：管理者的水平对评分没有显著影响。
操作步骤：①输入数据，如图9-1所示：②在菜单中，选取【工具】→【数据分析】，选定【方差分析：单因素方差分析】，点击【确定】，显示【单因素方差分析】对话框，如图9-2。
图9-1 管理者的评分数据图9-2 单因素方差分析对话框③在“输入区域”框输入数据矩阵（首坐标：尾坐标），可选为“A1：C8”，点选“标志位于第一行”，在“分组方式”框选定“列”，指定显著水平α＝0.05，输出选项的输出区域可为工作表的任何位置，本例选择在I4处。
④点击【确定】，则得输出结果，如下图9-3所示。
图9-3 单因素方差分析结果图9-3是一个单因素方差分析结果的报告。
第一个表是有关各样本的一些描述统计量，它可以作为方差分析的参考信息。
第二个表是方差分析结果。
其中SS 表示平方和，df 为自由度，MS 表示均方，F 为检验的统计量，P-value 为用于检验的P 值，F crit 为给定α水平下的临界值。
从方差分析表可以看到，由于68232.375573.11=>=αF F ，所以拒绝原假设，即管理者的水平对评分的影响是显著的。
在进行决策时，可以直接利用方差分析表中的P 值与显著性水平α的值进行比较，若 P ＜α，则拒绝原假设；若P ＞α，则不能拒绝原假设。
用excel进行方差分析
专业班次 组别
题 目 姓 名 日期
⒈ 用四种不同的发酵方法（A 、B 、C 、D ）所做成的面包的体积与重量之比如下表所示（数值己简化）。
试比较这四种发酵方法的体积重量比之间的差异。
如果处理效应为固定模型，并且处理间F 测验显著，用三种方法进行多重比较，并且讨论它们的结果。
第一种方法：标记字母法
由上面的结果可以看出：D 与C 、D 与A 、B 与C 、B 与A 的两两发酵方法都差异显著。
第二种方法：q 测验法
利用EXCEL 进行方差分析 09农信200930010621 张玲娟 2011.11.24
专业班次组别
题目姓名日期
由上面的表格可以看出：D与A、B与A差异极显著，D与C、B与C差异显著。
第三种方法：Duncan’s法
由上面的表格可以看出：D与A、B与A、D与C差异极显著，B与C差异显著。
⒉随机抽取四个品种的荔枝树在三种光照条件下测定它们的叶面积与干重之比值，结果如下表所示（数值己简化）。
如果品种为随机效应，光照条件为固定效应，试对资料进行适当的分析。
专业班次组别
题目姓名日期
因为P-value行=0.506023>0.05,P-value列=0.199336>0.05，所以接受原假设，即无显著差异。
⒊随机抽取五种年龄的游客两人，安排他们同时乘坐四种速度的过山车，然后测定他们
脉搏跳动的次数。
资料如下表（数值己简化）。
试对资料进行适当分析。
专业班次组别
题目姓名日期
由上面的结果可以看出：120转与100转、120转与80转、120转与60转、100转与60转、80转与60转差异显著。
Excel中的单因素方差分析
Excel中的单因素方差分析一、目的要求为了解决多个样本平均数差异显著性的测验问题，需要应用方差分析。
方差分析是把试验看成一个整体，分解各种变异的原因。
从总的方差中，将可能的变异原因逐个分出，并用误差的方法作为判断其他方差是否显著的标准，如果已知变异原因的方差比误差方差大得多，那么，该方差就不是随机产生的，试验的处理间的差异不会是由于误差原因造成的，这时处理的效应是应该肯定的。
通过学习Excel中方差分析，掌握基本的分析操作，能够处理实验的数据。
二、实验工具Microsoft Excel三、试验方法叶内平均含硼量的差异显著性。
在Excel统计中，完全随机试验设计的方差分析，只须经过单因素方差分析即可得出结果，具体步骤如下：①打开Excel，向单元格中输入文字与数字，建立表格；②单击“工具”，在出现的对话框中，选择“数据分析”，选取“方差分析：单因素方差分析”；③单击“确定”，单击“输入区域：”框右边的按钮，用鼠标选中数据，再次单击按钮；其他设置选择α为0.05。
分组方式：行。
点选标志位于第一列。
④单击“确定”，即可输出单因素方差分析结果。
4、方差分析输出结果：SUMMARY组观测数求和平均方差A 6 52 8.666667 4.666667B 6 245 40.83333 13.76667C 6 96 16 11.6D 6 169 28.16667 34.96667E 6 249 41.5 3.5差异源SS df MS F P-value F crit 组间5160.467 4 1290.117 94.1691 1.07E-14 2.75871 组内342.5 25 13.7总计5502.967 295、多重比较：由方差分析的结果，采用新复极差测验法，再稍加计算比较处理，即可得出：60.05显著，并可知除E与B二处理间无极显著差异外，其他均有极显著差异。
SPSS中的单因素方差分析一、基本原理单因素方差分析也即一维方差分析，是检验由单一因素影响的多组样本某因变量的均值是否有显著差异的问题，如各组之间有显著差异，说明这个因素（分类变量）对因变量是有显著影响的，因素的不同水平会影响到因变量的取值。
excel 方差 标准差
excel 方差标准差Excel 方差标准差。
在Excel中，我们经常需要计算数据的方差和标准差，以便对数据的离散程度进行分析。
本文将介绍如何在Excel中使用函数来计算方差和标准差。
首先，让我们来了解一下方差和标准差的概念。
方差是一组数据与其平均值之差的平方的平均值，用来衡量数据的离散程度。
标准差是方差的平方根，也是衡量数据离散程度的一种指标，通常用来描述数据的波动程度。
在Excel中，我们可以使用以下函数来计算数据的方差和标准差：1. 方差的计算：=VAR.P(数据范围) 或者 =VAR.S(数据范围)。
VAR.P函数用于计算总体方差，适用于整个数据总体。
VAR.S函数用于计算样本方差，适用于从总体中抽取的样本数据。
例如，我们有一组数据在A1:A10单元格中，我们可以使用以下公式来计算总体方差：=VAR.P(A1:A10)。
或者使用以下公式来计算样本方差：=VAR.S(A1:A10)。
2. 标准差的计算：=STDEV.P(数据范围) 或者 =STDEV.S(数据范围)。
STDEV.P函数用于计算总体标准差，适用于整个数据总体。
STDEV.S函数用于计算样本标准差，适用于从总体中抽取的样本数据。
例如，我们有一组数据在A1:A10单元格中，我们可以使用以下公式来计算总体标准差：=STDEV.P(A1:A10)。
或者使用以下公式来计算样本标准差：=STDEV.S(A1:A10)。
除了使用函数来计算方差和标准差之外，Excel还提供了数据分析工具包，可以帮助我们进行更复杂的数据分析。
在Excel中，我们可以通过以下步骤来使用数据分析工具包计算方差和标准差：1. 首先，点击“数据”选项卡，在“分析”组中找到“数据分析”命令，并点击打开“数据分析对话框”。
2. 在“数据分析对话框”中选择“方差分析”或“描述统计”选项，然后点击“确定”按钮。
3. 在弹出的对话框中，选择数据范围和输出范围，并选择需要计算的统计量，如方差和标准差。
excel求方差标准差
excel求方差标准差在Excel中，我们可以使用函数来求取一组数据的方差和标准差。
方差和标准差是统计学中常用的两个概念，它们可以帮助我们衡量数据的离散程度和波动程度。
在实际工作和研究中，我们经常需要对数据进行分析和处理，因此掌握如何在Excel中求取方差和标准差是非常重要的。
首先，让我们来了解一下方差和标准差的概念。
方差是指一组数据与其平均值之差的平方和的平均值，它可以衡量数据的离散程度。
而标准差则是方差的平方根，它可以更直观地表示数据的波动程度。
在实际应用中，我们经常使用标准差来衡量数据的稳定性和可靠性。
在Excel中，我们可以使用函数来求取一组数据的方差和标准差。
首先，我们需要准备一组数据，假设我们有一组数据存储在A1到A10的单元格中。
接下来，我们可以使用VAR.S函数来求取这组数据的方差，该函数的语法为“=VAR.S(数据范围)”。
例如，我们可以在B1单元格中输入“=VAR.S(A1:A10)”，然后按下回车键即可得到这组数据的方差。
类似地，我们可以使用STDEV.S函数来求取这组数据的标准差，该函数的语法为“=STDEV.S(数据范围)”。
例如，我们可以在C1单元格中输入“=STDEV.S(A1:A10)”，然后按下回车键即可得到这组数据的标准差。
除了VAR.S和STDEV.S函数外，Excel还提供了VAR.P和STDEV.P函数来分别求取总体方差和总体标准差。
如果我们需要对整个总体进行统计分析，可以选择使用这两个函数。
在实际工作中，我们经常需要对多组数据进行方差和标准差的比较。
在Excel 中，我们可以利用图表功能来直观地展示多组数据的方差和标准差。
通过创建柱状图或折线图，我们可以清晰地比较不同数据集之间的方差和标准差，从而更好地理解数据的分布情况。
除了单个数据集的方差和标准差外，Excel还提供了数据分析工具包，可以帮助我们对整个数据表格进行统计分析。
通过数据分析工具包中的方差分析和协方差分析功能，我们可以更加深入地了解数据之间的关系和差异，为决策提供更加可靠的依据。
Excel中进行表格做方差分析的操作技巧
Excel中进行表格做方差分析的操作技巧
如何用03版的excel做方差分析，很多答案是单击“工具”菜单上的“数据分析”，然而，当自己单击“工具”时，却没有“数据分析”这一选项，原来这是需要安装的。
今天，店铺就教大家在Excel中进行表格做方差分析的操作技巧。
Excel中进行表格做方差分析的操作步骤：
选择“工具”，找到“加载宏”。
会出现下面的活动框。
选择“分析工具库-VBA函数”。
确定后安装一下即可。
再次选择“工具”时，出现了方差分析。
其中很多项目可自行尝试。
Excel中进行表格做方差分析的操作。
excel单因素方差分析
excel单因素方差分析Excel的单因素方差分析（One-WayAnalysisofVariance,ANOVA）是一种统计技术，可以帮助我们检验某个变量在不同分组或组之间的差异。
它主要通过检验有效性的F检验，来分析两个或多个数据组之间的平均值是否具有统计学意义。
此外，Excel中的单因素方差分析技术还可以用来测量和比较不同因素对总体中样本值的影响程度，从而更好地判断因素之间的关联性。
Excel中的单因素方差分析是一种重要的统计分析工具，在许多研究领域中都得到了广泛应用，如市场营销研究中对用户满意度的比较，社会科学研究中对实验组和对照组的分析等。
它可以有效地帮助我们判断因素之间的关联性，从而更好地进行决策分析。
Excel中的单因素方差分析首先要准备数据，准备之前要注意几个问题：数据要符合正态分布，变量要是独立的，没有多重共线性等。
接下来，将准备好的数据输入Excel中。
进入数据分析对话框后，选择单因素方差分析，根据自己的分析需求，可以设置分析参数，比如比较的组别或因子，按照不同实验设置设定P值和alpha值等参数，最后点击确定，Excel就会根据我们的分析需求自动生成报告，包括F-检验和P-值等参数。
Excel中的单因素方差分析技术也具有一定的局限性要注意，它只能用于定量数据的分析，不能用于定性数据的分析，而且它不能用于多维数据分析，只能用于单维数据的分析。
此外，由于它的统计假设比较严格，不能适用于所有数据分析情形。
总之，Excel单因素方差分析是一种有效且易于使用的分析工具，能够用于在数据分析中帮助我们检验某个变量在不同分组或组之间的差异，比较实验组和对照组的差异，并用于测量和比较不同因素对总体样本值的影响程度，从而更好地判断因素之间的关联性。
但是，它也有一些局限性，在使用之前要仔细考虑，以确保最终的分析结果的准确性。
如何在Excel中使用ANOVA进行方差分析
如何在Excel中使用ANOVA进行方差分析方差分析（ANOVA）是一种常用的统计分析方法，用于比较两个或多个样本之间的均值是否存在统计显著性差异。
在Excel中，我们可以利用内置的数据分析工具paketo进行ANOVA分析，具体步骤如下：1. 数据准备首先，我们需要将待分析的数据准备好。
假设我们要比较三种不同药物对某种疾病的治疗效果，我们可以将每种药物的治疗结果记录在Excel的不同列中，每个样本的观测值放在不同行中，确保数据排列整齐。
2. 打开数据分析工具paketo点击Excel工具栏上的“数据”选项卡，在“数据分析”组中找到“数据分析”按钮，点击打开数据分析对话框。
3. 选择ANOVA工具在数据分析对话框中，找到并选中“方差分析（ANOVA）”工具，然后点击“确定”按钮。
4. 填写输入范围在ANOVA工具的对话框中，需要填写“输入范围”和“Alpha”值。
“输入范围”即为待分析的数据范围，可以手动输入或通过点击选择数据表中的相关数据区域。
“Alpha”值用于设置显著性水平，默认为0.05，可以根据需要适当调整。
5. 设置输出选项在ANOVA工具的对话框中，可以对输出结果进行设置。
一般情况下，选择“新工作表里输出”即可，这样可以在新的工作表中查看分析结果。
6. 点击确定，进行分析完成以上设置后，点击“确定”按钮开始进行ANOVA分析。
7. 分析结果解读分析完成后，Excel将会在指定的输出位置生成ANOVA的结果。
通过观察各个因素的P值，我们可以判断各组间的均值是否存在显著差异。
从ANOVA结果中，我们可以查看总体方差（Between groups）和误差方差（Within groups），并计算出F值和P值。
若P值小于显著性水平，则可以认为各个样本之间的均值存在显著差异。
总结：通过Excel中的数据分析工具paketo，我们可以轻松地进行ANOVA方差分析。
只需将待分析数据准备好，选择合适的工具，填入相应的参数，即可得到分析结果。
实验四 用EXCEL实现方差分析
壤种 B2(二合)
13.0 13.7 12.0 14.2 13.6 13.3
类 B3(黏土)
13.3 14.0 13.9 12.0 14.6 14.0
得其产量结果
1 21.4 19.6 17.6
(g)于表4.4，试 A3 2 21.2 18.8 16.6
作分析。
3 20.1 16.4 17.5
1 15.3 13.1 14.5
A因素 B因素
第三步： 获得F测验结 果，可以看出， A因素有极显 著差异，B因 素无显著差异。
F0.05值
为了下面的方便，注意 此处临界值的排列方向
第五步：多重比较 先计算标准误SE ，再手 工输入SSRα值，然后编 辑公式计算LSRα值，如 图。
“=$B39+C$38”， 然后用填充柄向右 和向下填充，然后 清除无效数据
差异显著性。
▼注意修正公式中的单元 格引用，使每一处理所在 行的最后一个差数均与 p=2时的LSRα值比较。
“=IF(D36>=D$32,FIXED(D36,1)&”**”,IF(D36>=D$31,FIXED(D 36,1)&”*”,FIXED(D36,1)))”，同理按住填充柄向左填充
▼注意修正公式中的单元 格引用，使每一处理所在 行的最后一个差数均与 p=2时的LSRα值比较。
分析。
D 25 26 21 27 22
第一步：打开一张工作表，并输入相应的数据， 如A2：F6。
第二步：单击“工具”菜单→“数据分析”命令 →选中“方差分析：单因素方差分析”命令，然 后单击“确定”按钮，如图。
输入区域：“$A$3：$F$6”
分组方式：“行”
选中“标志位于第一列”选 项 α(A)：“0.05”
(整理)实习四均值比较方差分析.
实习四均值比较和方差分析一均值比较与方差分析的概念统计分析常常采取抽样研究的方法。
即从总体中随机抽取一定数量的样本进行研究来推论总体的特性。
由于总体中的每个个体间均存在差异，即使严格遵守随机抽样原则也会由于多抽到一些数值较大或较小的个体致使样本统计量与总体参数之间有所不同。
由此可以得出这样的认识：均值不相等的两个样本不一定来自均值不同的总体。
能否用样本均数估计总体均数，两个变量均数接近的样本是否来自均值相同的总体？换句话说，两个样本某变量均值不同，其差异是否具有统计意义，能否说明总体差异？这是各种研究工作中经常提出的问题。
这就要进行均值比较。
对来自正态总体的两个样本进行均值比较常使用T检验的方法。
T检验要求两个被比较的样本来自正态总体。
两个样本方差相等与不等时使用的计算t值的公式不同。
进行方差齐次性检验使用F检验。
对应的零假设是：两组样本方差相等。
p值小于0．05说明在该水平上否定原假设，方差不齐；否则两组方差无显著性差异。
F值的计算公式是：F＝S12(较大)/S22(较小)方差分析（ANOVA）又称“变异数分析”或“F检验”，是R.A.Fisher发明的，用于两个及两个以上样本均数差别的显著性检验。
二实习目的和原理假设检验的目的：推断两个总体均数是否相等均值过程单一样本T检验(One-Sample T Test）独立样本T检验(Independent-Sample T Test)配对样本T检验(Paired-Sample T Test)方差分析（One-Way ANOVA）附正态分布的检验数据要求（t检验适用范围）：使用T检验法对两个独立样本的均值进行比较，除要求这两个样本都来自正态总体或近似正态分布（包括偏态转换），还要对两个正态总体的方差是否相等加以区分，即需要确定两个正态总体是否具有方差齐性。
t检验适用于可比性资料，即除了欲比较的因素外，其它所有可影响的因素应相似。
假设检验的注意事项1 假设检验的P值不能反映总体均数差别的大小。
用excel进行方差分析的实验报告
用excel进行方差分析的实验报告实验四：用excel进行方差分析的实验报告实验目的:学会在计算机上利用excel进行单因素方差分析和有交互的双因素分析以及无交互的双因素分析，实验背景：方差分析是从观测变量的方差入手，研究诸多控制变量中哪些变量是对观测变量有显著影响的变量。
一个复杂的事物，其中往往有许多因素互相制约又互相依存。
方差分析的目的是通过数据分析找出对该事物有显著影响的因素，各因素之间的交互作用，以及显著影响因素的最佳水平等。
方差分析是在可比较的数组中，把数据间的总的“变差”按各指定的变差来源进行分解的一种技术。
对变差的度量，采用离差平方和。
实验内容：实验（1）：单因素方差分析条件：单因素方差分析是对成组设计的多个样本均数比较，所以对数据格式有特殊要求，因素的不同水平作为表格的列（或行），在不同水平下的重复次数作为行（或列）。
例1：以下数据来自2009年中国统计年鉴，各地区农村居民家庭平均每人生活消费支出，按不同项目分组的不同地区：其中，1代表生活消费支出合计，2代表食品，3代表衣着，4代表居住， 5代表家庭设施及服务， 6代表交通和通讯， 7代表文教娱乐用品及服务，8代表医疗保健， 9代表其他商品及服务各地区农村居民家庭平均每人生活消费支出 (2009年)单位：元地区项目地区生活消费食品衣着居住家庭设备交通和文教娱乐医疗保健其他品支出合计及服务通讯用品及服务及务地区 1 2 3 4 5 6 7 8北京8897.59 2808.92 654.36 1798.88 528 1132.09 960.41 867.87 14天津4273.15 1848.11 324.63 674.67 187.83 481.27 371.85 299.79 8河北3349.74 1195.65 217.82 796.62 170.4 350.92 263.53 289.27 6山西3304.76 1224.6 283.2 584.07 156.27 324.89 416.94 240.94 7内蒙古3968.42 1578.57 271.88 609.29 148.03 466.34 390.85 416.87 8辽宁4254.03 1563.33 335.93 793.91 185.5 416.41 437.79 409.64 11吉林3902.9 1371.12 286.97 737.07 168.36 355.99 376.76 511.5 9黑龙江4241.27 1331.07 345.69 946.84 161.03 427.35 496.42 434.25 9上海9804.37 3639.14 496.14 2102.96 480.62 1212.38 942.76 738.94 19江苏5804.45 2275.28 306.62 969.76 286.37 691.56 818.45 322.99 13浙江7731.7 2812.39 473.11 1488.95 374.31 968.17 843.34 609.07 16安徽3655.02 1494.19 203.37 813.12 229.66 302.23 312.05 227.1 福建5015.72 2304.14 291.72 821.21 260.68 570.24 421.69 219.02 12江西3532.66 1609.2 162.58 725.11 181.91 295.76 254.77 232.78 7山东4417.18 1618.66 265.59 945.81 273.77 533.55 399.95301.55河南3388.47 1220.36 225.64 875.83 203.81 310.11 234.01 242.87 7湖北3725.24 1668.35 195.45 702.62 229.32 307.22 281.68 236.31 10步骤：（1）、在excel的分析工具库中中选择“方差分析：单因素方差分析”指定相应的数据区域和显著性水平，点击“确定”后输出最终输出结果：表一方差分析：单因素方差分析SUMMARY组观测数求和平均方差列 1 32 129281.5 4040.048 3465440列 2 32 52249.75 1632.805 428309.6列 3 32 7951.16 248.4738 15408.02列 4 32 25251.6 789.1125 162323.1列 5 32 6519.28 203.7275 10263列 6 32 13547.29 423.3528 66285.85列 7 32 11279.63 352.4884 55136列 8 32 9809.81 306.5566 31281.44列 9 32 2716.05 84.87656 1665.067 表一是各组数据的描述统计指标。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《田间试验设计与统计》实验
用EXCEL实现方差分析
▼注意修正公式中的单元 格引用，使每一处理所在 行的最后一个差数均与 p=2时的LSRα值比较。
“=IF(C37>=D$32,FIXED(C37,1)&”**”,IF(C37>=D$31, FIXED(C37,1)&”*”,FIXED(C37,1)))”
第一步：打开工作表，在适宜位置输入数据， 如图。
《田间试验设计与统计》实验
用EXCEL实现方差分析
第二步： 单击“工具”菜单→“数据分析”命令→ 选择“方差分析：可重复双因素分析”功能→单击 “确定”按钮，如图。
《田间试验设计与统计》实验
用EXC： 在弹出的对话框中的相应位置输 入有关参数，单击“确定”按钮，如图。
《田间试验设计与统计》实验
用EXCEL实现方差分析
《田间试验设计与统计》实验
用EXCEL实现方差分析
▼注意修正公式中的单元 格引用，使每一处理所在 行的最后一个差数均与 p=2时的LSRα值比较。
“=IF(D36>=D$32,FIXED(D36,1)&”**”,IF(D36>=D$31,FIXED(D 36,1)&”*”,FIXED(D36,1)))”，同理按住填充柄向左填充
《田间试验设计与统计》实验
用EXCEL实现方差分析
实验四 用EXCEL进行方差分析
一、单因素方差分析 二、无重复两因素方差分析 三、有重复两因素方差分析
《田间试验设计与统计》实验
用EXCEL实现方差分析
一、单因素方差分析
单因素试验可采用完全随机设计、随机区组 设计和拉丁方设计。而不同的试验设计方法所产 生的变异来源不同，完全随机设计可分为处理间 变异和误差变异两部分，随机区组设计则可分为 处理间变异、区组间变异和误差变异三部分，而 拉丁方设计则可以分为处理间变异、横向区组间 变异、纵向区组间变异以及误差变异四个部分。
《田间试验设计与统计》实验
用EXCEL实现方差分析
第一步 打开工作表，输入数据，然后单击“工 具”菜单→“数据分析”命令→“方差分析：无重 复双因素分析”，然后单击“确定”按钮，如图。
《田间试验设计与统计》实验
用EXCEL实现方差分析
选中“标志”选项，并在“α(A)”中输入 “0.05”
第二步：在方差分析对话框中，输入有关参数， 再单击“确定”按钮，如图。
第八步 获得 差异显著性结果， 从中可以看出， 除了A3、A4两个 品种间无显著差 异外，其余各品 种间均有极极显 著差异，由于B 因素无显著差异， A3或A4与任意一 个浸渍时间组合 均可获得最好的 结果，如图。
《田间试验设计与统计》实验
三、可重复两因素方差分析
用EXCEL实现方差分析
在EXCEL中可重复两因素试验的方差分析 实际上是采用方差分析方法来分析两因素试验 完全随机设计的结果，与无重复两因素的区别 在于除了分析两个试验的主效外，还可以分析 出两个试验因素间的交互作用的影响。
《田间试验设计与统计》实验
例4.4 施用 A1 、 A2 、 A3 、 A4 四 种 肥 料 于 B1 、 B2 、 B3 三 种土壤，以小 麦为指示作物， 每处理组合3盆， 得其产量结果 (g)于表4.4，试 作分析。
用EXCEL实现方差分析
《田间试验设计与统计》实验
用EXCEL实现方差分析
▼ 注意A、B两因素的 排列位置以及重复数据的 排列方向，否则将无法进 行方差分析。
用EXCEL实现方差分析
有重复两因素结果的方差分析中，一般情况下，如 果交互作用不显著，只需对有显著差异的因素进行多 重比较，再通过找出的最佳水平进行组合而获得最佳 的处理组合；但如果交互作用显著，则要求对处理组 合进行多重比较来确定最佳的处理组合。
当然，是否需要对各因素以及处理组合均进行多重 比较以及多重比较需采用的方法，主要是根据试验的 目的而确定。
第一步 打开工作表，输入数据，然后单击“工 具”菜单→“数据分析”命令→“方差分析：无重 复双因素分析”，然后单击“确定”按钮，如图。
《田间试验设计与统计》实验
“$A$2：$D$9”
用EXCEL实现方差分析
输出区域：“$A$11”
选中“标志”选项，并在“α(A)”中输入 “0.05”
第二步：在方差分析对话框中，输入有关参数， 再单击“确定”按钮，如图。
“=B37*B35”
“=B38*B35”
第四步：多重比较 采用LSD法(SSR法可参照 前述单因素方差分析方法)。
《田间试验设计与统计》实验
“=B41-$B$46”，并向下填充
用EXCEL实现方差分析
第五步：将处理 名称及其对应的平均 数复制到相应位置， 并按平均数大小进行 降序排列，然后再计 算与对照的平均数的 差数，如图。
《田间试验设计与统计》实验
用EXCEL实现方差分析
此部分数据存在于方差分析表之 前的汇总统计 (Summary)中
第六步：将处理名称及其对应的平均数复制到 所需位置，如图。
《田间试验设计与统计》实验
用EXCEL实现方差分析
“排序”命令
第七步 选中处理及其平均数所在的区域，单击 “数据”菜单→“排序”命令，进行数据排序，如 图。
对于多重比较的EXCEL方法请参考前述有关内容， 在此不再赘述；而其它试验设计方法所获得的试验结 果的方差分析方法，请大家参考其它有关书籍自行学 习掌握。
第七步： 复制一次梯形 表，在第二个 梯形表中删除 所有差数，然 后编制公式进 行比较，并进 行填充，以获 得所有差值的 差异显著性。
▼注意修正每一行最后边第一个差值的公式中的单元格引用，使 每一处理所在行的最后一个差数均与p=2时的LSRα值比较。
《田间试验设计与统计》实验
用EXCEL实现方差分析
输出区域：“$A$8”
第三步：在弹出的对话框中输入相应的参数，然后 再单击“确定”按钮，如图。
《田间试验设计与统计》实验
用EXCEL实现方差分析
此值为F=6.1973时的概率值，它如果≤0.01，则处理间有极显著差异，
如果介于[0.05,0.01)之间，则有显著差异，否则无显著差异。
处理平均数
F0.05
《田间试验设计与统计》实验
用EXCEL实现方差分析
“=IF(E35>=D$32,FIXED(E35,1)&”**”,IF(E35>=D$31,FIXED(E 35,1)&”*”,FIXED(E35,1)))”，并按住填充柄向左填充
第十步： 将梯形表中右 下角的无用数 据清除后，再 复制一次梯形 表，在第二个 梯形表中删除 所有差数，并 编制公式进行 填充，以获得 差异显著性。
《田间试验设计与统计》实验
例4.3 将A1、 A2 、 A3 、 A4 四 种 生 长 素 ， 并 用 B1 、 B2 、 B3 三 种 时 间 浸渍菜用大豆品 种 种 子 ， 45 天 后 测得各处理的平 均 单 株 干 物 重 (g) 于 表 4.3 ， 试 作 分 析。
用EXCEL实现方差分析
处理间
误差
s2
第四步：获得F测验结果，由于F=6.18>F0.05=3.24，因此 处理间有显著差异。
《田间试验设计与统计》实验
用EXCEL实现方差分析
“=SQRT(D21/5)”
为了下面的方便，注意 此处临界值的排列方向
“=B28*$B$25”， 再向右和向下填充
第五步：多重比较 先计算标准误SE ，再手工输入 SSRα值，然后编辑公式计算LSRα值，如图。
《田间试验设计与统计》实验
用EXCEL实现方差分析
第四步： 获得 分析结果，如图。
《田间试验设计与统计》实验
A因素 B因素
误差
用EXCEL实现方差分析
第四步： 获得分析结 果，可以看 出A因素和 A×B 交 互 有 极显著差异， 而B因素有 显著差异， 如图。
F0.05值
《田间试验设计与统计》实验
《田间试验设计与统计》实验
例4.1 设有A、 B、C、D四个 大豆品种，其 中D为对照，采 用完全随机设 计进行比较试 验，5次重复， 小区产量(㎏)列 于 表 4.1 ， 试 作 分析。
用EXCEL实现方差分析
《田间试验设计与统计》实验
用EXCEL实现方差分析
第一步：打开一张工作表，并输入相应的数据， 如A2：F6。
《田间试验设计与统计》实验
用EXCEL实现方差分析
“=$B39+C$38”， 然后用填充柄向右 和向下填充，然后 清除无效数据
第六步 复制处理名称及平均数，然后将各处理 及其平均数按平均数大小进行降序排列，再编制公 式计算处理平均数的差数，如图。
《田间试验设计与统计》实验
用EXCEL实现方差分析
《田间试验设计与统计》实验
用EXCEL实现方差分析
“=IF(ABS(C41)>=$D$38,FIXED(C41,2)&”**“,IF(ABS(C41)>=$ D$37,FIXED(C41,2)&”*“,FIXED(C41,2)))”，并向下填充
第六步：进行差异显著性的比较，可以看出， 除E品种与对照品种G有极显著差异外，其余品种 与对照间均无显著差异。
《田间试验设计与统计》实验
用EXCEL实现方差分析
在EXCEL中可采用编制公式的方法或使用方差分 析功能模块来实现方差分析。编制公式的方法比较繁 琐，但可以用在所有设计形式的试验结果中。相应地 ，使用方差分析功能模块比较简便，但直接只能进行 到F测验，同时EXCEL没有提供拉丁方设计、裂区设 计等复杂的试验结果的分析方法，因此，EXCEL只能 简化平方和和自由度的分解以及F测验的计算量，而无 法直接实现方差分析的完整过程。
《田间试验设计与统计》实验