自命题科目考试大纲 .doc
农学院自命题科目考试大纲
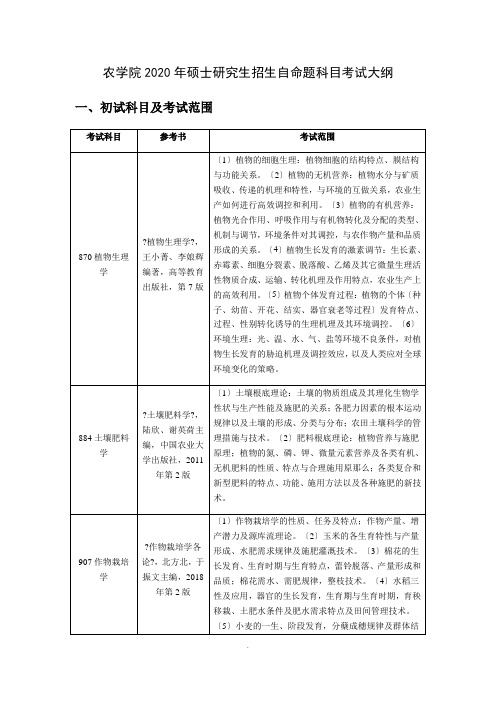
?细胞生物学?,翟中和、王喜忠、丁明孝主编,高等教育出版社,2011年第4版
〔1〕绪论:掌握细胞生物学的主要研究内容,了解细胞学开展中的关键事件。〔2〕细胞的统一性与多样性:植物细胞与动物细胞、原核细胞与真核细胞的主要结构差异。〔3〕细胞生物学研究方法:细胞形态结构的观察方法,细胞及其组分的分析及大分子动态变化的分析技术,细胞培养与细胞工程。〔4〕细胞基质与功能。〔5〕细胞器的结构与功能:内膜系统的概念及其组成成员;内质网、高尔基体、溶酶体、微体、线粒体、叶绿体。〔6〕细胞骨架的概念、组成及其功能;微丝、微管、中间纤维。〔7〕细胞核与染色体。〔8〕细胞膜和跨膜运输。〔9〕蛋白质分选与膜泡运输。〔10〕细胞通讯和信号转导。〔11〕细胞的连接。〔12〕细胞增殖及其调控与癌细胞。〔13〕细胞分化及其调控。〔14〕程序性细胞死亡,细胞衰老与凋亡。
639植物学
?植物学?,贺学礼,高等教育出版社,2010年第2版
〔1〕植物细胞:细胞的根本特征、植物细胞的根本结构植物细胞的后含物、植物细胞的分裂生长和分化死亡。〔2〕植物组织。〔3〕根:根尖的结构及其生长动态、根的初生生长和初生结构、根的次生生长与次生结构、根的变态。〔4〕茎:茎的形态、茎的初生生长和初生结构、茎的次生生长和次生结构、茎的变态。〔5〕叶:叶的发生和结构。〔6〕被子植物花的构造和发育:花的组成和发生、雌雄蕊的发育与结构、开花传粉和受精。〔7〕种子和果实:种子、果实的发育与结构、植物个体发育和被子植物生活史。〔8〕植物界的根本类群:植物分类的根底知识、植物界的发生与演化。〔9〕被子植物分类的形态学术语。〔10〕被子植物分类:双子叶植物纲和单子叶植物纲。〔11〕植物生态:植物的生态适应、植物种群与环境、植物群落与环境。
953保护生物学
自命题科目考试大纲

自命题科目考试大纲科目代码及名称:611马克思主义发展史适用专业:马克思主义基本原理一、考试目的及要求“马克思主义发展史”入学考试是为招收马克思主义基本原理类硕士生而实施的选拔性考试。
其主要目的是考查学生对马克思主义形成的历史背景、马克思主义产生的历史必然性、马克思主义发展的历史进程以及马克思主义在不同历史阶段发展的基本知识和马克思主义中国化等各项内容理解和掌握的程度。
在此基础上,提高学生运用马克思主义的立场、观点和方法分析问题和解决问题的能力。
二、考试内容奠基篇(1840-1895)第一章历史发展的必然成果第一节资本主义发展的历史性变化第二节人类先进思想的发展及困惑第三节马克思恩格斯向唯物主义和共产主义的转变第二章马克思主义的伟大发现(一)第一节发现唯物史观的历程第二节马克思主义的第一次公开阐述第三节《共产党宣言》的问世第三章马克思主义的伟大发现(二)第一节政治经济学的科学革命第二节《资本论》第一卷的问世第三节马克思主义同工人运动的结合第四章博大精深的理论体系(上)——系统化和多方面展开第一节《反杜林论》是马克思主义排科全书第二节马克思主义理论的多方面展开第五章博大精深的理论体系(下)——探索、深化和面向新世纪第一节东方社会发展道路的探索和研究第二节原始社会的研究和对唯物史观的进一步论证与深化第三节哲学发展的回顾和面向新世纪哲学纲领的提出第四节资本主义发展趋势的深索和无产阶级革命的斗争策略第五节面对世纪之交的理论分歧和挑战开拓篇(1895-1917)第六章历史转折的理论分歧第一节伯恩施坦主义及其对马克思主义的“修正”第二节德国社会民主党内反对伯恩施坦主义的斗争第三节法国和俄国马克思主义者的理论批判第七章捍卫真理的列宁主义第一节反对民粹派和“合法马克思主义者”的斗争第二节捍卫马克思主义世界观的斗争第八章实践呼唤的理论飞跃第一节列宁对辩证法的深刻研究第二节帝国主义理论的形成第三节社会主义革命的新理论发展篇(1917-1956)第九章十月革命的胜利和列宁建设社会主义的构想第十章斯大林关于社会主义建设的理论和苏联模式第十一章马克思主义中国化和毛泽东思想的历史性胜利第十二章毛泽东关建设新中国的战略思想第十三章西方学者对马克思主义理论与实践的探索创新篇(1956-1997)第十四章苏联东欧的改革和剧变第十五章当代资本主义国家围绕马克思主义出现的思潮和流派第十六章中国对社会主义道路的艰难探索第十七章邓小平理论的形成和科学体系第十八章马克思主义在中国发展的新阶段和跨越世纪的旗帜第十九章“三个代表”重要思想是坚持与时俱进、不断创新的理论成果第二十章新世纪的建设与不断开拓马克思主义理论发展的新境界三、考试题型及比例1、简答题(70%)2、论述题(30%)四、考核形式及时间考试形式为闭卷笔试。
安徽财经大学2024年硕士初试自命题大纲 822设计表现

安徽财经大学2024年硕士研究生入学考试
初试自命题科目考试大纲
考试科目代码及名称:822设计表现
一、考试总体目标
考察考生基本的设计表现能力,反应考生对画面整体的创作、组合、把握能力,考察考生的设计手绘基本功以及对设计语言和设计思想的理解表现力。
二、考试内容及要求
(一)考试内容:命题创作
(二)考试要求:
1.绘画表现材料不限,单色、彩色都可。
2.试卷尺寸:A3绘图纸。
3. 尺规、画材等用具自备。
三. 评分标准(满分150分)
(一)版式(完整、均衡)(15分)
(二)创作内容切题符合要求(60分)
(三)造型基本功(结构、线条、字体、卷面整洁度)(60分)
(四)创新能力(设计语言、设计思想的表达)(15分)。
北京科技大学2024年研究生自主命题考试大纲 《单独考试思想政治理论》(111)考试大纲

《单独考试思想政治理论》(111)考试大纲一、考试性质《单独考试思想政治理论》考试是北京科技大学为招收单独考试(非全日制)专业学位硕士研究生而设置的具有选拔性质的自主招生考试科目,其目的是科学、公平、有效地测试考生掌握大学本科阶段思想政治理论课程的基本知识和基本理论,以及运用马克思主义理论的立场、观点和方法分析和解决问题的能力,评价的标准是高等学校本科毕业生所能达到的相关课程的及格或及格以上水平,以保证被录取者具有基本的思想政治理论素养,并有利于本校相关专业(方向)择优选拔单独考试(非全日制)专业学位硕士研究生。
二、考查范围和目标1.考查范围。
《单独考试思想政治理论》考试,涵盖本科阶段《习近平新时代中国特色社会主义思想概论》《思想道德与法治》《马克思主义基本原理》《中国近现代史纲要》《毛泽东思想和中国特色社会主义理论体系概论》《形势与政策》课程的主要内容。
2.考查目标。
准确认知和记忆思想政治理论课的基础知识,正确理解课程相关的概念、范畴、命题和结论,能够初步运用马克思主义的基本立场、观点和方法分析和阐述中国特色社会主义事业和中华民族复兴伟业的历史与现实,深刻理解习近平新时代中国特色社会主义思想是马克思主义中国化时代化的最新理论成果,是21世纪的马克思主义。
三、考试形式和试卷结构1.试卷满分及考试时间本试卷满分为100分,考试时间为180分钟。
2.答题方式答题方式为闭卷、笔试。
3.试卷题型结构选择题 20分(10题,每题2分)简答题 40分(4题,每题10分)材料题 40分(2题,每题20分)四、参考书目《单独考试思想政治理论》科目考试以大学本科教材《习近平新时代中国特色社会主义思想概论》《思想道德与法治》(2023版)、《马克思主义基本原理》(2023版)、《中国近现代史纲要》(2023版)、《毛泽东思想和中国特色社会主义理论体系概论》(2023版)、《时事报告大学生版》(2022-2023学年度下学期、2023-2024学年度上学期)为主要参考书目。
2024年硕士研究生初试考试自命题大纲

2024 年硕士研究生初试考试自命题大纲科目:金融学考试范围:一、金融基础•金融的概念和作用•金融市场和工具•金融机构和监管二、资产定价•股票和债券定价•资本资产定价模型 (CAPM)•风险与收益三、投资管理•投资组合管理•风险管理•业绩评估四、公司金融•公司治理和代理问题•资本结构和融资•投资决策和资本预算五、国际金融•汇率和汇率制度•国际贸易与金融•外汇市场和衍生品六、实证金融学•金融数据的分析方法•时间序列分析•事件研究七、应用金融学•金融科技•行为金融学•绿色金融考试要求:•掌握基本概念和理论:理解金融学的基本原理和概念。
•解决实际问题的能力:运用所学知识解决金融领域中的实际问题。
•分析和批判性思维能力:分析金融数据和信息,提出有见地的结论。
•研究能力:熟悉金融学领域的最新研究进展。
•案例分析能力:对金融案例进行深入分析,提出合理的解决方案。
参考书目:•Ross, S. A., Westerfield, R. W., & Jordan, B. D. (2023). Fundamentals of Corporate Finance (12th ed.). McGraw-Hill Education.•Brealey, R. A., Myers, S. C., & Allen, F. (2023). Principles of Corporate Finance (13th ed.). McGraw-Hill Education.•Hull, J. C. (2023). Options, Futures, and Derivatives (10th ed.). Pearson Education.•Madura, J. (2023). International Financial Management (13th ed.). Cengage Learning.•Malkiel, B. G. (2022). The Elements of Investing (10th ed.). HarperCollins.考试时间: 3 小时考试题型:•单选题(50%)•多选题(20%)•判断正误题(10%)•简答题(10%)•论述题(10%)。
湖南师范大学2024年硕士研究生自命题考试大纲 专业外语

湖南师范大学硕士研究生入学考试自命题科目考试大纲考试科目代码:考试科目名称:专业外语(世界史)
一、考试内容及要点
考试内容:选取四段与世界历史各阶段相关的英文文献,要求考生把它们翻译成中文。
译文应最大程度忠实于原文,行文流畅,符合中文表达习惯。
考试为闭卷,不允许携带语言辞典及相关专业书籍。
要点:
八种不同模式的“世界史”;希腊人的世界;中国传统科学的基本范畴;明治晚期日本的意识形态;对比法国、俄罗斯和中国的社会革命;工业、民主、阶级、艺术及文化的基本概念;殖民时期印度的从属阶层;世界现代史上重要的转折点;乔治·华盛顿的启蒙运动理想;阿拉伯人的历史与文化;非洲人如何看待现代化;《寂静的春天》;《大宪章》;《我有一个梦》;《葛底斯堡演说》;《独立宣言》;《人权与公民权宣言》。
1。
湖南师范大学2024年硕士研究生自命题考试大纲 文艺学同等学力加试科目美学《考试大纲》
湖南师范大学硕士研究生入学考试自命题科目考试大纲考试科目代码:[文艺学复试科目] 考试科目名称:美学一、考试内容及要点(一)考试内容1、美学学科的基本概念、基本观点和基本理论,美学史的重要问题。
2、运用美学知识分析具体的审美现象。
(二)考试要点1、中西美学思想①中国美学的主要发展阶段:子学、经学、玄学、佛学、理学、心学、朴学。
②儒释道美学的代表性人物和基本观点。
③儒家与道家之美学对于中国文化发展的影响。
④西方美学的主要发展阶段:本体论美学、认识论美学、语言论美学。
⑤古希腊美学的代表人物——毕达哥拉斯、苏格拉底、柏拉图、亚里士多德、犬儒学派、伊壁鸠鲁学派、斯多噶学派——及其基本美学观点。
⑥中世纪教父哲学与经院哲学的代表人物及其基本美学观点。
⑦笛卡尔、康德、黑格尔等思想大师对于美学的贡献及影响。
2、美的本质①对“移情说”、“距离说”、“孤立说”、“美在关系”、“美是生活”等西方著名美学定义的了解。
②对中国50年代美学四大派及其基本美学定义的了解。
③从历史发生学角度理解“实践”与审美的关系。
④从静态和动态的角度对“美”的认识。
⑤美与真、善之关系。
⑥审美客体的特性。
①审美活动的概念与性质。
②审美活动发生的结构性要素。
③审美活动现实发生所需的主体条件——审美需要、审美能力、审美态度、审美理想、审美趣味等——以及各自的概念及内涵。
④审美活动中的主要心理因素——感觉、直觉、知觉、联想、想象、情感、理解等——以及各自的概念、特点及功能。
⑤审美活动与人类生存的关系。
4、艺术的本质①艺术的存在方式。
②艺术品的概念及其具体内涵。
③艺术品的层次结构。
④艺术创造的过程及基本能力。
⑤灵感、癫狂、天才的概念及内涵。
⑥艺术接受的意义。
5、自然美①自然美的概念及其特点。
②中国自然审美中的“比德说”与“畅神说”。
③自然美形成的原因。
④自然美的审美风格。
6、社会美①社会美的概念、类型及其特点。
②科学美的概念、特点及原因。
③饮食美的历史体现、要求以及中西饮食美的比较。
自命题科目考试大纲
自命题科目考试大纲科目代码与名称:831 经济学(含微观经济学与宏观经济学)适用专业:应用经济学一、考试目的与要求“经济学(含微观经济学与宏观经济学)”入学考试是为招收应用经济学硕士生而实施的选拔性考试。
其主要目的是考查考生对微观经济学和宏观经济学各项内容的理解和掌握的程度。
要求考生能够系统地掌握微观经济学和宏观经济学的基本知识,并具备运用所学的知识分析现实经济问题和解决问题的能力。
二、考试内容微观经济学部分:第一部分绪论1、经济学的产生和发展2、经济学的研究对象和主要内容3、经济学的研究方法第二部分均衡价格理论1、需求原理2、供给原理3、供求均衡——价格的决定4、弹性理论第三部分消费者行为理论1、消费者行为与其目标2、边际效用分析3、无差异曲线分析第四部分生产者行为理论1、生产者行为与其目标2、生产理论3、成本理论4、利润最大化原则第五部分市场结构理论1、市场结构与其划分2、完全竞争市场3、完全垄断市场4、垄断竞争市场5、寡头垄断市场第六部分要素价格理论1、要素价格决定的一般原理2、生产要素的价格3、收入分配的结果第七部分市场失灵与微观经济政策1、市场失灵与政府失灵2、垄断与其低效率3、外部性与其纠正4、公共产品与公共选择5、不完全信息与激励理论宏观经济学部分:第一部分国民收入核算理论1、与其核算方法2、国民经济中的其他总量指标3、核算的局限性与其纠正第二部分简单国民收入决定理论1、消费、储蓄与投资2、国民收入的均衡决定3、国民收入的变动第三部分产品市场与货币市场的一般均衡1、产品市场的均衡:曲线2、货币市场的均衡:曲线3、两个市场的同时均衡第四部分总需求-总供给模型1、总需求与总需求曲线2、总供给与总供给曲线3、总需求与总供给的均衡第五部分失业与通货膨胀理论1、失业理论2、通货膨胀理论3、失业与通货膨胀的关系第六部分经济增长与经济周期理论1、经济增长理论2、经济周期理论第七部分宏观经济政策1、宏观经济政策的目标与工具2、需求管理政策3、供给管理政策三、考试的题型与比例微观经济学部分(80分)单项选择题(10%)概念解释题(16%)计算题(20%)简答题(24%)论述题(10%)宏观经济学部分:(70分)单项选择题(10%)概念解释题(16%)计算题(10%)简答题(24%)论述题(10%)四、考试形式与时间考试形式为闭卷笔试。
自命题科目考试大纲
河北工业大学2021年硕士研究生招生考试自命题科目考试大纲科目代码:880科目名称:材料科学基础适用专业:材料科学与工程、材料与化工一、考试要求材料科学基础适用于河北工业大学材料科学与工程学院材料科学与工程、材料与化工专业研究生招生专业课考试。
主要考察考生对于材料科学基础的基本概念、基础理论的掌握情况及其运用所学知识分析和解决工程实际问题的能力。
二、考试形式试卷采用客观题型和主观题型相结合的形式,主要包括选择题、填空题、简答题、计算题、分析论述题等。
考试时间为3小时,总分为150分。
三、考试内容(一)原子结构与键合1、原子结构与原子的电子结构;原子结构、原子排列对材料性能的影响。
2、材料中的结合键的类型、本质,各结合键对材料性能的影响,键-能曲线及其应用。
3、原子的堆垛和配位数的基本概念及对材料性能的影响。
4、显微组织基本概念和对材料性能的影响。
(二)固体结构1、晶体与非晶体、晶体结构、空间点阵、晶格、晶胞、晶格常数、布拉菲点阵、晶面间距等基本概念。
2、晶体晶向指数与晶面指数的标定方法。
3、晶体结构及类型,常见晶体结构(bcc、fcc、hcp)及其几何特征、配位数、堆积因子(致密度)、间隙、密排面与密排方向,堆垛次序。
4、合金相结构,固溶体、中间相的基本概念和性能特点。
5、离子晶体和共价晶体机构,离子晶体结构规则、典型的离子晶体结构。
6、高分子材料的组成和结构的基本特征,高分子材料结晶形态、高分子链在晶体中的构象、高分子材料晶态结构模型、液晶态的结构特征与分类。
(三)点缺陷和扩散1、点缺陷的类型,肖脱基空位、弗兰克尔空位、间隙原子和置换原子,间隙固溶体和置换固溶体等基本概念,离子晶体中的点缺陷特点,点缺陷的平衡浓度、影响因素及其对材料性能的影响。
2、扩散概念,扩散第一定律、扩散第二定律。
3、扩散驱动力及扩散机制。
4、离子晶体中的扩散、聚合物中的扩散机制。
5、扩散系数、扩散激活能,影响扩散的因素及原理。
研究生入学考试自命题科目考试大纲o..doc
1,理解n阶线性微分方程解的结构,通解基本定理,掌握常数变易法和刘维尔公式;2,熟练掌握n阶线性常系数微分方程的解法。
参考资料:
东北师范大学编,《常微分方程》,第2版,2005,高等教育出版社
考试总分:100分考试时间:2小时考试方式:笔试
考试题型:计算题、证明题
魏宗舒等编,《概率论与数理统计教程》,高等教育出版社
(二、)常微分方程部分考试内容与范围:
一,初等积分法
1,熟练掌握初等积分法中的变量可分离方程解法、常数变易法、全微分方程解法(含积分因子的解法)及参数法和降阶法。
2,掌握证明一阶线性微分方程解的性质的基本方法。
3,掌握把实际问题抽象为常微分方程的基本方法。
5、随机变量的数字特征、切贝雪夫不等式;
6、条件分布与条件期望;
7、特征函数。
四、大数定律与中心极限定理
1、大数定律;
2、随机变量序列的两种收敛性;
3、中心极限定理。
五、数理统计的基本概念
1、母体与子样、经验分布函数;
2、统计量及其分布。
六、点估计
1、矩法估计;
2、极大似然估计;
3、估计的有效性。
参考资料:
二,基本定理
1,理解常微分方程解的几何解释,理解解的存在唯一性及延展定理的证明;
2,掌握奇解的求法。
3,掌握利用解的存在唯一性及延展定理证明有关方程解的某些性质的方法。
三,一阶线性微分方程组
1,理解线性微分方程组解的结构,通解基本定理,掌握常数变易法和刘维尔公式;
2,熟练掌握常系数线性微分方程组的解法。
7、贝努利概型。
二、离散型随机变量
1、一维随机变量及分布列;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自命题科目考试大纲
科目代码及名称:601 高等数学
适用专业:矿物学、岩石学、矿床学
一、考试目的及要求
“高等数学”入学考试是为矿物学、岩石学、矿床学等硕士生而实施的选拔性考试。
其主要目的是考查考生掌握一元微积分的基本概念、基本理论和基本运算等方面的数学基础。
要求考生具备能够综合运用所学微积分知识和数学素养去分析问题和解决问题的能力。
二、考试内容
第一部分函数、极限、连续
考试内容:函数的概念及表示法、函数的有界性、单调性、周期性和奇偶性,复合函数、反函数、分段函数和隐函数,基本初等函数的性质及其图形,初等函数、函数关系的建立,数列极限与函数极限的定义及其性质,函数的左极限和右极限,无穷小量和无穷大量的概念及其关系,无穷小量的性质及无穷小量的比较,极限的四则运算,极限存在的两个准则:单调有界准则和夹逼准则,两个重要极限,函数连续的概念,函数间断点的类型,初等函数的连续性,闭区间上连续函数的性质.
考试要求:
1. 理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系.
2. 了解函数的有界性、单调性、周期性和奇偶性.
3. 理解复合函数及分段函数的概念了解反函数及隐函数的概念
4. 掌握基本初等函数的性质及其图形,了解初等函数的概念.
5. 理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左、右极限之间的关系.
6. 掌握极限的性质及四则运算法则.
7. 掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.
8. 理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小
量求极限.
9. 理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.
10. 了解连续函数的性质和初等函数一的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.
第二部分一元函数微分学
考试内容:导数和微分的概念,导数的几何意义,函数的可导性与连续性之间的关系,平面曲线的切线与法线,导数和微分的四则运算,基本初等函数的导数,复合函数、反函数和隐函数的微分法,高阶导数,一阶微分形式的不变性,微分中值定理,洛必达(L'Hospital)法则,函数单调性的判别,函数的极值,函数图形的凹凸性,拐点及渐近线,函数图形的描绘,函数的最大值与最小值.
考试要求:
1. 理解导数和微分的概念,理解导数和微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.
2. 掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.
3. 了解高阶导数的概念,会求简单函数的高阶导数.
4. 会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.
5. 理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西( Cauchy )中值定理.
6. 掌握用洛必达法则求未定式极限的方法.
7. 理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.
8. 会用导数判断函数图形的凹凸性,会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.
第三部分一元函数积分学
考试内容:原函数和不定积分的概念,不定积分的基本性质,基本积分公式,定积分的概念和基本性质,定积分中值定理,积分上限的函数及其导数,牛顿-莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法、有理函数、三
角函数的有理式和简单无理函数的积分反常(广义)积分定积分的应用.考试要求:
1. 理解原函数的概念,理解不定积分和定积分的概念.
2. 掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.
3. 会求有理函数、三角函数有理式和简单无理函数的积分.
4. 理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.
5. 了解反常积分的概念,会计算反常积分.
6. 掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数的平均值.
第四部分常微分方程
考试内容:常微分方程的基本概念,变量可分离的微分方程,齐次微分方程,一阶线性微分方程,可降阶的高阶微分方程,线性微分方程解的性质及解的结构定理,二阶常系数齐次线性微分方程,简单的二阶常系数非齐次线性微分方程及微分方程的简单应用.
考试要求:
1. 了解微分方程及其阶、解、通解、初始条件和特解等概念.
2. 掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程.
3. 会用降阶法解微分方程.
4. 理解二阶线性微分方程解的性质及解的结构定理.
5. 掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.
6. 会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.
7. 会用微分方程解决一些简单的应用问题.
三、考试的题型及比例
卷面满分:150分
选择题(共32分,占 21%)
填空题(共24分,占 16%)
解答题(共94分,占 63%)
四、考试形式及时间
考试形式为闭卷笔试。
考试时间为3小时。
五、主要参考书目
1、同济大学应用数学系主编,《高等数学(上、下册)第六版》,北京:高等教育出版社,2007年。
