浅谈机械零件的强度(
机械零件的强度.
机械零件的强度.机械零件的强度.第⼀篇总论第三章机械零件的强度3-1 某材料的对称循环弯曲疲劳极限σ-1=180MPa，取循环基数N=5?106，m=9，试求循环次数N分别为7000，2500，620000次是时的有限寿命弯曲疲劳极限。
3-2 已知材料的⼒学性能为σS=260MPa，σ-1=170MPa，ψσ=0.2,试绘制此材料的简化极限应⼒线图（参看图3-3中的A’D’G’C）。
3-3 ⼀圆轴的轴肩尺⼨为：D=72mm，d=62mm，r=3mm。
材料为40CrNi，其强度极限σB =900MPa，屈服极限σS=750MPa，试计算轴肩的弯曲有效应⼒集中系数kσ。
3-4 圆轴轴肩处的尺⼨为：D=54mm，d=45mm，r=3mm。
如⽤题3-2中的材料，设其强度极限σB=420MPa，试绘制此零件的简化极限应⼒线图。
3-5 如题3-4中危险截⾯上的平均应⼒σm =20MPa，应⼒幅σa=900MPa，试分别按：a）r=C；b）σm=C，求出该截⾯的计算安全系数Sca。
第⼆篇联接第五章螺纹联接和螺旋传动5-1 分析⽐较普通螺纹、管螺纹、梯形螺纹和锯齿形螺纹的特点，各举⼀例说明它们的应⽤。
5-2 将承受轴向变载荷的联接螺栓的光杆部分做得细些有什么好处？5-3 分析活塞式空⽓压缩机⽓缸盖联接螺栓在⼯作时的受⼒变化情况，它的最⼤应⼒，最⼩应⼒如何得出？当⽓缸内的最⾼压⼒提⾼时，它的最⼤应⼒、最⼩应⼒将如何变化？5-4 图5-49所⽰的底板螺栓组联接受外⼒F∑的作⽤。
外⼒F∑作⽤在包含x轴并垂直于底板接合⾯的平⾯内。
试分析底板螺栓组的受⼒情况，并判断哪个螺栓受⼒最⼤？保证联接安全⼯作的必要条件有哪些？5-5 图5-50是由两块边板和⼀块承重板焊成的龙门起重机导轨托架。
两块边板各⽤4个螺栓与⽴柱相联接，托架所承受的最⼤载荷为20kN，载荷有较⼤的变动。
试问：此螺栓联接采⽤普通螺栓联接还是铰制孔⽤螺栓联接为宜？为什么？5-6 已知⼀个托架的边板⽤6个螺栓与相邻的机架相联接。
浅谈机械零件的疲劳强度
浅谈机械零件的疲劳强度内容摘要机械零件因生产制造不合格而毁坏，是造成机械设备运行出现异常的首要缘故。
在机械设备运作历程中，机械零件通过高温、高压等各种原因影响，产生衰老、损坏这些。
因此在机械零件的生产过程中，就必须对机械零件自身品质严格把关，尤其是对机械零件疲劳强度要良好掌握。
文中就提升机械零件疲劳强度的措施探讨，明确提出几个提议。
关键词：机械零件；疲劳强度；措施机械零件因生产制造不合格而毁坏，是造成机械设备运行出现异常的首要缘故。
在机械设备运作历程中，机械零件通过高温、高压等各种原因影响，产生衰老、损坏这些。
因此在机械零件的生产过程中，就需要对机械零件自身品质严格把关，尤其是对机械零件疲劳强度要良好掌握。
文中就提升机械零件疲劳强度的措施探讨，明确提出几个提议。
1 影响机械零件疲劳强度的因素1.1 应力集中的影响一切构造，像发动机轴、盘、机匣等都必然地存有阶梯、打孔、棒槽等造成横截面基因突变的地区。
当构造承受力时，在这种地区便会发生部分内应力集中扩大的状况，称之为应力集中。
很多疲惫毁坏安全事故和实验结果显示，疲惫源一直产生在应力集中的地区，应力集中使构造的疲劳强度减少，对疲劳强度有很大的影响，并且是影响疲劳强度众多要素中起关键功能的一个要素。
例如，法国陨星号飞机场便是由于整体机身枷钉孔处的应力集中造成气密性驾驶舱开裂而坠毁；原苏联设计的米文件格式飞机场就发生过很多飞机翼承重梁根处地脚螺栓孔处的疲惫裂痕；一IS发动机预制构件的疲惫裂痕大多数发生在有应力集中的斜角或健槽处这些。
1.2 表面状态的影响试样的制取技术对疲劳强度有较大影响，这一点早就在年就由不一样的专家学者表明了，那时候就已确立，试件表层上即使发生微小的伤疤也会使钢的疲劳强度显着降低。
进一步的研究表明，各种各样钢的疲惫特性所受表层问题的影响不一样。
钢的抗压强度愈高，缺点是疲劳强度减少愈大。
1.3 尺寸的影响尺寸对疲劳强度的不良影响的表述具体有内应力集中梯度方向的影响。
第3章 机械零件的强度(用)
汽车的齿轮和轴所承受的动载荷。
注意:在设计计算中，载荷又可分为名义载荷和计 算载荷，计算载荷等于载荷系数乘以名义载荷。
名义载荷： 根据机器在稳定和理想工作条件下的工作阻力，
按力学公式求出的载荷称为名义载荷. 计算载荷：
考虑机器在工作中载荷的变化和载荷在零件上
s
m rN
N
C (NC
N
ND)
D点以后(无限寿命区间):
s rN s r （N ND )
用N0及其相对应的疲劳极限σr来近
似代表ND和 σr∞,有：
s
m rN
N
s
m r
N0
C
s－N疲劳曲线
§3-1 材料的疲劳特性 疲劳曲线
２、 s－N疲劳曲线
有限寿命区间内循环次数N与
疲劳极限srN的关系为：
CＧ'直线的方程为：
s a s m s s
σ为试件受循环弯曲 应力时的材料常数，其值 由试验及下式决定：
s
2s 1 s 0 s0
对于碳钢，σ≈0.1~0.2，对于合金钢，σ≈0.2~0.3。
§3-2 机械零件的疲劳强度计算
1、零件的极限应力线图
如设弯曲疲劳极限的综合影响系数 Ｋσ ，且 s 1 ―材料对称循环弯曲疲劳极限
s rN s r
m
N0 N
KNsr
式中， N0为循环基数；
sr为与N0相对应的疲劳极限
s－N疲劳曲线
m为材料常数，值由材料试验确定。
疲劳曲线的意义
s rN
sr m
N0 N
KNsr
机械零件的强度和设计准则
• 减轻振动的一般措施：
（1）尽量采用对称结构（如花键联接）、减少悬臂长度、缩短中心距等； （2）对转动零件进行平衡，尽量满足动、静平衡条件；（3）采用阻尼 作用消耗引起振动的能量，比如设置滑动轴承的油膜阻尼器、液压缸端部 的阻尼孔等；（4）设置隔振零件，比如加装弹簧、橡胶垫、隔振层等都 具有减振作用。
• 同一种零件发生失效的形式可能有很多种； • 最常发生的失效形式主要是由于强度、刚度、耐磨性、耐温度性、
振动稳定性、可靠性等方面的问题。
提高机械零件强度的一般措施
1．合理布置零件，减少零件所受到的最大载荷
2. 采用等强度结构 3.减小载荷和应力集中
4.选用合理截面 比如梁的截面采用工字型、T字型；轴的截面采用圆形、 空心圆形等。
复习思考题
1、何谓零件的失效？常见形式有哪些？ 2、载荷、应力各如何分类？基本变应力有哪几种？用哪些参数描述变应 力？ 3、如何判断零件受力类型？ 4、两种判断零件强度的方式是什么？ 5、安全系数如何选择？其大小会产生什么影响？ 6、提高零件强度有哪些措施？ 7、表面强度有哪几种？如何计算挤压和磨损强度？ 8、何谓刚度和柔度？刚度不足会产生什么影响？影响刚度的因素有哪些？ 9、根据冲击模型推导解释冲击载荷的危害及如何缓和冲击作用。 10、何谓振动、共振及失稳？稳定性计算的准则是什么？减轻振动的措 施有哪些？ 11、什么是可靠度？
失效概率
Rt
Nt N
N Nf N
1 N f N
Ft
Nf N
1 Rt
Rt Ft 1
可靠性计算准则：保证零件在工作过程中能够满足规定的可靠性 要求。
如果试验时间不断延长，则Nf将不断增加，可靠度逐渐 减少，这说明零件的可靠度是随时间发生改变的，是时 间的函数。
《机械设计》第3章_机械零件的强度(正式)
2.最小应力 s min s m s a
3.平均应力
sm
s max
s min
2
4.应力幅
sa
s max
s min
2
5.应力循环特性
s min s max
第三章 机械零件的强度
(a)非对称循环变应力
(b)脉动循环变应力
(c)对称循环变应力
疲劳曲线
s max
s min
2
sa
s max
s min
2
r s min
s max
1 r 1 (r 0)
smax
sm
0
t
sm
sa
s max
2
s min 0
r0
sa= smax
0
t
smin
sm 0
s a s max s min
r 1
二、应力的描述
第三章 机械零件的强度
稳定循环变应力的基本参数 共有５个基本参数，知其２就能求其他
应力循环特性 r 一定的条件下，记录出在 不同最大应力σmax下引起试件疲劳破坏所经历 的应力循环次数N，即可得到σ-N疲劳曲线 。
静应力强度（AB段）：N≤103， σmax几乎不 随N变化，可近似看作是静应力强度。
(ND,σr∞)
低周疲劳（BC段）：N↑→ σmax↓。C点对应 的循环次数约为104。
（非周期变化）
循环变应力
（周期变化）
符合统计规律
稳定循环变应力
（等幅变应力）
非稳定循环变应力
（变幅变应力）
非对称循环变应力 对称循环变应力 脉动循环变应力
s
1、非循环变应力 符合统计规律
机械设计机械零件的强度
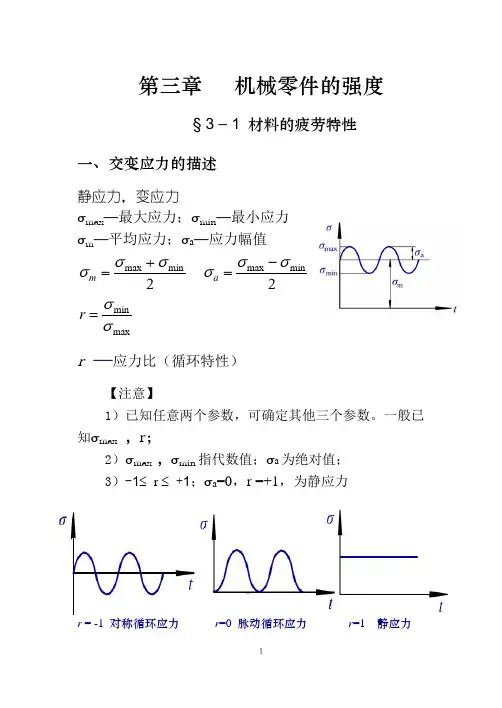
第三章 机械零件的强度§ 3 – 1 材料的疲劳特性一、交变应力的描述静应力，变应力σmax ─最大应力；σmin ─最小应力 σm ─平均应力；σa ─应力幅值2minmax σσσ+=m 2minmax σσσ-=amaxminσσ=r r─应力比（循环特性）【注意】1）已知任意两个参数，可确定其他三个参数。
一般已知σmax ，r ；2）σmax ，σmin 指代数值；σa 为绝对值； 3）-1≤ r ≤ +1；σa =0，r =+1，为静应力r = -1 对称循环应力 r =0 脉动循环应力 r =1 静应力σ－N 疲劳曲线二、 疲劳曲线（σ-N 曲线）1.材料的疲劳极限：σr N在一定应力比为г的循环变应力作用下，应力循环N 次后，材料不发生疲劳破坏时，所能承受的最大应力σmax 。
2.疲劳寿命：N材料疲劳失效前所经历的应力循环次数。
г不同或N 不同时，疲劳极限σrN 不同。
即σrN 与r 、N 有关。
疲劳强度计算中，就是以疲劳极限作为σlim 。
即σlim =σrN 。
通过试验可得，疲劳极限σrN 与循环次数N 之间关系的曲线，如上图所示。
AB段曲线：N<103，计算零件强度时按静强度计算。
（σrN≈σs）BC段曲线：103<N<104,零件的破坏为塑性破坏属于低周疲劳破坏。
特点：应力高，寿命低。
CD段曲线：σr N随N的增大而降低。
但是当N超过某一次数时（图中N D），曲线趋于水平。
即σr N不再减小。
N D与材料有关，有的相差很大，因此规定一个常数。
N0−循环基数当N>N D 时，σrN=σr∞=σr（简记）疲劳曲线以N0为界分为两个区：1）有限寿命区把曲线CD段上的疲劳极限σr称为有限疲劳极限（条件～）。
当材料受到的工作应力超过σr时，在疲劳破坏之前，只能经受有限次的应力循环。
即寿命是有限的。
【说明】不同应力比г时的疲劳曲线具有相似的形状。
但г↑，σrN↑。
机械零件的强度
σa
σa
σσ-1-1e A M’2 D
G
M
Oσm
潘存云教授研制
σm
σｓ C
通过联立直线M M’2和AG的方程可求解M’2点的坐标为
'max
1e
m 1
K
1
(K a ) m
K
'ae
1
a
K
m
计算安全系数及 疲劳强度条件为
Sca
lim
m ax max
-1 (K K ( a
K a m
计算安全系数及疲劳强度条件为
Sca
lim
m ax max
-1 K a m
≥S
N点的极限应力点N’1位于 直线CG上，
σa σσ-1-1e A
σ’ae σa
有 'max ae m e s
O
这说明工作应力为N点时，首先可能发生的是屈服失效。
故只需要进行静强度计算即可。
极限为 σ-1e
且总有 σ-1e ＜ σ-1
由于材料试件是一种特殊的结构，而实际零件的几何形状、
45˚
45˚
Ｏ σ0 /2
σS
Cσm
尺寸大小、加工质量及强化因素等与试件有区别，使得零件的
疲劳极限要小于材料试件的疲劳极限。
定义弯曲疲劳极限的综合影响系数
K
1 1e
1e 1 K
在不对称循环时，Ｋσ是试件与零件极限应力幅的比值。
σS
弯曲疲劳极限的综合影响系数Ｋσ 反映了应力集中、
尺寸因素、表面加工质量及强化等因素的综合影响结果。
其计算公式如下
K
k
1
1
1
q
其中：kσ ——有效应力集中系数；εσ ——尺寸系数； βσ ——表面质量系数； βq ——强化系数。
机械零件的强度计算
考虑弯曲应力和接触应力，确定齿轮的耐久性和承载能力。
3 螺纹的强度计算
考虑剪切应力和压紧应力，确定螺纹的稳定性和耐用性。
应力与应变的关系
应力
力对物体单位面积的作用，单 位为帕斯卡（Pa）。
应变
物体在受力下发生的形变，通 常以位移或拉伸比来表示。
弹性模量
反映物体在受力后恢复原状的 能力。
材料的物体抵抗拉伸试验中的最大拉力。 物体开始产生塑性变形的应力。
抗压强度
物体抵抗压缩试验中的最大压力。
设计中的安全系数
1
安全系数
将实际工作应力与材料抗拉强度之比，用于确保设计的安全性。
2
合理选择
根据使用环境、可靠性要求和破坏后果等因素确定合适的安全系数。
3
风险评估
评估潜在风险，确保安全系数能够保护机械零件免受破坏。
机械零件的强度计算
这个演示将介绍机械零件的强度计算。从定义和常见方法到应力应变关系、 材料强度参数以及设计中的安全系数等方面进行讨论。
强度计算的定义
强度计算是指通过确定材料能够承受的最大应力，评估机械零件在使用时能否安全工作的方法。
常见机械零件的强度计算方法
1 轴的强度计算
考虑弯曲应力和剪切应力，确定轴的最大承载能力。
弹性和塑性变形
机械零件在受力时可能发生两种类型的变形：弹性变形和塑性变形。弹性变形是可恢复的，而塑性变形是不可 恢复的。
强度计算的应用范围和局限性
应用范围
适用于设计和评估各种机械零件的强度。
局限性
无法考虑复杂的应力状态和材料的疲劳寿命。
机械设计第3章机械零件的强度
6
(一) σ—N疲劳曲线
图3—1中曲线CD段代表有限寿命疲劳阶段。在此
范围内，试件经过一定次数的交变应力作用后总会发
生疲劳破坏。曲线CD段上任何一点所代表的疲劳极限，
称为有限寿命疲劳极限，用符号σrN表示。脚标r代表该 变应力的应力比，N代表相应的应力循环次数。曲线 CD段可用式(3—1)来描述：
§3—2 机械零件的疲劳强度计算
由于零件尺寸及几何形状变化、加工质量及强
化因素等的影响，使得零件的疲劳极限要小于
材料试件的疲劳极限。如以弯曲疲劳极限的综
合影响系数Kσ表示材料对称循环弯曲疲劳极限 σ-1与零件对称循环弯曲疲劳极限σ-1e 的比值， 即
Kσ=σ-1 /σ-1 e 当已知Kσ及σ-1时，则
5
在循环次数约为103以前，相应于图3—1中的曲线AB 段，使材料试件发生破坏的最大应力值基本不变，或 者说下降得很小，因此我们可以把在应力循环次数 N≤103时的变应力强度看作是静应力强度的状况。
曲线的BC段，随着循环次数的增加，使材料发生疲 劳破坏的最大应力将不断下降。仔细检查试件在这一 阶段的破坏断口状况，总能见到材料已发生塑性变形 的特征。C点相应的循环次数大约在104左右(也有文 献中认为约在105，现在工程实践中多以104为准)。 这一阶段的疲劳破坏，因为这时已伴随着材料的塑性 变形，所以用应变—循环次数来说明材料的行为更为 符合实际。因此，人们把这一阶段的疲劳现象称为应 变疲劳,亦称低周疲劳。
零件材料(试件)的极限应力曲线即为 折线A＇G＇C。材料中发生的应力如 处于OA＇G＇C区域以内，则表示不 发生破坏；如在此区域以外，则表 示一定要发生破坏；如正好处于折 线上，则表示工作应力状况正好达 到极限状态。
机械设计-第三章 机械零件的强度(疲劳)
AB（103前）：最大应力值变化很小，相当于静强度状况； BC（103-104）：N增加，σmax减小，有塑性变形特征—应变疲
劳，低周疲劳，不讨论； CD（>104）：有限寿命疲劳阶段 ,任意点的疲劳极限--有限寿
命疲劳极限σrN ，该曲线近似双曲线。
公式描述：
c,m—材料常数 D点后：材料不发生疲劳破坏，无限寿命疲劳阶段,
件的疲劳极限，用综合影响系数Kσ 表示。 如：对称循环弯曲疲劳极限的综合影响系数Kσ。 则：
σ －1试件的对称循环弯曲疲劳极限； σ －1e零件的对称循环弯曲疲劳极限。
不对称时：Kσ 是试件与零件的极限应力幅的比值。
零件的极限应力线图—ADGC 试件线图A’ D’ G’C—综合修正系数Kσ—零件线图ADGC
机械设计
第三章：机械零件的强度（疲劳强度）
主讲老师：吴克勤
第三章 机械零件的强度（疲劳）
一、材料的疲劳特性 1、 σ － N曲线 ①疲劳断裂：变应力下的零件损坏形式，与循环次数有关。 ②特征： σmax< σlim； 脆性材料和塑性材料都突然断裂； 损伤的积累。 ③疲劳极限：循环特征r一定时，应力循环N次后，材料不 发生破坏的最大应力σrN ； ④疲劳曲线：r一定的条件下，表示N与σrN 关系的曲线。
零件的极限应力曲线：
φσe－零件受循环弯曲应力时的材料常数； σ’ae －零件受循环弯曲应力时的极限应力幅； σ’me－零件受循环弯曲应力时的极限平均应力。
Kσ 为弯曲疲劳极限的综合影响系数
kσ－零件的有效应力集中系数（σ 表示在正应力条 件下）；
εσ － 零件的尺寸系数； βσ －零件的表面质量系数； βq －零件的强化系数。 上面所有的计算公式，同样适用于剪切应力。
机械设计之机械零件的疲劳强度
机械设计之机械零件的疲劳强度引言在机械设计中，疲劳强度是评估机械零件是否能够在长时间使用过程中承受载荷和弯曲等作用力的重要指标之一。
疲劳强度不仅关乎机械零件的寿命和可靠性，还直接影响到机械装置的安全性能。
本文将介绍机械零件的疲劳强度分析方法，包括疲劳寿命预测、疲劳极限分析、疲劳强度评估等内容。
疲劳寿命预测疲劳寿命是机械零件在特定载荷下能够承受的循环次数。
疲劳寿命预测的目的是为了确定机械零件在特定工作条件下的可靠性。
常用的疲劳寿命预测方法有下面几种：1. 基于SN曲线的方法SN曲线（Stress Number Curve）揭示了应力与循环次数之间的关系。
通过测试材料在不同应力水平下的循环寿命，并绘制SN曲线图，可以预测不同应力水平下的寿命。
这种方法适用于不同材料在常温下的疲劳寿命预测。
2. 基于应力途径的方法应力途径是指机械零件在循环载荷下的相对应力历程和持续时间。
通过测量机械零件在不同应力途径下的寿命，并绘制应力途径图，可以预测不同应力途径下的寿命。
这种方法适用于复杂加载情况下的疲劳寿命预测。
3. 基于损伤积分的方法损伤积分是指在单位时间内损伤累积的指标。
通过测量机械零件在不同加载条件下的损伤积分，并与材料的损伤裕度相比较，可以预测机械零件的寿命。
这种方法适用于快速变化的加载情况下的疲劳寿命预测。
疲劳极限分析疲劳极限是指机械零件在循环载荷下的最大承载能力。
疲劳极限分析的目的是为了确定机械零件能够承受的最大载荷和疲劳寿命。
常用的疲劳极限分析方法有如下几种：1. 基于拉伸试验的方法拉伸试验是测量材料在拉伸载荷下的应变和应力变化的试验。
通过拉伸试验和应力-应变曲线，可以确定材料的疲劳极限。
这种方法适用于静态或低周疲劳加载条件下的疲劳极限分析。
冲击试验是测量材料在动态或高速加载条件下的力学性能的试验。
通过冲击试验和载荷-位移曲线，可以确定材料的疲劳极限。
这种方法适用于动态或高速加载条件下的疲劳极限分析。
浅谈机械零件的疲劳强度
网络教育学院本科生毕业论文（设计）题目：浅谈机械零件的疲劳强度学习中心：层次：专科起点本科专业：机械设计制造及其自动化年级：年季学号：学生：指导教师：完成日期：年月日内容摘要本文以机械零件的疲劳强度计算方法为切入点，首先阐述零件在工作中变应力的分类和变应力的参数，然后推导出变应力计算公式，进而讨论影响疲劳强度的因素以及提高疲劳强度的解决措施，最后介绍了疲劳强度在各领域中的应用。
关键词：疲劳强度；变应力；复合应力；可靠性目录内容摘要 (I)引言 (1)1 变应力的分类 (2)2 变应力参数 (3)3 疲劳曲线 (4)4 影响疲劳强度的因素 (5)4.1应力集中的影响 (5)4.2尺寸与形状的影响 (9)4.3表面质量的影响 (9)4.4表面强化的影响 (9)4.4其他因素的影响 (10)5 提高疲劳强度的解决措施 (11)5.1提高构件表面质量 (11)5.2提高构件表面强度 (11)5.3豪克能技术 (11)6 疲劳强度在各领域的应用以及前景展望 (12)6.1 疲劳强度在机械零件中的应用 (12)6.2 疲劳强度在航空航天领域的应用 (12)6.3前景展望 (13)结论 (15)参考文献 (16)引言通用机械零件的强度分为静应力和变应力强度范畴。
根据设计经验及材料的特性，通常认为在机械零件整个工作寿命期间应力变化次数小于103的通用零件，均可按静应力强度进行设计。
本论文以下主要讨论零件在变应力下的疲劳、影响疲劳强度因素、疲劳强度计算等问题。
1954 年，世界上第一款商业客机de Havilland Comet 接连发生了两起坠毁事故，这使得“金属疲劳”一词出现在新闻头条中，引起公众持久的关注。
这种飞机也是第一批使用增压舱的飞行器，采用的是方形窗口。
增压效应和循环飞行载荷的联合作用导致窗角出现裂纹，随着时间的推移，这些裂纹逐渐变宽，最后导致机舱解体。
Comet 空难夺去了68 人的生命，这场悲剧无时无刻不在提醒着工程师创建安全、坚固的设计。
机械零件的强度
1
相关概念： 1、失效 零件丧失工作能力或达不到要求的性能时，称为失效。
2、机械零件常见的失效形式：
（1）断裂 （2）过量变形（弹性或塑性）
（3）表面失效（过度磨损、打滑等）
2
相关概念： 3、工作能力：零件不发生失效时的安全工作限度。 4、强度是反映机械零件承受载荷时不发生失效的重要指标。
③、液体摩擦 摩擦表面被液体润滑膜完全隔离开的摩擦。
如轮船在水中行走，水把船底和河床隔离开；气垫、磁垫
使机车和导轨隔离开。在机械传动中，两零件表面之间处于液
体摩动的接触表面，大多数处于以上三种摩擦状态的混
合，称之为混合摩擦。 混合摩擦比前二种状态好，但比液体摩擦状态差些。
3、摩擦的分类： （ 1）
（2）根据摩擦副的运动状态分：
3、摩擦的分类：
（2）根据摩擦副的运动状态分：
（3）按表面润滑状态分：
①、干摩擦 没有润滑剂的摩擦面称为干摩擦。 如人在地面行走，脚后跟与地间形成的干摩擦。
（3）按表面润滑状态分：
②、边界摩擦 摩擦表面有一层极薄的润滑剂。 如人在湿润的地面行走；人在有粉尘的瓷砖上行走；洗脸盆边沾上一层很薄的油污后， 手与脸盆边之间的摩擦状态等都可看成边界摩擦，边界摩擦的摩擦因数比干摩擦略有改善。
一、载荷和应力
1、载荷 （1）静载荷 （2）变载荷
4
一、载荷和应力 2、应力
（1）应力：零件在载荷的作用下产生内力，单位截面上的内力称为应力。
应力的单位：Pa 1 Pa = 1 N/m2 （2）静应力和变应力 MPa 1MPa = 106 Pa = 1N/mm2
5
二、机械零件的强度 1、零件工作应力是静应力时，强度的主要表现为断裂或塑性变形。
机械设计第三章机械零件的强度
学习要求：
1． 了解疲劳曲线及极限应力曲线的来源，意义及用途， 能从材料的几个基本机械性能及零件的几何特性，绘 制零件的极限应力简化线图
2． 学会单向变应力时的强度计算方法 3． 了解疲劳损伤累积假说的意义及其应用
4． 学会双向变应力时的强度校核方法
学习重点：
极限应力线图的绘制及含义
强度准则是设计机械零件的最基本准则。
通用机械零件的强度分为静应力强度和变应力 强度两个范畴。
在机械零件整个工作寿命期间应力变化次数小 于103的通用零件，均按静应力强度进行设计。
即使是承受变应力的零件，在按疲劳强度进行 设计的同时，还有不少情况需要根据受载过程 中作用次数很少而数值很大的峰值载荷作静应 力强度校核。本章以下只讨论零件在变应力下的疲劳、低应力下 的脆断和接触强度等问题。
根据零件载荷的变化规律以及零件与相邻零件互相约 束情况的不同，可能发生的典型的应力变化规律通常 有下述三种：
a)变应力的应力比保持不变，即r=C(例如绝大 多数转轴中的应力状态)；
b)变应力的平均应力保持不变，即σm=C(例如 振动着的受载弹簧中的应力状态)；
c)变应力的最小应力保持不变， σmin=C(例如 紧螺栓联接中螺栓受轴向变载荷时的应力状 态)。以下分别讨论这三种情况。
e 可用下式计算
e
K
1 K
2 1 0 0
(3 11)
Kσ——弯曲疲劳极限的综合影响系数
K
k
1
1
1
q
(3 12)
式中：kσ——零件的有效应力集中系数 εσ——零件的尺寸系数； βσ——零件的表面质量系数； βq——零件的强化系数。
(一)单向稳定变应力时机械零件的疲劳强度计算
机械工程中的强度与刚度分析
机械工程中的强度与刚度分析机械工程是一门研究和应用机械原理、材料力学与结构力学等知识的学科，强度与刚度是机械设计中非常重要的两个参数。
强度与刚度的分析对于确保机械设备的安全运行和性能稳定起着至关重要的作用。
一、强度分析强度是材料抵抗外力破坏的能力。
在机械设计中，我们需要根据特定的工作条件和所使用的材料性能来计算和分析零部件的强度。
常见的强度计算方法有应力-应变分析、最大主应力理论、能量法等。
应力-应变分析是一种常用的强度分析方法。
材料在外力作用下产生应变，而应变又引起材料内部的应力分布。
通过确定材料的弹性模量和材料的极限强度，在受力状态下计算出材料的最大应力情况，从而判断零部件是否能够承受工作条件下的力量。
这种方法适用于弹性变形的情况，能够较准确地预测零部件的强度。
最大主应力理论是一种简化而实用的强度计算方法。
该理论认为，在受力情况下，材料的破坏主要发生在最大主应力达到材料的屈服强度时。
通过找出受力情况下的最大主应力，与材料的屈服强度进行比较，就可以得出零部件是否能够耐受外力的结论。
这种方法适用于一般工程实践中对零部件强度的初步评估，是一种快速而简单的分析方法。
能量法是一种综合考虑材料内部应力和应变分布的计算方法。
它基于能量守恒定律，通过计算材料受力时的应变能和应力能，确定零部件的强度。
能量法适用于非弹性变形情况下的强度分析，可考虑材料的塑性变形特性，对于工程实际中较为复杂的受力情况有着较准确的分析能力。
强度分析在机械工程中具有重要的意义。
只有保证零部件的强度满足要求，才能确保机械设备在工作条件下的稳定运行。
同时，强度分析也有助于减轻零部件的重量，提高整体性能，节约材料和成本。
二、刚度分析刚度是材料抵抗变形的能力。
在机械设计中，刚度分析是确定零部件在受力情况下变形程度的一种方法。
通过计算零部件的刚度，可以合理设计机械结构，确保其在工作条件下的稳定性和准确性。
刚度分析主要包括弹性刚度与局部和整体刚度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 机械零件的强度§ 3 – 1 材料的疲劳特性一、交变应力的描述静应力，变应力max ─最大应力； min ─最小应力 m ─平均应力； a ─应力幅值2minmax σσσ+=m 2minmax σσσ-=amaxminσσ=r r ─应力比（循环特性）【注意】1）已知任意两个参数，可确定其他三个参数。
一般已知 max，r；2） max， min指代数值； a为绝对值；3）-1≤r ≤ +1； a=0，r =+1，为静应力r = -1 对称循环应力r=0 脉动循环应力r=1静应力二、疲劳曲线（σ-N曲线）1.材料的疲劳极限：σr N在一定应力比为г的循环变应力作用下，应力循环N 次后，材料不发生疲劳破坏时，所能承受的最大应力σmax。
2.疲劳寿命：N材料疲劳失效前所经历的应力循环次数。
σ－N疲劳曲线г不同或N不同时，疲劳极限σrN不同。
即σrN与r、N 有关。
疲劳强度计算中，就是以疲劳极限作为σlim。
即σlim=σrN。
通过实验可得，疲劳极限σrN与循环次数N之间关系的曲线，如上图所示。
AB段曲线：N<103，计算零件强度时按静强度计算。
（σrN≈σs）BC段曲线：103<N<104,零件的破坏为塑性破坏属于低周疲劳破坏。
特点：应力高，寿命低。
CD段曲线：σr N随N的增大而降低。
但是当N超过某一次数时（图中N D），曲线趋于水平。
即σr N不再减小。
N D 与材料有关，有的相差很大，因此规定一个常数。
N 0−循环基数当N >N D 时，σrN =σr ∞=σr （简记）疲劳曲线以N 0为界分为两个区： 1）有限寿命区把曲线CD 段上的疲劳极限σr 称为有限疲劳极限（条件～）。
当材料受到的工作应力超过σr 时，在疲劳破坏之前，只能经受有限次的应力循环。
即寿命是有限的。
【说明】不同应力比г时的疲劳曲线具有相似的形状。
但г↑，σrN ↑。
2）无限寿命区当N >N 0时，曲线为水平直线，对应的疲劳极限是一个定值，——称为持久疲劳极限，用0rN σ表示 （简写为σr ）。
在工程设计中，一般认为：当材料受到的应力不超过σr 时，则可以经受无限次的循环应力而不疲劳破坏——即寿命是无限的。
------------------------------------------------------------------- 设计中经常用到的是σ-N 曲线的高周疲劳段（CD 段）。
CD 段曲线方程为：C N m rN =σ （N c N ND ）称为疲劳曲线方程显然D （N 0，σr ），也符合上述方程，即：C N mr =0σ代入上式得：C N N m r m rN ==0σσN r mrrN K NN σσσ==0（3-3） 式中:K N ——寿命系数m ——材料常数 【说明】1.计算K N 时，如N >N 0，则取N =N 0 此时K N =12. 对钢件：受拉、压、弯、扭时：m =6~20；N 0=（1~10）⨯106。
初步计算，受弯曲疲劳时，中等尺寸零件取m =9，N 0=5⨯106；大尺寸零件取m =9，N 0=107。
3．无限寿命设计：零件的寿命N≥N0，（强度指标为σr ）有限寿命设计：零件的寿命N<N0，（强度指标为σr N）有限寿命设计的意义：在于当零件的设计寿命低于N0时，可以适当提高疲劳极限应力。
亦即零件承受的工作应力可以更大些，以充分发挥材料的能力。
工程中经常用到的是对称循环（г=-1）下的疲劳极限σ-1或σ-1N，计算时，只需把式中σr，σrN，换成σ-1和σ-1N即可。
4．对于受切应力τ的情况，把σ换成τ即可。
5．大多数钢的疲劳曲线形状类似上图所示。
但是，高强度合金钢和有色金属的（σ-N）曲线没有水平部分，不存在无限寿命区，因此，工程上常规定一个循环基数N0，而将此基数N0下的条件疲劳极限作为材料疲劳强度的基本指标。
也记为σr。
请想想：σ-N曲线有什么用途？（−求任意r下的σrN）三、等寿命疲劳曲线（极限应力线图）σm−σa极限应力线图以上所讨论的σ－N曲线是材料承受单向稳定对称循环变应力的失效规律。
当零件材料承受非对称循环变应力时，必须考虑r 对疲劳破坏的影响。
这时用等寿命疲劳曲线。
σrN 与材料、r 、N 有关。
固定材料与N ，求σrN ～r 之间的极限应力曲线。
mamaam a m r σσσσσσσσσσ+-=+-==11maxmin σrN = σm + σaσa －σm 的关系即能表达σrN ～r 之间的关系。
疲劳寿命N 一定时，表示疲劳极限与应力比г之间关系的线图，称为极限应力线图。
下图为疲劳寿命为N 0时（无限寿命时的）的σm −σa 极限应力图。
它是极限应力图的表示形式之一，在疲劳设计中应用最广。
除此之外还有其他表示形式。
这里只介绍这种σm −σa 图。
（也是由实验得到的）曲线上的不同点，表示了不同应力比г下的疲劳极限σr （亦即σmax）。
横纵坐标之和σr=σrm+σra曲线上的四个特殊点：A'——对称循环疲劳极限D '——脉动循环疲劳极限 B ——抗拉强度极限σB C ——材料的屈服极限σS为了便于计算，工程设计中常对上图进行简化。
A 'G '线——疲劳强度线。
其上的各点表示了一定r 下的疲劳极限。
CG '线称为——屈服强度线。
其上的各点表示屈服极限。
σmax =σ'm +σ'a =σS横轴上的任一点都代表了应力幅等于零的应力−静应力 ♦如果材料承受的工作应力点落在折线A 'G 'C 以内，则不发生破坏。
且距离折线越远越安全。
♦如果落在折线以外，则一定发生破坏。
♦如果正好处于折线上，表示工作应力状况正好处于极限应力状态。
--------------------------------------------- 直线A 'G '的方程：由已知两点的坐标A '（0，σ-1）、D '（2σ，2σ）可推出，0022m1a010-'-'=----σσσσσσ 10a 0m 10222---'='⎪⎭⎫⎝⎛-σσσσσσσ m01a10222σσσσσσσ'⎪⎭⎫⎝⎛-+'=-- ()m 01a0102σσσσσσσ'-+'=-- m1a12σσσσσσ'-+'=-- σ-1 =σ'a +ϕσσ'm （3–4）式中： 012σσσϕσ-=- （3–6）碳钢：ϕσ≈0.10 ～ 0.2；合金钢：ϕσ≈0.2～0.3 直线CG '的方程为： σ'a +σ'm =σS （3–5）ϕσ——试件受循环弯曲应力时的材料常数。
（用于将平均应力等效地折算成应力幅的折算系数）σ'a ——试件受循环弯曲应力时的极限应力幅 σ'm ——试件受循环弯曲应力时的极限平均应力【强调】σm -σa 图的用途：根据σ-1，确定非对称循环应力下的疲劳极限σrN ，以计算安全系数。
§ 3 – 2 疲劳曲线和极限应力图由于零件的应力集中、绝对尺寸、表面质量及强化等影响，零件的疲劳极限小于规范试件的疲劳极限。
K σ−弯曲疲劳极限的综合影响系数 σ-1−材料的对称循环弯曲疲劳极限 σ-1e −零件的对称循环弯曲疲劳极限1e1K --=σσσ （3–7） σσσK e 11--=（3–8）（在非对称循环时，K σ是试件的与零件的极限应力幅的比值）由于K σ只影响应力幅，所以只有A '、D '两点的纵坐标计入K σ，得到零件的对称循环疲劳极限点A 和脉动循环疲劳极限点D 。
对CG 线，由于是按静强度考虑的，而静强度不受K σ的影响，所以CG 线不必修正。
因此，折线AGC 即为零件的极限应力图。
【方法】把材料的极限应力线图中的直线A 'D 'G '按比例向下移动→直线ADG直线AG 的方程： A (0，σσK 1-)，D (20σ，σσK 20) 直线AD 间的任一点的坐标 （meσ'，ae σ'） 0022me 1ae1-'-'=----σσσσσσσσσK K K →σσσσσσσσσσK K K 10ae 0me 10222---'='⎪⎪⎭⎫⎝⎛-me aeK K K σσσσσσσσσσ'⎪⎪⎭⎫⎝⎛-+'=--22201010 me ae K K K σσσσσσσσσσ'⎪⎪⎭⎫ ⎝⎛-+'=--22201010 me aeK K σσσσσσσσ'⎪⎪⎭⎫ ⎝⎛-+'=--001121 me e ae11e K σϕσσσσσ'+'==--（3–9） 或 me ae1K σϕσσσσ'+'=-（3–9a ） 直线CG 的方程：σ'ae +σ'me =σS （3–10） σ'ae ——零件受循环弯曲应力时的极限应力幅 σ'me ——零件受循环弯曲应力时的极限平均应力 ϕ'σe ——零件受循环弯曲应力时的材料常数1211σσσϕϕσσσσ-⋅=⋅=-K K e （3–11） qK K ββεσσσσ1)11(-+= （3–12）K σ−零件的有效应力集中系数 εσ−零件的尺寸系数 βσ−零件的表面质量系数 βq −零件的强化系数【注解】对于切向应力，将σ改为τ即可。
一、单向稳定变应力时机械零件的疲劳强度计算计算零件的疲劳强度时，应首先求出零件危险截面上的σmax ,σmin →σm ,σa ，即得到工作应力点M （σm ,σa ）。
然后将其标在零件的极限应力图上。
强度条件是S ca =m axlimσσ>S σlim 为零件的极限应力线AGC 上的点。
即：σlim =σ'max σmax 为零件的最大工作应力。
计算强度时，σlim 用AGC 线上的哪一点呢？这要根据零件载荷的变化规律决定。
典型的应力变化规律通常有三种：1. r =C （绝大多数转轴的应力状态）C rrm a =+-=+-=11min max min max σσσσσσ（常数）连接OM ，并延长，交AG 于M '1。
射线OM '1上任何一点的应力比都相同。
M '1点的应力值就是我们要的极限应力∵M '1 (σ'me ,σ'ae ) 在极限应力曲线AG 上， ∴σ'max =σ'ae +σ'me OM 方程：meae m a σσσσ''=⋯⋯（1） AG 方程：me ae1K σϕσσσσ'+'=-⋯⋯（2） 由（1）得 mmea aeσσσσ'='⋯⋯ （3） 将（3） 代入（2）得memmm me a K σσσϕσσϕσσσσσσσσσ'+='+'=-me 1K ma mK σϕσσσσσσ+='-1me ⋯⋯（4）将（4）代入（3）得ma aK σϕσσσσσσ+='-1ae⋯⋯（5）将（4）与（5）相加 σ'max =σ'ae +σ'me =ma a m a a m K K σϕσσσσϕσσσσσσσ+=++--max11)(强度条件： S ca =ma K σϕσσσσσσσσ+='=-1max max max lim ≥S （3–17）N 点的极限应力点N '在CG 上，此时的极限应力为σs ，属于屈服失效。