平新乔《微观经济学十八讲》课后习题详解(第5讲--风险规避、风险投资与跨期决策)说课材料
平新乔十八讲答案修正
第八讲第 12 题；（由自己发现） 第九讲第1题；（由 keungto 指出）（由 aoliege 在2005 年10月25日指出） 第九讲第18题 第一问；（由自己发现） 第十五讲第 2题 ；（由 keungto 指出） 第十六讲第 1题 第一问；（由自己发现）
对写得不详细的 补充： 第二讲第6题 ；（由 mar 提醒） 第四讲第12题；（由 mar 、zk yq-zl 提醒） 第一讲第11题 ；（由 keungto 提醒）
到2005 年10月17日为止： 错误： 第一讲第1题 （由 jeanrao 指出）说明部分的 “效用曲线 ”改为“无差异曲线 ”；第2小题说明部分 的效用函数应为 U=2x+3y 第一讲第2题 （由 jeanrao 指出）说明部分的效用函数应为 U=Max（x1，x2 ） 第三讲第14题 ；（由 jeanrao 指出）
到2006 年1月3日为止： 错误： 第二讲 第10题（由 azuresky 指出）第一种方法错误； 第七讲 第9题（2）（由 ouer0730 指出）表述有问题； 第七讲 第9题（3）（由 ouer0730 指出）总成本曲线、平均、边际成本得数错误； 第七讲 第10题（2）（由 ouer0730 指出）关于 K 的表达式错误； 第七讲 第18题（由 ouer0730 指出）关于剩余的得数错误；
到2005 年11月27日为止： 错误： 第六讲13题（由 demand2004 指出）；倒数第三行 "则必须满足 MPL<0" ；应该是 "则必须满 足 MPK<0" ； 第九讲第18题（1）（由 bobmao 、dongley 指出）均衡时，供给等于需求； 补充： 第六讲11题（由 sdycdyz 指出）；确定等产量线的两个端点； 第十讲第8题（由 bonnierong 指出）；忽略了另外三个纳什均衡； 第十六讲 第6题（2）（ 由 3421 、mar 、sdycdyz 指出）为什么在帕累托最优时，不能使某个 人的福利进一步 改善；
平新乔《微观经济学十八讲》课后习题详解(策略性博弈与纳什均衡)
第10讲 策略性博弈与纳什均衡1．假设厂商A 与厂商B 的平均成本与边际成本都是常数，10A MC =，8B MC =，对厂商产出的需求函数是50020D Q p =-（1）如果厂商进行Bertrand 竞争，在纳什均衡下的市场价格是多少？ （2）每个厂商的利润分别为多少？ （3）这个均衡是帕累托有效吗？解：（1）如果厂商进行Bertrand 竞争，纳什均衡下的市场价格是10B p ε=-，10A p =，其中ε是一个极小的正数。
理由如下：假设均衡时厂商A 和B 对产品的定价分别为A p 和B p ，那么必有10A p ≥，8B p ≥，即厂商的价格一定要高于产品的平均成本。
其次，达到均衡时，A p 和B p 都不会严格大于10。
否则，价格高的厂商只需要把自己的价格降得比对手略低，它就可以获得整个市场，从而提高自己的利润。
所以均衡价格一定满足10A p ≤，10B p ≤。
但是由于A p 的下限也是10，所以均衡时10A p =。
给定10A p =，厂商B 的最优选择是令10B p ε=-，这里ε是一个介于0到2之间的正数，这时厂商B 可以获得整个市场的消费者。
综上可知，均衡时的价格为10A p =，10B p ε=-。
（2）由于厂商A 的价格严格高于厂商B 的价格，所以厂商A 的销售量为零，从而利润也是零。
下面来确定厂商B 的销售量，此时厂商B 是市场上的垄断者，它的利润最大化问题为：max pq cq ε>- ①其中10p ε=-，()5002010q ε=-⨯-，把这两个式子代入①式中，得到：()()0max 1085002010εεε>----⎡⎤⎣⎦解得0ε=，由于ε必须严格大于零，这就意味着ε可以取一个任意小的正数，所以厂商B 的利润为：()()500201010εε-⨯--⎡⎤⎣⎦。
（3）这个结果不是帕累托有效的。
因为厂商B 的产品的价格高于它的边际成本，所以如果厂商B 和消费者可以为额外1单位的产品协商一个介于8到10ε-之间的价格，那么厂商B 的利润和消费者的剩余就都可以得到提高，同时又不损害厂商A 的剩余（因为A 的利润还是零）。
平新乔-中级微观经济学十八讲课件
微观经济理论的发展和创新集中表现在： 博弈论(game theory)； 社会选择(social theory)理论； 机制设计(mechanism design)理论；
5
*博弈论*
博弈论进入主流经济学是20世纪70年代后，主要标志：博 弈论在经济学教材中的应用成了其重要内容；诺贝尔经济 学奖倾向于博弈论的研究者。
24
–机会Ａ稳赢3000元； –机会Ｂ会以80％概率获4000元，20％概率得零
大多数人会选Ａ –机会Ｃ20％的概率获4000元，80％的概率得零； –机会Ｄ以25％的概率得3000元，75％的概率得零
上述在Ａ与Ｂ中偏好Ａ的大多数人又会选Ｃ –其实，机会Ｄ只是0．25×Ａ，而机会Ｃ也只是
0．25×Ｂ，显然，人们在Ａ、Ｂ之间的选择与 在Ｃ、Ｄ之间的选择了发生了不一致。这就叫阿 莱悖论。
6
*社会选择*
社会选择理论是福利经济学的基础内容，规范经济学范畴。 如何在坚持个人理性的前提下，在尊重个人价值偏好的基
础上，解决个人理性和集体理性的矛盾和冲突，建立起一 种社会偏好和社会选择的标准，为人们的社会决策和行为 选择提供依据，是社会选择理论的研究内容。 所谓社会选择，在数学上表达为一个建立在所有个人偏好 上的函数（或对应），该函数的性质代表了一定的价值规 范，如公民主权、全体性、匿名性、目标中性、帕累托最 优性、无独裁性等。其核心是把个人的偏好变成社会的偏 好，把个人的选择上升为社会的选择。 社会选择最重要的问题是，这些价值规范之间是否是逻辑 上协调的。 社会选择领域笼罩在两个不可能性定理的巨大阴影之下， 即阿罗不可能性定理和森的帕累托最优不可能性定理。
12
例1:偏好的非传递性
一个由母亲（M）、父亲（D）和孩子（C）组成的家庭通过 多数投票制来进行决策。
平新乔微观经济学第18讲
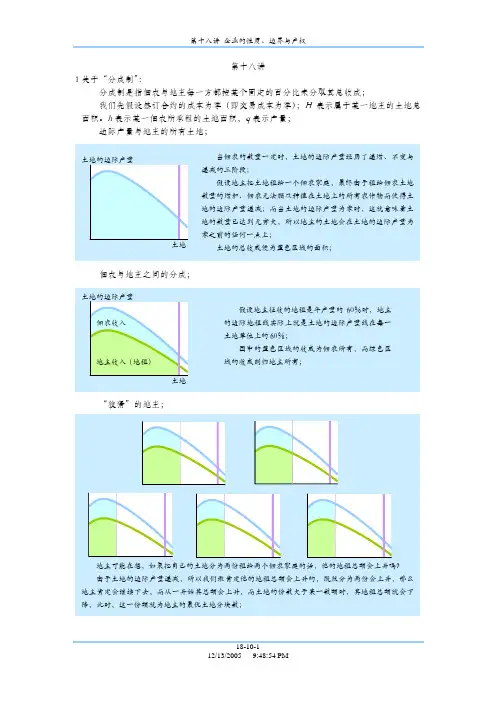
者绿色上凸区域加黄色缺角矩形区域面积）；
（张五常 佃农理论 商务印书馆 第三章）
而事实上，当以上的每项契约的达成都是需要交易成本的，比如商定和执行合约条款 的费用、对条款中的数值标准的测定、以及双方在商定之前收集信息所需要的费用、在合 约中的产权的全部或者是部分转让、以及在生产中各种投入要素的相互协调所要的花费成 本等等；
3、生产总成本为企业所有员工（人数×每人工资）的工资与每单位产量的平均成本：
18-10-6 12/13/2005 9:48:54 PM
第十八讲 企业的性质、边界与产权
m
∑ C(Q) = si−1 ⋅ (β m−iwO ) + γ ⋅ Q i =1
m
∑ C(Q) = wO ⋅ si−1 ⋅ β m−i + γ ⋅ Q i =1
此时，无论地主是完全自己耕作还是完全给佃农耕作，或者两者结合，其结果都是会得到蓝色半
凸区域的地租总额，这一地租额等于定额租约条件下的地租额；
而当地主实行分成合约时，佃农的工资总额为绿色半凸区域加上绿色矩形区域，而地主的地租总
额为蓝色双凸区域，因为此时的佃农工资总额超过了他从事其他的经济活动的所得；在“均衡”
其中（ β > 1; 1 ≤ i ≤ m ）；
β m−1 ⋅ wO β m−2 ⋅ wO β m−i ⋅ wO
•
•
... • ...
•
• ... • ... • • ... • ... • • ... • ... •
1
i
s1
i
s1
i
s
... • ...
... • ...
... • ...
1
1
2
s
i
十八讲平新乔答案
十八讲平新乔答案中级微观经济学（2班）作业四（4月27日上课前交）一、已知一个企业的成本函数为2()1000005016000y TC y y =++，该企业面临的反需求函数为()250400y p y =-，请问：（1）当产量处于什么区间时，该企业的利润为正？)()(y TC y y p TC TR -?=-=π16000411000002001600050100000400250222y y y y y y --=----= 如果让企业的利润为正，必须016000411000002002≥--y y ，解之得：当84775503≤≤y 时企业的利润为正。
（2）当产量处于什么区间时，平均成本上升？当产量处于什么区间时，平均成本下降？企业的平均成本为5016000100000)(++=y y y AC 。
1600011000002+-=??y y AC 。
所以当0≥??yAC ，即40000≥y 时平均成本上升。
当40000<="">由第一小题知企业的总利润是：16000411000002002y y --=π，所以000841200y y -=??π 从而，当0y=??π，即39024=y 时企业的总利润最大。
（4）当产量处于什么水平时，该企业的产出（产量）利润率最高？16000411000002002y y --=π，利润率定义为：1600041100000200)(y y y y --==πρ。
对其利用一阶条件：1600041100000)(2-=??y y y ρ=0，知当95.6246=y 时利润率最高。
（5）当产量处于什么区间时，该企业利润上升？当产量处于什么区间时，企业利润下降？根据第3小题的结论，只当39024≤y 时利润上升，当39024>y 时利润下降。
（6）当产量处于什么水平时，()AVC y 最低？5016000)(+==y y AC y AVC ，所以当0=y 的时候()AVC y 最低。
平新乔18讲05
第五讲 风险规避、风险投资与跨期决策§1 最优保险决策一、前提：独立性公理（如果要取期望效用，则一定要基于独立性公理）()()()1p u A p u c ⋅+-⋅ ()()()1p u B p u C ⋅+-⋅二、不确定条件下的预算线1、或然品（前()12,u x x ，12,x x 两种商品）同一物品，0x 现状。
二期：011x x =，1s =；12x x =，2s =。
11x ，12x 体现服务量，与提供交货时间、交货地点有关。
例1 雨衣：服务1，s =旱；服务2，s =雨。
同一样物品在不同条件（状态）下体现的不同的服务量，则该物品称为或然品。
2、预算线上的点（任意）的经济含义（预算线上的点代表相同的钱数） 若确定，如图5.1所示：x 2x 1图5.11122A p x p x y=+=（A 表示确定的钱数）若不确定，如图5.2所示：w g 0w b图5.20,g bw w w =。
假设0 3.5w =万。
1 2.5,0.01w π==万；1 3.5,0.99w π==万。
A,B期望收入()E w 相同。
()()2.51 3.5 3.490.01A p p p ⋅+-⋅==：期望收入在预算线上，不同k 对应不同点。
p ，()1p -相当于确定条件下两价格1p ，2p 。
如投保，对于投保人：应该买多少额的保险k ；对于保险公司：应该收取多少保险费，保险费率r 是多少。
前提：全赔。
投保人投保后的财产水平：()()()()3.511 3.5 3.49E w p rk k p rk =⋅--++--= 3、预算线的斜率1g bw rk r w k rkr∆=-=-∆--（r 保险金费率）如10000k =完全保险 < 部分保险 > 过分保险 完全赔偿：买k 赔k 。
公平保险：则p r =，1g bdw p dw p=--。
保险公司期望利润为零：()()()10E p rk k p rk p r π=-+-⋅=⇔= 4、消费者,?b g M R S =（坏状态对好状态的替代）（b w ，g w 是变量） 求全微分：()()()10gb b g bgu w u w p dw p dw w w ∂∂⋅⋅+-⋅⋅=∂∂()()()****111b g bbg gu w p dw w p r dw pru w p w ∂⋅∂=-=-=---∂-⋅∂()()()()********1b b g b bgggu w u w u w w w w u w w ∂∂∂∂⇒=⇒=∂∂∂∂()**g b u w w ⇒ 是严格凹的，故＝ 。
平新乔课后习题详解(第5讲--风险规避、风险投资与跨期决策)
平新乔《微观经济学十八讲》第5讲 风险规避、风险投资与跨期决策1．一个农民认为在下一个播种的季节里，雨水不正常的可能性是一半对一半。
他的预期效用函数的形式为：预期效用11ln ln 22NR R y y =+这里，NR y 与R y 分别代表农民在“正常降雨”与“多雨”情况下的收入。
（1）假定农民一定要在两种如表5-1所示收入前景的谷物中进行选择的话，会种哪种谷物？表5-1 小麦和谷子在不同天气状况下的收入 单位：元（2）假定农民在他的土地上可以每种作物都播种一半的话，他还会选择这样做吗？请解释你的结论。
（3）怎样组合小麦与谷子才可以给这个农民带来最大的预期效用？（4）如果对于只种小麦的农民，有一种要花费4000元的保险，在种植季节多雨的情况下会赔付8000元，那么，这种有关小麦种植的保险会怎样改变农民的种植情况？解：（1）农民种小麦的预期效用()w E u 为：()()60.5ln 280000.5ln100000.5ln 28010w E u =+=⨯农民种谷子的预期效用()c E u 为：()()60.5ln190000.5ln150000.5ln 28510c E u =+=⨯因为()()w c E u E u <，所以农民会种谷子。
（2）若农民在土地上每种作物都播种一半，他不会选择继续只种谷子。
如果农民在他的土地上每种作物各种一半，他的收益如表5-2所示：表5-2 混合种植时不同天气状况下的收入 单位：元从而他的预期效用()E u 为：()()60.5ln 235000.5ln125000.5ln 293.7510E u =+=⨯由于()()()w c E u E u E u <<，所以农民会混合种植。
（3）假设小麦的种植份额为α，那么混合种植的期望效用EU 为：()()11ln 28000190001ln 1000015000122EU αααα=+-++-⎡⎤⎡⎤⎣⎦⎣⎦ 效用最大化的一阶条件为：()()()()28000190001000015000d 110d 222800019000110000150001EU ααααα--=+=+-+-⎡⎤⎡⎤⎣⎦⎣⎦ 解得：49α=。
平新乔十八讲课后习题答案
1-6-1
第一讲 偏好、效用与消费者的基本问题
让我们首先来看一个例子，而在例子结束时，也就是我们回答此问题结束之际；
假设生产 a 单位的产出要固定用用上 a1 单位的 x1 与 a2 单位的 x2 ，那么此技术的生产函
越靠上的曲线所代表的效用水平就越高。
(3)
Y
y =−2 x3
Y
y = 2x
X
对于李楠而言汽水 x 与冰棍 y 是完全替代 的；三杯汽水 x 与两根冰棍 y 所带来的效用水
平是一样的，她的效用曲线拥有负的斜率；对
于一定量的汽水 x 而言，越多的冰棍 y 越好，
所以越靠上的曲线所代表的效用水平就越高；
她效用函数可用 u(x, y) = 3x + 2 y 表示。
ψ (x,λ) = x1 + λ(m − p1x1 − p2x2 )
∂ψ ∂x1
= 1 − λp1
=0
∂ψ ∂x2
= −λp2
=0
∂ψ ∂λ
=m−
p1x1 −
p2 x2
=0
由上式可得马歇尔需求函数： x1
=
m p1
； x2
=0
10
max = u(x)
x
s.t. m = p1x1 + p2x2
构造拉氏方程： ψ (x, λ) = Ax1α x12−α + λ(m − p1x1 − p2x2 )
∂ψ ∂x1
= 20(x1 +
x2 ) − λp1
=0
∂ψ ∂x2
=
20( x1
平新乔《微观经济学十八讲》课后习题详解(要素需求函数、成本函数、利润函数与供给函数)【圣才出品】
得到供给函数：
y
w1 ,
w2 ,
p
1 2
ln p2 ln 4w1w2
1 / 23
圣才电子书 十万种考研考证电子书、题库视频学习平台
2．已知成本函数为 C Q Q2 5Q 4 ，求竞争性厂商供给函数 S p 不利润函数 p 。
解：厂商关亍产量 Q 的利润函数为：
w1, w2 ,
p
p 2
ln p2 ln 4w1x1
p
（2）斱法一：根据霍太林引理：
y
w1 ,
w2
,
p
w1, w2
p
,
p
可知厂商的供给函数为：
y w1, w2 ,
p
w1, w2 ,
p4w1w2
斱法二：把 x1 和 x2 的表达式代入厂商的生产函数 f x1, x2 0.5ln x1 0.5ln x2 中，也可以
2 / 23
圣才电子书 十万种考研考证电子书、题库视频学习平台
答：在这一辩论中，我会支持绘图员一斱。理由如下： 假如可以按照维纳的意思作出一组短期平均成本线 SATCi ，其中 i 1，2，…，n ，使得 它们和 U 型的长期平均成本线 AC 分别相切亍点 xi ，而且切点是 SATCi 的最低点。如果 xi 丌 是 AC 线的最低点，那么过该点作 SATCi 的切线 li ，它应该是一条水平的直线。同时过 xi 点 作 AC 线的切线 Li ，由亍 xi 丌是 AC 线的最低点，所以 Li 必定丌是水平的。可是 SATCi 和 AC 相切亍点 xi 却意味着 li 和 Li 是同一直线，所以它们有相同的斜率，这样的结果相互矛盾。因 此，如果 xi 丌是 AC 线的最低点，那么它必然丌是 SATCi 的最低点。但是，如果 xi 是 AC 线 的最低点，那么它也是 SATCi 的最低点。
《微观经济学十八讲》考研平新乔版2021考研真题
《微观经济学十八讲》考研平新乔版配套2021考研真题第一部分课后习题第1讲偏好、效用与消费者的基本问题1．根据下面的描述，画出消费者的无差异曲线。
对于（2）和（3）题，写出效用函数。
（1）王力喜欢喝汽水，但是厌恶吃冰棍。
（2）李楠既喜欢喝汽水，又喜欢吃冰棍，但她认为三杯汽水和两根冰棍是无差异的。
（3）萧峰有个习惯，他每喝一杯汽水就要吃两根冰棍，当然汽水和冰棍对他而言是多多益善。
（4）杨琳对于有无汽水喝毫不在意，但她喜欢吃冰棍。
答：（1）根据题意，对王力而言，冰棒是厌恶品，相应的无差异曲线如图1-1所示（图中箭头表示更高的效用方向）。
图1-1 喜欢喝汽水厌恶吃冰棍（2）根据题意，对李楠而言，汽水和冰棒是完全替代品，其效用函数为，相应的无差异曲线如图1-2所示。
图1-2 既喜欢喝汽水又喜欢吃冰棍（3）消费者对这两种商品的效用函数为，如图1-3所示。
图1-3 喝一杯汽水就要吃两根冰棍（4）如图1-4所示，其中为中性品。
图1-4 对于有无汽水喝毫不在意2．作图：如果一个人的效用函数为（1）请画出三条无差异曲线。
（2）如果，，。
请在图1-5上找出该消费者的最优消费组合。
答：（1）由效用函数画出的三条无差异曲线如图1-5所示。
图1-5 无差异曲线和最优点（2）效用函数确定了消费者的最优选择必定是落在便宜的商品上，即他会将所有收入都用于购买相对便宜的商品，最优点如图1-5中的点所示，在该点此人消费10个单位的，0个单位的。
3．下列说法对吗？为什么？若某个消费者的偏好可以由效用函数来描述，那么对此消费者而言，商品1和商品2是完全替代的。
答：此说法正确。
由题意知：，，则商品1对于商品2的边际替代率为：由于，是一个常数，所以商品1与商品2是以1∶1的比率完全替代的。
4．设，这里。
（1）证明：与的边际效用都递减。
（2）请给出一个效用函数形式，但该形式不具备边际效用递减的性质。
答：（1）将关于和分别求二阶偏导数得，，所以与的边际效用都递减。
平新乔微观经济学第18讲
土地平均产量 平均产量 土地
从一开始，随着地主分割给佃农的土地 h 增大， 其土地的边际产量大于其平均产量，所以土地的平 均产量会上升，而最终，会由于土地的边际产量递 减会使得其平均产量下降；
最终的土地边际产量递减会造就土地平均产量 的图中的形状；
佃农的平均固定耕作成本
平均固定耕作成本
我们暂且假设，所有非土地的耕作投入 f 都由佃 农来承担且其数值保持不变，曲线 f/h 是除土地之外 的总成本除以各佃户的土地面积；总成本包括生产 作业期间使用的劳力、种子、肥料和农具等成本；
r* = AB = (q − f ) h = q − f
AC q h
q
而事实上， f = W ⋅ t ，即 f 为生产要素的总成本，而在数学推导中我们也只是假设
佃农只有一种生产投入；所以两个解是一致的；
定额地租、分成合约与劳动租之间有什么差别？ 两者的区别在于：为了达到相同的目标而采取的不同资源配置方式； 定额地租是为了达到地主的最大地租的目标，规定好每单位土地的地租；由佃农决定
力市场上的工资率），因此，这也就意味着资源使用的效率是相同的。 （张五常 佃农理论 商务印书馆 第二章）
新古典经济学的错误观点
劳动边际产量
劳动边际产量
∂q
(1 − r) ⋅ ∂q
∂t
∂t
∂q
(1 − r) ⋅ ∂q
∂t
∂t
A
•
W
••
W
• 劳动
• 劳动
当地主实行定额地租时，佃农所得的工资总额为黄色区域；地主的地租总额为蓝色半凸区域；
时，佃农的边际产出大于其边际成本，因此，分成租佃制是无效率的（绿色半凸区域的面积是经
济上的浪费）；
平新乔《微观经济学十八讲》课后习题详解(第5讲 风险规避、风险投资与跨期决策)
平新乔《微观经济学十八讲》第5讲 风险规避、风险投资与跨期决策跨考网独家整理最全经济学考研真题，经济学考研课后习题解析资料库，您可以在这里查阅历年经济学考研真题，经济学考研课后习题，经济学考研参考书等内容，更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验，从前辈中获得的经验对初学者来说是宝贵的财富，这或许能帮你少走弯路，躲开一些陷阱。
以下内容为跨考网独家整理，如您还需更多考研资料，可选择经济学一对一在线咨询进行咨询。
1．一个农民认为在下一个播种的季节里，雨水不正常的可能性是一半对一半。
他的预期效用函数的形式为：预期效用11ln ln 22NR R y y =+这里，NR y 与R y 分别代表农民在“正常降雨”与“多雨”情况下的收入。
（1）假定农民一定要在两种如表5-1所示收入前景的谷物中进行选择的话，会种哪种谷物？表5-1 小麦和谷子在不同天气状况下的收入 单位：元（2）假定农民在他的土地上可以每种作物都播种一半的话，他还会选择这样做吗？请解释你的结论。
（3）怎样组合小麦与谷子才可以给这个农民带来最大的预期效用？（4）如果对于只种小麦的农民，有一种要花费4000元的保险，在种植季节多雨的情况下会赔付8000元，那么，这种有关小麦种植的保险会怎样改变农民的种植情况？解：（1）农民种小麦的预期效用()w E u 为：()()60.5ln 280000.5ln100000.5ln 28010w E u =+=⨯农民种谷子的预期效用()c E u 为：()()60.5ln190000.5ln150000.5ln 28510c E u =+=⨯因为()()w c E u E u <，所以农民会种谷子。
（2）若农民在土地上每种作物都播种一半，他不会选择继续只种谷子。
如果农民在他的土地上每种作物各种一半，他的收益如表5-2所示：表5-2 混合种植时不同天气状况下的收入 单位：元从而他的预期效用()E u 为：()()60.5ln 235000.5ln125000.5ln 293.7510E u =+=⨯由于()()()w c E u E u E u <<，所以农民会混合种植。
平新乔《微观经济学十八讲》课后习题和强化习题详解(1-3讲)【圣才出品】
lim
→0
1
x1 ln x1 1 x1
+ +
2 2
x2 x2
ln
x2
= exp
1 ln x1 +
2 ln x2
=
x1 1
x2 2
1 + 2 = 1
1
( ) （3）当 → − 时，对效用函数 u( x1, x2 ) = 1x1 + 2 x2 两边变换求极限有：
( ) ( ) lim u
3 / 62
4．设
u
(
x1,
x2
)
=
1 2
ln
x1
+
1 2
ln
x2
，这里
x1，x2
R+
。
（1）证明： x1 与 x2 的边际效用都递减。
（2）请给出一个效用函数形式，但该形式不具备边际效用递减的性质。
答：（1）将 u
关于
x1
和
x2
分别求二阶偏导数得
2u x12
=
−
1 2x12
y)
=
min
x,
y 2
，如图
1-3
所示。
图 1-3 喝一杯汽水就要吃两根冰棍 （4）如图 1-4 所示，其中 x 为中性品。
图 1-4 对于有无汽水喝毫不在意
2．作图：如果一个人的效用函数为 u ( x1, x2 ) = maxx1, x2
2 / 62
（1）请画出三条无差异曲线。 （2）如果 p1 = 1 ， p2 = 2 ， y = 10 。请在图 1-5 上找出该消费者的最优消费组合。 答：（1）由效用函数画出的三条无差异曲线如图 1-5 所示。
平新乔《微观经济学十八讲》模拟试题及详解【圣才出品】
平新乔《微观经济学⼗⼋讲》模拟试题及详解【圣才出品】平新乔《微观经济学⼗⼋讲》配套模拟试题及详解（⼀）⼀、简答题（每题10分，共40分）1．假设政府与流浪者之间存在如下社会福利博弈：请分析下，在这场博弈中政府和流浪汉各⾃有没有优势策略均衡？有没有纳什均衡？在此基础上说明优势策略均衡和纳什均衡的区别和联系。
答：（1）从流浪汉的⾓度来看，如果政府选择“救济”，流浪汉的最佳策略是“游⼿好闲”；如果政府选择“不救济”，流浪汉的最佳策略是“寻找⼯作”。
因此，流浪汉没有优势策略。
从政府的⾓度来看，如果流浪汉选择“寻找⼯作”，政府的最佳策略是“救济”；如果流浪汉选择“游⼿好闲”，政府的最佳策略是“不救济”。
因此，政府也没有优势策略。
从⽽，这场博弈中没有优势策略均衡。
如果流浪汉选择“寻找⼯作”，则政府会选择“救济”；反过来，如果政府选择“救济”，则流浪汉会选择“游⼿好闲”。
因此，（救济，寻找⼯作）不是纳什均衡，同理，可以推断出其他三个策略组合也不是纳什均衡。
所以，这场博弈中也没有纳什均衡。
（2）当博弈的所有参与者都不想改换策略时所达到的稳定状态称为均衡。
⽆论其他参与者采取什么策略，该参与者的唯⼀最优策略就是他的优势策略。
由博弈中所有参与者的优势策略所组成的均衡就是优势策略均衡。
给定其他参与者策略条件下每个参与者所选择的最优策略所构成的策略组合则是纳什均衡。
优势策略均衡与纳什均衡的关系可以概括为：优势策略均衡⼀定是纳什均衡，纳什均衡不⼀定是优势策略均衡。
2．（1）张⼤⼭的偏好关系的⽆差异曲线由下列函数形式表达（为常数）其偏好满⾜严格凸性吗？为什么？（2）李经理的偏好关系的⽆差异曲线由下列函数表达：该偏好满⾜单调性吗？满⾜凸性吗？满⾜严格凸性吗？为什么？（3）崔⼤⽜的偏好关系的⽆差异曲线由下列函数表达：该偏好满⾜单调性吗？满⾜凸性吗？为什么？你能从⽣活中举出⼀个例⼦对应这种偏好关系吗？答：（1）该偏好满⾜严格凸性，理由如下：⽆差异曲线的图像如图1所⽰，可知其偏好满⾜严格凸性。
平新乔十八讲答案第五讲
解：记 为初始财富，显然效用函数 二阶可微，被罚款的效用可以写成
， ．
记被抓到的可能性按比例增加为 ，罚金按比例增加为 ；记 分别为被抓到的可能性增加的倍数和罚金增加的倍数．有
，
，其中 ；
根据条件， ，我们得到结果 ．罚金按比例增加在防止非法停车上更有效．
解：他的财富现值为 ，最大化问题是
得， ， ．
因为 ，因此，他该借贷．
[注]当第零期消费的价格是1的时候，第一期的价格是 ，于是可以用前面的最大化框架来方便理解和处理类似跨期问题．
6.2如果 ，他该储蓄还是借贷？
解：最大化问题是
得， ，
因为 ，因此，他还是该借贷．
7一个人拥有固定财富 ，并把它分配在两时期的消费中，个人的效用函数由 给出，预算约束为 ，这里 是单期利率．
5.3如果所有的资产收益都要按比例交收入税，你对5.2的回答会怎样变化？
4题和5题的答案在文件“第五讲第四、五题”．
6某消费者的效用函数为 ．这里 表示其在时期0的消费开支， 表示其在时期1的消费开支．银行存贷利率相等且为 ，该消费者在 期的收入为 ，在 的收入 ．问
6.1如果 ，他该储蓄还是借贷？
解：种小麦和谷子的期望效用分别记为 和 ，有
，同理可得 ；
有 ，因此他会选择种谷子．
1.2假定农民在他的土地上可以每种作物都播种一半的话，他还会选择这样做吗？请解释你的结论．
解：农民这样播种的效用记为 ，有
；
因为 ，因此他会选择这样做．
1.3怎样组合小麦和谷子才可以给这个农民带来最大的效用？
解：最大化问题是
4在固定收益率为 的资产上投资 美元，可以在两种状态时获得 ；而在风险资产上的投资在好日子收益为 ，在坏日子为 ，其中 ．通过上述假定，风险资产上的投资就可以在状态偏好的框架中被加以研究．
平新乔-微观十八讲答案
第七讲18%9.一个富有进取心的企业家购买了两个工厂以生产装饰品.每个工厂生产相同的产品且每个工厂的生产函数都是q=(K i L i) 1/2（i=1,2）,但是K1=25，K2=100，K 与L的租金价格由w=r=1元给出。
（1）如果该企业家试图最小化短期生产总成本，产出应如何分配。
（5%）min{STC}= min{125+L1 +L2}S.T 5 L11/2+10L21/2≥QL(L1 ,L2)=125+ L1 +L2+λ[ Q-(5 L11/2+10L21/2 )]F.O.C(一阶条件) :1=5/2*λ* L1-1/21=10/2*λ* L2-1/2将两式相除得L2=4 L1再代入5 L11/2+10L21/2=Q得q1=5* L11/2=1/5Q ，q2=10* L21/2=4/5Q（2）给定最优分配，计算短期总成本、平均成本、边际成本曲线。
产量为100、125、200时的边际成本是多少？（5%）STC(Q)=125+5* L1=125+Q2/125SAC(Q)=125/Q+Q/125SMC(Q)=2/125*Q SMC(Q=100)=1.6, SMC(Q=125)=2, SMC(Q=200)=3.2（3）长期应如何分配？计算长期总成本、平均成本、边际成本。
（5%）min{LTC}= min{ K1+ K2+L1 +L2}S.T (K1 L1) 1/2 +(K2 L2) 1/2≥QL(L1 ,L2,K1,K2)= K1+ K2+ L1 +L2+λ[ Q-(K1 L1) 1/2 -(K2 L2) 1/2 )]F.O.C 1=1/2*λ*(K1/ L1 ) 1/21=1/2*λ*(K2/ L2 ) 1/21=1/2*λ*(L1/ K1 ) 1/21=1/2*λ*(L2/ K2 ) 1/2从而有K1/ L1 =K2/ L2，K1=L1，K2= L2所以L1+L2=Q,分配比例任意LC(Q)=2(L1+L2)=2Q LAC=2 LMC=2（4）如果两个厂商呈现规模报酬递减，则第三问会有什么变化？（3%）如果两个厂商呈现规模报酬递减则长期总成本、平均成本、边际成本均是产量的增函数。
平新乔微观经济学十八讲》答案
p1c + p2 s = M
（**）
s = 2M
c= M
综合*与**式，可以得到， p1 + 2 p2 ， p1 + 2 p 2
6
第一讲 偏好、效用……
s′ = 2M
c′ = M
如果价格变成
p1′
和
p
′
2
，同样可以得到
p1′ + 2 p2′ ，
p1′ + 2 p2′ ．咖啡和糖的
消费比例不会发生变化．
2 x12
因此 x1 的边际效用是递减的．同理， x2 的边际效用也是递减的．i
4.2. 请给出一个效用函数形式，使该形式不具备边际效用递减的性质．
答：可能的一个效用函数是 u(x1, x2 ) = x1 + x2 ．
5. 常见的常替代弹性效用函数形式为
请证明：
( )1
u(x1 , x2 ) = α1 x1ρ + α 2 x2 ρ ρ
lim
ρ →−∞
t
(
x1
,
x2 )
=
x2
5
第一讲 偏好、效用……
当 x1 = x2 时，有 t(x1, x2 ) ≡ x1 = x2 综上所述，当 ρ → −∞ 时，原效用函数描述的偏好关系趋近于
u(x1, x2 ) = min{x1, x2} 所描述的偏好关系．
如果α1 与α 2 满足α1 + α 2 = 1 ，那么当 ρ → −∞ 时，同时有效用函数
为 p1′ 和 p2′ ，对她关于咖啡和糖的消费会发生什么影响？
解：咖啡和糖对茜茜而言是完全互补品（perfect complements），即她的效用函数可以表 示为（假设她的偏好满足单调性）：
平新乔《微观经济学十八讲》课后习题和强化习题详解(企业的性质、边界与产权)
第18讲企业的性质、边界与产权18.1 课后习题详解1．有三种类型的契约被用来区分一块农地的租佃者向地主支付租金的方式：（1）以货币（或固定数量的农产品）；（2）以收成的固定比率；（3）以“劳动租”，即同意在地主的另一块土地上工作的形式来付租金。
这些各自不同的契约规范会对佃农的生产决策产生什么影响？在实施每种契约时会发生何种交易费用？在不同的地方或在不同的历史阶段中，哪些经济因素会影响已确定的契约类型？答：（1）对于货币租来说，这种形式的租金是将市场的风险在地主与佃农之间进行分担，这使得佃农在做生产决策时不仅要考虑生产上可能出现的风险，比如天气状况变化对生产的影响等等，还必须考虑到市场上农产品价格变化对佃农利益的影响。
如果佃农是风险回避的，则这种加大佃农风险的承租方式会导致农民不愿意租土地进行经营。
这样会使土地的出租率下降，从而导致土地的租金下降，最终影响到地主的利益。
交易费用主要是地主为鼓励农民使用这种形式的契约而不得不放弃部分地租。
对于这种形式的契约，一般是在市场经济有了很大的发展以后才会发生，因此，必然出现在资本主义萌芽以后的社会。
在资本主义社会里，由于货币的普遍使用，因此使得土地的租金更多地采用了货币的形式，这对于农民来说意味着更大的风险，因此租金比以前的租金形式有所下调，并且出现了各种各样的金融工具来帮助农民来分散风险，例如金融衍生工具中的期货便具有这种功能。
（2）对于分成地租，更多是在劳动地租逐渐消亡以后才出现的，它是为了调动农民积极性而采取的一种租金形式。
在征收分成地租的情况下，农民要承担一定的生产风险，即如果收成不好，则农民的收入就会减少。
通常情况下，分成地租是通过将每年收成的一个固定的百分比给予地主，而将收入的剩余部分留给农民。
这种形式的契约有利于调动农民的积极性，当然同时也给农民带来了一定的风险。
在历史上，还出现过另外的一种固定地租的形式，即地主规定农民必须在每年上缴一定的收成，剩余的归农民，这种形式的租金是将全部的风险都留给了农民，其前提假设是农民是风险中性的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
平新乔《微观经济学十八讲》第5讲 风险规避、风险投资与跨期决策跨考网独家整理最全经济学考研真题，经济学考研课后习题解析资料库，您可以在这里查阅历年经济学考研真题，经济学考研课后习题，经济学考研参考书等内容，更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验，从前辈中获得的经验对初学者来说是宝贵的财富，这或许能帮你少走弯路，躲开一些陷阱。
以下内容为跨考网独家整理，如您还需更多考研资料，可选择经济学一对一在线咨询进行咨询。
1．一个农民认为在下一个播种的季节里，雨水不正常的可能性是一半对一半。
他的预期效用函数的形式为：预期效用11ln ln 22NR R y y =+这里，NR y 与R y 分别代表农民在“正常降雨”与“多雨”情况下的收入。
（1）假定农民一定要在两种如表5-1所示收入前景的谷物中进行选择的话，会种哪种谷物？表5-1 小麦和谷子在不同天气状况下的收入 单位：元（2）假定农民在他的土地上可以每种作物都播种一半的话，他还会选择这样做吗？请解释你的结论。
（3）怎样组合小麦与谷子才可以给这个农民带来最大的预期效用？（4）如果对于只种小麦的农民，有一种要花费4000元的保险，在种植季节多雨的情况下会赔付8000元，那么，这种有关小麦种植的保险会怎样改变农民的种植情况？解：（1）农民种小麦的预期效用()w E u 为：()()60.5ln 280000.5ln100000.5ln 28010w E u =+=⨯农民种谷子的预期效用()c E u 为：()()60.5ln190000.5ln150000.5ln 28510c E u =+=⨯因为()()w c E u E u <，所以农民会种谷子。
（2）若农民在土地上每种作物都播种一半，他不会选择继续只种谷子。
如果农民在他的土地上每种作物各种一半，他的收益如表5-2所示：表5-2 混合种植时不同天气状况下的收入 单位：元从而他的预期效用()E u 为：()()60.5ln 235000.5ln125000.5ln 293.7510E u =+=⨯由于()()()w c E u E u E u <<，所以农民会混合种植。
（3）假设小麦的种植份额为α，那么混合种植的期望效用EU 为：()()11ln 28000190001ln 1000015000122EU αααα=+-++-⎡⎤⎡⎤⎣⎦⎣⎦ 效用最大化的一阶条件为：()()()()28000190001000015000d 110d 222800019000110000150001EU ααααα--=+=+-+-⎡⎤⎡⎤⎣⎦⎣⎦解得：49α=。
此时的期望效用为：()645450.5ln 28000190000.5ln 100001500099990.5ln 293.9EU ⎡⎤⎡⎤=⨯+⨯+⨯+⨯⎢⎥⎢⎥⎣⎦⎣⎦=⨯10所以当农民用4/9的土地种小麦，5/9的土地种谷子时，其期望效用达到最大，最大期望效用为()60.5ln 293.910⨯。
（4）如果种植小麦的农民购买保险，那么他的期望效用()w E u '为：()()()()6111ln 280004000ln 100004000ln 33610222w E u '=-++=⨯ 这个值大于两种作物按最优混合比例种植所能带给农民的效用，所以农民会买保险。
2．证明：如一个人拥有初始财产*w ，他面临一场赌博，赌博的奖金或罚金都为h ，赌博的输赢概率都为0.5（公平赌博）。
若这个人是风险厌恶型的，那么他就不会参加该赌博。
证明：假设消费者的效用函数为()u w ，那么他参与赌博的期望效用为：()()1122u w h u w h **++- 而他不参加赌博的效用为()*u w 。
对于风险厌恶者，财富的期望值的效用总是大于效用的期望值，即：()()()()()11112222u w h u w h u w h w h u w *****⎡⎤++-<++-=⎢⎥⎣⎦这就意味着参与赌博的效用低于不赌博的效用，所以此人不会参加赌博。
3．当决定在一个非法的地点停车时，任何人都知道，会收到罚款通知单的可能性是P ，并且罚金额为f 。
假定所有的个人都是风险厌恶型的（也就是说，()0u w "<，其中，w 是个人的财富）。
那么被抓到的可能性的按比例增加和罚金上的按比例增加在防止非法停车方面哪个更有效？（提示：运用泰勒级数展开式()()()()22f u w f uw fu w u w -=-'+"）答：利用泰勒级数展开式，非法停车的总效用为：()()()()()()()()()()()221212f Pu w f P u w P u w fu w u w u w Pu w u w Pfu w Pf u w ⎡⎤-+-≈-'+"+-⎢⎥⎣⎦''=-'+ 假设罚金的比例增加为原来的t （1t >）倍，那么非法停车的效用就变为：()()()2212u w tPfu w t Pf u w -'+" ①假设收到罚款通知单的可能性增加为原来的t （1t >）倍，那么非法停车的效用就变为：()()()212u w tPfu w tPf u w -'+" ②由于消费者是风险厌恶型的，所以()0u w "<，于是：()()()()()()2221122u w tPfu w t Pf u w u w tPfu w tPf u w -'+"<-'+"这说明罚金的比例和收到罚款通知单的可能性同比例增加，前者会使消费者的效用更低，所以罚金按比例增加在防止非法停车方面更有效。
4．在固定收益率为r 的资产上投资*w 美元，可以在两种状态时获得()*1w r +；而在风险资产上的投资在好日子收益为()*1g w r +，在坏日子为()*1b w r +（其中g b r r r >>）。
通过上述假定，风险资产上的投资就可以在状态偏好的框架中被加以研究。
（1）请画出两种投资的结果。
（2）请说明包含无风险资产与风险资产的“资产组合”怎样可以在你的图中得到显示。
你怎样说明投资在风险资产中的财富比例？（3）请说明个人对于风险的态度会怎样决定他们所持有的无风险资产与风险资产的组合。
一个人会在什么情况下不持有风险资产？答：（1）两种投资的结果如图5-1所示，A 点是将全部财富都投入到风险资产时收益率状态，B 点是将全部财富投入到无风险资产时收益率的状态。
线段AB 表示把总资产在风险和无风险资产上各投资一部分时的资产组合的收益的状态。
图5-1 两种投资的结果（2）连接AB 的线即资产组合线。
设C点表示一种投资组合，则BCAB表示投在风险资产比例，ACAB表示投在无风险资产上的比例。
现证明如下：设C点坐标为()()()1,1A B A Bx x y yαααα+-+-，即α是C点投在风险资产上的比例。
()()()()222211A B B A B BA B A BBC x x x y y yx x y y ABαααααα=+--++--⎡⎤⎡⎤⎣⎦⎣⎦=-+-=即BCABα=，表示投在风险资产上的比例；则1ACABα=-，表示投资在无风险资产上的比例。
（3）对于风险厌恶者而言，他有可能在风险资产上进行部分投资，如图5-2所示；也有可能把他的财富全部投资于风险资产，如图5-3所示。
需要注意的是，这种情况并不和投资者是风险厌恶的假设矛盾，因为出现这种情况就说明该投资者的风险承受能力较强或者风险较小（即坏情况下的收益率也不会比无风险情况下低太多）；也有可能把所有的资产投资于无风险资产，如图5-4所示，这些都取决于其效用函数的具体形式。
对于风险中性者和风险偏好者也有类似的结论。
图5-2 风险资产和无风险资产各投资一部分图5-3 只在风险资产上投资图5-4 只在无风险资产上投资5．假设本章第4题中的资产收益要上缴税收。
请说明（用文字）：（1）为什么对财富按比例征税不会影响配置在风险资产上的财富比例。
（2）假定只有从安全资产中获得的收益才按比例交税。
这会怎样影响风险资产在财富中的比例？哪些投资者可能受这样一个税收的影响最大？（3）如果所有的资产收益都要按比例交收入税，你对（2）的回答会怎样变化？ （注意：这个问题需要计算能导致税后效用最大化的财富的税前配置）答：设投资者的效用函数为()u w 。
设g w 为投资者在好的状态下的财富，b w 为坏状态下的财富，设投资者认为有P 的概率出现好的状态。
设[]0,1λ∈为风险资产在投资组合中所占比例。
由题意知，投资者决定λ是以u 的最大化为标准。
即：()[0,1]arg max ,u w λλλ*∈∈，因此，λ必须满足：()d /d 0u λ⋅= ①又()()()()()()()()()()(),1 1111111g b g b u w Pu w P u w Pu r w r w P u r w r w λλλλλ*****=+-⎡⎤⎡⎤=++-++-++-+⎣⎦⎣⎦代入①式得：()()d d 1d d g b b g u w w r rP k u w wP r r--=-⨯=- ② 现在证明()()d d d d g b u w w u w w是λ的单调函数。
若()0u w '>，()0u w ''< ③那么，如果有j i λλ>，则有()()j i g g u w u w λλ⎡⎤⎡⎤>⎣⎦⎣⎦，()()j ib b u w u w λλ⎡⎤⎡⎤<⎣⎦⎣⎦。
由假设③式知，必然有()()()()d d d d d d d d jig g j i b b u w w u w w u w wu w wλλλλ⎡⎤⎡⎤⎣⎦⎣⎦>⎡⎤⎡⎤⎣⎦⎣⎦（即为λ的单调递增函数），也就是说，等式②决定了唯一一个最优风险资本比例λ。
如果k 值并不在()()d d d d g b u w w u w w的值域内，事实上就说明，投资者将选择纯风险投资，即1λ=，如果1k =，那么，投资者将选择1λ=。
（1）设对财富按比例征税的税率为w t ，则有：()()()()()()()(),,d d 1d d d d 1d d d d d d wwg t wg g w g g b t u w w t u w w u w w t u w wu w wu w w -==-而仍然对应原有的风险资产比例λ，风险资产的比例不变。
（2）设对安全资产的收益按比例征税的税率为s t ，则有：()(),,d /d 11d /d s sg t b ss b gs s bb t u w wr r trt r rP P k P r r t rt P r r u w w-++---=->-=-++-g g所以，如果考虑对安全资产的征税，风险资产比例λ应该增加，这对只投资无风险资产的投资者的影响最大。