最新人教A版必修2高中数学 2.1 空间点、直线、平面之间的位置关系(2)第1课时配套导学案(精品)
高中数学新课标人教A版必修2:空间点、直线、平面之间的位置关系 课件

2.(必修 2 第 45 页例 2 改编)已知空间四边形的两条对角线相互垂
直,顺次连接四边中点的四边形一定是
()
A.梯形
B.矩形
C.菱形
D.正方形
解析:如图所示,易证四边形 EFGH 为平行四
边形,因为 E,F 分别为 AB,BC 的中点,所以
EF∥AC,又 FG∥BD,所以∠EFG 或其补角为
AC 与 BD 所成的角,而 AC 与 BD 所成的角为
[提醒] 直线 l 和平面 α 相交、直线 l 和平面 α 平行统称为直线 l 在平面 α 外,记作 l⊄α.
[逐点清]
5.(易错题)若 a∥α,b∥β,α∥β,则 a,b 的位置关系是( )
A.平行
B.异面
C.相交
D.平行或异面或相交
解析:如图①②③所示,a,b 的关系分别是平行、异面、相交.
答案:D
B1C 与 EF 所成角的大小为
A.30°
B.45°
()
பைடு நூலகம்C.60°
D.90°
解析:连接 B1D1,D1C(图略),则 B1D1∥EF,故∠D1B1C 为所 求的角.又 B1D1=B1C=D1C, ∴∠D1B1C=60°. 答案:C
4.如图,在正方体 ABCD -A1B1C1D1 中,M,N
分别为棱 C1D1,C1C 的中点,有以下四个结论:
EF 相交的是
()
A.直线 AA1 C.直线 A1D1
B.直线 A1B1 D.直线 B1C1
解析:只有 B1C1 与 EF 在同一平面内,是相交的,选项 A,B, C 中直线与 EF 都是异面直线,故选 D.
答案:D
2.若直线上有两个点在平面外,则
()
人教A版高中数学必修二课件:2.1空间点、直线、平面之间的位置关系2-1-1

课后课时精练
A版 ·数学 ·必修2
解 (1)点 A 在平面 α 内,点 B 不在平面 α 内,如图①. (2)直线 l 在平面 α 内,直线 m 与平面 α 相交于点 A, 且点 A 不在直线 l 上,如图②. (3)直线 l 经过平面 α 外一点 P 和平面 α 内一点 Q,如 图③.
24
课前自主预习
17
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
A版 ·数学 ·必修2
【跟踪训练 1】 下列四种说法正确的是___②_____. ①平面的形状是平行四边形; ②任何一个平面图形都可以表示平面; ③平面 ABCD 的面积为 100 cm2; ④空间图形中,后作的辅助线都是虚线. 解析 ①错,通常用平行四边形表示平面,但平面的形 状不一定是平行四边形;③错,平面不能度量;④错,看不 到的线画成虚线.
27
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
A版 ·数学 ·必修2
[条件探究] 在本例中,若直线 a∥b∥c,直线 l∩a=A, l∩b=B,l∩c=C,又该如何证明直线 a,b,c,l 共面?
28
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
A版 ·数学 ·必修2
证明 如图所示. ∵a∥b,∴a,b 可确定一个平面 α. 又 l∩a=A,l∩b=B,∴A∈a,B∈b,A∈α,B∈α. ∴AB⊂α.又 A∈l,B∈l,∴l⊂α. 又 b∥c,∴b,c 可确定一个平面 β. 同理 l⊂β. ∵平面 α,β 均经过直线 b,l,且 b 和 l 是两条相交直 线,∴l 与 b 确定的平面是唯一的. ∴a,b,c,l 四线共面.
11
新人教A版必修2高中数学第二章点、直线、平面之间的位置关系单元总结

学习本章应着眼于以下几个方面:(1)从图形入手,学会识 图、画图,并注意图形语言、符号语言及文字语言之间的转 化;(2)整体把握空间点、线、面之间的位置关系,在具体的学 习中,对定理的学习要做到细致入微,从条件到结论,必须做 到准确的表达,论证要严谨,有理有据,计算要有依据,尽量 的追求简便;
(3)把握处理立体几何问题的思想方法,即把空间问题转化 为平面问题去解决,化繁为简,这是解决立体几何问题的基本 方法,也是最重要的思想方法;(4)培养处理立体几何问题必备 的三个方面能力:一是空间想象能力,二是逻辑思维能力,三 是推理论证能力.
9、 人的价值,在招收诱惑的一瞬间被决定 。21.4 .421.4 .4Sun day, April 04, 2021 10、低头要有勇气,抬头要有低气。 08:48 :1308 :48:1 308:4 84/4/ 2021 8:48:13 AM 11、人总是珍惜为得到。21.4.408: 48:13 08:48 Apr-2 14-Apr-21 12、人乱于心,不宽余请。08:48:1 308:4 8:130 8:48Sunday , April 04, 2021 13、生气是拿别人做错的事来惩罚自 己。21 .4.42 1.4.40 8:48: 1308: 48:13 April 4, 2021 14、抱最大的希望,作最大的努力。 2021 年4月4 日星期 日上午 8时48 分13秒 08:48 :1321. 4.4 15、一个人炫耀什么,说明他内心缺 少什么 。。20 21年4 月上午 8时48 分21.4 .408: 48Apri l 4, 2021 16、业余生活要有意义,不要越轨。 2021 年4月4 日星期 日8时4 8分13 秒08:4 8:134 April 2021 17、一个人即使已登上顶峰,也仍要 自强不 息。上 午8时4 8分13 秒上午 8时48 分08: 48:13 21.4.4
人教A版高中数学必修2第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系课件

C D
B A
C1 D1
B1 A1
知识小结
实例引 入平面
平面的画 法和表示
点和平面的 位置关系
平面三 个公理
空间图形
文字叙述
符号表示
2.1.2空间中两直线的位置 关系
平面有知识(复习 )
判断下列命题对错: 1、如果一条直线上有一个点在一个平面上,则这条直线上
的所有点都在这个平面内。( )
2、将书的一角接触课桌面,这时书所在平面和课桌所在平
直线。(既不相交也不平行的两条直线) 判断:
(1)
m
β
m
l
α
l
直线m和l是异面直线吗?
(2)
,则 与 是异面直线
(3)a,b不同在平面 内,则a与b异面
异面直线的画法:
通常用一个或两个平面来衬托,异面直线
不同在任何一个平面的特点
a
b
b
a
b
a
2、空间中两直线的三种位置关系
1、相交
m P
l
2、平行
m l
b′
平
a′ θ O
移
若两条异面直线所成角为90°,则称它们互相垂直。 异面直线a与b垂直也记作a⊥b 异面直线所成角θ的取值范围:
例 3 在正方体ABCD—A1B1C1D1中指出下列各对线段所
成的角:
D1
C1
1)AB与CC1; 2)A1 B1与AC; A1
B1
3)A1B与D1B1。
1)AB与CC1所成的角 = 9 0°
4、平面的基本性质
公理3 如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线.
符号表示为:
P l, Pl.
新课标人教A版高中数学必修2知识点总结
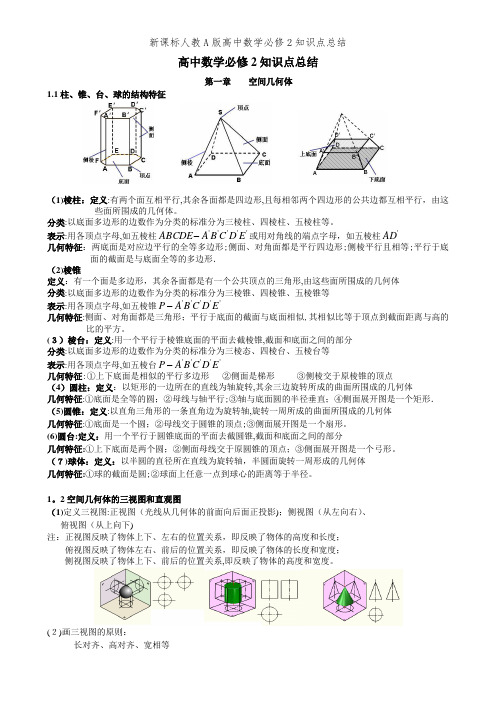
高中数学必修2知识点总结第一章 空间几何体1.1柱、锥、台、球的结构特征(1)棱柱:定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各顶点字母,如五棱柱'''''E D C B A ABCDE -或用对角线的端点字母,如五棱柱'AD几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.(2)棱锥定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体 分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示:用各顶点字母,如五棱锥'''''E D C B A P -几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
(3)棱台:定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分 分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示:用各顶点字母,如五棱台'''''E D C B A P -几何特征:①上下底面是相似的平行多边形 ②侧面是梯形 ③侧棱交于原棱锥的顶点(4)圆柱:定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形. (5)圆锥:定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体 几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
(6)圆台:定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
高中数学人教新课标A版 必修2 第二章 点、直线、平面之间的位置关系 2.1.3空间中直线与平面之间

高中数学人教新课标A版必修2 第二章点、直线、平面之间的位置关系 2.1.3空间中直线与平面之间的位置关系,2.1.4平面与平面之间的位置关系(II)卷姓名:________ 班级:________ 成绩:________一、选择题 (共7题;共14分)1. (2分)在下列命题中,不是公理的是()A . 平行于同一个平面的两个平面平行B . 过不在同一直线上的三个点,有且只有一个平面C . 如果一条直线上的两点在同一个平面内,那么这条直线上所有点都在此平面内D . 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线2. (2分)已知直线,平面,且,,给出下列四个命题:①若,则;②若,则;③若,则;④若,则.其中真命题的个数为()A . 1B . 2C . 3D . 43. (2分) (2017·南阳模拟) 已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列四个命题,错误的命题是()A . 若m∥α,m∥β,α∩β=n,则m∥nB . 若α⊥β,m⊥α,n⊥β,则m⊥nC . 若α⊥β,α⊥γ,β∩γ=m,则m⊥αD . 若α∥β,m∥α,则m∥β4. (2分)已知为两条不同直线为两个不同平面,给出下列命题: ()①②③④其中的正确命题序号A . ③④B . ②③C . ①②D . ①②③④5. (2分)点 E,F,G,H分别为空间四边形ABCD的边AB,BC,CD,AD的中点,则四边形EFGH是()A . 菱形B . 梯形C . 正方形D . 平行四边形6. (2分)设是两个不同的平面,是一条直线,则下列命题正确的是()A . 若,则B . 若,则C . 若,则D . 若,则7. (2分)已知l,m,n为两两垂直的三条异面直线,过l作平面α与m垂直,则n与α的关系是()A . n∥αB . n∥α或n⊊αC . n⊊α或n与α不平行D . n⊊α二、单选题 (共1题;共2分)8. (2分)如果直线l、m与平面α、β、γ满足:l=β∩γ,l∥α,m⊂α和m⊥γ,那么必有()A . α⊥γ且l⊥mB . α⊥γ且m∥βC . m∥β且l⊥mD . α∥β且α⊥γ三、填空题 (共3题;共3分)9. (1分) (2016高一上·天河期末) 已知α,β是两个平面,m,n是两条直线,则下列四个结论中,正确的有________(填写所有正确结论的编号)①若m∥α,n∥α,则m∥n;②若m⊥α,n∥α,则m⊥n;③若a∥β,m⊂α,则m∥β;④若m⊥n.m⊥α,n∥β,则α⊥β10. (1分) (2019高二上·慈溪期中) 设m,n是两条不同的直线,,,是三个不同的平面,给出如下命题:①若⊥ ,m// ,则m⊥ ;②若⊥ ,⊥ ,则 // ;③若⊥ ,m⊥ ,,则m// ;④若⊥ ,∩ =m,,n⊥m,则n⊥ .其中正确的是________.11. (1分)设l,m,n表示三条不同的直线,α,β,γ表示三个不同的平面,给出下列四个命题:①若l⊥α,m⊥l,m⊥β,则α⊥β;②若m⊂β,n是l在β内的射影,m⊥l,则m⊥l;③若m是平面α的一条斜线,A∉α,l为过A的一条动直线,则可能有l⊥m且l⊥α;④若α⊥β,α⊥γ,则γ∥β其中真命题的个数________ .四、解答题 (共3题;共20分)12. (5分)一个正方体的平面展开图及正方体的直观图的示意图如图所示:(Ⅰ)请将字母E,F,G,H标记在正方体相应的顶点处(不需说明理由);(Ⅱ)在正方体中,判断平面BEG与平面ACH的位置关系,并证明你的结论.13. (5分)已知三个平面两两相交,有三条交线,求证这三条交线交于一点或互相平行.14. (10分)如图所示是一个长方体截去一个角得到的几何体的直观图及正视图和侧视图(单位:cm).(1)画出该多面体的俯视图,并标上相应的数据;(2)设M为AB上的一点,N为BB’中点,且AM=4,证明:平面GEF∥平面DMN.参考答案一、选择题 (共7题;共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、二、单选题 (共1题;共2分)8-1、三、填空题 (共3题;共3分)9-1、10-1、11-1、四、解答题 (共3题;共20分)12-1、13-1、14-1、14-2、。
人教新课标A版高一数学《必修2》2.1.3 空间中直线与平面之间的位置关系

2.1 空间点、直线、平面之间的位置关系
2.1.3 空间中直线与平面之间的位置关系
2.1.3 空间中直线与平面之间的位置关系
1、了解空间中直线与平面的三种位置关系; 2、会用符号表示出直线和平面的三种位置 关系; 3、能准确地进行文字语言、图形语言和符 号语言的相互转化;
典例精析
直线与平面的位置关系
D
A
C
B
D
C
A B
典例精析
直线与平面的位置关系 )
例2 已知直线a在平面α外,则 ( (A)a∥α (C)aα=A
(B)直线a与平面α至少有一个公共点 (D)直线a与平面α至多有一个公共点
解析 准确理解直线在平面外的定义是解答本题的关键. 空间中的
直线a
与平面α探究点1 直线与平面源自位置关系DAC
B
D
C
A
面的位置关系
有哪些?
B
课堂探究
探究点1 直线与平面的位置关系 直线与平面的位置关系有且只有三种: a a a
α 直线在平面α内
有无数个交点 a⊂α 直线在平面内
α
A
α
直线与平面α相交
有且只有一个交点 直线与平面α平行 无交点 a∥α a ∩ α= A
直线与平面相交,记作a∩α=A(一个公共点)
直线与平面平行,记作a//α(没有公共点)
答案 D
知识识记
课堂达标训练
A
(A)0个 (B)1个 (C)2个 (D)3个
知识识记
课堂达标训练
D
C
知识识记
课堂达标训练 ( C)
(4).已知m,n为异面直线,m∥平面a,n∥平面b,a∩b=l,则l (A)与m,n都相交 (B)与m,n中至少一条相交 (C)与m,n都不相交 (D)与m,n中一条相交
数学:第二章《点、直线、平面之间的位置关系》教案(新人教A版必修2)

点、直线、平面之间的位置关系复习(一)课型:复习课一、教学目标1、知识与技能(1)使学生掌握知识结构与联系,进一步巩固、深化所学知识;(2)通过对知识的梳理,提高学生的归纳知识和综合运用知识的能力。
2、过程与方法利用框图对本章知识进行系统的小结,直观、简明再现所学知识,化抽象学习为直观学习,易于识记;同时凸现数学知识的发展和联系。
3情态与价值学生通过知识的整合、梳理,理会空间点、线面间的位置关系及其互相联系,进一步培养学生的空间想象能力和解决问题能力。
二、教学重点、难点重点:各知识点间的网络关系;难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。
三、教学设计(一)知识回顾,整体认识1、本章知识回顾(1)空间点、线、面间的位置关系;(2)直线、平面平行的判定及性质;(3)直线、平面垂直的判定及性质。
2、本章知识结构框图(二)整合知识,发展思维1、刻画平面的三个公理是立体几何公理体系的基石,是研究空间图形问题,进行逻辑推理的基础。
公理1——判定直线是否在平面内的依据;公理2——提供确定平面最基本的依据;公理3——判定两个平面交线位置的依据;公理4——判定空间直线之间平行的依据。
2、空间问题解决的重要思想方法:化空间问题为平面问题;3、空间平行、垂直之间的转化与联系:4、观察和推理是认识世界的两种重要手段,两者相辅相成,缺一不可。
(三)应用举例,深化巩固1、P.73 A 组第1题2、P.74 A 组第6、8题(四)、课堂练习:1.选择题 (1)如图BC 是R t ⊿ABC 的斜边,过A 作⊿ABC 所在平面α垂线AP ,连PB 、PC ,过A 作AD ⊥BC 于D ,连PD ,那么图中直角三角形的个数是( ) (A )4个 (B )6个 (C )7个 (D )8个(2)直线a 与平面α斜交,则在平面α内与直线a 垂直的直线( ) (A )没有 (B )有一条 (C )有无数条 (D )α内所有直线 答案:(1)D (2) C2.填空题(1)边长为a 的正六边形ABCDEF 在平面α内,PA ⊥α,PA =a ,则P 到CD 的距离为 ,P 到BC 的距离为 .(2)AC 是平面α的斜线,且AO =a ,AO 与α成60º角,OC ⊂α,AA '⊥α于A ',∠A 'OC =45º,则A 到直线OC 的距离是 , ∠AOC 的余弦值是 . 答案:(1)a a27,2; (2)42,414a 3.在正方体ABCD -A 1B 1C 1D 1中,求证:A 1C ⊥平面BC 1D .分析:A 1C 在上底面ABCD 的射影AC ⊥BD, A 1C 在右侧面的射影D 1C ⊥C 1D,所以A 1C ⊥BD, A 1C ⊥C 1D,从而有A 1C ⊥平面BC 1D .A A ′ CαOC1课后作业1、阅读本章知识内容,从中体会知识的发展过程,理会问题解决的思想方法;2、P.76 B组第2题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
符号语言:
二、新知探究【合作探究·展示能力】 . 空间两条直线的位置关系 文字语言:
平行公理与等角原理 公理 4:平行于 符号表述: 。 的两条直线平行。
平行公理表明:空间内平行于同一条直线的所有直线相互平行,因此它给出了 判定空间内两条直线平行的一个依据。 等角定理:如果一个角的两边与另一个角的两边分别平行,那么这两个角 。 检测练习: 例1:如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1、B1C1的中点。问:
AD 的位置关系是
时,四边形 EFGH 是菱形;当
;四边形 EFGH 是
;当
A
2
G B M
H D N C
时,四边形 EFGH 是矩形;当 时,四边形 EFGH 是正方形。
且
2、如图, A 是平面 BCD 外的一点 G, H 分别是 ABC , ACD 的重心,求证:
GH // BD .
合作探究:
1
(1)AM和CN是否是异面直线?说明理由; (2)D1B和CC1是否是异面直线?说明理由。
★例2、垂直于同一条直线的两条直线的位置关系是(
)
A.平行 B. 相交 C. 异面 D. A、B、C均有可能 【注】本例意在提醒学生比较平面几何与立体几何的异同。 小结: 证明两直线为异面直线的方法: 1、定义法(不易操作,很难实现) 2、反证法:先假设两条直线不是异面直线,即两直线平行或相交,由 假设的条件出发,经过严密的推理,导出矛盾,从而否定假设肯定两条直线异 面。此法在异面直线的判定中经常用到。 3、客观题中,也可用判定定理:过平面外一点和平面内一点的直线,与平面内 不过该点的直线是异面直线,如图所示。 三、总结检测【归纳总结·训练检测】 ◆挑战题 1、空间四边形 ABCD 中, E , F , G, H 分别是 AB, BC , CD, DA 的中点,则 BC 与
2.1 空间点、直线、平面之间的位置关系(2)
一、温故思考【自主学习·质疑思考】 仔细阅读课本44-47页,结合课本知识,完成下述概念. 异面直线: (1)定义:不同在 内的两条直线叫做异面直线;
(2)判定定理:连平面内一点与源自面外一点的直线与平面内不过此点的直线是异 面直线。
P a
图形语言:
A
教师点拨:
四、作业项目【课外作业·开展项目】 书面作业: 课后习题51页2.1A组第1、2、3题小题写在作业本上。 同时思考今天的拓展问题,将你的答案写在作业本上。 预习下一课时《等角定理》
3
