高中的常见函数图像及基本性质
最全高数基本初等函数概念图像及性质完整版

基本初等函数. 幂函数(a 为实数 )要记住最常见的几个幂函数的定义域及图形..指数函数定义域:,值域:,图形过( 0, 1)点, a>1 时,单调增加; a 时,单调减少。
今后用的较多。
.对数函数定义域:,值域:,与指数函数互为反函数,图形过(1, 0)点, a>1 时,单调增加;a<1 时,单调减少。
.三角函数,奇函数、有界函数、周期函数;,偶函数、有界函数、周期函数;,的一切实数,奇函数、周期函数,的一切实数,奇函数、周期函数;,.反三角函数;;;。
以上是五种基本初等函数,关于它们的常用运算公式都应掌握注:( 1)指数式与对数式的性质由此可知,今后常用关系式,如:( 2)常用三角公式积化和差sina*cosb=(sin(a+b)+sin(a-b))/2 cosa*sinb=(sin(a+b)-sin(a-b))/2cosa*cosb=(cos(a+b)+cos(a-b))/2 sina*sinb=-(cos(a+b)-cos(a-b))/2和差化积sinx+siny=2sin((x+y)/2)*cos((x-y)/2) sinx-siny=2cos((x+y)/2)*sin((x-y)/2) cosx+cosy=2cos((x+y)/2)*cos((x-y)/2) cosx-cosy=-2sin((x+y)/2)*sin((x-y)/2)赠送以下资料《二次函数的应用》中考题集锦10 题已知抛物线y x2mx 2m 2 (m 0).( 1)求证:该抛物线与x 轴有两个不同的交点;( 2)过点P(0,n)作y 轴的垂线交该抛物线于点 A 和点 B (点 A 在点 P 的左边),是否存在实数 m,n ,使得 AP2PB ?若存在,则求出m,n 满足的条件;若不存在,请说明理由.答案:解:( 1)证法 1:29 m2,y x2mx 2m2x m24当 m0 时,抛物线顶点的纵坐标为9 m20 ,4顶点总在 x 轴的下方.而该抛物线的开口向上,该抛物线与x 轴有两个不同的交点.(或者,当 m 0 时,抛物线与y 轴的交点(0,2m2)在x轴下方,而该抛物线的开口向上,该抛物线与 x 轴有两个不同的交点.)证法 2:m2 4 1 ( 2m2 ) 9m2,当 m0时, 9m20 ,该抛物线与 x 轴有两个不同的交点.( 2)存在实数m,n,使得AP2PB .设点 B 的坐标为(t,n),由 AP2PB 知,y①当点 B 在点 P 的右边时, t0,点 A 的坐标为(2t, n) ,A PBx 且 t, 2t是关于 x 的方程 x2mx2m2n 的两个实数根.O m24( 2m2n) 9m24n 0 ,即 n9 m2.4且 t ( 2t )m (I), t ( 2)t2(II)m n由( I)得,t m,即m 0.将 t m代入(II)得, n0 .y 当 m0且 n0 时,有 AP2PB .②当点 B 在点 P 的左边时, t0,点 A 的坐标为(2 t,n),且 t,2t 是关于x的方程 x 2mx2m2n 的两个实数根.xOm24( 2m2n) 9m24n 0 ,即 n9 m2.4AB P且 t 2t m (I),t 2t2m2n (II)由( I)得,t m0 .3,即m将 t m代入( II )得,n20 m2且满足 n9 m2.32094当 m0 且n m2时,有AP2PB9第 11 题一人乘雪橇沿如图所示的斜坡笔直滑下,滑下的距离S (米)与时间t (秒)间的关系式为S 10t t 2,若滑到坡底的时间为 2 秒,则此人下滑的高度为()A.24米B.12米C. 12 3 米D.6米答案:B第 12 题我市英山县某茶厂种植“春蕊牌”绿茶,由历年来市场销售行情知道,从每年的3月 25日起的 180 天内,绿茶市场销售单价y (元)与上市时间t (天)的关系可以近似地用如图( 1)中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价z (元)与上市时间t (天)的关系可以近似地用如图(2)的抛物线表示.y (天)z(元 )16060140( 180, 92)5012040100858036020401020140160100120O20 40 6080 100 120150 180t(天)O204060 80110140160 180t(天 )( 1)直接写出图(1)中表示的市场销售单价y (元)与上市时间t (天)(t0)的函数关图 (1)图 (2)系式;( 2)求出图( 2)中表示的种植成本单价z(元)与上市时间t (天)(t 0)的函数关系式;( 3 )认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大?(说明: 市场销售单价和种植成本单价的单位:元/500 克.)答案:解:( 1)依题意,可建立的函数关系式为:2 t 160 (0t,3 120)y 80 (120 ≤ t,150)2 20 (150 ≤t ≤ .5( 2)由题目已知条件可设za(t 110) 220 .85图象过点 (60, ) ,385 a(60 110) 2 20. a1 . 3300z1(t 110) 2 20 (t 0 ). 300( 3)设纯收益单价为W 元,则 W =销售单价 成本单价.2 1601110) 220 (0 t,t(t120)3300故W 801 (t 220(120 ≤t,300 110)150)2 201 220 (150 ≤ t≤.5300化简得1 2100(0,300W1(t 110)2 60 (120≤ t 150), 30012 56 (150 ≤ t ≤.300①当 W1 (t 10)2 100(0 t 120) 时,有 t 10时, W 最大,最大值为 100;300②当 W1 (t 110)2 60(120 ≤ t 150) 时,由图象知,有 t 120 时, W 最大,最大300值为 59 2 ;3③当 W1 (t 170)2 56(150 ≤ t ≤ 180) 时,有 t 170 时, W 最大,最大值为 56.300综上所述,在 t 10 时,纯收益单价有最大值,最大值为100 元.第 13 题如图,足球场上守门员在O 处开出一高球,球从离地面1 米的 A 处飞出( A 在 y 轴上),运动员乙在距O 点6 米的B 处发现球在自己头的正上方达到最高点M,距地面约 4 米高,球落地后又一次弹起.据实验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.( 1)求足球开始飞出到第一次落地时,该抛物线的表达式.( 2)足球第一次落地点 C 距守门员多少米?(取 43 7)( 3)运动员乙要抢到第二个落点D ,他应再向前跑多少米?(取26 5)y4 M2 1 AOBCDx答案:解:( 1)( 3 分)如图,设第一次落地时,抛物线的表达式为ya(x6) 2 4.y由已知:当 x 0 时 y 1.即 1 36a 4, a1 . 4M12E FN表达式为 y124. 2 ( x 6)1 A1 x2 12OBCDx(或 yx 1 )12 1( 2)(3 分)令 y0, ( x6)2 4 0.12(x6)2 48. x 4 3 6 ≈ 13,x4 3 6 0 (舍去).12足球第一次落地距守门员约 13 米.( 3)(4 分)解法一:如图,第二次足球弹出后的距离为CD根据题意: CDEF (即相当于将抛物线 AEMFC 向下平移了 2 个单位)21( x 6) 24解得 x6 2 6,x2 6 26.121CD x 1 x 2 4 6 ≈10.BD 13 6 1017 (米).解法二: 令1( x 6) 2 4 0.12解得x 1 6 4 3 (舍), x 26 4 3 ≈13.点 C 坐标为( 13, 0).设抛物线 CND 为 y1( x k) 2 2.12将 C 点坐标代入得:1(13 k) 2 2 0.12解得:k 1 13 2 613 (舍去),k 2 6 4 3 2 6 ≈ 6 7 5 18.y1( x 18)2 212 令 y0, 01( x 18)2 2.12x 118 2 6 (舍去), x 2 18 2 6≈23.BD 23 6 17 (米).解法三:由解法二知, k 18,所以 CD 2(18 13) 10, 所以 BD(136) 10 17.答:他应再向前跑17 米.第 14 题荆州市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知:平均修建每公顷大棚要用支架、农膜等材料费 2.7 万元;购置滴灌 设备,这项费用(万元)与大棚面积(公顷)的平方成正比,比例系数为 0.9 ;另外每公顷种植蔬菜需种子、化肥、农药等开支 0.3 万元.每公顷蔬菜年均可卖7.5 万元.y (万元),( 1)基地的菜农共修建大棚 x (公顷),当年收益(扣除修建和种植成本后)为写出 y 关于 x 的函数关系式.( 2)若某菜农期望通过种植大棚蔬菜当年获得 5 万元收益,工作组应建议他修建多少公项大棚.(用分数表示即可)( 3)除种子、化肥、农药投资只能当年受益外, 其它设施 3 年内不需增加投资仍可继续使用. 如果按 3 年计算,是否修建大棚面积越大收益越大?修建面积为多少时可以得到最大收益?请帮工作组为基地修建大棚提一项合理化建议.答案:( 1) y 7.5x2.7x 0.9x 20.3x0.9x 2 4.5x .( 2)当 0.9x 24.5x5 时,即 9x 245x 50 0 , x 15 , x 2 1033从投入、占地与当年收益三方面权衡,应建议修建5公顷大棚.(3)设3Z (万元)3年内每年的平均收益为Z 7.5x0.9x 0.3x20.3x0.3x2 6.3x20.3 x 10.5 33.075(10分)不是面积越大收益越大.当大棚面积为10.5 公顷时可以得到最大收益.建议:①在大棚面积不超过10.5公顷时,可以扩大修建面积,这样会增加收益.②大棚面积超过10.5公顷时,扩大面积会使收益下降.修建面积不宜盲目扩大.③当 0.3x2 6.3x0时, x10 , x2 21.大棚面积超过21公顷时,不但不能收益,反而会亏本.(说其中一条即可)第 15 题一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18 元,按定价 40元出售,每月可销售 20 万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价 1元,月销售量可增加 2 万件.(1)求出月销售量y(万件)与销售单价x(元)之间的函数关系式(不必写x的取值范围);(2)求出月销售利润z(万元)(利润=售价-成本价)与销售单价x(元)之间的函数关系式(不必写 x 的取值范围);(3)请你通过( 2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于 480 万元.答案:略.第 16 题一座隧道的截面由抛物线和长方形构成,长方形的长为8m ,宽为 2m ,隧道最高点P 位于 AB 的中央且距地面6m ,建立如图所示的坐标系(1)求抛物线的解析式;(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?yPA BO Cx答案:( 1)由题意可知抛物线经过点A0,2 ,P 4,6 ,B 8,2设抛物线的方程为y ax2bx c将 A,P,D 三点的坐标代入抛物线方程.解得抛物线方程为y1x22x 24( 2)令 y4 ,则有 1 x 2 2x2 44解得x 14 2 2, x 2 4 2 2x 2 x 14 2 2货车可以通过.( 3)由( 2)可知1x 2 x 1 2 2 22 货车可以通过.第 17 题如图,在矩形ABCD 中, AB 2 AD ,线段 EF 10 .在 EF 上取一点 M ,分别以EM , MF 为一边作矩形 EMNH 、矩形 MFGN ,使矩形 MFGN ∽ 矩形 ABCD .令 MN x ,当 x 为何值时,矩形 EMNH 的面积 S 有最大值?最大 D C值是多少?ABHN GEMF答案:解:矩形 MFGN ∽ 矩形 ABCD ,MN MF .AD ABAB2 AD , MN x ,MF 2x .EMEFMF 10 2x .Sx(10 2x) 2 x 2 10x22 52 x52.2当 x5时, S 有最大值为25.22第 18 题某企业信息部进行市场调研发现:信息一:如果单独投资A 种产品,则所获利润 y A (万元)与投资金额 x (万元)之间存在正比例函数关系: y A kx ,并且当投资 5 万元时,可获利润 2 万元.信息二:如果单独投资B 种产品,则所获利润y B (万元)与投资金额 x (万元)之间存在二次函数关系:y B ax 2 bx ,并且当投资2 万元时,可获利润 2.4 万元;当投资4 万元时,可获利润 3.2 万元.(1)请分别求出上述的正比例函数表达式与二次函数表达式;(2)如果企业同时对A,B两种产品共投资 10 万元,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?答案:解:(1)当x 5 时,y1,,0.4 ,2 25k ky A0.4x ,当x 2 时,y B 2.4 ;当x 4 时,y B 3.2.2.44a2b3.216a4ba0.2解得1.6by B0.2x2 1.6 x .( 2)设投资B种商品x万元,则投资 A 种商品(10x) 万元,获得利润W万元,根据题意可得W0.2x2 1.6 x0.4(10 x)0.2 x2 1.2x4W0.2( x3)2 5.8当投资 B 种商品 3 万元时,可以获得最大利润 5.8 万元,所以投资A种商品7万元, B种商品 3 万元,这样投资可以获得最大利润 5.8 万元.第 19 题如图所示,图(1)是一座抛物线型拱桥在建造过程中装模时的设计示意图,拱高为30m ,支柱 A3 B3 50m , 5 根支柱 A1 B1, A2 B2, A3 B3, A4 B4,A5 B5之间的距离均为15m ,B1B5∥ A1 A5,将抛物线放在图( 2)所示的直角坐标系中.(1)直接写出图( 2)中点 B1, B3, B5的坐标;(2)求图( 2)中抛物线的函数表达式;( 3)求图( 1)中支柱 A2 B2, A4 B4的长度.B3yB2B430m B3B1B5B1B5A1A2 A3 A4 A5O l图 (1)图(2)答案:B1 ( 30, 0) , B3 (0,30) , B5 (30,0) ;(1)( 2)设抛物线的表达式为y a(x 30)( x30) ,把 B3 (0,30) 代入得 y a(030)(030)30 .∴ a 1.301( x∵ 所求抛物线的表达式为:y30)( x30) .30( 3)∵B4点的横坐标为15,∴ B4的纵坐标 y41(1530)(1530)45.302∵ A3B350 ,拱高为30,∴立柱 A4B4 204585(m) .2285(m) 。
常用函数性质及图像

一次函数(一)函数1、确定函数定义域的方法:(1)关系式为整式时,函数定义域为全体实数;(2)关系式含有分式时,分式的分母不等于零;(3)关系式含有二次根式时,被开放方数大于等于零;(4)关系式中含有指数为零的式子时,底数不等于零;(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
(二)一次函数1、一次函数的定义一般地,形如y kx b =+(k ,b 是常数,且0k ≠)的函数,叫做一次函数,其中x 是自变量。
当0b =时,一次函数y kx =,又叫做正比例函数。
⑴一次函数的解析式的形式是y kx b =+,要判断一个函数是否是一次函数,就是判断是否能化成以上形式.⑵当0b =,0k ≠时,y kx =仍是一次函数.⑶当0b =,0k =时,它不是一次函数.⑷正比例函数是一次函数的特例,一次函数包括正比例函数.2、正比例函数及性质一般地,形如y=kx(k 是常数,k≠0)的函数叫做正比例函数,其中k 叫做比例系数.注:正比例函数一般形式y=kx (k 不为零)①k 不为零②x 指数为1③b 取零当k>0时,直线y=kx 经过三、一象限,从左向右上升,即随x 的增大y 也增大;当k<0时, 直线y=kx 经过二、四象限,从左向右下降,即随x 增大y 反而减小.(1)解析式:y=kx(k 是常数,k≠0)(2)必过点:(0,0)、(1,k)(3)走向:k>0时,图像经过一、三象限;k<0时, 图像经过二、四象限(4)增减性:k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小(5)倾斜度:|k|越大,越接近y 轴;|k|越小,越接近x 轴3、一次函数及性质一般地,形如y=kx +b(k,b 是常数,k≠0),那么y 叫做x 的一次函数.当b=0时,y=kx +b 即y=kx ,所以说正比例函数是一种特殊的一次函数.注:一次函数一般形式y=kx+b (k 不为零)①k 不为零②x 指数为1③b 取任意实数一次函数y=kx+b 的图象是经过(0,b)和(-kb,0)两点的一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx 平移|b|个单位长度得到.(当b>0时,向上平移;当b<0时,向下平移)(1)解析式:y=kx+b(k、b 是常数,k ≠0)(2)必过点:(0,b)和(-kb,0)(3)走向:k>0,图象经过第一、三象限;k<0,图象经过第二、四象限b>0,图象经过第一、二象限;b<0,图象经过第三、四象限⇔⎩⎨⎧>>00b k 直线经过第一、二、三象限⇔⎩⎨⎧<>00b k 直线经过第一、三、四象限⇔⎩⎨⎧><0b k 直线经过第一、二、四象限⇔⎩⎨⎧<<0b k 直线经过第二、三、四象限(4)增减性:k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小.(5)倾斜度:|k|越大,图象越接近于y 轴;|k|越小,图象越接近于x 轴.(6)图像的平移:当b>0时,将直线y=kx 的图象向上平移b 个单位;当b<0时,将直线y=kx 的图象向下平移b 个单位.4、一次函数y=kx+b的图象的画法.根据几何知识:经过两点能画出一条直线,并且只能画出一条直线,即两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线即可.一般情况下:是先选取它与两坐标轴的交点:(0,b),.即横坐标或纵坐标为0的点.b>0b<0b=0k>0经过第一、二、三象限经过第一、三、四象限经过第一、三象限图象从左到右上升,y随x的增大而增大k<0经过第一、二、四象限经过第二、三、四象限经过第二、四象限图象从左到右下降,y随x的增大而减小5、正比例函数与一次函数之间的关系一次函数y=kx+b的图象是一条直线,它可以看作是由直线y=kx平移|b|个单位长度而得到(当b>0时,向上平移;当b<0时,向下平移)6、正比例函数和一次函数及性质正比例函数一次函数概念一般地,形如y=kx(k 是常数,k≠0)的函数叫做正比例函数,其中k 叫做比例系数一般地,形如y=kx +b(k,b 是常数,k≠0),那么y 叫做x 的一次函数.当b=0时,是y=kx ,所以说正比例函数是一种特殊的一次函数.自变量范围X 为全体实数图象一条直线必过点(0,0)、(1,k)(0,b)和(-kb,0)走向k>0时,直线经过一、三象限;k<0时,直线经过二、四象限k>0,b>0,直线经过第一、二、三象限k>0,b<0直线经过第一、三、四象限k<0,b>0直线经过第一、二、四象限k<0,b<0直线经过第二、三、四象限增减性k>0,y 随x 的增大而增大;(从左向右上升)k<0,y 随x 的增大而减小。
高中数学的所有重要函数图像及其性质图像特点单调性定义域值域

数函数对数函数的一般形式为,它实际上就是指数函数的反函数。
因此指数函数里对于a的规定,同样适用于对数函数。
右图给出对于不同大小a所表示的函数图形:可以看到对数函数的图形只不过的指数函数的图形的关于直线y=x 的对称图形,因为它们互为反函数。
(1)对数函数的定义域为大于0的实数集合。
(2)对数函数的值域为全部实数集合。
(3)函数总是通过(1,0)这点。
(4)a大于1时,为单调递增函数,并且上凸;a小于1大于0时,函数为单调递减函数,并且下凹。
(5)显然对数函数无界。
指数函数指数函数的一般形式为,从上面我们对于幂函数的讨论就可以知道,要想使得x能够取整个实数集合为定义域,则只有使得如图所示为a的不同大小影响函数图形的情况。
可以看到:(1)指数函数的定义域为所有实数的集合,这里的前提是a大于0,对于a不大于0的情况,则必然使得函数的定义域不存在连续的区间,因此我们不予考虑。
(2)指数函数的值域为大于0的实数集合。
(3)函数图形都是下凹的。
(4)a大于1,则指数函数单调递增;a小于1大于0,则为单调递减的。
(5)可以看到一个显然的规律,就是当a从0趋向于无穷大的过程中(当然不能等于0),函数的曲线从分别接近于Y轴与X轴的正半轴的单调递减函数的位置,趋向分别接近于Y轴的正半轴与X轴的负半轴的单调递增函数的位置。
其中水平直线y=1是从递减到递增的一个过渡位置。
(6)函数总是在某一个方向上无限趋向于X轴,永不相交。
(7)函数总是通过(0,1)这点。
(8)显然指数函数无界。
奇偶性注图:(1)为奇函数(2)为偶函数1.定义一般地,对于函数f(x)(1)如果对于函数定义域内的任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数。
(2)如果对于函数定义域内的任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数。
(3)如果对于函数定义域内的任意一个x,f(-x)=-f(x)与f(-x)=f(x)同时成立,那么函数f(x)既是奇函数又是偶函数,称为既奇又偶函数。
高中各种函数图像画法与函数性质

一次函数(一)函数1、确定函数定义域的方法:(1)关系式为整式时,函数定义域为全体实数;(2)关系式含有分式时,分式的分母不等于零;(3)关系式含有二次根式时,被开放方数大于等于零;(4)关系式中含有指数为零的式子时,底数不等于零;(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
二次函数二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---2. 关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+- 4. 关于顶点对称(即:抛物线绕顶点旋转180°)2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.5. 关于点()m n ,对称 ()2y a x h k=-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-反比例函数1、反比例函数图象:反比例函数的图像属于以原点为对称中心的中心对称的双曲线反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交(K≠0)。
2、性质:1.当k>0时,图象分别位于第一、三象限,同一个象限内,y随x的增大而减小;当k<0时,图象分别位于二、四象限,同一个象限内,y随x的增大而增大。
高中数学常见函数图像
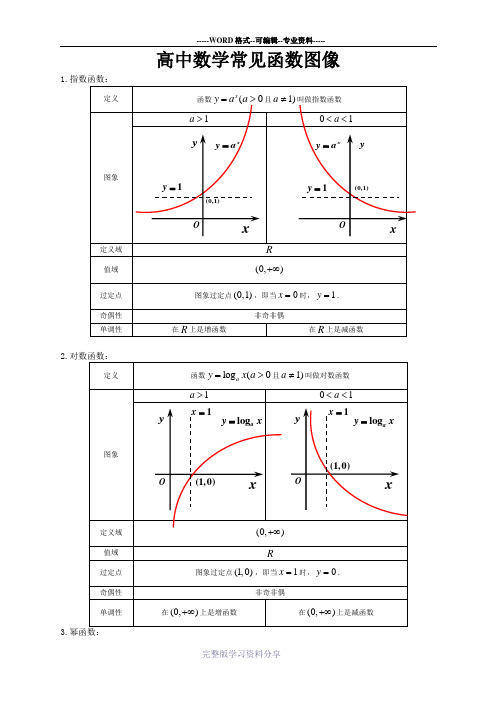
高中数学常见函数图像1.2.对数函数:3.定义形如αx y =(x ∈R )的函数称为幂函数,其中x 是自变量,α是常数.图像性质过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1). 单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴.4.函数sin y x =cos y x =tan y x =图象定义域R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时,max 1y =;当22xk ππ=-()k ∈Z 时,min 1y =-.当()2x k k π=∈Z 时,max 1y =;当2xk ππ=+()k ∈Z 时,min 1y =-.既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦ ()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦()k ∈Z 上是减函数.在[]()2,2k k k πππ-∈Z 上是增函数;在[]2,2k k πππ+()k ∈Z 上是减函数.在,22k k ππππ⎛⎫-+⎪⎝⎭()k ∈Z 上是增函数.对称性对称中心()(),0k k π∈Z对称轴()2x k k ππ=+∈Z对称中心(),02k k ππ⎛⎫+∈Z⎪⎝⎭ 对称轴()x k k π=∈Z对称中心(),02k k π⎛⎫∈Z ⎪⎝⎭无对称轴。
(完整版)高中各种函数图像及其性质(精编版)

高中各种函数图像及其性质一次函数(一)函数1、确定函数定义域的方法:(1)关系式为整式时,函数定义域为全体实数;(2)关系式含有分式时,分式的分母不等于零;(3)关系式含有二次根式时,被开放方数大于等于零;(4)关系式中含有指数为零的式子时,底数不等于零;(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
(二)一次函数1、一次函数的定义一般地,形如y kx b(k,b是常数,且k 0 )的函数,叫做一次函数,其中x 是自变量。
当b 0时,一次函数y kx,又叫做正比例函数。
⑴一次函数的解析式的形式是y kx b,要判断一个函数是否是一次函数,就是判断是否能化成以上形式.⑵当 b 0,k 0时,y kx仍是一次函数.⑶当 b 0,k 0时,它不是一次函数.⑷正比例函数是一次函数的特例,一次函数包括正比例函数.2、正比例函数及性质一般地,形如y=kx(k 是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数.注:正比例函数一般形式y=kx (k 不为零)① k 不为零② x 指数为 1 ③ b 取零当k>0 时,直线y=kx 经过三、一象限,从左向右上升,即随x 的增大y 也增大;当k<0 时,?直线y=kx经过二、四象限,从左向右下降,即随x增大y反而减小.(1)解析式:y=kx (k 是常数,k≠ 0)(2)必过点:(0,0)、(1,k)(3)走向:k>0时,图像经过一、三象限;k<0时,?图像经过二、四象限(4)增减性:k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小(5)倾斜度:|k| 越大,越接近y 轴;|k| 越小,越接近x 轴3、一次函数及性质一般地,形如y=kx +b(k,b 是常数,k≠0),那么y叫做x的一次函数.当b=0时,y=kx +b 即y=kx ,所以说正比例函数是一种特殊的一次函数.注:一次函数一般形式 y=kx+b (k 不为零) ① k 不为零 ②x 指数为 1 ③ b 取任意实 数一次函数 y=kx+b 的图象是经过( 0,b )和(- b , 0)两点的一条直线,我们称它为直k线 y=kx+b, 它可以看作由直线 y=kx 平移 |b| 个单位长度得到 . (当 b>0 时,向上平移; 当 b<0 时,向下平移)1)解析式: y=kx+b (k 、 b 是常数, k 0)2) 必过点:(0,b )和( - b ,0) k3) 走向: k>0 ,图象经过第一、三象限; k<0,图象经过第二、四象限b>0,图象经过第一、二象限;b<0,图象经过第三、四象限k 0 直线经过第一、二、三象限k 0 直线经过第一、三、四象限b 0b 0k 0 直线经过第一、二、四象限k 0 直线经过第二、三、四象限b 0b 04)增减性: k>0 , y 随 x 的增大而增大; k<0,y 随 x 增大而减小 . 5)倾斜度: |k| 越大,图象越接近于 y 轴; |k| 越小,图象越接近于 x 轴 .6)图像的平移: 当 b>0 时,将直线 y=kx 的图象向上平移 b 个单位; 当 b<0 时,将直线y=kx 的图象向下平移 b 个单位 .4、一次函数 y=kx + b 的图象的画法根据几何知识:经过两点能画出一条直线,并且只能画出一条直线,即两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线即可. 一般情况下:是先选取它与两坐标轴的交点:(0,b),或纵坐标为0 的点.. 即横坐标5、正比例函数与一次函数之间的关系一次函数y=kx +b的图象是一条直线,它可以看作是由直线y=kx平移|b| 个单位长度而得到(当b>0时,向上平移;当b<0 时,向下平移)6、正比例函数和一次函数及性质正比例函数一次函数概念一般地,形如y=kx(k 是常数,k≠0)的函数叫做正比例函数,其中k 叫做比例系数一般地,形如y=kx+b(k,b 是常数,k≠0),那么y 叫做x 的一次函数. 当b=0 时,是y=kx ,所以说正比例函数是一种特殊的一次函自变量范围X 为全体实数图象一条直线必过点(0,0)、(1,k)(0,b)和(- b,0)k走向k>0 时,直线经过一、三象限;k<0 时,直线经过二、四象限k>0,b>0, 直线经过第一、二、三象限k>0,b<0 直线经过第一、三、四象限k<0,b>0 直线经过第一、二、四象限k<0,b<0 直线经过第二、三、四象限增减性k>0 ,y 随x 的增大而增大;(从左向右上升)k<0 ,y 随x 的增大而减小。
常见函数的图像和性质
常见函数的图像和性质在数学的世界里,函数就像是一座桥梁,连接着不同的数量关系。
而函数的图像和性质,则是我们理解和把握这些关系的关键。
今天,咱们就来一起聊聊常见函数的图像和性质。
首先,咱们来看看一次函数。
一次函数的表达式一般写作 y = kx+ b (k、b 为常数,k ≠ 0)。
它的图像是一条直线。
当 k > 0 时,直线是上升的,意味着函数值 y 随着 x 的增大而增大;当 k < 0 时,直线是下降的,函数值 y 随着 x 的增大而减小。
b 呢,则决定了直线与 y轴的交点,当 b > 0 时,交点在 y 轴的正半轴;当 b < 0 时,交点在 y 轴的负半轴;当 b = 0 时,直线过原点。
再来说说反比例函数,它的表达式通常是 y = k / x (k 为常数,k ≠ 0)。
反比例函数的图像是两条曲线,叫做双曲线。
当 k > 0 时,双曲线在一、三象限,在每个象限内,y 随 x 的增大而减小;当 k < 0 时,双曲线在二、四象限,在每个象限内,y 随 x 的增大而增大。
二次函数也是常见函数中的重要一员,其表达式一般为 y = ax²+bx + c (a、b、c 为常数,a ≠ 0)。
二次函数的图像是一条抛物线。
当a > 0 时,抛物线开口向上,有最小值;当 a < 0 时,抛物线开口向下,有最大值。
抛物线的对称轴是直线 x = b / 2a 。
而且,判别式Δ = b²4ac 能帮助我们判断抛物线与 x 轴的交点情况。
当Δ > 0 时,抛物线与x 轴有两个交点;当Δ = 0 时,抛物线与 x 轴有一个交点;当Δ < 0 时,抛物线与 x 轴没有交点。
接下来看看指数函数,它的表达式是 y = a^x (a > 0 且a ≠ 1)。
当 a > 1 时,函数单调递增,图像从左到右逐渐上升;当 0 < a < 1 时,函数单调递减,图像从左到右逐渐下降。
指数函数的图像恒过点(0, 1)。
函数图像总结
函数图像总结函数图像总结函数图像总结一基本函数图像1y=kx(x≠0)2y=kx+b(k≠0)3y4yax2bxc(a0)5yxa6yxk(k0)xk(k0)7yax(a 0,a1)x8ylogax(a0,a1)二抽象图像平移f(x)f(x+1)f(x)f(x-1)f(x)f(x)+1f(x)f(x)-1f(x)f(2x)f(x)2f(x) f(x)f(2x+2)y=f(-x)变成y=f(-x+2)练习:cosxcos2xcos2xcos(2x+4)cosxcos2x+4三图像的变换1f(x)f(|x|)保留y轴右边的,左边关于右边y轴对称2f(x)|f(x)|保留x轴上方的,下方关于x轴对称3f(x)f(-x)y轴对称4f(x)-f(x)x轴对称5f(x)-f(-x)原点对称6f(x)f(|x+1|)先根据1方法变成f(|x|),在向左平移一个单位得到f(|x+1|)7f(x)f(|x|+1)先向左平移一个单位得到f(x+1),再根据1方法变成f(|x|+1)8f(x)与f1(x)的图象关于直线yx对称联想点(x,y),(y,x)9f(x)与f(2ax)的图象关于点(a,0)对称egf(x)= 2x与g(x)=-2x关于对称一、函数yf(x)与函数yf(x)的图象关系函数yf(x)的图象是由yf(x)的图象经沿y轴翻折180°而得到的(即关于y轴对称)。
注意它与函数yf(x)满足f(x)f(x)的图象是不同的,前者代表两个函数,后者表示函数yf(x)本身是关于y轴对称的。
(二)伸缩变换及其应用:函数yaf(bx)的图像可以看作是由函数yf(x)的图像先将横坐标伸长(|b|<1)或缩短(|b|>1)到原来的1倍,再把纵坐标伸长(|a|>1)或缩短(|a|<1)到原来的|a|倍即可得到。
如:|b|1的图像x1要求:1会画y=|x+1|y=-2会画f(x)=lg|x|以及f(x)=|lgx|3会画f(x)=|lg|x+1||以及f(x)=x2-4|x|+5f(x)=|x2-2x-3|二1由图像可知f(x+1)为偶函数对称轴为2由图像可知f(x+1)为奇函数关于点(,)对称Eg、对a,bR,记max{a,b}=(A)0(B) a,ab,函数f(x)=max{|x+1|,|x-2|}(xR)的最小值是b,a<b13(C)(D)3901(选讲)1、yf(x)绕原点顺时针方向旋转;yf(x)12、yf(x);yf (x)绕原点逆时针方向旋转9000yQP(a,b)(yf(x)yQ1xP1(b,a)(yf1(x))P(a,b)(yf(x)0P1(b,a)1(yf(x))0(乙)x(甲)(图五)0说明:关于绕原点旋转180的变换实际上就是关于原点对称的问题。
高中各种函数图像和性质(精编版)
高中各种函数图像及其性质一次函数(一)函数1、确定函数定义域的方法:(1)关系式为整式时,函数定义域为全体实数; (2)关系式含有分式时,分式的分母不等于零; (3)关系式含有二次根式时,被开放方数大于等于零; (4)关系式中含有指数为零的式子时,底数不等于零;(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
(二)一次函数1、一次函数的定义一般地,形如y kx b =+(k ,b 是常数,且0k ≠)的函数,叫做一次函数,其中x 是自变量。
当0b =时,一次函数y kx =,又叫做正比例函数。
⑴一次函数的解析式的形式是y kx b =+,要判断一个函数是否是一次函数,就是判断是否能化成以上形式.⑵当0b =,0k ≠时,y kx =仍是一次函数. ⑶当0b =,0k =时,它不是一次函数.⑷正比例函数是一次函数的特例,一次函数包括正比例函数.2、正比例函数及性质一般地,形如y=kx(k 是常数,k≠0)的函数叫做正比例函数,其中k 叫做比例系数. 注:正比例函数一般形式 y=kx (k 不为零) ① k 不为零 ② x 指数为1 ③ b 取零当k>0时,直线y=kx 经过三、一象限,从左向右上升,即随x 的增大y 也增大;当k<0时,•直线y=kx经过二、四象限,从左向右下降,即随x增大y反而减小.(1)解析式:y=kx(k是常数,k≠0)(2)必过点:(0,0)、(1,k)(3)走向:k>0时,图像经过一、三象限;k<0时,•图像经过二、四象限(4)增减性:k>0,y随x的增大而增大;k<0,y随x增大而减小(5)倾斜度:|k|越大,越接近y轴;|k|越小,越接近x轴3、一次函数及性质一般地,形如y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.当b=0时,y=kx +b即y=kx,所以说正比例函数是一种特殊的一次函数.注:一次函数一般形式y=kx+b (k不为零) ①k不为零②x指数为1 ③b取任意实数b,0)两点的一条直线,我们称它为一次函数y=kx+b的图象是经过(0,b)和(-k直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度得到.(当b>0时,向上平移;当b<0时,向下平移)(1)解析式:y=kx+b(k 、b 是常数,k ≠0) (2)必过点:(0,b )和(-kb,0) (3)走向: k>0,图象经过第一、三象限;k<0,图象经过第二、四象限 b>0,图象经过第一、二象限;b<0,图象经过第三、四象限⇔⎩⎨⎧>>00b k 直线经过第一、二、三象限 ⇔⎩⎨⎧<>00b k 直线经过第一、三、四象限 ⇔⎩⎨⎧><00b k 直线经过第一、二、四象限 ⇔⎩⎨⎧<<0b k 直线经过第二、三、四象限(4)增减性: k>0,y 随x 的增大而增大;k<0,y 随x 增大而减小.(5)倾斜度:|k|越大,图象越接近于y 轴;|k|越小,图象越接近于x 轴.(6)图像的平移: 当b>0时,将直线y=kx 的图象向上平移b 个单位;当b<0时,将直线y=kx 的图象向下平移b 个单位.4、一次函数y=kx+b的图象的画法.根据几何知识:经过两点能画出一条直线,并且只能画出一条直线,即两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线即可.一般情况下:是先选取它与两坐标轴的交点:(0,b),.即横坐标或纵坐标为0的点.5、正比例函数与一次函数之间的关系一次函数y=kx+b的图象是一条直线,它可以看作是由直线y=kx平移|b|个单位长度而得到(当b>0时,向上平移;当b<0时,向下平移)6、正比例函数和一次函数及性质6、直线11b x k y +=(01≠k )与22b x k y +=(02≠k )的位置关系 (1)两直线平行⇔21k k =且21b b ≠ (2)两直线相交⇔21k k ≠(3)两直线重合⇔21k k =且21b b = (4)两直线垂直⇔121-=k k7、用待定系数法确定函数解析式的一般步骤:(1)根据已知条件写出含有待定系数的函数关系式;(2)将x 、y 的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程;(3)解方程得出未知系数的值;(4)将求出的待定系数代回所求的函数关系式中得出所求函数的解析式.8、一元一次方程与一次函数的关系任何一元一次方程到可以转化为ax+b=0(a ,b 为常数,a ≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值. 从图象上看,相当于已知直线y=ax+b 确定它与x 轴的交点的横坐标的值.9、一次函数与一元一次不等式的关系任何一个一元一次不等式都可以转化为ax+b>0或ax+b<0(a ,b 为常数,a ≠0)的形式,所以解一元一次不等式可以看作:当一次函数值大(小)于0时,求自变量的取值范围.10、一次函数与二元一次方程组(1)以二元一次方程ax+by=c 的解为坐标的点组成的图象与一次函数y=bc x b a +-的图象相同.(2)二元一次方程组⎩⎨⎧=+=+222111c y b x a c y b x a 的解可以看作是两个一次函数y=1111b cx b a +-和y=2222b cx b a +-的图象交点.二次函数一、二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
高中数学第二章函数-函数及其性质(竞赛精讲)
第二章 函数§2.1 函数及其性质一、函数的基本性质:1. 函数图像的对称性(1) 奇函数与偶函数:奇函数图像关于坐标原点对称,对于任意x D ∈,都有()()f x f x -=-成立;偶函数的图像关于y 轴对称,对于任意x D ∈,都有()()f x f x -=成立。
(2) 原函数与其反函数:原函数与其反函数的图像关于直线y x =对称。
若某一函数与其反函数表示同一函数时,那么此函数的图像就关于直线y x =对称。
(3) 若函数满足()(2)f x f ax =-,则()f x 的图像就关于直线x a =对称;若函数满足()(2)f x f a x =--,则()f x 的图像就关于点(,0)a 对称。
(4) 互对称知识:函数()()y f x a y f a x =-=-与的图像关于直线x a =对称。
2.函数的单调性函数的单调性是针对其定义域的某个子区间而言的。
判断一个函数的单调性一般采用定义法、导数法或借助其他函数结合单调性的性质(如复合函数的单调性)特别提示:函数(0)ay x a x=+>的图像和单调区间。
3.函数的周期性对于函数()y f x =,若存在一个非零常数T ,使得当x 为定义域中的每一个值时,都有()()f x T f x +=成立,则称()y f x =是周期函数,T 称为该函数的一个周期。
若在所有的周期中存在一个最小的正数,就称其为最小正周期。
(1) 若T 是()y f x =的周期,那么()nT n Z ∈也是它的周期。
(2) 若()y f x =是周期为T 的函数,则()(0)y f ax b a =+≠是周期为Ta的周期函数。
(3) 若函数()y f x =的图像关于直线x a x b ==和对称,则()y f x =是周期为2()a b -的函数。
(4) 若函数()y f x =满足()()(0)f x a f x a +=-≠,则()y f x =是周期为2a 的函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常见函数性质汇总及简单评议对称变换常数函数 f (x )=b (b ∈R) 1)、y=a 和 x=a 的图像和走势2)、图象及其性质:函数f (x )的图象是平行于x 轴或与x 轴重合(垂直于y 轴)的直线一次函数 f (x )=kx +b (k ≠0,b ∈R)1)、两种常用的一次函数形式:斜截式——点斜式——2)、对斜截式而言,k 、b 的正负在直角坐标系中对应的图像走势: 3)、|k|越大,图象越陡;|k|越小,图象越平缓 4)、定 义 域:R 值域:R单调性:当k>0时 ;当k<0时奇 偶 性:当b =0时,函数f (x )为奇函数;当b ≠0时,函数f (x )没有奇偶性; 反 函 数:有反函数(特殊情况下:K=±1并且b=0的时候)。
补充:反函数定义:例题:定义在r 上的函数y=f (x ); y=g (x )都有反函数,且f (x-1)和g -1(x)函数的图像关于y=x 对称,若g (5)=2016,求=周 期 性:无 5)、一次函数与其它函数之间的练习 1、常用解题方法: xy b Of (x )=bxyOf (x )=kx +b R2、与曲线函数的联合运用反比例函数f(x)=xk(k≠0,k值不相等永不相交;k越大,离坐标轴越远)图象及其性质:永不相交,渐趋平行;当k>0时,函数f(x)的图象分别在第一、第三象限;当k<0时,函数f(x)的图象分别在第二、第四象限;双曲线型曲线,x轴与y轴分别是曲线的两条渐近线;既是中心对成图形也是轴对称图形定义域:),0()0,(+∞-∞ 值域:),0()0,(+∞-∞单调性:当k> 0时;当k< 0时周期性:无奇偶性:奇函数反函数:原函数本身补充:1、反比例函数的性质2、与曲线函数的联合运用(常考查有无交点、交点围城图行的面积)——入手点常有两个——⑴直接带入,利用二次函数判别式计算未知数的取值;⑵利用斜率,数形结合判断未知数取值(计算面积基本方法也基于此)3、反函数变形(如右图)1)、y=1/(x-2)和y=1/x-2的图像移动比较2)、y=1/(-x)和y=-(1/x)图像移动比较3)、f(x)=dcxbax++(c≠0且d≠0)(补充一下分离常数)(对比标准反比例函数,总结各项容)二次函数一般式:)0()(2≠++=acbxaxxf顶点式:)0()()(2≠+-=ahkxaxf两根式:)0)()(()(21≠--=axxxxaxf图象及其性质:①图形为抛物线,对称轴为,顶点坐标为②当0>a时,开口向上,有最低点当0<a时。
③当= >0时,函数图象与x轴有两个交点();当<0时,函数图象与x轴有一个交点();当=0时,函数图象与x轴没有交点。
④)0()(2≠++=acbxaxxf关系)0()(2≠=aaxxf定义域:R值域:当0>a时,值域为();当0<a时,值域为()单调性:当0>a时;当0<a时. 奇偶性:b=/≠0xyOf(x)=dcxbax++xyOf(x)=cbxax++2补充:1、a 的正/负;大/小与和函数图象的大致走向(所以,a 决定二次函数的 )2、3、二次函数的对称问题:关于x 轴对称;关于y 轴对称;关于原点对称;关于(m ,n )对称4、二次函数常见入题考法:⑴交点(交点之间的距离) ⑵值域、最值、极值、单调性 ⑶数形结合判断图形走势(选择题)指数函数)1,0()(≠>=a a a x f x,系数只能为1。
图象及其性质:1、恒过)1,0(,无限靠近x 轴;2、xa x f =)(与xx a ax f -==)1()(关于y 轴对称;但均不具有奇偶性。
3、在y 轴右边“底大图高”;在y 轴左边“底大图低”——靠近关系定 义 域:R 值 域:),0(+∞单 调 性:当0>a 时;当0<a 时。
奇 偶 性:无 反 函 数:对数函数)1,0(log )(≠>=a a x x f a 周 期 性:无 补充: 1、2、图形变换Log 21/x 和Log 2- xln (x-1)和lnx - 1对数函数(和指数函数互为反函数))1,0(log )(≠>=a a x x f a图象及其性质:①恒过)0,1(,无限靠近y 轴;②x x f a log )(=与x x x f a alog log )(1-==关于x 轴对称;③x >1时“底大图低”;0<x <1时“底大图高”(理解记忆)xyOf (x )=)1(>a a xf (x )=)10(<<a a xxyOf (x )=)1(log >a x af (x )=)10(log <<a x a定 义 域:R 值 域:),0(+∞单 调 性:当0>a 时;当0<a 时; 奇 偶 性:无 反 函 数:指数函数)1,0()(≠>=a a a x f x周 期 性:无 补充: 1、双钩函数xx x f 1)(+=(变形式 ) 图象及其性质:①两条渐近线: ②最值计算: 定 义 域: 值 域:单 调 性: 奇 偶 性:奇函数 反 函 数:定义域无反函数 周 期 性:无注意 :双沟函数在最值、数形结合、单调性的考察中用得较多,需特别注意最值得算法幂函数(考察时,一般不会太难)无论n 取任何实数,幂函数图象必然经过第一象限,并且一定不经过第四象限。
不需要背记,只要能够快速画出n=±1, ±1/2,±3,,1/3,0,的图象就行注意:掌握y=x 3的图像;掌握y=ax 3+bx 2+cx+d 的图像(当a>0,当a<0时);补充:利用数形结合,判断非常规方程的根的取值围。
例:P 393,例题10函数)(x f y 图象变换一.平移变换二.对称变换①y =f (-x )与y =f (x )关于y 轴对称; ②y =-f (x )与y =f (x )关于x 轴对称; ③y =-f (-x )与y =f (x )关于原点对称; ④y =f -1(x )与y =f (x )关于直线y =x 对称;⑤y =|f (x )|的图象可将y =f (x )的图象在x 轴下方的部分以x 轴为对称轴翻折到x 轴上方,其余部分不变.个单位b 个单位向左平移a 个单位向右a 平移个单位y=f x ()y=f x+a ())-by=f x ()+b y=f x-a ()三、伸缩变换①y=Af(x)(A>0)的图象,可将y=f(x)图象上每一点的纵坐标伸(A>1)缩(0<A<1)到原来的A倍,横坐标不变而得到.②y=f(ax)(a>0)的图象,可将y=f(x)的图象上每一点的横坐标伸(0<a<1)缩(a>1)到原来的a1,纵坐标不变而得到.四、函数及图象(大致图象)典型例题精讲例1:已知y=f(x)的图象如图2—7所示,则下列式子中能作为f(x)的解析式是(A)A.1||22+-xx B.x2-2|x|+1 C.|x2-1| D.122+-xx解析:当f(x)=1||22+-xx时,=-=-=|1|||)1|(|)(2xxxf⎪⎪⎩⎪⎪⎨⎧-<+-<≤-+<≤-≥-)1()1()01(1)10(1)1(1xxxxxxxx其图象恰好是上图.例2:画出函数y=lg|x+1|的图象.⎧->+)1()1lg(xx例3:要将函数y =12--x x 的图象通过平移变换得到y =x1的图象,需经过怎样的变换?解析:y =11-x -1,先沿x 轴方向向左平移1个单位,再沿y 轴方向向上平移1个单位,即可得到y =x1的图象. 例4:方程kx =2)2(1--x 有两个不相等的实根,数k 的取值围.解析:设y 1=kx①y 2=2)2(1--x②方程①表示过原点的直线,方程②表示半圆,其圆心(2,0),半径为1,如图2—9.易知当OA 与半圆相切时,33=OA k ,故当0≤k <33时,直线与半圆有两个交点,即0≤k <33时,原方程有两个不相等的实根.例5:作函数f (x )=x +x1的图象.分析:f (x )=x +x1不能由已知函数图象变换得到,故需对函数f (x )的性质进行研究.解析:函数的定义域是(-∞,0)∪(0,+∞),∵f (-x )=-f (x ),∴f (x )是(-∞,0)∪(0,+∞)上的奇函数, 又|f (x )|=|x +x1|=|x |+||1x ≥2,当且仅当|x |=1时等号成立,∴当x >0时y ≥2;当x <0时,y ≤-2; 当x ∈(0,1)时函数为减函数,且急剧递减;当x∈[1,+∞)时函数为增函数,且缓慢递增,又x≠0,y≠0,∴图象与坐标轴无交点,且y轴是渐近线,作出第一象限的函数的图象,再利用对称性可得函数在定义域上的图象,如图2—10所示.评述:(1)熟悉各种基本函数图的“原型”是函数作图的一项基本功;先研究函数的性质,再利用性质作图则能减少作图的盲目性,提高图象的准确性.(2)与图象有关的“辅助线”要用虚线作,以起到定形、定性、定位、定量的作用.例6:f(x)是定义在区间[-c,c]上的奇函数,其图象如图所示.令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是(B)A.若a<0,则函数g(x)的图象关于原点对称B.若a=-1,-2<b<0,则方程g(x)=0有大于2的实根C.若a≠0,b=2,则方程g(x)=0有两个实根D.若a≥1,b<2,则方程g(x)=0有三个实根解析:将f(x)图象上每点的纵坐标变为原来的a倍,横坐标不变,再将所得图象向上(b>0)或向下(b<0)平移|b|个单位,得g(x)=af(x)+b的图象.例6:(全国Ⅱ)把函数y=e x的图象按向量a=(2,3)平移,得到y=f(x)的图象,则f(x)=( C)(A)e x -3+2 (B)e x +3-2 (C)e x -2+3 (D)e x +2-3例7:(模拟)如图为函数y =m +lognx 的图象,其中m ,n 为常数,则下列结论正确的是 (D )(A)m<0,n>1 (B)m>O ,n>l (C)m>O ,0<n<1 (D)m<0,0<n<1例8:(模拟)函数y =e -|x -1|的图象大致是( D )例9:在直角坐标系xOy 中,已知△AOB 三边所在直线的方程分别为x =0,y =0,2x +3y =30,则△AOB 部和边上整点(即横、纵坐标均为整数的点)的总数是( B)A .95B .91C .88D .75解析:画出图象,补形做出长方形AOBC ,共有整点数11×16=176,而六点(0,10),(3,8),(6,6),(9,4),(12,2),(15,0)在长方形的对角线上,所以符合题意的点数为(176+6)×21=91.例10:将函数y =log21x 的图象沿x 轴方向向右平移一个单位,得到图象C ,图象C 1与C 关于原点对称,图象C 2与C 1关于直线y =x 对称,那么C 2对应的函数解析式是_____.解析:C :y =log21(x -1);由-y =log 21(-x -1)得C 1:y =log 2(-x -1);求C 1的反函数得y=-1-2x .直线有个交点.解析:(数形结合法)作y=|-x2+4x-3|的图象,知其顶点在M(2,1).过原点与点M(2,1)作直线y=kx,如图.∴曲线C与直线y=kx有四个交点.例12:作函数y=(21)|x-1|的图象.解析:(1)y=⎩⎨⎧<≥---).1(2),1(21)1(xxxx故它在区间[1,+∞)上的图象,可由y=2-x(x≥0)的图象沿x轴方向向右平移1个单位得到在区间(-∞,1)上的图象,可由y=2x(x<0)的图象沿x轴方向向右平移1个单位得到.例13:已知函数y=f(x)(x∈R)满足f(a+x)=f(a-x),求证y=f(x)的图象关于直线x =a对称.证明:设p(x0,y0)是y=f(x)图象上的任一点,则有y0=f(x0),设点P关于直线x=a的对称点为p′(x′,y′),则有⎩⎨⎧='-='2yyxax,即⎩⎨⎧'='-=yyxax2由y0=f(x0).. ⎭⎬⎫-=+'-+='-='⇒)()()]([)2(x a f x a f x a a f x a f y 又⇒ y ′=f [a -(a -x ′)]=f (x ′). 即点p ′(x ′,y ′)也在y =f (x )的图象上.∴y =f (x )的图象关于直线x =a 对称.例14:画出函数y =12+x 的图象,并利用此图象判定方程12+x =x +a 有两个不同的实数解时,实数a 所满足的条件.解析:图象是抛物线y 2=2x +1在y ≥0上的部分.把y =x +a 代入y 2=2x +1,得(x +a )2=2x +1,即x 2+2(a -1)x +a 2-1=0,由Δ=0得a =1,此时直线与抛物线相切.又因抛物线顶点是(-21,0), 可知当直线过点(-21,0)时,即a =21时直线与抛物线有两交点, 故当21≤a <1时直线与此抛物线有两个交点,即原方程有两不同实数解.。
