初一数学全等三角形难题全集

三角形的边角与全等三角形一、选择题1．如图，给出下列四组条件：①AB DE BC EF AC DF ===，，； ②AB DE B E BC EF =∠=∠=，，； ③B E BC EF C F ∠=∠=∠=∠，，； ④AB DE AC DF B E ==∠=∠，，．其中，能使ABC DEF △≌△的条件共有（） A ．1组 B ．2组 C ．3组 D ．4组2、已知图2中的两个三角形全等，则∠α度数是（）A.72°B.60°C.58°D.50° 3、如图，在等腰梯形ABCD 中，AB ＝DC ，AC 、BD 交于点O ，则图中全等三角形共有（） A ．2对 B ．3对C ．4对D ．5对ABC DO4、如图，将Rt △ABC(其中∠B ＝340，∠C ＝900）绕A 点按顺时针方向旋转到△AB 1 C 1的位置，使得点C 、A 、B 1 在同一条直线上，那么旋转角最小等于（） A.560B.680C.1240D.18005、如图，ACB A C B '''△≌△，BCB ∠'=30°，则ACA '∠的度数为（） A ．20° B ．30° C ．35° D ．40°6、尺规作图作AOB ∠的平分线方法如下：以O 为圆心，任意长为半径画弧交OA 、OB 于C 、D ，再分别以点C 、D 为圆心，以大于12CD 长为半径画弧，两弧交于点P ，作射线OP ，由作法得OCP ODP △≌△的根据是（） A ．SAS B ．ASA C ．AAS D ．SSS7、图(三)、图(四)、图(五)分别表示甲、乙、丙三人由A 地到B 地的路线图。

已知甲的路线为：A →C →B 。

乙的路线为：A →D →E →F →B ，其中E 为AB 的中点。

丙的路线为：A →I →J →K →B ，其中J 在AB 上，且AJ >JB 。

全等三角形难题集

全等三角形难题集引言全等三角形是初等数学中的一个重要概念，也是几何学的基础之一。

全等三角形指的是在形状、大小、角度等各方面完全相同的两个三角形。

解决全等三角形的难题对于培养学生的逻辑思维能力和几何直观能力具有重要意义。

本文将介绍一些关于全等三角形的难题，希望能够帮助读者更好地理解和掌握全等三角形的相关知识。

难题一：全等三角形的判定给定两个三角形ABC和XYZ，判断它们是否全等。

请根据下列条件判断并给出理由：1.两个三角形的三边分别相等，即AB = XY，BC = YZ，AC = XZ。

2.两个三角形的三个角度分别相等，即∠A = ∠X，∠B = ∠Y，∠C = ∠Z。

3.两个三角形的两边和夹角分别相等，即AB = XY，AC = XZ，∠BAC = ∠YXZ。

理由：1.两个三角形的三边分别相等，根据全等三角形的定义，可以判断它们为全等三角形。

因为边长相等可以保证三角形的形状和大小完全相同。

2.两个三角形的三个角度分别相等，根据全等三角形的定义，可以判断它们为全等三角形。

因为角度相等可以保证三角形的形状和大小完全相同。

3.两个三角形的两边和夹角分别相等，根据全等三角形的定义，可以判断它们为全等三角形。

因为两边和夹角的相等关系可以保证三角形的形状和大小完全相同。

综上所述，根据给定的条件判断两个三角形ABC和XYZ为全等三角形。

难题二：全等三角形的性质全等三角形具有以下性质，请证明或反驳：1.全等三角形的周长相等。

2.全等三角形的面积相等。

3.全等三角形的高度和中线相等。

证明或反驳：1.全等三角形的周长相等：假设三角形ABC和XYZ为全等三角形，根据全等三角形的定义，可以知道它们的边长相等。

所以，周长也相等。

2.全等三角形的面积相等：假设三角形ABC和XYZ为全等三角形，根据全等三角形的定义，可以知道它们的底边和高相等。

由于面积等于底边乘以高的一半，所以面积也相等。

3.全等三角形的高度和中线相等：反驳。

全等三角形难题含答案

全等三角形经典证明：AB=10，AC=2，D 是BC 中点，AD 是整数，求AD1.：D 是AB 中点，∠ACB=90°，求证：12CD AB2.：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23. ：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC4.：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C5.：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE6. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

7.：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠CCDBAADBC8、：AB=CD ，∠A=∠D ，求证：∠B=∠C9．〔5分〕如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．10．〔5分〕如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA11．〔6分〕如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，假设AB =CD ，AF =CE ，BD 交AC 于点M ．〔1〕求证：MB =MD ，ME =MF〔2〕当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？假设成立请给予证明；假设不成立请说明理由．12．〔7分〕：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，〔1〕求证：△AED ≌△EBC ．〔2〕观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．〔直接写出结果，不要求证明〕：/13.〔7分〕如图，△ABC 中，∠BAC =90度，AB =AC ，BD是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．14、〔10分〕如图：DF=CE ，AD=BC ，∠D=∠C 。

全等三角形证明难题

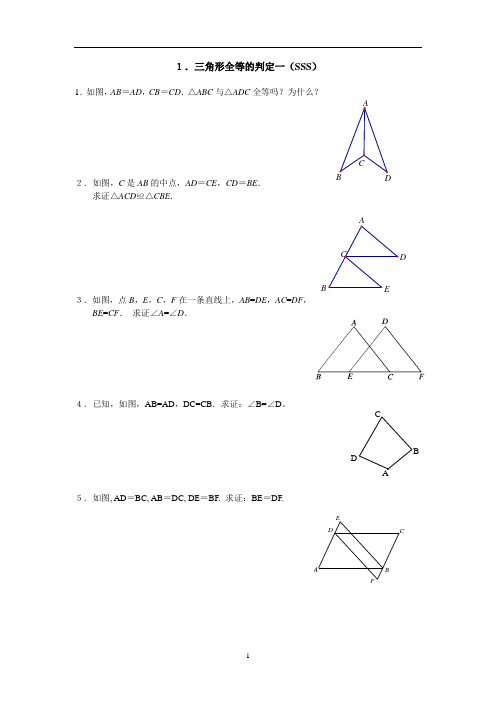
FE DCBA1．如图，AB ＝AD ，CB ＝CD ．△ABC 与△ADC 全等吗？为什么？２．如图，C 是AB 的中点，AD ＝CE ，CD ＝BE ．求证△ACD ≌△CBE ．３．如图，点B ，E ，C ，F 在一条直线上，AB =DE ，AC =DF ，BE =CF ．求证∠A =∠D ．４．已知，如图，AB=AD ，DC=CB ．求证：∠B=∠D 。

５．如图, AD ＝BC, AB ＝DC, DE ＝BF. 求证：BE ＝DF.AD C B1．如图，AC 和BD 相交于点O ，OA =OC ，OB =OD ．求证DC ∥AB ．2．如图，△ABC ≌△A B C '''，AD ，A D ''分别是△ABC ，△A B C '''的对应边上的中线，AD 与A D ''有什么关系？证明你的结论．3．如图，已知AC ⊥AB ，DB ⊥AB ，AC ＝BE ，AE ＝BD ，试猜想线段CE 与DE 的大小与位置关系，并证明你的结论．4．已知：如图，AD ∥BC ，AD=CB ，求证：△ADC ≌△CBA ．5．已知：如图AD ∥BC ，AD=CB ，AE=CF 。

求证：△AFD ≌△CEB ．6．已知，如图，AB=AC ，AD=AE ，∠1=∠2。

求证：△ABD ≌△ACE ．AC EDBAE B CFDAB CD2A CBE1H F ED CB A 7．已知:如图,点B,E,C,F 在同一直线上,AB ∥DE,且AB=DE,BE=CF. 求证:AC ∥DF ．8．已知:如图,AD 是BC 上的中线 ,且DF=DE ．求证:BE ∥CF ．9．如图, 在△ABC 中, 分别延长中线BE 、CD 至F 、H, 使EF ＝BE, DH ＝CD, 连结AF 、AH ．求证：(1) AF ＝AH ；(2)点A 、F 、H 三点在同一直线上； (3)HF ∥BC.10．如图, 在△ABC 中, AC ⊥BC, AC ＝BC, 直线EF 交AC 于F, 交AB 于E, 交BC 的延长线于D, 连结AD 、BF, CF ＝CD. 求证：BF ＝AD, BF ⊥AD.11．证明：如果两个三角形有两条边和其中一边上的中线对应相等，那么这两个三角形全等．（提示：首先分清已知和求证，然后画出图形，再结合图形用数学符号表示已知和求证）AB E F12．证明：如果两个三角形有两条边和第三边上的中线对应相等，那么这两个三角形全等．13.已知：如图，正方形ABCD ，BE =CF ，求证：(1)AE =BF ；（2）AE ⊥BF . 14．已知：E 是正方形ABCD 的边长AD 上一点，BF 平分∠EBC ，交CD 于F ，求证BE=AE+CF.（提示：旋转构造等腰）15.如图,△ABD 和△ACE 是△ABC 外两个等腰直角三角形,∠BAD=∠CAE=900.（1）判断CD 与BE 有怎样的数量关系;（2）探索DC 与BE 的夹角的大小.（3）取BC 的中点M ，连MA ，探讨MA 与DE 的位置关系。

全等三角形难题(含答案.解析)

∵∠BFE+∠CFE=180o
∴∠D=∠CFE
又∵∠DCE=∠FCE
CE平分∠BCD
CE=CE
∴⊿DCE≌⊿FCE（AAS）
∴CD=CF
∴BC=BF+CF=AB+CD
8. 已知：AB//ED，∠EAB=∠BDE，AF=CD，EF=BC，求证：∠F=∠C
ED
C
F
AB
AB‖ED，得：∠EAB+∠AED=∠BDE+∠ABD=180度，
1＜AD＜3
∴AD=2
1
2.已知：D是AB中点，∠ACB=90°，求证：
CDAB
2
A
D
CB
延长CD与P，使D为CP中点。连接AP,BP
∵DP=DC,DA=DB
∴ACBP为平行四边形
又∠ACB=90
∴平行四边形ACBP为矩形
∴AB=CP=1/2AB
3.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2
AB=AE,BF=EF,
∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF
∴三角形ABF和三角形AEF全等。
∴∠BAF=∠EAF (∠1=∠2)。
4.已知：∠1=∠2，CD=DE，EF//AB，求证：EF=AC
A
2
1
F
C
D
E
B
过C作CG∥EF交AD的延长线于点G
CG∥EF，可得，∠EFD＝CGD
DE＝DC
∠FDE＝∠GDC（对顶角）
∴△EFD≌△CGD
EF＝CG
∠CGD＝∠EFD
又，EF∥AB
∴，∠EFD＝∠1
∠1=∠2
∴∠CGD＝∠2

(完整版)全等三角形难题超级好题汇总

1. 如图，已知等边△ ABC，P在AC延长线上一点，以PA为边作等边△ APE,EC延长线交BP于M，连接AM,求证：（1）BP=CE；（2）试证明：EM-PM=AM.3.已知，如图①所示，在△ABC和△ ADE中，AB AC，AD AE，BAC DAE ，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：① BE CD ；② AM AN ；2）在图①的基础上，将△ADE 绕点 A 按顺时针方向旋转180o，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立4、如图１，以△ ABC的边AB 、AC为边分别向外作正方形ABDE和正方形ACFG ，连结EG ，试判断△ABC与△AEG 面积之间的关系，并说明理由．2、点 C 为线段AB 上一点，△ ACM, △ CBN 都是等边三角形，线段AN,MC 交于点E，BM,CN交于点F。

求证：1）AN=MB. （2）将△ ACM 绕点 C 按逆时针方向旋转一定角度，如图②所示，其他条件不变，1）中的结论是否依然成立？（3）AN 与BM 相交所夹锐角是否发生变化。

B图①CB图１）F7、已知 Rt △ ABC 中， AC BC ，∠C 90，D 为AB 边的中点， EDF 90°，EDF 绕 D 点旋转，它的两边分别交 AC 、 CB （或它们的延长线）于 E 、 F．1 当 EDF 绕 D 点旋转到 DE AC 于E时（如图1），易证S △DEF S △CEF S △ ABC ．DEF CEF 2 ABC当 EDF 绕 D 点旋转到 DE 和 AC 不垂直时，在图 2 和图 3 这两种情况下，上述结论是否成立？若成立，请给予证明；8. 已知 AC//BD, ∠CAB 和∠ DBA 的平分线 EA 、EB 与 CD 相交于点 E. 求证 :AB=AC+BD.5、如图所示，已知△ ABC 和△ BDE 都是等边三角形，且 A 、 HB 平分∠ AHD ；④∠ AHC=60 °，⑤△ BFG 是等边三角形；⑥ A ．3个 B ．4 个 C ．5个 D ．6 个B 、D 三点共线．下列结论：① AE=CD ；② BF=BG ；③ FG ∥AD ．其中正确的有（）6. 如图所示，△ ABC 是等腰直角三角形，∠ ACB ＝90°，AD 交 AD 于点 F ，求证：∠ ADC ＝∠ BDE ．是 BC 边上的中线，过 C 作 AD 的垂线，交 AB 于点 E ，、 S △CEF 、 S △ABC 又有怎样的数量关系？请写出你的猜想，不需证明．图1若不成立，S △ DEF 图2图210、已知，如图1，在四边形ABCD 中，BC>AB，AD=DC，BD 平分∠ ABC 。

全等三角形难题集锦

1、（2007 年）已知：如图，△ ABC中，∠ ABC=45 °，CD⊥AB于D，BE平分∠ ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连结DH与BE相交于点G。

（!）求证：BF=AC；1（2）求证：CE= BF；2（3）CE与BC 的大小关系如何？试证明你的结论2.（2012?江）已知△ABC为等边三角形，点D为直线BC上的一动点（点D不与B、C 重合），以AD 为边作菱形ADEF（A、D、E、F按逆时针排列），使∠ DAF=60°，连接CF．（1）如图1，当点 D 在边BC上时，求证：① BD=CF；② AC=CF+CD；（2）如图2，当点D在边BC的延长线上且其他条件不变时，结论AC=CF+CD是否成立？若不成立，请写出AC、CF、CD 之间存在的数量关系，并说明理由；（3）如图3，当点 D 在边BC的延长线上且其他条件不变时，补全图形，并直接写出AC、CF、CD 之间存在的数量关系．3（08中考第24题）如图14-1，在△ABC中，BC边在直线l上，AC⊥BC，且AC = BC．△ EFP的边FP也在直线l 上，边EF与边AC 重合，且EF= FP．（1）在图14-1 中，请你通过观察、测量，猜想并写出AB与AP所满足的数量关系和位置关系；（2）将△ EFP沿直线l 向左平移到图14-2 的位置时，EP交AC 于点Q，连结AP，BQ．猜想并写出BQ 与AP 所满足的数量关系和位置关系，请证明你的猜想；（3）将△ EFP沿直线l 向左平移到图14-3 的位置时，EP的延长线交AC的延长线于点Q，连结AP，BQ．你认为（2）中所猜想的BQ与AP的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由．4.如图1、图2、图3，△ AOB，△ COD 均是等腰直角三角形，∠ AOB＝∠COD＝90o，（1）在图1中，AC与BD相等吗，有怎样的位置关系？请说明理由。

全等三角形难题集锦超级好

1.如图，已知等边△ABC ，P 在AC 延长线上一点，以PA 为边作等边△APE,EC 延长线交BP 于M ，连接AM,求证：（1）BP=CE ；（2）试证明：EM-PM=AM.2.已知，如图①所示，在ABC △和ADE △中，AB AC =，AD AE =，BAC DAE ∠=∠，且点B A D ，，在一条直线上，连接BE CD M N ，，，分别为BE CD ，的中点．（1）求证：①BE CD =；②AN AM =；（2）在图①的基础上，将ADE △绕点A 按顺时针方向旋转180，其他条件不变，得到图②所示的图B E3.已知：如图，ABC △是等边三角形，过AB 边上的点D 作DG BC ∥，交AC 于点G ，在GD 的延长线上取点E ，使DE DB ，连接AE CD ，．（1）求证：AGE DAC △≌△；（2）过点E 作EF DC ∥，交BC 于点F ，请你连接AF ，并判断AEF △是怎样的三角形，试证明你的结论．CGAEDBF4、在ABC △中，2120AB BC ABC ==∠=，°，将ABC △绕点B 顺时针旋转角α(0<°α90)<°得A BC A B 111△，交AC 于点E ，11A C 分别交AC BC 、于D F 、两点．如图1，观察并猜想，在旋转过程中，线段1EA 与FC 有怎样的数量关系？并证明你的结论；ADBECF 1A1CADBECF 1A1C5. 如图所示，△ABC 是等腰直角三角形，∠ACB ＝90°，AD 是BC 边上的中线，过C 作AD 的垂线，交AB 于点E ，交AD 于点F ，求证：∠ADC ＝∠BDE ．ABCD EF6已知Rt ABC △中，90AC BC C D ==︒，∠，为AB 边的中点，90EDF ∠=°， EDF ∠绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F ．当EDF ∠绕D 点旋转到DE AC ⊥于E 时（如图1），易证12DEF CEF ABC S S S +=△△△．当EDF ∠绕D 点旋转到DE AC 和不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，DEF S △、CEF S △、ABC S △又有怎样的数量关系？请写出你的猜想，不需证明．A EC F BD图1图3ADFECBADBCE 图2F7、已知AC//BD,∠CAB和∠DBA的平分线EA、EB与CD相交于点E.求证:AB=AC+BD.8.等边△ABC，D为△ABC外一点，∠BDC=120°，BD=DC．∠MDN=60°射线DM与直线AB相交于点M，射线DN与直线AC相交于点N，①当点M、N在边AB、AC上，且DM=DN时，直接写出BM、NC、MN之间的数量关系．②当点M、N在边AB、AC上，且DM≠DN时，猜想①中的结论还成立吗？若成立，请证明．③当点M、N在边AB、CA的延长线上时，请画出图形，并写出BM、NC、MN之间的数量关系．DCBA9.如图1，BD 是等腰ABC Rt Δ的角平分线， 90=∠BAC .（1）求证BC =AB +AD ；（2）如图2，BD AF ⊥于F ，BD CE ⊥交延长线于E ，求证：BD =2CE ；10、如图，四边形ABCD 中，AC 平分∠BAD ，CE ⊥AB 于E ，AD+AB=2AE ，则∠B 与∠ADC 互补.为什么？ABCD FE 图2DBEAC图十一11如图，在△ABC 中∠ABC,∠ACB 的外角平分线交P.求证:AP 是∠BAC 的角平分线12、如图在四边形ABCD 中，AC 平分∠BAD ，∠ADC ＋∠ABC ＝180度，CE ⊥AD 于E ，猜想AD 、AE 、AB 之间的数量关系，并证明你的猜想，EBAC图2DCB13如图，已知在△ABC 中，∠B=60°，△ABC 的角平分线AD,CE 相交于点O ，求证：OE=OD14如图所示，已知在△AEC 中，∠E=90°，AD 平分∠EAC ，DF ⊥AC ，垂足为F ，DB=DC ，求证：BE=CF15如图①，OP 是∠MON 的平分线，请你利用该图形画一对以OP 所在直线为对称轴的全等三角形。

全等三角形难题集锦超级好

2、点C 为线段AB 上一点，△ ACM, △ CBN 都是等边三角形，线段 AN,MC 交于点E ，BM,CN 交于点F 。

求证:(1) AN=MB.(2)将厶ACM 绕点C 按逆时针方向旋转一定角度，如图②所示，其他条件不变，(1)中的结论是否依然成立？ ( 3) AN 与BM 相交所夹锐角是否发生变化。

5.已知，如图①所示，在 △ ABC 和厶ADE 中，AB AC ，AD AE ， BAC DAE ，且点B ，A ，D 在一条直线上，连接 BE ，CD ，M ，N 分别为BE ，CD 的中点.(1)求证：① BE CD :② AM AN ；(2)在图①的基础上，将 △ ADE 绕点A 按顺时针方向旋转180°，其他条件不变，得到图出(1)中的两个结论是否仍然成立6.如图，C 为线段AE 上一动点(不与点 A ，E 重合)，在AE 同侧分别作正三角形ABC 和正三角形CDE AD 与BE 交于点O, AD 与BC 交于点P, BE 与CD 交于点 Q 连结PQ 以下五个结论：① AD=BE ;② PQ // AE ;③ AP=BQ;④DE=DP ⑤ / AOB=60 ⑥CP=CQ ⑦厶CPQ 为等边三角形. ⑧共有2对全等三角形⑨CO 平分/ AOP ⑩CO 平分/ BCD恒成立的结论有 _________________ (把你认为正确的序号都填上).10.已知：如图，△ ABC 是等边三角形, 使 DE DB ，连接 AE ，CD .(1)求证：△ AGE ◎△ DAC ；过AB 边上的点D 作DG // BC ，交AC 于点G ，在GD 的延长线上取点 E ， 1.如图，已知等边厶ABC P 在AC 延长线上一点，以PA 为边作等边△ APE,EC 延长线交BP 于M 连接AM,求证：(1) BP=CE(2)试证明：EM-PM=AM.（把你认为正确的序号都填A. 3个1、在厶 ABC 中，AB BC 2, ABC 120°将△ ABC 绕(0 ° 90 °得厶ABG , AB 交AC 于点E , A 1C 1分别点B 顺时针旋转角交 AC 、BC 于 D 、F2.如图所示，△ ABC 是等腰直角三角形，/ ACB= 90° AB 于点E ,交AD 于点F ,求证：/ ADC=Z BDE（2）过点E 作EF // DC ,交BC 于点F ,请你连接AF ,并判断△ AEF 是怎样的三角形，试证明你的结论.11、如图1,以 △ ABC 的边AB 、AC 为边分别向外作正方形 ABDE 和正方形 ACFG ，连结EG ，试判断△ ABC与厶AEG 面积之间的关系，并说明理由.9如图，C 为线段AE 上一动点（不与点A, E 重合），在AE 同侧分别作正三角形 AD 与BC 交于点P, BE 与CD 交于点Q,连结PQ 以下五个结论:① AD=BE ; ② PQ // AE ③ AP=BQ ④ DE=DP ⑤ / AOB=60 .恒成立的结论有 ________________ 10.如图所示，已知△ ABC^n ^ BDE 都是等边三角形，且 A 、B 、D 三点共线.下列结论： ①AE=CD ②BF=BG ③HB 平分/ AHD ④/ AHC=60，⑤A BFG 是等边三角形； ⑥FG// AD.其中正确的有（）两点•如图1,观察并猜想，在旋转过程中，线段EA 与FC 有怎样的数量关系？并证明你的结论;Q113. 如图1，四边形ABCD 是正方形，M 是AB 延长线上一点。

全等三角形难题集锦超级好题汇总

1.如图，已知等边△ABC ，P 在AC 延长线上一点，以PA 为边作等边△APE,EC 延长线交BP 于M ，连接AM,求证：（1）BP=CE ；（2）试证明：EM-PM=AM.2、点C 为线段AB 上一点，△ACM, △CBN 都是等边三角形，线段AN,MC 交于点E ，BM,CN 交于点F 。

求证：（1）AN=MB.（2）将△ACM 绕点C 按逆时针方向旋转一定角度，如图②所示，其他条件不变，（1）中的结论是否依然成立（3）AN与BM 相交所夹锐角是否发生变化。

3.已知，如图①所示，在ABC △和ADE △中，AB AC =，ADAE =，BAC DAE ∠=∠，且点B A D ，，在一条直线上，连接BE CD M N ，，，分别为BE CD ，的中点．（1）求证：①BE CD =；②AN AM =；（2）在图①的基础上，将ADE △绕点A 按顺时针方向旋转180，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立.22题PB EAB A B N CNA4、如图１，以ABC △的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ，连结EG ，试判断ABC △与AEG △面积之间的关系，并说明理由．5、如图所示，已知△ABC 和△BDE 都是等边三角形，且A 、B 、D 三点共线．下列结论：①AE=CD ；②BF=BG ；③HB 平分∠AHD ；④∠AHC=60°，⑤△BFG 是等边三角形；⑥FG ∥AD ．其中正确的有（）A ．3个B ．4个C ．5个D ．6个6. 如图所示，△ABC 是等腰直角三角形，∠ACB ＝90°，AD 是BC 边上的中线，过C 作AD 的垂线，交AB 于点E ，交AD 于点F ，求证：∠ADC ＝∠BDE ．AGFCBDE（图１）ABC DEF7、已知Rt ABC △中，90AC BC C D ==︒，∠，为AB 边的中点，90EDF ∠=°，EDF ∠绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F ．当EDF ∠绕D 点旋转到DE AC ⊥于E 时（如图1），易证12DEF CEFABC S S S +=△△△．当EDF ∠绕D 点旋转到DE AC 和不垂直时，在图2和图3这两种情况下，上述结论是否成立若成立，请给予证明；若不成立，DEF S △、CEF S △、ABC S △又有怎样的数量关系请写出你的猜想，不需证明．8.已知AC 求证:AB=AC+BD.A E C FBD图1图3ADFECBADBCE 图2FDCBA9.如图1，BD 是等腰ABC Rt Δ的角平分线， 90=∠BAC .（1）求证BC =AB +AD ；（2）如图2，BD AF ⊥于F ，BD CE ⊥交延长线于E ，求证：BD =2CE ；10、已知，如图1，在四边形ABCD 中，BC ＞AB ，AD=DC ，BD 平分∠ABC 。

全等三角形难题(含答案)

全等三角形经典证明已知：AB=10，AC=2，D 是BC 中点，AD 是整数，求AD1. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB2. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC4. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C5. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BECDB AADBC6. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

7.已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C8、已知：AB=CD ，∠A=∠D ，求证：∠B=∠C9．（5分）如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ． 10．（5分）如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA 11．（6分）如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，DCB A FEBD 交AC 于点M ．（1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．12．（7分）已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：/13.（7分）如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．14、（10分）如图：DF=CE ，AD=BC ，∠D=∠C 。

(完整)全等三角形难题及答案

1、如图，在ABC ∆中，AB BC =，90ABC ∠=。

F 为AB 延长线上一点，点E 在BC 上，BE BF =,连接,AE EF 和CF 。

求证:AE CF =.2、如图,D 是ABC ∆的边BC 上的点，且CD AB =，ADB BAD ∠=∠，AE 是ABD ∆的中线。

求证：2AC AE =.3、如图，在ABC ∆中，AB AC >，12∠=∠,P 为AD 上任意一点。

求证：AB AC PB PC ->-。

4、如图，BD 、CE 分别是ABC ∆的边AC 、AB 上的高，F 、G 分别是线段DE 、BC 的中点求证:DE FG ⊥5、如图所示，△ABC 是等腰直角三角形，∠ACB ＝90°，AD 是BC 边上的中线，过C 作AD 的垂线,交AB 于点E,交AD 于点F ，求证:∠ADC＝∠BDE6、如图,在锐角ABC ∆中，已知C ABC ∠=∠2,ABC ∠的平分线BE 与AD 垂直，垂足为D ，若cm BD 4=，求AC 的长参考答案1、思路分析：可以利用全等三角形来证明这两条线段相等，关键是要找到这两个三角形.以线段AE 为边的ABE ∆绕点B 顺时针旋转90到CBF ∆的位置，而线段CF 正好是CBF ∆的边，故只要证明它们全等即可。

解答过程：90ABC ∠=，F 为AB 延长线上一点∴90ABC CBF ∠=∠=在ABE ∆与CBF ∆中AB BC ABC CBF BE BF =⎧⎪∠=∠⎨⎪=⎩∴ABE CBF ∆≅∆(SAS)∴AE CF =。

解题后的思考：利用旋转的观点，不但有利于寻找全等三角形，而且有利于找对应边和对应角。

小结：利用三角形全等证明线段或角相等是重要的方法，但有时不容易找到需证明的三角形。

这时我们就可以根据需要利用平移、翻折和旋转等图形变换的观点来寻找或利用辅助线构造全等三角形。

2、思路分析：要证明“2AC AE =”，不妨构造出一条等于2AE 的线段，然后证其等于AC 。

全等三角形难题集锦

1、（2007年成都）已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC 于E，与CD相交于点F，H是BC边的中点，连结DH与BE相交于点G。

(!)求证：BF=AC；(2)求证：CE=12 BF；(3)CE与BC的大小关系如何？试证明你的结论。

2.（2012•内江）已知△ABC为等边三角形，点D为直线BC上的一动点（点D不与B、C重合），以AD为边作菱形ADEF（A、D、E、F按逆时针排列），使∠DAF=60°，连接CF．（1）如图1，当点D在边BC上时，求证：①BD=CF；②AC=CF+CD；（2）如图2，当点D在边BC的延长线上且其他条件不变时，结论AC=CF+CD是否成立？若不成立，请写出AC、CF、CD之间存在的数量关系，并说明理由；（3）如图3，当点D在边BC的延长线上且其他条件不变时，补全图形，并直接写出AC、CF、CD之间存在的数量关系．3（08河北中考第24题）如图14-1，在△ABC 中，BC 边在直线l 上，AC ⊥BC ，且AC = BC ．△EFP 的边FP 也在直线l 上，边EF 与边AC 重合，且EF =FP ．（1）在图14-1中，请你通过观察、测量，猜想并写出AB 与AP 所满足的数量关系和位置关系；（2）将△EFP 沿直线l 向左平移到图14-2的位置时，EP 交AC 于点Q ，连结AP ，BQ ．猜想并写出BQ 与AP 所满足的数量关系和位置关系，请证明你的猜想；（3）将△EFP 沿直线l 向左平移到图14-3的位置时，EP 的延长线交AC 的延长线于点Q ，连结AP ，BQ ．你认为（2）中所猜想的BQ 与AP 的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由．4.如图1、图2、图3，△AOB ，△COD 均是等腰直角三角形，∠AOB ＝∠COD ＝90º，（1）在图1中，AC 与BD 相等吗，有怎样的位置关系？请说明理由。

全等三角形的的性质与判定难题50道(含详细答案)

全等三角形的的性质与判定难题50道1．边长为a 的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），⋯，按此方式依次操作，则第6个正六边形的边长为( )A ．511()32a ⨯B ．511()23a ⨯C ．611()32a ⨯D ．611()23a ⨯2．如图，在等边ABC ∆中，点D ，E 分别在边BC ，AC 上，且//DE AB ，过点E 作EF DE ⊥，交BC 的延长线于点F ，（1）求F ∠的度数；（2）若3CD =，求DF 的长．3．数学课上，李老师出示了如下的题目：“在等边三角形ABC 中，点E 在AB 上，点D 在CB 的延长线上，且ED EC =，如图，试确定线段AE 与DB 的大小关系，并说明理由”．小敏与同桌小聪讨论后，进行了如下解答：（1）特殊情况，探索结论当点E 为AB 的中点时，如图1，确定线段AE 与DB 的大小关系，请你直接写出结论：AEDB （填“>”，“ <”或“=” )．（2）特例启发，解答题目解：题目中，AE 与DB 的大小关系是：AE DB （填“>”，“ <”或“=” )．理由如下：如图2，过点E 作//EF BC ，交AC 于点F ．（请你完成以下解答过程）（3）拓展结论，设计新题在等边三角形ABC 中，点E 在直线AB 上，点D 在直线BC 上，且ED EC =．若ABC ∆的边长为1，2AE =，求CD 的长（请你直接写出结果）．4．如图，过等边ABC ∆的边AB 上一点P ，作P E A C ⊥于E ，Q 为BC 延长线上一点，且PA CQ =，连PQ 交AC 边于D ．（1）求证：PD DQ =；（2）若ABC ∆的边长为1，求DE 的长．5．如图所示，已知等边ABC ∆的边长为a ，P 是ABC ∆内一点，//PD AB ，//PE BC ，//PF AC ，点D 、E 、F 分别在BC 、AC 、AB 上，猜想：PD PE PF ++= ，并证明你的猜想．6．如图，已知ABC ∆和CDE ∆均为等边三角形，且点B 、C 、D 在同一条直线上，连接AD 、BE ，交CE 和AC 分别于G 、H 点，连接GH ．（1）请说出AD BE =的理由；（2）试说出BCH ACG ∆≅∆的理由；（3）试猜想：CGH ∆是什么特殊的三角形，并加以说明．7．如图，已知ABC ∆是边长为6cm 的等边三角形，动点P ，Q 同时从A 、B 两点出发，分别沿AB 、BC 方向匀速运动，其中点P 运动的速度是1/cm s ，点Q 运动的速度是2/cm s ，当点Q 运动到点C 时，P ，Q 都停止运动．（1）出发后运动2s 时，试判断BPQ ∆的形状，并说明理由；那么此时PQ 和AC 的位置关系呢？请说明理由；（2）设运动时间为t ，BPQ ∆的面积为S ，请用t 的表达式表示S ．8．已知：在等边ABC ∆中，点D 、E 、F 分别为边AB 、BC 、AC 的中点，点G 为直线BC 上一动点，当点G 在CB 延长线上时，有结论“在直线EF 上存在一点H ，使得DGH ∆是等边三角形”成立（如图①)，且当点G 与点B 、E 、C 重合时，该结论也一定成立．问题：当点G 在直线BC 的其它位置时，该结论是否仍然成立？请你在下面的备用图②③④中，画出相应图形并证明相关结论．9．已知点C 为线段AB 上一点，分别以AC 、BC 为边在线段AB 同侧作ACD ∆和BCE ∆，且CA CD =，CB CE =，ACD BCE ∠=∠，直线AE 与BD 交于点F ，（1）如图1，若60ACD ∠=︒，则AFB ∠= ；如图2，若90ACD ∠=︒，则AFB ∠= ；如图3，若120ACD ∠=︒，则AFB ∠= ；（2）如图4，若ACD α∠=，则AFB ∠= （用含α的式子表示）；（3）将图4中的ACD ∆绕点C 顺时针旋转任意角度（交点F 至少在BD 、AE 中的一条线段上），变成如图5所示的情形，若ACD α∠=，则AFB ∠与α的有何数量关系？并给予证明．10．如图1，ABC ∆为等边三角形，面积为S ．1D 、1E 、1F 分别是ABC ∆三边上的点，且11112AD BE CF AB ===，连接11D E 、11E F 、11F D ，可得△111D E F 是等边三角形，此时△11AD F 的面积114S S =，△111D E F 的面积114S S =．（1）当2D 、2E 、2F 分别是等边ABC ∆三边上的点，且22213AD BE CF AB ===时如图2，①求证：△222D E F 是等边三角形；②若用S 表示△22AD F 的面积2S ，则2S = ；若用S 表示△222D E F 的面积2S '，则2S '= ．（2）按照上述思路探索下去，并填空：当n D 、n E 、n F 分别是等边ABC ∆三边上的点，11n n n AD BE CF AB n ===+时，(n 为正整数）△n n n D E F 是三角形；若用S 表示△n n AD F 的面积n S ，则n S = ；若用S 表示△n n n D E F 的面积n S '，则n S '= ．11．如图，在等边ABC ∆的三边上分别取点D 、E 、F ，使AD BE CF ==．（1）试说明DEF ∆是等边三角形；（2）连接AE 、BF 、CD ，两两相交于点P 、Q 、R ，则PQR ∆为何种三角形？试说明理由．12．如图所示，一个六边形的六个内角都是120︒，其中连续四边的长依次是1、9、9、5．求这个六边形的周长．13．如图，已知D 是ABC ∆的边BC 上的一点，CD AB =，BDA BAD ∠=∠，AE 是ABD ∆的中线．（1）若60B ∠=︒，求C ∠的值；（2）求证：AD 是EAC ∠的平分线．14．如图，ABC ∆为等边三角形，BD 平分ABC ∠交AC 于点D ，//DE BC 交AB 于点E ．（1）求证：ADE ∆是等边三角形．（2）求证：12AE AB =．15．如图．在等边ABC ∆中，ABC ∠与ACB ∠的平分线相交于点O ，且//OD AB ，//OE AC ．（1）试判定ODE ∆的形状，并说明你的理由；（2）线段BD 、DE 、EC 三者有什么关系？写出你的判断过程．16．如图，ABC ∆是等边三角形，DF AB ⊥，DE CB ⊥，EF AC ⊥，求证：DEF ∆是等边三角形．17．用三根火柴棒可以搭成一个等边三角形，你能用9根火柴搭出5个等边三角形吗？ 18．如图，ABC ∆是等边三角形，AD 是高，并且AB 恰好是DE 的垂直平分线．求证：ADE ∆是等边三角形．19．如图，60AOB ∠=︒，OC 平分AOB ∠，C 为角平分线上一点，过点C 作CD OC ⊥，垂足为C ，交OB 于点D ，//CE OA 交OB 于点E ．（1）判断CED ∆的形状，并说明理由；（2）若3OC=，求CD的长．20．如图，在ABC∆中，AB AC=，120BAC∠=︒，D、F分别为AB、AC的中点，且DE AB⊥，FG AC⊥，点E、G在BC上，18BC cm=，求线段EG的长．（提示：需要添加辅助线）21．已知，如图，ABC∆是正三角形，D，E，F分别是各边上的一点，且AD BE CF==．请你说明DEF∆是正三角形．22．如图所示，DEF∆是等边三角形，且123∠=∠=∠，试问：ABC∆是等边三角形吗？请说明理由．23．如图，ABC∆为等边三角形，BD平分ABC∠，//DE BC．（1）求证：ADE∆是等边三角形；（2）求证：12AE AB=．24．如图ABC∆是等边三角形（1）如图①，//∆是等边三角形；DE BC，分别交AB、AC于点D、E．求证：ADE（2）如图②，ADE∆仍是等边三角形，点B在ED的延长线上，连接CE，判断BEC∠的度数及线段AE、BE、CE之间的数量关系，并说明理由．25．如图，E是AOB⊥，C、D是垂足，连接CD ∠的平分线上一点，EC OB⊥，ED OA交OE于点F，若60∠=︒．AOB（1）求证：OCD∆是等边三角形；（2）若5EF=，求线段OE的长．26．如图，ABCBCD CBE∠=∠=︒，BAC∆中，60∠=︒，点D、E分别在AB、AC上，30 BE、CD相交于点O，OG BC+=．OE OD OG⊥于点G，求证：227．如图，在ABC∠=∠=︒，EBC E∠，60∆中，AB AC=，D、E是ABC∆内两点，AD平分BAC若30=，则BC=cm．DE cmBE cm=，228．如图，已知ABC=，∆为等边三角形，D为BC延长线上的一点，CE平分ACD∠，CE BD 求证：ADE∆为等边三角形．29．如图，ABC∆∠=︒，DE与ABC ∆为等边三角形，D为BC边上一点，以AD为边作60ADE的外角平分线CE交于点E，连接AE，且CE BD∆是等边三角形．=．求证：ADE30．如图，在ABC+=．求ABD∠=︒，BD DC AB ∆中，AB AC=，D是三角形外一点，且60证：60∠=︒．ACD31．如图，在等边ABCOD AB，//OE AC．∠与ACB∠的平分线相交于点O，且//∆中，ABC（1）求证：ODE∆是等边三角形．（2）线段BD、DE、EC三者有什么数量关系？写出你的判断过程．（3）数学学习不但要能解决问题，还要善于提出问题．结合本题，在现有的图形上，请提出两个与“直角三角形”有关的问题．（只要提出问题，不需要解答）32．已知：如图，在ABC∠=︒，BD是中线，延长BC至点E，使C E C D=．A=，60∆中，AB AC求证：DB DE=．33．如图，ABD∆和BCD∆均是边长为2的等边三角形，E、F分别是AD、CD上的两个动点，且满足2+=．AE CF（1）求证：BDE BCF∆≅∆；（2）判断BEF∆的形状，并说明理由．34．已知：如图，四边形ABCD中，AB BC CD DA a∠=︒，M为BC上====，120BAD的点(M不与B、C重合），若AMN∆有一角等于60︒．（1）当M 为BC 中点时，则ABM ∆的面积为（结果用含a 的式子表示）；（2）求证：AMN ∆为等边三角形；（3）设AMN ∆的面积为S ，求出S 的取值范围（结果用含a 的式子表示）．35．如图，点O 是等边ABC ∆内一点，110AOB ∠=︒，BOC α∠=，将B O C ∆绕点C 按顺时针方向旋转60︒得ADC ∆，连接OD ．（1）COD ∆是什么三角形？说明理由；（2）若21AO n =+，21AD n =-，2(OD n n =为大于1的整数），求α的度数；（3）当α为多少度时，AOD ∆是等腰三角形？36．已知：如图，ABC ∆、CDE ∆都是等边三角形，AD 、BE 相交于点O ，点M 、N 分别是线段AD 、BE 的中点．（1）求证：AD BE =；（2）求DOE ∠的度数；（3）求证：MNC ∆是等边三角形．37．已知：在AOB ∆和COD ∆中，OA OB =，OC OD =．（1）如图①，若60AOB COD ∠=∠=︒，求证：①AC BD =②60APB ∠=︒．（2）如图②，若A O B C O D α∠=∠=，则AC 与BD 间的等量关系式为，APB ∠的大小为（直接写出结果，不证明）38．如图，ABC ∆是等边三角形，D 是AC 上一点，BD CE =，12∠=∠，试判断ADE ∆形状，并证明你的结论．39．等边ABC ∆边长为6，P 为BC 上一点，含30︒、60︒的直角三角板60︒角的顶点落在点P 上，使三角板绕P 点旋转．（1）如图1，当P 为BC 的三等分点，且PE AB ⊥时，判断EPF ∆的形状；（2）在（1）问的条件下，FE 、PB 的延长线交于点G ，如图2，求EGB ∆的面积；（3）在三角板旋转过程中，若2CF AE ==，()CF BP ≠，如图3，求PE 的长．40．为了使同学们更好地解答本题，我们提供了思路点拨，你可以依照这个思路填空，并完成本题解答的全过程，当然你也可以不填空，只需按照解答的一般要求，进行解答即可．如图，已知AB AD =，60BAD ∠=︒，120BCD ∠=︒，延长BC ，使C E C D =，连接DE ，求证：BC DC AC +=．思路点拨：（1）由已知条件AB AD=，60BAD∠=︒，可知：ABD∆是三角形；（2）同理由已知条件120BCD∠=︒得到DCE∠=，且CE CD=，可知；（3）要证BC DC AC+=，可将问题转化为两条线段相等，即=；（4）要证（3）中所填写的两条线段相等，可以先证明⋯．请你完成证明过程：41．已知ABC∆是等边三角形，点P是AC上一点，PE BC⊥于点E，交AB于点F，在CB 的延长线上截取BD PA=，PD交AB于点I，PA nPC=．（1）如图1，若1n=，则EBBD=，FIED=；（2）如图2，若60EPD∠=︒，试求n和FIED的值；（3）如图3，若点P在AC边的延长线上，且3n=，其他条件不变，则EBBD=．（只写答案不写过程）42．如图ABC∆为等边三角形，直线//a AB，D为直线BC上任一动点，将一60︒角的顶点置于点D处，它的一边始终经过点A，另一边与直线a交于点E．（1）若D恰好在BC的中点上（如图1)求证：ADE∆是等边三角形；（2）若D为直线BC上任一点（如图2)，其他条件不变，上述（1）的结论是否成立？若成立，请给予证明；若不成立，请说明理由．43．如图，在等边ABC=，点P从点C出发沿CB边向点B点以2/cm s的速AB cm∆中，9度移动，点Q点从B点出发沿BA边向A点以5/cm s速度移动．P、Q两点同时出发，它们移动的时间为t秒钟．（1）你能用t表示BP和BQ的长度吗？请你表示出来．（2）请问几秒钟后，PBQ∆为等边三角形？（3）若P、Q两点分别从C、B两点同时出发，并且都按顺时针方向沿ABC∆三边运动，请问经过几秒钟后点P与点Q第一次在ABC∆的哪条边上相遇？44．如图：在ABC⊥于Q．==，AE CD∆中，AB BC AC=，AD与BE相交于点P，BQ AD求证：①ADC BEA∆≅∆；②2=．BP PQ45．如图1，点B是线段AD上一点，ABC∆分别是等边三角形，连接AE和CD．∆和BDE（1）求证：AE CD=；（2）如图2，点P、Q分别是AE、CD的中点，试判断PBQ∆的形状，并证明．46．如图：已知ABC∆是等边三角形，D、E、F分别是AB、AC、BC边的中点，M是直线BC上的任意一点，在射线EF上截取EN，使EN FM=，连接DM、MN、DN．（1）如图①，当点M在点B左侧时，请你按已知要求补全图形，并判断DMN∆是怎样的特殊三角形（不要求证明）；（2）请借助图②解答：当点M在线段BF上（与点B、F不重合），其它条件不变时，（1）中的结论是否依然成立？若成立，请证明；若不成立，请说明理由；（3）请借助图③解答：当点M在射线FC上（与点F不重合），其它条件不变时，（1）中的结论是否仍然成立？不要求证明．47．如图，ABC∆是等边三角形，点D、E、F分别是线段AB、BC、CA上的点，（1）若AD BE CF∆是等边三角形吗？试证明你的结论；==，问DEF（2）若DEF∆是等边三角形，问AD BE CF==成立吗？试证明你的结论．48．如图，已知ABC=，连∆为等边三角形，延长BC到D，延长BA到E，并且使AE BD 接CE，DE．求证：EC ED=．49．如图，已知ABC ∆与ACD ∆都是边长为2的等边三角形，如图有一个60︒角的三角板绕着点A 旋转分别交BC 、CD 于点P 、Q 两点（不与端点重合）．（1）试说明：PAQ ∆是等边三角形；（2）求四边形APCQ 的面积；（3）填空：当BP = 时，APQ S ∆最小．50．如图，A 、B 、C 三点在同一直线上，ABM ∆和BCN ∆是正三角形，P 是AN 中点，Q 是CM 中点．求证：BPQ ∆是正三角形．全等三角形的的性质与判定难题50道参考答案与试题解析一．选择题（共1小题）1．边长为a 的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），⋯，按此方式依次操作，则第6个正六边形的边长为( )A ．511()32a ⨯B ．511()23a ⨯C ．611()32a ⨯D ．611()23a ⨯【解答】解：连接AD 、DF 、DB ．六边形ABCDEF 是正六边形，ABC BAF AFE ∴∠=∠=∠，AB AF =，120E C ∠=∠=︒，EF DE BC CD ===， 30EFD EDF CBD BDC ∴∠=∠=∠=∠=︒， 120AFE ABC ∠=∠=︒， 90AFD ABD ∴∠=∠=︒，在Rt ABD ∆和RtAFD 中 AF ABAD AD =⎧⎨=⎩Rt ABD Rt AFD(HL)∴∆≅∆， 1120602BAD FAD ∴∠=∠=⨯︒=︒，60120180FAD AFE ∴∠+∠=︒+︒=︒， //AD EF ∴，G 、I 分别为AF 、DE 中点，////GI EF AD ∴，60FGI FAD ∴∠=∠=︒，六边形ABCDEF 是正六边形，QKM ∆是等边三角形， 60EDM M ∴∠=︒=∠，ED EM ∴=，同理AF QF =，即AF QF EF EM ===，等边三角形QKM 的边长是a ，∴第一个正六边形ABCDEF 的边长是13a ，即等边三角形QKM 的边长的13，过F 作FZ GI ⊥于Z ，过E 作EN GI ⊥于N ，则//FZ EN ， //EF GI ，∴四边形FZNE 是平行四边形，13EF ZN a ∴==，11112236GF AF a a ==⨯=，60FGI ∠=︒（已证）， 30GFZ ∴∠=︒，11212GZ GF a ∴==，同理112IN a =， 1111123122GI a a a a ∴=++=，即第二个等边三角形的边长是12a ，与上面求出的第一个正六边形的边长的方法类似，可求出第二个正六边形的边长是1132a ⨯；同理第第三个等边三角形的边长是1122a ⨯，与上面求出的第一个正六边形的边长的方法类似，可求出第三个正六边形的边长是111322a ⨯⨯；同理第四个等边三角形的边长是111222a ⨯⨯，第四个正六边形的边长是11113222a ⨯⨯⨯；第五个等边三角形的边长是11112222a ⨯⨯⨯，第五个正六边形的边长是1111132222a ⨯⨯⨯⨯；第六个等边三角形的边长是1111122222a ⨯⨯⨯⨯，第六个正六边形的边长是111111322222a ⨯⨯⨯⨯⨯，即第六个正六边形的边长是511()32a ⨯，故选：A ．二．解答题（共49小题）2．如图，在等边ABC ∆中，点D ，E 分别在边BC ，AC 上，且//DE AB ，过点E 作EF DE ⊥，交BC 的延长线于点F ，（1）求F ∠的度数；（2）若3CD =，求DF 的长．【解答】解：（1）ABC ∆是等边三角形，60B ∴∠=︒， //DE AB ，60EDC B ∴∠=∠=︒，EF DE ⊥，90DEF ∴∠=︒，9030F EDC ∴∠=︒-∠=︒；（2）60ACB ∠=︒，60EDC ∠=︒，EDC∴∆是等边三角形．∴==，ED DC3∠=︒，F90∠=︒，30DEF∴==．DF DE263．数学课上，李老师出示了如下的题目：“在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED EC=，如图，试确定线段AE与DB的大小关系，并说明理由”．小敏与同桌小聪讨论后，进行了如下解答：（1）特殊情况，探索结论当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE =DB（填“>”，“<”或“=”)．（2）特例启发，解答题目解：题目中，AE与DB的大小关系是：AE DB（填“>”，“<”或“=”)．理由如下：如图2，过点E作//EF BC，交AC于点F．（请你完成以下解答过程）（3）拓展结论，设计新题在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED EC∆的边=．若ABC 长为1，2AE=，求CD的长（请你直接写出结果）．【解答】解：（1）故答案为：=．（2）过E作//EF BC交AC于F，等边三角形ABC，∴∠=∠=∠=︒，AB AC BC==，ABC ACB A60AFE ACB∴∠=∠=︒，60∠=∠=︒，AEF ABC60即60∠=∠=∠=︒，AEF AFE A∴∆是等边三角形，AEFAE EF AF ∴==，60ABC ACB AFE ∠=∠=∠=︒，120DBE EFC ∴∠=∠=︒，60D BED FCE ECD ∠+∠=∠+∠=︒，DE EC =，D ECD ∴∠=∠，BED ECF ∴∠=∠，在DEB ∆和ECF ∆中DEB ECF DBE EFC DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，DEB ECF ∴∆≅∆，BD EF AE ∴==，即AE BD =，故答案为：=．（3）解：1CD =或3，理由是：分为两种情况：①如图1过A 作AM BC ⊥于M ，过E 作EN BC ⊥于N ，则//AM EN ，ABC ∆是等边三角形，1AB BC AC ∴===，AM BC ⊥， 1122BM CM BC ∴===， DE CE =，EN BC ⊥，2CD CN ∴=，//AM EN ，AMB ENB ∴∆∆∽， ∴AB BM BE BN=， ∴11221BN=-， 12BN ∴=， 13122CN ∴=+=， 23CD CN ∴==；②如图2，作AM BC ⊥于M ，过E 作EN BC ⊥于N ，则//AM EN ，ABC ∆是等边三角形，1AB BC AC ∴===，AM BC ⊥，1122BM CM BC ∴===， DE CE =，EN BC ⊥，2CD CN ∴=，//AM EN ， ∴AB BM AE MN=， ∴1122MN=， 1MN ∴=，11122CN ∴=-=，21CD CN ∴==，即3CD =或1．4．如图，过等边ABC ∆的边AB 上一点P ，作P E A C ⊥于E ，Q 为BC 延长线上一点，且PA CQ =，连PQ 交AC 边于D ．（1）求证：PD DQ =；（2）若ABC ∆的边长为1，求DE 的长．【解答】（1）证明：如图，过P 做//PF BC 交AC 于点F ，AFP ACB ∴∠=∠，FPD Q ∠=∠，PFD QCD ∠=∠ABC ∆为等边三角形，60A ACB ∴∠=∠=︒，60A AFP ∴∠=∠=︒，APF ∴∆是等边三角形；AP PF =，AP CQ =，PF CQ ∴=PFD QCD ∴∆≅∆，PD DQ ∴=．（2）APF ∆是等边三角形，PE AC ⊥，AE EF ∴=，PFD QCD ∆≅∆，CD DF ∴=，12DE EF DF AC =+=， 1AC =，12DE =． 5．如图所示，已知等边ABC ∆的边长为a ，P 是ABC ∆内一点，//PD AB ，//PE BC ，//PF AC ，点D 、E 、F 分别在BC 、AC 、AB 上，猜想：PD PE PF ++= a ，并证明你的猜想．【解答】解：PD PE PF a ++=．理由如下：如图，延长EP 交AB 于G ，延长FP 交BC 于H ，//PE BC ，//PF AC ，ABC ∆是等边三角形，60PGF B ∴∠=∠=︒，60PFG A ∠=∠=︒，PFG ∴∆是等边三角形，同理可得PDH ∆是等边三角形，PF PG ∴=，PD DH =，又//PD AB ，//PE BC ，∴四边形BDPG是平行四边形，∴=，PG BD∴++=++==．PD PE PF DH CH BD BC a故答案为a．6．如图，已知ABC∆均为等边三角形，且点B、C、D在同一条直线上，连接AD、∆和CDEBE，交CE和AC分别于G、H点，连接GH．（1）请说出AD BE=的理由；（2）试说出BCH ACG∆≅∆的理由；（3）试猜想：CGH∆是什么特殊的三角形，并加以说明．【解答】解：（1）ABC∆均为等边三角形∆和CDE=∴=，EC DCAC BC∠=∠=︒ACB ECD60∴∠=∠ACD ECBACD BCE∴∆≅∆∴=；AD BE（2）ACD BCE∆≅∆∴∠=∠CBH CAGACB ECD∠=∠=︒，点B、C、D在同一条直线上60∴∠=∠=∠=︒ACB ECD ACG60又AC BC=ACG BCH∴∆≅∆；（3）CGH∆是等边三角形，理由如下：ACG BCH∆≅∆∴=（全等三角形的对应边相等）CG CH又60∠=︒ACG∴∆是等边三角形（有一内角为60度的等腰三角形为等边三角形）；CGH7．如图，已知ABC∆是边长为6cm的等边三角形，动点P，Q同时从A、B两点出发，分别沿AB、BC方向匀速运动，其中点P运动的速度是1/cm s，cm s，点Q运动的速度是2/当点Q运动到点C时，P，Q都停止运动．（1）出发后运动2s时，试判断BPQ∆的形状，并说明理由；那么此时PQ和AC的位置关系呢？请说明理由；（2）设运动时间为t，BPQ∆的面积为S，请用t的表达式表示S．【解答】解：（1）BPQ∆是等边三角形，//PQ AC，（2分）运动至2s时，2AP=，4BQ=，BP AB AP BQ∴=-==（4分）4又ABC∆是边长为6cm的等边三角形∴∠=︒B60∴∆是等边三角形（6分）BPQ∴∠=∠=︒60BPQ A∴．//PQ AC（2）过Q作QH AB⊥于H，=，30∠=︒，BQHBQ t2∴=，QH=．（10分）BH t=-BP t6213(6)3(6)2S t t t t ∴=-=-=+．（12分）8．已知：在等边ABC ∆中，点D 、E 、F 分别为边AB 、BC 、AC 的中点，点G 为直线BC上一动点，当点G 在CB 延长线上时，有结论“在直线EF 上存在一点H ，使得DGH ∆是等边三角形”成立（如图①)，且当点G 与点B 、E、C 重合时，该结论也一定成立．问题：当点G 在直线BC 的其它位置时，该结论是否仍然成立？请你在下面的备用图②③④中，画出相应图形并证明相关结论．【解答】证明：连接DE 、EF 、DF ．（1）当点G 在线段BE 上时，如图①，在EF 上截取EH 使EH BG =．D 、E 、F 是等边ABC ∆三边中点，DEF ∴∆、DBE ∆也是等边三角形且12DE AB BD ==．在DBG ∆和DEH ∆中，60DB DE DBG DEH BG EH =⎧⎪∠=∠=︒⎨⎪=⎩，()DBG DEH SAS ∴∆≅∆，DG DH ∴=．BDG EDH ∴∠=∠．60BDE GDE BDG ∠=∠+∠=︒，60GDH GDE EDH ∴∠=∠+∠=︒∴在直线EF 上存在点H 使得DGH ∆是等边三角形．（2）当点G 在射线EC 上时，如图②，在EF 上截取EH 使EH BG =．由（1）可证DBG DEH ∆≅∆．DG DH ∴=，BDG EDH ∠=∠．60BDE BDG EDG ∠=∠-∠=︒，60GDH EDH EDG ∴∠=∠-∠=︒．∴在直线EF 上存在点H 使得DGH ∆是等边三角形．（3）当点G 在BC 延长线上时，如图③，与（2）同理可证，结论成立．综上所述，点G 在直线BC 上的任意位置时，该结论成立．9．已知点C 为线段AB 上一点，分别以AC 、BC 为边在线段AB 同侧作ACD ∆和BCE ∆，且CA CD =，CB CE =，ACD BCE ∠=∠，直线AE 与BD 交于点F ，（1）如图1，若60ACD ∠=︒，则AFB ∠= 120︒ ；如图2，若90ACD ∠=︒，则AFB ∠= ；如图3，若120ACD ∠=︒，则AFB ∠= ；（2）如图4，若ACDα∠=（用含α的式子表示）；∠=，则AFB（3）将图4中的ACD∆绕点C顺时针旋转任意角度（交点F至少在BD、AE中的一条线段上），变成如图5所示的情形，若ACDα∠与α的有何数量关系？并给予∠=，则AFB证明．【解答】解：（1）如图1，CA CD∠=︒，ACD=，60所以ACD∆是等边三角形．∠=∠=︒，ACD BCE=，60CB CE所以ECB∆是等边三角形．AC DC∠=∠+∠，BCD BCE DCE∠=∠+∠，=，ACE ACD DCE又ACD BCE∠=∠，∴∠=∠．ACE BCDAC DC=，=，CE BC∴∆≅∆．ACE DCB∴∠=∠．EAC BDC∠是ADFAFB∆的外角．∴∠=∠+∠=∠+∠+∠=∠+∠+∠=∠+∠=︒AFB ADF FAD ADC CDB FAD ADC EAC FAD ADC DAC120．如图2，AC CD=，∠=∠=︒，EC CBACE DCB=，90∴∆≅∆．ACE DCB∴∠=∠，AEC DBC又FDE CDB∠=︒，DCB∠=∠，9090EFD ∴∠=︒．90AFB ∴∠=︒．如图3，ACD BCE ∠=∠，ACD DCE BCE DCE ∴∠-∠=∠-∠．ACE DCB ∴∠=∠．又CA CD =，CE CB =，ACE DCB ∴∆≅∆．EAC BDC ∴∠=∠．180180(180)120BDC FBA DCB ACD ∠+∠=︒-∠=︒--∠=︒， 120FAB FBA ∴∠+∠=︒．60AFB ∴∠=︒．故填120︒，90︒，60︒．（2）ACD BCE ∠=∠，ACD DCE BCE DCE ∴∠+∠=∠+∠．ACE DCB ∴∠=∠．CAE CDB ∴∠=∠．DFA ACD ∴∠=∠．180180180AFB DFA ACD α∴∠=︒-∠=︒-∠=︒-．（3）180AFB α∠=︒-；证明：ACD BCE α∠=∠=，则ACD DCE BCE DCE ∠+∠=∠+∠，即ACE DCB ∠=∠．在ACE ∆和DCB ∆中AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩，则()ACE DCB SAS ∆≅∆．则CBD CEA ∠=∠，由三角形内角和知EFB ECB α∠=∠=． 180180AFB EFB α∠=︒-∠=︒-．10．如图1，ABC ∆为等边三角形，面积为S ．1D 、1E 、1F 分别是ABC ∆三边上的点，且11112AD BE CF AB ===，连接11D E 、11E F 、11F D ，可得△111D E F 是等边三角形，此时△11AD F 的面积114S S =，△111D E F 的面积114S S =．（1）当2D 、2E 、2F 分别是等边ABC ∆三边上的点，且22213AD BE CF AB ===时如图2，①求证：△222D E F 是等边三角形； ②若用S 表示△22AD F 的面积2S ，则2S = 29S ；若用S 表示△222D E F 的面积2S '，则2S '= ．（2）按照上述思路探索下去，并填空：当n D 、n E 、n F 分别是等边ABC ∆三边上的点，11n n n AD BE CF AB n ===+时，(n 为正整数）△n n n D E F 是三角形；若用S 表示△n n AD F 的面积n S ，则n S = ；若用S 表示△n n n D E F 的面积n S '，则n S '= ．【解答】解：（1）①ABC ∆为等边三角形，AB BC AC ∴==，60A B ∠=∠=︒，（1分）由已知得213AD AB =，213BE BC =，213CF AC =223AF AC ∴=，223BD AB = 22AD BE ∴=，22AF BD =（2分）△22AD F ≅△22BE D （3分） 2222D E F D ∴=同理可证△22AD F ≅△22CF E 2222F D E F =（4分） 222222D E E F F D ∴==∴△222D E F 为等边三角形；（5分）②229S S =；（6分）221393S S S S '=-⨯=（7分）（2）由（1）可知：△n n n D E F 等边三角形；（8分）由（1）的方法可知：229S S =，3316S S =，2(1)n n S S n ⋯=+；（9分） 213S S '=，232711621n n n S S S S n n '-+'=⋯=++．（10分） 11．如图，在等边ABC ∆的三边上分别取点D 、E 、F ，使AD BE CF ==．（1）试说明DEF ∆是等边三角形；（2）连接AE 、BF 、CD ，两两相交于点P 、Q 、R ，则PQR ∆为何种三角形？试说明理由．【解答】证明：（1）ABC ∆是等边三角形， AB BC AC ∴==， AD BE CF ==，AF BD ∴=，在ADF ∆和BED ∆中，AD BEA B AF BD =⎧⎪∠=∠⎨⎪=⎩，()ADF BED SAS ∴∆≅∆，DF DE ∴=，同理DE EF =，DE DF EF ∴==． DEF ∴∆是等边三角形；（2）PQR ∆是等边三角形，理由：由（1）证得ADF BED ∆≅∆，BD AF ∴=，在ABF ∆与CBD ∆中，AB BC BAC CBD AF BD =⎧⎪∠=∠⎨⎪=⎩，ABF CBD ∴∆≅∆， ABF BCD ∴∠=∠， 60ABF CBF ∠+∠=︒， 60CBF BCD ∴∠+∠=︒，60RPQ FBC BCD ∠=∠+∠=︒，同理60PQR PRQ ∠=∠=︒， PQR ∴∆是等边三角形．12．如图所示，一个六边形的六个内角都是120︒，其中连续四边的长依次是1、9、9、5．求这个六边形的周长．【解答】解：如图，延长并反向延长AB ，CD ，EF ，两两相交于点G 、H 、I ，六边形ABCDEF 的每个内角都是120︒，60G H I ∴∠=∠=∠=︒，60GCB GBC ∠=∠=︒， GHI ∴∆，GBC ∆是等边三角形，同理：HAF ∆，DEI ∆是等边三角形，9BG GC BC ∴===，5DE DI EI ===， 99523GI GC CD DI ∴=++=++=， 23GH GI HI ∴===， 13AH GH BG AB ∴=--=，13AF AH FH ∴===， 5EF HI EI FH ∴=--=，∴六边形ABCDEF 的周长113559942AB AF EF DE CD BC =+++++=+++++=．13．如图，已知D 是ABC ∆的边BC 上的一点，CD AB =，BDA BAD ∠=∠，AE 是ABD ∆的中线．（1）若60B ∠=︒，求C ∠的值；（2）求证：AD 是EAC ∠的平分线．【解答】（1）解：60B ∠=︒，BDA BAD ∠=∠， 60BAD BDA ∴∠=∠=︒，AB AD ∴=，CD AB =， CD AD ∴=， DAC C ∴∠=∠，2BDA DAC C C ∴∠=∠+∠=∠， 60BAD ∠=︒， 30C ∴∠=︒；（2）证明：延长AE 到M ，使EM AE =，连接DM ，在ABE ∆和MDE ∆中， EM AE AEB MED BE DE =⎧⎪∠=∠⎨⎪=⎩， ABE MDE ∴∆≅∆，B MDE ∴∠=∠，AB DM =，ADC B BAD MDE BDA ADM ∠=∠+∠=∠+∠=∠，在MAD ∆与CAD ∆，DM CD ADM ADC AD AD =⎧⎪∠=∠⎨⎪=⎩，MAD CAD ∴∆≅∆， MAD CAD ∴∠=∠，AD ∴是EAC ∠的平分线．14．如图，ABC ∆为等边三角形，BD 平分ABC ∠交AC 于点D ，//DE BC 交AB 于点E ．（1）求证：ADE ∆是等边三角形．（2）求证：12AE AB =．【解答】证明：（1）ABC ∆为等边三角形， 60A ABC C ∴∠=∠=∠=︒． //DE BC ，60AED ABC ∴∠=∠=︒，60ADE C ∠=∠=︒．ADE ∴∆是等边三角形．（2）ABC ∆为等边三角形， AB BC AC ∴==．BD 平分ABC ∠，12AD AC ∴=．ADE ∆是等边三角形， AE AD ∴=．12AE AB ∴=． 15．如图．在等边ABC ∆中，ABC ∠与ACB ∠的平分线相交于点O ，且//OD AB ，//OE AC ．（1）试判定ODE ∆的形状，并说明你的理由；（2）线段BD 、DE 、EC 三者有什么关系？写出你的判断过程．【解答】解：（1）ODE ∆是等边三角形，其理由是：ABC ∆是等边三角形， 60ABC ACB ∴∠=∠=︒，（2分） //OD AB ，//OE AC ，60ODE ABC ∴∠=∠=︒，60OED ACB ∠=∠=︒（3分）ODE ∴∆是等边三角形；（4分）（2）答：BD DE EC ==，其理由是：OB 平分ABC ∠，且60ABC ∠=︒， 30ABO OBD ∴∠=∠=︒，（6分） //OD AB ，30BOD ABO ∴∠=∠=︒， DBO DOB ∴∠=∠，DB DO ∴=，（7分）同理，EC EO =， DE OD OE ==，BD DE EC ∴==．（8分） 16．如图，ABC ∆是等边三角形，DF AB ⊥，DE CB ⊥，EF AC ⊥，求证：DEF ∆是等边三角形．【解答】证明：ABC∆是等边三角形，ABC ACB CAB∠=∠=∠=︒，∴==，60AB AC BC⊥，DE CBDF AB⊥，⊥，EF AC∴∠=∠=∠=︒，DAB ACF CBE90∴∠=∠=∠=︒，FAC BCE DBA30∴∠=∠=∠=︒-︒-︒=︒，D E F180903060∴==，DF DE EFDEF∴∆是等边三角形，17．用三根火柴棒可以搭成一个等边三角形，你能用9根火柴搭出5个等边三角形吗？【解答】解：等边三角形各边长相等，故按照上图搭出图形，即为9根火柴搭出5个等边三角形．18．如图，ABC∆是等边三角形，AD是高，并且AB恰好是DE的垂直平分线．求证：ADE∆是等边三角形．【解答】证明：A在DE的垂直平分线上，∴=，AE AD∴∆是等腰三角形，ADE⊥，AB DE90ADE BAD ∴∠=︒-∠，AD BD ⊥，90B BAD ∴∠=︒-∠，由90ADE BAD ∠=︒-∠，90B BAD ∠=︒-∠，得：60B ADE ∠=∠=︒，ADE ∴∆是等边三角形．19．如图，60AOB ∠=︒，OC 平分AOB ∠，C 为角平分线上一点，过点C 作CD OC ⊥，垂足为C ，交OB 于点D ，//CE OA 交OB 于点E ．（1）判断CED ∆的形状，并说明理由；（2）若3OC =，求CD 的长．【解答】解：（1）CED ∆是等边三角形，理由如下： OC 平分AOB ∠，60AOB ∠=︒， 30AOC COE ∴∠=∠=︒， //CE OA ，30AOC COE OCE ∴∠=∠=∠=︒，60CED ∠=︒， CD OC ⊥， 90OCD ∴∠=︒， 60EDC ∴∠=︒， CED ∴∆是等边三角形；（2）CED ∆是等边三角形， CD CE ED ∴==，又COE OCE ∠=∠， OE EC ∴=， CD ED OE ∴==，设CD x =，则2OD x =，在Rt OCD ∆中，根据勾股定理得：2294x x +=，解得：x =则CD =．20．如图，在ABC ∆中，AB AC =，120BAC ∠=︒，D 、F 分别为AB 、AC 的中点，且DE AB ⊥，FG AC ⊥，点E 、G 在BC 上，18BC cm =，求线段EG 的长．（提示：需要添加辅助线）【解答】解：如图，连接AE 、AGD 为AB 中点，ED AB ⊥， EB EA ∴=，ABE ∴∆为等腰三角形，又30B EAB ∠=∠=︒， 30BAE ∴∠=︒， 60AEG ∴∠=︒，同理可证：60AGE ∠=︒， AEG ∴∆为等边三角形， AE EG AG ∴==，又AE BE =，AG GC =，BE EG GC ∴==，又18()BE EG GC BC cm ++==， 6()EG cm ∴=．21．已知，如图，ABC ∆是正三角形，D ，E ，F 分别是各边上的一点，且AD BE CF ==．请你说明DEF ∆是正三角形．【解答】解：ABC==，∆为等边三角形，且AD BE CF∴==，AE BF CD又60∠=∠=∠=︒，A B CADE BEF CFD SAS∴∆≅∆≅∆，()∴==，DE EF FD∴∆是等边三角形．DEF22．如图所示，DEF∆是等边三角形，且123∆是等边三角形吗？请∠=∠=∠，试问：ABC说明理由．【解答】解：ABC∆是等边三角形，理由：DEF∆是等边三角形，∴∠=︒，DEF60∴∠=︒，BEC120BCE∴∠+∠=︒，260∠=∠，23BCE∴∠+∠=︒，360ACB∴∠=︒，60同理60∠=∠=︒，ABC BACABC ∴∆是等边三角形．23．如图，ABC ∆为等边三角形，BD 平分ABC ∠，//DE BC ．（1）求证：ADE ∆是等边三角形；（2）求证：12AE AB =．【解答】证明：（1）ABC ∆为等边三角形，60A ABC ACB ∴∠=∠=∠=︒，//DE BC ，60AED ABD ∴∠=∠=︒，60ADE ACB ∴∠=∠=︒，A AED ADE ∴∠=∠=∠，ADE ∴∆是等边三角形；（2）ADE ∆是等边三角形AD AE ∴=ABC ∆为等边三角形，AB AC ∴= BD 平分ABC ∠，D ∴是AC 的中点（三线合一）1122AD AC AB ==， 12AE AB ∴=． 24．如图ABC ∆是等边三角形（1）如图①，//DE BC ，分别交AB 、AC 于点D 、E ．求证：ADE ∆是等边三角形；（2）如图②，ADE ∆仍是等边三角形，点B 在ED 的延长线上，连接CE ，判断BEC ∠的度数及线段AE 、BE 、CE 之间的数量关系，并说明理由．【解答】（1）证明：ABC ∆是等边三角形，60B C ∴∠=∠=︒，//DE BC ，60ADE B ∴∠=∠=︒，60AED C ∠=∠=︒，ADE ∴∆是等边三角形；（2）解：AE CE BE +=．60BAD DAC ∠+∠=︒，60CAE DAC ∠+∠=︒，BAD CAE ∴∠=∠，在BAD ∆和CAE ∆中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，BAD CAE ∴∆≅∆，BD CE ∴=，120AEC ADB ∠=∠=︒，BE BD DE AE CE ∴=+=+，CE BD DE ==，30EBC ∴∠=︒，60BEC ∴∠=︒．25．如图，E 是AOB ∠的平分线上一点，EC OB ⊥，ED OA ⊥，C 、D 是垂足，连接CD交OE 于点F ，若60AOB ∠=︒．（1）求证：OCD ∆是等边三角形；（2）若5EF =，求线段OE 的长．【解答】解：（1）点E 是AOB ∠的平分线上一点，EC OB ⊥，ED OA ⊥，垂足分别是C ，D ，DE CE ∴=，在Rt ODE ∆与Rt OCE ∆中，DE CE OE OE =⎧⎨=⎩Rt ODE Rt OCE(HL)∴∆≅∆，OD OC ∴=，60AOB ∠=︒，OCD ∴∆是等边三角形；（2）OCD ∆是等边三角形，OF 是COD ∠的平分线，OE DC ∴⊥，60AOB ∠=︒，30AOE BOE ∴∠=∠=︒，60ODF ∠=︒，ED OA ⊥，30EDF ∴∠=︒，210DE EF ∴==，220OE DE ∴==．26．如图，ABC ∆中，60BAC ∠=︒，点D 、E 分别在AB 、AC 上，30BCD CBE ∠=∠=︒，BE 、CD 相交于点O ，OG BC ⊥于点G ，求证：2OE OD OG +=．【解答】证明：延长OE 至点M ，使OM OC =，连接CM ，30BCD CBE ∠=∠=︒，OB OC ∴=，303060MOC ∠=︒+︒=︒，OM OC =，OMC ∴∆为等边三角形，CM OC OB ∴==，60M ∠=︒，DBO MCE ∴∠=∠，在BOD ∆和CME ∆中，DBO MCE BO CMDOB M ∠=∠⎧⎪=⎨⎪∠=∠⎩， BOD MCE ∴∆≅∆，DO EM ∴=，OE OD OM OB ∴+==，在Rt OBG ∆中，30OBG ∠=︒，OG BC ⊥，2OG OB ∴=，2OE OD OG ∴+=．27．如图，在ABC ∆中，AB AC =，D 、E 是ABC ∆内两点，AD 平分BAC ∠，60EBC E ∠=∠=︒，若30BE cm =，2DE cm =，则BC = 32 cm ．【解答】解：延长ED交BC于M，延长AD交BC于N，∠，AB AC=，AD平分BAC=，AN BC∴⊥，BN CN∠=∠=︒，EBC E60∴∆为等边三角形，BEMEFD∴∆为等边三角形，DE=，30BE=，2∴=，28DM∆为等边三角形，BEMEMB∴∠=︒，60⊥，AN BC∴∠=︒，90DNM∴∠=︒，30NDM∴=，NM14∴=，16BN∴==，BC BN232故答案为32．28．如图，已知ABC=，∠，CE BD ∆为等边三角形，D为BC延长线上的一点，CE平分ACD 求证：ADE∆为等边三角形．【解答】证明：ABC ∆为等边三角形，60B ACB ∴∠=∠=︒，AB AC =，即120ACD ∠=︒， CE 平分ACD ∠，1260∴∠=∠=︒，在ABD ∆和ACE ∆中，1AB AC B BD CE =⎧⎪∠=∠⎨⎪=⎩，()ABD ACE SAS ∴∆≅∆，AD AE ∴=，BAD CAE ∠=∠，又60BAC ∠=︒，60DAE ∴∠=︒，ADE ∴∆为等边三角形．29．如图，ABC ∆为等边三角形，D 为BC 边上一点，以AD 为边作60ADE ∠=︒，DE 与ABC ∆的外角平分线CE 交于点E ，连接AE ，且CE BD =．求证：ADE ∆是等边三角形．【解答】解：过D 作//DG AC 交AB 于G ，则13∠=∠，GDB ∆为等边三角形，120AGD DCE ∠=∠=︒，AG DC =．又60ADE ACE ∠=∠=︒，ACE ECF ∠=∠，12∴∠=∠，31∴∠=∠．在AGD ∆和DCE ∆中，31AGD DCE AG DC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AGD DCE AAS ∴∆≅∆，AD DE ∴=，60ADE ∠=︒，ADE ∴∆是等边三角形．30．如图，在ABC ∆中，AB AC =，D 是三角形外一点，且60ABD ∠=︒，BD DC AB +=．求证：60ACD ∠=︒．【解答】证明：延长BD 至E ，使CD DE =，连接AE ，AD ，BD CD AB +=，BE BD DE =+，BE AB ∴=，60ABD ∠=︒，ABE ∴∆是等边三角形，AE AB AC ∴==，60E ∠=︒，在ACD ∆和ADE ∆中，AC AE CD DE AD AD =⎧⎪=⎨⎪=⎩，()ACD ADE SSS ∴∆≅∆，60ACD E ∴∠=∠=︒．31．如图，在等边ABC ∆中，ABC ∠与ACB ∠的平分线相交于点O ，且//OD AB ，//OE AC ．（1）求证：ODE ∆是等边三角形．（2）线段BD 、DE 、EC 三者有什么数量关系？写出你的判断过程．（3）数学学习不但要能解决问题，还要善于提出问题．结合本题，在现有的图形上，请提出两个与“直角三角形”有关的问题．（只要提出问题，不需要解答）【解答】（1）证明：ABC ∆是等边三角形，60ABC ACB ∴∠=∠=︒，//OD AB ，//OE AC ，60ODE ABC ∴∠=∠=︒，60OED ACB ∠=∠=︒，ODE ∴∆是等边三角形；。

(专题精选)初中数学三角形难题汇编含答案

（专题精选）初中数学三角形难题汇编含答案一、选择题1．如图所示，将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上，若∠1=38°，则∠2的度数（）A．28°B．22°C．32°D．38°【答案】B【解析】【分析】延长AB交CF于E，求出∠ABC，根据三角形外角性质求出∠AEC，根据平行线性质得出∠2=∠AEC，代入求出即可．【详解】解：如图，延长AB交CF于E，∵∠ACB=90°，∠A=30°，∠ABC=60°，∵∠1=38°，∴∠AEC=∠ABC-∠1=22°，∵GH∥EF，∴∠2=∠AEC=22°，故选B．【点睛】本题考查了三角形的内角和定理，三角形外角性质，平行线性质的应用，主要考查学生的推理能力．2．如图，已知△ABC是等腰直角三角形，∠A＝90°，BD是∠ABC的平分线，DE⊥BC于E，若BC＝10cm，则△DEC的周长为（）A ．8cmB ．10cmC ．12cmD ．14cm【答案】B【解析】【分析】根据“AAS”证明 ΔABD ≌ΔEBD .得到AD ＝DE ，AB ＝BE ，根据等腰直角三角形的边的关系，求其周长.【详解】∵ BD 是∠ABC 的平分线，∴ ∠ABD ＝∠EBD .又∵ ∠A ＝∠DEB ＝90°，BD 是公共边，∴ △ABD ≌△EBD (AAS)，∴ AD ＝ED ，AB ＝BE ，∴ △DEC 的周长是DE ＋EC ＋DC＝AD ＋DC ＋EC＝AC ＋EC ＝AB ＋EC＝BE ＋EC ＝BC＝10 cm.故选B.【点睛】本题考查了等腰直角三角形的性质，角平分线的定义，全等三角形的判定与性质. 掌握全等三角形的判定方法（即SSS 、SAS 、ASA 、AAS 和HL ）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．3．如图，ABCD 的对角线AC 与BD 相交于点O ，AD BD ⊥，30ABD ∠=︒，若23AD =．则OC 的长为（）A ．3B ．3C 21D ．6【答案】C【解析】【分析】先根据勾股定理解Rt ABD △求得6BD =，再根据平行四边形的性质求得3OD =，然后根据勾股定理解Rt AOD △、平行四边形的性质即可求得OC OA ==【详解】解：∵AD BD ⊥∴90ADB ∠=︒∵在Rt ABD △中，30ABD ∠=︒，AD =∴2AB AD ==∴6BD ==∵四边形ABCD 是平行四边形 ∴132OB OD BD ===，12OA OC AC ==∴在Rt AOD △中，AD =3OD =∴OA =∴OC OA ==故选：C【点睛】本题考查了含30角的直角三角形的性质、勾股定理、平行四边形的性质等知识点，熟练掌握相关知识点是解决问题的关键．4．下列长度的三条线段能组成三角形的是（）A ．2, 2,5B ．C ．3,4,8D ．4,5,6【答案】D【解析】【分析】三角形的任何一边大于其他两边之差，小于两边之和，满足此关系的可组成三角形，其实只要最小两边的和大于最大边就可判断前面的三边关系成立．【详解】根据三角形三边关系可知，三角形两边之和大于第三边．A 、2+2=4＜5，此选项错误；B 、＜3，此选项错误；C 、3+4＜8，此选项错误；D 、4+5=9＞6，能组成三角形，此选项正确．故选：D ．【点睛】此题考查三角形三边关系，解题关键在于掌握三角形两边之和大于第三边．即：两条较短的边的和小于最长的边，只要满足这一条就是满足三边关系．5．如图，已知AB ∥CD ，直线AB ，CD 被BC 所截，E 点在BC 上，若∠1＝45°，∠2＝35°，则∠3＝（）A ．65°B ．70°C ．75°D ．80°【答案】D【解析】【分析】由平行线的性质可求得∠C ，在△CDE 中利用三角形外的性质可求得∠3．【详解】解：∵AB ∥CD ，∴∠C ＝∠1＝45°，∵∠3是△CDE 的一个外角，∴∠3＝∠C+∠2＝45°+35°＝80°，故选：D ．【点睛】本题主要考查平行线的性质，掌握平行线的性质和判定是解题的关键，即①两直线平行⇔同位角相等，②两直线平行⇔内错角相等，③两直线平行⇔同旁内角互补，④a ∥b ，b ∥c ⇒a ∥c ．6．将一个边长为4的正方形ABCD 分割成如图所示的9部分，其中ABE △，BCF ，CDG ，DAH 全等，AEH △，BEF ，CFG △，DGH 也全等，中间小正方形EFGH 的面积与ABE △面积相等，且ABE △是以AB 为底的等腰三角形，则AEH △的面积为（）A ．2B ．169C ．32D 2【答案】C【解析】【分析】【详解】解：如图，连结EG 并向两端延长分别交AB 、CD 于点M 、N ，连结HF ，∵四边形EFGH 为正方形，∴EG FH =，∵ABE △是以AB 为底的等腰三角形，∴AE BE =，则点E 在AB 的垂直平分线上，∵ABE △≌CDG ，∴CDG 为等腰三角形，∴CG DG =，则点G 在CD 的垂直平分线上，∵四边形ABCD 为正方形，∴AB 的垂直平分线与CD 的垂直平分线重合，∴MN 即为AB 或CD 的垂直平分线，则,EM AB GN CD ，EM GN ，∵正方形ABCD 的边长为4，即4AB CDAD BC ， ∴4MN =，设EM GN x ，则42EG FH x ， ∵正方形EFGH 的面积与ABE △面积相等，即2114(42)22x x ，解得：121,4x x ==，∵4x =不符合题意，故舍去，∴1x =，则S 正方形EFGH 14122==⨯⨯=ABE S ， ∵ABE △，BCF ，CDG ，DAH 全等， ∴2====ABE BCF CDG DAHS S S S ， ∵正方形ABCD 的面积4416=⨯=，AEH △，BEF ，CFG △，DGH 也全等， ∴1(4=AEH S S 正方形ABCD − S 正方形EFGH 134)(16242)42-=⨯--⨯=ABE S ，故选：C ．【点睛】本题考查了正方形的性质、全等三角形的性质和等腰三角形的性质，解题的关键是求得ABE △的面积．7．图中的三角形被木板遮住了一部分，这个三角形是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．以上都有可能【答案】D【解析】从图中，只能看到一个角是锐角，其它的两个角中，可以都是锐角或有一个钝角或有一个直角，故选D ．8．如图，直线a b ∥，点A 、B 分别在直线a 、b 上，145∠︒＝，若点C 在直线b 上，105BAC ∠︒＝，且直线a 和b 的距离为3，则线段AC 的长度为（）A ．32B ．33C ．3D ．6【答案】D【解析】【分析】过C 作CD ⊥直线a ，根据30°角所对直角边等于斜边的一半即可得到结论．【详解】过C 作CD ⊥直线a ，∴∠ADC =90°．∵∠1=45°，∠BAC =105°，∴∠DAC =30°．∵CD =3，∴AC =2CD =6．故选D ．【点睛】本题考查了平行线间的距离，含30°角的直角三角形的性质，正确的理解题意是解题的关键．9．如图，在菱形ABCD 中，对角线AC ＝8，BD ＝6，点E ，F 分别是边AB ，BC 的中点，点P在AC上运动，在运动过程中，存在PE＋PF的最小值，则这个最小值是（）A．3 B．4 C．5 D．6【答案】C【解析】【分析】先根据菱形的性质求出其边长，再作E关于AC的对称点E′，连接E′F，则E′F即为PE+PF 的最小值，再根据菱形的性质求出E′F的长度即可．【详解】解：如图∵四边形ABCD是菱形，对角线AC=6，BD=8，∴22，34作E关于AC的对称点E′，连接E′F，则E′F即为PE+PF的最小值，∵AC是∠DAB的平分线，E是AB的中点，∴E′在AD上，且E′是AD的中点，∵AD=AB，∴AE=AE′，∵F是BC的中点，∴E′F=AB=5．故选C．10．如图，△ABC的角平分线CD、BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG＝2∠DCB；②∠ADC＝∠GCD；③CA平分∠BCG；④∠DFB＝12∠CGE．其中正确的结论是( )A．②③B．①②④C．①③④D．①②③④【答案】B【解析】【分析】根据平行线的性质、角平分线的定义、垂直的性质及三角形内角和定理依次判断即可得出答案．【详解】①∵EG∥BC，∴∠CEG=∠ACB，又∵CD是△ABC的角平分线，∴∠CEG=∠ACB=2∠DCB，故正确；②∵∠A=90°，∴∠ADC+∠ACD=90°，∵CD平分∠ACB，∴∠ACD=∠BCD，∴∠ADC+∠BCD=90°．∵EG∥BC，且CG⊥EG，∴∠GCB=90°，即∠GCD+∠BCD=90°，∴∠ADC=∠GCD，故正确；③条件不足，无法证明CA平分∠BCG，故错误；④∵∠EBC+∠ACB=∠AEB，∠DCB+∠ABC=∠ADC，∴∠AEB+∠ADC=90°+12（∠ABC+∠ACB）=135°，∴∠DFE=360°-135°-90°=135°，∴∠DFB=45°=12∠CGE，，正确．故选B．【点睛】本题主要考查了角平分线的定义，平行线的性质，三角形内角和定理及多边形内角和，三角形外角的性质，熟知直角三角形的两锐角互余是解答此题的关键．11．如图，△ABC ≌△A E D ，∠C =40°，∠E AC =30°，∠B =30°，则∠E AD =（）；A ．30°B ．70°C ．40°D ．110°【答案】D【解析】【分析】【详解】∵△ABC ≌△AED ， ∴∠D=∠C=40°，∠C=∠B=30°，∴∠E AD=180°－∠D －∠E ＝110°，故选D.12．如图，在菱形ABCD 中，60BCD ∠=︒，BC 的垂直平分线交对角线AC 于点F ，垂足为E ，连接BF 、DF ，则DFC ∠的度数是（）A ．130︒B ．120︒C ．110︒D ．100︒【答案】A【解析】【分析】首先求出∠CFB=130°，再根据对称性可知∠CFD=∠CFB 即可解决问题；【详解】∵四边形ABCD 是菱形，∴∠ACD ＝∠ACB ＝12∠BCD=25°， ∵EF 垂直平分线段BC ，∴FB=FC ，∴∠FBC=∠FCB=25°，∴∠CFB=180°-25°-25°=130°，根据对称性可知：∠CFD=∠CFB=130°，故选：A ．【点睛】此题考查菱形的性质、线段的垂直平分线的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．13．如图，在平面直角坐标系中，已知点A （﹣2，0），B （0，3），以点A 为圆心，AB 长为半径画弧，交x 轴的正半轴于点C ，则点C 的横坐标介于（）A ．0和1之间B ．1和2之间C ．2和3之间D ．3和4之间【答案】B【解析】【分析】先根据点A ，B 的坐标求出OA ，OB 的长度，再根据勾股定理求出AB 的长，即可得出OC 的长，再比较无理数的大小确定点C 的横坐标介于哪个区间．【详解】∵点A ，B 的坐标分别为（﹣2，0），（0，3），∴OA ＝2，OB ＝3，在Rt △AOB 中，由勾股定理得：AB 222+313=∴AC ＝AB 13，∴OC 132，∴点C 132，0）， ∵3134<< ， ∴11322<< ，即点C 的横坐标介于1和2之间，故选：B ．【点睛】本题考查了弧与x 轴的交点问题，掌握勾股定理、无理数大小比较的方法是解题的关键．14．满足下列条件的是直角三角形的是（）A ．4BC =，5AC =，6AB =B ．13BC =，14AC =，15AB = C ．::3:4:5BC AC AB =D ．::3:4:5A B C ∠∠∠= 【答案】C【解析】【分析】要判断一个角是不是直角，先要知道三条边的大小，用较小的两条边的平方和与最大的边的平方比较，如果相等，则三角形为直角三角形；否则不是．【详解】A．若BC=4，AC=5，AB=6，则BC2+AC2≠AB2，故△ABC不是直角三角形；B.若13BC=，14AC=，15AB=，则AC2+AB2≠CB2，故△ABC不是直角三角形；C．若BC：AC：AB=3：4：5，则BC2+AC2=AB2，故△ABC是直角三角形；D．若∠A：∠B：∠C=3：4：5，则∠C＜90°，故△ABC不是直角三角形；故答案为：C．【点睛】本题主要考查了勾股定理的逆定理，如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．15．等腰三角形的一个角比另一个角的2倍少20度，则等腰三角形顶角的度数是（）A．140B．20或80C．44或80D．140或44或80【答案】D【解析】【分析】设另一个角是x，表示出一个角是2x-20°，然后分①x是顶角，2x-20°是底角，②x是底角，2x-20°是顶角，③x与2x-20°都是底角根据三角形的内角和等于180°与等腰三角形两底角相等列出方程求解即可．【详解】设另一个角是x，表示出一个角是2x-20°，①x是顶角，2x-20°是底角时，x+2（2x-20°）=180°，解得x=44°，∴顶角是44°；②x是底角，2x-20°是顶角时，2x+（2x-20°）=180°，解得x=50°，∴顶角是2×50°-20°=80°；③x与2x-20°都是底角时，x=2x-20°，解得x=20°，∴顶角是180°-20°×2=140°；综上所述，这个等腰三角形的顶角度数是44°或80°或140°．故答案为：D．【点睛】本题考查了等腰三角形两底角相等的性质，三角形的内角和定理，难点在于分情况讨论，特别是这两个角都是底角的情况容易漏掉而导致出错．16．如图，90ACB ∠=︒，AC CD =，过D 作AB 的垂线，交AB 的延长线于E ，若2AB DE =，则BAC ∠的度数为（）A ．45°B ．30°C ．22.5°D ．15°【答案】C【解析】【分析】连接AD ，延长AC 、DE 交于M ，求出∠CAB=∠CDM ，根据全等三角形的判定得出△ACB ≌△DCM ，求出AB=DM ，求出AD=AM ，根据等腰三角形的性质得出即可．【详解】解：连接AD ，延长AC 、DE 交于M ，∵∠ACB=90°，AC=CD ，∴∠DAC=∠ADC=45°，∵∠ACB=90°，DE ⊥AB ，∴∠DEB=90°=∠ACB=∠DCM ，∵∠ABC=∠DBE ，∴∠CAB=∠CDM ，在△ACB 和△DCM 中CAB CDM AC CDACB DCM ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ACB ≌△DCM （ASA ），∴AB=DM ，∵AB=2DE ，∴DM=2DE ，∴DE=EM ，∵DE ⊥AB ，∴AD=AM ，114522.522BAC DAE DAC ︒︒∴∠=∠=∠=⨯= 故选：C ．【点睛】本题考查了全等三角形的性质和判定，等腰直角三角形，等腰三角形的性质和判定等知识点，能根据全等求出AB=DM 是解此题的关键．17．如图为一个66⨯的网格，在ABC ∆，A B C '''∆和A B C ''''''∆中，直角三角形有（）个A ．0B ．1C ．2D ．3【答案】C【解析】【分析】根据题中的网格，先运用勾股定理计算出各个三角形的边长，再根据勾股定理的逆定理判断是否为直角三角形即可．【详解】设网格的小正方形的边长是1，由勾股定理（两直角边的平方等于斜边的平方）可知，ABC ∆的三边分别是：10，5，5；由于2225510+=，根据勾股定理的逆定理得：ABC ∆是直角三角形； '''A B C ∆的三边分别是：''A B 10， ''B C 5 ，''AC 13 由于22210513，根据勾股定理的逆定理得：'''A B C ∆不是直角三角形；A B C ''''''∆的三边分别是：A B ''''18B C ''''8 ，A C ''''26；由于22218826，根据勾股定理的逆定理得：A B C ''''''∆是直角三角形；因此有两个直角等三角形；故选C ．【点睛】本题主要考查了勾股定理和勾股定理的逆定理，能灵活运用所学知识是解题的关键．18．如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为(3，3)，点C的坐标为(12，0)，点P为斜边OB上的一个动点，则PA＋PC的最小值为( )A．132B．312C．3+192D．2 7【答案】B【解析】如图，作点A关于OB的对称点点D，连接CD交OB于点P，此时PA＋PC最小，作DN⊥x 轴交于点N，∵B（33OA=3，AB3OB3BOA=30°，∵在Rt△AMO中，∠MOA=30°，AO=3，∴AM=1.5，∠OAM=60°，∴∠ADN=30°，∵在Rt△AND中，∠ADN=30°，AD=2AM=3，∴AN=1.5，DN 33 2∴CN=3－12－1.5=1，∴CD2=CN2+DN2=12+3322=314，∴CD=312.故选B.点睛：本题关键在于先借助轴对称的性质确定出P点的位置，然后结合特殊角30°以及勾股定理计算.19．如图，Rt△ABC中，∠C =90°，∠ABC的平分线BD交AC于D，若AD =5cm，CD=3cm，则点D到AB的距离DE是（）A ．5cmB ．4cmC ．3cmD ．2cm【答案】C【解析】 ∵点D 到AB 的距离是DE ，∴DE ⊥AB ，∵BD 平分∠ABC ，∠C =90°，∴把Rt △BDC 沿BD 翻折后，点C 在线段AB 上的点E 处，∴DE=CD ，∵CD =3cm ，∴DE=3cm.故选：C.20．如图，在ABC 中，90C ∠=︒，60CAB ∠=︒，按以下步骤作图：①分别以A ，B 为圆心，以大于12AB 的长为半径画弧，两弧分别相交于点P 和Q ． ②作直线PQ 交AB 于点D ，交BC 于点E ，连接AE ．若4CE =，则AE 的值为（） A ．6B ．2C ．43D ．8 【答案】D【解析】【分析】根据垂直平分线的作法得出PQ 是AB 的垂直平分线，进而得出∠EAB ＝∠CAE ＝30°，即可得出AE 的长．【详解】由题意可得出：PQ 是AB 的垂直平分线，∴AE ＝BE ，∵在△ABC中，∠C＝90°，∠CAB＝60°，∴∠CBA＝30°，∴∠EAB＝∠CAE＝30°，∴CE＝12AE＝4，∴AE＝8．故选D．【点睛】此题主要考查了垂直平分线的性质以及直角三角形中，30°所对直角边等于斜边的一半，根据已知得出∠EAB＝∠CAE＝30°是解题关键．。

(完整版)全等三角形难题集锦超级好题汇总

1.如图，已知等边△ABC ，P 在AC 延长线上一点，以PA 为边作等边△APE,EC 延长线交BP 于M ，连接AM,求证：（1）BP=CE ；（2）试证明：EM-PM=AM.2、点C 为线段AB 上一点，△ACM, △CBN 都是等边三角形，线段AN,MC 交于点E ，BM,CN 交于点F 。

求证：（1）AN=MB.（2）将△ACM 绕点C 按逆时针方向旋转一定角度，如图②所示，其他条件不变，（1）中的结论是否依然成立？（3）AN 与BM 相交所夹锐角是否发生变化。

3.已知，如图①所示，在ABC △和ADE △中，AB AC =，AD AE =，BAC DAE ∠=∠，且点B A D ，，在一条直线上，连接BE CD M N ，，，分别为BE CD ，的中点．（1）求证：①BE CD =；②AN AM =；（2）在图①的基础上，将ADE △绕点A 按顺时针方向旋转180，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立.22题PB EA B A B N CN 图①图②4、如图１，以ABC △的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ，连结EG ，试判断ABC △与AEG △面积之间的关系，并说明理由．5、如图所示，已知△ABC 和△BDE 都是等边三角形，且A 、B 、D 三点共线．下列结论：①AE=CD ；②BF=BG ；③HB 平分∠AHD ；④∠AHC=60°，⑤△BFG 是等边三角形；⑥FG ∥AD ．其中正确的有（） A ．3个 B ．4个 C ．5个 D ．6个6. 如图所示，△ABC 是等腰直角三角形，∠ACB ＝90°，AD 是BC 边上的中线，过C 作AD 的垂线，交AB 于点E ，交AD 于点F ，求证：∠ADC ＝∠BDE ．AG FC BDE （图１） ABCD EFDCB A7、已知Rt ABC △中，90AC BC C D ==︒，∠，为AB 边的中点，90EDF ∠=°，EDF ∠绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F ．当EDF ∠绕D 点旋转到DE AC ⊥于E 时（如图1），易证12DEF CEF ABC S S S +=△△△．当EDF ∠绕D 点旋转到DE AC 和不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，DEF S △、CEF S △、ABC S △又有怎样的数量关系？请写出你的猜想，不需证明．8.已知AC//BD,∠CAB 和∠DBA 的平分线EA 、EB 与CD 相交于点E. 求证:AB=AC+BD.9.如图1，BD 是等腰ABC Rt Δ的角平分线， 90=∠BAC .（1）求证BC =AB +AD ；（2）如图2，BD AF ⊥于F ，BD CE ⊥交延长线于E ，求证：BD =2CE ；A E C F BD图1图3ADFECBADBCE图2FAD FE图十一4321P A BC 10、已知，如图1，在四边形ABCD 中，BC ＞AB ，AD=DC ，BD 平分∠ABC 。

全等三角形的的性质与判定难题50道(含详细答案)

全等三角形的的性质与判定难题50道1．边长为a 的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），⋯，按此方式依次操作，则第6个正六边形的边长为( )A ．511()32a ⨯B ．511()23a ⨯C ．611()32a ⨯D ．611()23a ⨯2．如图，在等边ABC ∆中，点D ，E 分别在边BC ，AC 上，且//DE AB ，过点E 作EF DE ⊥，交BC 的延长线于点F ，（1）求F ∠的度数；（2）若3CD =，求DF 的长．3．数学课上，李老师出示了如下的题目：“在等边三角形ABC 中，点E 在AB 上，点D 在CB 的延长线上，且ED EC =，如图，试确定线段AE 与DB 的大小关系，并说明理由”．小敏与同桌小聪讨论后，进行了如下解答：（1）特殊情况，探索结论当点E 为AB 的中点时，如图1，确定线段AE 与DB 的大小关系，请你直接写出结论：AEDB （填“>”，“ <”或“=” )．（2）特例启发，解答题目解：题目中，AE 与DB 的大小关系是：AE DB （填“>”，“ <”或“=” )．理由如下：如图2，过点E 作//EF BC ，交AC 于点F ．（请你完成以下解答过程）（3）拓展结论，设计新题在等边三角形ABC 中，点E 在直线AB 上，点D 在直线BC 上，且ED EC =．若ABC ∆的边长为1，2AE =，求CD 的长（请你直接写出结果）．4．如图，过等边ABC ∆的边AB 上一点P ，作P E A C ⊥于E ，Q 为BC 延长线上一点，且PA CQ =，连PQ 交AC 边于D ．（1）求证：PD DQ =；（2）若ABC ∆的边长为1，求DE 的长．5．如图所示，已知等边ABC ∆的边长为a ，P 是ABC ∆内一点，//PD AB ，//PE BC ，//PF AC ，点D 、E 、F 分别在BC 、AC 、AB 上，猜想：PD PE PF ++= ，并证明你的猜想．6．如图，已知ABC ∆和CDE ∆均为等边三角形，且点B 、C 、D 在同一条直线上，连接AD 、BE ，交CE 和AC 分别于G 、H 点，连接GH ．（1）请说出AD BE =的理由；（2）试说出BCH ACG ∆≅∆的理由；（3）试猜想：CGH ∆是什么特殊的三角形，并加以说明．7．如图，已知ABC ∆是边长为6cm 的等边三角形，动点P ，Q 同时从A 、B 两点出发，分别沿AB 、BC 方向匀速运动，其中点P 运动的速度是1/cm s ，点Q 运动的速度是2/cm s ，当点Q 运动到点C 时，P ，Q 都停止运动．（1）出发后运动2s 时，试判断BPQ ∆的形状，并说明理由；那么此时PQ 和AC 的位置关系呢？请说明理由；（2）设运动时间为t ，BPQ ∆的面积为S ，请用t 的表达式表示S ．8．已知：在等边ABC ∆中，点D 、E 、F 分别为边AB 、BC 、AC 的中点，点G 为直线BC 上一动点，当点G 在CB 延长线上时，有结论“在直线EF 上存在一点H ，使得DGH ∆是等边三角形”成立（如图①)，且当点G 与点B 、E 、C 重合时，该结论也一定成立．问题：当点G 在直线BC 的其它位置时，该结论是否仍然成立？请你在下面的备用图②③④中，画出相应图形并证明相关结论．9．已知点C 为线段AB 上一点，分别以AC 、BC 为边在线段AB 同侧作ACD ∆和BCE ∆，且CA CD =，CB CE =，ACD BCE ∠=∠，直线AE 与BD 交于点F ，（1）如图1，若60ACD ∠=︒，则AFB ∠= ；如图2，若90ACD ∠=︒，则AFB ∠= ；如图3，若120ACD ∠=︒，则AFB ∠= ；（2）如图4，若ACD α∠=，则AFB ∠= （用含α的式子表示）；（3）将图4中的ACD ∆绕点C 顺时针旋转任意角度（交点F 至少在BD 、AE 中的一条线段上），变成如图5所示的情形，若ACD α∠=，则AFB ∠与α的有何数量关系？并给予证明．10．如图1，ABC ∆为等边三角形，面积为S ．1D 、1E 、1F 分别是ABC ∆三边上的点，且11112AD BE CF AB ===，连接11D E 、11E F 、11F D ，可得△111D E F 是等边三角形，此时△11AD F 的面积114S S =，△111D E F 的面积114S S =．（1）当2D 、2E 、2F 分别是等边ABC ∆三边上的点，且22213AD BE CF AB ===时如图2，①求证：△222D E F 是等边三角形；②若用S 表示△22AD F 的面积2S ，则2S = ；若用S 表示△222D E F 的面积2S '，则2S '= ．（2）按照上述思路探索下去，并填空：当n D 、n E 、n F 分别是等边ABC ∆三边上的点，11n n n AD BE CF AB n ===+时，(n 为正整数）△n n n D E F 是三角形；若用S 表示△n n AD F 的面积n S ，则n S = ；若用S 表示△n n n D E F 的面积n S '，则n S '= ．11．如图，在等边ABC ∆的三边上分别取点D 、E 、F ，使AD BE CF ==．（1）试说明DEF ∆是等边三角形；（2）连接AE 、BF 、CD ，两两相交于点P 、Q 、R ，则PQR ∆为何种三角形？试说明理由．12．如图所示，一个六边形的六个内角都是120︒，其中连续四边的长依次是1、9、9、5．求这个六边形的周长．13．如图，已知D 是ABC ∆的边BC 上的一点，CD AB =，BDA BAD ∠=∠，AE 是ABD ∆的中线．（1）若60B ∠=︒，求C ∠的值；（2）求证：AD 是EAC ∠的平分线．14．如图，ABC ∆为等边三角形，BD 平分ABC ∠交AC 于点D ，//DE BC 交AB 于点E ．（1）求证：ADE ∆是等边三角形．（2）求证：12AE AB =．15．如图．在等边ABC ∆中，ABC ∠与ACB ∠的平分线相交于点O ，且//OD AB ，//OE AC ．（1）试判定ODE ∆的形状，并说明你的理由；（2）线段BD 、DE 、EC 三者有什么关系？写出你的判断过程．16．如图，ABC ∆是等边三角形，DF AB ⊥，DE CB ⊥，EF AC ⊥，求证：DEF ∆是等边三角形．17．用三根火柴棒可以搭成一个等边三角形，你能用9根火柴搭出5个等边三角形吗？ 18．如图，ABC ∆是等边三角形，AD 是高，并且AB 恰好是DE 的垂直平分线．求证：ADE ∆是等边三角形．19．如图，60AOB ∠=︒，OC 平分AOB ∠，C 为角平分线上一点，过点C 作CD OC ⊥，垂足为C ，交OB 于点D ，//CE OA 交OB 于点E ．（1）判断CED ∆的形状，并说明理由；（2）若3OC=，求CD的长．20．如图，在ABC∆中，AB AC=，120BAC∠=︒，D、F分别为AB、AC的中点，且DE AB⊥，FG AC⊥，点E、G在BC上，18BC cm=，求线段EG的长．（提示：需要添加辅助线）21．已知，如图，ABC∆是正三角形，D，E，F分别是各边上的一点，且AD BE CF==．请你说明DEF∆是正三角形．22．如图所示，DEF∆是等边三角形，且123∠=∠=∠，试问：ABC∆是等边三角形吗？请说明理由．23．如图，ABC∆为等边三角形，BD平分ABC∠，//DE BC．（1）求证：ADE∆是等边三角形；（2）求证：12AE AB=．24．如图ABC∆是等边三角形（1）如图①，//∆是等边三角形；DE BC，分别交AB、AC于点D、E．求证：ADE（2）如图②，ADE∆仍是等边三角形，点B在ED的延长线上，连接CE，判断BEC∠的度数及线段AE、BE、CE之间的数量关系，并说明理由．25．如图，E是AOB⊥，C、D是垂足，连接CD ∠的平分线上一点，EC OB⊥，ED OA交OE于点F，若60∠=︒．AOB（1）求证：OCD∆是等边三角形；（2）若5EF=，求线段OE的长．26．如图，ABCBCD CBE∠=∠=︒，BAC∆中，60∠=︒，点D、E分别在AB、AC上，30 BE、CD相交于点O，OG BC+=．OE OD OG⊥于点G，求证：227．如图，在ABC∠=∠=︒，EBC E∠，60∆中，AB AC=，D、E是ABC∆内两点，AD平分BAC若30=，则BC=cm．DE cmBE cm=，228．如图，已知ABC=，∆为等边三角形，D为BC延长线上的一点，CE平分ACD∠，CE BD 求证：ADE∆为等边三角形．29．如图，ABC∆∠=︒，DE与ABC ∆为等边三角形，D为BC边上一点，以AD为边作60ADE的外角平分线CE交于点E，连接AE，且CE BD∆是等边三角形．=．求证：ADE30．如图，在ABC+=．求ABD∠=︒，BD DC AB ∆中，AB AC=，D是三角形外一点，且60证：60∠=︒．ACD31．如图，在等边ABCOD AB，//OE AC．∠与ACB∠的平分线相交于点O，且//∆中，ABC（1）求证：ODE∆是等边三角形．（2）线段BD、DE、EC三者有什么数量关系？写出你的判断过程．（3）数学学习不但要能解决问题，还要善于提出问题．结合本题，在现有的图形上，请提出两个与“直角三角形”有关的问题．（只要提出问题，不需要解答）32．已知：如图，在ABC∠=︒，BD是中线，延长BC至点E，使C E C D=．A=，60∆中，AB AC求证：DB DE=．33．如图，ABD∆和BCD∆均是边长为2的等边三角形，E、F分别是AD、CD上的两个动点，且满足2+=．AE CF（1）求证：BDE BCF∆≅∆；（2）判断BEF∆的形状，并说明理由．34．已知：如图，四边形ABCD中，AB BC CD DA a∠=︒，M为BC上====，120BAD的点(M不与B、C重合），若AMN∆有一角等于60︒．（1）当M 为BC 中点时，则ABM ∆的面积为（结果用含a 的式子表示）；（2）求证：AMN ∆为等边三角形；（3）设AMN ∆的面积为S ，求出S 的取值范围（结果用含a 的式子表示）．35．如图，点O 是等边ABC ∆内一点，110AOB ∠=︒，BOC α∠=，将B O C ∆绕点C 按顺时针方向旋转60︒得ADC ∆，连接OD ．（1）COD ∆是什么三角形？说明理由；（2）若21AO n =+，21AD n =-，2(OD n n =为大于1的整数），求α的度数；（3）当α为多少度时，AOD ∆是等腰三角形？36．已知：如图，ABC ∆、CDE ∆都是等边三角形，AD 、BE 相交于点O ，点M 、N 分别是线段AD 、BE 的中点．（1）求证：AD BE =；（2）求DOE ∠的度数；（3）求证：MNC ∆是等边三角形．37．已知：在AOB ∆和COD ∆中，OA OB =，OC OD =．（1）如图①，若60AOB COD ∠=∠=︒，求证：①AC BD =②60APB ∠=︒．（2）如图②，若A O B C O D α∠=∠=，则AC 与BD 间的等量关系式为，APB ∠的大小为（直接写出结果，不证明）38．如图，ABC ∆是等边三角形，D 是AC 上一点，BD CE =，12∠=∠，试判断ADE ∆形状，并证明你的结论．39．等边ABC ∆边长为6，P 为BC 上一点，含30︒、60︒的直角三角板60︒角的顶点落在点P 上，使三角板绕P 点旋转．（1）如图1，当P 为BC 的三等分点，且PE AB ⊥时，判断EPF ∆的形状；（2）在（1）问的条件下，FE 、PB 的延长线交于点G ，如图2，求EGB ∆的面积；（3）在三角板旋转过程中，若2CF AE ==，()CF BP ≠，如图3，求PE 的长．40．为了使同学们更好地解答本题，我们提供了思路点拨，你可以依照这个思路填空，并完成本题解答的全过程，当然你也可以不填空，只需按照解答的一般要求，进行解答即可．如图，已知AB AD =，60BAD ∠=︒，120BCD ∠=︒，延长BC ，使C E C D =，连接DE ，求证：BC DC AC +=．思路点拨：（1）由已知条件AB AD=，60BAD∠=︒，可知：ABD∆是三角形；（2）同理由已知条件120BCD∠=︒得到DCE∠=，且CE CD=，可知；（3）要证BC DC AC+=，可将问题转化为两条线段相等，即=；（4）要证（3）中所填写的两条线段相等，可以先证明⋯．请你完成证明过程：41．已知ABC∆是等边三角形，点P是AC上一点，PE BC⊥于点E，交AB于点F，在CB 的延长线上截取BD PA=，PD交AB于点I，PA nPC=．（1）如图1，若1n=，则EBBD=，FIED=；（2）如图2，若60EPD∠=︒，试求n和FIED的值；（3）如图3，若点P在AC边的延长线上，且3n=，其他条件不变，则EBBD=．（只写答案不写过程）42．如图ABC∆为等边三角形，直线//a AB，D为直线BC上任一动点，将一60︒角的顶点置于点D处，它的一边始终经过点A，另一边与直线a交于点E．（1）若D恰好在BC的中点上（如图1)求证：ADE∆是等边三角形；（2）若D为直线BC上任一点（如图2)，其他条件不变，上述（1）的结论是否成立？若成立，请给予证明；若不成立，请说明理由．43．如图，在等边ABC=，点P从点C出发沿CB边向点B点以2/cm s的速AB cm∆中，9度移动，点Q点从B点出发沿BA边向A点以5/cm s速度移动．P、Q两点同时出发，它们移动的时间为t秒钟．（1）你能用t表示BP和BQ的长度吗？请你表示出来．（2）请问几秒钟后，PBQ∆为等边三角形？（3）若P、Q两点分别从C、B两点同时出发，并且都按顺时针方向沿ABC∆三边运动，请问经过几秒钟后点P与点Q第一次在ABC∆的哪条边上相遇？44．如图：在ABC⊥于Q．==，AE CD∆中，AB BC AC=，AD与BE相交于点P，BQ AD求证：①ADC BEA∆≅∆；②2=．BP PQ45．如图1，点B是线段AD上一点，ABC∆分别是等边三角形，连接AE和CD．∆和BDE（1）求证：AE CD=；（2）如图2，点P、Q分别是AE、CD的中点，试判断PBQ∆的形状，并证明．46．如图：已知ABC∆是等边三角形，D、E、F分别是AB、AC、BC边的中点，M是直线BC上的任意一点，在射线EF上截取EN，使EN FM=，连接DM、MN、DN．（1）如图①，当点M在点B左侧时，请你按已知要求补全图形，并判断DMN∆是怎样的特殊三角形（不要求证明）；（2）请借助图②解答：当点M在线段BF上（与点B、F不重合），其它条件不变时，（1）中的结论是否依然成立？若成立，请证明；若不成立，请说明理由；（3）请借助图③解答：当点M在射线FC上（与点F不重合），其它条件不变时，（1）中的结论是否仍然成立？不要求证明．47．如图，ABC∆是等边三角形，点D、E、F分别是线段AB、BC、CA上的点，（1）若AD BE CF∆是等边三角形吗？试证明你的结论；==，问DEF（2）若DEF∆是等边三角形，问AD BE CF==成立吗？试证明你的结论．48．如图，已知ABC=，连∆为等边三角形，延长BC到D，延长BA到E，并且使AE BD 接CE，DE．求证：EC ED=．49．如图，已知ABC ∆与ACD ∆都是边长为2的等边三角形，如图有一个60︒角的三角板绕着点A 旋转分别交BC 、CD 于点P 、Q 两点（不与端点重合）．（1）试说明：PAQ ∆是等边三角形；（2）求四边形APCQ 的面积；（3）填空：当BP = 时，APQ S ∆最小．50．如图，A 、B 、C 三点在同一直线上，ABM ∆和BCN ∆是正三角形，P 是AN 中点，Q 是CM 中点．求证：BPQ ∆是正三角形．全等三角形的的性质与判定难题50道参考答案与试题解析一．选择题（共1小题）1．边长为a 的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），⋯，按此方式依次操作，则第6个正六边形的边长为( )A ．511()32a ⨯B ．511()23a ⨯C ．611()32a ⨯D ．611()23a ⨯【解答】解：连接AD 、DF 、DB ．六边形ABCDEF 是正六边形，ABC BAF AFE ∴∠=∠=∠，AB AF =，120E C ∠=∠=︒，EF DE BC CD ===， 30EFD EDF CBD BDC ∴∠=∠=∠=∠=︒， 120AFE ABC ∠=∠=︒， 90AFD ABD ∴∠=∠=︒，在Rt ABD ∆和RtAFD 中 AF ABAD AD =⎧⎨=⎩Rt ABD Rt AFD(HL)∴∆≅∆， 1120602BAD FAD ∴∠=∠=⨯︒=︒，60120180FAD AFE ∴∠+∠=︒+︒=︒， //AD EF ∴，G 、I 分别为AF 、DE 中点，////GI EF AD ∴，60FGI FAD ∴∠=∠=︒，六边形ABCDEF 是正六边形，QKM ∆是等边三角形， 60EDM M ∴∠=︒=∠，ED EM ∴=，同理AF QF =，即AF QF EF EM ===，等边三角形QKM 的边长是a ，∴第一个正六边形ABCDEF 的边长是13a ，即等边三角形QKM 的边长的13，过F 作FZ GI ⊥于Z ，过E 作EN GI ⊥于N ，则//FZ EN ， //EF GI ，∴四边形FZNE 是平行四边形，13EF ZN a ∴==，11112236GF AF a a ==⨯=，60FGI ∠=︒（已证）， 30GFZ ∴∠=︒，11212GZ GF a ∴==，同理112IN a =， 1111123122GI a a a a ∴=++=，即第二个等边三角形的边长是12a ，与上面求出的第一个正六边形的边长的方法类似，可求出第二个正六边形的边长是1132a ⨯；同理第第三个等边三角形的边长是1122a ⨯，与上面求出的第一个正六边形的边长的方法类似，可求出第三个正六边形的边长是111322a ⨯⨯；同理第四个等边三角形的边长是111222a ⨯⨯，第四个正六边形的边长是11113222a ⨯⨯⨯；第五个等边三角形的边长是11112222a ⨯⨯⨯，第五个正六边形的边长是1111132222a ⨯⨯⨯⨯；第六个等边三角形的边长是1111122222a ⨯⨯⨯⨯，第六个正六边形的边长是111111322222a ⨯⨯⨯⨯⨯，即第六个正六边形的边长是511()32a ⨯，故选：A ．二．解答题（共49小题）2．如图，在等边ABC ∆中，点D ，E 分别在边BC ，AC 上，且//DE AB ，过点E 作EF DE ⊥，交BC 的延长线于点F ，（1）求F ∠的度数；（2）若3CD =，求DF 的长．【解答】解：（1）ABC ∆是等边三角形，60B ∴∠=︒， //DE AB ，60EDC B ∴∠=∠=︒，EF DE ⊥，90DEF ∴∠=︒，9030F EDC ∴∠=︒-∠=︒；（2）60ACB ∠=︒，60EDC ∠=︒，EDC∴∆是等边三角形．∴==，ED DC3∠=︒，F90∠=︒，30DEF∴==．DF DE263．数学课上，李老师出示了如下的题目：“在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED EC=，如图，试确定线段AE与DB的大小关系，并说明理由”．小敏与同桌小聪讨论后，进行了如下解答：（1）特殊情况，探索结论当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE =DB（填“>”，“<”或“=”)．（2）特例启发，解答题目解：题目中，AE与DB的大小关系是：AE DB（填“>”，“<”或“=”)．理由如下：如图2，过点E作//EF BC，交AC于点F．（请你完成以下解答过程）（3）拓展结论，设计新题在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED EC∆的边=．若ABC 长为1，2AE=，求CD的长（请你直接写出结果）．【解答】解：（1）故答案为：=．（2）过E作//EF BC交AC于F，等边三角形ABC，∴∠=∠=∠=︒，AB AC BC==，ABC ACB A60AFE ACB∴∠=∠=︒，60∠=∠=︒，AEF ABC60即60∠=∠=∠=︒，AEF AFE A∴∆是等边三角形，AEFAE EF AF ∴==，60ABC ACB AFE ∠=∠=∠=︒，120DBE EFC ∴∠=∠=︒，60D BED FCE ECD ∠+∠=∠+∠=︒，DE EC =，D ECD ∴∠=∠，BED ECF ∴∠=∠，在DEB ∆和ECF ∆中DEB ECF DBE EFC DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，DEB ECF ∴∆≅∆，BD EF AE ∴==，即AE BD =，故答案为：=．（3）解：1CD =或3，理由是：分为两种情况：①如图1过A 作AM BC ⊥于M ，过E 作EN BC ⊥于N ，则//AM EN ，ABC ∆是等边三角形，1AB BC AC ∴===，AM BC ⊥， 1122BM CM BC ∴===， DE CE =，EN BC ⊥，2CD CN ∴=，//AM EN ，AMB ENB ∴∆∆∽， ∴AB BM BE BN=， ∴11221BN=-， 12BN ∴=， 13122CN ∴=+=， 23CD CN ∴==；②如图2，作AM BC ⊥于M ，过E 作EN BC ⊥于N ，则//AM EN ，ABC ∆是等边三角形，1AB BC AC ∴===，AM BC ⊥，1122BM CM BC ∴===， DE CE =，EN BC ⊥，2CD CN ∴=，//AM EN ， ∴AB BM AE MN=， ∴1122MN=， 1MN ∴=，11122CN ∴=-=，21CD CN ∴==，即3CD =或1．4．如图，过等边ABC ∆的边AB 上一点P ，作P E A C ⊥于E ，Q 为BC 延长线上一点，且PA CQ =，连PQ 交AC 边于D ．（1）求证：PD DQ =；（2）若ABC ∆的边长为1，求DE 的长．【解答】（1）证明：如图，过P 做//PF BC 交AC 于点F ，AFP ACB ∴∠=∠，FPD Q ∠=∠，PFD QCD ∠=∠ABC ∆为等边三角形，60A ACB ∴∠=∠=︒，60A AFP ∴∠=∠=︒，APF ∴∆是等边三角形；AP PF =，AP CQ =，PF CQ ∴=PFD QCD ∴∆≅∆，PD DQ ∴=．（2）APF ∆是等边三角形，PE AC ⊥，AE EF ∴=，PFD QCD ∆≅∆，CD DF ∴=，12DE EF DF AC =+=， 1AC =，12DE =． 5．如图所示，已知等边ABC ∆的边长为a ，P 是ABC ∆内一点，//PD AB ，//PE BC ，//PF AC ，点D 、E 、F 分别在BC 、AC 、AB 上，猜想：PD PE PF ++= a ，并证明你的猜想．【解答】解：PD PE PF a ++=．理由如下：如图，延长EP 交AB 于G ，延长FP 交BC 于H ，//PE BC ，//PF AC ，ABC ∆是等边三角形，60PGF B ∴∠=∠=︒，60PFG A ∠=∠=︒，PFG ∴∆是等边三角形，同理可得PDH ∆是等边三角形，PF PG ∴=，PD DH =，又//PD AB ，//PE BC ，∴四边形BDPG是平行四边形，∴=，PG BD∴++=++==．PD PE PF DH CH BD BC a故答案为a．6．如图，已知ABC∆均为等边三角形，且点B、C、D在同一条直线上，连接AD、∆和CDEBE，交CE和AC分别于G、H点，连接GH．（1）请说出AD BE=的理由；（2）试说出BCH ACG∆≅∆的理由；（3）试猜想：CGH∆是什么特殊的三角形，并加以说明．【解答】解：（1）ABC∆均为等边三角形∆和CDE=∴=，EC DCAC BC∠=∠=︒ACB ECD60∴∠=∠ACD ECBACD BCE∴∆≅∆∴=；AD BE（2）ACD BCE∆≅∆∴∠=∠CBH CAGACB ECD∠=∠=︒，点B、C、D在同一条直线上60∴∠=∠=∠=︒ACB ECD ACG60又AC BC=ACG BCH∴∆≅∆；（3）CGH∆是等边三角形，理由如下：ACG BCH∆≅∆∴=（全等三角形的对应边相等）CG CH又60∠=︒ACG∴∆是等边三角形（有一内角为60度的等腰三角形为等边三角形）；CGH7．如图，已知ABC∆是边长为6cm的等边三角形，动点P，Q同时从A、B两点出发，分别沿AB、BC方向匀速运动，其中点P运动的速度是1/cm s，cm s，点Q运动的速度是2/当点Q运动到点C时，P，Q都停止运动．（1）出发后运动2s时，试判断BPQ∆的形状，并说明理由；那么此时PQ和AC的位置关系呢？请说明理由；（2）设运动时间为t，BPQ∆的面积为S，请用t的表达式表示S．【解答】解：（1）BPQ∆是等边三角形，//PQ AC，（2分）运动至2s时，2AP=，4BQ=，BP AB AP BQ∴=-==（4分）4又ABC∆是边长为6cm的等边三角形∴∠=︒B60∴∆是等边三角形（6分）BPQ∴∠=∠=︒60BPQ A∴．//PQ AC（2）过Q作QH AB⊥于H，=，30∠=︒，BQHBQ t2∴=，QH=．（10分）BH t=-BP t6213(6)3(6)2S t t t t ∴=-=-=+．（12分）8．已知：在等边ABC ∆中，点D 、E 、F 分别为边AB 、BC 、AC 的中点，点G 为直线BC上一动点，当点G 在CB 延长线上时，有结论“在直线EF 上存在一点H ，使得DGH ∆是等边三角形”成立（如图①)，且当点G 与点B 、E、C 重合时，该结论也一定成立．问题：当点G 在直线BC 的其它位置时，该结论是否仍然成立？请你在下面的备用图②③④中，画出相应图形并证明相关结论．【解答】证明：连接DE 、EF 、DF ．（1）当点G 在线段BE 上时，如图①，在EF 上截取EH 使EH BG =．D 、E 、F 是等边ABC ∆三边中点，DEF ∴∆、DBE ∆也是等边三角形且12DE AB BD ==．在DBG ∆和DEH ∆中，60DB DE DBG DEH BG EH =⎧⎪∠=∠=︒⎨⎪=⎩，()DBG DEH SAS ∴∆≅∆，DG DH ∴=．BDG EDH ∴∠=∠．60BDE GDE BDG ∠=∠+∠=︒，60GDH GDE EDH ∴∠=∠+∠=︒∴在直线EF 上存在点H 使得DGH ∆是等边三角形．（2）当点G 在射线EC 上时，如图②，在EF 上截取EH 使EH BG =．由（1）可证DBG DEH ∆≅∆．DG DH ∴=，BDG EDH ∠=∠．60BDE BDG EDG ∠=∠-∠=︒，60GDH EDH EDG ∴∠=∠-∠=︒．∴在直线EF 上存在点H 使得DGH ∆是等边三角形．（3）当点G 在BC 延长线上时，如图③，与（2）同理可证，结论成立．综上所述，点G 在直线BC 上的任意位置时，该结论成立．9．已知点C 为线段AB 上一点，分别以AC 、BC 为边在线段AB 同侧作ACD ∆和BCE ∆，且CA CD =，CB CE =，ACD BCE ∠=∠，直线AE 与BD 交于点F ，（1）如图1，若60ACD ∠=︒，则AFB ∠= 120︒ ；如图2，若90ACD ∠=︒，则AFB ∠= ；如图3，若120ACD ∠=︒，则AFB ∠= ；（2）如图4，若ACDα∠=（用含α的式子表示）；∠=，则AFB（3）将图4中的ACD∆绕点C顺时针旋转任意角度（交点F至少在BD、AE中的一条线段上），变成如图5所示的情形，若ACDα∠与α的有何数量关系？并给予∠=，则AFB证明．【解答】解：（1）如图1，CA CD∠=︒，ACD=，60所以ACD∆是等边三角形．∠=∠=︒，ACD BCE=，60CB CE所以ECB∆是等边三角形．AC DC∠=∠+∠，BCD BCE DCE∠=∠+∠，=，ACE ACD DCE又ACD BCE∠=∠，∴∠=∠．ACE BCDAC DC=，=，CE BC∴∆≅∆．ACE DCB∴∠=∠．EAC BDC∠是ADFAFB∆的外角．∴∠=∠+∠=∠+∠+∠=∠+∠+∠=∠+∠=︒AFB ADF FAD ADC CDB FAD ADC EAC FAD ADC DAC120．如图2，AC CD=，∠=∠=︒，EC CBACE DCB=，90∴∆≅∆．ACE DCB∴∠=∠，AEC DBC又FDE CDB∠=︒，DCB∠=∠，9090EFD ∴∠=︒．90AFB ∴∠=︒．如图3，ACD BCE ∠=∠，ACD DCE BCE DCE ∴∠-∠=∠-∠．ACE DCB ∴∠=∠．又CA CD =，CE CB =，ACE DCB ∴∆≅∆．EAC BDC ∴∠=∠．180180(180)120BDC FBA DCB ACD ∠+∠=︒-∠=︒--∠=︒， 120FAB FBA ∴∠+∠=︒．60AFB ∴∠=︒．故填120︒，90︒，60︒．（2）ACD BCE ∠=∠，ACD DCE BCE DCE ∴∠+∠=∠+∠．ACE DCB ∴∠=∠．CAE CDB ∴∠=∠．DFA ACD ∴∠=∠．180180180AFB DFA ACD α∴∠=︒-∠=︒-∠=︒-．（3）180AFB α∠=︒-；证明：ACD BCE α∠=∠=，则ACD DCE BCE DCE ∠+∠=∠+∠，即ACE DCB ∠=∠．在ACE ∆和DCB ∆中AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩，则()ACE DCB SAS ∆≅∆．则CBD CEA ∠=∠，由三角形内角和知EFB ECB α∠=∠=． 180180AFB EFB α∠=︒-∠=︒-．10．如图1，ABC ∆为等边三角形，面积为S ．1D 、1E 、1F 分别是ABC ∆三边上的点，且。

全等三角形难题集锦(整理)

1、（1）如图1，点O 是线段AD 的中点，分别以AO 和DO 为边在线段AD 的同侧作等边三角形OAB 和等边三角形OCD ，连结AC 和BD ，相交于点E ，连结BC ．求∠AEB 的大小；（2）如图2，ΔOAB 固定不动，保持ΔOCD 的形状和大小不变，将ΔOCD 绕着点O 旋转（ΔOAB 和ΔOCD 不能重叠），求∠AEB 的大小.图1 图22、（1）如图1，现有一正方形ABCD ，将三角尺的指直角顶点放在A 点处，两条直角边也与CB 的延长线、DC 分别交于点E 、F ．请你通过观察、测量，判断AE 与AF 之间的数量关系，并说明理由．（2）将三角尺沿对角线平移到图2的位置，PE 、PF 之间有怎样的数量关系，并说明理由．（3）如果将三角尺旋转到图3的位置，PE 、PF 之间是否还具有（2）中的数量关系？如果有，请说明3、E 、F 分别是正方形ABCD 的边BC 、CD 上的点，且45EAF =︒∠，AH EF ⊥，H 为垂足，求证：AH AB =．CHF ED BA4、C 为线段AE 上一动点（不与点A ，E 重合），在AE 同侧分别作等边ABC ∆和等边CDE ∆，AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连结PQ ．以下五个结论： ① AD=BE ； ② AE PQ //； ③ AP=BQ ；④ DE=DP ； ⑤ ︒=∠60AOB ⑥CP=CQ ⑦△CPQ 为等边三角形． ⑧共有2对全等三角形 ⑨CO 平分AOE ∠ ⑩CO 平分BCD ∠ 恒成立的结论有______________（把你认为正确的序号都填上）．ABC ED O P Q5、D 为等腰ABC Rt ∆斜边AB 的中点，DM ⊥DN ，DM ，DN 分别交BC ，CA 于点E ，F 。

（1）当MDN ∠绕点D 转动时，求证：DE=DF 。

（2）若AB=2，求四边形DECF 的面积。