数学建模--路灯问题
路灯跟路灯的间隔的数学题目

路灯跟路灯的间隔的数学题目在解决路灯跟路灯之间的间隔问题时,可以运用数学中的相关概念和公式来辅助计算。
这些公式可以通过数学模型来描述题目中的情况,并且可以通过数值计算来求解。
首先,我们需要确定问题中涉及到的各个参数。
题目中没有具体给出参数的数值,因此我们假设以下几个参数:1. 路灯的数量:设为N。
2. 路灯之间的间隔:设为D。
3. 道路的长度:设为L。
首先,我们可以求解出路灯之间的实际平均间隔,即每两个路灯之间的距离。
由于题目没有给出具体的数值,我们可以按照以下公式进行计算:实际平均间隔 = 道路的长度 / (路灯的数量 - 1)接下来,我们可以计算出实际平均间隔和设定的间隔之间的差值。
如果差值为正数,则说明实际平均间隔大于设定的间隔,反之则说明实际平均间隔小于设定的间隔。
差值的绝对值可以衡量路灯之间的间隔是否均匀。
公式如下:差值 = 实际平均间隔 - 设定的间隔在计算这些差值时,我们可以将设定的间隔与实际平均间隔进行比较,从而得到相应的差值。
如果要进一步研究路灯之间的分布情况,我们可以利用概率统计中的均匀分布问题来描述。
设定每个路灯落在道路上的位置服从均匀分布,我们可以用概率密度函数来描述这种分布。
对于均匀分布的情况,概率密度函数是一个常数,可以通过以下公式进行计算:概率密度函数 = 1 / (道路的长度 / N)其中,道路的长度除以N表示每个路灯在道路上的平均间隔。
概率密度函数可以用来描述落在某个区间的路灯的概率。
除了上述的数学公式,我们还可以通过绘制图表来直观地表示路灯之间的间隔情况。
例如,我们可以绘制一个道路长度与路灯数量的关系图,以及一个差值与路灯数量的关系图。
通过观察这些图表,我们可以更好地理解路灯之间的间隔情况。
在实际应用中,还可以采用更复杂的数学方法和模型来解决类似的问题。
例如,可以采用最优化方法来寻找最佳的路灯布局,使得路灯之间的间隔最小或者最均匀。
此外,可以利用统计学方法来分析路灯之间的分布情况,以及预测未来的路灯需求等。
数学建模作业_路灯问题
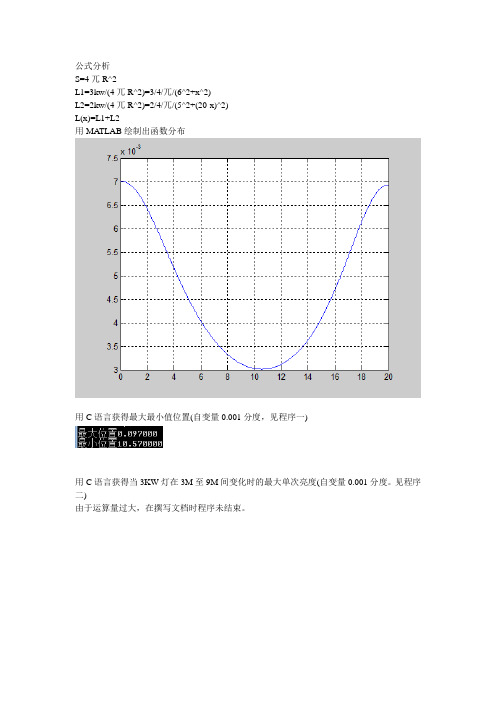
用 C 语言获得最大最小值位置(自变量 0.001 分度,见程序一)
用 C 语言获得当 3KW 灯在 3M 至 9M 间变化时的最大单次亮度(自变量 0.001 分度。见程序 二) 由于运算量过大,在撰写文档时程序未结束。Βιβλιοθήκη 程序一:获得最大最小亮度的位置
#include "stdafx.h" #include "math.h" double fLight(double x,float h3,float h2) {
static double PI=3.141592653589793; double L1,L2; L1=300000/4/PI/(pow(h3,2)+pow(x,2));printf("%f;",L1); L2=200000/4/PI/(pow(h2,2)+pow((20-x),2));printf("%f\n",L2); return (L1+L2); }
return 0; }
程序二:3KW 路灯从 3M 到 9M 的最暗点
#include "stdafx.h" #include "math.h" struct PointLight{double Light;float Point;}; double fLight(double x,float h3,float h2) {
static double PI=3.141592653589793; double L1,L2; L1=300000/4/PI/(pow(h3,2)+pow(x,2));printf("%f;",L1); L2=200000/4/PI/(pow(h2,2)+pow((20-x),2));printf("%f\n",L2); return (L1+L2); }
数学建模 绿色波浪红绿灯

评分栏1、设计"绿色波浪"红绿灯摘要:本文主要研究交通问题中的“绿色波浪”线控模型,把主干道相邻交通交通信号联动起来,通过对其距离和信号周期的分析,给出“时间-距离”图,利用图解法对简单系统优化求解;提出对复杂系统的数值计算法,用精确的数值进一步研究红绿灯控制问题,并实地考察从哈尔滨秋林公司到太平桥各路口的实际情况,采集了数据,用此法给出了对此路段的“绿色波浪”红绿灯的设计方案。
从而政府可以逐渐改变道路的结构和尽可能多地设置“绿色波浪”道路,大大节约整个行车组的汽油消耗,改善环境。
一、问题重述随着全球温室效应的加剧和石油资源的逐渐减少,很多国家都将节能减排提到了政府工作的重要议事日程之中。
城市拥堵的交通是造成汽油消耗和大量尾气排放的重要元凶,而汽车在反复刹车减速和提速的过程中不但耗油量是正常行驶的数倍以至十多倍,所排放的有害气体也是成倍增加。
哈尔滨秋林公司到太平桥路线,该路段长约4公里,但是地处繁华地带,红绿灯密集,一路上有大约10多处红绿灯,行车缓慢经常拥堵,行车时间长达20分钟。
需要依照“绿色波浪”想法设计一套红绿灯系统。
在保证安全的前提下尽可能实现顺畅通行,并在最后向司机写一份推广文,介绍想法做法,和司机应该如何顺利实现“绿色波浪”。
二、问题的分析与假设1、假设从秋林公司到太平桥这一段,马路的宽度相等、各向车道数相等。
2、假设此路段上车总量大于与其他交叉的其他路口的车流量。
3、从各个路口进入此路段的车流量等于注入此路口的车流量。
即各个路口对此路段的车流量没有影响,此路段与它们相交叉时自身的车流量不会改变。
4、假设此路段从西到东的车流量相等,而且两个方向汽车的平均速度相等。
5、信号灯只有红灯、绿灯两种,不考虑黄灯。
6、各个路口的信号周期(红灯+绿灯时间)相等。
7、不考虑转盘等设施,认为在这些路口仍然使用红绿灯。
三、模型的建立与求解在提出模型之前,现进行符号说明和参数解释。
数学建模(路灯)

数学模型实验论文路灯安置优化问题一、摘要:现代社会,经济不断发展人民生活水平不断提高,国家采取了一系列的措施让人民生活得更舒适,而在路上安装路灯就是其中一项重要的举措。
这里我从一盏灯的照明情况的分析出发,研究怎样合理的设计路灯的度和路灯之间的间距才能满足人们的需求。
首先分析路灯照明的特性,然后建立一盏灯时面积使最大的模型及两盏灯时时路灯间距最大的模型,在此基础上建立一排路灯及两排路灯的数学模型,分析两种情况何时须灯数最少即最节约能源,其中由实际情况和生活经验来看,两排灯时交错分布照明是比较均匀的,所以在两排灯时考虑灯交错分布的情况。
关键词:照明强度、路灯设计、路灯高度、间距的优化二、问题的提出:目前大多数公共场所都安装了路灯,路灯的高度和路灯之间的间距一般是依靠经验进行设置的,并没有从优化的角度进行考虑。
在能源日益减少的今天,我们应该考虑怎样尽可能的节约能源,并且作为路段整体设计的一部分路灯的安排也直接影响到社会公共环境。
经过对我校校园内几条道路的路灯设计的观察,对校园整体室外照明有了一定的了解。
在调查时A路正在安装路灯,为获取数据的方便取该路段为研究对象。
三、背景知识:1.光强度:光源在一定范围内发出可见光辐射强弱的物理量。
以光源在某一方向上单位立体角辐射的能量来量度。
(单位:坎德拉)2.照度:单位面积上得到的光通量。
(单位:勒克司)3.通量:人眼所能感觉到的光辐射的功率。
单位时间光辐射的能 和相对视见率的乘积。
(单位:流明)4.对于眼睛最敏感的 波长的黄绿光来说,1流明相当于1/685瓦特。
一般常见或需要的照度:晴朗夏天室外背荫处得照度为1000-10000流明。
5.为保证在该路段上处处都能有满足正常活动需要的照明强度,取照度的最小值为 ,即为13700流明。
6.照度定律:点光源O 预备照明平面中心A 的距离为h 时,平面上A 点的照度。
符号规定:p 为 O 点的光强度,a 为平面的法线方向与光源到A 点的连线之间的夹角,h 为光源的高度,l 为光源到A 点的距离。
数学路灯照明问题

数学实验与数学建模1-2.路灯照明问题(1)解:2^/sin .r p k I α=(光照强度公式),由题意的假设两只路灯照射半径之和为20m ,可得路面上任一点的光照强度等于两路灯光照强度之和。
由题意建立如下坐标系建立方程:2^1/1sin 1.1x p k I α= 2/1)^2^2^1/(11sin x h h +=α2^2)/(2sin 2.2x s p k I -=α 2/1]^2)^(2^2/[12sin x s h h -+=α此题只考虑强度的大小,故设k=1;2/3]^2)^(2^2/[2.22/3)^2^2^1/(1.121x s h h p x h h p I I I -+++=+= 要求最亮与最暗,即求I 的最大与最小值,先求I 的极值点用MA TLAB 求取clear alls=solve('(-30*x)/((25+x^2)^(5/2))+(54*(20-x))/((36+(20-x)^2)^(5/2))') s1=vpa(s,8);s1综上所述,当x=9.33m 时,为最暗点;当x=19.97m 时,为最亮点。
(2)~1. 3KW 的路灯高度在变化,此时2/3]^2)^(2^2/[2.22/3)^2^2^1/(1.121x s h h p x h h p I I I -+++=+=(此时h2也为未知数)因此求偏导数3))^2)^(2^2((/2^2233)^2^2^2((/22/x s h h p x h p h I -++-=∂∂=0同理用MA TLAB 求取(2)~2. 两只路灯的高度都在变化时2/3]^2)^(2^2/[2.22/3)^2^2^1/(1.121x s h h p x h h p I I I -+++=+=(此时h1,h2也都为未知数)3)^2^2^2((/2^2233)^2^2^2((/12/x h h p x h p h I ++-=∂∂=0 3))^2)^(2^2((/2^2233)^2^2^2((/22/x s h h p x h p h I -++-=∂∂=0 同理用MA TLAB 求取 2—2小型火箭初始。
交通灯数学建模

欢迎阅读驾车通过校园一、摘要本文通过对康奈尔大学交通路况以及在不同时间段人流量和车流量的调查,建立适当的优化模型着重解决六个问题中的四个问题。
问题一中,首先提出车辆尾部增长速度的概念,建立一个目标函数,使得一个交通周期内积累的车辆长度最小,并以行人通过人行道的最短时间为约束条件,然后求解出一个交通周期整。
?Find a good way to “synchronize” the new traffic light with the three existing ones (at the Thurston Ave Bridge, at Garden Ave. & Tower Rd., and at Central Ave. & Campus Rd.)? Suggest several different possible modes / synchronization programs based on the time of the day. (E.g., note that on weekdays the pedestrian traffic spikes in between classes.)? Will some of the motorists (or pedestrians) switch to alternative routes once this traffic light is installed?? Will the resulting vehicular traffic flow become more efficient than it is at present?? How much of a delay would this plan add for an average pedestrian at this intersection?? Assuming that the majority of pedestrians will follow the rules, are the sidewalks near that intersection wide enough for the crowd waiting to cross the road?三、问题分析3.1 针对问题一的分析本问题主要目标是要通过分析康奈尔大学的交通状况,在交叉路口设置一个交通灯与已经有的三个交通灯同步,让校园内的交通更加顺畅。
路灯模型
路灯照明
30. 关于 h2 极大化 E(x) 给定 h1, 对于每个 h2 都存在一个最小照明点 xm(h2) 求 h2*使得在其最小照明点xm(h2*)处照度最高. 即
E ( x m ( h )) max E ( x m ( h 2 ))
* 2
E x 3 P1 h1 x (h
20. 最低照明点
dE dx dE 1 dx dE 2 dx 3 P1 h1 x (h x )
2 1 2 5/2
3 P2 h 2 ( s x ) (h (s x) )
2 2 2 5/2
0
令 P1=2000W,P2=3000W,h1=5m,h2=6m, s=20m. 可求得 x =(0.028, 9.34,19.98) E =(81.98,18.24,84.48) xe = 9.00
路灯照明
计算 E x 0 , 可以得到
h2
*
E h1 0 ,
E h2 0
P2[( s - xm)2 - 2h2*2] = 0 和 P1(xm2 – 2h1*2)=0
tan 2 s xm
*
2 2
tan 1
h1
*
2 2
xm
1 2 35 . 26
路灯照明
照度定律:点光源 O 与被照明平面中心 A 的距 离为 h 时,平面上 A 点的照度 E= (I / h2) cos a, 其中,I 为 O 点的光强度,a 为平面的法线方向与 光源到 A点连线之间的夹角。
路灯照明
基于数学建模的城市路灯优化与节能研究
关键词: 路灯优化; 照明强度; 节能
中图分类号: O221. 1
文献标识码: A
文章编号: 1673- 8772( 2011) 01- 0053- 03
R esearch on Street Lamps Optim ization and Energy- saving Based onM athem aticalM odeling
可。此时 B ( o, y, 0)B 是 A ( x, y, 0)在 x = 0时, 地面上照明强度最小的点。此时 B 点位于三盏灯形成的三
角形外接圆圆心在轴上的投影, 且 y 与 d、l 满足关系 ( y - d ) 2 + h2 =
l2 4
+
y2
+
h2,
y
I
[ 0, d ]
( 2)
由 ( 2)式变形得 y = d +
d2 + 2l2 + l2 + h2 E 5l2 + d2 + l2 + h2
8
16
16 4 16
d = 10
lE 0
灯
o1 到
o1 o3 中点 C 的距离为
d2
满足
d
2 2
=
d2 4
+
l2 + 16
h 2。
比较上述两个式子可以很快得出结论: d1 E d2。即只需考虑路灯在 B 点的照度大于等于最低照度即
基于数学建模的城市路灯优化与节能研究
张家昕, 仇海全, 卢中其
(安徽科技学院 理学院, 安徽 凤阳 233100)
摘 要: 本文提出了一种优化的城市路灯排列设计方法。利用该方法优化出的路灯交错排列方式, 与现在
数学建模 红绿灯问题解答
05年研究生竞赛D 题参考解答问题1的解答 1 模型假设1)市场上对该商品的需求速率是连续均匀的,记为r ; 2)每次进货的订货费为常数1c ;3)使用自己仓库贮存产品时,单位产品每天的存贮费用记为2c ,使用租借仓库贮存产品时,单位产品每天的存贮费用记为3c ,且32c c ≤;4)对于一个订货周期,允许产品缺货,单位产品每天的缺货损失记为4c ;5)自己仓库用于存贮该产品的最大容量为0Q ,每次订货后使下周期初的储存量达到固定值Q ,且Q Q <0;6)当存贮量降到L 时开始订货;7)交货时间X 是随机的,如下图中的,,,21 x x 这就使得每个订货周期为随机变量,设X 的概率密度函数为)(x p ;8)购进货物时需事先支出产品本身的费用,每单位产品的费用记为k ;9)1t 、2t 、3t 分别表示每个订货周期内当库存量q 从Q 降至L 、0Q 、0的时刻,4t 表示当出现缺货时一个订货周期结束的时刻。
2 模型建立产品到货后,首先将自己的仓库装满,剩余的0Q Q -部分存入租借的仓库;而使用产品时,首先使用租借仓库中的产品,待使用完后,再使用自己仓库中的产品。
由于市场上对该商品的需求速率是常数r ,在一个销售周期内,t 时刻产品库存量q 呈直线rt Q q -=下降。
情形1 Q L Q ≤<0此时形成如下的存贮状态图1。
图1 情形1的存贮状态图Fig.1 storage state chart in case 1建模目的是选择合适的目标函数,并确定最佳订货点*L ,使一个订货周期内发生的总费用最小。
下面先考虑一个订货周期内所发生的各种费用。
1)订货费1c ,这可看成一个常数,与订货数量、时间等均无关; 2)购进产品本身的平均费用 注意到当q 降至L 时,rL Q t -=1(可见只要求出最佳时刻*1t ,便可换算出最佳订货点*L ),因此一个订货周期长度是X t T +=1,周期结束时的库存量是rT Q -,因此要购进产品)(1X t r rT +=,购买产品本身的平均费用为)]([)(11X E t kr t +=α (1)这里⎰∞+=)()(dx x xp X E 。
(完整版)数学建模--路灯问题
最终报告课题名称:关于城市街道路灯分布规划问题一、问题描述1.问题背景随着城市化水平的不断提高,城市街道越来越多,街道上的路灯数量也会大量增加,如何合理安放路灯便成为一个重要问题。
在能源日益紧张的今天,更需要一种能够尽可能节约能源的路灯安置方案。
2.主要问题对某一条街道两侧的路灯,在照明强度的要求已知时,寻求一种路灯安置方案,(选定合适的路灯高度、路灯之间的间距),使路灯的安置达到要求,同时路灯的数量尽可能减少,路灯的能耗达到最低。
3.问题研究的意义通过对路灯问题的研究,找到一种安置方案,优化现有路灯布局,使路灯能耗降低,以节省经济投入。
二、问题分析要使能耗最小,在路灯功率一定的情况下,只能减少路灯的使用量。
因此,在满足最低照明功率的前提下,通过改变路灯的高度来使路灯之间的距离达到最优是本问题的一个解决方案。
三、模型假设所有路灯都紧靠在路的边界线上,且照明效果都相同。
光源是点光源。
在单个光源照射下,距光源L的点的光照强度为C=f(L);在多光源照射下,某一点的光照强度为各光源对该点光照强度的代数和。
道路处处等宽,路面上每一点的光照强度至少要达到C0。
四、说明1. 照度定律:点光源O的发光强度是P,则距点光源O为l的点的照度为E=Pℎ32. 参量变量说明:(1)设路灯的高度:ℎ,路的宽度:d=7m(2)经过实际考察,路灯的功率:P=2200W(3)路灯的间距:l(4)查阅资料可知,使物体可见的最低照明强度:c0=20W/m2五、模型建立与求解㈠单排路灯平直道路的路灯优化问题首先考虑直路上只安装一排路灯时的最优化方案,目的是通过调整路灯的高度和间距,使路灯的间距尽可能大,以减少路灯数量,节约成本。
忽略相邻的四盏路灯之外路灯对该点的影响。
建立如图坐标系,假设四盏路灯下最暗点坐标为(x,d)(x∈[0,l2]),设该点照度为E,则有E =Pℎ[ℎ2+d 2+(x −3l2)2]32+Pℎ[ℎ2+d 2+(x −l2)2]32+Pℎ[ℎ2+d 2+(x +l2)2]32+Pℎ[ℎ2+d 2+(x +3l2)2]32E ′=−2Pℎx(1[ℎ2+d 2+(x−3l2)2]52+1[ℎ2+d 2+(x−l2)2]52+1[ℎ2+d 2+(x+l2)2]52+1[ℎ2+d 2+(x+3l2)2]52)易求得当x =0时E 有最小值E m =2Pℎ[ℎ2+d 2+(3l 2)2]32+2Pℎ[ℎ2+d 2+(l2)2]32令E m =c 0,c 0=2Pℎ[ℎ2+d 2+(3l 2)2]32+2Pℎ[ℎ2+d 2+(l2)2]32用C 程序求解 程序源代码: #include <stdio.h> #include <math.h>double s(double l, double h);void main(){double c, h, t[51], delta, left, right, mid; int i; c = 20;while (1) {scanf("%lf", &h); if (h == 0) break; t[0] = 30;for (i = 1; i <= 50; i++) { t[i] = s(i, h); if ((t[i] - c) * (t[i-1] - c) <= 0)break;}left = i-1;right = i;do{mid = left * 0.618 + right * 0.382;if (s(mid, h) <= c)left = mid;elseright = mid;delta = s(left, h) - c;}while (delta <= -1);printf("l=%lf,%lf\n", left, delta);}}double s(double l, double h){double s, p, d, k1, k2;p = 2200;d = 7;k1 = h * h + d * d + l * l * 2.25;k1 = sqrt(k1 * k1 * k1);k2 = h * h + d * d + l * l * 0.25;k2 = sqrt(k2 * k2 * k2);s = 2 * p * h * (1 / k1 + 1 / k2);return s;}解得当ℎ=9.6m时,l的值最大,l m=13.38m㈡两排路灯直路的优化问题两排路灯安置有对称和非对称两种形式,考虑美观,本方案针对对称安置优化问题进行讨论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
校园路灯问题优化
一、问题描述
1.问题背景
路灯已成为夜晚比不可少的工具,不管是在街道,还是校园都随处可见。
随着路灯的增加,如何合理解决路灯问题便成为一个重要问题。
在能源日益减少的今天,我们应该考虑怎样尽可能的节约能源,并且作为校园整体设计的一部分路灯的安排也直接影响到学校环境,对于夜晚校园环境的烘托具有非常重要的意义。
2. 主要问题
经过对校园内几条道路的路灯设计的观察,对校园整体室外照明有了一定的了解。
主要从三个方面优化校园路灯问题。
主要侧重于其布局优化。
(1)校园路灯分布规划:在照明强度的要求已知时,寻求一种路灯安置方案,(选定合适的路灯高度、路灯之间的间距),使路灯的安置达到要求,同时路灯的数量尽可能减少,路灯的能耗达到最低。
(2)校园路灯开放时间优化。
(3)校园路灯维护优化。
3. 问题研究的意义
通过对路灯问题的研究,找到一种安置方案,优化现有路灯布局,使路灯能耗降低,以节省经济投入。
二、问题分析
要使能耗最小,在路灯功率一定的情况下,只能减少路灯的使用量。
因此,在满足最低照明功率的前提下,通过改变路灯的高度来使路灯之间的距离达到最优是本问题的一个解决方案。
三、模型假设
(1)所有路灯都紧靠在路的边界线上,且照明效果都相同。
光源是点光源。
在单个光源照射下,距光源L的点的光照强度为C=f(L);在多光源照射下,某一点的光照强度为各光源对该点光照强度的代数和。
道路处处等宽,路面上每一点的光照强度至少要达到C0。
(2)假设路灯为完全规范的,即处处等宽,一排路灯的宽度为,两排路灯的宽度为。
四、变量说明
1. 照度定律:点光源O的发光强度是,则距点光源O为的点的照度为
2. 参量变量说明:
(1)设路灯的高度:h,路的宽度:
(2)经过实际考察,路灯的功率:=2200W
(3)路灯的间距:
O
x
y
( x , d ) (4)查阅资料可知,使物体可见的最低照明强度:=20W/m 2
五、模型建立与求解
㈠单排路灯平直道路的路灯优化问题
首先考虑直路上只安装一排路灯时的最优化方案,目的是通过调整路灯的高度和间距,使路灯的间距尽可能大,以减少路灯数量,节约成本。
忽略相邻的四盏路灯之外路灯对该点的影响。
建立如图坐标系,不难发现路面上光强最弱的点分布在路的另一边界。
假设四盏路灯下最暗点坐标为(∈[0,),设该点照度为E ,则有
E=ph/[(h^2+d^2+(x-3l/2)^2)^(3/2)]+ph/[(h^2+d^2+(x-l/2)^2)
^(3/2)]+ph/[(h^2+d^2+(x+l/2)^2)^(3/2)]+ph/[(h^2+d^2+(x+3l/2)^2)^(3/2)]
E’=-2phx(1/[(h^2+d^2+(x-3l/2)^2)^(5/2)]+1/[(h^2+d^2+(x-l/2)^2)^(5/2)]+1/[(h^2+d^2+(x+l/2)^2)^(5/2)]+1/[(h^2+d^2+(x+3l/2)^2)^(5/2)])
易求得当 =0时E 有最小值
令=,
用C 程序求解
程序源代码:
#include <stdio.h>
#include <math.h>
double s(double l, double h);
void main()
{
double c, h, t[51], delta, left, right, mid;
int i;
c = 20;
while (1)
{
scanf("%lf", &h);
if (h == 0)
break;
t[0] = 30;
for (i = 1; i <= 50; i++)
{
t[i] = s(i, h);
if ((t[i] - c) * (t[i-1] - c) <= 0)
break;
}
left = i-1;
right = i;
do
{
mid = left * 0.618 + right * 0.382;
if (s(mid, h) <= c)
left = mid;
else
right = mid;
delta = s(left, h) - c;
}
while (delta <= -1);
printf("l=%lf,%lf\n", left, delta);
}
}
double s(double l, double h)
{
double s, p, d, k1, k2;
p = 2200;
d = 7;
k1 = h * h + d * d + l * l * 2.25;
k1 = sqrt(k1 * k1 * k1);
k2 = h * h + d * d + l * l * 0.25;
k2 = sqrt(k2 * k2 * k2);
s = 2 * p * h * (1 / k1 + 1 / k2);
return s;
}
解得当h=9.6m时,的值最大,
㈡两排路灯直路的优化问题
两排路灯安置有对称和非对称两种形式,考虑美观,本方案针对对称安置优化问题进行讨论。
同(1)中研究方法,试图寻找路面光照度最小点,使其不小于c0即可。
如图,易得,八盏路灯构成的平行四边形中心为光强最弱点。
则在满足照度最低要求下h与的关系式
同样利用C程序求解,解得当h=7.4时,的值最大,
㈢十字路口的路灯安置
根据两排路灯直路的讨论,满足照度要求的路灯最大间距为25米。
那么两条7米宽的路交叉,可看作在一条道路相临两盏灯之间插入一条道路,即不改变当前路灯分布是完全可行的。
若考虑美观,可将路灯对称地排在十字路口的四个角上。
㈣丁字路口的路灯安置
丁字路与十字路类似,亦可看作在一条道路的一侧相临两盏灯之间插入一条道路,不改变当前路灯分布也是完全可行的。
此时若考虑路口安全问题,可在支路所对方向安置一盏灯。
六、结论及扩展
到此为止,本小组关于校园路灯分布规划问题的研究暂时结束。
本课题中主要讨论了单排路灯、两排路灯、十字路口、丁字路口的路灯安置优化问题,按照国家标准,路灯间距的最大值应为路灯的高度的3.5倍,这与我们的研究结果是相符的。
但此次建模也存在着一定的缺陷,例如对于更加复杂的路况,小组曾集中讨论,但并未得到理想的结果;在考虑两排路灯安置的优化问题时,从美观出发,只考虑了道路两侧路灯对称分布的情况。
参考文献:《数学建模》谢金星
《数学建模简明教程》戴朝寿孙世良
二、开放时间优化
设置路灯的作用是为了校园的美观,更是为了方便广大学生的出行,根据天气的具体情况,灵活机动地开启或者关闭路灯,可以使路灯切实发挥自身的作用。
路灯开关的时间应该根据天气的实际情况来决定,灵活机动一些,不能墨守成规。
如果天气状况不好,到了规定的关闭时间,天空阴暗,能见度很低,就应该适当地延长;如果天气很好,即使没有到了关闭时间也应该立即关闭,可以尽可能地节省能源,降低路灯使用的成本。
天气状况很好,能见度很高,路灯还亮着,浪费能源。
三、维修优化
在校园,常可见坏了的路灯,而无人管理。
针对目前校园路灯维护方式的不合理性,为了广大师生出行的方便,以及尽可能的节约能源和节省经费,制定出合理的维修方式是很有必要的。
