数学建模香烟过滤嘴作用
香烟过滤嘴的作用1

在x=0处点燃的烟草单位时间内放出的毒物量 记作H0,根据假设可得:
q(0) aH 0 , H 0 uw0
2、在燃烧过程的任意时刻,计算q( x,l)
假设时刻t点燃的烟草单位时间放出的毒物量为
H(t),则可得 H( t ) uw( ut,t )
且 q(ut,t) aH(t)
香烟过滤嘴的作用
问题的提出
吸烟有害健康,这是众所周知的,但是仍有不少 人不抛弃香烟的嗜好,香烟制造商既要满足消费者的 需求,又要顺应减少吸烟危害的潮流,还获取丰厚的 利润,于是在香烟上要装了过滤嘴,过滤嘴的作用到 底有多大,于是用的材料和过滤嘴的长度有什么关系, 能否从定量的角度回答这些问题,分析吸入的毒物数 量与哪些因素有关,并建立它们之间的数量表达式。
目标量:
吸入毒物量Q就是在x=l处的毒物流量在吸一只烟的 时间内的总和。
T
Q 0 q(l,t)dt,T l1 / u
Hale Waihona Puke 毒物流量函数q(x,t)的分析
q(x+△x)
q(x)
0
x x+△x
l1
x
1、在燃烧开始的时刻t =0,计算q( x,0) ,记为q( x)
: 当t=0时,由假设条件及守恒定律可得
auw(l, t)e v e
(l l1 ) v
毒物密度函数 w(ut,t) 的分析
在吸烟过程中未点燃的烟草不断吸收毒物,所
以毒物在烟草中的密度w(x,t)是变化的,考察
截面x处△t时间内毒物密度的增量,根据假设
知:
w( x,
t
t )
w(
x,
t)
b
q(
x,
数学建模技术与案例 20151127

+ ⋯+
������
������
������������ ������!
������ − ������������
������
+ ������������ ������
只取泰勒展开的一次项������ ������ =
程 ������
������������ 近似为: ������������
a. 如何控制捕捞使持续产量最大化 b. 如何控制捕捞使效益最大化 c. 捕捞过度问题
∴ 渔场鱼量的变化量=增长量−捕捞量
案例6 捕鱼业的持续收获
分析
• 在鱼群自然增长和人工捕捞的情况下, 渔场鱼量如何变化?
– 渔场的鱼量按规律增长
– 捕捞
∴ 渔场鱼量的变化量=增长量−捕捞量
案例6 捕鱼业的持续收获
分析:渔场鱼量按规律增长
• 鱼量增长到一定程度后增长率下降:
– 原因:自然资源、环境条件等的阻滞作用。 – 趋势:随着鱼量的增加,阻滞作用也变大。
课程大纲
• • • • • • 第1章:什么是数学建模 第2章:数学建模的基本技能与方法 第3章:交通与运输案例分析 第4章:健康与医疗案例分析 第5章:环境与生态保护案例分析 第6章:生产与制造案例分析
2015/11/30
Mathematical Modeling
3
第5章:环境与生态保护案例分析
������→∞
lim ������ ������ = ������������ ⋯ ������
则平衡点������ = ������������ 是稳定的;否则是不稳定的。
微分方程的稳定性理论
•
������������ ������������
数学建模香烟过滤嘴作用

数学建模-----微分方程模型香烟过滤嘴的作用问题:尽管科学家们对于吸烟的危害提出了许多的无可辩驳的证据,不少国家的政府与有关部门也一直致力于减少或禁止吸烟,但就是仍有不少人不愿抛弃对香烟的嗜好。
香烟制造既要满足瘾君子的需要,又要顺应减少吸烟危害潮流,还要获取丰厚的利润,于就是普遍地在香烟上安装了过滤嘴。
过滤嘴的作用到底有多大,与使用的材料与过滤嘴的长度有什么关系,要从定量的角度回答这些问题就要建立一个描述吸烟过程的数学模型,分析人体吸入的毒物数量与哪些因素有关,以及她们之间的数量表达式。
问题描述与分析:吸烟时毒物吸入人体的大致过程时这样的:毒物基本上均匀的分布在烟草中,吸烟时点燃处的烟草大部分化为烟雾,毒物由烟雾携带着一部分直接进入空气,另一部分沿香烟穿行。
在穿行过程中又部分的被未点燃的烟草与过滤嘴吸收而沉积下来,剩下的进入人体。
被烟草吸收而沉积下来的那一部分毒物,当香烟燃烧到哪里的时候又通过烟草部分进入空气,部分沿香烟穿行,这个过程一直继续到香烟燃烧到过滤嘴处为止。
于就是我们瞧到,原来分布在烟草中的毒物除去了进入空气与被过滤嘴吸收的一部分外,剩下的全部被人体吸入。
实际的及烟过程非常复杂并且因人而异,点燃处毒物随烟雾进入空气与沿香烟穿行的数量比例,与吸烟的方式、环境等多种因素有关;烟雾穿过香烟的速度随着吸烟动作的变化而不断地改变;过滤嘴与烟草对毒物的吸收作用也会随烟雾穿行速度等影响而有所变化。
如果要考虑类似于上面这些复杂情况,将使我们寸步难行。
为了能建立一个初步的模型,可以设想一个机器人在典型的环境下吸烟,“她”吸烟的动作、方式及外部环境在整个过程中不变,于就是可以认为毒物随烟进入空气与沿香烟穿行的数量比例、烟雾穿行的速度、过滤嘴与烟草对毒物的吸收率等在吸烟过程中都就是常数。
模型假设基于上述分析,这个模型的假设如下。
1. 烟草与过滤嘴的长度分别就是1l 与2l ,香烟总长度l = 1l +2l ,毒物M(毫克)均匀分布在烟草中,密度为10/M l ω=2. 点燃处毒物随烟雾进入空气与沿香烟穿行的数量比例就是a ’:a,a ’+a=1、3. 未点燃的烟草与过滤嘴对随烟雾穿行的毒物的吸收率(单位时间内毒物被吸收的比例)分别就是常数b 与β4. 烟雾沿香烟穿行的速度就是常数v,香烟燃烧速度就是常数u,且v>>u将一支烟吸完,毒物进入人体的总量(不考虑从空气的烟雾中吸入的)记作Q,在建立模型以得到Q 的数量表达式之前,让我们先根据常识分析一下Q 应与那些因素有关,采取什么方法可以降低Q 。
311香烟过滤嘴的作用问题

3.11香烟过滤嘴的作用问题1)问题的提出普遍认为香烟过滤嘴的作用可使吸烟者对尼古丁和烟焦油等毒物的吸收率减少,肺癌死亡率下降。
这有何根据呢?本节从定量的角度介绍一个模型,描述烟雾通过香烟的过程,分析人体吸入毒物的数量与哪些因素相关,说明过滤嘴的作用与使用的材料和过滤嘴的长度之间的关系。
2)模型机理假设毒物均匀地分布在香烟中,吸烟时点燃处的烟草化为烟雾,毒物由烟雾携带着一部分0q 直接进入空气,另一部分q 沿着香烟穿行。
在穿行过程中,q 又有一部分被未点燃的烟草和过滤嘴吸收而沉积下来,剩下的部分进入人体。
q q :0的数量比例随吸烟的方式、环境等多种因素的变化而不同。
烟雾沿香烟穿行的速度v 随着吸烟动作变化也不断地变化。
为了建立模型,我们希望避开这个复杂的过程。
为此,设想吸烟者是架机器,吸烟的动作、方式及外部环境在整个吸烟过程中不变,于是可以认为毒物随烟雾进入空气和沿香烟穿行的数量比例q q :0、烟雾穿行的速度v 、过滤嘴和烟草对毒物的吸收率等在吸烟过程中都是常数。
香烟燃烧速度u 与v 相比,可认为燃点处于静止状态。
下面用数学语言来描述。
3)模型假设1.点燃处毒物随烟雾进入空气部分0q 和沿香烟穿行部分q 的数量比例是)10( ,:)1(:0<<-=a a a q q ;2.烟雾沿着香烟穿行的速度v 和香烟燃烧速度u 都是常数。
且u v >>; 3.未点燃的烟草和过滤嘴对毒物的吸收率(单位时间内毒物被吸收的比例)分别为常数b 和β;4.香烟总长为l ,烟草部分长1l ,则过滤嘴长为1l l -。
整支香烟所含毒物总量M 均匀分布在长1l 的烟草当中。
于是毒物的平均密度10l M w =;5.坐标系如图3-19所示。
设0=t 时刻,在0=x 处点燃香烟,则在ul T 1=时整支香烟燃尽。
图3-19 0)0(=x 香烟点燃状态4)模型建立首先定义几个基本函数:毒物流量),(t x q :在燃烧过程中的时刻)0( ≥t t ,单位时间内通过香烟截面)0( l x x ≤≤处的毒物量。
数学建模5香烟过滤嘴的作用分解

b q x q x x q x v dq lim dx x 0 x b q x v
在x
0 x l1
⑵
l1 x l.
0 处点燃的烟草单位时间内放出的毒物量记作
根据假设1、3、4,则可得微分方程2的初始条件为
w x, t t w x, t b q x, t v t ,
位长度烟雾中的毒物被吸收的部分,由假设4,则有
令 t
0, 并将⑸、⑹代入得方程
b x ut w abu w ut , t e v v t w x, 0 w . 0
即方程的解可以表达为
bx v aH e 0 q x x l1 b l aH e v 1 e v , 0
0 x l1 ,
⑷
l1 x l.
2. 在香烟燃烧的任何时刻 t , 求毒物在单位时间内通 过x
l 的数量q l , t .
此方程为偏微分方程,该方程的解为
but abut a bx w x, t w0 1 e v e v e v a abut w0 v w ut , t a 1 ae
q 0 aH 0 , H 0 uw0 .
求解微分方程⑵。首先由方程及初始条件
⑶
b dq q x v dx q 0 aH 0 ,
方程的通解为 q x Ce 从而得到方程的解为
b x v
, 再由初始条件得 C aH0 .
q x aH 0 e
滤嘴吸收而沉淀下来,剩下的进入人体。被烟草吸收而
滤嘴对卷烟主流烟气中Cd和Pb截留效率的影响

滤嘴对卷烟主流烟气中Cd和Pb截留效率的影响【摘要】本文主要探讨了滤嘴对卷烟主流烟气中Cd和Pb截留效率的影响。
在分析了滤嘴对Cd和Pb的截留效率、滤嘴构成、烟草品种、烟支燃烧温度以及烟草燃烧速率对Cd和Pb截留效率的影响。
研究表明滤嘴在降低主流烟气中Cd和Pb含量方面发挥着重要作用。
结论部分指出,影响Cd和Pb截留效率的主要因素包括滤嘴构成及烟草燃烧温度等,这对减少Cd和Pb对吸烟者健康的风险具有重要意义。
研究的意义在于为卷烟生产和吸烟者提供了相关的参考,有望减少卷烟主流烟气中有害金属Cd和Pb的释放,保护吸烟者健康。
【关键词】关键词:滤嘴,Cd,Pb,主流烟气,截留效率,烟草品种,燃烧温度,燃烧速率,健康风险1. 引言1.1 研究背景Cd和Pb是卷烟烟气中的两种主要重金属污染物,它们对人体健康造成了严重的危害。
Cd具有强大的毒性,长期暴露可能导致肾功能损害、骨质疏松等疾病;而Pb同样具有毒性,可引起神经系统损伤、生殖系统疾病等。
卷烟是造成Cd和Pb进入人体的主要途径,因此降低卷烟烟气中Cd和Pb的含量对保障吸烟者健康至关重要。
目前,卷烟滤嘴被广泛应用于降低烟气中有害物质的含量。
滤嘴对Cd和Pb的截留效率并不十分明确,其受到滤嘴构成、烟草品种、烟支燃烧温度以及烟草燃烧速率等因素的影响。
研究滤嘴对Cd和Pb 的截留效率及影响因素,对于制定减少Cd和Pb对吸烟者健康风险的措施具有重要意义。
本研究旨在探讨滤嘴对卷烟主流烟气中Cd和Pb 截留效率的影响,为人们提供科学依据和指导。
1.2 研究目的本研究的目的是探讨滤嘴对卷烟主流烟气中镉(Cd)和铅(Pb)的截留效率,并分析影响截留效率的因素。
通过对不同滤嘴结构、烟草品种、烟支燃烧温度以及烟草燃烧速率等因素的研究,旨在揭示滤嘴在降低主流烟气中Cd和Pb含量方面的作用机制,并为减少Cd和Pb对吸烟者健康风险提供科学依据。
通过本研究可以深入了解Cd和Pb在卷烟烟气中的行为特征,为卷烟生产和吸烟者健康保护提供具体指导和建议。
建模必修课课程设计题目
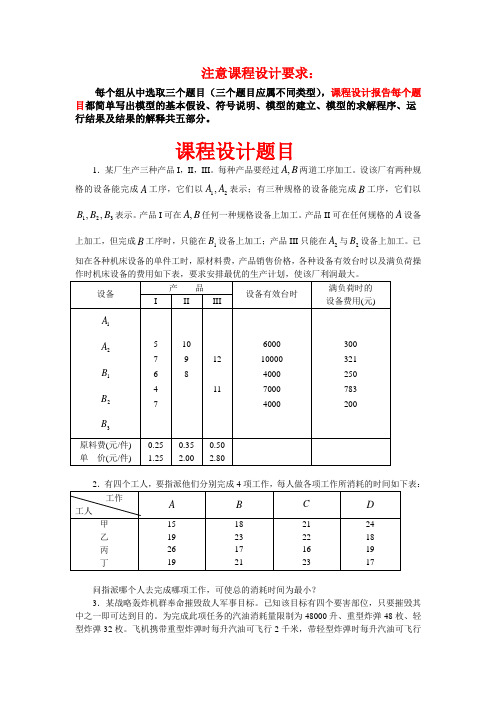
注意课程设计要求:每个组从中选取三个题目(三个题目应属不同类型),课程设计报告每个题目都简单写出模型的基本假设、符号说明、模型的建立、模型的求解程序、运行结果及结果的解释共五部分。
课程设计题目1.某厂生产三种产品I ,II ,III 。
每种产品要经过B A ,两道工序加工。
设该厂有两种规格的设备能完成A 工序,它们以21,A A 表示;有三种规格的设备能完成B 工序,它们以321,,B B B 表示。
产品I 可在B A ,任何一种规格设备上加工。
产品II 可在任何规格的A 设备上加工,但完成B 工序时,只能在1B 设备上加工;产品III 只能在2A 与2B 设备上加工。
已知在各种机床设备的单件工时,原材料费,产品销售价格,各种设备有效台时以及满负荷操问指派哪个人去完成哪项工作,可使总的消耗时间为最小?3.某战略轰炸机群奉命摧毁敌人军事目标。
已知该目标有四个要害部位,只要摧毁其中之一即可达到目的。
为完成此项任务的汽油消耗量限制为48000升、重型炸弹48枚、轻型炸弹32枚。
飞机携带重型炸弹时每升汽油可飞行2千米,带轻型炸弹时每升汽油可飞行3千米。
又知每架飞机每次只能装载一枚炸弹,每出发轰炸一次除来回路程汽油消耗(空载为了使摧毁敌方军事目标的可能性最大,应如何确定飞机轰炸的方案,要求建立这个问题的线性规划模型。
4. 某钻井队要从以下10个可供选择的井位中确定5个钻井探油,使总的钻探费用为最小。
若10个井位的代号为1021,,,s s s ,相应的钻探费用为1021,,,c c c ,并且井位选择上要满足下列限制条件:(1) 或选择1s 和7s ,或选择钻探9s ;(2) 选择了3s 或4s 就不能选5s ,或反过来也一样;(3) 在8765,,,s s s s 中最多只能选两个;试建立这个问题的整数规划模型。
5. 设位于坐标原点的甲舰向位于x 轴上点)0,1(A 处的乙舰发射导弹,导弹始终对准乙舰。
烟嘴的作用

烟嘴的作用第一篇:烟嘴的作用在吞云吐雾的同时,我们必须了解:烟草中含有数百种复杂的化学成分,大部分对人体有害,其中焦油、尼古丁、酚类、醇类、酸类、醛类等40种是有毒和有致癌作用的物质。
凯龙烟嘴在做市场调研的时候发现,大多数人只认识到香烟有尼古丁的危害,却不知道烟在点燃后,所产生的烟雾,包含了烟草中所有的化学成分,同时比烟草本身又增加了一些有害物质,如一氧化碳和烟焦油等。
这是因为除烟草本身外,在制成卷烟的过程中,要在原料中加入一些可可、甘草、糖、甘油、乙二醇等调味、湿润、产香、助燃物质。
这些添加剂虽然本身无害,但在燃烧过程中却起了变化。
所以抽烟的时候,不但吸进了大量的有害物质,还有一些燃烧过程中形成的灰尘状物质,利用凯龙烟嘴,就是用凯龙烟嘴的多重过滤原理,滤除了香烟中的有害化学成分,而且也把烟气中的灰尘截流在了烟嘴里面,抽进的就是醇和的烟了,自然对身体好,呼吸系统了没有了大量灰尘的堆积,自然咳嗽、咳痰就减轻了,对喉咙的刺激也减少了。
目前市场上陆续出现的戒烟产品始终无法真正解决戒烟的问题,人们总是戒而复吸,香烟中有2540多种成分,燃烧后发生复杂的物理化学变化,产生的烟气中有400多种致癌物质,还有10多种会促进癌发展的物质,其中对人体危害最大的是烟碱、焦油、一氧化碳、氰化物及放射性物质。
烟民在想戒烟而又戒不掉的时候,借助凯龙牌健康烟嘴,可高效分离香烟中80%以上有害物质!能有效缓解因吸烟引起的咳嗽、多痰、咽喉肿痛等症状;基于此,烟嘴产品将蕴含庞大的市场潜力,烟嘴也从稀有产品逐渐被公众所接受,正成为烟民的主力日用消费产品。
长期使用健康烟嘴,会有以下明显功效:1、滤除卷烟内大部份焦油,减少了吸烟者焦油的摄入量,降低焦油对心、脑血管的硬化起到加速的作用。
2、痰液减少,痰液色泽渐浅:使用”凯龙”牌保健过滤烟嘴,可高效分离香烟中80%以上有害物质,能有效缓解因吸烟引起咳嗽、多痰、咽喉肿痛等症状。
3、延缓牙黄、牙黑等症状:实验证明过去每年洗一次牙齿的吸烟者,使用“凯龙”牌保健过滤烟嘴后可延长3一5年。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模-----微分方程模型香烟过滤嘴的作用问题:尽管科学家们对于吸烟的危害提出了许多的无可辩驳的证据,不少国家的政府和有关部门也一直致力于减少或禁止吸烟,但是仍有不少人不愿抛弃对香烟的嗜好。
香烟制造既要满足瘾君子的需要,又要顺应减少吸烟危害潮流,还要获取丰厚的利润,于是普遍地在香烟上安装了过滤嘴。
过滤嘴的作用到底有多大,与使用的材料和过滤嘴的长度有什么关系,要从定量的角度回答这些问题就要建立一个描述吸烟过程的数学模型,分析人体吸入的毒物数量与哪些因素有关,以及他们之间的数量表达式。
问题描述与分析:吸烟时毒物吸入人体的大致过程时这样的:毒物基本上均匀的分布在烟草中,吸烟时点燃处的烟草大部分化为烟雾,毒物由烟雾携带着一部分直接进入空气,另一部分沿香烟穿行。
在穿行过程中又部分的被未点燃的烟草和过滤嘴吸收而沉积下来,剩下的进入人体。
被烟草吸收而沉积下来的那一部分毒物,当香烟燃烧到哪里的时候又通过烟草部分进入空气,部分沿香烟穿行,这个过程一直继续到香烟燃烧到过滤嘴处为止。
于是我们看到,原来分布在烟草中的毒物除去了进入空气和被过滤嘴吸收的一部分外,剩下的全部被人体吸入。
实际的及烟过程非常复杂并且因人而异,点燃处毒物随烟雾进入空气和沿香烟穿行的数量比例,与吸烟的方式、环境等多种因素有关;烟雾穿过香烟的速度随着吸烟动作的变化而不断地改变;过滤嘴和烟草对毒物的吸收作用也会随烟雾穿行速度等影响而有所变化。
如果要考虑类似于上面这些复杂情况,将使我们寸步难行。
为了能建立一个初步的模型,可以设想一个机器人在典型的环境下吸烟,“他”吸烟的动作、方式及外部环境在整个过程中不变,于是可以认为毒物随烟进入空气和沿香烟穿行的数量比例、烟雾穿行的速度、过滤嘴和烟草对毒物的吸收率等在吸烟过程中都是常数。
模型假设基于上述分析,这个模型的假设如下。
1. 烟草和过滤嘴的长度分别是1l 和2l ,香烟总长度l = 1l +2l ,毒物M (毫克)均匀分布在烟草中,密度为10/M l ω=2. 点燃处毒物随烟雾进入空气和沿香烟穿行的数量比例是a ’:a,a ’+a=1.3. 未点燃的烟草和过滤嘴对随烟雾穿行的毒物的吸收率(单位时间内毒物被吸收的比例)分别是常数b 和β 4. 烟雾沿香烟穿行的速度是常数v ,香烟燃烧速度是常数u ,且v>>u将一支烟吸完,毒物进入人体的总量(不考虑从空气的烟雾中吸入的)记作Q ,在建立模型以得到Q 的数量表达式之前,让我们先根据常识分析一下Q 应与那些因素有关,采取什么方法可以降低Q 。
首先,提高过滤嘴吸收率β 、增加过滤嘴长度2l 、减少烟草中毒物的初始含量M ,显然可以降低吸入毒物量Q 。
其次,当毒物随烟雾沿香烟穿行的比例a 和烟雾速度v 减小时,预料Q 也会降低。
至于在假设条件中涉及的其他因素,如烟草对毒物的吸收率b 、烟草长度1l 、香烟燃烧速度u ,对Q 的影响就不容易估计了。
下面通过建摸对这些作定性分析,对提出的问题作出定量的验证和回答。
模型建立设t=0时在x=0处点燃香烟,坐标系如图1所示。
吸入毒物量Q 由毒物穿过香烟的流量确定,后者又与毒物在烟草中的密度有关,为研究这些关系,定义两个基本函数:毒物流量 q(x,t)表示时刻t 单位时间内通过香烟截面x 处(0≤x ≤l )的毒物量。
毒物密度 (,)x t ω 表示时刻t 截面x 处单位长度烟草中的毒物含量(0≤x ≤1l )。
由假设1,0(,0)x ωω=,,图1 x=0处点燃的香烟如果知道了流量函数q(x,t),吸入毒物量Q 就是x=l 处的流量在吸一支烟时间内的总和。
注意到关于烟草长度和香烟燃烧速度的假设,我们得到(,),TQ q l t dt =⎰ 1/T l u = (1)下面分步计算Q 。
1.求t=0瞬间由烟雾携带的毒物单位时间内通过x 处的数量q(x,0)。
由假设4中关于v ﹥﹥u 的假定,可以认为香烟点燃处x=0 静止不动。
为简单起见,记 q(x,0) =q(x) ,考察 (x, x+△x ) 一段香烟(图1),毒物通过 x 和 x+△x 处的流量分别是 q(x) 和q(x+△x),根据守恒定律这两个流量之差应该等于这一段未点燃的烟草或过滤嘴对毒物的吸收量,于是由假设2、4有11(),,()()(),,bq x o x l q x q x x q x l x l τβτ∆≤≤⎧-+∆=⎨∆≤≤⎩x v τ∆∆=其中 △τ 是香烟穿过 △x 所需时间,令 △x →0得到微分方程11(),0(),bq x x l dq v dx q x l x l vβ⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩ (2)在x=0处点燃的烟草单位时间内放出的毒物量记作0H ,根据假设1、3、4可以写出方程(2)的初始条件为000(0),q aH H uw == (3)求解(2)、(3)式时先解出q(x)(0≤x ≤1l ),再利用q(x)在x=1l 处的连续确定q(x)( 1l ≤x ≤l ),其结果为10x l ≤≤ (4) 1l x l ≤≤2、在香烟燃烧过程的任意时刻t ,求毒物单位时间内通过 x=l 的数量q ( l , t).因为在t 时刻香烟燃至x=ut 处,记此时点燃的烟草单位时间放出的毒物量为H (t ),则H (t )=(,)uw ut t (5) 根据与第1步完全相同的分析和计算可得11()1()()1(),(,)(),b x ut vb l ut x l v v aH t e ut x l q x t aH t e e l x l β------⎧≤≤⎪=⎨⎪≤≤⎩ (6)实际上在(4)式中将坐标原点平移至x=ut 处即可得到(6)式。
由(5)、(6)式能够直接写出12()(,)(,)b l ut lv vq l t auw ut t eeβ---= (7)110()0(),bxvbl x l v v aH e q x aH e e β----⎧⎪=⎨⎪⎩3.确定w(ut,t)因为在吸烟过程中未点燃的烟草不断地吸收烟雾中的毒物,所以毒物在烟草中的密度w(ut,t)由初始值0w 逐渐增加。
考察烟草截面x 处⊿t 时间内毒物密度的增量w(x,t+⊿t)-w(x,t),根据守恒定律它应该等于单位长度烟雾中的毒物被吸收的部分,按照假设2、4有w(x,t+⊿t)-w(x,t)=(,)q x t bt v∆ 令0t ∆→并将(5)、(6)式代入得()0(,)(,0)b x ut v w abuw ut t e t v w x w--⎧∂=⎪∂⎨⎪=⎩(8)方程(8)的解为()0''0'(,)1(,)(1)but bxabutv e e v va butv a w x t w e a w w ut t ae a---⎡⎤⎢⎥=+⎢⎥⎢⎥⎢⎥⎣⎦=-⎧⎪⎪⎨⎪⎪⎩(9)其中a ’=1-a (假设2) 4.计算Q将(9)代入(7)式得120'(,)()bl l but abut v v v vautw q l t e e e ae aβ----=- (10)最后将(10)代入(1)式作积分得到'211/00'(,)(1)l a bl l u vvaw v Q q l t dt eea bβ--==-⎰(11)为便于下面的分析将上式化作12'11'a bl l vve Q aMea bl vβ---=•(12)记'11,()x a bl e r x v x ϕ--==(13)则(12)式可写作2()l vQ aMer βϕ-= (14)(13),(14)式是我们得到的最终结果,表示了吸入有毒物质量Q 与21,,,,,,a M l v b l β等的因素之间的数量关系。
结果分析1. Q 与烟草的含毒物质量的M ,毒物随烟雾沿香烟穿行比例a 成正比*,设想将毒物M 集中在x=l 处,则吸入量为aM 。
2. 因子2l veβ-体现了过滤嘴的减少毒物进入人体的作用,提高过滤嘴吸收率β和增长长度2l 能够对Q 起到负质数衰减的效果,并且β和2l 在数量上增加一定比例时起作用相同。
降低烟雾穿行速度v 也可减少Q 。
设想将毒物M 集中在X=1l 处,利用上述建模方法不难证明,吸入毒物量为2l vaMeβ-。
3. 因子 ()r ϕ表示的是由于未点燃烟草对毒物的吸收而起到的减少Q 的作用。
虽然被吸收的毒物还要被点燃,随烟雾沿香烟穿行的部分的进入人体,但是因为烟草中毒物的密度(,)x t ϖ 越来越高,所以按照固定的比例跑到空气中的毒物增多,相应的减少了进入人体的毒物量。
根据实际资料'1a bl r v=<<1在(13)试()r ϕ 中的re - 取Taylor 展开的前3项可得 , ()r ϕ1/2r ≈-,于是(14)试为2'1(1)2l va bl Q aMevβ-≈- (15)可知,提高烟草吸收率b 和增加长度1l (毒物量M 不变)对减少Q 的作用是线性的,与β和2l 是负指数衰减作用相比,效果要小得多。
4. 为了更清楚的了解过滤嘴的作用,不妨比较两支香烟,一只是上述模型讨论的,另一支长度为l ,不带过滤嘴,参数0w ,b,a,v与第一支香烟相同,并且吸到x=1l 处就扔掉。
吸第一支香烟和第二支香烟进入人体的毒物量分别记着1,21,Q Q Q 当然可由(11)式给出,Q 2也不必重新计算,只需把第二支烟设想成吸收率为b (与烟草相同)的假过滤嘴香烟就行了,这样由(11)式可以直接写出'2102'(1)bl a bl vvaw v Q e ea b--=-与(11)式给出的Q 1相比,我们得到2()12b l vQ e Q β--=所以只要b β> 就有 Q 1< Q 2,过滤嘴是起作用的,并且,提高吸收率之差b β- 与加长过滤嘴长度l 2,对于降低比例Q 1/Q 2的效果相同,不过提高需要研制新材料,将更困难一些。
评注:这个模型在于基本合理的简化假设下,运用精确的数学工具解决了一个粗看起来不易下手的实际问题,从提出假设,引入两个基本函数q(x,t)和w(x,t),到运用物理学上常用的守恒定律建立微分方程,从而构造出动态模型,最后到对结果的分析,整个过程可以说是用建模方法解决实际问题的一个范例.11。
