明渠水流速度分布测量
超声波明渠流量计测量原理

超声波明渠流量计测量原理
超声波明渠流量计是利用超声波传播的特性来测量明渠流量的仪器。
它的测量原理主要包括以下几个步骤:
1. 发射超声波:流量计中的发射器会发射一束超声波信号,这个信号会通过明渠向下传播。
2. 接收超声波:在明渠中,超声波会被水体反射和散射,其中一部分会被接收器接收。
3. 计算时间差:接收器会记录超声波发射和接收的时间差。
由于超声波在水中的传播速度是已知的,根据时间差可以计算出超声波在水中传播的距离。
4. 测量流速:通过连续测量超声波的传播距离,可以获得明渠中的流速分布。
5. 计算流量:根据已知的明渠横截面积和流速分布,可以计算出明渠的流量。
超声波明渠流量计的优点是测量精度高、测量范围广、不受温度、压力等因素的影响,并且无需对明渠进行改造,对流体不会造成干扰。
但也有一些局限性,例如在特定情况下可能受到空气泡存在的干扰。
明渠水流速度分布测量
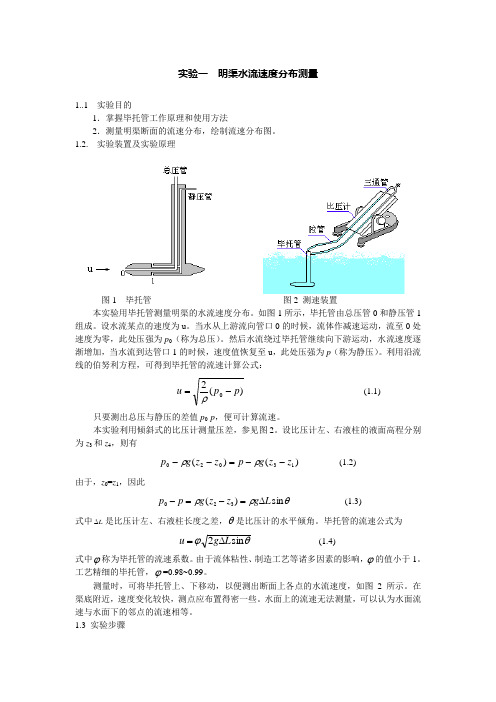
实验一 明渠水流速度分布测量1..1 实验目的1.掌握毕托管工作原理和使用方法2.测量明渠断面的流速分布,绘制流速分布图。
1.2. 实验装置及实验原理图1 毕托管 图2 测速装置本实验用毕托管测量明渠的水流速度分布。
如图1所示,毕托管由总压管0和静压管1组成。
设水流某点的速度为u 。
当水从上游流向管口0的时候,流体作减速运动,流至0处速度为零,此处压强为p 0(称为总压)。
然后水流绕过毕托管继续向下游运动,水流速度逐渐增加,当水流到达管口1的时候,速度值恢复至u ,此处压强为p (称为静压)。
利用沿流线的伯努利方程,可得到毕托管的流速计算公式:)(20p p u -=ρ (1.1)只要测出总压与静压的差值p 0-p ,便可计算流速。
本实验利用倾斜式的比压计测量压差,参见图2。
设比压计左、右液柱的液面高程分别为z 3和z 4,则有)()(13020z z g p z z g p --=--ρρ (1.2)由于,z 0=z 1,因此θρρsin )(320L g z z g p p ∆=-=- (1.3)式中L ∆是比压计左、右液柱长度之差,θ是比压计的水平倾角。
毕托管的流速公式为θϕsin 2L g u ∆= (1.4)式中ϕ称为毕托管的流速系数。
由于流体粘性、制造工艺等诸多因素的影响,ϕ的值小于1。
工艺精细的毕托管,ϕ=0.98~0.99。
测量时,可将毕托管上、下移动,以便测出断面上各点的水流速度,如图2所示。
在渠底附近,速度变化较快,测点应布置得密一些。
水面上的流速无法测量,可以认为水面流速与水面下的邻点的流速相等。
1.3 实验步骤1.毕托管的注水及排气。
毕托管的总压与静压之差是利用比压计的水柱高差计算的,因此,在使用前应该将水注入毕托管、传压胶管、比压计测压管。
注水时,应打开比压计上方的密封夹,并将毕托管的管口没入明渠的水中(也可以没入防水盒的水中),然后将水注入比压计的测压管。
注水后,如果发现传压胶管或比压计的测压管残存气泡,应设法排除。
明渠流量计方法

明渠流量计方法明渠流量计方法是用于测量明渠中水流的流量的一种方法。
以下是关于明渠流量计方法的50条详细描述:1. 明渠流量计方法是通过测量明渠中水流的流速与流量来进行流量测量的方法。
2. 明渠流量计方法可以用于测量小型河流、溪流和排水渠道等明渠的流量。
3. 明渠流量计方法适用于无压力水流的测量。
4. 明渠流量计方法常用于农田灌溉、城市雨水排放和水资源管理等领域。
5. 明渠流量计方法根据水流速度测量原理可分为几种不同的方法,包括浮子法、梳齿法、流速计法等。
6. 浮子法是一种常用的明渠流量计方法,它利用在水流中浮动的物体的速度来测量水流速度。
7. 浮子法中,测量水流速度的常用浮子有木块、铁球、塑料球等。
8. 浮子法需要在明渠上游设置起点和终点,通过观察浮子从起点到终点所用的时间来计算水流速度。
9. 梳齿法是另一种常用的明渠流量计方法,它利用在水流中插入的齿状物体的数量和间距来测量水流速度。
10. 梳齿法中,水流速度与梳齿数和间距的比值成正比。
11. 梳齿法需要在明渠上游设置起点和终点,并在水流中插入一根梳齿,通过观察梳齿从起点到终点所用的时间和梳齿数来计算水流速度。
12. 流速计法是一种使用流速计测量水流速度的明渠流量计方法。
13. 流速计法中,流速计被放置在明渠中,通过测量流速计的转速或脉冲数来计算水流速度。
14. 流速计法适用于需要连续测量水流速度的情况。
15. 明渠流量计方法还可以通过测量水位差来间接测量水流速度和流量。
16. 明渠流量计方法中,通过在明渠的起始和终点处设置水位计来测量水位差。
17. 明渠流量计方法中,可以使用流量-水位关系曲线来将水位差转换为流量。
18. 明渠流量计方法中,流量-水位关系曲线通常是在实验室中获得的,通过一系列水位差和已知流量的测量来建立。
19. 明渠流量计方法也可以使用流量计测量水流量。
20. 明渠流量计方法中,可以使用电磁流量计、涡街流量计、超声波流量计等不同类型的流量计。
矩形断面明渠流速分布特性的试验研究_严军

第38卷第5期2005年10月武汉大学学报(工学版)Enginee ring Jour nal of W uhan U niver sity Vo l.38N o.5O ct.2005收稿日期:2005-04-08作者简介:严 军(1971-),湖北武汉人,博士研究生,主要从事水力学及河流动力学教学与研究.基金项目:河南省科技攻关项目(2000570001).文章编号:1671-8844(2005)05-057-06矩形断面明渠流速分布特性的试验研究严 军1,王二平1,孙东坡1,董志慧2(1.华北水利水电学院,河南郑州 450011;2.珠江水利委员会科学研究所,广东广州 510611)摘要:通过对明渠流速的水槽试验研究,建立了矩形断面明渠沿垂线流速的抛物线分布公式和横向平均流速的乘幂函数分布公式,同时给出了相关系数的确定方法.采用不同渠道流速资料进行验证,表明所提出的明渠流速分布律与实际分布一致,对应测点流速相对误差较小,可以满足明渠流速分布及流量计算精度要求.关键词:流速分布律;边界摩阻;无量纲流速;边界效应中图分类号:T V 133 文献标识码:A Experimental study on distribution properties ofvelocity in rectangular open channelYAN Jun 1,WANG Er -ping 1,SUN Dong -po 1,DONG Zhi -hui2(1.N or th China Institute of Wa te r Conse rvancy and Hydro electric Pow er ,Zheng zho u 450011,China ;2.Institute of P RCC ,Guang zho u 510611,China )A bstract :Through the flum e expe rimental research ,the velocity distributio n fo rmulas for rectang ular open channel hav e been found ,including parabola form of v elocity distribution on the vertical and pow er fo rm of mean velocity distribution on the transverse direction ;meanw hile ,the means o f ascertaining cor -relative coefficient have been given in this paper.Validation of the observing velocity data in different channels indicate s that the velocity -distribution law given by authors is in acco rdance w ith the real v eloc -ity -distributio n perfectly in open channel ;and the relative erro r betw een observing value and calculating value of point velo city is sm all ,w hich can satisfy the precision requirement in the calculatio n of velocity distribution and discharge in open channel.Key words :velocity distribution ;boundary friction ;dimensionless velocity ;boundary effect 引水明渠流量的精确度量是进行水资源科学管理的重要环节,这也是灌区取水动态、连续计量急需解决的技术问题.若不改变明渠边界,一般多采用流速-面积法测定流量.以有限点的流速表征断面流动状况,需要准确掌握明渠过流断面上的流速分布规律.在明渠断面上如何正确布点测量特征点流速,能否采用准确合理的流速分布公式,对计量明槽流量的精确度都会产生很大影响.近年来为了这些问题,Coles 和Coleman 提出添加尾迹函数给对数流速分布律进行修正可以更好地符合实际流速分布,王晋军也有类似的研究,但瑞士的Graf 则通过试验认为尾迹函数对二维均匀流的影响并不明显而且使用繁琐.胡春宏基于大量试验提出了在不同区域采用不同形式流速公式的方法解决问题,研究焦点多集中在流速沿垂线分布上[1].本文研究了在矩形断面明渠中水流垂向及横向流速分布的特点,借助水槽试验,探求符合实际流速分布特点的明槽流速垂线分布律与横向分布律.通过建武汉大学学报(工学版)2005立准确的流速分布公式及相应参数的确定方法,为精确计量明槽流量提供理论计算依据.1 明槽流速分布的试验1.1 试验设备概化明槽为长60m 的室内大型玻璃水槽,断面为矩形,槽宽B =1.2m ,槽深H =0.6m ,糙率n =0.009,底坡i =1/1000.为保证均匀流条件与流态的稳定,流速测量段选取在水槽中间的20m 范围内(试验区上下游的过渡段均大于20m );水槽进口布置两道消能栅和压波排使水面波动迅速衰减.流量采用E -m ag 电磁流量计测量,测量精度为0.30%;流速测量使用LC -3光电式旋桨流速仪,校验后精度为0.1m m /s.1.2 测速点布设及试验控制条件根据对称性原则,自水槽中垂线至边壁布设8条测速垂线,每条测线布置9个测速点,测点分布参照国际标准ISO1088和国家JJG835《速度-面积法》计量检测规程有关规定[2],保证测点密度可以准确反映流速分布.试验流量范围为106~250L /s ,每个流量级控制水深为20~40cm ,保持明渠宽深比B /h 在3~6之间,每个测点流速样本不低于8个,试验水温在T =11.3℃左右.1.3 测量成果采用不同流量级与不同水深的组合进行试验,水流保持恒定均匀紊流状态.雷诺数范围Re =49733~146127,佛汝德数范围Fr =0.112~0.707,实测流速为0.12~1.64m /s.2 垂向流速分布规律的分析2.1 垂向流速分布在明渠流量量测时,通常采用1/7指数分布律与对数分布律.由于公式形式自身的缺陷及边壁的影响,实际垂向流速分布与对数拟合曲线相比较,中心区的相关系数均在0.85左右,而边壁附近相关系数一般在0.5左右甚至更小.分析作者水槽试验成果和前人研究的相关资料,都表明实际明渠流速的最大值应该在水面以下,流速的垂线分布更接近于二次函数曲线的特征.统计整理各试验组次的流速测量成果,引入无量纲相对流速u /v 与相对水深y /H ,通过拟合分析表明,各垂线的这两个无量纲因子之间的相关曲线具有很好的相似性.明渠任一垂线上流速与水深的无量纲函数关系可以一般的表示为u v=a y H 2+b yH +c(1)式中:u ,v 分别为测线上任一点流速与测线平均流速;y ,H 意义同前;a ,b ,c 为待定系数.图1为实测相对流速u /v 与相对水深y /H 之间的关系曲线,测流断面上各条测线的垂向流速分布都具有相同的特性,曲线拟合的相关系数一般均在0.95左右,可见上述关系式更接近于真实反映了矩形明渠流速的分布特征.受水槽断面几何特性、边界阻力及水力特性等要素影响,虽然沿横向各垂线流速分布的规律一致,但决定垂线流速分布曲线形状的流速垂向分布系数a ,b ,c 却有所变化.分析试验成果表明,它们与水流宽深比B /H ,糙率n ,水力半径R ,水力坡度J ,横向位置z /B (B 为矩形渠宽,z 为测线至中垂线的距离),相对水深y /H 等因素有关,但在不同区域主要受其中某个或某几个因素影响.图1 u/v 与y /H 的关系示意图2.2 a ,b ,c 系数的分析与确定统计分析室内矩形玻璃水槽的试验资料表明,在明渠中心区和边壁区影响流速函数垂向分布系数a ,b ,c 的因素也不相同.分析边壁区实测流速拟合曲线的变化,可以发现在这一区域的系数a ,b ,c 主要受测线至边壁的横向位置的影响.分析中心区实测流速拟合曲线的变化,发现这一区域的系数a ,b ,c 与横向位置基本无关,主要受表征水流强度的Fr 数控制.统计实测流速拟合曲线的资料,可以得到系数a ,b ,c 与无量纲横向坐标Z /H (Z =B /2-z )的相关关系如图2所示.在图2中系数a 和c 的变化相类似,随着Z /H 值的增加,a 值和c 值先减小,大约在Z /H 为0.5左右,两值又开始随Z /H 值的增加而增大,而后趋于常数,即当Z /H ≥2.5时a 值和c 值都主要受F r 值的影响.在图2中,b 值则是先随Z /H 值的增加而增大;大约在58 第5期严 军等:矩形断面明渠流速分布特性的试验研究图2 系数a ,b ,c 与无量纲Z /H 的关系图Z /H 为0.5左右,b 值又开始随Z /H 值的增加而减小;而后趋于平缓,即在Z /H ≥2.5时b 值主要受Fr 值的影响.通过分析拟合,得到在不同区域流速垂向分布系数a ,b ,c 与Z /H ,Fr 间的拟合函数关系:在边壁区,当Z /H ≤0.5时:a =-1.17(Z /H )-0.4282(2)b =1.5261(Z /H )+0.4106(3)c =-0.4168(Z /H )+0.9211(4) 当0.5<Z /H <2.5时:a =0.1804(Z /H )-0.9085(5)b =-0.1704(Z /H )+1.0781(6)c =0.0141(Z /H )+0.7556(7) 在中心区,当Z /H ≥2.5、满足缓流(Fr <1)条件时有a =13.851Fr 3-25.739Fr 2+15.345Fr -3.4831(8)b =-25.985Fr 3+46.449Fr 2-26.361Fr +5.5073(9)c =11.017Fr 3-19.205Fr 2+10.561Fr -1.0329(10)2.3 流速垂线分布律的校核验证采用本次试验和前人观测资料,依据《明渠水流测量》[2]相关规范进行数据验证校核,对比结果如表1所示.为了检验作者提出的流速分布律与流速垂向分布系数公式,收集了一些水槽试验和明渠的实测流速资料,与按拟合流速分布律计算的相应点流速进行比照.比较表1中数字可以看到,测线上各测点计算流速与实测流速非常接近,相对误差一般均小于3%;在相对水深等于0.4处的流速,计算流速与实测流速更接近,相对误差都小于2.5%.这表明根据试验研究提出的矩形明渠流速分布律比较准确地反映了实际明槽的流速分布规律.实际引水渠道由于边界糙率较大,边壁区的影响范围相应会较大.试验成果分析表明,当相对水深较小时,测点的计算流速比较接近实测流速,当相对水深较大时,明渠水流强烈的紊动使测点计算流速与实测流速的相对误差会相应增大.3 流速横向分布规律的探讨由实际观测与流速资料的整理统计发现,沿明渠横断面的边壁区与中心区,测线平均流速还是连续变化并与其横向位置有关;边壁区变化大些,中心区变化小些.如果采用无量纲流速与无量纲横向位置,按照对称性原则,明渠实际流速的横向分布特点如图3所示,基本反映了乘幂函数的分布特征.通过分析水槽试验的流速实测成果,采用无量纲分析法可以将沿横断面相对流速与相对位置的函数关系表示为vv m=nB 2-z B 2m(11)图3 半槽宽内流速横向分布特性示意式中:v 为测线平均流速;v m 为中垂线平均流速;B 为渠道宽度;z 为测线至中垂线的横向距离;m ,n为待定参数.显然测线平均流速沿渠宽的分布特性除了与其横向位置、中垂线平均流速有关外,还与参数m ,n 有关,我们就称其为流速横向分布参数.3.1 流速横向分布特性参数的确定根据量纲分析,可以确定横向分布参数m ,n 均受断面几何特性及水力特性等要素的影响,如B /H ,z /B ,y /H ,n ,R ,J 与运动粘滞系数υ等因59武汉大学学报(工学版)2005表1 明渠流速分布成果对比Z/H Fr y/H v/(m s-1)u′/(m s-1)u/(m s-1)R/%0.1030.226160.10.3130.29060.286 1.610.20.3130.30320.3020.450.30.3130.31240.3130.140.40.3130.31810.3170.420.50.3130.32050.3210.280.60.3130.31930.3160.950.80.3130.30680.312-1.630.90.3130.29540.2930.970.950.3130.28840.293-1.641.5380.3260.10.4520.38510.3762.490.20.4520.41340.408 1.320.30.4520.43600.447-2.420.40.4520.45290.463-2.230.50.4520.46410.472-1.650.60.4520.46970.471-0.350.80.4520.46360.473-1.890.90.4520.45200.454-0.510.950.4520.44410.452-1.642.8990.73090.1 1.0410.84610.8450.090.2 1.0410.92150.943-2.280.3 1.0410.9843 1.013-2.850.4 1.041 1.0344 1.053-1.790.5 1.041 1.0718 1.077-0.510.6 1.041 1.0965 1.0960.060.8 1.041 1.1079 1.114-0.530.9 1.041 1.0946 1.110 1.420.95 1.041 1.0831 1.099 1.41*0.3330.150.40.5800.59860.600-0.23*0.2670.330.4 1.680 1.6637 1.680-0.97#1.0340.2190.20.6400.58980.580 1.690.80.66990.690 2.85#2.6790.2730.40.6400.63490.6400.81*1.7860.1820.20.6750.61550.600 2.590.40.67250.675-0.370.80.69150.680 1.69*90.5860.20.4130.37410.380-1.540.40.41150.420-2.030.80.43280.4300.66注:u为模型试验测线上任一测点的实测流速;u′为相应测点的计算流速;R=(u′-u)/u×100%,为测线上任一测点流速计算值与实测值的相对误差;#,*分别为矩形断面实际明渠和水槽模型试验的实测流速数据;Fr一般在0.15~0.65之间.素.为了便于研究,对式(11)取对数可以转换为lnvv m=m lnB2-zB2+ln(n)(12)或为ln v=m ln(B/2-z)/B/2+ln(n v m)(13) 大量明渠研究表明[1],当宽深比B/H>5且Z>2.5H时,渠道断面存在一个准二维流动的中心区,区内各垂线流速分布基本相同,故各测线的平均流速相等,即有v=v m.在此区域流速横向分布系数m=0,n=1.当B/H>5且Z≤2.5H时,这部分渠道断面为具有三维流动特性边壁区,区内各垂线流速分布均不同程度地受壁面影响.60 第5期严 军等:矩形断面明渠流速分布特性的试验研究当宽深比B /H >5时,按中心区边界条件:取Z =2.5H ,v =v m ,可得:n =(2/5H /(B /2))-m(14) 则指数m 可利用水槽、明渠的实测流速资料以最小二乘法来拟合确定[3].当B ≤5H 时无中心区,按明槽中轴线条件:取z =0,v =v m ,可得系数n =1,m 也可根据实测流速资料采用最小二乘法来拟合确定.令y =ln vx =ln ((B /2-z )/(B /2))k =ln (n v m )则式(13)可以表示为y =mx |+k 设在某一过流断面设置p 条测线,测得各测线的垂线平均流速为v i(i =1~p ),根据最小二乘法原理有p∑pi =1xi∑p i =1x i∑pi =1x2imk=∑pi =1yi∑p i =1y ixi(15)方程组(15)中系数矩阵为一对称阵,根据断面实测流速资料求解式(16),即可确定未知的流速横向分布参数m 及k.根据明槽宽深比,还可以确定系数n 和v m .按以上方法确定了各参数,就可根据式(11)计算相应测流断面任一测线的平均流速,进而就可以利用垂线平均流速的横向分布确定明渠流量.3.2 垂线平均流速横向分布律的校核比较根据水槽与明渠的流速实测资料,对垂线平均流速横向分布规律进行比较验证,并以测线平均流速与中垂线平均流速比值为纵坐标,以测线位置与槽宽比值为横坐标,将分析成果绘于图4中.图4 相对流速与相对宽度的关系 图4(a )和(b )反映了两类不同的明槽宽深比(B /H >5和B /H ≤5)情况下,在对数坐标中相对流速与横向位置间都存在着很好的线性关系,测点与趋势线的相关系数均在0.98以上.图4(a )反映在大宽深比(B /H >5)有中心区的情况下,Z /H ≤2.5的测线相对流速与相对位置的关系,从图中不难看出m 值的变化范围不大.在Fr =0.344~0.731,m =0.095~0.138,n =0.972~1.035.图4(b )反映在小宽深比(B /H <5)无中心区的情况下,测线相对流速与相对位置的对数关系,从图中容易看出,趋势线基本都均经过原点,与前述边界条件结果是一致的.小宽深比(B /H <5)时,m 值的变化范围稍大,Fr =0.116~0.430,m =0.078~0.14,n =0.978~1.019.由于测量设备精度及测量验证资料的限制,此种流速分布律的验证还只局限在有限宽深比和边界糙率基本一致的矩形渠道,梯形及复式断面明渠的分布率还有待进一步探讨.在准确掌握了明槽流速的垂向分布律与横向分布律之后,就可以根据流速分布律特点,选择几个特征点;通过量测特征点流速就可以很快确定垂线平均流速与断面平均流速,进而比较精确地计算明槽流量.4 结 语(1)矩形渠道测线流速的垂向分布律采用二次抛物线拟合,更加符合实际流速分布特点.实测资料分析表明,作者提出的流速垂向分布律拟合精度较高,流速计算值与实际测量值的相对误差较小.(2)矩形渠道测线平均流速的横向分布符合乘幂函数分布形式,不同宽深比明槽流速横向分布律61武汉大学学报(工学版)2005的幂指数有所不同.通过最小二乘法拟合确定各参数后,可以很方便地确定出任一测线的平均流速及横向分布.(3)根据作者提出的流速分布律按照特征点布点测量,可以采用计算机编程处理垂向流速分布和横向平均流速分布,可以大大地减少流速实测工作量和计算工作量.同时根据比较准确的流速分布律,可以进行无边界干扰的明槽流量精确计算.参考文献:[1] 胡春宏,惠遇甲.明渠挟沙水流运动的力学和统计规律[M].北京:科学出版社,1995.[2] 明渠水流测量续集[M].水利部水文司译.北京:中国科学技术出版社,1992.[3] 陈森林,肖 舸,赵云发,等.河道断面流速分布函数研究[J].水利学报,1999(4):70-74.(上接第56页)的比较分析可见,对于水工模型实验主要关心的流量系数和堰面压强值,数值计算结果都与模型实验值极为一致.由此可以认为,以目前的计算技术水平,数值计算方法替代部分模型试验是可能的,这对降低这类水工建筑物的设计成本和设计周期有着积极的意义.参考文献:[1] 李志勤.溢流丁坝附近自由水面的实验研究与数值模拟[J].水利学报,2003(8):53-57.[2] 王志东,汪德.含闸墩溢流坝三维过坝水流数值模拟[J].水科学进展,2004(6):735-738.[3] Savag e B M,Jo hnson M C.F low over o gee spillw ay: phy sical and numerical model case study[J].J.of Hydraulic Eng ineering,2001,127(8):640-649. [4] U nami K.T wo-dimensio nal nume rical model of spillw ay flow[J].J.of Hy draulic Eng ineering,1999,125(4):369-375.[5] Har low F H,Welch J E.N umerical calculation oftime-dependent viscous incompressible flo w of fluidw ith free surface[J].T he Phy sics of Fluids,1965,8:2182-2189.[6] H ir t C W,Nicho ls B D.V olume of fluid me tho d fo rthe dy namics of free surface bounda ries[J].J.ofComput.P hy s.,1981,39:201-225.[7] 孙 建.越过矩形分流墩的流态及急流自由水面[J].西安理工大学学报,1994(3):208-214.62。
明渠流量计方法范文

明渠流量计方法范文一、流速-流量法流速-流量法是一种通过测量明渠中的水流速度来计算流量的方法。
该方法适用于明渠中水流比较均匀、流速变化较小的情况。
1.测量点的选择:在明渠的一侧选择一段足够长的测量段,该段应处于流量较为均匀的区域。
在该段中,选择若干个等距离的测点。
2.测量流速:使用流速测量仪器,如流速计或流速仪,将其放置在每个测点上,测量每个测点处的流速。
应该注意,测点处的流速应该代表该处整个截面的流速,因此在不同深度的不同位置进行多次测量,并取平均值。
3.计算平均流速:根据每个测点处的流速计算出平均流速。
常用的计算方法包括等距离测点法、梯形法、圆形法等。
4.测量截面面积:测量明渠的横截面形状,使用测量仪器测量其截面的宽度和深度,计算出截面的面积。
5.计算流量:根据平均流速和截面面积,使用流量公式计算出流量。
其中,最常用的流量公式是曼宁公式:Q=K*M*N*A*R^(2/3)*S^(1/2)。
其中,Q为流量,K为修正系数,M为河道断面形状系数,N为河道断面粗糙系数,A为横截面积,R为水力半径,S为水流沿程坡降。
6.验证和纠正:根据实际情况,可能需要对计算结果进行验证和纠正,以提高计算精度。
二、水位-流量法水位-流量法是一种通过测量明渠中的水位来计算流量的方法。
该方法适用于水流速度较大,无法直接测量的情况。
1.测量点的选择:与流速-流量法相似,也需要在明渠的一侧选择一个测量段。
不同之处是,在该段中,选择若干个等距离的测点,并测量每个测点处的水位高度。
2.建立水位-流量关系曲线:根据实测的水位高度和对应的流量数据,建立水位-流量关系曲线。
可以通过多次测量,采用回归分析法、插值法等方法获得较为准确的关系曲线。
3.测量水位:在使用明渠流量计时,通过合适的仪器测量明渠中的水位。
4.计算流量:根据测量到的水位,通过水位-流量关系曲线,计算出对应的流量。
5.验证和纠正:同样,根据实际情况,可能需要对计算结果进行验证和纠正,以提高计算精度。
明渠流量监测系统方案设计

明渠流量监测系统方案设计一、系统概述明渠流量监测系统是一个集数据采集、传输、处理和分析于一体的综合性系统,其主要目的是实时、准确地获取明渠中的水流流量信息,并将这些数据提供给相关部门和人员,以便进行水资源管理、水利工程调度以及灾害预警等工作。
二、系统组成(一)传感器部分1、水位传感器用于测量明渠中的水位高度。
常见的水位传感器有压力式水位计、超声波水位计和雷达水位计等。
压力式水位计通过测量水对传感器的压力来计算水位,适用于较浅的渠道;超声波水位计和雷达水位计则利用声波或电磁波的反射原理来测量水位,适用于各种深度和环境的渠道。
2、流速传感器用于测量明渠中水流的速度。
常用的流速传感器有旋桨式流速仪、电磁流速仪和多普勒流速仪等。
旋桨式流速仪通过水流推动桨叶旋转来测量流速,适用于低流速的情况;电磁流速仪基于电磁感应原理测量流速,适用于较大的渠道和较高的流速;多普勒流速仪则利用多普勒效应测量水流中粒子的运动速度,从而得到流速信息,适用于含有杂质较多的水流。
(二)数据采集与传输部分1、数据采集器负责将传感器采集到的水位和流速数据进行数字化处理,并按照一定的格式进行存储。
数据采集器通常具有多个输入通道,可以同时连接多个传感器,提高系统的集成度和可靠性。
2、传输设备将采集到的数据传输到远程监控中心。
传输方式可以选择有线传输(如以太网、RS485 等)或无线传输(如GPRS、NBIoT、LoRa 等)。
有线传输具有稳定性高、传输速度快的优点,但布线成本较高;无线传输则具有安装方便、灵活性强的特点,但受信号覆盖和传输距离的限制。
(三)监控中心部分1、服务器用于接收和存储来自各个监测点的数据,并提供数据处理和分析的计算资源。
2、监控软件运行在服务器上,实现对数据的实时显示、历史查询、统计分析、报表生成等功能。
监控软件还应具备报警功能,当流量超过设定的阈值时,能够及时发出警报通知相关人员。
三、系统工作原理明渠流量的计算通常基于水位流量关系曲线或流速面积法。
流体力学实验

(1.1.2)
(1.1.3)
水的密度 是已知的,只要读取各管液面的高程读数,就可以求出未知密度 和 。
1.1.4实验步骤
1.关闭密封阀,并检查密封效果。其方法是,移动调压筒至某一高程位置,这时各管的液面也随之移动。如果密封效果良好,各管液面的升降的速度越来越慢,并最终停止在某一高程位置,不再变化。如果密封效果不好,各管的液面总是不停升降,直至各管液面与调压筒以及水箱的液面平齐。这就说明水箱漏气。
(1.3.1)
图1.3.2动量方程用图
射流的冲击力也可以由动量方程算出,图1.3.2是计算用图,设射流的偏转角度为 (即入射速度矢量转到出流速度矢量所旋转的角度),射流的流量为Q,入射速度为V,则有
(1.3.2)
本实验的射流偏角有90°,135°,180°等3种。
1.3.3 实验步骤
1.实验前,调节平衡锤的位置,使杠杆处于水平状态。
1.请自己推导方程(1.3.2)
2.实验中如何确定砝码的作用力臂?
3.本实验的流量是用什么方法调节的?
图1.3.3动量方程实验数据表
1.4 沿程水头损失实验
1.4.1 实验目的
测量管流的沿程水头损失系数,绘制沿程损失系数与雷诺数的变化曲线,并与尼古拉兹曲相比较。
1.3.2 实验装置
图1.4.1 沿程损失实验仪
水流从设在水箱下部的管嘴射击,冲击一个轴对称曲面档板,档板将射流冲击力传递给杠杆。移动砝码到某一位置,可使杠杆保持平衡。
本实验用杠杆平衡原理测量射流的冲击力。另外,再用流体力学的动量方程计算射流对档板的作用力,并比较这两个冲周力的大小,以便进行误差分析。
设砝码的重量为G,作用力臂为L1,射流的作用力为F,作用力臂为L。当杠杆平衡时,有
明渠流量的测定方法
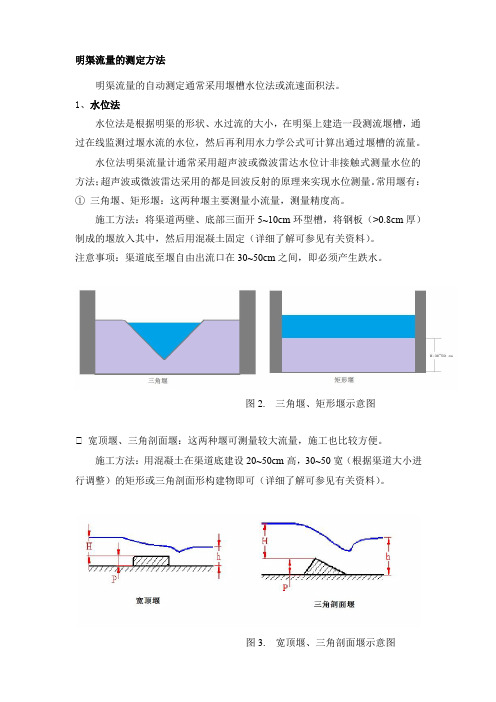
明渠流量的测定方法明渠流量的自动测定通常采用堰槽水位法或流速面积法。
1、水位法水位法是根据明渠的形状、水过流的大小,在明渠上建造一段测流堰槽,通过在线监测过堰水流的水位,然后再利用水力学公式可计算出通过堰槽的流量。
水位法明渠流量计通常采用超声波或微波雷达水位计非接触式测量水位的方法;超声波或微波雷达采用的都是回波反射的原理来实现水位测量。
常用堰有:①三角堰、矩形堰:这两种堰主要测量小流量,测量精度高。
施工方法:将渠道两壁、底部三面开5~10cm环型槽,将钢板(>0.8cm厚)制成的堰放入其中,然后用混凝土固定(详细了解可参见有关资料)。
注意事项:渠道底至堰自由出流口在30~50cm之间,即必须产生跌水。
图2. 三角堰、矩形堰示意图② 宽顶堰、三角剖面堰:这两种堰可测量较大流量,施工也比较方便。
施工方法:用混凝土在渠道底建设20~50cm高,30~50宽(根据渠道大小进行调整)的矩形或三角剖面形构建物即可(详细了解可参见有关资料)。
图3. 宽顶堰、三角剖面堰示意图2、流速面积法流速面积法是明渠中常用的流量测验方法,不需修建量水建筑物,通过测定过水断面流速和过水断面面积来求得流量。
流速面积法明渠流量计是由流量显示仪、流速计、液位计组成的流速面积法自动测量明渠流量的设备。
流速计可选用电磁式流量计或多普勒流速测试仪。
如选用电磁式流量计,则由流量显示仪将流量信号转换成与流速信号成正比的数字量信号,由此实现流速的测量。
电磁式流量计测量不受水中漂浮物、泥沙、气泡和水位大幅度变化的影响,流速传感器结构简单、体积小、安装方便对水流不产生阻力。
水位计多采用微波雷达或超声波水位计。
超声波水位计价格廉价,便于安装,被广泛进行使用;微波雷达水位计测量精度高、相应快、稳定性好,是今后水利项目首选的仪表之一。
水位测量仪表一般采用立杆安装,远程遥测器RTU、蓄电池等设备集中放置在密封箱内,可放置在杆架上。
如图4所示。
图4. 立杆设计图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 明渠水流速度分布测量
1..1 实验目的
1.掌握毕托管工作原理和使用方法
2.测量明渠断面的流速分布,绘制流速分布图。
1.2. 实验装置及实验原理
图1 毕托管 图2 测速装置
本实验用毕托管测量明渠的水流速度分布。
如图1所示,毕托管由总压管0和静压管1组成。
设水流某点的速度为u 。
当水从上游流向管口0的时候,流体作减速运动,流至0处速度为零,此处压强为p 0(称为总压)。
然后水流绕过毕托管继续向下游运动,水流速度逐渐增加,当水流到达管口1的时候,速度值恢复至u ,此处压强为p (称为静压)。
利用沿流线的伯努利方程,可得到毕托管的流速计算公式:
)(2
0p p u -=ρ (1.1)
只要测出总压与静压的差值p 0-p ,便可计算流速。
本实验利用倾斜式的比压计测量压差,参见图2。
设比压计左、右液柱的液面高程分别为z 3和z 4,则有
)()(13020z z g p z z g p --=--ρρ (1.2)
由于,z 0=z 1,因此
θρρsin )(320L g z z g p p ∆=-=- (1.3)
式中L ∆是比压计左、右液柱长度之差,θ是比压计的水平倾角。
毕托管的流速公式为
θϕsin 2L g u ∆= (1.4)
式中ϕ称为毕托管的流速系数。
由于流体粘性、制造工艺等诸多因素的影响,ϕ的值小于1。
工艺精细的毕托管,ϕ=0.98~0.99。
测量时,可将毕托管上、下移动,以便测出断面上各点的水流速度,如图2所示。
在渠底附近,速度变化较快,测点应布置得密一些。
水面上的流速无法测量,可以认为水面流速与水面下的邻点的流速相等。
1.3 实验步骤
1.毕托管的注水及排气。
毕托管的总压与静压之差是利用比压计的水柱高差计算的,因此,在使用前应该将水注入毕托管、传压胶管、比压计测压管。
注水时,应打开比压计上方的密封夹,并将毕托管的管口没入明渠的水中(也可以没入防水盒的水中),然后将水注入比压计的测压管。
注水后,如果发现传压胶管或比压计的测压管残存气泡,应设法排除。
2.调节明渠流量控制阀门,调节明渠尾水闸门,将明渠水深控制在15cm左右。
3.用水位探针测量渠底高程和水面高程,并计算水深。
4.逐点测量水流速度u。
渠底附近速度变化快,测点间距应为2mm,远离渠底的测点间距可取2~3cm。
测量内容:毕托管高程读数,比压计左、右液面读数。
1.4 注意事项
1.实验前应先熟悉电源开关及起动水泵电机的操作方法,流量计的使用方法,并注意用电安全,实验结束后立即关闭电源。
2.注水、排气工作比较麻烦,自已应摸索最佳方法。
3.毕托管的管口应正对来流。
注意:不能将毕托管的管口露出水面。
4.测量时,如果比压计液面发生波动,液面读数可取平均值。
1.5思考题
1.渠底附近的流速变化较大,这是为什么?
2.明渠水流的速度大致符合什么样的分布?
3.你认为,影响毕托管速度系数 的因素有哪些?
4.测量时,通常调节比压计的水平倾角小于直角,θ<90°,这样做有什么好处?改变倾角θ的值,对速度u的计算值是否有影响?
5.比压计安放位置的高低,对测量结束是否有影响?
6.如何判断毕托管口是否正对来流方向?
7.测量时,你是从水面开始逐点往下布置测点,还是从渠底开始往上布置测点,或者是随意布置测点?为什么要这样做?你认为测点总数应为多少才比较合适?
8.根据各点流速的分布值用积分法可以计算断面流量,并与流量计读数比较,请估算流量值的误差是多少?
1.6 参考数据表
图3是流速测量数据表,图4是流速分布图。
由图看出,靠近壁面的1cm范围内,流速变化比较大,这与边界层的对数分布比较接近。
但近壁附近的实验点不够密,因而不能得到对数分布。
如要测量近壁的速度分布,应多布置一些测点。
图3 明渠流速测量数据表
图4 明渠流速分布曲线。
