二次函数中特殊四边形的存在性问题
二次函数背景下的特殊四边形存在性判定(解析版)
备战2020年中考数学压轴题之二次函数专题06 二次函数背景下的特殊四边形存在性判定【方法综述】知识准备：特殊四边形包括平行四边形、菱形、矩形和正方形。
它们的判定方法如下：平行四边形的判定方法:两组对边分别平行的四边形是平行四边形；两组对角分别相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形两条对角线互相平分的四边形是平行四边形；矩形判的定方法有一个角是直角的平行四边形是矩形；对角线相等的平行四边形是矩形有三个角是直角的四边形是矩形菱形判定方法有一组邻边相等的平行四边形是菱形；对角线互相垂直的平行四边形是菱形四条边相等的四边形是矩形正方形的判定方法平行四边形+矩形的特性；平行四边形+菱形的特性解答时常用的技巧：（1）.根据平行四边形的对角线互相平分这条性质，应用中点坐标公式，可以采用如下方法：已知点A、B、C三点坐标已知，点P在某函数图像上，是否存在以点A、B、C、P为顶点的四边形为平行四边形，求点P的坐标。
如，当AP、BC为平行四边形对角线时，由中点坐标公式，可得a+m=c+e，n+b=d+f则m= c+e-a;n= d+f-b，点P坐标可知，将其带入到函数关系式进行验证，如果满足函数关系式，即为所求P点，同理，根据分类讨论可以得到其它情况的解答方法。
（2）.菱形在折叠的情况下，可以看成是等腰三角形以底边所在直线折叠所得，因此，菱形的存在性讨论，亦可以看做等腰三角形的存在性讨论。
（3）.矩形中的直角证明出来常规直角的探究外，还有主要是否由隐形圆的直径所对圆周角得到。
【典例示范】类型一平行四边形的存在性探究例1：如图，在平面直角坐标系中，已知抛物线经过A(－4，0)，B(0，－4)，C(2，0)三点．(1)求抛物线的解析式；(2)若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S，求S关于m的函数关系式，并求出S的最大值；(3)若点P是抛物线上的动点，点Q是直线y＝－x上的动点，判断有几个位置能使以点P，Q，B，O为顶点的四边形为平行四边形(要求PQ∥OB)，直接写出相应的点Q的坐标．【答案】（1）y＝12x2＋x－4；（2）当m＝－2时，S有最大值，S最大＝4；（3）满足题意的Q点的坐标有三个，分别是（－2＋2－，（－2－2＋，（－4，4）.【思路引导】（1）已知抛物线与x轴的两个交点的横坐标，一般选用两点式，利用待定系数法求解即可；（2）利用抛物线的解析式表示出点M 的纵坐标，从而得到点M 到x 轴的距离，然后根据三角形面积公式表示并整理即可得解，根据抛物线的性质求出第三象限内二次函数的最值，然后即可得解；（3）利用直线与抛物线的解析式表示出点P 、Q 的坐标，然后求出PQ 的长度，再根据平行四边形的对边相等列出算式，然后解关于x 的一元二次方程即可得解．【解析】（1）设抛物线的解析式为y=a （x+4）（x -2），把B （0，-4）代入得，-4=a×（0+4）（0-2），解得a=12， ∴抛物线的解析式为：y=12（x+4）（x -2），即y=12x 2+x -4； （2）过点M 作MD ⊥x 轴于点D ，设M 点的坐标为（m ，n ）， 则AD=m+4，MD=-n ，n=12m 2+m -4， ∴S=S △AMD +S 梯形DMBO -S △ABO =111(4)()(4)()44222m n n m +-+-+--⨯⨯= -2n -2m -8=-2×（12m 2+m -4）-2m -8=-m 2-4m =-（m+2）2+4（-4＜m ＜0）；∴S 最大值=4．（3）设P （x ，12x 2+x -4）． ①如图1，当OB 为边时，根据平行四边形的性质知PQ ∥OB ，∴Q 的横坐标等于P 的横坐标，又∵直线的解析式为y=-x ，则Q （x ，-x ）．由PQ=OB ，得|-x -（12x 2+x -4）|=4，解得x=0，-4，-x=0不合题意，舍去．由此可得Q （-4，4）或（-2--2-；②如图2，当BO 为对角线时，知A 与P 应该重合，OP=4．四边形PBQO 为平行四边形则BQ=OP=4，Q 横坐标为4，代入y=-x 得出Q 为（4，-4）．故满足题意的Q 点的坐标有四个，分别是（-4，4），（4，-4），（-，2-，（-2-．【方法总结】本题是二次函数综合题，交点式求解析式，二次函数与三角形面积最值问题的公共底的辅助线的做法要注意，二次函数中存在平行四边形的方法，要分别对已知边的分别为平行四边形的边或是对角线进行分类讨论.针对训练1．如图，二次函数的图象与x 轴交于A 、B 两点，与y 轴交于点C ，已知点A （﹣4，0）．（1）求抛物线与直线AC 的函数解析式；（2）若点D （m ，n ）是抛物线在第二象限的部分上的一动点，四边形OCDA 的面积为S ，求S 关于m 的函数关系式；（3）若点E 为抛物线上任意一点，点F 为x 轴上任意一点，当以A 、C 、E 、F 为顶点的四边形是平行四边形时，请求出满足条件的所有点E 的坐标．【答案】（1）（2）S=﹣m 2﹣4m+4（﹣4＜m ＜0）（3）（﹣3，2）、（，﹣2）、（，﹣2）【解析】 （1）∵A （﹣4，0）在二次函数y=ax 2﹣x+2（a≠0）的图象上， ∴0=16a+6+2，解得a=﹣， ∴抛物线的函数解析式为y=﹣x 2﹣x+2； ∴点C 的坐标为（0，2），设直线AC 的解析式为y=kx+b ，则， 232(0)2y ax x a =-+≠122y x =+32--32-3212123204{2k b b=-+=解得，∴直线AC 的函数解析式为：；（2）∵点D （m ，n ）是抛物线在第二象限的部分上的一动点，∴D （m ，﹣m 2﹣m+2），过点D 作DH ⊥x 轴于点H ，则DH=﹣m 2﹣m+2，AH=m+4，HO=﹣m ，∵四边形OCDA 的面积=△ADH 的面积+四边形OCDH 的面积，∴S=（m+4）×（﹣m 2﹣m+2）+（﹣m 2﹣m+2+2）×（﹣m ），化简，得S=﹣m 2﹣4m+4（﹣4＜m ＜0）；（3）①若AC 为平行四边形的一边，则C 、E 到AF 的距离相等，∴|y E |=|y C |=2，∴y E =±2．当y E =2时，解方程﹣x 2﹣x+2=2得，x 1=0，x 2=﹣3，∴点E 的坐标为（﹣3，2）；当y E =﹣2时，解方程﹣x 2﹣x+2=﹣2得，x 1=，x 2=，∴点E 的坐标为（，﹣2）或（，﹣2）；②若AC 为平行四边形的一条对角线，则CE ∥AF ，∴y E =y C =2，∴点E 的坐标为（﹣3，2）．综上所述，满足条件的点E 的坐标为（﹣3，2）、（，﹣2）、（，﹣2）．1{22k b ==122y x =+123212321212321212321232123232-32-+32-32-32--32-+2．（云南省弥勒市2019届九年级上学期期末考试数学试题）如图，抛物线y =x 2−2x −3与x 轴交A 、B 两点（A 点在B 点左侧），直线l 与抛物线交于A 、C 两点，其中C 点的横坐标为2.（1）求A 、B 两点的坐标及直线AC 的函数表达式；（2）P 是线段AC 上的一个动点，过P 点作y 轴的平行线交抛物线于E 点，求线段PE 长度的最大值；（3）点G 是抛物线上的动点，在x 轴上是否存在点F ，使A 、C 、F 、G 四个点为顶点的四边形是平行四边形？如果存在，写出所有满足条件的F 点坐标（请直接写出点的坐标，不要求写过程）；如果不存在，请说明理由.【答案】（1）A(−1,0)，B(3,0)，y =−x −1。
二次函数专题提优》。特殊四边形存在性问题
二次函数专题提优》。
特殊四边形存在性问题二次函数专题提优：特殊四边形存在性问题一、平行四边形存在性原理：1.实验与探究：给出平行四边形ABCD的顶点A、B、C、D的坐标，并归纳发现：无论平行四边形ABCD处于直角坐标系中哪个位置，当其顶点坐标为A(a，b)，B(c，d)，C(m，n)，D(e，f)时，则四个顶点的横坐标a，c，m，e之间的等量关系为；纵坐标b，d，n，f之间的等量关系为（不必证明）。
2.运用与推广：在同一直角坐标系中有抛物线和三个点G，S，H，且c＞0.求当c为何值时，该抛物线上存在点P，使得以G，S，H，P为顶点的四边形是平行四边形，并求出所有符合条件的P点坐标。
二、平行四边形的存在性问题：1.已知抛物线y=ax²+bx+c的对称轴是x=1，经过(-2,-5)和(5,-12)两点。
1）求此抛物线的解析式。
2）设此抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于C点，D是线段BC上一点（不与点B、C 重合）。
若以B、O、D为顶点的三角形与△BAC相似，求点D的坐标。
3）点P在y轴上，点M在此抛物线上，若要使以点P、M、A、B为顶点的四边形是平行四边形，请直接写出点M的坐标。
2.如图，抛物线y=ax²+bx+c交x轴于点A(-3,0)、点B(1,0)，交y轴于点E(0,-3)，点C是点A关于点B的对称点，点F是线段BC的中点，直线l过点F且与y轴平行，直线y=-x+m过点C，交y轴于点D。
1）求抛物线的函数表达式。
2）点K为线段AB上一动点，过点K作x轴的垂线与直线CD交于点H，与抛物线交于点G，求线段HG长度的最大值。
3、在直线l上取点M，在抛物线上取点N，使得以点A、C、M、N为顶点的四边形是平行四边形。
求点N的坐标。
解析：根据题意，可以得到以下条件：1.点A在抛物线上，坐标为（0，c）；2.点C在直线l上，坐标为（0，b）；3.点M在直线l上，坐标为（x，kx+b）；4.点N在抛物线上，坐标为（y，ay^2+by+c）。
专题21二次函数与特殊四边形存在型问题(解析版)【苏科版】
2020年中考数学必考经典题讲练案【苏科版】专题21二次函数与特殊四边形存在型问题【方法指导】【题型剖析】【类型1】二次函数与平行四边形存在型问题已知抛物线28(0)y ax bx a =++≠经过点(3,7)A --，(3,5)B ，顶点为点E ，抛物线的对称轴与直线AB 交于点C ．（1）求直线AB 的解析式和抛物线的解析式．（2）在抛物线上A ，E 两点之间的部分（不包含A ，E 两点），是否存在点D ，使得2DAC DCE S S ∆∆=？若存在，求出点D 的坐标；若不存在，请说明理由．（3）若点P 在抛物线上，点Q 在x 轴上，当以点A ，E ，P ，Q 为顶点的四边形是平行四边形时，直接写出满足条件的点P 的坐标．【分析】（1）把点(3,7)A --，(3,5)B 的坐标分别代入一次函数表达式和二次函数表达式，即可得出直线AB 的解析式和抛物线的解析式；（2）设点2(,28)D m m m -++，分别用m 的代数式表示出DAC S ∆和DCE S ∆，再根据2DAC DCE S S ∆∆=列出方程，解方程即可得出点D 的坐标；（3）设点(,)P x y ，分三种情形讨论：①当AE 为对角线时；②当AP 为对角线时；③当PE 为对角线时，根据中点坐标公式求得点Q 的坐标，再根据点Q 在x 轴上，即可得出点P 的坐标． 【解答】解：（1）设直线AB 的解析式为y kx m =+， 把点(3,7)A --，(3,5)B 代入，得7353k m k m -=-+⎧⎨=+⎩，解得：21k m =⎧⎨=-⎩，∴直线AB 的解析式为21y x =-，把点(3,7)A --，(3,5)B 代入抛物线28(0)y ax bx a =++≠， 得79385938a b a b -=-+⎧⎨=++⎩，解得12a b =-⎧⎨=⎩， ∴抛物线的解析式为228y x x =-++．（2）2228(1)9y x x x =-++=--+，∴顶点(1,9)E ，设点2(,28)D m m m -++，(1,1)C ，过点D 作y 轴的平行线交直线AB 于点M ，则(,21)M m m -， 221(2821)42182DAC S m m m m ∆=⨯-++-+⨯=-+，18(1)442DCE S m m ∆=⨯⨯-=-，2DAC DCE S S ∆∆=22182(44)m m ∴-+=-， 解得1m =-或5m =（舍去），∴存在点(1,5)D -，使得2DAC DCE S S ∆∆=（3）(3,7)A --，(1,9)E ， 设点(,)P x y ，当以点A ，E ，P ，Q 为顶点的四边形是平行四边形时，分三种情况讨论： ①当AE 为对角线时，根据中点坐标公式可得点Q 坐标为(2,2)x y ---， 点Q 在x 轴上， 2y ∴=，当2y =时，2282x x -++=，解得1x =+1x =∴点P 坐标为(1+2)或(1-，2)，②当AP 为对角线时，根据中点坐标公式可得点Q 坐标为(4,16)x y --， 点Q 在x 轴上， 16y ∴=，当16y =时，22816x x -++=， 方程无解，舍去③当PE 为对角线时，根据中点坐标公式可得点Q 坐标为(4,16)x y ++， 点Q 在x 轴上， 16y ∴=-，当16y =-时，22816x x -++=-，解得6x =或4x =-∴点P 坐标为(6,16)-或(4,16)--，综上所述，点P 的坐标为(17+，2)或(17-，2)或(6,16)-或(4,16)--．【点评】此题考查了用待定系数法求二次函数和一次函数表达式，还考查了坐标系中三角形的面积计算，平行四边形性质以及分类讨论思想．合理的分类讨论来表示出点D 的坐标是解决（3）问的关键． 【变式训练】如图，抛物线25(0)y ax bx a =+-≠经过x 轴上的点(1,0)A 和点B 及y 轴上的点C ，经过B 、C 两点的直线为y x n =+． ①求抛物线的解析式．②点P 从A 出发，在线段AB 上以每秒1个单位的速度向B 运动，同时点E 从B 出发，在线段BC 上以每秒2个单位的速度向C 运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为t 秒，求t 为何值时，PBE ∆的面积最大并求出最大值．③过点A 作AM BC ⊥于点M ，过抛物线上一动点N （不与点B 、C 重合）作直线AM 的平行线交直线BC 于点Q ．若点A 、M 、N 、Q 为顶点的四边形是平行四边形，求点N 的横坐标．【分析】①点B 、C 在直线为y x n =+上，则(,0)B n -、(0,)C n ，点(1,0)A 在抛物线上，所以250505a b an bn n +-=⎧⎪--=⎨⎪=-⎩，解得1a =-，6b =，因此抛物线解析式：265y x x =-+-； ②先求出点P 到BC 的高h为sin 45)BP t ︒=-，于是2112)22)2222PBE S BE h t t t ∆==⨯-⨯=-+2t =时，PBE ∆的面积最大，最大值为 ③由①知，BC 所在直线为：5y x =-，所以点A 到直线BC 的距离d =过点N 作x 轴的垂线交直线BC 于点P ，交x 轴于点H ．设2(,65)N m m m -+-，则(,0)H m 、(,5)P m m -，易证PQN ∆为等腰直角三角形，即NQ PQ ==4PN =，Ⅰ．4NH HP +=，所以265(5)4m m m -+---=解得11m =（舍去），24m=，Ⅱ．14N H HP +=，25(65)4m m m ---+-=解得1m =2m =，Ⅲ．24N H HP -=，2(65)[(5)]4mm m --+----=，解得1m =，2m ． 【解答】解：①点B 、C 在直线为y x n =+上， (,0)B n ∴-、(0,)C n ，点(1,0)A 在抛物线上， ∴250505a b an bn n +-=⎧⎪--=⎨⎪=-⎩， 1a ∴=-，6b =，∴抛物线解析式：265y x x =-+-；②由题意，得， 4PB t=-，2BE t =，由①知，45OBC ∠=︒，∴点P 到BC 的高h为sin 45)2BP t ︒=-， 2112)22)22PBE S BEh t t t ∆∴==⨯-⨯=-+， 当2t =时，PBE ∆的面积最大，最大值为 ③由①知，BC 所在直线为：5y x =-，∴点A 到直线BC 的距离d =过点N 作x 轴的垂线交直线BC 于点P ，交x 轴于点H ， 设2(,65)N m m m -+-，则(,0)H m 、(,5)P m m -，易证PQN ∆为等腰直角三角形，即NQ PQ == 4PN ∴=，Ⅰ．4NH HP +=，265(5)4m m m ∴-+---= 解得11m =，24m =，点A 、M 、N 、Q 为顶点的四边形是平行四边形， 4m ∴=；Ⅱ．14N H HP +=，25(65)4m m m ∴---+-=解得1m =2m =， 点A 、M 、1N 、1Q 为顶点的四边形是平行四边形， 5m >，m ∴=， Ⅲ．24N H HP -=，2(65)[(5)]4m m m ∴--+----=，解得1m =2m =， 点A 、M 、2N 、2Q 为顶点的四边形是平行四边形， 0m <，52m ∴=，综上所述，若点A 、M 、N 、Q 为顶点的四边形是平行四边形，点N 的横坐标为：4．【点评】本题考查了二次函数，熟练掌握二次函数的性质、平行四边形的判定与性质是解题的关键． 【类型2】二次函数与矩形存在型问题3．如图，抛物线2y ax bx c =++与x 轴交于点(1,0)A -，点(3,0)B -，且OB OC =． （1）求抛物线的解析式；（2）点P 在抛物线上，且POB ACB ∠=∠，求点P 的坐标；（3）抛物线上两点M ，N ，点M 的横坐标为m ，点N 的横坐标为4m +．点D 是抛物线上M ，N 之间的动点，过点D 作y 轴的平行线交MN 于点E ． ①求DE 的最大值；②点D 关于点E 的对称点为F ，当m 为何值时，四边形MDNF 为矩形．【分析】（1）已知抛物线与x 轴两交点坐标，可设交点式(1)(3)y a x x =++；由3OC OB ==得(0,3)C -，代入交点式即求得1a =-．（2）由POB ACB ∠=∠联想到构造相似三角形，因为求点P 坐标一般会作x 轴垂线PH 得Rt POH ∆，故可过点A 在BC 边上作垂线AG ，构造ACG POH ∆∆∽．利用点A 、B 、C 坐标求得AG 、CG 的长，由相似三角形对应边成比例推出12PH AG OH CG ==．设点P 横坐标为p ，则OH 与PH 都能用p 表示，但需按P 横纵坐标的正负性进行分类讨论．得到用p 表示OH 与PH 并代入2OH PH =计算即求得p 的值，进而求点P 坐标．（3）①用m 表示M 、N 横纵坐标，把m 当常数求直线MN 的解析式．设D 横坐标为d ，把x d =代入直线MN 解析式得点E 纵坐标，D 与E 纵坐标相减即得到用m 、d 表示的DE 的长，把m 当常数，对未知数d 进行配方，即得到当2d m =+时，DE 取得最大值．②由矩形MDNF 得MN DF =且MN 与DF 互相平分，所以E 为MN 中点，得到点D 、E 横坐标为2m +．由①得2d m =+时，4DE =，所以8MN =．用两点间距离公式用m 表示MN 的长，即列得方程求m 的值． 【解答】解：（1）抛物线与x 轴交于点(1,0)A -，点(3,0)B -∴设交点式(1)(3)y a x x =++3OC OB ==，点C 在y 轴负半轴(0,3)C ∴-把点C 代入抛物线解析式得：33a =- 1a ∴=-∴抛物线解析式为2(1)(3)43y x x x x =-++=---（2）如图1，过点A 作AG BC ⊥于点G ，过点P 作PH x ⊥轴于点H 90AGB AGC PHO ∴∠=∠=∠=︒ ACB POB ∠=∠ ACG POH ∴∆∆∽∴AG CGPH OH =∴AG PHCG OH=3OB OC ==，90BOC ∠=︒45ABC ∴∠=︒，BC ==ABG ∴∆是等腰直角三角形2AG BG AB ∴==CG BC BG ∴=-=∴12PH AG OH CG == 2OH PH ∴=设2(,43)P p p p ---①当3p <-或10p -<<时，点P 在点B 左侧或在AC 之间，横纵坐标均为负数 OH p ∴=-，22(43)43PH p p p p =----=++22(43)p p p ∴-=++解得：1p =2p =P ∴或 ②当31p -<<-或0p >时，点P 在AB 之间或在点C 右侧，横纵坐标异号22(43)p p p ∴=++ 解得：12p =-，232p =-(2,1)P ∴-或3(2-，3)4综上所述，点P 的坐标为、、(2,1)-或3(2-，3)4．（3）①如图2，4x m =+时，22(4)4(4)31235y m m m m =-+-+-=---2(,43)M m m m ∴---，2(4,1235)N m m m +--- 设直线MN 解析式为y kx n =+∴2243(4)1235km n m m k m n m m ⎧+=---⎨++=---⎩解得：22843k m n m m =--⎧⎨=+-⎩ ∴直线2:(28)43MN y m x m m =--++-设(D d ，243)(4)d d m d m ---<<+ //DE y 轴E D x x d ∴==，(E d ，2(28)43)m d m m --++-2222243[(28)43](24)4[(2)]4DE d d m d m m d m d m m d m ∴=------++-=-++--=--++∴当2d m =+时，DE 的最大值为4．②如图3，D 、F 关于点E 对称DE EF ∴=四边形MDNF 是矩形MN DF ∴=，且MN 与DF 互相平分12DE MN ∴=，E 为MN 中点422D E m m x x m ++∴===+ 由①得当2d m =+时，4DE = 28MN DE ∴==22222(4)[1235(43)]8m m m m m m ∴+-+-------= 解得：134m =--，234m =-+ m ∴的值为34--或34-+时，四边形MDNF 为矩形．【点评】本题考查了求二次函数解析式，求二次函数最大值，等腰三角形的性质，相似三角形的判定和性质，一元二次方程的解法，二元一次方程组的解法，矩形的性质．第（3）题没有图要先根据题意画草图帮助思考，设计较多字母运算时抓住其中的常量和变量来分析和计算．【变式训练】如图，抛物线223y x x =--+的图象与x 轴交于A 、B 两点（点A 在点B 的左边），与y 轴交于点C ，点D 为抛物线的顶点． （1）求点A 、B 、C 的坐标；（2）点(,0)M m 为线段AB 上一点（点M 不与点A 、B 重合），过点M 作x 轴的垂线，与直线AC 交于点E ，与抛物线交于点P ，过点P 作//PQ AB 交抛物线于点Q ，过点Q 作QN x ⊥轴于点N ，可得矩形PQNM ．如图，点P 在点Q 左边，试用含m 的式子表示矩形PQNM 的周长；（3）当矩形PQNM 的周长最大时，m 的值是多少？并求出此时的AEM ∆的面积；（4）在（3）的条件下，当矩形PMNQ 的周长最大时，连接DQ ，过抛物线上一点F 作y 轴的平行线，与直线AC 交于点G （点G 在点F 的上方）．若22FG DQ =，求点F 的坐标．【分析】（1）利用函数图象与坐标轴的交点的求法，求出点A ，B ，C 的坐标； （2）先确定出抛物线对称轴，用m 表示出PM ，MN 即可；（3）由（2）得到的结论判断出矩形周长最大时，确定出m ，进而求出直线AC 解析式，即可；（4）在（3）的基础上，判断出N 应与原点重合，Q 点与C 点重合，求出2DQ DC ==2(3)(23)4n n n +---+=即可． 【解答】解：（1）由抛物线223y x x =--+可知，(0,3)C ． 令0y =，则2023x x =--+， 解得，3x =-或x l =， (3,0)A ∴-，(1,0)B ．（2）由抛物线223y x x =--+可知，对称轴为1x =-．(,0)M m ，223PM m m ∴=--+，(1)222MN m m =--⨯=--，∴矩形PMNQ 的周长222()(2322)2282PM MN m m m m m =+=--+--⨯=--+．（3）222822(2)10m m m --+=-++，∴矩形的周长最大时，2m =-．(3,0)A -，(0,3)C ，设直线AC 的解析式y kx b =+， ∴303k b b -+=⎧⎨=⎩解得k l =，3b =，∴解析式3y x =+，令2x =-，则1y =， (2,1)E ∴-，1EM ∴=，1AM =，1122S AM EM ∴=⨯=． （4）(2,0)M -，抛物线的对称轴为x l =-， N ∴应与原点重合，Q 点与C 点重合，DQ DC ∴=，把1x =-代入223y x x =--+，解得4y =， (1,4)D ∴-，DQ DC ∴== 2FG =，4FG ∴=．设2(,23)F n n n --+，则(,3)G n n +， 点G 在点F 的上方且4FG =，2(3)(23)4n n n ∴+---+=．解得4n =-或1n =， (4,5)F ∴--或(1,0)．【类型3】二次函数与菱形存在型问题【例3】如图，在平面直角坐标系中，Rt ABC ∆的边BC 在x 轴上，90ABC ∠=︒，以A 为顶点的抛物线2y x bx c =-++经过点(3,0)C ，交y 轴于点(0,3)E ，动点P 在对称轴上． （1）求抛物线解析式；（2）若点P 从A 点出发，沿A B →方向以1个单位/秒的速度匀速运动到点B 停止，设运动时间为t 秒，过点P 作PD AB ⊥交AC 于点D ，过点D 平行于y 轴的直线l 交抛物线于点Q ，连接AQ ，CQ ，当t 为何值时，ACQ ∆的面积最大？最大值是多少？（3）若点M 是平面内的任意一点，在x 轴上方是否存在点P ，使得以点P ，M ，E ，C 为顶点的四边形是菱形，若存在，请直接写出符合条件的M 点坐标；若不存在，请说明理由．【分析】（1）将点C 、E 的坐标代入二次函数表达式，即可求解； （2）12ACQ S DQ BC ∆=⨯⨯，即可求解；（3）分EC 是菱形一条边、EC 是菱形一对角线两种情况，分别求解即可．【解答】解：（1）将点C 、E 的坐标代入二次函数表达式得：9303b c c -++=⎧⎨=⎩，解得：23b c =⎧⎨=⎩，故抛物线的解析式为：223y x x =-++， 则点(1,4)A ；（2）将点A 、C 的坐标代入一次函数表达式并解得： 直线AC 的表达式为：26y x =-+，点(1,4)P t -，则点2(2t D +，4)t -，设点2(2t Q +，24)4t -，21124ACQ S DQ BC t t ∆=⨯⨯=-+，104-<，故ACQ S ∆有最大值，当2t =时，其最大值为1； （3）设点(1,)P m ，点(,)M x y ， ①当EC 是菱形一条边时， 当点M 在点P 右方时，点E 向右平移3个单位、向下平移3个单位得到C ， 则点P 向右平移3个单位、向下平移3个单位得到M ， 则13x +=，3m y -=，而M P EP =得：2221(3)(1)()m x y m +-=-+-，解得：3y m =-=，故点M ； 当点M 在点P 左方时，同理可得：点(2,3M -+； ②当EC 是菱形一对角线时， 则EC 中点即为PM 中点， 则13x +=，3y m +=，而PE PC =，即221(3)4m m +-=+， 解得：1m =，故2x =，3312y m =-=-=， 故点(2,2)M ；综上，点M 或(2,3-+或(2,2)M ．【点评】本题考查的是二次函数综合运用，涉及到菱形的性质、图形的平移、面积的计算等，其中（3），要注意分类求解，避免遗漏． 【变式训练】综合与探究如图，抛物线2y x bx c =++与x 轴交于A 、B 两点，与y 轴交于C 点，2OA =，6OC =，连接AC 和BC ． （1）求抛物线的解析式；（2）点D 在抛物线的对称轴上，当ACD ∆的周长最小时，点D 的坐标为 1(2，5)- ．（3）点E 是第四象限内抛物线上的动点，连接CE 和BE ．求BCE ∆面积的最大值及此时点E 的坐标； （4）若点M 是y 轴上的动点，在坐标平面内是否存在点N ，使以点A 、C 、M 、N 为顶点的四边形是菱形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．【分析】（1）由2OA =，6OC =得到(2,0)A -，(0,6)C -，用待定系数法即求得抛物线解析式．（2）由点D 在抛物线对称轴上运动且A 、B 关于对称轴对称可得，AD BD =，所以当点C 、D 、B 在同一直线上时，ACD ∆周长最小．求直线BC 解析式，把对称轴的横坐标代入即求得点D 纵坐标．（3）过点E 作EG x ⊥轴于点G ，交直线BC 与点F ，设点E 横坐标为t ，则能用t 表示EF 的长．BCE ∆面积拆分为BEF ∆与CEF ∆的和，以EF 为公共底计算可得12BCE S EF OB ∆=，把含t 的式子代入计算即得到BCE S ∆关于t 的二次函数，配方即求得最大值和t 的值，进而求得点E 坐标．（4）以AC 为菱形的边和菱形的对角线进行分类画图，根据菱形邻边相等、对边平行的性质确定点N 在坐标．【解答】解：（1）2OA =，6OC = (2,0)A ∴-，(0,6)C -抛物线2y x bx c =++过点A 、C ∴420006b c c -+=⎧⎨++=-⎩ 解得：16b c =-⎧⎨=-⎩∴抛物线解析式为26y x x =--（2）当0y =时，260x x --=，解得：12x =-，23x = (3,0)B ∴，抛物线对称轴为直线23122x -+==点D 在直线12x =上，点A 、B 关于直线12x =对称 12D x ∴=，AD BD = ∴当点B 、D 、C 在同一直线上时，ACD C AC AD CD AC BD CD AC BC ∆=++=++=+最小设直线BC 解析式为6y kx =- 360k ∴-=，解得：2k =∴直线:26BC y x =-12652D y ∴=⨯-=-1(2D ∴，5)-故答案为：1(2，5)-（3）过点E 作EG x ⊥轴于点G ，交直线BC 与点F 设(E t ，26)(03)t t t --<<，则(,26)F t t -2226(6)3EF t t t t t ∴=----=-+22111113327()3(3)()22222228BCE BEF CEF S S S EF BG EF OG EF BG OG EF OB t t t ∆∆∆∴=+=+=+==⨯-+=--+∴当32t =时，BCE ∆面积最大 23321()6224E y ∴=--=-∴点E 坐标为3(2，21)4-时，BCE ∆面积最大，最大值为278． （4）存在点N ，使以点A 、C 、M 、N 为顶点的四边形是菱形． (2,0)A -，(0,6)C -AC ∴=①若AC 为菱形的边长，如图3，则//MN AC 且，MN AC ==1(2N ∴-，，2(2,N --，3(2,0)N②若AC 为菱形的对角线，如图4，则44//AN CM ，44AN CN = 设4(2,)N n -n ∴-解得：103n =- 410(2,)3N ∴--综上所述，点N 坐标为(2-，210)，(2,210)--，(2,0)，10(2,)3--．【点评】本题考查了二次函数的图象与性质，轴对称求最短路径，一次函数的图象与性质，一次方程（组)的解法，菱形的性质，勾股定理．第（4）题对菱形顶点存在性的判断，以确定的边AC 进行分类，再画图讨论计算．【类型4】二次函数与正方形存在型问题【例4】如图，已知抛物线2y x bx c =++的图象经过点(1,0)A ，(3,0)B -，与y 轴交于点C ，抛物线的顶点为D ，对称轴与x 轴相交于点E ，连接BD ． （1）求抛物线的解析式．（2）若点P 在直线BD 上，当PE PC =时，求点P 的坐标．（3）在（2）的条件下，作PF x ⊥轴于F ，点M 为x 轴上一动点，N 为直线PF 上一动点，G 为抛物线上一动点，当以点F ，N ，G ，M 四点为顶点的四边形为正方形时，求点M 的坐标．【分析】（1）利用待定系数法即可得出结论；（2）先确定出点E 的坐标，利用待定系数法得出直线BD 的解析式，利用PC PE =建立方程即可求出a 即可得出结论；（3）设出点M 的坐标，进而得出点G ，N 的坐标，利用FM MG =建立方程求解即可得出结论． 【解答】解：（1）抛物线2y x bx c =++的图象经过点(1,0)A ，(3,0)B -， ∴10930b c b c ++=⎧⎨-+=⎩，∴23b c =⎧⎨=-⎩，∴抛物线的解析式为223y x x =+-；（2）由（1）知，抛物线的解析式为223y x x =+-； (0,3)C ∴-，抛物线的顶点(1,4)D --， (1,0)E ∴-，设直线BD 的解析式为y mx n =+， ∴304m n m n -+=⎧⎨-+=-⎩，∴26m n =-⎧⎨=-⎩， ∴直线BD 的解析式为26y x =--，设点(,26)P a a --， (0,3)C -，(1,0)E -，根据勾股定理得，222(1)(26)PE a a =++--，222(263)PC a a =+--+， PC PE =，2222(1)(26)(263)a a a a ∴++--=+--+， 2a ∴=-，2(2)62y ∴=-⨯--=-， (2,2)P ∴--，（3）如图，作PF x ⊥轴于F ， (2,0)F ∴-，设(,0)M d ，2(,23)G d d d ∴+-，2(2,23)N d d -+-，以点F ，N ，G ，M 四点为顶点的四边形为正方形，必有FM MG =，2|2||23|d d d ∴+=+-， 121d -±∴=或313d -±=， ∴点M 的坐标为121(2-+，0)，121(2--，0)，313(-+，0)，313(--，0)．【点评】此题是二次函数综合题，主要考查了待定系数法，抛物线的顶点坐标，勾股定理，正方形的性质，解（2）的关键是用PC PE =建立方程求解，解（3）的关键是解绝对值方程，是一道中等难度的中考常考题．【变式训练】已知抛物线2(1)3(0)y a x a =-+≠与y 轴交于点(0,2)A ，顶点为B ，且对称轴1l 与x 轴交于点M （1）求a 的值，并写出点B 的坐标；（2）有一个动点P 从原点O 出发，沿x 轴正方向以每秒2个单位的速度运动，设运动时间为t 秒，求t 为何值时PA PB +最短；（3）将此抛物线向右平移所得新的抛物线与原抛物线交于点C ，且新抛物线的对称轴2l 与x 轴交于点N ，过点C 作//DE x 轴，分别交1l ，2l 于点D 、E ，若四边形MDEN 是正方形，求平移后抛物线的解析式．【分析】（1）利用待定系数法即可解决问题；（2）如图1中，作点A 关于x 轴的对称点A '，连接BA '交x 轴于P ，点P 即为所求．（3）如图2中，设抛物线向右平移后的解析式为2()3y x m =--+．想办法用m 表示点C 的坐标，分两种情形，利用待定系数法即可解决问题；【解答】解：（1）把(0,2)A 代入抛物线的解析式可得，23a =+， 1a ∴=-，∴抛物线的解析式为2(1)3y x =--+， ∴抛物线的顶点B 坐标为(1,3)．（2）如图1中，作点A 关于x 轴的对称点A '，连接BA '交x 轴于P ，点P 即为所求． (0,2)A '-，(1,3)B ，∴直线A B '的解析式为52y x =-，2(5P ∴，0)，21525t ∴==时，PA PB +最短（3）如图2中，设抛物线向右平移后的解析式为2()3y x m =--+．由22(1)3()3y x y x m ⎧=--+⎨=--+⎩，解得12m x +=， ∴点C 的横坐标12m +， 1MN m =-，四边形MDEN 是正方形，1(2m C +∴，1)m -， 把点C 的坐标代入2(1)3y x =--+， 得到2(1)134m m --=-+， 解得3m =或5-（舍弃），∴移后抛物线的解析式为2(3)3y x =--+．当点C 在x 轴下方时，1(2m C +，1)m -， 把点C 的坐标代入2(1)3y x =--+， 得到2(1)134m m --=-+， 解得7m =或1-（舍弃），∴移后抛物线的解析式为2(7)3y x =--+．【达标检测】1．如图，抛物线y ＝a （x +1）2+4（a ≠0）与x 轴交于A ，C 两点，与直线y ＝x ﹣1交于A ，B 两点，直线AB 与抛物线的对称轴交于点E ．（1）求抛物线的解析式；（2）若点P在直线AB上方的抛物线上运动．①点P在什么位置时，△ABP的面积最大，求出此时点P的坐标；②当点P与点C重合时，连接PE，将△PEB补成矩形，使△PEB上的两个顶点成为矩形一边的两个顶点，第三个顶点落在矩形这一边的对边上，求出矩形未知顶点的坐标．【分析】（1）先确定出点A的坐标，进而用待定系数法求出抛物线解析式；（2）先确定出点B的坐标，①设点P（m，﹣m2﹣2m+3），得出PG＝﹣m2﹣3m+4，利用三角形的面积公式建立函数关系式即可得出结论；②先确定出点E的坐标，进而判断出△BPE是直角三角形，即可作出图形，利用两直线的交点坐标的求法即可得出结论．【解答】解：（1）∵点A是直线y＝x﹣1与x轴的交点，∴A（1，0），∵过点A（1，0）在y＝a（x+1）2+4，∴a（1+1）2+4＝0，∴a＝﹣1，∴抛物线的解析式为y＝﹣（x+1）2+4＝﹣x2﹣2x+3（2）由题意知，，∴（是点A的纵横坐标）或，∴B（﹣4，﹣5），①如图，设点P（m，﹣m2﹣2m+3），过点P作PG∥y轴交AB于G，∴G（m，m﹣1），∴PG＝﹣m2﹣2m+3﹣（m﹣1）＝﹣m2﹣3m+4，∴S△ABP＝S△PBG+S△P AG PG×（x A﹣x B|（﹣m2﹣3m+4）（1+4）（m）2，当m时，S△ABP最大，为，此时点P（，）；②方法1、由（1）知，抛物线的解析式为y＝﹣x2﹣2x+3，∴C（﹣3，0）抛物线的对称轴为直线x＝﹣1，∵点E在直线y＝x﹣1上，∴E（﹣1，﹣2），∵点P与点C重合，∴P（﹣3，0），∵B（﹣4，﹣5），∴PE2＝8，BE2＝18，BP2＝26，∴PE2+BE2＝BP2，∴△BPE是直角三角形，且∠BEP＝90°，∵C（﹣3，0），E（﹣1，﹣2），∴直线CE的解析式为y＝﹣x﹣3，∵△PEB上的两个顶点成为矩形一边的两个顶点，第三个顶点落在矩形这一边的对边上，∴Ⅰ、作出如图1所示的矩形BECD（以BE为矩形的一边），∴AB∥CD，BD∥CE，∵B（﹣4，﹣5），∴直线BD的解析式为y＝﹣x﹣9①，∵直线AB的解析式为y＝x﹣1，且AB∥CD，∴直线CD的解析式为y＝x+3②，联立①②解得，，∴D（﹣6，﹣3），即：矩形未知顶点的坐标（﹣6，﹣3）．Ⅱ、以BP为矩形的一边，如图1所示的矩形BD'F'P，∵P（﹣3，0），B（﹣4，﹣5），∴直线BP的解析式为y＝5x+15，∵D'F'∥BP，E（﹣1，﹣2），∴D'F'的解析式为y＝5x+3③，∵PF'⊥D'F'，且P（﹣3，0），∴PF'的解析式为y x④，联立③④解得，，∴F'（，），同理：D'（，）；方法2、Ⅰ、由（1）知，抛物线的解析式为y＝﹣x2﹣2x+3，∴C（﹣3，0）抛物线的对称轴为直线x＝﹣1，∵点E在直线y＝x﹣1上，∴E（﹣1，﹣2），∵四边形BDCE是矩形，∵C（﹣3，0），∴点C看作点E平移得到，向左平移2个单位，再向上平移2个单位，∴点D也是向左平移2个单位，再向上平移2个单位，且B（﹣4，﹣5），∴D（﹣6，﹣3），Ⅱ、以BP为矩形的一边，如图1所示的矩形BD'F'P，∵P（﹣3，0），B（﹣4，﹣5），∴直线BP的解析式为y＝5x+15，∵D'F'∥BP，E（﹣1，﹣2），∴D'F'的解析式为y＝5x+3③，∵PF'⊥D'F'，且P（﹣3，0），∴PF'的解析式为y x④，联立③④解得，，∴F'（，），同理：D'（，）；2．如图，抛物线y＝﹣x2+bx+c交x轴于点A，B，交y轴于点C．点B的坐标为（3，0）点C的坐标为（0，3），点C与点D关于抛物线的对称轴对称．（1）求抛物线的解析式；（2）若点P为抛物线对称轴上一点，连接BD，以PD，PB为边作平行四边形PDNB，是否存在这样的点P，使得▱PDNB是矩形？若存在，请求出tan∠BDN的值；若不存在，请说明理由；（3）点Q在y轴右侧抛物线上运动，当△ACQ的面积与△ABQ的面积相等时，请直接写出点Q的坐标．【分析】（1）把B点坐标、点C点坐标为代入抛物线y＝﹣x2+bx+c方程，即可求解；（2）存在．设点P（1，m），由k1k2＝﹣1，即可求解；（3）设点Q坐标为（t，﹣t2+2t+3），则：AQ所在的直线方程为：y＝（3﹣t）x+（3﹣t），△ACQ的面积与△ABQ的面积相等时，即：S四边形ACQB＝2S△ABQ，即可求解．【解答】解：（1）把B点坐标、点C点坐标为代入抛物线y＝﹣x2+bx+c方程，解得，抛物线方程为：y＝﹣x2+2x+3；点A坐标为（﹣1，0），点D坐标为（2，3），函数的对称轴为x＝1；（2）存在．设点P（1，m），设函数对称轴交x轴于点N，过点D作DM⊥PN于点M，则∠MDP＝∠BPN，则tan∠MDP＝tan∠BPN，即：，解得：m＝1或m＝2；则点P（1，1）或（1，2），则：PD或，则PB＝2或，tan∠BDN1或；（3）设点Q坐标为（t，﹣t2+2t+3），则：AQ所在的直线方程为：y＝（3﹣t）x+（3﹣t），如图所示，连接CA、QB，过点Q作x轴的垂线QN交x轴于N点，当△ACQ的面积与△ABQ的面积相等时，即：S四边形ACQB＝2S△ABQ，S四边形ACQB＝S梯形CONQ+S△AOC+S△BQN（﹣t2+2t+3+3）×t1×3（3﹣t）（﹣t2+2t+3），（﹣t2+3t+4），S△ABQ（3+1）（﹣t2+2t+3），∵S四边形ACQB＝2S△ABQ，化简得：5t2﹣7t﹣12＝0，解得：t＝﹣1或（舍去负值），当Q在x轴下方时，由△ACQ的面积与△ABQ的面积相等，可得：点Q坐标为（4，﹣5），则点Q坐标为（，）或（4，﹣5）．3．如图，已知二次函数y＝ax2+2x+c的图象经过点C（0，3），与x轴分别交于点A，点B（3，0）．点P 是直线BC上方的抛物线上一动点．（1）求二次函数y＝ax2+2x+c的表达式；（2）连接PO，PC，并把△POC沿y轴翻折，得到四边形POP′C．若四边形POP′C为菱形，请求出此时点P的坐标；（3）当点P运动到什么位置时，四边形ACPB的面积最大？求出此时P点的坐标和四边形ACPB的最大面积．【分析】（1）根据待定系数法，可得函数解析式；（2）根据菱形的对角线互相垂直且平分，可得P点的纵坐标，根据自变量与函数值的对应关系，可得P 点坐标；（3）根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得PQ的长，根据面积的和差，可得二次函数，根据二次函数的性质，可得答案．【解答】解：（1）将点B和点C的坐标代入函数解析式，得，解得，二次函数的解析式为y＝﹣x2+2x+3；（2）若四边形POP′C为菱形，则点P在线段CO的垂直平分线上，如图1，连接PP′，则PE⊥CO，垂足为E，∵C（0，3），∴E（0，），∴点P的纵坐标，当y时，即﹣x2+2x+3，解得x1，x2（不合题意，舍），∴点P的坐标为（，）；（3）如图2，P在抛物线上，设P（m，﹣m2+2m+3），设直线BC的解析式为y＝kx+b，将点B和点C的坐标代入函数解析式，得，解得．直线BC的解析为y＝﹣x+3，设点Q的坐标为（m，﹣m+3），PQ＝﹣m2+2m+3﹣（﹣m+3）＝﹣m2+3m．当y＝0时，﹣x2+2x+3＝0，解得x1＝﹣1，x2＝3，OA＝1，AB＝3﹣（﹣1）＝4，S四边形ABPC＝S△ABC+S△PCQ+S△PBQAB•OC PQ•OF PQ•FB4×3（﹣m2+3m）×3（m）2，当m时，四边形ABPC的面积最大．当m时，﹣m2+2m+3，即P点的坐标为（，）．当点P的坐标为（，）时，四边形ACPB的最大面积值为．4．如图，抛物线y＝﹣x2+bx+c和直线y＝x+1交于A，B两点，点A在x轴上，点B在直线x＝3上，直线x＝3与x轴交于点C．（1）求抛物线的解析式；（2）点P从点A出发，以每秒个单位长度的速度沿线段AB向点B运动，点Q从点C出发，以每秒2个单位长度的速度沿线段CA向点A运动，点P，Q同时出发，当其中一点到达终点时，另一个点也随之停止运动，设运动时间为t秒（t＞0）．以PQ为边作矩形PQNM，使点N在直线x＝3上．①当t为何值时，矩形PQNM的面积最小？并求出最小面积；②直接写出当t为何值时，恰好有矩形PQNM的顶点落在抛物线上．【分析】（1）利用待定系数法即可；（2）①分别用t表示PE、PQ、EQ，用△PQE∽△QNC表示NC及QN，列出矩形PQNM面积与t的函数关系式问题可解；②由①利用线段中点坐标分别等于两个端点横纵坐标平均分的数量关系，表示点M坐标，分别讨论M、N、Q在抛物线上时的情况，并分别求出t值．【解答】解：（1）由已知，B点横坐标为3∵A、B在y＝x+1上∴A（﹣1，0），B（3，4）把A（﹣1，0），B（3，4）代入y＝﹣x2+bx+c得解得∴抛物线解析式为y＝﹣x2+3x+4；（2）①过点P作PE⊥x轴于点E．∵直线y＝x+1与x轴夹角为45°，P点速度为每秒个单位长度∴t秒时点E坐标为（﹣1+t，0），Q点坐标为（3﹣2t，0）∴EQ＝4﹣3t，PE＝t∵∠PQE+∠NQC＝90°∠PQE+∠EPQ＝90°∴∠EPQ＝∠NQC∴△PQE∽△QNC∴∴矩形PQNM的面积S＝PQ•NQ＝2PQ2∵PQ2＝PE2+EQ2∴S＝2（）2＝20t2﹣48t+32当t时，S最小＝20×（）2﹣4832②由①点Q坐标为（3﹣2t，0），P坐标为（﹣1+t，t）∴△PQE∽△QNC，可得NC＝2EQ＝8﹣6t∴N点坐标为（3，8﹣6t）由矩形对角线互相平分∴点M坐标为（3t﹣1，8﹣5t）当M在抛物线上时8﹣5t＝﹣（3t﹣1）2+3（3t﹣1）+4解得t或当点Q到A时，Q在抛物线上，此时t＝2当N在抛物线上时，8﹣6t＝4∴t综上所述当t或或或2时，矩形PQNM的顶点落在抛物线上．5．如图，在平面直角坐标系xOy中，已知抛物线y＝ax2﹣2x+c与直线y＝kx+b都经过A（0，﹣3）、B（3，0）两点，该抛物线的顶点为C．（1）求此抛物线和直线AB的解析式；（2）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，求点M的坐标；若不存在，请说明理由；（3）设点P是直线AB下方抛物线上的一动点，当△P AB面积最大时，求点P的坐标，并求△P AB面积的最大值．【分析】（1）将A（0，﹣3）、B（3，0）两点坐标分别代入二次函数的解析式和一次函数解析式即可求解；（2）先求出C点坐标和E点坐标，则CE＝2，分两种情况讨论：①若点M在x轴下方，四边形CEMN 为平行四边形，则CE＝MN，②若点M在x轴上方，四边形CENM为平行四边形，则CE＝MN，设M （a，a﹣3），则N（a，a2﹣2a﹣3），可分别得到方程求出点M的坐标；（3）如图，作PG∥y轴交直线AB于点G，设P（m，m2﹣2m﹣3），则G（m，m﹣3），可由，得到m的表达式，利用二次函数求最值问题配方即可．【解答】解：（1）∵抛物线y＝ax2﹣2x+c经过A（0，﹣3）、B（3，0）两点，∴，∴，∴抛物线的解析式为y＝x2﹣2x﹣3，∵直线y＝kx+b经过A（0，﹣3）、B（3，0）两点，∴，解得：，∴直线AB的解析式为y＝x﹣3，（2）∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴抛物线的顶点C的坐标为（1，﹣4），∵CE∥y轴，∴E（1，﹣2），∴CE＝2，①如图，若点M在x轴下方，四边形CEMN为平行四边形，则CE＝MN，设M（a，a﹣3），则N（a，a2﹣2a﹣3），∴MN＝a﹣3﹣（a2﹣2a﹣3）＝﹣a2+3a，∴﹣a2+3a＝2，解得：a＝2，a＝1（舍去），∴M（2，﹣1），②如图，若点M在x轴上方，四边形CENM为平行四边形，则CE＝MN，设M（a，a﹣3），则N（a，a2﹣2a﹣3），∴MN＝a2﹣2a﹣3﹣（a﹣3）＝a2﹣3a，∴a2﹣3a＝2，解得：a，a（舍去），∴M（，），综合可得M点的坐标为（2，﹣1）或（）．（3）如图，作PG∥y轴交直线AB于点G，设P（m，m2﹣2m﹣3），则G（m，m﹣3），∴PG＝m﹣3﹣（m2﹣2m﹣3）＝﹣m2+3m，∴S△P AB＝S△PGA+S△PGB，∴当m时，△P AB面积的最大值是，此时P点坐标为（）．6．如图，抛物线y＝﹣x2+bx+c与x轴交于A、B两点（A在B的左侧），与y轴交于点N，过A点的直线l：y＝kx+n与y轴交于点C，与抛物线y＝﹣x2+bx+c的另一个交点为D，已知A（﹣1，0），D（5，﹣6），P点为抛物线y＝﹣x2+bx+c上一动点（不与A、D重合）．（1）求抛物线和直线l的解析式；（2）当点P在直线l上方的抛物线上时，过P点作PE∥x轴交直线l于点E，作PF∥y轴交直线l于点F，求PE+PF的最大值；（3）设M为直线l上的点，探究是否存在点M，使得以点N、C，M、P为顶点的四边形为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．【分析】（1）将点A、D的坐标分别代入直线表达式、抛物线的表达式，即可求解；（2）PE+PF＝2PF＝2（﹣x2+3x+4+x+1）＝﹣2（x﹣2）2+18，即可求解；（3）分NC是平行四边形的一条边、NC是平行四边形的对角线，两种情况分别求解即可．【解答】解：（1）将点A、D的坐标代入直线表达式得：，解得：，故直线l的表达式为：y＝﹣x﹣1，将点A、D的坐标代入抛物线表达式，同理可得抛物线的表达式为：y＝﹣x2+3x+4；（2）直线l的表达式为：y＝﹣x﹣1，则直线l与x轴的夹角为45°，即：则PE＝PF，设点P坐标为（x，﹣x2+3x+4）、则点F（x，﹣x﹣1），PE+PF＝2PF＝2（﹣x2+3x+4+x+1）＝﹣2（x﹣2）2+18，∵﹣2＜0，故PE+PF有最大值，当x＝2时，其最大值为18；（3）NC＝5，①当NC是平行四边形的一条边时，设点P坐标为（x，﹣x2+3x+4）、则点M（x，﹣x﹣1），由题意得：|y M﹣y P|＝5，即：|﹣x2+3x+4+x+1|＝5，解得：x＝2或0或4（舍去0），则点M坐标为（2，﹣3）或（2，﹣3）或（4，﹣5）；②当NC是平行四边形的对角线时，则NC的中点坐标为（0，），设点P坐标为（m，﹣m2+3m+4）、则点M（n，﹣n﹣1），N、C，M、P为顶点的四边形为平行四边形，则NC的中点即为PM中点，即：0，，解得：n＝0或﹣4（舍去0），故点M（﹣4，3）；故点M的坐标为：（2，﹣3）或（2，﹣3）或（4，﹣5）或（﹣4，3）．7．如图，在平面直角坐标系xOy中，抛物线L1：y＝x2+bx+c过点C（0，﹣3），与抛物线L2：y x2x+2的一个交点为A，且点A的横坐标为2，点P、Q分别是抛物线L1、L2上的动点．（1）求抛物线L1对应的函数表达式；（2）若以点A、C、P、Q为顶点的四边形恰为平行四边形，求出点P的坐标；（3）设点R为抛物线L1上另一个动点，且CA平分∠PCR．若OQ∥PR，求出点Q的坐标．【分析】（1）先求出A点的坐标，再用待定系数法求出函数解析式便可；（2）设点P的坐标为（x，x2﹣2x﹣3），分两种情况讨论：AC为平行四边形的一条边，AC为平行四边形的一条对角线，用x表示出Q点坐标，再把Q点坐标代入抛物线L2：y x2x+2中，列出方程求得解便可；（3）当点P在y轴左侧时，抛物线L1不存在点R使得CA平分∠PCR，当点P在y轴右侧时，不妨设点P在CA的上方，点R在CA的下方，过点P、R分别作y轴的垂线，垂足分别为S、T，过点P作PH ⊥TR于点H，设点P坐标为（x1，），点R坐标为（x2，），证明△PSC∽△RTC，由相似比得到x1+x2＝4，进而得tan∠PRH的值，过点Q作QK⊥x轴于点K，设点Q坐标为（m，），由tan∠QOK＝tan∠PRH，移出m的方程，求得m便可．【解答】解：（1）将x＝2代入y x2x+2，得y＝﹣3，故点A的坐标为（2，﹣3），将A（2，﹣3），C（0，﹣3）代入y＝x2+bx+c，得，解得，∴抛物线L1：y＝x2﹣2x﹣3；（2）如图，设点P的坐标为（x，x2﹣2x﹣3），第一种情况：AC为平行四边形的一条边，①当点Q在点P右侧时，则点Q的坐标为（x+2，x2﹣2x﹣3），将Q（x+2，x2﹣2x﹣3）代入y x2x+2，得x2﹣2x﹣3（x+2）2（x+2）+2，解得x＝0或x＝﹣1，因为x＝0时，点P与C重合，不符合题意，所以舍去，此时点P的坐标为（﹣1，0）；②当点Q在点P左侧时，则点Q的坐标为（x﹣2，x2﹣2x﹣3），将Q（x﹣2，x2﹣2x﹣3）代入y x2x+2，得y x2x+2，得x2﹣2x﹣3（x﹣2）2（x﹣2）+2，解得，x＝3，或x，此时点P的坐标为（3，0）或（，）；第二种情况：当AC为平行四边形的一条对角线时，由AC的中点坐标为（1，﹣3），得PQ的中点坐标为（1，﹣3），故点Q的坐标为（2﹣x，﹣x2+2x﹣3），将Q（2﹣x，﹣x2+2x﹣3）代入y x2x+2，得﹣x2+2x﹣3═（2﹣x）2（2﹣x）+2，。
【中考数学几何模型】第二十二节：二次函数特殊平行四边形存在性问题
中考数学几何模型第二十二节:二次函数特殊平行四边形存在性问题422.二次函数正方形存在性问题(初三)在平面直角坐标系中,抛物线y =―13x 2+bx +c 交x 轴于A(―3,0),B(4,0)两点,交y 轴于点C .(1)求抛物线的表达式,(2)如图,直线y =34x +94与抛物线交于A,D 两点,与直线BC 交于点E .若M(m,0)是线段AB 上的动点,过点M 作x 轴的垂线,交抛物线于点F ,交直线AD 于点G ,交直线BC 于点H .①当点F 在直线AD 上方的抛物线上,且S △EFG =59S △OFG 时,求m 的值;②在平面内是否存在点P ,使四边形EFHP 为正方形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.423.二次函数面积最大值矩形存在性问题(初三)如图,在平面直角坐标系中,抛物线y =ax 2+2x +c(a ≠0)与x 轴交于点A 、B ,与y 轴交于点C ,连接BC,OA =1,对称轴为直线x =2,点D 为此拋物线的顶点.(1)求抛物线的解析式(2)抛物线上C 、D 两点之间的距离是_______(3)点E 是第一象限内抛物线上的动点,连接BE 和CE ,求△BCE 面积的最大值;(4)点P 在抛物线对称轴上，平面内存在点Q ，使以点B 、C 、P 、Q 为顶点的四边形为矩形,请直接写出点Q 的坐标.424.二次函数线段最大值相等角矩形存在性问题(初三)如图,抛物线y=ax2+bx+c与x轴交于点A(―1,0),点B(―3,0),且0O=OC.(1)求抛物线的解析式(2)点P在抛物线上,且∠POB=∠ACB,求点P的坐标;(3)抛物线上两点M,N,点M的横坐标为m,点N的横坐标为m+4.点D是抛物线上M,N之间的动点,过点D作y轴的平行线交MN于点E.①求DE的最大值②点D关于点E的对称点为F,当m为何值时,四边形MDNF为矩形.425.二次函数菱形存在性三角形相似存在性问题(初三)如图,已知直线y=―2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x 轴于点C,交抛物线于点D.(1)若抛物线的解析式为y=―2x2+2x+4,设其顶点为M,其对称轴交AB于点N.①求点M、N的坐标;②是否存在点P,使四边形MNPD为菱形?并说明理由(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.426.二次函数菱形存在性问题(初三)如图,抛物线y=x2+2x―8与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.(1)求A,B,C三点的坐标(2)连接AC,直线x=m(―4<m<0)与该抛物线交于点E,与AC交于点D,连接OD.当OD⊥AC时,求线段DE的长;(3)点M在y轴上，点N在直线AC上,点P为拋物线对称轴上一点,是否存在点M,使得以C、M、N、P为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.427.二次函数菱形存在性问题三角形面积相等问题(初三)x2+2x―6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.如图,抛物线y=12(1)求A、B,C三点的坐标并直接写出直线AC,BC的函数表达式.(2)点P是直线AC下方抛物线上的一个动点,过点P作BC的平行线1,交线段AC于点D.①试探究:在直线1上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,求出点E的坐标,若不存在,请说明理由;②设抛物线的对称轴与直线1交于点M,与直线AC交于点N.当S△DWN=S△AOC时,请直接写出DM的长.428.二次函数三角形面积最大值菱形存在性问题(初三)如图,在平面直角坐标系中,Rt△ABC的边BC在x轴上,∠ABC=90∘,以A为顶点的抛物线y=―x2+bx+c经过点C(3,0),交y轴于点E(0,3),动点P在对称轴上.(1)求抛物线解析式;(2)若点P从A点出发,沿A→B方向以1个单位/秒的速度匀速运动到点B停止,设运动时间为t秒,过点P作PD⊥AB 交AC于点D,过点D平行于y轴的直线1交抛物线于点Q,连接AQ,CQ,当t为何值时,△ACQ的面积最大?最大值是多少?(3)若点M是平面内的任意一点,在x轴上方是否存在点P,使得以点P,M,EC为顶点的四边形是菱形,若存在,请直接写出符合条件的M点坐标;若不存在,请说明理由.429.二次函数菱形存在性问题(初三)已知抛物线F:y=x2+bx+c的图象经过坐标原点0,且与x轴另一交点为(―33,0).(1)求抛物线F的解析式.x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限)，求y2―y1的(2)如图1,直线1:y=33值(用含m的式子表示);,设点A′是点A关于原点0的对称点,如图2.(3)在(2)中,若m=43①判断△AA′B的形状,并说明理由;②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.430.二次函数线段最大值菱形存在性问题(初三)如图,二次函数y =x 2+bx +c 的图象交x 轴于点A(―3,0),B(1,0),交y 轴于点C .点P(m,0)是x 轴上的一动点，PM ⊥x 轴，交直线AC 于点M ，交抛物线于点N .(1)求这个二次函数的表达式:(2)①若点P 仅在线段A0上运动，如图，求线段MN 的最大值;②若点P 在x 轴上运动,则在y 轴上是否存在点Q ,使以M,N,C,Q 为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q 的坐标;若不存在,请说明理由.431.二次函数菱形存在性问题(初三)如图,一次函数y =33x ―3图象与坐标轴交于点A 、B ,二次函数y =33x 2+bx +c 图象过A 、B 两点.(1)求二次函数解析式(2)点B 关于抛物线对称轴的对称点为点C ,点P 是对称轴上一动点,在抛物线上是否存在点Q ,使得以B 、C 、P 、Q 为顶点的四边形是菱形?若存在,求出Q 点坐标;若不存在,请说明理由.答案422【解】(1)∵抛物线y =―13x 2+bx +c 交x 轴于A(―3,0),B(4,0)两点,∴y =―13(x +3)(x ―4)=―13x 2+13x +4;(2)①如图1,∵B(4,0),C(0,4),∴设BC 的解析式为:y =kx +n,则{4k +n =0n =4,解得{k =―1n =4∴BC 的解析式为:y =―x +4,∴―x +4=34x +94,解得:x =1,∴E(1,3),∵M(m,0),且MH ⊥x 轴,∴G (m,34m +94),F (m,―13m 2+13m +4),∴FG =―13m 2+13m +4―(34m +94)=―13m 2―512m +74∵S △EFG =59S △OEG ,△EFG 和△OEG 的水平宽度相同,∴FG =59ON,∴―13m 2―512m +74=59×94解得:m 1=34,m 2=―2;②存在,由①知:E(1,3),且∠CBM =45∘∴过点E 作AB 的平行线,与抛物线的交点就是正方形EFHP 的顶点F.∴FH =EF,∠EFH =∠FHP =∠HPE =90∘,∵M(m,0),且MH ⊥x 轴,∴H(m,―m +4),F (m,―13m 2+13m +4),分两种情况:第一种情况:当―3⩽m <1时,如图1,点F 在EP 的左侧∴FH =(―m +4)―(―13m 2+13m +4)=13m 2―43m,∴13m 2―43m =1―m,解得:m 1=1+132(舍),m 2=1―132,∴H(1―132,7+132),∴P (1,7+132),第二种情况:当1<m <4时,点F 在PE 的右边,如图2,同理得―13m 2+43m =m ―1,解得:m 1=1+132,m 2=1―132(舍)，同理得P (1,7―132);综上,点P 的坐标为:(1,7+132)或(1,7―132).423【解】(1)∵OA =1,∴A(―1,0),又∵对称轴为x =2,∴B(5,0),将A,B 代入解析式得:{0=a ―2+c0=25a +10+c ,解得{a =―12c =52,∴y =―12x 2+2x +52(2)由(1)得:C (0,52),D (2,92),∴由两点距离公式可得:CD =22,故答案为22;(3)∵B(5,0),C (0,52),∴直线BC 的解析式为:y =―12x +52,设E (x,―12x 2+2x +52),且0<x <5,如图,作EF ⊥x 轴交BC 于点F,则F (x,―12x +52),∴EF =―12x 2+2x +52―(―12x +52)=―12x 2+52x,S △BCE =12×EF ×BO =12×(―12x 2+52x )×5=―54(x ―52)2+12516当x =52时,S △BCE 有最大值为12516;(4).设P(2,y),Q(m,n),由(1)知B(5,0),C (0,52),分三种情况讨论:①若BC 为矩形的对角线,由中点坐标公式得:{5+0=2+m 0+52=y +n ,解得:{m =3n =52―y ,又∵∠BPC =90∘,∴PC 2+PB 2=BC 2,即:22+(52―y )2+32+y 2=52+(52)2,解得y =4或y =―32,∴n =―32或n =4,∴Q (3,―32)或Q(3,4)，②若BP 为矩形的对角线,由中点坐标公式得{5+2=0+m 0+y =52+n ,解得:{m =7n =y ―52,又∵∠BCP =90∘,BC 2+CP 2=BP 2即:52+(52)2+22+(52―y )2=32+y 2,解得y =132,∴Q(7,4),③若BQ 为矩形的对角线,由中点坐标公式得:{5+m =2+00+n =y +52,解得:{m =―3n =y +52,又∵∠BCQ =90∘,∴BC 2+CQ 2=BQ 2,即:52+(52)2+m 2+(52―n )2=(5―m)2+n 2,解得n =―72,∴Q (―3,―72),综上,点Q 的坐标为(3,―32)或(3,4),或(7,4)或(―3,―72).解法二,也可以构造利用一线三等角三角形相似来解决。
专题05二次函数中特殊平行四边形存在性问题(原卷版)
挑战2023年中考数学解答题压轴真题汇编专题05 二次函数中特殊平行四边形存在性问题一．平行四边形的存在性1．（2022•重庆）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于点A（4，0），与y轴交于点B（0，3）．（1）求抛物线的函数表达式；（2）点P为直线AB上方抛物线上一动点，过点P作PQ⊥x轴于点Q，交AB于点M，求PM+AM的最大值及此时点P的坐标；（3）在（2）的条件下，点P′与点P关于抛物线y＝﹣x2+bx+c的对称轴对称．将抛物线y＝﹣x2+bx+c向右平移，使新抛物线的对称轴l经过点A．点C在新抛物线上，点D在l上，直接写出所有使得以点A、P′、C、D为顶点的四边形是平行四边形的点D的坐标，并把求其中一个点D的坐标的过程写出来．2．（2022•郴州）已知抛物线y＝x2+bx+c与x轴相交于点A（﹣1，0），B（3，0），与y轴相交于点C．（1）求抛物线的表达式；（2）如图1，将直线BC向上平移，得到过原点O的直线MN．点D是直线MN上任意一点．①当点D在抛物线的对称轴l上时，连接CD，与x轴相交于点E，求线段OE的长；②如图2，在抛物线的对称轴l上是否存在点F，使得以B，C，D，F为顶点的四边形是平行四边形？若存在，求出点F与点D的坐标；若不存在，请说明理由．3．（2022•攀枝花）如图，二次函数y＝ax2+bx+c的图象与x轴交于O（O为坐标原点），A两点，且二次函数的最小值为﹣1，点M（1，m）是其对称轴上一点，y轴上一点B（0，1）．（1）求二次函数的表达式；（2）二次函数在第四象限的图象上有一点P，连结P A，PB，设点P的横坐标为t，△P AB的面积为S，求S与t的函数关系式；（3）在二次函数图象上是否存在点N，使得以A、B、M、N为顶点的四边形是平行四边形？若存在，直接写出所有符合条件的点N的坐标，若不存在，请说明理由．4．（2022•内蒙古）如图，抛物线y＝ax2+x+c经过B（3，0），D（﹣2，﹣）两点，与x轴的另一个交点为A，与y轴相交于点C．（1）求抛物线的解析式和点C的坐标；（2）若点M在直线BC上方的抛物线上运动（与点B，C不重合），求使△MBC面积最大时M点的坐标，并求最大面积；（请在图1中探索）（3）设点Q在y轴上，点P在抛物线上，要使以点A，B，P，Q为顶点的四边形是平行四边形，求所有满足条件的点P的坐标．（请在图2中探索）5．（2022•资阳）已知二次函数图象的顶点坐标为A（1，4），且与x轴交于点B （﹣1，0）．（1）求二次函数的表达式；（2）如图，将二次函数图象绕x轴的正半轴上一点P（m，0）旋转180°，此时点A、B的对应点分别为点C、D．①连结AB、BC、CD、DA，当四边形ABCD为矩形时，求m的值；②在①的条件下，若点M是直线x＝m上一点，原二次函数图象上是否存在一点Q，使得以点B、C、M、Q为顶点的四边形为平行四边形，若存在，求出点Q的坐标；若不存在，请说明理由．二．矩形的存在性6．（2022•泸州）如图，在平面直角坐标系xOy中，已知抛物线y＝ax2+x+c经过A（﹣2，0），B（0，4）两点，直线x＝3与x轴交于点C．（1）求a，c的值；（2）经过点O的直线分别与线段AB，直线x＝3交于点D，E，且△BDO与△OCE的面积相等，求直线DE的解析式；（3）P是抛物线上位于第一象限的一个动点，在线段OC和直线x＝3上是否分别存在点F，G，使B，F，G，P为顶点的四边形是以BF为一边的矩形？若存在，求出点F的坐标；若不存在，请说明理由．8．（2021•齐齐哈尔）综合与探究如图，在平面直角坐标系中，抛物线y＝ax2+2x+c（a≠0）与x轴交于点A、B，与y轴交于点C，连接BC，OA＝1，对称轴为直线x＝2，点D为此抛物线的顶点．（1）求抛物线的解析式；（2）抛物线上C、D两点之间的距离是2；（3）点E是第一象限内抛物线上的动点，连接BE和CE，求△BCE面积的最大值；（4）点P在抛物线对称轴上，平面内存在点Q，使以点B、C、P、Q为顶点的四边形为矩形，请直接写出点Q的坐标．9．（2022•随州）如图1，平面直角坐标系xOy中，抛物线y＝ax2+bx+c（a＜0）与x轴分别交于点A和点B（1，0），与y轴交于点C，对称轴为直线x＝﹣1，且OA＝OC，P为抛物线上一动点．（1）直接写出抛物线的解析式；（2）如图2，连接AC，当点P在直线AC上方时，求四边形P ABC面积的最大值，并求出此时P点的坐标；（3）设M为抛物线对称轴上一动点，当P，M运动时，在坐标轴上是否存在点N，使四边形PMCN为矩形？若存在，直接写出点P及其对应点N的坐标；若不存在，请说明理由．10．（2023•秦都区校级二模）如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0）、B两点（点B在点A的右侧），与y轴交于点C，且OC＝3OA，点D为抛物线的对称轴与x轴的交点，连接CD．（1）求抛物线的函数表达式；（2）点F为坐标平面内一点，在第一象限的抛物线上是否存在点E，使得以点C、D、E、F为顶点的四边形是以CD为边的矩形？若存在，请求出符合条件的点E的横坐标；若不存在，请说明理由．7．（2022•元宝区校级二模）如图，在平面直角坐标系中，抛物线y＝ax2+bx+3（a≠0）与x轴交于点A、B，与y轴交于点C，连接BC，OA＝1，对称轴为直线x＝2，点D为此抛物线的顶点．（1）求抛物线的解析式；（2）抛物线上C、D两点之间的距离是11；（3）点E是第一象限内抛物线上的动点，连接BE和CE，求△BCE面积的最大值；（4）点P在抛物线对称轴上，平面内存在点Q，使以点B、C、P、Q为顶点的四边形为矩形，请直接写出点Q的坐标．8．（2022•鱼峰区模拟）如图，在平面直角坐标系中，抛物线y＝x2+bx+c与坐标轴交于A（0，﹣2），B（4，0）两点，直线BC：y＝﹣2x+8交y轴于点C．（1）求该抛物线的解析式；（2）在第二象限内是否存在一点M，使得四边形ABCM为矩形？如果存在，求出点M的坐标；如果不存在，请说明理由．三．菱形的存在性9．（2022•朝阳）如图，在平面直角坐标系中，抛物线y＝ax2+2x+c与x轴分别交于点A（1，0）和点B，与y轴交于点C（0，﹣3），连接BC．（1）求抛物线的解析式及点B的坐标．（2）如图，点P为线段BC上的一个动点（点P不与点B，C重合），过点P 作y轴的平行线交抛物线于点Q，求线段PQ长度的最大值．（3）动点P以每秒个单位长度的速度在线段BC上由点C向点B运动，同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动，在平面内是否存在点N，使得以点P，M，B，N为顶点的四边形是菱形？若存在，请直接写出符合条件的点N的坐标；若不存在，请说明理由．10．（2021•湘潭）如图，一次函数y＝x﹣图象与坐标轴交于点A、B，二次函数y＝x2+bx+c图象过A、B两点．（1）求二次函数解析式；（2）点B关于抛物线对称轴的对称点为点C，点P是对称轴上一动点，在抛物线上是否存在点Q，使得以B、C、P、Q为顶点的四边形是菱形？若存在，求出Q点坐标；若不存在，请说明理由．11．（2021•鄂尔多斯）如图，抛物线y＝x2+2x﹣8与x轴交于A，B两点（点A 在点B左侧），与y轴交于点C．（1）求A，B，C三点的坐标；（2）连接AC，直线x＝m（﹣4＜m＜0）与该抛物线交于点E，与AC交于点D，连接OD．当OD⊥AC时，求线段DE的长；（3）点M在y轴上，点N在直线AC上，点P为抛物线对称轴上一点，是否存在点M，使得以C、M、N、P为顶点的四边形是菱形？若存在，请直接写出点M的坐标；若不存在，请说明理由．12．（2021•通辽）如图，抛物线y＝ax2+bx+3交x轴于A（3，0），B（﹣1，0）两点，交y轴于点C，动点P在抛物线的对称轴上．（1）求抛物线的解析式；（2）当以P，B，C为顶点的三角形周长最小时，求点P的坐标及△PBC的周长；（3）若点Q是平面直角坐标系内的任意一点，是否存在点Q，使得以A，C，P，Q为顶点的四边形是菱形？若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．13．（2021•娄底）如图，在直角坐标系中，二次函数y＝x2+bx+c的图象与x轴相交于点A（﹣1，0）和点B（3，0），与y轴交于点C．（1）求b、c的值；（2）点P（m，n）为抛物线上的动点，过P作x轴的垂线交直线l：y＝x于点Q．①当0＜m＜3时，求当P点到直线l：y＝x的距离最大时m的值；②是否存在m，使得以点O、C、P、Q为顶点的四边形是菱形，若不存在，请说明理由；若存在，请求出m的值．14．（2021•山西）综合与探究如图，抛物线y＝x2+2x﹣6与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，连接AC，BC．（1）求A、B，C三点的坐标并直接写出直线AC，BC的函数表达式．（2）点P是直线AC下方抛物线上的一个动点，过点P作BC的平行线l，交线段AC于点D．①试探究：在直线l上是否存在点E，使得以点D，C，B，E为顶点的四边形为菱形，若存在，求出点E的坐标，若不存在，请说明理由；②设抛物线的对称轴与直线l交于点M，与直线AC交于点N．当S△DMN ＝S△AOC时，请直接写出DM的长．15．（2020•阜新）如图，二次函数y＝x2+bx+c的图象交x轴于点A（﹣3，0），B（1，0），交y轴于点C．点P（m，0）是x轴上的一动点，PM⊥x轴，交直线AC于点M，交抛物线于点N．（1）求这个二次函数的表达式；（2）①若点P仅在线段AO上运动，如图，求线段MN的最大值；②若点P在x轴上运动，则在y轴上是否存在点Q，使以M，N，C，Q为顶点的四边形为菱形．若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．。
二次函数中考压轴题四边形的存在性问题解析
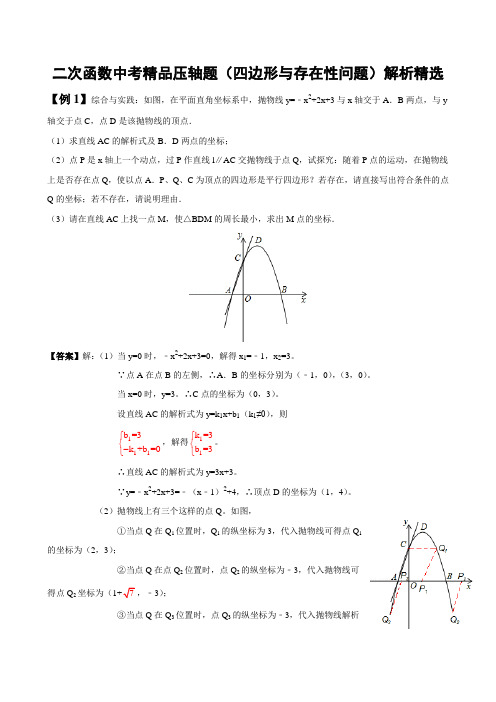
二次函数中考精品压轴题（四边形与存在性问题）解析精选【例1】综合与实践：如图，在平面直角坐标系中，抛物线y=﹣x 2+2x+3与x 轴交于A ．B 两点，与y 轴交于点C ，点D 是该抛物线的顶点．（1）求直线AC 的解析式及B ．D 两点的坐标；（2）点P 是x 轴上一个动点，过P 作直线l ∥AC 交抛物线于点Q ，试探究：随着P 点的运动，在抛物线上是否存在点Q ，使以点A ．P 、Q 、C 为顶点的四边形是平行四边形？若存在，请直接写出符合条件的点Q 的坐标；若不存在，请说明理由．（3）请在直线AC 上找一点M ，使△BDM 的周长最小，求出M 点的坐标．【答案】解：（1）当y=0时，﹣x 2+2x+3=0，解得x 1=﹣1，x 2=3。
∵点A 在点B 的左侧，∴A ．B 的坐标分别为（﹣1，0），（3，0）。
当x=0时，y=3。
∴C 点的坐标为（0，3）。
设直线AC 的解析式为y=k 1x+b 1（k 1≠0），则111b =3k +b =0⎧⎨-⎩，解得11k =3b =3⎧⎨⎩。
∴直线AC 的解析式为y=3x+3。
∵y=﹣x 2+2x+3=﹣（x ﹣1）2+4，∴顶点D 的坐标为（1，4）。
（2）抛物线上有三个这样的点Q 。
如图，①当点Q 在Q 1位置时，Q 1的纵坐标为3，代入抛物线可得点Q 1的坐标为（2，3）；②当点Q 在点Q 2位置时，点Q 2的纵坐标为﹣3，代入抛物线可得点Q 2坐标为（1+7，﹣3）；③当点Q 在Q 3位置时，点Q 3的纵坐标为﹣3，代入抛物线解析式可得，点Q 3的坐标为（1﹣7，﹣3）。
综上可得满足题意的点Q 有三个，分别为：Q 1（2，3），Q 2（1+7，﹣3），Q 3（1﹣7，﹣3）。
（3）点B 作BB′⊥AC 于点F ，使B′F=BF ，则B′为点B 关于直线AC 的对称点．连接B′D 交直线AC 与点M ，则点M 为所求。
过点B′作B′E ⊥x 轴于点E 。
重难点06二次函数中四边形的存在性问题(原卷版)
重难点06 二次函数中四边形的存在性问题技巧方法类型一：已知三点的平行四边形问题1、知识内容：已知三点后，其实已经固定了一个三角形（平行四边形的一半），如图ABC．第四个点M则有3种取法，过3个顶点作对边的平行线且取相等长度即可（如图中3个M点）．2、解题思路：（1）根据题目条件，求出已知3个点的坐标；（2）用一点及其对边两点的关系，求出一个可能点；（3）更换顶点，求出所有可能的点；（4）根据题目实际情况，验证所有可能点是否满足要求并作答．类型二：存在动边的平行四边形问题1、知识内容：在此类问题中，往往是已知一条边，而它的对边为动边，需要利用这组对边平行且相等列出方程，进而解出相关数值．更复杂的有，一组对边的两条边长均为变量，需要分别表示后才可列出方程进行求解．2、解题思路：（1）找到或设出一定平行的两条边（一组对边）；（2）分别求出这组对边的值或函数表达式；（3）列出方程并求解；（4）返回题面，验证求得结果．能力拓展一、填空题1．（2020·浙江·九年级期中）如图，已知在平面直角坐标系xOy 中，抛物线24(0)y x x c c =--+>的顶点为D ，与y 轴的交点为C ，过点C 的直线CA 与抛物线交于另一点A （点A 在对称轴左侧），点B 在AC 的延长线上，连结,,OA OB DA 和3,5BC DB AC =．当四边形AOBD 是平行四边形时，则点A 的坐标为_______．二、解答题2．（2020·浙江温州·模拟预测）如图，直线l ：112y x =-+ 与x 轴、y 轴分别交于点B 、C ，经过B 、C 两点的抛物线 2y x bx c =++ 与x 轴的另一个交点为A ．(1)求该抛物线的解析式；(2)若点P 在直线l 下方的抛物线上，过点P 作//PD x 轴交l 于点D ，//PE y 轴交l 于点E ，求PD PE +的最大值；(3)设F 为直线l 上的点，点P 仍在直线l 下方的抛物线上，以A 、B 、P 、F 为顶点的四边形能否构成平行四边形？若能，求出点F 的坐标；若不能，请说明理由．3．（2022·浙江湖州·一模）如图已知二次函数2y x bx c =++（b ，c 为常数）的图像经过点(3,1)A -，点(0,4)C -，顶点为点M ，过点A 作AB x ∥轴，交y 轴于点D ，交二次函数2y x bx c =++的图象于点B ，连接BC ．(1)求该二次函数的表达式及点M的坐标；(2)若将该二次函数图象向上平移(0)m m 个单位，使平移后每到的二次函数图象的顶点落在ABC的内部（不包括ABC的边界），求m的取值范围；(3)若E为y轴上且位于点C下方的一点，P为直线AC上一点，在第四象限的抛物线上是否存在一点Q，使以C、E、P、Q为顶点的四边形是菱形？若存在，请求出点Q的横坐标；若不存在，请说明理由．4．（2020·浙江温州·九年级阶段练习）如图，抛物线y＝﹣x2＋2x＋3与y轴相交于A，B两点（点A在点B 左侧），与y轴相较于点C，顶点为D．(1)直接写出A、B、C三点的坐标；(2)连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；①用含m的代数式表示PF的长，并求出当m为何值时四边形PEDF为平行四边形？②设△BCF的面积为S，求S与m的函数关系式．5．（2021·浙江·嘉兴一中一模）已知抛物线y＝a（x－m）2＋n与y轴交于点A，它的顶点为点B，点A、B 关于原点O的对称点分别为C、D．若A、B、C、D中任何三点都不在一直线上，则称四边形ABCD为抛物线的伴随四边形，直线AB为抛物线的伴随直线．(1)如图1，求抛物线y ＝（x －3）2＋1的伴随直线的解析式．(2)如图2，若抛物线y ＝a （x －m ）2＋n （m ＞0）的伴随直线是y ＝x －3，伴随四边形的面积为12，求此抛物线的解析式．(3)如图3，若抛物线y ＝a （x －m ）2＋n 的伴随直线是y ＝－2x ＋b （b ＞0），且伴随四边形ABCD 是矩形． ①用含b 的代数式表示m 、n 的值；②在抛物线的对称轴上是否存在点P ，使得△PBD 是一个等腰三角形？若存在，请直接写出点P 的坐标（用含b 的代数式表示）；若不存在，请说明理由．6．（2022·浙江台州·模拟预测）如图，抛物线21=-++2y x bx c 的图象经过点C (0，2)，交x 轴于点A (﹣1，0)和B ，连接BC ，直线y ＝kx +1与y 轴交于点D ，与BC 上方的抛物线交于点E ，与BC 交于点F ．(1)求抛物线的表达式及点B的坐标；(2)求EFDF的最大值及此时点E的坐标；(3)在（2）的条件下，若点M为直线DE上一点，点N为平面直角坐标系内一点，是否存在这样的点M和点N，使得以点B、D、M、N为顶点的四边形是菱形？若存在，直接写出点M的坐标；若不存在，请说明理由．7．（2016·浙江·海盐县滨海中学九年级期中）如图，在平面直角坐标系中，已知抛物线经过A（﹣4，0），B （0，﹣4），C（2，0）三点．(1)求抛物线的解析式；(2)若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S ，求S 关于m 的函数关系式，并求出S 的最大值；(3)若点P 是抛物线上的动点，点Q 是直线y ＝﹣x 上的动点，判断有几个位置能使以点P ，Q ，B ，O 为顶点的四边形为平行四边形（要求PQ OB ∥），直接写出相应的点Q 的坐标．8．（2022·浙江金华·一模）如图，把两个全等的Rt AOB 和Rt COD 分别置于平面直角坐标系中，使直角边OB 、OD 在x 轴上．已知点()2,4A ，过A 、C 两点的直线分别交x 轴、y 轴于点E 、F ，抛物线2y ax bx c=++经过O 、A 、C 三点．(1)求该抛物线的函数解析式；(2)点G 为抛物线上位于线段OC 所在直线上方部分的一动点，求G 到直线OC 的最大距离和此时点G 的坐标；(3)点P 为线段OC 上一个动点，过点P 作y 轴的平行线交抛物线于点M ，交x 轴于点N ，问是否存在这样的点P ，使得四边形ABPM 的边AM 与边BP 相等？若存在，求出此时点P 的坐标；若不存在，请说明理由．9．（2020·浙江宁波·九年级期中）如图，抛物线y ＝﹣213222x x ++与x 轴交于点A ，点B ，与y 轴交于点C ，点D 与点C 关于x 轴对称，点P 是x 轴上的一个动点，设点P 的坐标为（m ，0），过点P 作x 轴的垂线l 交抛物线于点Q ．(1)求点A 、点B 、点C 的坐标；(2)求直线BD 的解析式；(3)当点P 在线段OB 上运动时，直线l 交BD 于点M ，试探究m 为何值时，四边形CQMD 是平行四边形；(4)在点P 的运动过程中，是否存在点Q ，使△BDQ 是以BD 为直角边的直角三角形？若存在，求出点Q 的坐标；若不存在，请说明理由．10．（2020·浙江·浣江教育九年级期中）如图，已知抛物线2y x bx c =++的图象经过点(1,0)A ，(3,0)B -，与y 轴交于点C ，抛物线的顶点为D ，对称轴与x 轴相交于点E ，连接BD ．（1）求抛物线的解析式．（2）在抛物线上点B 和点D 之间是否存在一点H 使得四边形OBHC 的面积最大，若存在求出四边形OBHC的最大面积，若不存在，请说明理由．（3）直线BD 上有一点P ，使得PE PC =时，过P 作PF x ⊥轴于F ，点M 为x 轴上一动点，N 为直线PF 上一动点，G 为抛物线上一动点，当以点F ，N ，G ，M 四点为顶点的四边形为正方形时，求点M 的坐标．11．（2022·浙江·舟山市定海区第七中学一模）【基础巩固】（1）如图1，AC ∥DF ，Rt △ABC ≌Rt △DEF ，连结AD ，BE ，求证：四边形ABED 是平行四边形．【尝试应用】（2）如图2，在平面直角坐标系xOy 中，已知点A ，B 的坐标分别是A （1，3），B （4，1），点C 在x 轴上，点D 在y 轴上．若以AB 为边，其余两个顶点为C ，D 的四边形是平行四边形，求点C ，D 的坐标．【拓展提高】（3）如图3，抛物线y ＝x 2﹣4x +3与直线y ＝x +3交于C ，D 两点，点E 是抛物线上任意一点，在对称轴上是否存在点F ，使得以CD 为边，其余两个顶点为E ，F 的四边形是平行四边形，若存在，求出点E 的坐标，若不存在，请说明理由．12．（2021·浙江金华·九年级期中）如图，已知抛物线24y ax bx =++经过(1,0)A -，(4,0)B 两点，交y 轴于点C ．（1）求抛物线的解析式；（2）连接BC ，求直线BC 的解析式；（3）请在抛物线的对称轴上找一点P ，使AP PC +的值最小，求点P 的坐标，并求出此时AP PC +的最小值；（4）点M 为x 轴上一动点，在抛物线上是否存在一点N ，使得以A 、C 、M 、N 四点为顶点的四边形是平行四边形？若存在，求出点N 的坐标；若不存在，请说明理由．13．（2021·浙江·一模）如图，在平面直角坐标系中，直线443y x =+与x 轴交于点A ，与y 轴交于点C ，抛物线2(0)y ax bx c a =++≠经过A 、C 两点，与x 轴的另一交点为点B ．（1）求A 、C 两点的坐标；（2）当ABC 为轴对称图形时，求抛物线的解析式；（3）当ABC 关于y 轴成轴对称时，若点M 、N 是抛物线上的动点，且有//MN x 轴，点P 是x 轴上的动点，在坐标平面内是否存在一点Q ，使以M 、N 、P 、Q 为顶点的四边形构成正方形？若存在，求出Q 点坐标：若不存在，请说明理由．14．（2020·浙江·九年级期中）如图，已如在平面直角坐标系xOy 中，直线33y x =x 轴交于点A ，与y 轴交于点B ，点F 是点B 关于x 轴的对称点，抛物线23y bx c ++经过点A 和点F ，与直线AB 交于点C ．（1）求A 和F 的坐标，并求出抛物线的函数表达式；（2）点P 是直线AC 下方的抛物线上的一动点，连结,PA PB ．求PAB △的最大面积并写出点P 的坐标； （3）点Q 是抛物线上一点，点D 在x 轴上，在（2）的条件下，是否存在以,,,A P D Q 为顶点且AP 为边的平行四边形，若存在，直接写出点Q 的坐标；若不存在，说明理由．15．（2020·浙江绍兴·模拟预测）定义：如果一条直线把一个封闭的平面图形分成面积相等的两部分，我们把这条直线称为这个平面图形的一条中分线．如三角形的中线所在的直线是三角形的一条中分线．（1）按上述定义，分别作出图1，图2的一条中分线．（2）如图3，已知抛物线2132y x x m =-+与x 轴交于点(2,0)A 和点B ，与y 轴交于点C ，顶点为D ． ①求m 的值和点D 的坐标；②探究在坐标平面内是否存在点P ，使得以A ，C ，D ，P 为顶点的平行四边形的一条中分线经过点O ．若存在，求出中分线的解析式；若不存在，请说明理由．16．（2020·浙江省温岭市第四中学九年级期中）如图，点A 、D 是平面直角坐标系中y 轴正半轴上的点，B 、C 分别在x 轴的负半轴和x 轴的正半轴上，且OA=OB=6，BD=AC ，OC=m ，E 、F 、G 分别是AB 、CD 、BC的中点．（1）求证：BD⊥AC；（2）用含m的式子表示△EFG的面积，并直接写出当∠BDO=4∠ACD时．△EFG的面积：（3）抛物线l₁：y=ax²+bx+c经过 A、B、C三点，顶点为P．①求a的值（用m的式子表示），并判断是否存在m的值，使得四边形APDC为平行四边形，若存在，求出此时m的值，若不存在，请说明理由．②连结AF，当经过G、O、F三点的抛物线h与抛物线l关于某点成中心对称，点Q是△AEF的外接圆上的动点，求GQ的最小值与最大值的和．。
二次函数中的存在性问题
二次函数中特殊四边形的存在性问题（三）——与正方形的结合一、教材分析：结合最近几年的中考真题，不难发现，第28题压轴题一定是二次函数的综合性题目，在这道题的第3问中，大致可以分为以下几类：1、存在性问题：（1）二次函数中的特殊三角形存在性问题（这里的三角形可以是等腰三角形、等边三角形、等腰直角三角形）；（2）二次函数中与已知三角形相似的三角形存在性问题；话（3）二次函数中与已知三角形面积产生联系的三角形存在性问题；（4）二次函数中特殊四边形存在性问题（这里的特殊四边形可以是平行四边形、矩形、菱形、正方形）。
2、最值问题。
3、动点问题（路径）。
由此可见，将存在性问题分为多个小专题来授课是非常必要的。
二、学情分析：在八年级学过一次函数后，我们已经在该背景下研究过特殊三角形的存在性问题，其中不乏等腰三角形等，也研究过在已知三角形的前提下，是否有点存在，构成全等三角形。
对处理存在性问题有了一定的感悟，往往是：假设存在——尝试画图，在该过程中分析是否具有多种可能性——选择合适的分类标准，进行讨论——结合题意推理计算。
在此背景下，经历了九年级的反比例函数、二次函数和相似三角形、特殊平行四边形的学习后，便可以将存在性问题放到反比例函数和二次函数中来研究，学生也有了一定的方向和研究策略，可以进一步体会存在性问题的本质。
三、教学目标：1、能根据题中给出的条件，选择恰当的表达式（一般式、顶点式、交点式），用待定系数法求出抛物线解析式2、在二次函数的综合性题目中，能结合图象，在题意中抽取出有用的信息，并能用数学语言表达（若没有图形则可自己尝试画图），找出符合题意的点，尝试解答3、在学习的过程中，经历独自思考、小组讨论的过程，增强自信心，树立健全人格四、教学重、难点：教学重点：在二次函数的综合性题目中，能结合图象，在题意中抽取出有用的信息，并能用数学语言表达（若没有图形则可自己尝试画图），尝试解答教学难点：归纳总结怎么处理二次函数中的存在性问题，存在性问题的本质是什么。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
网课：二次函数中特殊四边形的存在性问题
学习目标：
1、通过二次函数中的特殊四边形存在性问题的探究、学习，获取解决这类问题的基本方法；经历解决二次函数中的特殊四边形存在性问题的探索过程，培养学生的理解能力，抽象能力，能正确认识问题的本质，提高知识迁移能力，积累解决问题的经验，感受数学知识对解决问题的价值；
2、通过函数中的特殊四边形存在性问题的解决，渗透“转化”、“分类”、“方程”、“数形结合”等数学思想，并在问题解决中体验成功的快乐，感受数学的魅力.
学习重点：利用“特殊四边形的性质”，或者“点在函数上”来建立等量关系，解决“点是否存在的问题”.
学习难点：从复杂的函数背景中提炼问题的本质，利用“特殊四边形的性质”，或者“点在函数上”来建立等量关系，解决“点是否存在的问题”.
背景问题：
如图，抛物线中，点A在x轴的正半轴上，点C在y轴的正半轴上，
OC=3，点D是直线AC与抛物线的交点。
问题一：在平面内是否存在一点B，使得以A、B、O、D为顶点的
四边形是平行四边形?
若存在，请直接写出B点的坐标；若不存在，请说明理由。
归纳：_________________________________________________
问题二：若点M在抛物线上，点N在x轴上，是否存在以A、D、M、N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由;
（备图1）（备图2）
归纳：
_____________________________________________________________________________
问题三：若点E（2,3）在抛物线上，点F、P在直线AC上，当EF所在直线与x轴垂直时，平面内是否存在一点Q，使得以点E、F、P、Q为顶点的四边形是菱形？若存在，求出点Q 的坐标；若不存在，请说明理由;
（备图1）（备图2）
归纳：
______________________________________________________________________________
问题四：点是直线AC上一点，若点N是平面内一点，M是抛物线对称轴上的一点，是否存在一点M使得以点A，P，M，N为顶点的四边形是矩形？若能，求出点M的坐标；若不能，请说明理由．
归纳：
_______________________________________________________________________
课后练习：
如图1，抛物线y＝﹣﹣x+2与x轴交于A，B两点，与y轴交于点C，点D为线段AC的中点，直线BD与抛物线交于另一点E，与y轴交于点F．
（1）如图1，点P是直线BE上方抛物线上一动点，连接PD，PF，当△PDF的面积最大
时，在线段BE上找一点G，使得PG﹣EG的值最小，求出PG﹣EG的最小值；（2）如图2，点M为抛物线上一点，点N在抛物线的对称轴上，点K为平面内一点，当以点A、M、N、K为顶点的四边形是正方形时，直接写出点N的坐标．。