matlab课程论文要求
高校《MATLAB及其应用》课程教学论文

高校《MATLAB及其应用》课程教学的研究与思考【摘要】《matlab及其应用》课程是国内高校广泛开设的一门电子信息类专业基础课。
如何完成好该课程的教学工作,是高校教务管理部门和任课教师十分关心的课题。
本文首先对《matlab及其应用》课程的安排、实施进行了系统的论述,然后对该课程教学中存在的若干问题进行了思考,并对相应的改进和提高措施进行了探讨。
本文对规范《matlab及其应用》课程的教学工作、保障该课程的教学质量、提高对学生的培养水平等具有重要意义。
【关键词】matlab;课程教学;研究;思考0 引言matlab是matrix laboratory(矩阵实验室)的缩写,是美国mathwork公司推出的—种集矩阵分析、数值计算、符号计算、绘图操作、系统建模仿真等多种功能于一体的计算机程序语言和软件[1-2],被广泛应用于科研、工程技术等领域,已成为国际上影响最广泛的计算机软件之一。
matlab在数学计算、数据处理等方面具备其它计算机语言所不具备的优势,其主要特点是操作方便、语言简洁、语法规则简单、库函数丰富、编程效率高、绘图功能强大、开放性的源程序、良好的人机交互等[1,3]。
matlab在9o年代中期开始在我国逐渐兴起,并在各高校和科研单位得到应用。
目前,其已成为在读本、专科学生、研究生、科研人员、工程技术人员等需要掌握的重要计算机语言[4]。
河南工业大学相继为电子信息类专业的本科生、专科生开设了《matlab及其应用》课程,获得了本、专科学生和相关专业课任课教师的一致好评。
开设《matlab及其应用》课程的目的是为了使电子信息类专业学生能熟练使用matlab语言和软件、具备一定的编程能力、掌握matlab在相关专业课中的应用方法。
作为一门电子信息类专业基础课,《matlab及其应用》课程内容涉及了学生在大学期间的大部分主要课程,例如:高等数学、线性代数、概率统计、大学物理、电路分析、信号与系统、数字信号处理、通信原理等[5]。
基于Matlab的脉冲编码调制(PCM)系统设计与仿真

课程设计(论文)任务书信息工程学院通信工程专业14-2 班一、课程设计(论文)题目脉冲编码调制(PCM)系统设计与仿真二、课程设计(论文)工作自2017年1 月3日起至2017年1月 13日止。
三、课程设计(论文) 地点: 图书馆、寝室、通信实验室(4-410)。
四、课程设计(论文)内容要求:1.本课程设计的目的(1)使学生掌握通信系统各功能模块的基本工作原理;(2)培养学生采用Matlab与Simulink相结合对各种编码与解码进行仿真的方法;(3)培养学生对PCM的理解能力;(4)能提高和挖掘学生对所学知识的实际应用能力即创新能力;(5)提高学生的科技论文写作能力。
2.课程设计的任务及要求1)基本要求:(1)学习Matlab与Simulink仿真软件的使用;(2)对PCM,DPCM,ΔM编码与解码各功能模块的工作原理进行分析;(3)提出各种编码与解码电路的设计方案,选用合适的模块;(4)对所设计系统进行仿真;(5)并对仿真结果进行分析。
a. 采样定理的原理仿真b. PCM编码与解码c. DPCM编码与解码;增量调制(至少选做一种)2)创新要求:3)课程设计论文编写要求(1)要按照书稿的规格打印誊写毕业论文(2)论文包括目录、绪论、正文、小结、参考文献、谢辞、附录等(3)毕业论文装订按学校的统一要求完成4)答辩标准:(1)完成原理分析(20分)(2)系统方案选择(30分)(3)仿真结果分析(30分)(4)论文写作(20分)5)参考文献:(1)王俊峰.《通信原理MATLAB仿真教程》人民邮电出版社第1版 .2010.11.1 (2)赵静.《基于MATLAB的通信系统仿真》北京航空航天大学出版社6)课程设计进度安排内容天数地点构思及收集资料 2 图书馆仿真 5 实验室撰写论文 3 实验室学生签名:2017年1月3日课程设计(论文)评审意见(1)完成原理分析(20分):优()、良()、中()、一般()、差();(2)系统方案选择(30分):优()、良()、中()、一般()、差();(3)仿真结果分析(30分):优()、良()、中()、一般()、差();(4)论文写作(20分):优()、良()、中()、一般()、差();(5)格式规范性及考勤是否降等级:是()、否()评阅人:职称:副教授2017年1月13日目录摘要 (I)Abstract............................................................................................................................................................... I I1 绪论 (1)2 PCM脉冲编码原理 (2)2.1 模拟信号的抽样及频谱分析 (2)2.1.1 信号的采样 (2)2.1.2 抽样定理 (2)2.1.3 采样信号的频谱分析 (3)2.2 量化 (3)2.2.1 量化的定义 (3)2.2.2 量化的分类 (4)2.2.3 MATLAB的A律13折线量化 (10)2.3 PCM编码 (10)2.3.1 编码的定义 (10)2.3.2 码型的选择 (11)2.3.3 PCM脉冲编码的原理 (11)3 PCM的MA TLAB实现 (13)3.1 PCM抽样的MATLAB实现 (13)3.2 PCM量化的MATLAB实现 (16)3.2.1 PCM均匀量化的MATLAB实现 (16)3.2.2 PCM A律非均匀量化的MATLAB实现 (18)3.3 PCM A律13折线编码的MATLAB实现 (20)4结果分析及总结 (23)参考文献 (24)。
Matlab的应用-论文.docx

MATLAB在控制系统中的应用结课论文所在学院:信息工程学院专业名称:自动化10-3学生姓名:王思嘉学号代码: 1005130315指导教师:崔新忠MATLAB在控制系统中的应用1 MATLAB简介MATLAB是Mathworks公司开发的一种集数值计算、符号计算和图形可视化三大基本功能于一体的功能强大、操作简单的优秀工程计算应用软件。
MATLAB不仅可以处理代数问题和数值分析问题,而且还具有强大的图形处理及仿真模拟等功能。
从而能够很好的帮助工程师及科学家解决实际的技术问题。
MATLAB的含义是矩阵实验室(Matrix Laboratory),最初主要用于方便矩阵的存取,其基本元素是无需定义维数的矩阵。
经过十几年的扩充和完善,现已发展成为包含大量实用工具箱(Toolbox)的综合应用软件,不仅成为线性代数课程的标准工具,而且适合具有不同专业研究方向及工程应用需求的用户使用。
MATLAB最重要的特点是易于扩展。
它允许用户自行建立完成指定功能的扩展MATLAB函数(称为M文件),从而构成适合于其它领域的工具箱,大大扩展了MATLAB的应用范围。
目前,MATLAB已成为国际控制界最流行的软件,控制界很多学者将自己擅长的CAD方法用MATLAB加以实现,出现了大量的MATLAB配套工具箱,如控制系统工具箱(control systems toolbox),系统识别工具箱(system identification toolbox),鲁棒控制工具箱(robust control toolbox),信号处理工具箱(signal processing toolbox)以及仿真环境SIMULINK等。
2 MATLAB在控制系统中的应用1.稳定性分析模块:包含系统的稳定性的判断和显示闭环系统所有的特征根,很直观地显示系统的稳定性判断是否正确,快捷地表示已知系统的稳定性。
2.时域分析响应模块:包括了一阶系统、典型二阶系统、任意阶系统三个主要界面,可以通过此界面绘制时域的响应曲线并且计算相关参数。
运用MATLAB软件进行潮流计算论文

摘要本文运用MATLAB软件进行潮流计算,对给定题目进行分析计算,再应用DDRTS软件,构建系统图进行仿真,最终得到合理的系统潮流。
潮流计算是电力系统最基本最常用的计算。
根据系统给定的运行条件,网络接线及元件参数,通过潮流计算可以确定各母线的电压幅值和相角,各元件流过的功率,整个系统的功率损耗。
潮流计算是实现电力系统安全经济发供电的必要手段和重要工作环节。
因此,潮流计算在电力系统的规划计算,生产运行,调度管理及科学计算中都有着广泛的应用。
首先,画出系统的等效电路图,在计算出各元件参数的基础上,应用牛顿—拉夫逊Newton-Raphson法以及MATLAB软件进行计算对给定系统图进行了四种不同负荷下的潮流计算,经过调节均得到符合电压限制及功率限制的潮流分布。
其次,牛顿—拉夫逊Newton-Raphson法具有较好的收敛性,上述计算过程经过四到五次迭代后均能收敛。
根据运算结果,分析各支路损耗和系统总损耗。
最后,应用DDRTS软件,构建系统图,对给定负荷重新进行分析,潮流计算后的结果也能满足相应的参数要求。
关键词:牛顿-拉夫逊法MATLAB DDRTS 潮流计算目录1.摘要 (2)2.题目原始资料 (2)3.题目分析 (5)4.题目求解 (6)1)根据题意要求画出等值电路 (6)2)读程序画出拉夫逊法的流程图 (7)3)变电所负荷为题目所给数据进行求解 (8)4)编写程序并运行 (10)5)具体调压调损耗过程 (10)1.改变变压器变比调压 (10)2.改变发电机机端电压调压 (12)3.负荷按照一定比例变化的潮流计算分析 (15)4.轮流断开支路双回线中的一条的潮流计算 (19)5.仿真并比较 (26)6.设计心得 (28)7.参考文献 (29)一、 题目原始资料:1.系统图:两个发电厂分别通过变压器和输电线路与四个变电所相连。
变电所1变电所2母线2、发电厂资料:母线1和2为发电厂高压母线,发电厂一总装机容量为(300MW ),母线3为机压母线,机压母线上装机容量为(100MW),最大负荷和最小负荷分别为50MW和20MW;发电厂二总装机容量为(200MW )。
基于matlab gui的控制系统界面设计毕业设计论文

基于MATLAB GUI的控制系统界面设计摘要:MATLAB语言是一种十分有效的工具,能容易地解决在系统仿真及控制系统设计领域的教学与研究中遇到的问题,它可以将使用者从频繁的底层编程中解放出来,把有限的宝贵时间更多地华仔解决科学问题上。
MATLABA GUI是MATLAB人际交互界面。
由于GUI本身提供了windows基本控件的支持,并且具有良好的时间驱动机制,同时提供了MATLAB数学库的接口,所以GUI对于控制系统仿真的平台设计显得十分合适。
GUI对于每个用户窗口生成.fig和.m 文件。
前者负责界面的设计信息,后者负责后台代码的设计。
本文界面设计主要基于MATLAB GUI平台,结合控制系统基础理论和MATLAB控制系统工具箱,实现了用于控制系统界面的设计。
主要包括:进行常规控制环节(比如PID)的图形界面设计,能够在已知传输函数的情况下,输出常用响应曲线。
关键词:控制系统;MATLAB GUI;计算机设计Control system based on MATLAB GUI interface designAbstract: MATLAB language is a very effective tool,and can be easily resolved in the system simulation and control system of teaching in the field of computer-aided design and research problems,it could be the bottom of the user from tedious programming liberate the limted spend more valuable time to solve scientific problems. The MATLAB GUI is the interative interface.As the GUI itself provides the basic control windows support,and has a good mechanism for event-driven,while providing the MATLAB Math Library interface,the GUI for control system simulation platform for the design of it is suitable. GUI window generated for each user.Figand .M file. The former is responsible for the design of the interfaceinformation,which is responsible for the design of the background code.Research done in this article is mainly based on MATLAB GUI platform,the basis of combination of control syetem theory and MATLAB Control System Toolbox,the realization of control systems for computer-aided analysis and design software.Mainly includes:routine control links,such as PID,graphical interface design,can in the known transfer function of the case,the output respnonse curve is commonly used.Key words: Control System;MATLAB GUI;Computer design目录1 概述 (1)1.1 本文研究的目的以及意义 (1)1.2 已了解的本课题国内外研究现状 (1)1.3 本课题研究内容 (3)2 控制系统与MATLAB语言 (3)2.1 控制系统理论基础 (3)2.1.1 控制系统的古典理论与现代理论 (3)2.1.2 控制系统理论的基本内容 (4)2.2 MATLAB语言与控制系统工具箱 (4)2.2.1 MATLAB软件介绍 (5)2.2.2 控制系统工具箱介绍 (7)3 MATLAB简介及应用 (9)3.1 MATLAB GUI (9)3.2 图形用户界面设计工具的启动 (10)3.2.1图形用户界面设计工具的启动方式 (10)3.2.2 菜单方式 (10)3.2.3 图形用户界面设计窗口 (13)3.3 图形用户界面开发环境(GUIDE) (14)3.4 控件对象及属性 (16)3.5 菜单设计 (18)3.5.1 建立用户菜单 (18)3.5.2 菜单对象常用属性 (18)3.5.3 快捷菜单 (18)3.5.4 对话框设计 (19)3.5.5 公共对话框 (19)3.6 GUI程序设计 (19)4 GUI控制系统界面 (20)4.1 GUI控制系统界面设计 (20)4.1.1 具体设计步骤 (20)4.2 具体实现过程 (23)4.2.1 运行效果 (23)4.2.2 实现代码 (24)[参考文献] (25)附录 (26)谢辞 (29)1 概述1.1 本文研究的目的以及意义自动控制原理是自动控制专业和自动化专业的主要课程之一[3],是研究自动控制技术的基础理论课,是必修的专业基础课程。
毕业设计(论文)基于matlab的数字基带通信系统仿真
基于matlab的数字基带通信系统仿真1.课程设计的目的(1)增加对仿真软件的认识,学会对各种软件的操作和使用方法(2)加深理解数字基带通信系统的概念(3)初步掌握系统的设计方法,培养独立工作能力2.设计方案论证2.1数字基带传输系统在数字传输系统中,其传输的对象通常是二进制数字信号,它可能是来自计算机、电传打字机或其它数字设备的各种数字脉冲,也可能是来自数字终端的脉冲编码调制(PCM)信号。
这些二进制数字信号的频带范围通常从直流和低频开始,直到某一频率m f ,我们称这种信号为数字基带信号。
在某些有线信道中,特别是在传输距离不太远的情况下,数字基带信号可以不经过调制和解调过程在信道中直接传送,这种不使用调制和解调设备而直接传输基带信号的通信系统,我们称它为基带传输系统。
而在另外一些信道,特别是无线信道和光信道中,数字基带信号则必须经过调制过程,将信号频谱搬移到高频处才能在信道中传输,相应地,在接收端必须经过解调过程,才能恢复数字基带信号。
我们把这种包括了调制和解调过程的传输系统称为数字载波传输系统。
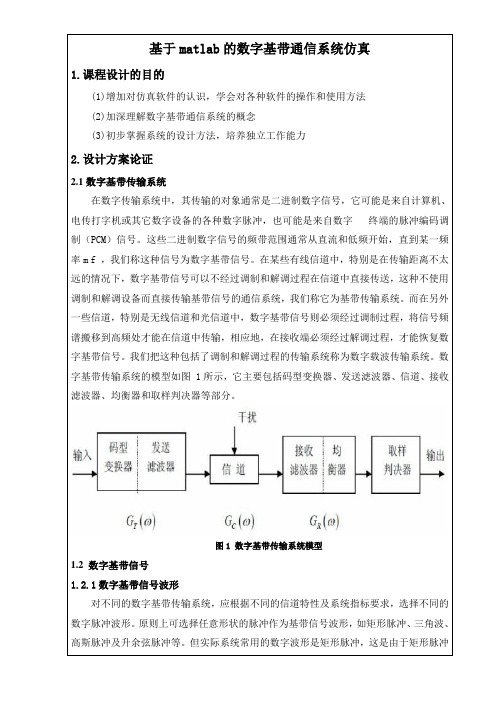
数字基带传输系统的模型如图 1所示,它主要包括码型变换器、发送滤波器、信道、接收滤波器、均衡器和取样判决器等部分。
图1 数字基带传输系统模型1.2 数字基带信号1.2.1数字基带信号波形对不同的数字基带传输系统,应根据不同的信道特性及系统指标要求,选择不同的数字脉冲波形。
原则上可选择任意形状的脉冲作为基带信号波形,如矩形脉冲、三角波、高斯脉冲及升余弦脉冲等。
但实际系统常用的数字波形是矩形脉冲,这是由于矩形脉冲纤数字传输系统中的线路传输码型。
此外,CMI 码和曼彻斯特码一样都是将一位二进制码用一组两位二进制码表示,因此称其为1B2B 码。
(5)4B/3T 码4B/3T 码是1B/1T 码的改进型它把4 个二进制码元变换为3个三进制码元。
显然,在相同信息速率的条件下,4B/3T 码的码元传输速率要比1B/1T 码的低,因而提高了系统的传输效率。
基于MATLAB的线性分组码课程设计论文
目录TOC \o "1-3" \h \u HYPERLINK \l _Toc6750 前言.... PAGEREF _Toc6750 1HYPERLINK \l _Toc26804 工程概况................ PAGEREF _Toc26804 1HYPERLINK \l _Toc14622 正文.................... PAGEREF _Toc14622 2 HYPERLINK \l _Toc4430 3.1设计的目的和意义... PAGEREF _Toc4430 2HYPERLINK \l _Toc31075 3.1.1设计的目的. PAGEREF _Toc31075 2HYPERLINK \l _Toc18535 3.1.2设计的意义. PAGEREF _Toc18535 2 HYPERLINK \l _Toc31236 3.2 线性分组码的编码与译码原理 PAGEREF _Toc31236 2 HYPERLINK \l _Toc11233 3.2.1线性分组码的编码原理 PAGEREF _Toc11233 2HYPERLINK \l _Toc6682 3.2.2 线性分组码的译码原理 PAGEREF _Toc6682 3 HYPERLINK \l _Toc31791 3.3 2PSK的调制与解调原理 PAGEREF _Toc31791 4 HYPERLINK \l _Toc26402 3.3.1调制的原理. PAGEREF _Toc26402 4HYPERLINK \l _Toc27747 3.3.2解调的原理. PAGEREF _Toc27747 4 HYPERLINK \l _Toc23880 3.4 不同信噪比是的测试结果 PAGEREF _Toc23880 5 HYPERLINK \l _Toc20433 3.4.1 信噪比为1时 PAGEREF _Toc20433 5HYPERLINK \l _Toc4861 3.4.2 信噪比为5时. PAGEREF _Toc4861 5HYPERLINK \l _Toc31183 3.4.3 信噪比为10时 PAGEREF _Toc31183 6HYPERLINK \l _Toc29253 3.4.4译码时当检测到错码结果如图 PAGEREF _Toc29253 6 HYPERLINK \l _Toc2127 致谢...................... PAGEREF _Toc2127 7HYPERLINK \l _Toc30045 参考文献................ PAGEREF _Toc30045 7前言近年来,随着计算机、卫星通信及高速数据网的飞速发展,数据的交换、数据的交换理和存储技术得到了广泛的应用,人们对数据传输和存储系统的可靠性提出了越来越高的要求。
毕业设计(论文)-信号与系统中的典型问题的matlab分析[管理资料]
2011届学士学位论文信号与系统中典型问题的MATLAB分析系别: 电子信息系专业: 电子信息科学与技术学号:姓名:指导教师:指导教师职称: 教授2011年4月30日信号与系统中典型问题的MATLAB分析摘要从信号与系统课程的特点出发,结合MATLAB软件优势,针对实例进行分析。
主要从连续信号、离散信号两方面应用MATLAB软件进行仿真和分析。
分别对连续信号和离散信号中线性时不变(LTI)系统信号分析,应用MATLAB软件进行仿真和分析。
对连续时间信号和离散时间信号的线性时间不变(LTI)系统的变换域,卷积和采样定理进行了模拟。
实例中运用了连续模块库、离散模块库等。
通过实例表明了MATLAB软件的便捷性,可以提高工作效率。
实践证明,采用MATLAB软件进行辅助分析可以我们对知识点的理解更深入更透彻。
关键词MATLAB仿真;时域分析;频域分析;卷积;序列卷和;冲激响应;阶跃响应;The Applied Research of Signal ProcessingBased on MATLABAbstract we give an overview of the examples from the characteristics of signal and system course, combining with MATLAB software advantages. The main idea is that MATLAB simulation and analysis software were applied in the continuous-time signals and discrete-time signals. In continuous-time signals and discrete-time signals the response signal of linear time invariant(LTI) system and its analysis of the transform domain and convolution and Sampling theorem were simulated. The examples used the continuous and discrete blocks library and communication toolbox, etc. Some examples show that processing signals can bring us great convenience and high efficiency. Practice has proved, using MATLAB software were aided analysis on knowledge points we can understand deeper and more thoroughly.Key-words MATLAB; the Time-domain Analysis;Frequency domain analysis;convolution ;Sequence convolution ;Impulse response ;Order step-response目录1引言 (1)2 MATLAB软件介绍 (2)3 MATLAB对连续时间信号的分析 (3)MATLAB仿真线性时不变(LTI)系统响应的信号表示 (3)MATLAB对连续信号变换域的分析 (4)连续时间信号的卷积计算及MATLAB的实现 (5)连续时间系统抽样定理的验证 (6)84 MATLAB对离散时间信号的分析 (10)离散系统的单位样值响应 (11)离散系统的变换域分析 (12)离散时间信号的卷积计算 (13)结论 (15)参考文献 (16)致谢 (17)附录一 (18)附录二 (19)附录三 (21)1 引言随着软件的发展,为仿真实验提供了另一思路,MATLAB软件具有强大的数值计算和矩阵处理功能。
MATLAB论文 12010245346 李星辰解读
《MATLAB语言》课程论文MATLAB在研究物体振动方面的应用姓名:李星辰学号:12010245346专业:电子信息工程班级:电子信息工程指导老师:汤全武学院:物理电气信息学院完成日期:2011-12-26MATLAB在研究物体振动方面的应用(李星辰电子信息工程12010245346)[摘要] 物体振动这样一个看似简单但又包含着很多复杂计算的运动中,在人为的计算时是很难精确的实现,而通过MATLAB可以处理诸多科学中的许多问题,利用它来研究物理学中的机械振动,不仅特别方便还非常有效。
[关键字]Matlab、物体振动、应用一、问题的提出从广义上说振动是指描述系统状态的参量(如位移、电压)在其基准值上下交替变化的过程。
狭义的指机械振动,即力学系统中的振动。
电磁振动习惯上称为振荡。
力学系统能维持振动,必须具有弹性和惯性。
由于弹性,系统偏离其平衡位置时,会产生回复力,促使系统返回原来位置;由于惯性,系统在返回平衡位置的过程中积累了动能,从而使系统越过平衡位置向另一侧运动。
正是由于弹性和惯性的相互影响,才造成系统的振动。
按系统运动自由度分,有单自由度系统振动(如钟摆的振动)和多自由度系统振动。
有限多自由度系统与离散系统相对应,其振动由常微分方程描述;无限多自由度系统与连续系统(如杆、梁、板、壳等)相对应,其振动由偏微分方程描述。
方程中不显含时间的系统称自治系统;显含时间的称非自治系统。
按系统受力情况分,有自由振动、衰减振动和受迫振动。
按弹性力和阻尼力性质分,有线性振动和非线性振动。
振动又可分为确定性振动和随机振动,后者无确定性规律,如车辆行进中的颠簸。
振动是自然界和工程界常见的现象。
振动的消极方面是:影响仪器设备功能,降低机械设备的工作精度,加剧构件磨损,甚至引起结构疲劳破坏;振动的积极方面是:有许多需利用振动的设备和工艺(如振动传输、振动研磨、振动沉桩等)。
振动分析的基本任务是讨论系统的激励(即输入,指系统的外来扰动,又称干扰)、响应(即输出,指系统受激励后的反应)和系统动态特性(或物理参数)三者之间的关系。
MATLAB 结课小论文
基于MATLAB的控制系统分析摘要MATLAB具有强大的图形处理功能、符号运算功能和数值计算功能。
MATLAB 工具几乎涵盖了整个科学技术运算领域。
其中系统的仿真(Simulink)工具箱是从底层开发的一个完整的仿真环境和图形界面。
在这个环境中,用户可以完成面向框图系统仿真的全部过程,并且更加直观和准确地达到仿真的目标。
此次,以数字电路中的时序逻辑电路为线索来学习Simulink,了解了许多数字电路中常用模块的使用方法.时序电路中除具有逻辑运算功能的组合电路外,还必须有能够记忆电路状态的存储单元或延迟单元,这些存储或延迟单元主要由本次设计所用到的触发器来实现。
D触发器、RS触发器、JK触发器等这些时序逻辑电路中常用的器件在Simulink中都有相应的仿真模块,除此之外,用户还可以自行设计封装模块来一步一步完成更大的电路系统,实现更强大的逻辑功能。
关键词:MATLAB、Simulink、时序电路1 Matlab内容简介MATLAB拥有了更丰富的数据类型和结构,更好的面向对象的快速精美的图形界面,更多的数学和数据分析资源,MATLAB工具几乎涵盖了整个科学技术运算领域。
在大部分大学里,应用代数、数理统计、自动控制、数字信号处理、模拟与数字通信、时间序列分析、动态系统仿真等课程的教材都把MATLAB作为必不可少的内容。
在国际学术界,MATLAB被确认为最准确可靠的科学计算标准软件,在许多国际一流的学术刊物上都可以看到MATLAB在各个领域里的应用。
2系统的稳定性分析稳定是控制系统的重要性能,也是系统能够正常运行的首要条件。
在分析控制系统时,首先遇到的问题就是系统的稳定性。
对线性系统来说,如果一个系统的所有几点都位于左半s 平面,则该系统是稳定的。
对于离散系统来说,如果一个系统的全部极点都在单位圆内,则该系统可以被认为是稳定的。
由此可见,线性系统的稳定性完全取决于系统的极点在根平面上的位置。
判断一个线性系统稳定性的一种最有效的方法是直接求出系统所用的极点,然后根据极点的分布情况来确定系统的稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab课程论文要求一、时间安排(一)2016年X月X日之前必须提交纸质版(时间待定,另行通知,尽早完成,以免影响其他科目的复习考试)。
(二)电子版统一写清楚学号(学号在前)+姓名+专业发送给学委。
打包文件夹发送给我,不接受单独发给我的。
二、选题(一)选题要紧密结合本学科专业的教学科研和MATLAB,符合专业培养目标的要求。
(二)论文一般为一人一题,严格控制与往年的重复率。
三、成绩评定平时成绩(0.3)+课程论文(0.7)=最终成绩。
四、论文写作规范要求(一)封面:封面要使用统一格式。
(二)目录:“目录”两字黑体小二号、居中,“目录”两字间空四格、与正文空一行。
各部分名为宋体小四号字,各小部分名间有缩进。
(三)题目:题目要对论文的内容有高度的概括性,简明、易读,字数应在20个字以内,论文题目用黑体三号字。
(四)署名:论文署名的顺序为:专业学号学生姓名指导老师姓名,用宋体小四号字。
可用以下表示:专业:XXXXX 学号:XXXXX 学生姓名:XXXXX 指导老师姓名:XXXX (五)内容摘要:中文内容摘应简要说明所研究的内容、目的、实验方法、主要成果和特色,一般为200-300字,用宋体小四号字,其中“内容摘要”四个字加粗。
(六)关键词:一般为3-6个,用分号隔开,用宋体小四号字,其中“关键词”三个字加粗。
(七)正文:正文要符合一般学术论文的写作规范,统一用宋体小四号字,行距为1.5倍。
字数一般要求为不得少于5000字。
内容要理论联系实际,涉及到他人的观点、统计数据或计算公式的要注明出处(引注),涉及计算内容的数据要求准确。
标题序号从大到小的顺序为:“1”“1.1”“1.1.1”……。
(八)注释:论文中所引用文献按学术论文规范注明出处,注序要与文中提及的序号一致。
注释方法参见参考文献顺序。
(九)参考文献:论文后要标注参考文献和附录,参考文献按照以下格式排列:1.专著、论文集、学位论文、报告[序号]主要责任者.文献题名[文献类型标识].出版地:出版者,出版年.起止页码。
[1]刘国钧,陈绍业,王凤.图书馆目录[M].北京:高等教育出版社,1957.10-12.[2]辛希孟.信息技术与信息服务国际研讨会论文集:A集[C].北京:中国社会科学出版社,1994.12-13.[3] 查正军.《基于机器学习方法的视觉信息标注研究》.[D].北京.中国科技大学.2010年.32-352.期刊文章[序号]主要责任者.文献题名[J].刊名,年卷(期):起止页码.[1]何龄修.读顾城《南明史》[J].中国史研究,1998(3):12-13.[2]金显贸,王昌长,王忠东等.一种用于在线检测局部放电的数字滤波技术 [J].清华大学学报(自然科学版),1993(4):12-13.3.电子文献[序号]主要责任者.电子文献题名[电子文献及载体类型标识] .电子文献的出处或可获得地址,发表或更新日期/引用日期(任选).[1]王明亮.关于中国学术期刊标准化数据库系统工程的进展[EB/OL]. /pub/wml.txt/980810-2.html,1998-08-16/1998-10-04.[2]万锦坤.中国大学学报论文文摘(1983-1993).英文版[DB/CD].北京:中国大百科全书出版社,1996.(十)图表、附注、公式:图表、附注、公式一律采用阿拉伯数字连续编号。
图序及图名置于图的下方;表序及表名置于表的上方;用宋体五号字。
论文中的公式编号,用圆括弧括起写在右边行末,其间不加虚线。
MATLAB课程论文(设计)( 届)论文(设计)题目:学院:数学与统计学院专业:学号:姓名:分数:目录1 引言 (6)1.1信赖域算法 (6)1.2三次自适应算法 (7)1.3非单调线性搜索 (8)2 加权平均的非单调三次自适应算法 (9)3 加权平均的非单调三次自适应算法收敛 (10)参考文献 (17)一种加权平均的非单调三次自适应算法专业:XXXXXX 学号:XXXXXX 学生姓名:XXXX 指导老师:XXXX摘要 这篇文章提出了一种非单调三次自适应算法. 不同于传统的三次自适应算法, 本文算法XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX 下降量引入了函数加权平均值, 即表达式为()k k k C f x s -+. 在适当条件下,证明算法的全局收敛性.关键词 无约束优化问题; 三次模型; 非单调自适应; 全局收敛性1 引言本文考虑无约束优化问题:min (),n f x x R ∈, (1.1) 其中()f x :n R R →是二次连续可微函数.1.1 信赖域算法解此问题一般都采用二次模型逼近()f x , 信赖域算法和线性搜索是解决无约束优化问题两种最常用的方法. 信赖域方法是一类较新的方法, 对它的研究开始于 Powell 1970 年的工作, 他提出了一个求解无约束优化问题的算法, 该算法的基本思想是通过求解近似的二次函数在信赖域中的极小点的方法来求最优化问题的解, 即:对于当前的迭代点k x , 给定一个信赖域半径0k ∆>, 然后在以k x 为中心k ∆为半径的小邻域内, 构造一个逼近目标函数的模型1min ()2n T T k k k s R q s g s s B s ∈=+, ..s t s ≤∆.这个模型称为信赖域子问题, 求解子问题得到试探步k s , 然后利用某一评价函数即目标函数的实际下降量与预测下降量的比值()()(0)()k k k k k k k f x f x s r q q s -+=- 来决定是否接受该试探步以及确定下一次迭代的信赖域半径, 如果试探步被接受, 则1k k k x x d +=+, 否则1k k x x +≈; 信赖域半径的大小通过迭代逐步调节, 粗略地说, 如果当前迭代模型较好地逼近原问题, 则信赖域半径可扩大, 否则将缩小. 下面将给出信赖域算法的基本步骤.信赖域算法:步1:取初始点(0)n x R ∈, 010,(0,),[0,)4η--∆>∆∈∆∈,精度0ε>. 令0k =. 步2:若()()k f x ε∇≤, 则算法终止.得到问题的解()k x . 否则转步2.步3:由信赖域子问题()k q s 计算比值k r若{}3,min 24k+1k 则令=,k r ->∆∆∆. 若11,42k+1k 则令=k r η<<∆∆. 若13,44k+1k 则令=k r ≤<∆∆. 步4:若k r η≤, 令(1)()k k x x +=, 1k k =+, 转步2.否则令(1)()()k k k x x s +=+, 1k k =+.1.2 三次自适应算法该算法用三次模型作为目标函数的近似. :n f R R →是无约束优化问题的一个连续可微函数, 找到f 的一个局部极小值, 则k x 是当前最好的估计. 假设目标函数的Hessian 矩阵在n R 是全局Lipschitz 连续的. 得到101()()()()(1)[()()]2TT T k k k k k k f x s f x s g x s H x s s H x s H x sd τττ+=+++-+-⎰ 3211()()()()26T T C k k k k f x s g x s H x s L s m s ≤+++=, 其中n s R ∈,定义()()x g x f x =∇, ()()xx H x f x =∇. 只要()(0)()C c k k k k m s m f x <=.(1.2), 新的迭代点1k k k x x s +=+使得函数()f x 下降. 通过()C k m s 的极小值找到步长k s .文献[1]中的作者整合这些知识得到一个渐进的, 有效的数值算法框架. 在较弱的假设条件下, 可以证明这种算法是全局收敛和渐进收敛的. 首先, 降低要求去求一个全局的最小值, 然而一个局部的极小值是满足目标函数的复杂条件的. 然后, 用一个动态的正参数k σ代替(1.1)中的Lipschitz 常量12L , 不再要求()H x 是全局的, 甚至是局部的Lipschitz 连续. 最后用一个对称近似矩阵k B 代替在近似函数的每一次迭代中的Hessian 矩阵. 这就得到 311()()()23T T k k k k k m s f x s g x s B s s σ=+++. (1.3) 在算法的每一次迭代中, 用三次模型(近似函数)代替目标函数f .1.3 非单调线性搜索在20世纪80年代, Grippo 等人在牛顿算法提中出一种非单调线性搜索[6], 其中步长k s 满足下面的条件0()max ()()kT k k k k j k k k j m f x s d f x s f x d β-≤≤+≤+∇, 其中(0,1)β∈, {}10min 1,k k m m M -≤≤+, M 是一个非负整数. 然而, Grippo 等人提出非单调技术还是有一定不足的地方. 为了克服这不足, Zhang 和Hager 提出的另外一种非单调线性搜索. 这种新的线性搜索用函数值的加权平均代替函数的最大值, 具体表达即()()T k k k k k k k f x s d C s f x d β+≤+∇.其中 111(),0(())/,1k k k k k k k f x k C Q C f x Q k γ---⎧=⎪=⎨⎪+≥⎩ (1.4)11,01,1k K k Q Q k γ-⎧=⎪=⎨+≥⎪⎩ (1.5)1min max [,]k γγγ-∈, min [0,1)γ∈和max min [,1]γγ∈, 其中min max ,γγ是两个选择参数.从(1.4)和(1.5), 知道k C 是由函数值01(),(),...,()k f x f x f x 组成的凸组合. 所以可知k C 是连续函数值的一个特殊加权平均. 在这个算法中, 函数值序列{}k f 是非单调的, {}k C 序列是非增的.本文将给出一类新的非单调自适应算法, 进一步丰富自适应算法的研究. 本文将三次算法和基于函数值加权平均的线性搜索方法结合起来. 这种算法跟三次算法的主要不同点是预测下降量. 在本文中, 实际下降量的表达式为()k k k C f x s -+. 接下来, 本文将给出具体的算法步骤, 以及算法收敛性的证明.2 加权平均的非单调三次自适应算法先介绍一些本文出现的基本的符号. 范数指的是在n R 上的欧氏范数. 用k f 表示()k f x , 用k g 表示()k g x , 其中()n k g x R ∈是函数f 在k x 上的一阶梯度,n n k B R ⨯∈是函数f 在k x 处的Hessian 矩阵或者其近似.算法步骤如下:步0:取初始点0x , 211a a ≥>, 2110b b >≥>和00σ>, 当0,1,...k =. 步1:算出一个步长k s , 使得()()c k k k k m s m s ≤.(2.1) 其中Cauchy 点c c k k k s g α=-, arg c k α= min ()k k Rm g αα∈-. (2.2) 步2:计算()k k f x s +, 并求实际下降量与预测下降量的比值 ()()()k k k k k k k C f x s f x m s ρ-+=-, (2.3) 其中 111(),0(())/,1k k k k k k k f x k C Q C f x Q k γ---⎧=⎪=⎨⎪+≥⎩,11,01,1k K k Q Q k γ-⎧=⎪=⎨+≥⎪⎩. 步3:令 11,,如果其他k k k k k x s b x x ρ+⎧+>⎪⎨⎪⎩. (2.4)步4:校正1k σ+, 2111212[0,],[,],[,],如果(非常成功)如果(成功)其他(不成功)k k k k k k k kb a b b a a σρσσσρσσ+⎧>⎪⎪∈≤≤⎨⎪⎪⎩ . (2.5) 给出函数f 的一个临界估计值k x , 求出一个满足条件(2.1)的步长k s . 求出近似函数(1.3)的一个近似最小值作为步长k s , k B 是目标函数f 的Hessian 矩阵的近似. 其中比值k ρ从某种角度反映了三次函数()k k m s 与目标函数()k k f x s +的近似程度. 若k ρ接近于1, 则认为三次函数()k k m s 与目标函数()k k f x s +的近似程度很好. 反之, 若k ρ离1较远, 可认为()k k m s 在定义域上与目标函数()k k f x s +的近似程度不好. 所以, 可用k ρ与1的近似程度作为1k σ+是否合适的准则.常数12,(0,1)b b ∈满足2110b b >≥>. 若2k b ρ>, 我们可认为()k k m s 在定义域中是f 的一个很好的近似, 或者说得到一个非常成功的迭代点1k x +=k k x s +. 此时, k m 有可能在更小的区域内也是f 的一个很好的近似, 因此, 我们可令1k k σσ+<. 若12k b b ρ≤≤, 即k m 是f 的一个好的近似, 或者说得到一个好的迭代点1k x +=k k x s +. 此时可以增大k σ, 令1k k σσ+>(为了在下一次迭代中得到一个更成功的点). 若b ρ≤, 即k m 在定义域中跟f 的近似程度不好, 或者说1k x +是一个不成功的迭代点; 说明k σ太小, 此时需要增大k σ, 即令11k k a σσ+>. 在上面的基础上, 我们给出算法收敛性的证明.3 加权平均的非单调三次自适应算法收敛在这部分, 将证明算法的全局收敛, 在证明之前, 先给出下列的一些假设. 假设1 集合{}0|()n A x R f x f =∈≤是有界的.假设2 ()f x 的一阶梯度函数()g x 在集合A 上是Lipschitz 连续的. 假设3 对称矩阵k B 是一致有界的,即,0,0k B B B k κκ≤≥≥.为了简单起见, 我们定义两个集合:{}1:k I k b ρ=≥和{}1:k J k b ρ=<.引理3.1 假设步长k s 满足式子(2.1). 当0k ≥时, 则有()()k k k f x m s -()()ck k k f x m s ≥-2kk g B ≥+1k k g B +. (3.1)证明 由(1.2)()()ck k k k m s m s ≤, 可得到()()()()ck k k k k k f x m s f x m s -≥-.对任意0α≥, 由Cauchy-Schwarz 不等式得到()()()()c k k k k k k m s f x m g f x α-≤--23231123Tkk k k k g g B g g ααα=-++ {}2211123k k k k g B g ααασ≤-++. (3.2)要使()()ck k m s f x ≤成立,即要求2111023k k k B g αασ-++≤和0α≥成立,所以有_[0,],k αα∈其中_3122kkk B g ασ⎡=-⎢⎣ .将分子有理化, 可以把_α化成下面的形式1_122k B α-⎡=⎢⎣. 令1k k B θ-⎤=+⎦ (3.3)112max(22k k B B ≤,k B ≤+, 和1,2k k B B ≤+ 所以得到_0k k θα<≤. 用k θ代入(3.2)中的不等式, 得到()()ck k k m s f x -≤2111023k k k k k B g θθσ⎛⎫⨯-++≤ ⎪⎝⎭. (3.4)从(3.3)k θ的定义中知道, 1k k B θ≤和21k k k g θσ≤, 所以(3.4)中括号里的表达式的上界是16-. 可知引理3.1成立.引理3.2 当{}k x 是由算法产生. 则对所有k , 有下面的不等式成立11k k k f C C ++≤≤ . (3.5) 证明 首先证明当k I ∈时, (3.5)式成立. 即对任意k I ∈有11k k k f C C ++≤≤.(3.6) 对k I ∈, 由1k b ρ≥, (2.3)和(3.1)得到11k k k k g f C B +≤-+. (3.7)又由(1.4), (1.5)和(3.7)得到111k k k k k k Q C f C Q γ++++=1k+≤1kkkgCB=+. (3.8)从(1.4)和(1.5)知, 如果0kγ≠则有111k kk kk kf CC CQγ+++--=. (3.9)如果0kγ=, 则有11k kC f++=. (3.10)由(3.8)—(3.10), 可知(3.6)成立.接下来, 我们证明当k J∈时, (3.5)成立. 由算法步3中的(2.4)对k J∈,我们得1k kx x+=和1k kf f+=. 我们先证明11k kf C++≤, 先考虑两种情形:情形1:1k I-∈. 由(3.6)得到k kf C≤. 又由(1.4), (1.5)和1k kf f+=得到111k k k kkkQ f fCQγ++++≥111k k k kkQ f fQγ++++=1kf+=. (3.11)情形2:1k J-∈. 在这种情况下, 令{}|1,K i i k k i I=<≤-∈. 如果K=∅,由算法的步3可知01,0,1,...,1k j kf f f j k-+===-. 因此, 由(1.4), (1.5)得到11k k kC C f++==. (3.12)又假设K≠∅. 令{}min:m i i K=∈. 则有1,0,1,...,1k j k kf f f j m-+===- . (3.13)从(1.4)得到111,1k k k k k k Q C Q C f k γ--+=+≥. (3.14) 再次运用(1.4)得到1211111000jm m k k k k k k m k m k i k j k i j i Q C f Q C f f γγγ--+--+-+--+===+=∏+∑∏+. (3.15)通过K 和m 的定义, 知k m I -∈, 从(3. 6)得到11k m k m C f -+-+≥. 从(3.13)和(3.15), 又1211111000jm m k k k k k k m k m k i k j k i j i Q C f Q f f f γγγ--+--+-+--+===+≥∏+∑∏+1211000(1)jm m k i k m k i k i j i Q f γγ----+-+====∏+∑∏+11k k Q f ++=. (3.16) 因此, 由(1.4)和(3.16)得到111k k k k k k Q C f C Q γ++++=111k k k Q f Q +++≥1k f += . (3.17) 由(3.11),(3.12)和(3.17), 对任意k J ∈可以得到11k k f C ++≤. (3.18) 如果0k γ≠, 从(3.9)和(3.18)得到11k k k f C C ++≤≤. 如果0k γ=, 由(1.4), (1.5)和k J ∈, 11k k k C f f ++==. 结合1k J -∈和(3.18), 可以得到k k f C ≤. 所以对于任意k J ∈, 11k k k f C C ++≤≤成立.引理3.3 根据假设1, 可知由算法求出的{}k x 序列包含于集合A 中. 引理3.4 如果假设2和假设3成立, {}k x 序列是由算法产生; 并且假设 k g δ≥ (3.19) 对任意k 成立, 其中(0,1)δ∈的一个常数. 则对所有的k , 存在一个正的整数m 使得1k m x ++是一个成功的迭代点.证明 假设存在一个整数k , 使得对任意的m , 1k m x ++是一个不成功的迭代点, 即1k m b ρ+<, 0,1,2,...m = (3.20) 由算法的步3、步4得到1k m k x x ++=, 0,1,2,...m = (3.21)0→, 当m 充分大时, 由假设2, (3.21)和k s ≤,()()(()())k k k m k k k m f x f x s f x m s ++-+--()101[()]2T Tk m k m k m k k m k k m s B s g x ts g x s dt +++++=-+-⎰()kk mkg O B o σ+≤+. (3.22)对充分大的m , 由(3.1), (3.19), (3.21)和(3.22)得到()()1()()k k k m k k k m f x f x s f x m s ++-+-≤-又因为假设3和上面所述得到 ()()lim1()()k k k m m k k k m f x f x s f x m s +→∞+-+=-. (3.23)综上所述, 从(2.3), (3.5)和(3.21)得到()()()k m k k m k m k k k m C f x s f x m s ρ++++-+=-()()()()k k k m k k k m f x f x s f x m s ++-+≥-. (3.24)所以, 当m 充分大时, 1(0,1)b ∈, 由(3.23)和(3.24)得到1k m b ρ+≥.这与(3.20)是矛盾, 所以引理是成立的.定理3.5 如果假设1, 假设2, 假设3成立, {}k x 序列是由算法求得, 则有lim inf 0k k g →∞=. (3.25)证明 假设(3.25)不成立, 设存在一个常数(0,1)α∈, 使得对任意k 有k g ε≥.(3.26) 由(3.26)可以知道k I∞∈∑∞. (3.27)又知道由(2.3), (2.4), (3.1)假设假设3和(3.26)得到1()k k C f x +- 1[()()]k k k b f x m s ≥-1B εκ≥+. (3.28)又{}k C 是非增的序列. 通过假设1, 引理3. 3和函数f 的连续知道{}()k f x 是有下界的, 所以{}k C 是收敛的. 所以得到(3.28)不等式右边的最小值是并且(3.28)不等式左边收敛到0. 所以当k I ∈,k 充分大时得到1()k k C f x +-≥概括所有充分大的迭代点得到00011,,()[()]jjk j k k k k k I k k IC f x C f x ++=∈=∈-=∑-≥∑, (3.29)其中一些迭代下标0k 充分大, 0,j I j k ∈≥. 所以当(3.29)中j →∞时,{}1()j f x +是收敛的.接下来我们证明迭代序列{}k x , 0k ≥是Cauchy 序列. 由(3.27)知, 当,k k I →∞∈时有0. (3.30)又k s k S ≤∈, S 是一个无穷大的集合, 则算法的解{}k x 有下面的关系,当0,0l r ≥≥, l 充分大有111,l r l r l r l k k k k lk l k Ix x x x s +-+-++==∈-≤∑-=∑1,3l r k l k I+-=∈≤∑由式(3.27)知, 当l →∞时上面不等式右边趋于. 所以{}k x 是一个Cauchy 序列, 且对*nx R ∈有, *kx x →, k →∞. (3.31)由(3.26), (3. 30), (3.31)知道S I =. 又集合I 的定义, 我们知道k I ∈是成功的, 即当k 充分大的时没有不成功的迭代点, 又因为[1]1k k σσ+≤,{}k σ, 0k ≥, 是有上界的. 这与(3.26)和(3.30)的k σ→∞是矛盾的, 所以(3.26)不成立. 所以定理3.1是成立的.参考文献[1]Coralia Cartis, Nicholas I.M.Gould, Philippe L.Toint. A daptive cubic regularization methods[J]. Math Program, 2011(127):245-258.[2] Jiangtao Mo, Chunyan Liu, ShicuiYan. A nonmonotone trust region method based on nonincreasing technique of weighted average of the successive function values[J]. Journal of Computational and Applied Mathematics, 2007(209):97-108. [3]陈俊,张纯. 两种非单调信赖域算法的数值比较研究[J]. 南京晓庄学院学报, 2011(6). 18-22.[4]李董辉,童小娇,万中. 数值最优化算法与理论(第二版)[M]. 北京:科学出版社, 2010. 92-100.[5] H.C.Zhang, W.Y.Hager. A nonmonotone line search technique and its application tounconstrained optimization[J]. SIAM,2004(14):1043-1056.[6]L.Grippo, mpariello, S.Lucidi. A nonmonotone line search technique for Newton’s method[J]. SIAM,1986(23):707-716.[7]Y.H.Dai. A nonmonotone conjugate gradient algorithm for unconstrained optimization[J]. J.Systems plex, 2002(15):139-145.[8]J.L.Zhang, X.S..Zhang. A nonmonotone adaptive trust region method and its convergence[J]. Comput Math Appl, 2003 (45):1469-1477.[9]Nesterov Yu. Accelerating the cubic regularization of Newton’s method on convex problems[J]. Math Program, 2008(112):159-181.[10]Weiser M, Deuflhard P Erdmann. Affine conjugate adaptive Newton methods fornonlinear elastomechanics[J]. Optim Methods Softw, 2007(22):413-417.。
