极点配置控制器的设计法则(97)980707
控制系统的极点配置设计法
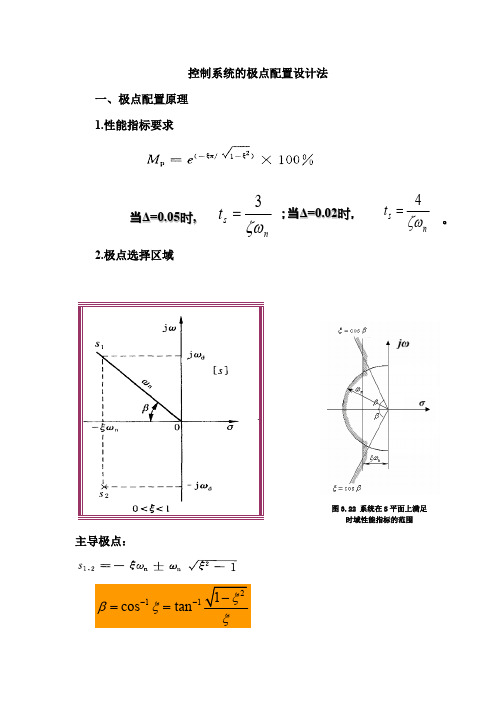
控制系统的极点配置设计法一、极点配置原理1.性能指标要求n s t ζω4=;当Δ=0.02时,。
ns t ζω3= 当Δ=0.05时,2.极点选择区域主导极点:2111cos tan ξβξξ---==3.其它极点配置原则系统传递函数极点在s 平面上的分布如图(a )所示。
极点s 3距虚轴距离不小于共轭复数极点s 1、s 2距虚轴距离的5倍,即(此处,对应于极点s 1、s 2);同时,极点n s s ξω5Re 5Re 13=≥ξn ωs 1、s 2的附近不存在系统的零点。
由以上条件可算出与极点s 3所对应的过渡过程分量的调整时间为1351451s n s t t =⨯≤ξω式中是极点s 1、s 2所对应过渡过程的调整时间。
1s tn x o (t)(a )(b系统极点的位置与阶跃响应的关系图(b )表示图(a )所示的单位阶跃响应函数的分量。
由图可知,由共轭复数极点s 1、s 2确定的分量在该系统的单位阶跃响应函数中起主导作用,即主导极点。
因为它衰减得最慢。
其它远离虚轴的极点s 3、s 4、s 5所对应的单位阶跃响应衰减较快,它们仅在极短时间内产生一定的影响。
因此,对系统过渡过程进行近似分析时。
可以忽略这些分量对系统过渡过程的影响。
二、极点配置实例磁悬浮轴承控制系统设计1.1磁悬浮轴承系统工作原理图1是一个主动控制的磁悬浮轴承系统原理图。
主要由被悬浮转子、传感器、控制器和执行器(包括电磁铁和功率放大器)四大部分组成。
设电磁铁绕组上的电流为I0,它对转子产生的吸力F和转子的重力mg相平衡,转子处于悬浮的平衡位置,这个位置称为参考位置。
(a)(b)图1 磁悬浮轴承系统的工作原理Fig.1 The magnetic suspension bearing system principledrawing假设在参考位置上,转子受到一个向下的扰动,转子就会偏离其参考位置向下运动,此时传感器检测出转子偏离其参考位置的位移,控制器将这一位移信号变换成控制信号,功率放大器又将该控制信号变换成控制电流I0+i,控制电流由I0增加到I0+i,因此,电磁铁的吸力变大了,从而驱动转子返回到原来的平衡位置。
极点配置法设计状态反馈控制器——自动控制原理理论篇

设计算法--适用于用能控标准形表示的SI系统的算法
a0 f1 0 a1 f 2 1
an1 f n n1
f1 0 a0 f2 1 a1
fn n1 an1
举例
例8-21 设系统的状态空间描述为
x(t)
0 6
1 0 5x(t) 1u(t)
y(t) 2 1x(t)
试求:(1)求状态反馈矩阵F使闭环系统有期望 极点s1,2=-3±2j; (2)绘制带有状态反馈控制器的状态变量图
举例----求解过程
解: 0
B 1
0 1 0 1 AB 6 51 5
rankS
rankB
AB
0 1
1 5
2
系统能控。
举例----求解过程
期望闭环系统特征多项式为:
(s s1)(s s2 ) (s 3 2 j)(s 3 2 j) s2 6s 13
设: F f1 f2
s sI A BF
6 f1
SI系统,所以设 F f1 f2 fn
| sI A BF |
0 1
0 0
s 0
0
s
s
0
a0
0 a1
1
0
1
0
f1
f
2
f
n
an1 1
极点配置法设计状态反馈控制器
——《自动控制原理-理论篇》第8.8节
极点配置法设计状态反馈控制器——自动控制原理理论篇

——《自动控制原理-理论篇》第8.8节
自动化工程学院自动控制原理课程组制 2015年11月
主要内容
状态反馈控制系统 状态反馈控制器设计条件 用极点配置法设计状态反馈控制器 举例
主要内容
状态反馈控制系统 状态反馈控制器设计条件 用极点配置法设计状态反馈控制器 举例
SI系统,所以设 F f1 f2 fn
| sI A BF |
0 1
0 0
s 0
0
s
s
0
a0
0 a1
1
0
1
0
f1
f
2
f
n
an1 1
设计算法--适用于用能控标准形表示的SI系统的算法
a0 f1 0 a1 f 2 1
an1 f n n1
f1 0 a0 f2 1 a1
fn n1 an1
举例
例8-21 设系统的状态空间描述为
x(t)
0 6
1 0 5x(t) 1u(t)
rankB
AB
0 1
1 5
2
系统能控。
举例求解过程
期望闭环系统特征多项式为:
(s s1)(s s2 ) (s 3 2 j)(s 3 2 j) s2 6s 13
设: F f1 f2
s sI A BF
6 f1
1x(t)
F 7 1
基于极点配置的控制器设计与仿真

计算机控制理论与设计作业题目:基于极点配置方法的直流调速系统的控制器设计摘要本文目的是用极点配置方法对连续的被控对象设计控制器。
基本思路是对连续系统进行数学建模,将连续模型进行离散化,针对离散的被控对象,用极点配置的方法分别在用状态方程和传递函数两种描述方法下设计前馈和反馈控制器,并用MATLAB仿真。
文中具体以直流调速系统作为研究对象,对直流调速系统的组成和结构进行了分析,把各个部分进行数学建模,求出其传递函数,组成系统结构框图,利用自控原理的知识对结构图化简,求出被控对象的传递函数和状态方程,进一步得将其离散化。
第一种是通过极点配置设计方法的原理,用状态方程设计被控对象的控制律,因为直流调速系统存在噪声,实际状态不可测,故选择了全阶的观测器,又因为采样时间小于计算延时,所以选择了预报观测器。
利用所学知识对此闭环系统设计前馈和反馈控制器[1]。
第二种利用传统的离散传递函数,从代数多项式的角度进行复合控制器的设计,在保证系统稳定的情况下,分析系统的可实现性,稳定性,静态指标,动态指标,抗干扰等方面性能研究前馈反馈相结合控制器设计。
重点是保证被控对象的不稳定的零极点不能被抵消。
最后利用MATLAB的Simulink进行仿真,观察系统的输出的y和u和收敛性,并加入扰动看其抗干扰性能,得出结论。
经研究分析,对于直流调速系统,基于极点配置设计的前馈反馈相结合的控制器,具有良好的稳定性能和抗干扰性能。
运行结果符合实际情况。
关键词:极点配置;状态方程;直流调速系统;代数多项式;Matlab;1绪论1.1论文的背景及意义在工业生产和日常生活中,自动控制系统分为确定性系统和不确定性系统两类,确定性系统是指系统的结构和参数是确定的,确定的输入下,输出也确定的一类系统。
确定性系统相对于不确定性系统而言的。
在确定的系统中所用的变量都可用确切的函数关系来描述,系统的运动特性可以完全确定。
以确定性系统为研究对象的控制理论称为确定性控制理论。
极点配置法设计状态反馈控制器——自动控制原理

这两个多项式的系数相等,可得出:
0 0
1
1
n n1
i中含F阵系数fij
当F阵为1 n时
n个方程可解n个系数 fi
(i 1,2,...,n)
设计算法--适用于用能控标准形表示的SI系统的算法
设系统期望的闭环极点为s1、s2、sn ,则其
闭环特征式为s s1 s s2 s s3 s sn
SI系统,所以设 F f1 f2 fn
ห้องสมุดไป่ตู้
设计算法--适用于用能控标准形表示的SI系统的算法
s
1
0
0
0
0
s
1
0
0
0
0
0
s
1
a0 f1 a1 f2 a2 f3 an2 fn1 an1 fn s
sn (an1 fn )sn1 a1 f2 s a0 f1
设计算法--适用于用能控标准形表示的SI系统的算法
解:
系统能控。
举例----求解过程
期望闭环系统特征多项式为:
设: F f1 f2
F 7 1
w
u+
x2 ∫
--
++ -5
x2 x1
∫ x1
-
F 7 1
1
+
2
+
y
-6 1
7
a0 f1 0 a1 f 2 1
an1 f n n1
f1 0 a0 f2 1 a1
fn n1 an1
举例
例8-21 设系统的状态空间描述为
试求:(1)求状态反馈矩阵F使闭环系统有期望 极点s1,2=-3±2j; (2)绘制带有状态反馈控制器的状态变量图
线性系统的状态反馈及极点配置

线性系统的状态反馈及极点配置1.前言随着现代控制理论的不断发展和成熟,线性系统的状态反馈控制在控制理论中得到了广泛的应用,并成为了控制领域中重要的一种控制方法。
状态反馈控制能够将系统的状态进行反馈,并利用反馈得到的信息对系统进行控制,从而达到使系统达到预期控制目标的目的。
本文将从状态反馈控制的原理和实现方法两方面介绍线性系统的状态反馈及极点配置。
2.状态反馈控制的原理状态反馈控制是建立在现代控制理论的基础上的一种高级控制方法。
状态反馈控制的基本思想是在系统中引入反馈环节,设计一个反馈控制器,将系统的状态量反馈给控制器,控制器再根据反馈信号输出控制量,以期望控制系统按照预期的运动轨迹运行。
因此,状态反馈控制要实现以下两个步骤:- 系统状态量的测量:首先要在系统中安装测量传感器,实时地测量系统状态量,使得状态量可以被反馈到控制器中。
- 反馈控制器的设计:设计一个反馈控制器,将系统的状态量反馈给控制器,控制器再根据反馈信号输出控制量,实现对系统的精确控制。
因此,状态反馈控制的基本原理就是将系统状态量反馈到控制器中,以期望控制系统按照预期的运动轨迹运行。
2.2 状态空间模型与状态反馈控制状态空间模型是状态反馈控制的基础。
状态空间模型是一种方便描述线性系统动态行为和控制器的模型。
对于线性时不变系统,我们可以用如下的状态变量描述:x(t) = [x1(t),x2(t),...,xn(t)]T其中,x(t) 是系统在时刻 t 的状态量,n 是状态量的数量,x1(t),x2(t),...,xn(t) 分别是系统的每个状态量。
状态空间模型可以用一组线性常微分方程描述:dx/dt = Ax + Bu其中,A 是系统的状态方程矩阵,B 是输入矩阵,C 是输出矩阵,D 是直接耦合矩阵。
系统的状态反馈控制可以表示为:u(t) = -Kx(t)其中,K 是状态反馈矩阵。
将状态反馈控制引入到状态空间模型中,可以得到控制器的状态空间模型为:y = Cx上述控制器的状态空间模型就是一个闭环系统,通过反馈控制器将系统状态返回到系统,形成了一个反馈环。
(完整版)控制系统的极点配置设计法
控制系统的极点配置设计法一、极点配置原理1.性能指标要求2.极点选择区域主导极点:2111cos tanξβξξ---==图3.22 系统在S平面上满足时域性能指标的范围nstζω4=;当Δ=0.02时,。
nstζω3=当Δ=0.05时,3.其它极点配置原则系统传递函数极点在s 平面上的分布如图(a )所示。
极点s 3距虚轴距离不小于共轭复数极点s 1、s 2距虚轴距离的5倍,即n s s ξω5Re 5Re 13=≥(此处ξ,n ω对应于极点s 1、s 2);同时,极点s 1、s 2的附近不存在系统的零点。
由以上条件可算出与极点s 3所对应的过渡过程分量的调整时间为1351451s n s t t =⨯≤ξω 式中1s t 是极点s 1、s 2所对应过渡过程的调整时间。
图(b )表示图(a )所示的单位阶跃响应函数的分量。
由图可知,由共轭复数极点s 1、s 2确定的分量在该系统的单位阶跃响应函数中起主导作用,即主导极点。
因为它衰减得最慢。
其它远离虚轴的极点s 3、s 4、s 5 所对应的单位阶跃响应衰减较快,它们仅在极短时间内产生一定的影响。
因此,对系统过渡过程进行近似分析时。
可以忽略这些分量对系统过渡过程的影响。
n x o (t)(a )(b )系统极点的位置与阶跃响应的关系二、极点配置实例磁悬浮轴承控制系统设计1.1磁悬浮轴承系统工作原理图1是一个主动控制的磁悬浮轴承系统原理图。
主要由被悬浮转子、传感器、控制器和执行器(包括电磁铁和功率放大器)四大部分组成。
设电磁铁绕组上的电流为I0,它对转子产生的吸力F和转子的重力mg相平衡,转子处于悬浮的平衡位置,这个位置称为参考位置。
(a)(b)图1 磁悬浮轴承系统的工作原理Fig.1 The magnetic suspension bearing system principledrawing假设在参考位置上,转子受到一个向下的扰动,转子就会偏离其参考位置向下运动,此时传感器检测出转子偏离其参考位置的位移,控制器将这一位移信号变换成控制信号,功率放大器又将该控制信号变换成控制电流I0+i,控制电流由I0增加到I0+i,因此,电磁铁的吸力变大了,从而驱动转子返回到原来的平衡位置。
现代控制理论 极点配置
−
=
=
,
−
= −
1 1
18 −14
(6)状态反馈增益
ഥ − = − 25 9
=
−
1
18
1
−14
−3
= −5.6
24
7.8
−3
24
5.2
极点配置问题
算法2 给定线性定常系统 ሶ =A+B 和一组期望的闭环极点 ∗ ,∗ , ⋯ ,∗ 确定状
⋱
…
⋯
ഥ
ഥ = =
取
ഥ
ഥ− = ∗ −
⋯
ഥ = − A
0
⋮
1
−−1
0
ഥ = − = ⋮
0
1
∗ −
ഥ = =
⋯ ∗− − −
⋯
−
5.2
极点配置问题
于是
0
ഥ −
ഥ
ഥ= ⋮
3.计算由期望极点 ∗ ,∗ , ⋯ ,∗ 所确定的特征多项式
∗ = ෑ − ∗ = + ∗− − + ⋯ + ∗ + ∗
=
ഥ = ∗ − ∗ − ⋯ ∗− − −
4. 计算变换为能控标准型后系统的状态反馈矩阵:
0
−0
1
⋮
0
−1
⋯
⋱
…
⋯
0
⋮
1
−−1
0
− ⋮ ∗ −
0
1
∗ −
⋯ ∗− − −
0
⋮
= 0
极点配置的原理
极点配置的原理今天来聊聊极点配置的原理。
我不是一开始就接触到极点配置这个概念的,之前做项目的时候遇到了控制系统的性能优化问题,就开始研究起它来了。
极点配置就像是给控制系统这个大机器调音一样。
咱们先从生活现象说起,想象一下开车。
汽车有个速度控制系统,我们想要汽车的速度按照我们期望的方式变化,比如说快速稳定地达到一个设定速度,并且在遇到一些小干扰(像路面有点小坡度)的时候还能保持稳定。
这个时候极点配置就像调整汽车的“脾气秉性”的工具一样。
在控制系统里,系统的特性跟极点的位置密切相关。
从原理上讲呢,极点就是系统传递函数分母等于零的根。
我记得第一次接触这个理论公式的时候,觉得满脑袋都是浆糊。
比如说一个简单的二阶系统,它的极点会影响系统的响应速度和稳定性,就像一个跷跷板,两个极点要处于一个合适的位置,系统才会又快又稳。
这可是我琢磨了好久才有点理解的地方。
说到这里,你可能会问,这个极点怎么才能配置到我们想要的位置呢?这就要用到反馈控制理论了。
就像我们在训练宠物一样,通过反馈(知道宠物做的好不好,然后奖惩)来让系统的特性符合我们的要求。
比如说,通过调整反馈增益,就可以改变极点的位置。
老实说,我一开始也不明白极点配置到底为啥这么重要。
后来遇到好多实际例子才恍然大悟。
实际在航空航天领域,飞行器的姿态控制系统要很精确才行,极点配置就大有用武之地。
合理的极点配置能让飞行器快速准确地调整姿态且保持稳定,就像杂技演员总能在高空钢丝上保持平衡一样。
再讲讲相关的注意事项吧。
极点配置虽然很强大,但并不是随心所欲的,要考虑系统的物理可实现性以及对于外部干扰和不确定性的鲁棒性。
比如说,不能要求汽车做到像火箭那样的加速能力,因为汽车有它的物理限制。
这就像我们人一样,虽然有潜力可以挖掘,但是也有自身的极限。
我觉得极点配置这个原理还有很多可以延伸思考的地方。
比如如何在更加复杂多变的环境下进行适当地极点配置,这就像在不断变化的天气下管理一个大农场,要根据不同情况调整策略。
第4章 极点配置设计课件
Wc和 Wc 分别是系统(4.2)式和(4.5)式的能达性矩阵。
注 意:
注1:方程(4.14)称为阿克曼(Ackerman)公式。
注2:把上述极点配置问题形式化为下面的抽象问题:
给定矩阵和,寻找一个矩阵L以便使得矩阵 -L有
规定的特征值。
注3:根据式(4.11)和(4.12),可得:
T 1 ( Γ Φ Γ a 1 ΓΦ n 1 Γ a 1 Φ n 2 Γ a n - 1 Γ )( 4 . 1 5 )
u (k 1)
C Γ u (k 1)
y (k n 1)
Yk
y(k
n
2
)
y (k )
把方程(4.24)写成:
Y k W o x ( k n 1 ) W u U k 1
其中矩阵Wo和Wu由下式给出:
C
0
0
0
CΦ
CΓ
0
0
Wo CΦ2 Wu CΦΓ
CΓ
0
CΦn1
CΦn2 Γ CΦn3Γ
CΓ
如 果 系 统 是 能 观 测 的 , 矩 阵 Wo 就 是 可 逆 的 , 就 能 解 出 x(k-n+1),反复利用方程(4.23),得到:
典型的例子是阶跃,斜坡和正弦信号。
过程的不确定性
用状态空间描述可以处理矩阵A和B中各元素的不确定性, 但是状态空间描述不便于处理其他形式的未建模动力学特 性。因此,当建立更合适的工具之后,我们再来讨论过程 的不确定性。
性能准则
➢ 调节问题 受扰之后,其性能准则是力图使状态归零。 在极点配置表达中,这种状态衰减速率是通过规定闭
P ( z ) z n p 1 z n 1 p n( 4 . 8 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12 10
Position(mm)
8 6 4 2 0 0
PID控制器: Kp=21 Ki=0.5 Kd=0.5
0.1
0.2 0.3 time(SEC)
0.4
0.5
Real-Time Estimation of Induction Motor Parameters by LSE
內容:
主旨 感應馬達模型 狀態變數濾波器
N s Ls As D s M s N s
PP控制器設計步驟:
利用 As Ds M s N s D p s X s F s 順利解出控制器的參數
How to choose
X s
依據系統抗干擾能力及 系統的強健性來做判斷
a0 1 Ts Tr
- isd - isq
Lr Rr
dv sd v sq r dt dv sq - v sd r dt
a1 v sd a 0 b v sq 1 b 0
V
強健性的設計:
觀念:系統對任何的步階干擾輸入的響應都能
消為零,則系統有抗步階干擾的能力。 lim y p t 0 設計 A 0 0
t
Ps Y p s
H s
Y p s H s Ps
N s As a D p s X s s
4-th order Butterworth lowpass filter
z Az Bu u F Cz
C 1 0 0 0
1 0 0 0 0 0 1 0 A 0 0 1 0 - a F0 - a F1 - a F2 - a F3
LSE演算法
主旨
A application Least Square Estimation
algorithm to the identification of the induction machine parameters. Advantage It is possible to estimate the four fundamental parameters of an induction machine at the same time.
規格:使用ITAE最佳化設計閉迴路特徵方程式
並且設計系統速度閉迴路頻寬為30赫茲。 自由參數:X s 則以系統抗干擾能力做為準則 挑選 X s ( s 620)2 A0 0
s 4 2.1o s 3 3.4o 2 s 2 2.7o3s o 4
速度步階命令:800 mm/s
Four Identified Parameters
Stator resistance :
due to temperature change
Stator inductance :
due to difference input signal frequency
Rotor time constant
Total leakage factor : 磁損
The Induction Motor Model
由於三相感應馬達之數學模型為一複雜
且相互耦合的,一般可透過一些座標轉 換式將方程式簡化[1] 馬達電壓或電流之三相交流表示式,不 如用二相交流表示式簡單。更進一步仍 可用二軸直流表示[2]
[1]劉竟成, “交流調速系統”, 上海交通大學出版社, 1984 [2]姚武松, “縫紉機用之感應馬達全數位伺服控制器研製”, 國立成功大學機械工程學系碩士論文, 1997
is a very large positive scalar, and I
is the identity matrix. They apply the LSE with 0 put to zero during a locked rotor test
In fact, at motor standstill with zero rotor speed, the identification of parameters is easier thanks to the linearity of IM equations
-1 T x k yk
Fresh experimental data are continuously in supply
y k 1 xT k 1
Combine
y k 1 x k 1
To achieve the identification algorithm (LSE)
Ts
Ls Rs
Tr
b0
The measured variables • Stator currents • Stator voltages
1 1 a1 Ts Tr
c0 a 0 b1 1 b0 Ts
1 Ls Tr
b1
1 Ls
• Rotor angular speed
பைடு நூலகம்
N s As a aN 0 A0 lim y p t lim s D p 0 X 0 t s 0 D p s X s s
實例模擬結果:
3621 .51 4 2 1800 7.5 mm s PLANT: s 371.16 254.76 j s 371.16 - 254.76 j Volt
-1 T
x k 1 p k
Let
K k 1 p k x k 1 I x k 1p k x k 1
T
Then
p k p k 1 I - K k 1x k 1p k k 1 p k 1 x T y x k 1 y k 1
IM Equations
disq d 2isd disd isq r c0 2 r dt dt dt 2 disd d isq - disq dt 2 - r dt - isd r c0 dt
M2 1 Ls Lr
PP控制器設計步驟:
• step 2
選擇自由參數 X s ,使得 degD p s X s 的階數 至少為2N+1次 極零點相消
N s N p s D p s N s N p s X s D p s X s
• step 3
G f s
自由參數的選擇:
• 我們必頇知道: X s 的選擇(1)並不影響系統的輸出
(2)也不影響系統驅動信號的大小
P
+
Vref
Ls
+
A -1s
+
Cout
Gs
V
Ms
± ¨ ¹ î ¾
s G s N s As H s -1 P s 1 G s M s A s DP X s
T
-1
k k
simplify
k 1 k K k 1 y k 1 - x T k 1 k
How to choose the initial values
Take the first k data points and solve k and p k directly Set 0 arbitrarily and p0 I where
報告人:郭洲成 日 期:1998/7/7
報告內容:
第一部份
極點配置控制器的介紹
控制器設計流程
強健性的設計
實例模擬結果
第二部份
感應馬達參數的判認
極點配置控制器的介紹:
F Vref
+ +
傳統的架構
1 S
+
KI KP 極點配置控制器 PDFF Pole-Placement控制器是設計者依據
G(s)
V
PDF控制器 (ID控制器)
PDFF控制器 所要的系統性能(performance),例 F=0 如系統慣量或欲設計的閉迴路系統頻寬 F=1 來決定控制器的參數 PI控制器
PP控制器設計步驟:
• 已知:
N s 系統的轉移函數 G s D s
• 要求規格:
使用ITAE最佳化設計閉迴路特 徵方程式,並給定系統閉迴路頻寬
• 自由參數的選擇:
以系統的強健性作為選擇的準則
PP控制器設計步驟:
• 實現架構:
Vref
Ls
+
A -1s
Cout
Gs
V
Ms
± ¨ ¾ î ¹
• step 1
計算 N s D s N s D s f p
G f s
N f s
N p s
LSE ( Recursive Form )
yk
T x k ek
They choose a State Variable Filter (SVF) of the 4-th order to improve the filtering properties and identifier performance.
速度迴路 As s 4 252.04s 3 58016.49s 2 2001183.57 s
Ls 7.27s 2 9011.57s 2793586.79 M s 66.94s 2 46185.09 s 2793586.79
1000 800
Velocity(mm/s)
System Identification
