极点配置法设计状态反馈控制器——自动控制原理共19页
状态反馈极点配置基本理论与方法
状态反馈极点配置基本理论与方法IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】第2章 状态反馈极点配置设计基本理论引言大多数的控制系统的基本结构是由被控对象和反馈控制器构成的闭环系统。
反馈的基本类型包括状态反馈和输出反馈。
其中状态反馈能够提供更加丰富的状态信息。
状态反馈是将系统的每一个状态变量乘相应的反馈系数，然后反馈到输入端与参考输入相加形成的控制规律，作为被控系统的控制输入。
图是一个多输入多输出线性时不变系统状态反馈的基本结构：图 多输入-多输出系统的状态反馈结构图其中受控系统的状态空间表达式为：x Ax Buy Cx=+=由图可知，加入状态反馈后，受控系统的输入为：u Fx v =+其中v 为参考输入，F 为状态反馈增益阵，因此可以得到状态反馈闭环系统的状态空间表达式：()x A BF x Bv y Cx=++=闭环系统的传递函数矩阵：()()1s W s C sI A BF B -=-+⎡⎤⎣⎦由此可见，引入状态反馈后，通过F 的选择，可以改变闭环系统的特征值，是系统获得所要求的性能。
极点配置方法的选择对于一个线性时不变系统进行状态反馈极点配置，一般有四种方法： （1） 传统方法—将系统转化为一个或多个单输入单输出系统。
（2） 直接法—使用稳定的酉矩阵，将这种系统转化为标准型。
（3）矩阵方程法—对矩阵F ，直接解方程AX X BG -Λ=FX G =（4）特征向量法—先找到特征向量x j （等式中矩阵X 的列向量），然后利用等式求解F 。
方法（1）一般难以应用或者数值不稳定。
方法（3）需要解方程，并且对于系统矩阵A 的特征值不能再分配。
最有效并且数值稳定的方法是方法（2）和方法（4）。
其中方法（4）通过使用一系列的迭代算法找到最优解，所以比较复杂。
对于方法（2），当系统的输入多于一个信号输入时，不能确定系统的鲁棒性。
本文结合以上方法提出了一种新的设计方法：首先通过酉变换将状态方程化为一种控制规范形，然后利用最小二乘法解方程的得到最佳的状态反馈矩阵。
状态反馈和极点配置
为了根据期望的闭环极点位置来设计输出反馈矩阵h的参数，只需将期望的 系统特征多项式与该输出反馈系统特征多项式 hC) 相比较即可。
15
输出反馈到参考输入
设被控对象的状态方程为 x Ax Bu
y Cx
输出量反馈到参考输入时， u=r-hy，则该输出反馈系统的动态
方程为 x (A BhC)x Bv
为
0 0 1
Q [ B AB A2 B ] 0
1
6
1
6 31
得出detQ = -1。因此，rankQ = 3。因而该系统是状态完全可控的，可任意
配置极点。
下面用两种方法求解。
11
极点配置 例1
方法1：利用刚才介绍的求解步骤，计算系统矩阵A的特征多项式，求特征值。
7
极点配置定理_充分性
a0 k0 a0 a1 k1 a1
an1
kn1
a n1
求解上述方程组，得到 ki 的值，则
K KP1 [k0 k1
kn 1 ]P 1
[ a0 a0 a1 a1
an1 an1 ] P1
如果系统是状态完全可控的，则通过对应于上式所选取的矩阵K，可任意 配置所有的特征值。
充分性得证。
8
极点配置定理_必要性
即已知闭环系统可任意配置极点，证明被控系统状态完全可控。 现利用反证法证明。 先证明如下命题：如果系统不是状态完全可控的，则矩阵A-BK 的特征值不可能由线性状态反馈来控制。 假设原线性系统 x Ax Bu 状态不可控，则其可控性矩阵的 秩小于n，即
rank[ B AB An1B ] q n
◆考察系统的可控性条件。如果系统是状态完全可控的，则可按下列步骤继续。
控制系统的极点配置设计法
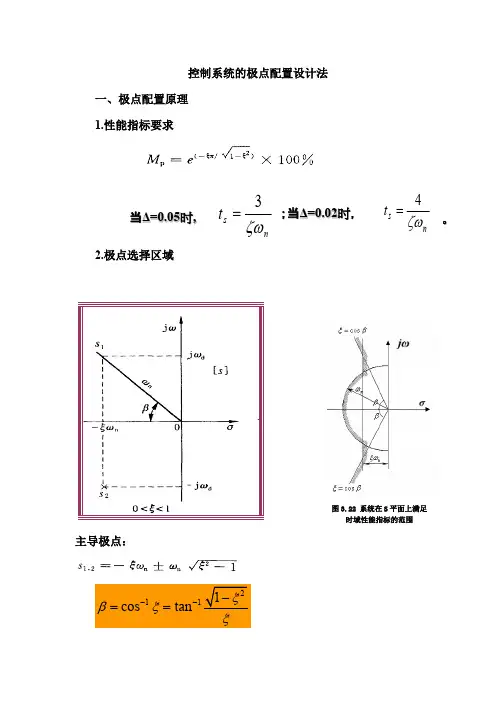
控制系统的极点配置设计法一、极点配置原理1.性能指标要求n s t ζω4=；当Δ=0.02时，。
ns t ζω3= 当Δ=0.05时,2.极点选择区域主导极点：2111cos tan ξβξξ---==3.其它极点配置原则系统传递函数极点在s 平面上的分布如图（a ）所示。
极点s 3距虚轴距离不小于共轭复数极点s 1、s 2距虚轴距离的5倍，即（此处，对应于极点s 1、s 2）；同时，极点n s s ξω5Re 5Re 13=≥ξn ωs 1、s 2的附近不存在系统的零点。
由以上条件可算出与极点s 3所对应的过渡过程分量的调整时间为1351451s n s t t =⨯≤ξω式中是极点s 1、s 2所对应过渡过程的调整时间。
1s tn x o (t)（a ）（b系统极点的位置与阶跃响应的关系图（b ）表示图（a ）所示的单位阶跃响应函数的分量。
由图可知，由共轭复数极点s 1、s 2确定的分量在该系统的单位阶跃响应函数中起主导作用，即主导极点。
因为它衰减得最慢。
其它远离虚轴的极点s 3、s 4、s 5所对应的单位阶跃响应衰减较快，它们仅在极短时间内产生一定的影响。
因此，对系统过渡过程进行近似分析时。
可以忽略这些分量对系统过渡过程的影响。
二、极点配置实例磁悬浮轴承控制系统设计1.1磁悬浮轴承系统工作原理图1是一个主动控制的磁悬浮轴承系统原理图。
主要由被悬浮转子、传感器、控制器和执行器(包括电磁铁和功率放大器)四大部分组成。
设电磁铁绕组上的电流为I0，它对转子产生的吸力F和转子的重力mg相平衡，转子处于悬浮的平衡位置，这个位置称为参考位置。
（a）（b）图1 磁悬浮轴承系统的工作原理Fig.1 The magnetic suspension bearing system principledrawing假设在参考位置上，转子受到一个向下的扰动，转子就会偏离其参考位置向下运动，此时传感器检测出转子偏离其参考位置的位移，控制器将这一位移信号变换成控制信号，功率放大器又将该控制信号变换成控制电流I0+i，控制电流由I0增加到I0+i，因此，电磁铁的吸力变大了，从而驱动转子返回到原来的平衡位置。
控制器极点配置方法
控制器极点配置方法如果已知系统的模型或传递函数，通过引入某种控制器，使得闭环系统的极点可以移动到指定的位置，从而使系统的动态性能得到改善。
这种方法称为极点配置法。
例6－12 有一控制系统如图6－38，其中，要求设计一个控制器，使系统稳定。
图6-38解：（1）校正前，闭环系统的极点：> 0因而控制系统不稳定。
（2）在控制对象前串联一个一阶惯性环节，c>0，则闭环系统极点：显然，当，时，系统可以稳定。
但此对参数c 的选择依赖于 a 、b 。
因而，可选择控制器，c 、d ，则有特征方程：当，时，系统稳定。
本例由于原开环系统不稳定，因而不能通过简单的零极点相消方式进行控制器的设计，其原因在于控制器的参数在具体实现中无法那么准确，从而可能导致校正后的系统仍不稳定。
例6－13 已知一单位反馈控制系统的开环传递函数：要求设计一串联校正装置Gc(s) ，使校正后系统的静态速度误差系统，闭环主导极点在处。
解：首先，通过校正前系统的根轨迹可以发现，如图6－39所示，其主导极点为：。
图6-39为使主导极点向左偏移，宜采用超前校正装置。
（2）令超前校正装置，可采用待定系数法确定相关参数：又其中、、、为待定系数。
进一步可得：即将代入式子可以得到：，，，。
进一步可得超前校正装置的传递函数：校正后系统的根轨迹如图6-39所示。
该校正装置与例6－7中由超前装置获取的校正装置结果基本相同，说明结果是正确的。
在matlab中，亦有相应的命令可进行极点配置，主要有三个算法可实现极点配置算法：Bass-Gura算法、Ackermann 算法和鲁棒极点配置算法。
这些算法均以状态空间进行表征，通过设定期望极点位置，获取状态反馈矩阵K。
下面通过示例介绍其中的一种算法。
例6－14 考虑给定的系统，其状态方程模型如下：，期望的闭环系统配置在，，，试设计其控制器。
解：可以使用下面的MATLAB语句来实现极点的配置：A=[0,1,0,0;0,0,-1,0;0,0,0,1;0,0,11,0]; B=[0;1;0;-1];eig(A)'ans =0 0 3.3166 -3.3166P=[-1;-2;-1+sqrt(-1);-1-sqrt(-1)];K=place(A,B,P)place: ndigits= 15Warning: Pole locations are more than 10% in error.K =-0.4000 -1.0000 -21.4000 -6.0000eig(A-B*K)'ans =-1.0000 - 1.0000i -1.0000 + 1.0000i -2.0000 -1.0000。
极点配置法设计状态反馈控制器——自动控制原理理论篇
——《自动控制原理-理论篇》第8.8节
自动化工程学院自动控制原理课程组制 2015年11月
主要内容
状态反馈控制系统 状态反馈控制器设计条件 用极点配置法设计状态反馈控制器 举例
主要内容
状态反馈控制系统 状态反馈控制器设计条件 用极点配置法设计状态反馈控制器 举例
SI系统，所以设 F f1 f2 fn
| sI A BF |
0 1
0 0
s 0
0
s
s
0
a0
0 a1
1
0
1
0
f1
f
2
f
n
an1 1
设计算法--适用于用能控标准形表示的SI系统的算法
a0 f1 0 a1 f 2 1
an1 f n n1
f1 0 a0 f2 1 a1
fn n1 an1
举例
例8-21 设系统的状态空间描述为
x(t)
0 6
1 0 5x(t) 1u(t)
rankB
AB
0 1
1 5
2
系统能控。
举例求解过程
期望闭环系统特征多项式为：
(s s1)(s s2 ) (s 3 2 j)(s 3 2 j) s2 6s 13
设： F f1 f2
s sI A BF
6 f1
1x(t)
F 7 1
反馈控制与极点配置
2021/1/23
h
15
因此,在反馈律u=-Kx+v下,闭环系统状态方程为
0 1 0 0
x
0
0
10 0 0 ]x
在例6-3中,由给定的传递函数通过状态反馈进行极点配置时 需先求系统实现,即需选择状态变量和建立状态空间模型。 ➢ 这里就存在一个所选择的状态变量是否可以直接测量、 可以直接作反馈量的问题。
2021/1/23
h
10
解 1： 判断系统的能控性。
➢ 开环系统的能控性矩阵为
[B
AB]12
-4 1
则开环系统为状态能控,可以进行任意极点配置。
2. 求能控规范II形:
T1 [0 1][B AB]1 1/6 1/3
Tc21
T1 T1A
1 6
1 1
2 8
A~
Tc21ATc2
0 5
1 2
B~
Tc21B
2021/1/23
h
4
• 下面分别讨论:
– 状态反馈极点配置定理 – SISO系统状态反馈极点配置方法 – 输出反馈极点配置
2021/1/23
h
5
6.2.1 状态反馈极点配置定理
在进行极点配置时,存在如下问题: ➢ 被控系统和所选择的期望极点满足哪些条件,则是可以进 行极点配置的。 ➢ 下面的定理就回答了该问题。
2 8
-7/3 26/3
则在反馈律u=-Kx+v下的闭环系统的状态方程为
2021/1/23
h
12
x13141 1578x12u
通过验算可知,该闭环系统的极点为-1±j2,达到设计要求。
状态反馈极点配置基本理论与方法
第2章 状态反馈极点配置设计基本理论2.1引言大多数的控制系统的基本结构是由被控对象和反馈控制器构成的闭环系统。
反馈的基本类型包括状态反馈和输出反馈。
其中状态反馈能够提供更加丰富的状态信息。
状态反馈是将系统的每一个状态变量乘相应的反馈系数，然后反馈到输入端与参考输入相加形成的控制规律，作为被控系统的控制输入。
图2.1是一个多输入多输出线性时不变系统状态反馈的基本结构：图2.1 多输入-多输出系统的状态反馈结构图其中受控系统的状态空间表达式为：x Ax Buy Cx=+= (2.1)由图2.1可知，加入状态反馈后，受控系统的输入为：u Fx v =+ (2.2)其中v 为参考输入，F 为状态反馈增益阵，因此可以得到状态反馈闭环系统的状态空间表达式：()x A BF x Bv y Cx=++= (2.3)闭环系统的传递函数矩阵：()()1s W s C sI A BF B -=-+⎡⎤⎣⎦ (2.4)由此可见，引入状态反馈后，通过F 的选择，可以改变闭环系统的特征值，是系统获得所要求的性能。
2.2极点配置方法的选择对于一个线性时不变系统进行状态反馈极点配置，一般有四种方法： （1） 传统方法—将系统转化为一个或多个单输入单输出系统。
（2） 直接法—使用稳定的酉矩阵，将这种系统转化为标准型。
（3） 矩阵方程法—对矩阵F ，直接解方程AX X BG -Λ= (2.5a)FX G = (2.5b)（4） 特征向量法—先找到特征向量x j （等式(2.5)中矩阵X 的列向量），然后利用等式(2.5b)求解F 。
方法（1）一般难以应用或者数值不稳定。
方法（3）需要解(2.5a)方程，并且对于系统矩阵A 的特征值不能再分配。
最有效并且数值稳定的方法是方法（2）和方法（4）。
其中方法（4）通过使用一系列的迭代算法找到最优解，所以比较复杂。
对于方法（2），当系统的输入多于一个信号输入时，不能确定系统的鲁棒性。
极点配置法设计状态反馈控制器——自动控制原理
这两个多项式的系数相等，可得出：
0 0
1
1
n n1
i中含F阵系数fij
当F阵为1 n时
n个方程可解n个系数 fi
(i 1,2,...,n)
设计算法--适用于用能控标准形表示的SI系统的算法
设系统期望的闭环极点为s1、s2、sn ,则其
闭环特征式为s s1 s s2 s s3 s sn
SI系统，所以设 F f1 f2 fn
ห้องสมุดไป่ตู้
设计算法--适用于用能控标准形表示的SI系统的算法
s
1
0
0
0
0
s
1
0
0
0
0
0
s
1
a0 f1 a1 f2 a2 f3 an2 fn1 an1 fn s
sn (an1 fn )sn1 a1 f2 s a0 f1
设计算法--适用于用能控标准形表示的SI系统的算法
解：
系统能控。
举例----求解过程
期望闭环系统特征多项式为：
设： F f1 f2
F 7 1
w
u+
x2 ∫
--
++ -5
x2 x1
∫ x1
-
F 7 1
1
+
2
+
y
-6 1
7
a0 f1 0 a1 f 2 1
an1 f n n1
f1 0 a0 f2 1 a1
fn n1 an1
举例
例8-21 设系统的状态空间描述为
试求：（1）求状态反馈矩阵F使闭环系统有期望 极点s1,2=-3±2j; (2)绘制带有状态反馈控制器的状态变量图
线性系统的状态反馈及极点配置
线性系统的状态反馈及极点配置1.前言随着现代控制理论的不断发展和成熟，线性系统的状态反馈控制在控制理论中得到了广泛的应用，并成为了控制领域中重要的一种控制方法。
状态反馈控制能够将系统的状态进行反馈，并利用反馈得到的信息对系统进行控制，从而达到使系统达到预期控制目标的目的。
本文将从状态反馈控制的原理和实现方法两方面介绍线性系统的状态反馈及极点配置。
2.状态反馈控制的原理状态反馈控制是建立在现代控制理论的基础上的一种高级控制方法。
状态反馈控制的基本思想是在系统中引入反馈环节，设计一个反馈控制器，将系统的状态量反馈给控制器，控制器再根据反馈信号输出控制量，以期望控制系统按照预期的运动轨迹运行。
因此，状态反馈控制要实现以下两个步骤：- 系统状态量的测量：首先要在系统中安装测量传感器，实时地测量系统状态量，使得状态量可以被反馈到控制器中。
- 反馈控制器的设计：设计一个反馈控制器，将系统的状态量反馈给控制器，控制器再根据反馈信号输出控制量，实现对系统的精确控制。
因此，状态反馈控制的基本原理就是将系统状态量反馈到控制器中，以期望控制系统按照预期的运动轨迹运行。
2.2 状态空间模型与状态反馈控制状态空间模型是状态反馈控制的基础。
状态空间模型是一种方便描述线性系统动态行为和控制器的模型。
对于线性时不变系统，我们可以用如下的状态变量描述：x(t) = [x1(t),x2(t),...,xn(t)]T其中，x(t) 是系统在时刻 t 的状态量，n 是状态量的数量，x1(t),x2(t),...,xn(t) 分别是系统的每个状态量。
状态空间模型可以用一组线性常微分方程描述：dx/dt = Ax + Bu其中，A 是系统的状态方程矩阵，B 是输入矩阵，C 是输出矩阵，D 是直接耦合矩阵。
系统的状态反馈控制可以表示为：u(t) = -Kx(t)其中，K 是状态反馈矩阵。
将状态反馈控制引入到状态空间模型中，可以得到控制器的状态空间模型为：y = Cx上述控制器的状态空间模型就是一个闭环系统，通过反馈控制器将系统状态返回到系统，形成了一个反馈环。
(完整版)控制系统的极点配置设计法
控制系统的极点配置设计法一、极点配置原理1.性能指标要求2.极点选择区域主导极点：2111cos tanξβξξ---==图3.22 系统在S平面上满足时域性能指标的范围nstζω4=；当Δ=0.02时，。
nstζω3=当Δ=0.05时,3.其它极点配置原则系统传递函数极点在s 平面上的分布如图（a ）所示。
极点s 3距虚轴距离不小于共轭复数极点s 1、s 2距虚轴距离的5倍，即n s s ξω5Re 5Re 13=≥（此处ξ，n ω对应于极点s 1、s 2）；同时，极点s 1、s 2的附近不存在系统的零点。
由以上条件可算出与极点s 3所对应的过渡过程分量的调整时间为1351451s n s t t =⨯≤ξω 式中1s t 是极点s 1、s 2所对应过渡过程的调整时间。
图（b ）表示图（a ）所示的单位阶跃响应函数的分量。
由图可知，由共轭复数极点s 1、s 2确定的分量在该系统的单位阶跃响应函数中起主导作用，即主导极点。
因为它衰减得最慢。
其它远离虚轴的极点s 3、s 4、s 5 所对应的单位阶跃响应衰减较快，它们仅在极短时间内产生一定的影响。
因此，对系统过渡过程进行近似分析时。
可以忽略这些分量对系统过渡过程的影响。
n x o (t)（a ）（b ）系统极点的位置与阶跃响应的关系二、极点配置实例磁悬浮轴承控制系统设计1.1磁悬浮轴承系统工作原理图1是一个主动控制的磁悬浮轴承系统原理图。
主要由被悬浮转子、传感器、控制器和执行器(包括电磁铁和功率放大器)四大部分组成。
设电磁铁绕组上的电流为I0，它对转子产生的吸力F和转子的重力mg相平衡，转子处于悬浮的平衡位置，这个位置称为参考位置。
（a）（b）图1 磁悬浮轴承系统的工作原理Fig.1 The magnetic suspension bearing system principledrawing假设在参考位置上，转子受到一个向下的扰动，转子就会偏离其参考位置向下运动，此时传感器检测出转子偏离其参考位置的位移，控制器将这一位移信号变换成控制信号，功率放大器又将该控制信号变换成控制电流I0+i，控制电流由I0增加到I0+i，因此，电磁铁的吸力变大了，从而驱动转子返回到原来的平衡位置。
(第11讲)极点配置与状态反馈
Ao P 1 AP, bo P 1b, co cP
第一能观标准型 四川理工自动化教研室
tgq77@
Review
SISO系统第二能控、能观标准型
第二能控标准型 1 0 0 0 0 0 0 0 0 1 0 0 Ac 0 0 0 1 0 , b c 0, cc b0 b1 b2 b3 b4 0 0 0 0 1 0 a0 a1 a2 a3 a4 1 1 n 1 1 cAn 1
•在外扰下无静差跟踪。如使状态和控制的 二次型积分函数最小，即最优控制。
J (x, u) xT Qx uT Ru dt
0
四川理工自动化教研室
tgq77@
SISO系统的极点配置：问题表述
已知系统方程
x Ax bv y cx
* * 1 , * ,, * 和n个期望闭环极点值 2 n
A
y
四川理工自动化教研室
tgq77@
Review
0 1 Ac 0 0 0
SISO系统第一能控、能观标准型
T Qc b Ab An 1b
第一能控标准型
Ao
0 0 0 a0 1 Ac T 1 AT , b c T 1b, c c cT 0 0 0 0 a1 1 0 0 a2 , b c 0, c c 1 2 3 4 5 0 1 0 a3 0 0 0 0 1 a4 T T T T P 1 Qo c cA cAn1 A ,b c ,c b
u
B
x
A
H
极点配置状态反馈控制器的设计
极点配置状态反馈控制器的设计王俊伟于新海(河套学院机电工程系)摘要围绕双级倒立摆案例，对极点配置状态反馈控制器的设计方法展开讨论，对最终的计算结果进行仿真,并通过仿真结果分析了系统的稳定性、动态性能和稳态误差情况。
倒立摆的开环系统状态空间模型状态不稳定且动态性能较差，通过引进极点配置状态反馈控制器，倒立摆的闭环系统状态达到稳定，而且动态性能得到改善。
关键词状态反馈控制器双级倒立摆极点配置能控标准型爱克曼公式动态特性稳态误差中图分类号TH865文献标识码B文章编号1000-3932(2021)01-0015-05极点配置状态反馈控制器设计得好坏直接决定了控制系统动态性能的优劣！配置极点的目的不仅是使系统稳定还要使系统的动态性能满足控制要求[1]!在配置状态反馈控制器时，根据被控制对象的要求，可以采用3种方法实现:极点配置状态反馈控制器的直接法、极点配置状态反馈控制器的变换法和爱克曼公式[2]'这3种方法仅适用于单输入系统，优点是只要系统能控，就可以实现极点配置的状态反馈，缺点是不能用于多输入系统的极点配置状态反馈控制器。
对于单输入系统，如果系统能控可以实现极点的任意配置,改善动态性能，但有可能使闭环控制系统的稳态误差变大[3]!1极点配置状态反馈控制器的直接法线性时不变系统如下:x=Ax+Bu(])'=Cx其中,X是系统的*维状态向量;*是状态向量对时间的导数;u是状态反馈控制律；#、B和C是适当维数的已知常数矩阵;'是系统的输出。
采用的状态反馈控制律是:u=-kx+v(2)其中，-是一维外部输入;k是反馈增益矩阵。
将式(2)代入式(1)得到闭环系统状态方程：*二(.-Bk)x+B-(3)极点配置状态反馈控制器的直接法分5步实现⑷。
第1步,检验系统(1)的能控性,如果系统能控,进行第2步。
第2步，计算闭环系统特征多项式：)et[!0—(#—Bk)]二！*+(3*_]+k*_14!*i1--------(3]+k])!+30+,0(4)其中，！是闭环极点。
5.状态反馈控制器的设计
Chapter5状态反馈控制器设计控制方式有“开环控制”和“闭环控制”。
“开环控制”就是把一个确定的信号（时间的函数）加到系统输入端，使系统具有某种期望的性能。
然而，由于建模中的不确定性或误差、系统运行过程中的扰动等因素使系统产生一些意想不到的情况，这就要求对这些偏差进行及时修正，这就是“反馈控制”。
在经典控制理论中，我们依据描述控制对象输入输出行为的传递函数模型来设计控制器，因此只能用系统输出作为反馈信号，而在现代控制理论中，则主要通过更为广泛的状态反馈对系统进行综合。
通过状态反馈来改变和控制系统的极点位置可使闭环系统具有所期望的动态特性。
利用状态反馈构成的调节器，可以实现各种目的，使闭环系统满足设计要求。
参见R38例5.3.3,通过状态反馈的极点配置，使闭环系统的超调量匚p乞5%，峰值时间（超调时间）t p乞0.5s，阻尼振荡频率壮乞10。
5.1线性反馈控制系统的结构与性质设系统S=（A, B,C）为x 二Ax Bu y 二Cx （5-1）图5-1 经典控制-输岀反馈闭环系统经典控制中采用输出（和输出导数）反馈（图5-1 ）:其控制规律为：u二-Fy v F为标量，v为参考输入（5-2）x 二Ax Bu 二Ax B （- Fy V （A-BFC）x Bv可见，在经典控制中，通过适当选择F ,可以利用输出反馈改善系统的动态性能现代控制中采用状态反馈（图5-2 ）:其控制规律为：u - -Kx v，K〜m n （5-3）（K的行=u的行，K的列=x的行）称为状态反馈增益矩阵。
状态反馈后的闭环系统S K =（A K，B,C）的状态空间表达式为x =（A-BK）x Bv = A K X Bv y = Cx （5-4）式中：|A K三A-BK若K -FC ，“状态反馈”退化成“输出反馈”，表明“输出反馈”只是“状态反馈”的一种特例，因此，在经典控制理论中的输出反馈”(比例控制P )和 输出导数反馈”(微分控制D )能实现的任务，状态反馈必能实现，反之则未必。
控制系统的极点配置设计法
3其它极点配置原则
系统传递函数极点在s平面上的分布如图（a）所示。极点S3距
虚轴距离不小于共轭复数极点Si、S2距虚轴距离的5倍，即
Res^| 5Resi5n（此处，n对应于极点Si、S2）；同时，极点Si、
S2的附近不存在系统的零点。由以上条件可算出与极点S3所对应的过
渡过程分量的调整时间为
°N2A I
式中，o为真空磁导率，N为线圈匝数，A为铁心与气隙的横截面面 积，I为电流，x为气隙大小.
设转子处于平衡位置时的气隙为go，当转子离开平衡位置向电磁 铁方向产生偏移量x，则通过减小流进绕组的电流i来调节使转子回 复到平衡位置，把电流表示成I 10i。在转子位移变化很小（xvvg。） 时，将其线性化得
FxKxx Kii（2）
3222
式中，Kx0A'1。为位移刚度系数；KiOAN2I0为电流刚度系数。
2g°2g°
其拉普拉斯变换为：
Fx(s) KxX(s) Kil(s)
2.电磁绕组端电压方程
由于常导电磁轴承的转子位移变化时，其自感系数也要变化，即
常导电磁轴承的线圈的电感系数是转子位移x的函数，因此其端电压
、极点配置原理
控制系统的极点配置设计法
1•性能指标要求
Mp=占七x100%
当2 0.05时,ts
;当A=0.02时，tsFra bibliotek2.极点选择区域
K
_!VX
L
—gs0
J
1
1
1
1
1
J”
MM,
^2
0<f< L
* Jwd
主导极点:
s=coa
= lasjd
图3.22系统在S平面上满足
状态反馈极点配置基本理论与方法
第2章 状态反馈极点配置设计基本理论2.1引言大多数的控制系统的基本结构是由被控对象和反馈控制器构成的闭环系统。
反馈的基本类型包括状态反馈和输出反馈。
其中状态反馈能够提供更加丰富的状态信息。
状态反馈是将系统的每一个状态变量乘相应的反馈系数，然后反馈到输入端与参考输入相加形成的控制规律，作为被控系统的控制输入。
图2.1是一个多输入多输出线性时不变系统状态反馈的基本结构：图2.1 多输入-多输出系统的状态反馈结构图其中受控系统的状态空间表达式为：x Ax Buy Cx=+= (2.1)由图2.1可知，加入状态反馈后，受控系统的输入为：u Fx v =+ (2.2)其中v 为参考输入，F 为状态反馈增益阵，因此可以得到状态反馈闭环系统的状态空间表达式：()x A BF x Bv y Cx=++= (2.3)闭环系统的传递函数矩阵：()()1s W s C sI A BF B -=-+⎡⎤⎣⎦ (2.4)由此可见，引入状态反馈后，通过F 的选择，可以改变闭环系统的特征值，是系统获得所要求的性能。
2.2极点配置方法的选择对于一个线性时不变系统进行状态反馈极点配置，一般有四种方法： （1） 传统方法—将系统转化为一个或多个单输入单输出系统。
（2） 直接法—使用稳定的酉矩阵，将这种系统转化为标准型。
（3） 矩阵方程法—对矩阵F ，直接解方程AX X BG -Λ= (2.5a) FX G = (2.5b)（4） 特征向量法—先找到特征向量x j （等式(2.5)中矩阵X 的列向量），然后利用等式(2.5b)求解F 。
方法（1）一般难以应用或者数值不稳定。
方法（3）需要解(2.5a)方程，并且对于系统矩阵A 的特征值不能再分配。
最有效并且数值稳定的方法是方法（2）和方法（4）。
其中方法（4）通过使用一系列的迭代算法找到最优解，所以比较复杂。
对于方法（2），当系统的输入多于一个信号输入时，不能确定系统的鲁棒性。
现代控制理论-第四章 极点配置问题
现代控制理论-第四章极点配置问题第四章线性定常系统的综合第四章线性定常系统的综合内容：4.1 线性反馈控制系统的基本结构及其对系统特性的影响4.2 SISO系统的极点配置4.3 系统镇定问题4.4 系统解耦问题4.5 状态观测器4.6 利用状态观测器实现状态反馈前面介绍的内容都属于系统的描述与分析。
系统的描述：主要解决系统的建模、各种数学模型(时域、频域、内部、外部描述)之间的相互转换等。
系统的分析：主要研究系统的定量变化规律(如状态方程的解，即系统的运动分析等)和定性行为(如能控性、能观测性、稳定性等)。
在本章中，将主要讨论在不同形式的性能指标下线性定常系统的反馈控制规律的综合方法，包括建立可综合的条件及建立控制规律及其算法。
综合与设计问题：在已知系统结构、参数(被控系统数学模型) 及期望的系统运动形式或特征的基础上，确定施加于受控系统的控制规律与参数，称为综合。
当系统以状态空间描述以后，系统的状态含有系统的全部运动信息。
若将控制信号设计为状态与参考信号的函数形成闭环控制，便可得到相当好的控制效果。
无论在抗扰动或抗参数变动方面，反馈系统的性能都远优于非反馈系统。
综合问题中的性能指标可区分为非优化型性能指标和优化型性能指标两种类型，它们都规定着综合所得系统运动过程的期望性能。
两者的差别是：非优化指标是—类不等式型的指标，即只要性能值达到或好于期望指标就算实现了综合目标；优化型指标则是一类极值型指标，综合目的是要使性能指标在所有可能值中取极值。
本章讨论的综合问题主要涉及的是非优化型指标，它们可能以一组期望的闭环系统极点作为性能指标，来讨论极点配置问题。
系统运动的状态也即其动态性能，主要是由系统的极点位置所决定。
把闭环极点组配置到所希望的位置上，实际上等价于使综合得到的系统的动态性能达到期望的要求。
以渐近稳定作为性能指标，主要讨论各种反馈结构对系统稳定性的影响。
使“多输入—多输出”系统实现“一个输入只控制相应的某个输出”作为性1第四章线性定常系统的综合能指标，其相应的综合问题即为解耦控制问题。
自控原理实验极点配置
实验3 控制系统极点的任意配置一、实验目的1. 掌握用全状态反馈的设计方法实现控制系统极点的任意配置2. 用电路模拟的方法，研究参数的变化对系统性能的影响二、实验设备1.THSSC-4型信号与系统·控制理论·计算机控制技术实验箱2.PC机一台(含上位机软件)、USB数据采集卡、37针通信线1根、16芯数据排线、USB接口线三、实验内容1. 用全状态反馈实现二阶系统极点的任意配置，并用电路模拟的方法予以实现2. 用全状态反馈实现三阶系统极点的任意配置，并通过电路模拟的方法予以实现四、实验原理由于控制系统的动态性能主要取决于它的闭环极点在S平面上的位置，因而人们常把对系统动态性能的要求转化为一组希望的闭环极点。
一个单输入单输出的N阶系统，如果仅靠系统的输出量进行反馈，显然不能使系统的n个极点位于所希望的位置。
基于一个N阶系统有N个状态变量，如果把它们作为系统的反馈信号，则在满足一定的条件下就能实现对系统极点任意配置，这个条件就是系统能控。
理论证明，通过状态反馈的系统，其动态性能一定会优于只有输出反馈的系统。
设系统受控系统的动态方程为=Axbux+y=cx图3-1为其状态变量图。
图3-1 状态变量图令Kx r u -=，其中]...[21n k k k K =，r 为系统的给定量，x 为1⨯n 系统状态变量，u 为1×1控制量。
则引入状态反馈后系统的状态方程变为bu x bK A x+-=)( 相应的特征多项式为)](det[bK A SI --，调节状态反馈阵K 的元素]...[21n k k k ，就能实现闭环系统极点的任意配置。
图3-2为引入状态反馈后系统的方框图。
图3-2 引入状态变量后系统的方框图1. 典型二阶系统全状态反馈的极点配置二阶系统方框图如3-3所示。
图3-3 二阶系统的方框图1.1 由图得)15.0(10)(+=S S S G ，然后求得：223.0=ξ，%48≈p δ同时由框图可得：2115.01)(X S X R =+- ，2110X X = 所以：R X X X 222212+--= R X X ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=2022100[]X X y 011==1.2 系统能控性[]242200=⎥⎦⎤⎢⎣⎡-=rank Ab b rank 所以系统完全能控，即能实现极点任意配置。
状态反馈的极点配置
东南大学自动化学院实验报告课程名称：自动控制基础实验名称：控制系统极点的任意配置院（系）：自动化学院专业：自动化姓名：吴静学号：08008419实验室：实验组别：同组人员：实验时间：2011年4月29日评定成绩：审阅教师：一、实验目的1. 掌握用状态反馈的设计方法实现控制系统极点的任意配置；2. 用电路模拟的方法，研究参数的变化对系统性二、实验原理内容用全状态反馈实现二阶系统极点的任意配置，并用电路模拟的方法予予以实现； 理论证明，通过状态反馈的系统，其动态性能一定会优于只有输出反馈的系统。
设系统受控系统的动态方程为bu Ax x+= cx y =图6-1为其状态变量图。
图6-1 状态变量图令Kx r u -=，其中]...[21n k k k K =，r 为系统的给定量，x 为1⨯n 系统状态变量，u 为11⨯控制量。
则引入状态反馈后系统的状态方程变为bu x bK A x+-=)( 相应的特征多项式为)](det[bK A SI --，调节状态反馈阵K 的元素]...[21n k k k ，就能实现闭环系统极点的任意配置。
图6-2为引入状态反馈后系统的方框图。
图6-2 引入状态变量后系统的方框图实验时，二阶系统方框图如6-3所示。
图6-3 二阶系统的方框图引入状态反馈后系统的方框图如图6-4所示。
根据状态反馈后的性能指标：20.0≤p δ，s 5.0T p ≤，试确定状态反馈系数K1和K2图6-4 引入状态反馈后的二阶系统方框图三、实验步骤1．引入状态反馈前根据图6-3二阶系统的方框图，设计并组建该系统相应的模拟电路，如图6-9所示。
图6-9 引入状态反馈前的二阶系统模拟电路图在系统输入端加单位阶跃信号，用上位机软件观测c(t)输出点并记录相应的实验曲线，测量其超调量和过渡时间。
2．引入状态反馈后请预先根据前面给出的指标计算出状态反馈系数K1、K2。
根据图6-4引入状态反馈后的二阶系统的方框图，设计并组建该系统相应的模拟电路，如图6-10所示。