现代控制理论-第四章 极点配置问题
控制系统的极点配置设计法
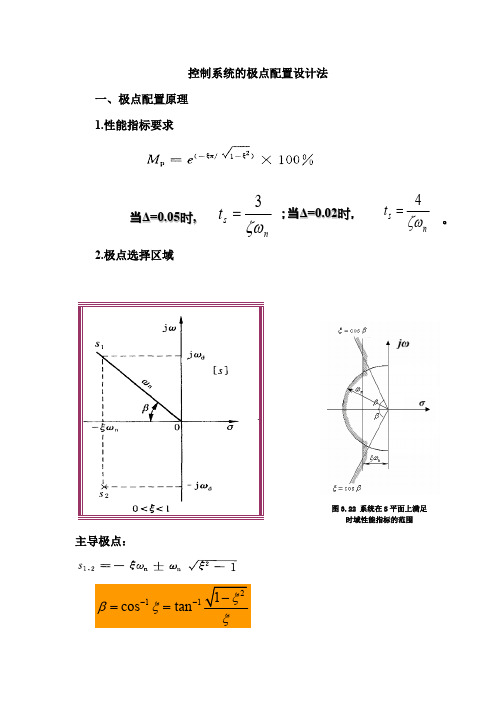
控制系统的极点配置设计法一、极点配置原理1.性能指标要求n s t ζω4=;当Δ=0.02时,。
ns t ζω3= 当Δ=0.05时,2.极点选择区域主导极点:2111cos tan ξβξξ---==3.其它极点配置原则系统传递函数极点在s 平面上的分布如图(a )所示。
极点s 3距虚轴距离不小于共轭复数极点s 1、s 2距虚轴距离的5倍,即(此处,对应于极点s 1、s 2);同时,极点n s s ξω5Re 5Re 13=≥ξn ωs 1、s 2的附近不存在系统的零点。
由以上条件可算出与极点s 3所对应的过渡过程分量的调整时间为1351451s n s t t =⨯≤ξω式中是极点s 1、s 2所对应过渡过程的调整时间。
1s tn x o (t)(a )(b系统极点的位置与阶跃响应的关系图(b )表示图(a )所示的单位阶跃响应函数的分量。
由图可知,由共轭复数极点s 1、s 2确定的分量在该系统的单位阶跃响应函数中起主导作用,即主导极点。
因为它衰减得最慢。
其它远离虚轴的极点s 3、s 4、s 5所对应的单位阶跃响应衰减较快,它们仅在极短时间内产生一定的影响。
因此,对系统过渡过程进行近似分析时。
可以忽略这些分量对系统过渡过程的影响。
二、极点配置实例磁悬浮轴承控制系统设计1.1磁悬浮轴承系统工作原理图1是一个主动控制的磁悬浮轴承系统原理图。
主要由被悬浮转子、传感器、控制器和执行器(包括电磁铁和功率放大器)四大部分组成。
设电磁铁绕组上的电流为I0,它对转子产生的吸力F和转子的重力mg相平衡,转子处于悬浮的平衡位置,这个位置称为参考位置。
(a)(b)图1 磁悬浮轴承系统的工作原理Fig.1 The magnetic suspension bearing system principledrawing假设在参考位置上,转子受到一个向下的扰动,转子就会偏离其参考位置向下运动,此时传感器检测出转子偏离其参考位置的位移,控制器将这一位移信号变换成控制信号,功率放大器又将该控制信号变换成控制电流I0+i,控制电流由I0增加到I0+i,因此,电磁铁的吸力变大了,从而驱动转子返回到原来的平衡位置。
极点配置问题

5.2 极点配置问题5.2.1 问题提出控制系统的性能主要取决于系统极点在根平面上的分布。
因此,作为综合系统性能指标的一种形式,往往是给定一组期望极点,或者根据时域指标转换成一组等价的期望极点。
极点配置问题,就是通过选择反馈增益矩阵,将闭环系统的极点恰好配置在根平面上所期望的位置,以获得所希望的动态性能。
在经典控制理论中所介绍的根轨迹法就是一种极点配置法,不过它只是通过改变一个参数使闭环系统的极点沿着某一组特定的根轨迹曲线配置而已。
因此,广义地说,不论综合系统的性能指标怎样不同,究其实质都是运用各种技术手段来实现系统极点零点的重新配置,以期获得所期望的性能。
本节讨论在指定极点分布的情况下,如何设计反馈增益阵的问题。
为简单起见,只讨论单输入—单输出系统。
5.2.2 状态反馈与极点配置定理三 采用状态反馈对系统()0,,A B C =∑任意配置极点的充要条件是0∑完全能控。
证明 只证充分性。
若∑完全能控,通过状态反馈必成立[]*det ()()I A bK f λλ-+= (5.26) 式中*()f λ—期望特征多项式。
***1*1101()()nn n in i f a a a λλλλλλ--==-=++++∏ (5.27)式中*(1,2,,)i i n λ= —期望的闭环极点(实数极点或共轭复数极点)。
① 若∑完全能控,必存在非奇异变换CI x T x = 式中CI T —能控标准I 型变换矩阵。
能将∑化成能控标准I 型x+xA bu =y Cx =式中 1012101000010CI CI n A T AT a a a a --⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥----⎣⎦1001CI b T b -⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦[]011=C CI n C T b b b -=受控系统∑的传递函数为121121001110()=()n n n n n n n b s b s b s b W s C sI A b s a s a s a -------++⋅⋅⋅++-=++⋅⋅⋅++ (5.28) ② 加状态反馈增益阵 011n K k k k -⎡⎤=⎣⎦ (5.29)可求得对x 的闭环状态空间表达式()+x A bK x bu y Cx ⎫=+⎪⎬=⎪⎭(5.30)式中 0110110100001001()()()n n A b K a k ak a k --⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥------⎣⎦闭环特征多项式为()()f I A bK λλ=-+1110110()()()n n n n a k a k a k λλλ---=+-++-+- (5.31) 闭环传递函数为1212101110110()=()()()n n n n k n n n n b s b s b s b W s s a k s a k s a k -------++⋅⋅⋅+++-+⋅⋅⋅+-+- (5.32) ③ 使闭环极点与给定的期望极点相符,必须满足 *()()f f λλ=由等式两边同次幂系数对应相等,可解出反馈阵各系数*(0,1,,1)i i i k a a i n =-=- (5.33)于是得 ***001111n n K a a a a a a --⎡⎤=---⎣⎦ ④ 最后,把对应于X 的K ,通过如下变换,得到对应于状态X 的K 。
现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Prepared on 22 November 2020《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有相应的模拟结构图如下: 1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图 (2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P(或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P )当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为(1)⎥⎦⎤⎢⎣⎡=11b解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
现代控制理论实验指导书4-极点配置

现代控制理论实验指导书4-极点配置实验五利⽤MATLAB 求解极点配置问题实验⽬的:1、学习极点配置状态反馈控制器的设计算法;2、通过编程、上机调试,掌握系统极点配置设计⽅法。
实验原理:给定⼀个连续时间系统的状态空间模型:xA xB u =+ (5.1)其中:nx R ∈是系统的n 维状态向量,mu R ∈是m 维的控制输⼊,A 和B 分别是适当维数的已知常数矩阵。
在状态反馈u K x =- (5.2)作⽤下,闭环系统的状态⽅程是()xA B K x =- (5.3)由线性时不变系统的稳定性分析可知,闭环系统(5.3)的稳定性由闭环系统矩阵A B K -的特征值决定,即闭环系统(5.3)渐近稳定的充分必要条件是矩阵A B K -的所有特征值都具有负实部。
⽽由经典控制理论知道,矩阵A B K -的特征值也将影响诸如衰减速度、振荡、超调等过渡过程特性。
因此,若能找到⼀个适当的矩阵K ,使得矩阵A B K -的特征值位于复平⾯上预先给定的特定位置,则以矩阵K 为增益矩阵的状态反馈控制器(5.2)就能保证闭环系统(5.3)是渐近稳定的,且具有所期望的动态响应特性。
这种通过寻找适当的状态反馈增益矩阵K ,使得闭环系统极点(即矩阵A B K -的特征值)位于预先给定位置的状态反馈控制器设计问题称为是状态反馈极点配置问题,简称为极点配置问题。
对给定的线性定常系统(5.1)和⼀组给定的期望闭环极点12{,,}n λλλΩ= ,按以下步骤可以设计出使得闭环系统(5.3)具有给定极点}12{,,}n λλλΩ= 的状态反馈控制器(5.2)。
第1步:检验系统的能控性。
如果系统是能控的,则继续第2步。
第2步:利⽤系统矩阵A 的特征多项式1110det()n n n I A a a a λλλλ---=++++确定011,,,n a a a - 的值。
第3步:确定将系统状态⽅程变换为能控标准形的变换矩阵T 。
若给定的状态⽅程已是能控标准形,那么1T =。
现代控制理论 极点配置

− −
= [ − − A − ]
= [ − − + ( − )( )]
ഥ−
ഥ
ഥ )]
= [ − (
ഥ −
其中, = , 即 =
这说明对于任意给定的期望极点 ∗ ,∗ , ⋯ ,∗ ,都可以找到状态反馈矩阵
,
= 2
1 3
满秩,系统是完全能控的,可由状态反馈任意配置系统的闭环极点。
(2)闭环系统的期望特征多项式为 :
∗ = ( − 1 )( − 2 ) = 2 + 2 + 5
(3)设状态反馈阵为: =
− −
=
−
−2
4Hale Waihona Puke ,则状态反馈控制系统的特征多项式为:
二. 状态反馈极点可配置的条件
定理:线性定常系统
ሶ =A+B , 0 = , ≥0
=
可通过状态反馈 = − + 任意配置全部极点的充要条件是系统完全能控。
5.2
极点配置问题
证明:充分性(只讨论单输入单输出系统)
已知系统为完全能控,证明可任意配置极点。
即通过状态反馈必成立 − −
1. 利用非动态输出反馈 = − + ,不能任意地配置系统的全部极点。
以单输入单输出系统为例,设受控系统的传递函数为 (),则输出反馈系统的传递函
数为:
()
=
1 + ()
因此,闭环系统的根轨迹方程为: 1 + =
当从0到∞ 变化时,就得到了闭环系统的根轨迹。
5.2
极点配置问题
三.单输入单输出系统状态反馈极点配置的算法
《现代控制理论基础》讲义教案第4章.docx

III、综合部分第四早线性多变量系统的综合与设计4.1引言前面我们介绍的内容都属于系统的描述与分析。
系统的描述主要解决系统的建模、各种数学模型(时域、频域、内部、外部描述)Z间的相互转换等;系统的分析,则主要研究系统的定量变化规律(如状态方程的解,即系统的运动分析等)和定性行为(如能控性、能观测性、稳定性等)。
而综合与设计问题则与此相反,即在己知系统结构和参数(被控系统数学模型)的基础上,寻求控制规律,以使系统具有某种期望的性能。
一般说来,这种控制规律常取反馈形式,因为无论是在抗干扰性或鲁棒性能方面,反馈闭环系统的性能都远优于非反馈或开环系统。
在本章中,我们将以状态空间描述和状态空间方法为基础,仍然在吋域中讨论线性反馈控制规律的综合与设计方法。
4. 1. 1问题的提法给定系统的状态空间描述若再给定系统的某个期望的性能指标,它既可以是时域或频域的某种特征量(如超调量、过渡过程时间、极、零点),也可以是使某个性能函数取极小或极大。
此时,综合问题就是寻求一个控制作用u,使得在该控制作用下系统满足所给定的期望性能指标。
对于线性状态反馈控制律u = -Kx + r对于线性输岀反馈控制律u = -Ffy + r其中r e R'为参考输入向量。
由此构成的闭环反馈系统分别为x - {A- BK)x+ Br y-Cx或x = {A-BHC)x+Br y = Cx闭坏反馈系统的系统矩阵分别为九=A — BKA H=A-BHC即工K = (A—BK,B,C)或工〃=(A—BHC,B,C)°闭环传递函数矩阵G K⑶=C '[si-(A-BK)Y] BG H G) = C_,[si-(A-BHOf B我们在这里将着重指出,作为综合问题,将必须考虑三个方面的因素,即1)抗外部干扰问题;2)抗内部结构与参数的摄动问题,即鲁棒性(Robustness)问题;3)控制规律的工程实现问题。
一般说来,综合和设计是两个有区别的概念。
线性系统的状态反馈及极点配置

线性系统的状态反馈及极点配置1.前言随着现代控制理论的不断发展和成熟,线性系统的状态反馈控制在控制理论中得到了广泛的应用,并成为了控制领域中重要的一种控制方法。
状态反馈控制能够将系统的状态进行反馈,并利用反馈得到的信息对系统进行控制,从而达到使系统达到预期控制目标的目的。
本文将从状态反馈控制的原理和实现方法两方面介绍线性系统的状态反馈及极点配置。
2.状态反馈控制的原理状态反馈控制是建立在现代控制理论的基础上的一种高级控制方法。
状态反馈控制的基本思想是在系统中引入反馈环节,设计一个反馈控制器,将系统的状态量反馈给控制器,控制器再根据反馈信号输出控制量,以期望控制系统按照预期的运动轨迹运行。
因此,状态反馈控制要实现以下两个步骤:- 系统状态量的测量:首先要在系统中安装测量传感器,实时地测量系统状态量,使得状态量可以被反馈到控制器中。
- 反馈控制器的设计:设计一个反馈控制器,将系统的状态量反馈给控制器,控制器再根据反馈信号输出控制量,实现对系统的精确控制。
因此,状态反馈控制的基本原理就是将系统状态量反馈到控制器中,以期望控制系统按照预期的运动轨迹运行。
2.2 状态空间模型与状态反馈控制状态空间模型是状态反馈控制的基础。
状态空间模型是一种方便描述线性系统动态行为和控制器的模型。
对于线性时不变系统,我们可以用如下的状态变量描述:x(t) = [x1(t),x2(t),...,xn(t)]T其中,x(t) 是系统在时刻 t 的状态量,n 是状态量的数量,x1(t),x2(t),...,xn(t) 分别是系统的每个状态量。
状态空间模型可以用一组线性常微分方程描述:dx/dt = Ax + Bu其中,A 是系统的状态方程矩阵,B 是输入矩阵,C 是输出矩阵,D 是直接耦合矩阵。
系统的状态反馈控制可以表示为:u(t) = -Kx(t)其中,K 是状态反馈矩阵。
将状态反馈控制引入到状态空间模型中,可以得到控制器的状态空间模型为:y = Cx上述控制器的状态空间模型就是一个闭环系统,通过反馈控制器将系统状态返回到系统,形成了一个反馈环。
极点配置的原理

极点配置的原理今天来聊聊极点配置的原理。
我不是一开始就接触到极点配置这个概念的,之前做项目的时候遇到了控制系统的性能优化问题,就开始研究起它来了。
极点配置就像是给控制系统这个大机器调音一样。
咱们先从生活现象说起,想象一下开车。
汽车有个速度控制系统,我们想要汽车的速度按照我们期望的方式变化,比如说快速稳定地达到一个设定速度,并且在遇到一些小干扰(像路面有点小坡度)的时候还能保持稳定。
这个时候极点配置就像调整汽车的“脾气秉性”的工具一样。
在控制系统里,系统的特性跟极点的位置密切相关。
从原理上讲呢,极点就是系统传递函数分母等于零的根。
我记得第一次接触这个理论公式的时候,觉得满脑袋都是浆糊。
比如说一个简单的二阶系统,它的极点会影响系统的响应速度和稳定性,就像一个跷跷板,两个极点要处于一个合适的位置,系统才会又快又稳。
这可是我琢磨了好久才有点理解的地方。
说到这里,你可能会问,这个极点怎么才能配置到我们想要的位置呢?这就要用到反馈控制理论了。
就像我们在训练宠物一样,通过反馈(知道宠物做的好不好,然后奖惩)来让系统的特性符合我们的要求。
比如说,通过调整反馈增益,就可以改变极点的位置。
老实说,我一开始也不明白极点配置到底为啥这么重要。
后来遇到好多实际例子才恍然大悟。
实际在航空航天领域,飞行器的姿态控制系统要很精确才行,极点配置就大有用武之地。
合理的极点配置能让飞行器快速准确地调整姿态且保持稳定,就像杂技演员总能在高空钢丝上保持平衡一样。
再讲讲相关的注意事项吧。
极点配置虽然很强大,但并不是随心所欲的,要考虑系统的物理可实现性以及对于外部干扰和不确定性的鲁棒性。
比如说,不能要求汽车做到像火箭那样的加速能力,因为汽车有它的物理限制。
这就像我们人一样,虽然有潜力可以挖掘,但是也有自身的极限。
我觉得极点配置这个原理还有很多可以延伸思考的地方。
比如如何在更加复杂多变的环境下进行适当地极点配置,这就像在不断变化的天气下管理一个大农场,要根据不同情况调整策略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明 由{A, B} 为不完全能控,则必可对其引入线性非奇异变换而进行结构分
解:
10
第四章 线性定常系统的综合
3.极点配置问题 当反馈形式确定之后,极点配置问题就是依据希望的指定极点位置来计算反
3、从输出到 X 处的反馈 方框图如图 4.3 所示
原受控系统动态方程为
图 4.3
⎧X = AX + BU
⎨ ⎩
Y = CX
反馈后,系统的动态方程为
⎧ X = AX + BU − GY = ( A − GC) X + BU
⎨ ⎩
Y = CX
其中 G 为 Gn×l 阵。 l 为 Y 的维数,n 为状态向量的维数。 记为 {A − GC, B,C} ,其传递矩阵为
2、输出反馈 系统的状态常常不能全部测量到,状态反馈方法就有一定的工程限制。在此
3
第四章 线性定常系统的综合
情况下,人们常常采用输出反馈方法。输出反馈的目的首先是使系统闭环成为稳 定系统,然后在此基础上进一步改善闭环系统的性能。
输出反馈方框图如图 4.2 所示。
原受控系统动态方程为
图 4.2
⎧X = AX + BU
综合问题中的性能指标可区分为非优化型性能指标和优化型性能指标两种 类型,它们都规定着综合所得系统运动过程的期望性能。两者的差别是:非优化 指标是—类不等式型的指标,即只要性能值达到或好于期望指标就算实现了综合 目标;优化型指标则是一类极值型指标,综合目的是要使性能指标在所有可能值 中取极值。
本章讨论的综合问题主要涉及的是非优化型指标,它们可能以一组期望的闭 环系统极点作为性能指标,来讨论极点配置问题。系统运动的状态也即其动态性 能,主要是由系统的极点位置所决定。把闭环极点组配置到所希望的位置上,实 际上等价于使综合得到的系统的动态性能达到期望的要求。
GF (s) = C [sI − ( A − BFC ]) −1 B
特点:F:m× l 维; K:m×n 维,由于 m<n,故 F 的可供选择的自由度比 K 小,所以输出反馈效果不如状态反馈,但是比较容易实现。
不难看出,不管是状态反馈还是输出反馈,部可以改变系统状态方程的系数 矩阵 A,但这并不是说两者具有等同的性能。由于状态能完整地表征系统的动态 行为,因而利用状态反馈时,其信息量大而完整,可在不增加系统的维数的情况 下,自由地支配响应持性;而输出反馈仅利用了状态变量的线性组合来进行反馈, 其信息量便较小,所引入的串、并联补偿装置将使系统维数增加,且难于得到任 意期望的响应特性。
SISO 系统,又适于 MIMO 系统。
定理 设受控系统 ∑0 状态方程为
⎧X = AX + BU
⎨ ⎩
Y = CX
要通过状态反馈的方法,使闭环系统 ∑K
⎧ X = ( A − BK ) X + BV
图 4.4 这类系统的典型例子是使用状态观测器的状态反馈系统。这类系统的维数等 于受控系统与动态补偿器二者维数之和。采用反馈连接比采用串联连接容易获得 更好的性能。
二、 反馈结构对系统特性的影响 反馈引入后,系统状态方程的系数矩阵有了变化,对系统的能控性、能观测
性、系统的稳定性、系统的响的影响及对闭环极点位置的影响。 1.对能控性与能观测性的影响
控。
7
第四章 线性定常系统的综合
再来证明状态反馈系统不—定能保持能观测性。对此只需举反例说明,设
∑0 为能观的,但 ∑K 不一定为能观测的。如考察系统:
结论 2 输出反馈的引入能同时不改变系统的能控性和能观性,即输出反馈系统
∑K 为能控(能观测)的充分必要条件是受控系统 ∑0 为能控(能观)。
证 首先,由于对任一输出反馈系统都可找到一个等价的状态反馈系统 K=FC,
一个输出反馈系统的性能,定有对应的状态反馈系统与之等同,因为只需令
4
第四章 线性定常系统的综合
FC=K,这时确定状态反馈增益矩阵 K 是方便的。但是,一个状态反馈系统的性 能,却不一定有对应的输出反馈系统与之等同,这是由于令 K=FC 来确定 F 的解 时,未必能够实现(或者形式上过于复杂而不易实现,或者 F 阵含有高阶导数项 而不能实现,或对于非最小相位的受控对象,如古有右极点,而选择了有校正零 点来加以对消时,便会潜藏有不稳定的隐患,见周凤岐 PP.86-87,93)。不过, 输出反馈所用的输出变量总是容易测得的,因而实现是方便的;而有些状态变量 不便测量或不能测量,需要重构,给实现带来麻烦是需要克服的障碍。因此,若 我们要实现状态反馈,则必须根据可利用的信息 V、Y 来产生状态向量估值。这 种建立近似状态向量的装置,在确定性系统中即为状态观测器,在不确定性系统 中为 Kalman 滤波器。状态观测器理论的建立,拓宽了状态反馈综合方法的应用 范围。
依据极点配置的基本定理可知,如果系统{A, B} 为能控,则必存在状态反馈
增益短阵 K,使得(A—BK)的全部特征值配置到任意指定的一组位置上。当然, 这也包含了使(A—BK)的
Re λi < 0, i = 1, 2, , n
因此,{A, B} 为能控是系统可由状态反馈实现镇定的充分条件。状态反蚀镇
的闭环系统成为稳定系统.就称为镇定。鉴于状态反馈的优越性,这里只讨论状 态反馈的镇定向题。对于线性定常受控系统
9
第四章 线性定常系统的综合
是渐近稳定的,也即其特征值均具有负实部,则称系统实现了状态反馈镇定。在 镇定向题中,综合的目标不是要使闭环系统的极点严格地配置到任意指定的一组 位置上,而是使其配置于复数平面的左半开平面上,因此这类问题属于极点区域 配置问题,是指定极点配置的一类特殊情况。利用这一点,可以很容易导出镇定 向题的相应结论。
反馈后,系统的动态方程为
⎧ X = ( A − BK ) X + BV
⎨ ⎩
Y = CX
其中 K 为 Km×n 阵。m 为 U 的维数,n 为状态向量的维数。 记为 {A − BK, B,C} ,其传递矩阵为
GK (s) = C [sI − ( A − BK ]) −1 B
特点:状态反馈并没有增加系统的维数,通过改变 K,可以选择系统的特征值, 使系统获得所要求的性能
对此,有如下两个结论。 结论 1 状态反馈的引入,不改变系统的能控性,但可能改变系统的能观测性。
也就是说,状态反馈保持了系统的能控性,即闭环系统{A − BK, B,C} 状态 完全能控的充分必要条件是受控系统{A, B,C} 状态完全能控;状态反馈不一定保
6
第四章 线性定常系统的综合
持系统的能观性,即闭环系统{A − BK, B,C} 状态完全观性与受控系统{A, B,C} 状
⎨ ⎩
Y = CX
将系统的控制量 U 取为输出变量 Y 的线性函数
动态输出反馈,简称输出反馈。
反馈后,系统的动态方程为
U = V − FY ,称其为线性非
⎧ X = ( A − BFC) X + BV
⎨ ⎩
Y = CX
其中 F 为 Km×l 阵。m 为 U 的维数, l 为 Y 的维数,n 为状态向量的维数。 记为 {A − BFC, B,C} ,其传递矩阵为
4.1 线性反馈控制系统的基本结构及其对系统特性的影响
无论是在经典控制理论还是在现代控制理论中,反馈都是系统设计的主要方 式。但由于经典控制理论是用传递函数来描述的,因此它只能以输出量作为反馈 量。而现代控制理论由于是采用系统内部的状态变量来描述系统的物理特性,因 而除了输出反馈外,还可采用状态反馈这种新的控制方式。 一、 反馈的两种基本形式
8
第四章 线性定常系统的综合
而巴知状态反馈可保持能控性,从而证明输出反馈的引入不改变系统的能控性。
其次,表示 ∑0 和 ∑K 的能观测判别阵分别为
⎡C ⎤
Qo
⎢
=
⎢ ⎢
CA
⎥ ⎥ ⎥
⎢⎣CAn−1
⎥ ⎦
⎡
C
⎤
和
⎢
QoF
=
⎢ ⎢
C( A − BFC)
⎥ ⎥ ⎥
⎢⎣C
(
A
−
BFC
)
n−1
⎥ ⎦
2.稳定性与镇定 状态反馈和输出反馈都能影响系统的稳定性。加入反馈,使得通过反馈构成
在本章中,将主要讨论在不同形式的性能指标下线性定常系统的反馈控制规 律的综合方法,包括建立可综合的条件及建立控制规律及其算法。
综合与设计问题:在已知系统结构、参数(被控系统数学模型) 及期望的系 统运动形式或特征的基础上,确定施加于受控系统的控制规律与参数,称为综合。
当系统以状态空间描述以后,系统的状态含有系统的全部运动信息。若将控 制信号设计为状态与参考信号的函数形成闭环控制,便可得到相当好的控制效 果。无论在抗扰动或抗参数变动方面,反馈系统的性能都远优于非反馈系统。
第四章 线性定常系统的综合
第四章 线性定常系统的综合
内容: 4.1 线性反馈控制系统的基本结构及其对系统特性的影响 4.2 SISO 系统的极点配置 4.3 系统镇定问题 4.4 系统解耦问题 4.5 状态观测器 4.6 利用状态观测器实现状态反馈
前面介绍的内容都属于系统的描述与分析。 系统的描述:主要解决系统的建模、各种数学模型(时域、频域、内部、外 部描述)之间的相互转换等。 系统的分析:主要研究系统的定量变化规律(如状态方程的解,即系统的运 动分析等)和定性行为(如能控性、能观测性、稳定性等)。
本章最后讨论状态观测器。在状态反馈中,假定所有状态变量如输出量一样 是可以得到的。实际上,这一假定通常是不成立的。因此,若我们要实现状态反 馈,则必须根据可利用的信息来产生状态向量估值。这种建立近似状态向量的装 置,在确定性系统中即为状态观测器,在不确定性系统中为 Kalman 滤波器。状 态观测器理论的建立,拓宽了状态反馈综合方法的应用范围。
