第6章 动力学
第6章操作臂动力学

zc
1 2
w
l
h
C Izz
m (w2 12
l2 )
,
C Ixy 0
第 6 章: 操作臂动力学 6.3 质量分布
其它参量由对称性得出:
m 12
(l
2
h2
)
CI
0
0
0 m (w2 h2) 12
0
0
0
m 12
(l
2
w2
)
第 6 章: 操作臂动力学 6.3 质量分布
惯性张量的其他性质: ---如果由坐标系的两个坐标轴构成的平面为刚体质量分布的 对称平面,则正交于这个对称平面的坐标轴与另一个坐标轴 的惯量积为0. ---惯量距永远是正值,而惯量积可能正,可能负. ---三个惯量距的和保持不变. ---惯性张量的特征值为刚体的主惯量距,相应的特征矢量为 主轴。
h2
)
AI
m wl 4
m hw 4
m wl 4
m (w2 h2) 3
m hl 4
m hw 4
m hl 4
m 3
(l 2
w2
)
惯性张量是坐标系位姿的函数.
第 6 章: 操作臂动力学 6.3 质量分布
平行移轴定理 :
A Izz C Izz m(xc2 yc2 ) A Ixy C I xy mxc yc
刻的角速度、线加速度和角加速度. 可应用迭代方法完成这些计算。 首先对连杆1进行计算,接着计算下一个连杆,这样一直向外迭代到连 杆n – 计算出每个连杆质心的线加速度和角加速度之后,运动牛顿欧拉公式 计算出作用在连杆质心上的惯性力和力矩 .
第 6 章: 操作臂动力学 6.4 牛顿欧拉方程
角速度在连杆之间的“传递问题”:
26第6章第二十六讲 动力学普遍定理-相对动点的动量矩定理
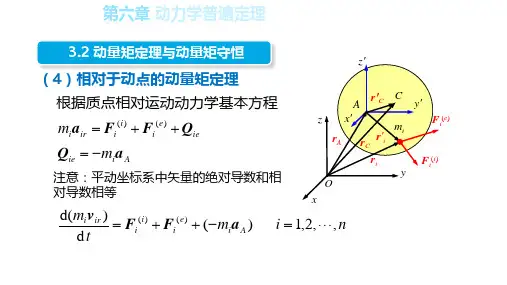
3.2 动量矩定理与动量矩守恒根据质点相对运动动力学基本方程注意:平动坐标系中矢量的绝对导数和相对导数相等(e )(4)相对于动点的动量矩定理iee ii i ir i m Q F F a ++=)()(Ai ie m a Q −=ni m tm A i e i i i ir i ,,2,1)(d )d()()( =−++=a F F v3.2 动量矩定理与动量矩守恒两边叉乘r i ′,并求和(对动点A 取矩)注意到:内力系的主矩等于零;质心计算公式;叉乘性质n i m tm A i e i i i ir i ,,2,1)(d )d()()( =−++=a F F v ()=×′=′=∑∑ir i ir Cii i ie im M m v v r r F[])(d d)(A Ce iiiri iM m ta r Fr v r −×′+×′=×′∑∑是质点系相对动点A是外力系对动点A 的主矩是牵连惯性力的合力对动点A 的力矩注意平动系惯性力合力作用点3.2 动量矩定理与动量矩守恒Ar ir i i m L v r =×′∑ )()(e Ae iiMFr =×′∑ )()(e A A CM Q M a r =−×′d t[∑r i′×m i v ir])(d )(A Ce iiM a r Fr −×′+×′=∑(e )质点系相对动点的动量矩定理=质点系相对动点的动量矩对时间的导数外力系对该点的主矩加在质心上的牵连惯性力的合力对该点之矩+3.2 动量矩定理与动量矩守恒3.2 动量矩定理与动量矩守恒①如果动点为质心C ,则动点的动量矩定理为相对质心的动量矩定理)(d d )(e A e A Ar tQ M M L +=3.2 动量矩定理与动量矩守恒②如果a A = 0,则③如果A 点的加速度方向通过质心,则)(d d )(e A e A Ar tQ M M L +=)(d d e A Ar tM L =)(d d e AAr tM L =3.2 动量矩定理与动量矩守恒④对质心的动量矩守恒定律则对质心的动量矩守恒)(d d e CCr tM L =0)(=e CM()=e Cz M cL =cr constL cz =3.2 动量矩定理与动量矩守恒【例】质量为m半径为r的均质圆盘从静止开始,沿倾角为θ的斜面无滑动的滚下。
6第六章 发酵动力学

2.随着时间的延长,培养液中微生物细胞的 量c’(X)增加,但细胞的浓度却保持不变,即
dc(X) dt
= 0
3.因而µ≌D
这种微生物细胞的培养状态称为 ——“准恒定状态”
在“ቤተ መጻሕፍቲ ባይዱ恒定状态”下
c(S) ≈ DKs µm - D (4)
c’(X) = c0’(X) + F · Yx/s · c ’0 (S) · t 补料液浓度
动力学方程
c0(S)——开始时培养基中限制性基质的浓度 g/L F——培养基的流速 L/h V——培养基的体积 L F/V=D——稀释率 c0(X)——刚接种时培养液中的微生物细胞浓度 g/L c(X)——某一瞬间培养液中微生物细胞浓度 g/L c(X) = c0(X) + Yx/s [c0 (S) -c (S)]
v =
µ
YG
v =
+ m +
Qp Yp
+
(6)
µ Yx/s
(5)
少量的其他代谢产物和其他忽略 1 Yx/s 1 m + µ (7)
=
YG
YG和m很难直接测定,只要得出细胞在不同 比生长速率下的Yx/s,可根据(7)式用作图法 求出YG和m值。 YG和m值用于衡量发酵时限制性营养基质的 起始最低浓度。
µ µm
b µm/2
c
µ =
a
µm c(S)
Ks + c(S)
c(S)
Ks
Ks的物理意义
Ks的大小表示了微生物对营养物质的吸收亲 和力大小 Ks越大,表示微生物对营养物质的吸收亲 和力越小; Ks越小,表示微生物对营养物质的吸收亲 和力越大
发酵工程 第6章 发酵动力学

■将细胞作为与培养液分离的生物相处理所建立的模 型为分离化模型。在细胞浓度很高时采用。
如果把细胞和培养液视为一相,建立的模型为均一化 模型。
非结构模型
结构模型
最理想情况
确定论模型 不考虑细胞内部结构
各种细胞均一
均衡 细胞之间无差异, 生长 是均一的,细胞内
如果在考虑细胞组成变化的基础上建立的模型,称为结 构模型,一般选取RNA、DNA、糖类及蛋白含量做为过 程变量。
■菌体视为单组分的模型为非结构模型,通过物料平 衡建立超经验或半经验的关联模型。
如果细胞内的各种成分均以相同的比例增加,称为 均衡生长。
如果由于各组分的合成速率不同而使各组分增加比 例不同,称为非均衡生长。
(3)质量平衡法(质量守恒定律)
发酵系统中物 物质进入系统的速度+物质在系统生成的速度 =
质积累的速度 -物质排出系统的速度-物质在系统消耗的速度
研究发酵动力学的步骤
(1). 为了获得发酵过程变化的第一手资料,要尽 可能寻找能反映过程变化的各种理化参数。
(2). 将各种参数变化和现象与发酵代谢规律联系 起来,找出它们之间的相互关系和变化规律。
S ——基质量,mol;
t ——发酵时间,h
注:这里的“维持”是指活细胞群体没有净生长和产物没有净合成的生 命活动,所需能量有细胞物质氧化或降解产生,这种用于“维持”的物 质代谢称为维持代谢(内源代谢),代谢释放的能量叫维持能。
(2)得率系数(或产率,转化率,Y): 是指被消耗的物质和所合成产物之间的量的关系。包括生
基于关键生化反应限速步及其关键酶的动力学特征及其影响因素采用一系列分子水平的方法?细胞层次代谢网络与细胞工厂基于细胞信号传导代谢网络细胞物质运输的系列关键生化反应的综合表现采用一系列细胞水平的方法包括细胞群体行为分析?反应器层次过程工程基于细胞群体生长及产物合成对外部环境综合响应采用一系列优化反应器发酵条件的方法主要针对微生物发酵的表观动力学通过研究微生物群体的生长代谢定量反映细胞群体酶促反应体系的宏观变化速率主要包括
化学动力学第六章链反应动力学

ddC tOkCH3CHO1/2
当n=3/2时,断链方式:CH3+CH3→C2H6
dC dtH4k'CH3CHO3/2
第七节 支链反应
直链反应: 支链反应:在链传递过程中一个旧的自由基的小事往往伴随2个或更多个新
的自由基的产生,是一个自由基数目迅速增殖的过程。反应以爆 炸的形式发生。
1. 引发反应 有机物分子在其最弱的链上产生原始自由基。
2. 持续反应——链传递 原始自由基中的一个自母体分子夺取H形成一个饱和分子和一个外自由基。
3. 断链反应——链中止 自由基复合或歧化
引发: 持续:
断链:
M1 k 1R1+M2 R 1+M 1 k 2 R 1H +R 2 R2 k 3R1+M3 R1+R2 k 4M4
1/2
1/2
2k3k2kk k3 1 5B B rr22 k4H H 2 B rB r22k2k k 11 5 kk43H H B 2 B r2 rB r21/2A 1 H B 2H B B B rr2 2r1 /2
1/ 2
A
2k2
k1 k5
B k4 k3
∴得证
附:H2+X2 → 2HX反应历程的比较
链引发 支链反应步骤 链传递
链中止
2. 链传递:
CH3+CH3CHO→CH4+CH3CO CH3CO→CH3+CO
3. 推测链终止反应: 引发反应一般为一级,总级数为1/2或3/2时: n=1/2时,为SS简单断链或RSM三体断链 n=3/2时,为SS简单断链。
R——简单自由基。S——含2个以上自由基,M——阻化剂。 乙醛热解无需阻化剂,因而不会采用RSM断链方式。
机器人学-第6章_机器人动力学

H 2 L2
0
0
CI
M 12
0 0
W2 H2 0
0
L2 W 2
Z
结果是对角矩阵,此时坐标系{C}的坐标轴是刚体的
惯性主轴。
L X
H Y
W
6
刚体的牛顿-欧拉方程
在动力学分析过程中,把刚体的运动分解为质心的平移运动和绕质心的转动 。一般将连体坐标系的原点固定在刚体的质心,这样坐标原点的运动描述刚 体的平移运动,坐标系的转动描述刚体绕质心的旋转运动。
m2 L1LC 2 s2
K
1
1 2
q&T
M
1
q&
0
m2
L1LC 0
2
s2
&&12
m2
L1LC
2
s2
&12 &1&2
M&q& 2mm22LL11LLCC22ss22&&22
m2
L1LC 0
2
s2&2
&&12
m2
L1LC
2
s2&2 12
1 0
&&12
m2L1LC2s2 2&1&2 &22 m2 L1LC 2 s2&1&2
&1
其中
M11 IC1 IC2 m1L2C1 m2 L12 L2C2 2L1LC2c2
&2
M11 M 21
M M
12 22
&&12
M 21 M12 IC2 m2 (L2C2 L1LC2c2 ) M 22 IC2 mL2C2
机器人学及其智能控制第6章 机器人的动力学
(式 6.10)
下面再用牛顿力学求解,对系统进行受力分析后,很容易就可以得到系统的受力方程为:
F ma
(式 6.11)
其中:
F kx ma
(式 6.12)
整理之后可以得到:
F ma kx
(式 6.13)
很容易得出这样一个结论,对于一个简单系统,用牛顿力学求解更容易,下面我们求解 一个稍微复杂一点的系统。
m2l
cos
m2l
2
sin
L kx x
F (m1 m2 )x m2l cos m2l 2 sin kx
(式 6.20)
(式 6.21) (式 6.22) (式 6.23)
对于旋转运动: 得到:
L
m2l 2
m2lx cos
d dt
L
m2l 2
m2lx
cos
m2lx
sin
L
m2gl sin
(式 6.29)
为方便分析,将其写成矩阵的形式:
F T
m1 m2l
m2
cos
m2l cos
m2l 2
x
0 0
m2l
sin 0
x2
2
kx m2
gl
sin
(式 6.30)
由此可以看出,对于求解复杂系统的运动方程,采用拉格朗日力学进行求解更加方便。
动力学仿真
为了对操作臂的运动进行仿真,必须采用前面建立的动力学模型,由封闭形式的动力学 方程(6.66),可通过仿真求出动力学方程中的加速度
q(t t) q(t) q(t)t 1 q(t)t 2 2
式中,每次迭代要用式(6.67)计算一次 q 。这样,通过输入已知的力矩函数,用数值积分
第六章化学动力学
•
v
def
ξ
V
1 vB V
d nB dt
1 vB
d cB dt
恒 容
(11.1.3)
设将计量反应写作:
νAA νBB . ... νYY νZZ
研究中经常用指定反应物A的消耗速率,或指定产物Z的 生成速率来表示反应的进行速率:
反应物A的消耗速率:
vA
1 V
dnA dt
1 1 .1 . 4
基元反应是组成一切化学反应的基本单元。所谓的反应机 理(或反应历程),是指该反应是由哪些基元反应组成的。
例如,上述①②③个基元反应即构成了总反应:
的反应机理。
H2 + I2 2HI
除非特别注明,一般的化学反应都属于化学计量方程,并 不代表基元反应。
例如:
N2 + 3 H2 2 NH3
它仅指参加反应的各组分在反应中的数量变化符合方程式系 数间的比例关系
质量作用定律只适用于基元反应。对于非基元反应需要分 解为若干个基元反应,然后对每一个基元反应逐个应用质量作 用定律。
在这种情况下,若某一物质同时出现在两个或两个以上的 基元反应中,则对于该物质的净消耗速率或净生成速率为这几 个基元反应的总和。
基元反应
A P A B P 2A B P
反应分子数 单分子反应 双分子反应 三分子反应
另一种定义是所谓的基于浓度的反应速率 v :
•
def
v
ξ
1
dnB
V νB V dt
11.1.2
即用单位时间、单位体积内的化学反应进度来定义反应速率。
反应速率的单位是 mol ·m-3 ·s– 1 。该定义同样与物质B 的选择无关,但与化学计量式的写法有关。
第六章 多底物酶促反应动力学
第六章 多底物 酶促反应动力学
Cleland分析大量动力学数据,总结两条重要规则:
应用Cleland方法方法的关键: 看产物是否抑制和抑制方式,取决 于抑制性产物是P或Q中的哪一个?
如浓度变化的底物是那一个,A或B? 同样,与另一个固定浓度的底物是 否饱和有关。 实验结果与判断结果一致。全部 结果列表于下。
1/v 1 = 1/v 2 Kia /[A][B]1+1/[B]1 )= (Kia /[A][B]2+1/[B]2) Kia/A(1/[B]1-1/[B]2)=- (1/[B]1 -1/[B]2) 1/[A]=-1/Kia
第六章 多底物 酶促反应动力学
1/[A] == 1/Kia 斜率, 截距都可用此法取得。 问题:从作图看出,从直线方程取得的 是复合未知数,要用二次作图法 求出KmA,KmB,Vm。 斜率
第六章 多底物 酶促反应动力学
Cleland分析大量动力学数据,总结两条重 要规则: 1. 浓度变化的底物和一种形式的酶结合, 抑制性产物和另一种形式的酶结合。 双倒数作图,只有纵坐标截距变化。
2. a) 浓度变化的底物和抑制性产物都结合 在同一个酶上。双倒数作图则产生斜率 变化。 b)浓度变化的底物所结合的酶形式和抑 制性产物结合的酶形式间可在酶的反应 历程中通过可逆变化而互相联接。双倒 数作图产生斜率变化。
第六章 多底物 酶促反应动力学
且交点在1/[A]上截距可计算出来。 设有两个固定浓度[B]1,[B]2,有两个
相应的1/v1,1/v2,而且在交点处的截 距相等
第六章 多底物 酶促反应动力学
1
v 1 =
KmB
Vm[B] 1
+
KmA
Vm[A] Vm[A][B] Vm
无机化学 第六章 化学动力学.
3. 实验测得aA + bB →cC + dD的动力学方程式为 r=kca(A)cb(B) ,下列说法错误的是( )
A. 该反应是基元反应 B. 反应级数为a+b C. 对反应物A是a级 D.对反应物 B是b级
4. 已知某反应是放热反应,如果升高温度,则( )
A. k增加,Kθ减小
B. k,Kθ均增加
6. 催化剂可以使反应的( )
A. Kθ增大
B. 反应自由能增大
C. 活化能改变
D. 反应焓减小
7. 反应2NO(g) + Br2(g) →2NOBr(g)的反应历程是: (1) NO(g) + Br2(g) →2NOBr2(g) 快 (2) NO(g) + NOBr2(g) →2NOBr2(g) 慢,则该反应对NO的反应 级数为( )
三、速率常数
速率方程中的 k 称为速率常数,物理意义是速率方程式 中各种物质浓度均为1 mol/L时的反应速率。
速率常数的量纲由速率方程确定,总反应级数不同,单位 不同。
速率常数越大,表明反应进行得越快。但应注意,两个反 应级数不同的反应,对比速率常数的大小是毫无意义的。
速率常数的大小取决于反应物的本质,而与浓度无关。 速率常数是温度的函数,当其他条件相同时,T 升高,则 k 增大。
第6章 化学动力学 6-1 化学反应速率
1. 平均速率: 指反应进程中某时间间隔(t)内反应物浓度的减少或生成
物浓度的增加来表示: r ≡ ︱cB / t︱ 或:r ≡ (1/B )cB / t
2. 瞬时速率
指某一瞬时(时刻)的速率,即时间间隔无限小,t→0时的 平均速率。
r ≡ ︱dcB / dt︱或 r ≡ (1/B )dcB / dt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
刚体的线加速度(1)
坐标系{B}和{A}原点重合,P点的线加速度为:
A A A A VP = B R BVP + A Ω B × A P = B R BVP + A Ω B × B R BP ⇒ A ɺ ɺ ɺ ɺ ɺ ɺ V = AR BV + AR BV + A Ω × A R BP + A Ω × A R BP + AR BP P B P B P B B B
列出平衡方程
牛顿-欧拉迭代动力学方程(5)
整理得到:
通过计算力或力矩在Z方向的分量即可求得关节力矩: 对于转动关节
对于移动关节
牛顿-欧拉迭代动力学方程(6)
题目:一连杆动力学方程
首先,确定牛顿-欧拉公式中各 参量的值。连杆质心位置矢量 为:
1
g
Pc = [a / 2,0,0]T
0 0 0 ma C I1 = 0 1 0 12 0 0 1
ɺ N = Iω + ω× Iω
c c
牛顿-欧拉迭代动力学方程(2)
连杆i+1角速度和角加速度
i +1
ɺ ˆ ωi +1 = i +i1R iωi + θ i +1 i +1Z i +1
i +1
ɺ ɺ ˆ ɺ ɺ ωi +1 = i +i1R iωi + i +i1R iωi + θɺi +1 i +1Z i +1
(
B
A A A A ɺ ɺ A = A Ω B × B R BVP + B R BVP + A Ω B × B R BP + A Ω B × A Ω B × B R BP + B R BVP ⇒ A ɺ ɺ ɺ V = AR B V + A Ω × A R B P + A Ω × A Ω × A R B P + 2 A Ω × A R B V P B P B B B B B B B P
i +1
ɺ i +1×i +1PCi +1 + i +1ωi +1 ×( i +1ωi +1×i +1PCi +1 )+ i +1vi +1 ɺ ɺ vCi +1 = ω
i +1 0
ɺ ω0 = 0 ω0 = 0
教材P137页式(6-34) (6-36)有误
牛顿-欧拉迭代动力学方程(4)
得到连杆质心线加速度和角加速度 后,运用牛顿-欧拉公式便可求出作 用在连杆质心上的惯性力和力矩。即
题目:RP连杆动力学方程
0
X1 Z2 Y1 X2
ω0 = 0,0 v0 = 0
0 1 0 0 1 0 ɺ T θ
当P点相对{B}静止时,P点的线加速度简化为:
A A ɺ ɺ ɺ A VP = AVBORG + A Ω B × B R BP + A Ω B × A Ω B × B R BP
P132页,式(6-12)有误。
刚体的角加速度
坐标系{B}相对{A}转动 ,坐标系{C}相对{B},则A
A A Ω c = A Ω B + B R B ΩC
A Aɺ A A Aɺ A A ɺ ɺ P = AVP = B R BP + B R BP⇒ R )T A P = B R BVP + A Ω B × A P
坐标系{B}和{A}原点不重合,其在另一个坐标系{A}中的描述为 AP=A R BP+AP B BORG。那么P点的速度为:
2
在坐标系{1}中的惯性张量为:
其余:
ɺ ɺ f 2 = n2 = 0; ω0 = ω0 = 0; v0 = [− g ,0,0]
0
T
题目:一连杆动力学方程(2)
旋转变换阵为:
cθ 0 1 R = sθ 0 − sθ cθ 0 0 0 1
应用方程(6-45)-(6-53)对连杆1向外迭代法求解如下:
C为
坐标系{C}相对{A} 的角加速度为:
A Aɺ A ɺ ɺ ɺ Ωc = A Ω B + B R B ΩC + B R B ΩC ⇒ A ɺ ɺ ɺ Ω = A Ω + A Ω × A R B Ω + AR B Ω c B B B C B
C
刚体的质心、惯性张量
物体的质心定义为:
c= 1 A ∫ PρdV mV
ɺ ˆ ˆ ɺ ɺ = i +i1R iωi − θ i +1 i +1Z i +1×i +i1R iωi + θɺi +1 i +1Z i +1 ɺ ɺ ˆ ˆ ɺ = i +1R iω + i +1R iω × θ i +1Z + θɺ i +1Z
i i i i i +1 i +1 i +1 i +1
上式称为欧拉-拉格朗日方程。
拉格朗日动力学方程(2)
对于操作臂第i个连杆的动能可表达为:
整个系统的动能为各个连杆动能之和: 速度的函数 对于操作臂第i个连杆的势能可表达为:
它是关节位置和
整个系统的动能为各个连杆势能之和: 函数
它是关节位置的
拉格朗日动力学方程(3)
操作臂的拉格朗日函数可表达为:
操作臂运动方程为:
A
ɺ AR T Ω B ×= R B
A B
( )
0 = Ωz − Ω y
− Ωz 0 Ωx
Ωy − Ωx 0
于是有:AVP = A Ω B × A P 坐标系{B}相对于{A}的角速度等于,B到A的旋转矩阵的微分 乘以B到A的旋转矩阵的转置
刚体的线速度
坐标系{B}和{A}原点重合,假定固定矢量BP相对于坐标系 {B}是时变的,其在另一个坐标系{A}中的描述为AP=ABR BP. 如果坐标系{B}相对于坐标系{A}是旋转的,即 ABR是时变 的。那么P点的速度为:
第六章 动力学
动力学是机器人控制的基础,本章将考虑由 驱动器施加的力矩使操作臂运动。 解决问题: 已知关节的位置、速度和加速度,求出驱动关节 运动所需的力矩矢量; 方法: 牛顿-欧拉法 拉格朗日法
刚体的角速度
坐标系{B}和{A}原点重合,假定固定矢量BP相对于坐标系 {B}是不变的,其在另一个坐标系{A}中的描述为AP=ABR BP. 如果坐标系{B}相对于坐标系{A}是旋转的,即 ABR是时变 A ɺ ɺ ɺ A ɺ A 的。那么P点的速度为:P = AVP = BAR BP⇒ AVP = BAR( B R) −1 A P⇒ AVP = BAR( B R)T A P 定义角速度矢量 A Ω B = [Ω x Ω y Ω z ]T
式中m是物体的质量,ρ是密度 坐标系{A}中物体的惯性张量为:
平等轴定理
坐标系{C}是以刚体的质心为原点,坐标系{A}与{C}平行,那么 惯性张量AI和CI存在在下关系:
A
式中:m为物体质量,Pc = [xc 1 0 0 中的位置。E3 = 0 1 0 0 0 1
I = C I + m( PcT Pc E3 − Pc PcT )
(
B
)
)
相对加速度
转动加速度
向心加速度
科氏加速度
牵引加速度
刚体的线加速度(2)
坐标系{B}和{A}原点不重合,P点的线加速度为:
A A A A ɺ ɺ ɺ ɺ A VP = AVBORG + B R BVP + A Ω B × B R BP + A Ω B × A Ω B × B R BP + 2 A Ω B × B R BVP
yc
zc ] 表示刚体质心在坐标系{ A}
T
一般是通过测量装置来得到连杆的惯性张量。
长方体的惯性张量
牛顿-欧拉迭代动力学方程(1)
问题:已知关节的位置、速度和加速度,如何计算出驱动关节运 动所需要的力矩 牛顿方程描述了移动物体的力与加速度的关系:
ɺ F = mvC
欧拉方程描述了转动物体的力矩与角速度、角加速度的关系:
题目:一连杆动力学方程(3)
应用方程(6-45)-(6-53)对连杆1向外迭代法求解如下:
ɺ ɺ − gcθ − aθ 2 / 2 − m1 gcθ − m1aθ 2 / 2 ɺ 1 ɺ F1 = m1 aθɺ / 2 + gsθ = m1aθɺ / 2 + m1 gsθ 0 0 0 0 0 0 2 2 ma 0 + ma 1 C 1 1 C 1 ɺ N1 = I1 ω1 + ω1× I1 ω1 = 0 1 0 12 12 ɺ 0 0 1 θɺ 0 ma = 0 12 ɺɺ θ
1
ɺˆ ɺ ɺ ɺ ɺ ˆ ω1 =θ 1Z1 = [0,0, θ ]T ,1ω1 =θɺ1Z1 = [0,0, θɺ]T
cθ sθ 0 − g − gcθ 1 ɺ v1 = − sθ cθ 0 0 = gsθ 0 0 1 0 0 ɺ ɺ ɺ 0 − θɺ 0 a / 2 0 − θ 0 0 − θ 0 a / 2 − gcθ ɺ ɺ ɺ 1 ɺ vc = θɺ 0 0 0 + θ 0 0 θ 0 0 0 + gsθ 0 0 0 0 0 0 0 0 0 0 0 0 ɺ2 ɺ2 0 − aθ / 2 − gcθ − gcθ − aθ / 2 ɺ ɺ = aθɺ / 2 + 0 + gsθ = aθɺ / 2 + gsθ 0 0 0 0
