立体几何中的最值问题(一)
高中数学立体几何中的最值问题专题辅导

高中数学立体几何中的最值问题 海红楼 立体几何主要研究空间中点、线、面之间的位置关系,与空间图形有关的线段、角、体积等最值问题常常在试题中出现。
下面举例说明解决这类问题的常用方法。
一、运用变量的相对性求最值例1. 在正四棱锥S-ABCD 中,SO ⊥平面ABCD 于O ,SO=2,底面边长为2,点P 、Q 分别在线段BD 、SC 上移动,则P 、Q 两点的最短距离为( )A. 55B. 552C. 2D. 1解析:如图1,由于点P 、Q 分别在线段BD 、SC 上移动,先让点P 在BD 上固定,Q 在SC 上移动,当OQ 最小时,PQ 最小。
过O 作OQ ⊥SC ,在Rt △SOC 中,552=OQ 中。
又P 在BD 上运动,且当P 运动到点O 时,PQ 最小,等于OQ 的长为552,也就是异面直线BD 和SC 的公垂线段的长。
故选B 。
图1二、定性分析法求最值例2. 已知平面α//平面β,AB 和CD 是夹在平面α、β之间的两条线段。
AB ⊥CD ,AB=3,直线AB 与平面α成30°角,则线段CD 的长的最小值为______。
解析:如图2,过点B 作平面α的垂线,垂足为O ,连结AO ,则∠BAO=30°。
过B 作BE//CD 交平面α于E ,则BE=CD 。
连结AE ,因为AB ⊥CD ,故AB ⊥BE 。
则在Rt △ABE 中,BE=AB ·tan ∠BAE ≥AB ·tan ∠BAO=3·tan30°=3。
故3≥CD 。
图2三、展成平面求最值例3. 如图3-1,四面体A-BCD 的各面都是锐角三角形,且AB=CD=a ,AC=BD=b ,AD=BC=c 。
平面α分别截棱AB 、BC 、CD 、DA 于点P 、Q 、R 、S ,则四边形PQRS 的周长的最小值是( )A. 2aB. 2bC. 2cD. a+b+c图3-1解析:如图3-2,将四面体的侧面展开成平面图形。
几何中的最值问题

几何中的最值问题作为一门重要的数学学科,几何中有许多重要的概念和方法,其中最值问题是一个广泛研究的内容。
在几何中,最值问题是指在某些条件下,某个几何量(如长度、面积、体积等)的最大值或最小值问题。
本文将从不同角度介绍几何中的最值问题及其应用。
一、最值问题的基础概念在几何问题中,最值问题最常见的便是一些面积、长度和体积的最值问题。
最常见的方法是使用微积分的极值定理,通过计算导数为0的点来找到函数的最大值和最小值。
此外,还有最大和最小的边界问题。
这些问题需要考虑的是给定条件下的最大可行解或最小可行解。
例如,给定一个面积固定的矩形,我们需要求出其长度和宽度的最大或最小值。
这些问题与微积分密切相关,但在解决这些问题时需要更多的几何知识和直觉。
二、平面几何中的最值问题在平面几何中,最值问题通常涉及三角形、四边形和圆形等形状。
这些形状的特性可以用来求解最值问题,通常需要使用各种几何知识和技巧。
例如,对于一个给定面积的三角形,在其周长恒定的情况下,需要求出该三角形的最大或最小长度。
为解决这类问题,我们可以利用三角形的海涅定理或余弦定理,通过微积分的极值定理得到最优解。
对于圆形,最值问题可能涉及到面积和周长问题,这些需要用到圆相关的特点和公式,如半径、直径、周长和面积等,通常需要通过微积分的方法求解。
另一方面,对于四边形最值问题,我们需要利用它们的对角线和相邻边的关系来解决,这通常需要将四边形划分为三角形或矩形来计算。
三、空间几何中的最值问题在空间几何中,最值问题通常涉及立体体积,包括长方体、正方体、棱锥和棱柱等。
这些问题需要利用空间几何的特点和公式来求解,常用的方法包括微积分的极值定理和立体几何的体积计算公式。
例如,对于一个矩形长方体,在其表面积固定的情况下,需要求出其有最大或最小的体积。
如果我们设该矩形长方体的长、宽和高分别为x、y和z,那么该矩形长方体的体积可以表示为V(x,y,z)=xyz。
通过微积分的方法,可以证明只有当x=y=z时,该方体的体积最大。
立体几何中线段长度的最值问题
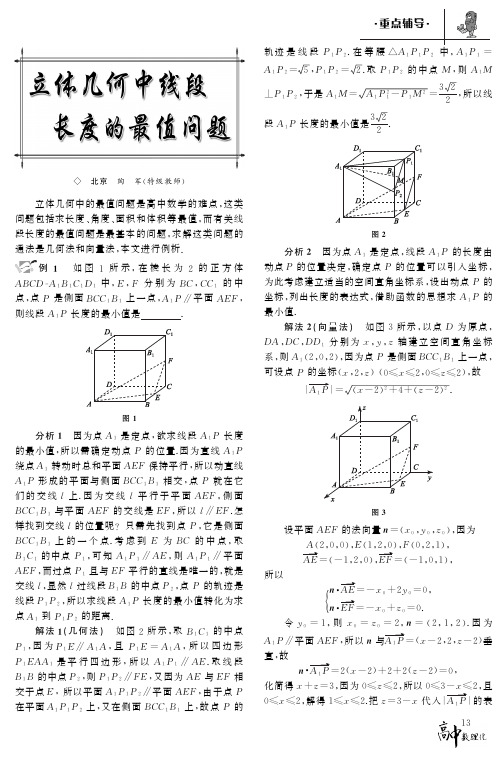
重点辅导Җ㊀北京㊀陶㊀军(特级教师)㊀㊀立体几何中的最值问题是高中数学的难点,这类问题包括求长度㊁角度㊁面积和体积等最值,而有关线段长度的最值问题是最基本的问题,求解这类问题的通法是几何法和向量法,本文进行例析.例1㊀如图1所示,在棱长为2的正方体A B C D GA 1B 1C 1D 1中,E ,F 分别为B C ,C C 1的中点,点P 是侧面B C C 1B 1上一点,A 1P ʊ平面A E F ,则线段A 1P 长度的最小值是.图1分析1㊀因为点A 1是定点,欲求线段A 1P 长度的最小值,所以需确定动点P 的位置.因为直线A 1P 绕点A 1转动时总和平面A E F 保持平行,所以动直线A 1P 形成的平面与侧面B C C 1B 1相交,点P 就在它们的交线l 上.因为交线l 平行于平面A E F ,侧面B C C 1B 1与平面A E F 的交线是E F ,所以l ʊE F .怎样找到交线l 的位置呢?只需先找到点P ,它是侧面B C C 1B 1上的一个点.考虑到E 为B C 的中点,取B 1C 1的中点P 1,可知A 1P 1ʊA E ,则A 1P 1ʊ平面A E F ,而过点P 1且与E F 平行的直线是唯一的,就是交线l ,显然l 过线段B 1B 的中点P 2,点P 的轨迹是线段P 1P 2,所以求线段A 1P 长度的最小值转化为求点A 1到P 1P 2的距离.解法1(几何法)㊀如图2所示,取B 1C 1的中点P 1,因为P 1E ʊA 1A ,且P 1E =A 1A ,所以四边形P 1E A A 1是平行四边形,所以A 1P 1ʊA E .取线段B 1B 的中点P 2,则P 1P 2ʊF E ,又因为A E 与E F 相交于点E ,所以平面A 1P 1P 2ʊ平面A E F ,由于点P 在平面A 1P 1P 2上,又在侧面B C C 1B 1上,故点P 的轨迹是线段P 1P 2.在等腰әA 1P 1P 2中,A 1P 1=A 1P 2=5,P 1P 2=2.取P 1P 2的中点M ,则A 1M ʅP 1P 2,于是A 1M =A 1P 21-P 1M 2=322,所以线段A 1P 长度的最小值是322.图2分析2㊀因为点A 1是定点,线段A 1P 的长度由动点P 的位置决定,确定点P 的位置可以引入坐标,为此考虑建立适当的空间直角坐标系,设出动点P 的坐标,列出长度的表达式,借助函数的思想求A 1P 的最小值.解法2(向量法)㊀如图3所示,以点D 为原点,D A ,D C ,D D 1分别为x ,y ,z 轴建立空间直角坐标系,则A 1(2,0,2),因为点P 是侧面B C C 1B 1上一点,可设点P 的坐标(x ,2,z )(0ɤx ɤ2,0ɤz ɤ2),故|A 1P ң|(x -2)2+4+(z -2)2.图3设平面A E F 的法向量n =(x 0,y 0,z 0),因为A (2,0,0),E (1,2,0),F (0,2,1),A E ң=(-1,2,0),E F ң=(-1,0,1),所以n A E ң=-x 0+2y 0=0,n E F ң=-x 0+z 0=0.{令y 0=1,则x 0=z 0=2,n =(2,1,2).因为A 1P ʊ平面A E F ,所以n 与A 1P ң=(x -2,2,z -2)垂直,故n A 1P ң=2(x -2)+2+2(z -2)=0,化简得x +z =3,因为0ɤz ɤ2,所以0ɤ3-x ɤ2,且0ɤx ɤ2,解得1ɤx ɤ2.把z =3-x 代入|A 1P ң|的表31重点辅导达式,整理得|A 1P ң|=2(x -32)2+92,x ɪ[1,2],故当x =32时,|A 1P ң|取得最小值322.例2㊀如图4所示,在棱长为2的正方体A B C D GA 1B 1C 1D 1中,E 为B C 的中点,点P 在线段D 1E 上,点P 到直线C C 1的距离的最小值为.图4分析1㊀求点P 到直线C C 1的距离的最小值,就是找点P 到直线C C 1的垂线段P Q 长度的最小值.求线段P Q 的长度涉及空间上两个动点长度的距离问题,不易处理.注意到C C 1ʅ平面A B C D ,P Q ʅC C 1,则P Q ʊ平面A B C D .因此,我们可以把P Q 正投影在平面A B C D 上,点P 在平面A B C D 上的正投影H 落在线段D E 上,点Q 在平面A B C D 上的正投影是点C ,于是P Q =H C ,求P Q 的最小值转化为在平面A B C D 上求定点C 与线段D E 上的动点H 之间距离的最小值,就是求定点C 到D E 的距离.解法1(几何法)㊀如图5所示,过点P 作P Q ʅC C 1,Q 为垂足,因为C C 1ʅ平面A B CD ,所以P Q ʊ平面A B C D ,过点P 作PH ʅDE ,H 为垂足,则PH ʅ平面A B C D ,所以PH ʊQ C ,且P Q ʊH C ,Q C ʅH C ,故四边形P Q C H 是矩形,P Q =H C ,在R t әC D E 中,当C H ʅD E 时,C H 长度最小,因为C E =1,C D =2,D E =5,所以C H =1ˑ25=255,故点P 到直线C C 1的距离的最小值为255.图5分析2㊀设点P 到直线C C 1的距离为P Q ,因为P ,Q 分别在线段D 1E 和C C 1上,故可以引入两个变量控制点P ,Q 的位置.设E P ң=λE D 1ң(0ɤλɤ1),C Q ң=μC C 1ң(0ɤμɤ1),根据正方体的特殊性建立适当的空间直角坐标系,利用向量的坐标运算推出点P ,Q 的坐标,进而用λ,μ表示P Q ң,利用P Q ң C C 1ң=0找出λ,μ的关系式,代入P Q 长度的表达式,转化为一元函数求最值.解法2(向量法)㊀如图6所示,以D 为原点,D A ,D C ,D D 1分别为x ,y ,z 轴建立空间直角坐标系,则D 1(0,0,2),E (1,2,0),C 1(0,2,2),C (0,2,0),E D 1ң=(-1,-2,2),由于点P 在线段D 1E 上,可设E P ң=λE D 1ң(0ɤλɤ1),即E P ң=(-λ,-2λ,2λ),由此得点P 的坐标为(,,).图6过点P 作P Q 垂直于C C 1,Q 为垂足,设点Q 的坐标(0,2,m ),P Q ң=(λ-1,2λ,m -2λ),C C 1ң=(0,0,2),因为P Q ңʅC C 1ң,所以P Q ң C C 1ң=0,即2(m -2λ)=0,m =2λ,P Q ң=(λ-1,2λ,0),|P Q ң|=(λ-1)2+(2λ)2+02=5(λ-15)2+45,λɪ[0,1].当λ=15,P Q 取得最小值255.综上所述,利用几何法求线段长度的最值,要点是先用立体几何知识确定动点的轨迹,再用平面几何知识求最值;利用向量法求线段长度的最值,要点是建立适当的坐标系,设出动点坐标,建立线段长度的表达式,借助向量知识把题目中的几何条件合理转化为代数条件,找到动点坐标的关系,把线段长度的表达式转化为一元函数,用函数的思想求最值.(作者单位:北京市怀柔区第一中学)41。
高数140招之71-立体几何中的最值问题的解题策略

一、与线段长有关的最值问题【典例1】在直三棱柱ABC A 1B 1C 1中,底面为直角三角形, ∠ACB =90°,AC =6,BC =CC 1=2,P 是BC 1上一动点,如图所示,则CP +PA 1的最小值为________.[解析]PA 1在平面A 1BC 1内,PC 在平面BCC 1内,将其铺平后转化为平面上的问题.铺平平面A 1BC 1,平面BCC 1,如图所示,计算得A 1B =AB 1=210,BC 1=2.又A 1C 1=6,故△A 1BC 1是∠A 1C 1B =90°的直角三角形. 设P 是BC 1上任一点,CP +PA 1≥A 1C ,即当A 1,P ,C 三点共线时,CP +PA 1有最小值. 在△A 1C 1C 中,由余弦定理得A 1C =62+ 2 2-2×6×2×cos 135°=52, 故(CP +PA 1)min =52.【变式练习】1.如图所示,在棱长为1的正方体ABCD A 1B 1C 1D 1的面对角线A 1B 上存在一点P ,使得AP +D 1P 取得最小值,则此最小值为()A .2B.6+22C .2+2 D.2+2解析:选D将△A 1AB 与△A 1BD 1放在同一平面内,如图所示.连接AD 1,则AD 1为AP +D 1P 的最小值.因为AA 1=A 1D 1=1,∠AA 1D 1=90°+45°=135°,所以由余弦定理得AD 1=AA 21+A 1D 21-2×AA 1×A 1D 1×cos 135°=2+2. 2.某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy 的最大值为________.解析:由三视图知三棱锥如图所示,底面ABC 是直角三角形,AB ⊥BC , PA ⊥平面ABC ,BC =27, PA 2+y 2=102,(27)2+PA 2=x 2, 因此xy =x 102-[x 2- 27 2] =x128-x 2≤x 2+ 128-x 22=64,当且仅当x 2=128-x 2,即x =8时取等号,因此xy 的最大值是64.3.已知直三棱柱ABC A 1B 1C 1的侧棱长为6,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱AA 1,BB 1,CC 1分别交于三点M ,N ,Q ,若△MNQ 为直角三角形,则该直角三角形斜边长的最小值为()A .22B .3C .23D .4解析:选C 如图,不妨设N 在B 处,设AM =h ,CQ =m ,则MB 2=h 2+4,BQ 2=m 2+4,MQ 2=(h -m )2+4,由MB 2=BQ 2+MQ 2,得m 2-hm +2=0.Δ=h 2-8≥0⇒h 2≥8,该直角三角形斜边MB =4+h 2≥23,故该直角三角形斜边长的最小值为23.故选C.二、与面积有关的最值问题【典例2】已知正四面体S ABC 的棱长为1,如果一个高为36的长方体能在该正四面体内任意转动,则该长方体的长和宽形成的长方形的面积的最大值为________.解析:如图,易知正四面体S ABC 的内切球的球心O 必在高线SH 上,延长AH 交BC 于点D ,则D 为BC 的中点,连接SD ,设内切球切SD 于点E ,连接AO .因为H 是正三角形ABC 的中心,所以AH ∶DH =2∶1.易得Rt △OAH ∽Rt △DSH ,所以OA OH =DSDH=3,可得OA =3OH =SO ,因此SH =4OH ,可得内切球的半径R =OH =14SH .因为正四面体S ABC 的棱长为1,所以在Rt △DSH中,DS =SH 2+DH 2= 4R 2+(13×32)2=32,解得R 2=124.要满足一个高为36的长方体能在该正四面体内任意转动,则长方体的体对角线长不超过正四面体内切球的直径,设该长方体的长和宽分别为x ,y ,其长和宽形成的长方形的面积为S ,则4R 2≥(36)2+x 2+y 2,所以x 2+y 2≤112,所以S =xy ≤x 2+y 22≤124,当且仅当x =y =612时等号成立,即该长方体的长和宽形成的长方形的面积的最大值为124. 【变式练习】1.(2018·全国卷Ⅰ)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为() A .334B .233C .324D .32【答案】A【解析】如图所示,在正方体ABCD A 1B 1C 1D 1中,平面AB 1D 1与棱A 1A ,A 1B 1,A 1D 1所成的角都相等,又正方体的其余棱都分别与A 1A ,A 1B 1,A 1D 1平行,故正方体ABCD A 1B 1C 1D 1的每条棱所在直线与平面AB 1D 1所成的角都相等.如图所示,取棱AB ,BB 1,B 1C 1,C 1D 1,D 1D ,DA 的中点E ,F ,G ,H ,M ,N ,则正六边形EFGHMN 所在平面与平面AB 1D 1平行且面积最大,此截面面积为S 正六边形EFGHMN =6×12×22×22×sin 60°=334.故选A.2.已知球O 是正三棱锥A BCD 的外接球,BC =3,AB =23,点E 在线段BD 上,且BD =3BE ,过点E 作球O 的截面,则所得截面中面积最小的截面圆的面积是________.【答案】2π【解析】如图,设△BCD 的中心为点O 1,球O 的半径为R ,则A ,O ,O 1三点共线.连接O 1D ,O 1E ,OD ,OE ,则O 1D =3,AO 1=AD 2-O 1D 2=3.在Rt △OO 1D 中,R 2=3+(3-R )2,即R =2,所以OO 1=1.在△O 1DE 中,DE =23BD =2,∠O 1DE =30°,所以由余弦定理得O 1E =3+4-2×3×2× cos 30°=1.所以OE =2.过点E 作圆O 的截面,当截面与OE 垂直时,截面的面积最小,此时截面圆的半径为22-(2)2=2,所以截面圆的面积为2π.3.在长方体ABCD A 1B 1C 1D 1中,AB =AD =4,AA 1=2.过点A 1作平面α与AB ,AD 分别交于M ,N 两点,若AA 1与平面α所成的角为45°,则截面A 1MN 面积的最小值是________.【答案】2π【解析】如图,过点A 作AE ⊥MN ,连接A 1E ,因为A 1A ⊥平面ABCD ,所以A 1A ⊥MN ,所以MN ⊥平面A 1AE ,所以A 1E ⊥MN ,平面A 1AE ⊥平面A 1MN ,所以∠AA 1E 为AA 1与平面A 1MN 所成的角,所以∠AA 1E =45°,在Rt △A 1AE 中,因为AA 1=2,所以AE =2,A 1E =22,在Rt △MAN 中,由射影定理得ME ·EN =AE 2=4,由基本不等式得MN =ME +EN ≥2ME ·EN =4,当且仅当ME =EN ,即E 为MN 的中点时等号成立,所以截面A 1MN 面积的最小值为12×4×22=42.三、与体积有关的最值问题【典例3】(2017·全国卷Ⅰ)如图,圆形纸片的圆心为O ,半径为5 cm ,该纸片上的等边三角形ABC 的中心为O .D ,E ,F 为圆O 上的点,△DBC ,△ECA ,△FAB 分别是以BC ,CA ,AB 为底边的等腰三角形.沿虚线剪开后,分别以BC ,CA ,AB 为折痕折起△DBC ,△ECA ,△FAB ,使得D ,E ,F 重合,得到三棱锥.当△ABC 的边长变化时,所得三棱锥体积(单位:cm 3)的最大值为________.【答案】415【解析】如图,连接OD 交BC 于点G ,由题意知,OD ⊥BC .易得OG =36BC ,设OG =x ,则BC =23x ,DG =5-x , S △ABC =12×23x ×3x =33x 2,故所得三棱锥的体积V =13×33x 2× 5-x 2-x 2=3x 2×25-10x =3×25x 4-10x 5.令f (x )=25x 4-10x 5,x ∈(0,52),则f ′(x )=100x 3-50x 4,令f ′(x )>0,即x 4-2x 3<0,得0<x <2; 令f ′(x )<0,得2<x <52,则当x ∈(0,52)时,f (x )≤f (2)=80, ∴V ≤3×80=415.∴所求三棱锥的体积的最大值为415.【变式练习】1.(2018·全国卷Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为93,则三棱锥D ABC 体积的最大值为()A .123B .183C .243D .543【答案】B【解析】由等边△ABC 的面积为93,可得34AB 2=93,所以AB =6,所以等边△ABC的外接圆的半径为r =33AB =23.设球的半径为R ,球心到等边△ABC 的外接圆圆心的距离为d ,则d =R 2-r 2=16-12=2.所以三棱锥D ABC 高的最大值为2+4=6,所以三棱锥D ABC 体积的最大值为13×93×6=183.2.已知圆锥的侧面展开图是半径为3的扇形,则该圆锥体积的最大值为________. 【答案】23π【解析】由题意得圆锥的母线长为3,设圆锥的底面半径为r ,高为h ,则h =9-r 2,所以圆锥的体积V =13πr 2h =13πr 29-r 2=13π9r 4-r 6.设f (r )=9r 4-r 6(r >0),则f ′(r )=36r 3-6r 5,令f ′(r )=36r 3-6r 5=6r 3(6-r 2)=0,得r =6,所以当0<r <6时,f ′(r )>0,f (r )单调递增;当r >6时,f ′(r )<0,f (r )单调递减,所以f (r )max =f (6)=108,所以V max =13π×108=23π.3.已知A ,B ,C 是球O 的球面上三点,且AB =AC =3,BC =33,D 为该球面上的动点,球心O 到平面ABC 的距离为球半径的一半,则三棱锥D ABC 体积的最大值为________.【答案】274【解析】如图,在△ABC 中, ∵AB =AC =3,BC =33, ∴由余弦定理可得cos A =32+32- 33 22×3×3=-12,∴sin A =32.设△ABC 外接圆O ′的半径为r ,则3332=2r ,得r =3.设球的半径为R ,连接OO ′,BO ′,OB , 则R 2=(R 2)2+32,解得R =23.由图可知,当点D 到平面ABC 的距离为32R 时,三棱锥D ABC 的体积最大,∵S △ABC =12×3×3×32=934,∴三棱锥D ABC 体积的最大值为13×934×33=274.4.如图,等腰梯形ABCD 中,AB ∥CD ,AD =AB =BC =1,CD =2,E 为CD 的中点,将△ADE 沿AE 折到△APE 的位置.(1)证明:AE ⊥PB ;(2)当四棱锥P ABCE 的体积最大时,求二面角A PE C 的余弦值.解:(1)证明:在等腰梯形ABCD 中,连接BD ,交AE 于点O , ∵AB ∥CE ,AB =CE ,∴四边形ABCE 为平行四边形, ∴AE =BC =AD =DE ,∴△ADE 为等边三角形, ∴在等腰梯形ABCD 中,∠C =∠ADE =π3,BD ⊥BC ,∴BD ⊥AE .如图,翻折后可得OP ⊥AE ,OB ⊥AE ,又OP ⊂平面POB ,OB ⊂平面POB ,OP ∩OB =O ,∴AE ⊥平面POB ,∵PB ⊂平面POB ,∴AE ⊥PB .(2)当四棱锥P ABCE 的体积最大时,平面PAE ⊥平面ABCE .又平面PAE ∩平面ABCE =AE ,PO ⊂平面PAE ,PO ⊥AE ,∴OP ⊥平面ABCE .以O 为坐标原点,OE所在的直线为x 轴,OB 所在的直线为y 轴,OP 所在的直线为z轴,建立空间直角坐标系,由题意得,P(0,0,32),E(12,0,0),C(1,32,0),∴PE―→=(12,0,-32),EC―→=(12,32,0),设平面PCE的法向量为n1=(x,y,z),则{·n1=0,·n1=0,)即{12x-32z=0,12x+32y=0,)设x=3,则y=-1,z=1,∴n1=(3,-1,1)为平面PCE的一个法向量,易知平面PAE的一个法向量为n2=(0,1,0),cos n1,n2 =n1·n2|n1||n2|=-11×5=-55.由图知所求二面角APEC为钝角,∴二面角APEC的余弦值为-5 5 .[解题技法]立体几何中的最值问题的解题策略空间几何体中的某些对象,如点、线、面,在约束条件下运动,带动相关的线段长度、体积等发生变化,进而就有了面积与体积的最值问题.定性分析:在空间几何体的变化过程中,通过观察运动点的位置变化,确定其相关量的变化规律,进而发现相关面积或体积的变化规律,求得其最大值或最小值.定量分析:将所求问题转化为某一个相关量的问题,即转化为关于其中一个量的函数,求其最大值或最小值的问题.根据具体情况,有函数法、不等式法、三角函数法等多种方法可供选择.。
高中数学立体几何中的最值问题

高中数学立体几何中的最值问题在高中数学的学习中,立体几何一直是一个重点和难点,而其中的最值问题更是让许多同学感到头疼。
这类问题往往需要我们综合运用空间想象力、几何知识以及数学方法来求解。
接下来,让我们一起深入探讨立体几何中的最值问题。
一、常见类型及解法1、距离最值问题(1)两点间距离最值在立体几何中,求两点间距离的最值,常常需要我们将空间中的两点转化到同一平面内。
例如,在长方体中,求异面直线上两点的最短距离,就需要通过平移将其转化为共面直线,然后利用平面几何中的知识求解。
(2)点到直线距离最值求点到直线的距离最值时,通常要找到点在直线上的投影。
如果直线是某一平面的斜线,那么可以通过作垂线找到投影,再利用勾股定理计算距离。
(3)点到平面距离最值对于点到平面的距离最值,一般可以利用空间向量法。
先求出平面的法向量,然后通过向量的数量积来计算点到平面的距离。
2、面积最值问题(1)三角形面积最值在立体几何中,涉及三角形面积的最值问题,可能需要考虑三角形的边长关系或者角度大小。
例如,已知三角形的两边及其夹角,当夹角为直角时,面积最大。
(2)四边形面积最值对于四边形,如平行四边形,其面积可以表示为底边乘以高。
当底边长度固定时,高取得最大值时面积最大;或者当四边形的对角线相互垂直时,面积等于对角线乘积的一半。
3、体积最值问题(1)柱体体积最值对于柱体,如圆柱、棱柱,其体积等于底面积乘以高。
当底面积不变时,高最大则体积最大;反之,高最小时体积最小。
(2)锥体体积最值锥体体积为三分之一底面积乘以高。
在求解锥体体积最值时,需要关注底面积和高的变化。
二、例题分析例 1:在棱长为 2 的正方体 ABCD A1B1C1D1 中,E、F 分别是棱AB、BC 的中点,求点 A1 到直线 EF 的距离。
解:连接 A1C1、C1F、EF,因为 A1C1 平行于 EF,所以点 A1 到直线 EF 的距离等于点 A1 到直线 C1F 的距离。
立体几何的最值问题

立体几何最值问题立体几何是数学中的一个重要分支,它研究的是空间图形的性质和数量关系。
在立体几何中,我们经常遇到最值问题,即寻找某个量的最大值或最小值。
本文将介绍立体几何中最值问题的几个方面:1.立体几何位置关系立体几何中的位置关系是指空间中点、线、面之间的相对位置。
解决位置关系问题需要运用空间想象和逻辑推理。
在立体几何中最值问题中,位置关系往往与距离、角度等问题交织在一起,需要综合考虑多种因素。
2.立体几何中的距离立体几何中的距离是指空间中两点之间的直线距离,或者是点与线、线与面之间的距离。
在解决最值问题时,我们需要考虑如何利用距离公式来计算最短路径、最大距离等。
3.立体几何中的体积立体几何中的体积是指空间中封闭图形的体积,或者是两个平面图形之间的距离。
计算体积需要运用体积公式,而解决最大或最小面积问题则需要考虑如何调整图形的形状和大小。
4.立体几何中的最短路径立体几何中的最短路径问题是指寻找空间中两点之间的最短距离。
解决这类问题需要运用距离公式和几何定理,有时还需要借助对称、旋转等技巧。
5.立体几何中的最大/最小面积立体几何中的最大/最小面积问题通常涉及到平面图形在空间中的展开和折叠。
解决这类问题需要运用面积公式和平面几何定理,同时要注意图形的对称性和边长之间的关系。
6.立体几何中的角度问题立体几何中的角度问题是指空间中两条直线或两个平面之间的夹角。
解决这类问题需要运用角度公式和空间向量,同时要注意图形的对称性和边长之间的关系。
7.立体几何中的轨迹问题立体几何中的轨迹问题是指一个点或一条线在空间中按照一定规律移动所形成的轨迹。
解决这类问题需要运用轨迹方程和运动学原理,同时要注意轨迹的形状和大小随时间的变化情况。
立体几何中体积与面积最值问题的解法

1 声明本文首先以体积最大和面积最小的物体为例,讨论它们的最大/小值的解决方案。
接下来,给定指定的条件,通过拉格朗日型最优化技术对最大化体积最小化面积问题进行剖析。
最后,在说明了结果及其分析之后,讨论此类问题的求解思路及扩展性。
2 体积最大和面积最小的物体体积最大和面积最小的物体是立体几何的典型问题,它可以被看作是一种拉格朗日型优化问题,即在完成最大化体积和最小化面积的条件下寻求平衡点。
典型的体积最大和面积最小物体有球形、柱形、长方体等,也可以拓展到多边形,例如三角形等。
2.1 球形球形是一种立体几何体,其体积最大,面积最小,可以通过满足一定条件解决最大体积最小面积问题。
大体积最小面积问题的解法主要有两种:1) 根据体积最大的物体的方程,可以求出球的半径r,其中`V=4/3πr^3`;2) 因为球的周长是最长,周长和平面面积是相关的,因此可以求出球的周长C,从而计算球的面积`S=4πr^2`;这两个方程使用上面的公式,可以求出球的体积和面积。
根据拉格朗日型优化例子求出:当半径r=1时,体积最大,体积V=4/3πr^3=4.19,面积最小,面积S=4πr^2=12.57;当半径r=2时,体积最小,体积V=33.51,面积最大,面积S=50.27。
2.2 柱形柱形也是一种常用的立体几何物体,它的体积最大,面积最小的条件也可以满足。
柱的体积的最大/小值可以利用柱体的内切球的半径r求出,其中`V=πr²h`; 柱的面积最大/小值可以求出其元表面积`S=(2πrh+2πr²)`。
根据拉格朗日型优化例子求出:当半径r=1时,体积最大,体积V=πr²h=2.14,面积最小,面积S=2πr²+2πrh=10.30;当半径r=2时,体积最小,体积V=12.56,面积最大,面积S=18.85。
2.3 长方体长方体也是常用的立体几何物体,其体积最大,面积最小的条件也可以满足。
长方体的体积的最大/小值可以利用它的公式`V=a*b*c`进行求解,其中a,b,c分别为直角坐标三边的长度;长方体的表面积最大/小值可以求出其元表面积`S=2(a*b+b*c+a*c)`。
高三数学选择填空难题突破 立体几何中最值问题

高三数学选择填空难题突破立体几何中最值问题高三数学选择填空难题突破——立体几何中的最值问题一、方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目,而几何问题中的最值与范围类问题,既可以考查学生的空间想象能力,又考查运用运动变化观点处理问题的能力,因此,将是有中等难度的考题。
此类问题,可以充分考查图形推理与代数推理,同时往往也需要将问题进行等价转化,比如求一些最值时,向平面几何问题转化,这些常规的降维操作需要备考时加强关注与训练。
立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面,此类问题多以规则几何体为载体,涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合。
解决此类问题一般可从三个方面思考:一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解;二是根据几何体的结构特征,变动态为静态,直观判断在什么情况下取得最值;三是将几何体平面化,如利用展开图,在平面几何图中直观求解。
二、解题策略类型一:距离最值问题例1:如图,矩形ADFE,矩形CDFG,正方形ABCD两两垂直,且AB=2,若线段DE上存在点P使得GP⊥BP,则边CG长度的最小值为()解:建立空间直角坐标系,设CG长度为a及点P的坐标,求BP与GP的坐标,得到函数关系式,利用函数求其最值。
举一反三:如图,在棱长为1的正方体ABCD-A中,点E、F分别是棱BC、CC'的中点,P是侧面BCC'B内一点,若A'P⊥平面AEF,则线段A'P长度的取值范围是_____。
二、改写后的文章高三数学选择填空难题突破——立体几何中的最值问题一、方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目。
而几何问题中的最值与范围类问题,不仅可以考查学生的空间想象能力,还可以考查运用运动变化观点处理问题的能力,因此这类问题将是有中等难度的考题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
252 52 53 3立体几何中的最值问题(一)立体几何主要研究空间中点、线、面之间的位置关系,与空间图形有关的线段、角、体积等最值问题常常在试题中出现。
下面举例说明解决这类问题的常用方法。
一、运用变量的相对性求最值例1. 在正四棱锥S-ABCD 中,SO⊥平面ABCD 于O,SO=2,底面边长为,点P、Q 分别在线段BD、SC 上移动,则P、Q 两点的最短距离为()A. B. C. 2 D. 15 5解析:如图1,由于点P、Q 分别在线段BD、SC 上移动,先让点P 在BD 上固定,Q 在SC 上移动,当OQ 最小时,PQ 最小。
过O 作OQ⊥SC,在Rt△SOC 中,OQ = 中。
又P 在BD 上运动,且当5P 运动到点O 时,PQ 最小,等于OQ 的长为,也就是异面直线BD 和SC 的公垂线段的长。
故选B。
5图 1二、定性分析法求最值例2. 已知平面α//平面β,AB 和CD 是夹在平面α、β之间的两条线段。
AB⊥CD,AB=3,直线AB 与平面α成30°角,则线段CD 的长的最小值为。
解析:如图2,过点B 作平面α的垂线,垂足为O,连结AO,则∠BAO=30°。
过B 作BE//CD 交平面α于E,则BE=CD。
连结AE,因为AB⊥CD,故AB⊥BE。
则在Rt△ABE 中,BE=AB·tan∠BAE≥AB·tan ∠BAO=3·tan30°= 。
故CD ≥。
2 5图 2三、展成平面求最值例 3. 如图 3-1,四面体 A-BCD 的各面都是锐角三角形,且 AB=CD=a ,AC=BD=b ,AD=BC=c 。
平面α分别截棱 AB 、BC 、CD 、DA 于点 P 、Q 、R 、S ,则四边形 PQRS 的周长的最小值是()A. 2aB. 2bC. 2cD. a+b+c图 3-1解析:如图 3-2,将四面体的侧面展开成平面图形。
由于四面体各侧面均为锐角三角形,且 AB=CD , AC=BD ,AD=BC ,所以,A 与 A’、D 与 D’在四面体中是同一点,且 AD// BC // A ' D ' , AB // CD ',A 、C 、A’共线,D 、B 、D’共线, AA ' = DD ' = 2BD 。
又四边形 PQRS 在展开图中变为折线 S’PQRS , S’与 S 在四面体中是同一点。
因而当 P 、Q 、R 在 S’S 上时, S ' P + PQ + QR + RS 最小,也就是四边形 PQRS 周长最小。
又 S ' A = SA ',所以最小值 L = SS ' = DD ' = 2BD = 2b 。
故选 B 。
图 3-2四、利用向量求最值例 4. 在棱长为 1 的正方体 ABCD-EFGH 中,P 是 AF 上的动点,则 GP+PB 的最小值为 。
2x 2 - 4x +3 (x - 1)2+ 0 - ⎝ ⎛ ⎪ 2 ⎭ 2 ⎫2 2 1 + 22 2 + 2 2 解析:以 A 为坐标原点,分别以 AB 、AD 、AE 所在直线为 x ,y ,z 轴,建立如图 4 所示的空间直角→坐标系, 则 B ( 1, 0, 0), G ( 1, 1, 1)。
根据题意设 P ( x , 0, x ), 则 BP = (x - 1,0,x ) , →GP = (x - 1,- 1,x - 1) ,那么图 4GP + PB = +⎛ ⎫⎪ = ⎪ ⎪ ⎝ ⎭式子 ⎛ 2 ⎫ + ⎛ 1 1 ⎫ 可以看成 x 轴正半轴上一点(x ,0, 0)到 xAy 平面上两点 1, ,0⎪ 、 , ,0⎪ 的距离之和,其最小值为 。
所以 GP+PB 的最⎝ 2 ⎭ ⎝ 2 2 ⎭小值为 ⋅ = 。
立体几何中的最值问题一、线段长度最短或截面周长最小问题例 1. 正三棱柱 ABC —A 1B 1C 1 中,各棱长均为 2,M 为 AA 1 中点,N 为 BC 的中点,则在棱柱的表面上从点 M 到点 N 的最短距离是多少?并求之.2x 2 - 2x + 1⎛ 1 ⎫2 x - + 0 - ⎝ 2 ⎭ ⎪ ⎛ 1 ⎫2 ⎝ 2 ⎭ ⎪(x -1)2+ 0 - ⎝⎛ ⎪ 2 ⎭ 2 ⎫2⎛ 1 ⎫2 x - + 0 - ⎝ 2 ⎭ ⎪ ⎛ 1 ⎫2⎝ 2 ⎭ ⎪ 1 + 2 2 +AM 2 + AN 2 10 AM 2 + AN 2- 2 A M ⋅ AN cos120︒ 12 + ( 3)2 + 2 ⨯1⨯ 3 ⨯ 124 + 34 + 310 4 + 3(1 - CP ) 2 + BQ 2 =解析: (1)从侧面到N ,如图1,沿棱柱的侧棱AA 1剪开,并展开,则MN ===(2) 从底面到 N 点,沿棱柱的 AC 、BC 剪开、展开,如图 2.则 MN ===∵<∴ MN min =.例 2.如图,正方形 ABCD 、ABEF 的边长都是 1,而且平面 ABCD 、ABEF 互相垂直。
点 M 在 AC 上移动, 点 N 在 BF 上移动,若 CM=BN= a (0 < a <2). (1)求 MN 的长;(2)当 a 为何值时,MN 的长最小; (3)当 MN 长最小时,求面 MNA 与面 MNB 所成的二面角的大小。
解析:(1)作 MP ∥AB 交 BC 于点 P ,NQ ∥AB 交 BE 于点 Q ,连接 PQ ,依题意可得 MP ∥NQ ,且MP=NQ ,即 MNQP 是平行四边形。
∴MN=PQ,由已知,CM=BN=a,CB=AB=BE=1,∴ AC = BF = CPa BQ , , 1 2 1a, 即2 CP = BQ = a , 2∴ MN = PQ == = (a -2) 2 + 1(0 < a < 2) 2 2(2)由(1)知:当a =时,MN = 2 ,即M , N 分别移动到AC , BF 的中点时2MN 的长最小,最小值为 2212 + (2 +1)22 22(1 - a ) 2 + ( a ) 2 2 2 =2(1 + cos )(x - a )2 + 1 (1 - cos )a 22 2 (3) 取 MN 的中点 G ,连接 AG 、BG ,∵AM=AN,BM=BN ,∴AG ⊥MN,BG ⊥MN ,∴∠AGB 即为二面角α的平面角。
又 AG = BG =定理有,所以由余弦 4CD G M( 6 )2 + ( 6)2 - 1B P A1 H Ncos= 44 = - 1 。
故所求二面角= arccos(- 3) 。
EF2 • 6 • 6 34 4例 3. 如图,边长均为 a 的正方形 ABCD 、ABEF 所在的平面所成的角为(0 << 点 N 在 BF 上,若 AM=FN ,(1)求证:MN//面 BCE ; (2)求证:MN ⊥ AB;) 。
点 M 在 AC 上,2(3)求 MN 的最小值.解析:(1)如图,作 MG//AB 交 BC 于 G, NH//AB 交 BE 于 H, MP//BC 交 AB 于 P, 连 PN, GH , 易证 MG//NH, 且 MG=NH, 故 MGNH 为平行四边形,所以 MN//GH , 故 MN//面 BCE ; (2)易证 AB ⊥ 面 MNP, 故 MN ⊥ AB ;(3)∠MPN 即为面 ABCD 与 ABEF 所成二面角的平面角,即∠MPN =,设 AP=x , 则 BP=a -x , NP=a -x , 所以: MN =x 2 + (a - x )2 - 2x (a - x ) cos=,故当 x =a 时,MN有最小值21(1 - cos)a .2例4.如图,正方形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直。
点 M 在 AC 上移动,点 N 在 BF 上移动,若 DECM=x ,BN=y, (0 < x , y <2). (1)求 MN 的长(用 x,y 表示);(2)求 MN 长的最小值,该最小值是否是异面直线 AC ,BF 之间的 A距离。
6CMBPNFMP 2 + PN 2 x 2 + y 2 - x y - 2x + 1 2 2b 2 sin 2+ a 2 cos 2+ (a s in - b cos )22 解析:在面 ABCD 中作 MP ⊥ AB 于 P ,连 PN ,则 MP ⊥ 面 ABEF ,所以 MP ⊥ PN ,PB=1-AP=2x 在∆PBN 中,由余弦定理得:PN 2= (2x )2+ y 2 + - 2xy cos 450= 1x 2 + y 2 - xy ,在 Rt ∆PMN 中,MN= = 2= (0 < x , y < 2). ;(2)MN =,故当 x = ,3y = 时,MN 有最小值 3 3。
且该最小值是异面直线 AC ,BF 之间的距离。
3例 5. 如图,在ΔABC 中,∠ACB=90°,BC =a,AC =b,D 是斜边 AB 上的点,以 CD 为棱把它折成直二面角 A —CD —B 后,D 在怎样的位置时,AB 为最小,最小值是多少?解析: 设∠ACD=θ,则∠BCD=90°-θ,作 AM⊥CD 于 M ,BN⊥CD 于 N ,于是 AM =bsinθ,CN=asinθ.∴MN=|asinθ-bcosθ|,因为 A —CD —B 是直二面角,AM⊥CD,BN⊥CD,∴AM 与 BN 成 90°的角,于是 AB== a2+ b 2 - ab sin 2≥ a2+ b 2 - ab .∴当θ=45°即 CD 是∠ACB 的平分线时,AB 有最小值,最小值为a 2 +b 2 - ab .例 6. 正三棱锥 A-BCD ,底面边长为 a ,侧棱为 2a ,过点 B 作与侧棱 AC 、AD 相交的截面,在这样的截面三角形中,求(1)周长的最小值;(2)周长为最小时截面积的值,(3)用这周长最小时的截面截得的小三棱锥的 体积与三棱锥体积之比.22 (1 - 2 x )2 + 1 x 2 + y 2 - xy2 2 x 2+ y 2- x y - 2x + 1 ( y - x )2 + 3 (x -2 2 43 2 )2 + 1 3BE2- EG 2a 2 - (3a )2 8 55 3 55解析:(1)沿侧棱 AB 把正三棱锥的侧面剪开展成平面图.如图 1,当周长最小时,EF 在直线 BB′上,∵ΔABE≌ΔB′AF,∴AE=AF ,AC =AD ,∴B′B∥CD,∴∠1=∠2=∠3,∴BE=BC =a , DF DB ' DF a同理 B′F=B′D=a.∵ΔFDB′∽ΔADB′,∴= , =1 1 3DB ' AB '3 a2a11 = ,∴DF= a,AF = a.又∵ΔAEF∽ΔACD ,∴BB′=a+ a+a =a,∴2 2 24411 截面三角形的周长的最小值为a.4(2) 如图2,∵ΔBEF 等腰,取EF 中点G ,连BG ,则BG⊥EF.∴BG=== 81 1 3 a ∴S ΔBEF =·EF·BG= · a·a = a 2.2248 64(3)∵V A-BCD =V B-ACD ,而三棱锥 B —AEF ,三棱锥 B —ACD 的两个高相同,所以它们体积之比于它们的两底面积之比,即VSEF 29B - AEF= △ A EF==V B -CADS △ ACDCD 216评析 把曲面上的最短路线问题利用展开图转化为平面上两点间距离的问题,从而使问题得到解决,这是求曲面上最短路线的一种常用方法.本题中的四面体,其中任何一个面都可以做为底面,因而它可有四个底面和与之对应的四条高,在解决有关三棱锥体积题时,需要灵活运用这个性质.55。
