合肥工业大学电磁场与电磁波(孙玉发版)第6章答案
电磁场与电磁波课后习题及答案六章习题解答

第六章 时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场5cos mT z e t ω=B 之中,如题6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定,轨道终端接有电阻0.2R =Ω,试求电流i.解 穿过导体回路abcda 的磁通为5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为 00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为0000()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面,如题6.3图所示。
设0.2a m =、0.1m b c d ===、71.0cos(210)A i t π=⨯,求回路中的感应电动势。
电磁场与电磁波课后习题及答案六章习题解答

第六章 时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场5cos mT z e t ω=B 之中,如题 6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定,轨道终端接有电阻0.2R =Ω,试求电流i.解 5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰g g B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为00()(P r r r a e r σεεωε==⋅=-⋅=-P n B e 则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面,如题6.3图所示。
设0.2a m=、0.1m b c d ===、71.0cos(210)A i t π=⨯,求回路中的感应电动势。
解 由题给定的电流方向可知,双线中的电流产生的磁感应强度的方向,在回路中都是垂直于纸面向内的。
[汇编]合肥工业大学电磁场与电磁波(孙玉发版)第5章答案
![[汇编]合肥工业大学电磁场与电磁波(孙玉发版)第5章答案](https://img.taocdn.com/s3/m/caf9f82e0a4c2e3f5727a5e9856a561252d321af.png)
第5章时变电磁场5.1 有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场5cos mT z e t ω=B 之中,如题6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定,轨道终端接有电阻0.2R =Ω,试求电流i.穿过导体回路abcda 的磁通为)cos [0.70.35(1cos )]0.35cos (1cos )z z x t t t t ωωωωΦ-=--=+ 故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E5.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =Be 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X 极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P 极化电荷面密度为0000()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-5.3 平行双线传输线与一矩形回路共面,如题6.3图所示。
设0.2a m =、0.1mb c d ===、71.0cos(210)A i t π=⨯,求回路中的感应电动势。
解 由题给定的电流方向可知,双线中的电流产生的磁感应强度的方向,在回路中都是垂直于纸面向内的。
信息电子技术中的场与波第六章习题答案

3、请给出ITU-T对三种单模光纤的具体命名。
G.652 常规单模光纤 零色散点在1300nm,当工作波长在1300nm时,光 纤色散很小,系统的传输距离只受损耗限制 零色散点在1550nm,使低损耗与零色散在同一工 作波长上。产生一种称为四波混频(FWM)的非 线性光学效应,导致信道间发生串扰。 在1550nm附近的损耗最小,仅为0.185dB/km,但 在此区域色散比较大,约17~20 ps/(nm· km),但在 1300nm波长区域色散为零。主要用于跨洋光缆。 主要特点是1550nm的色散接近零,但不是零。是 一种改进的色散位移光纤,以抑制四波混频。
6.1 试说明为什么规则金属波导内不能传播TEM模。
t (u, v) 0 ,位函数Φ 满足 • 传TEM播波时,kc=ez=hz=0, 拉普拉斯方程。位函数Φ 和静电场中的电位一样。波导 横截面上场的分布就和静电场的分布一样[Φ =常数的面 代表一系列的等位面,波导内壁代表在边界上的等位面]。
6.27 以半径为a,内充空气的金属圆波导和芯半径为a、芯区 与包层折射率为n1、n2的介质圆波导为例,比较金属波导和介 质波导的导波特性。
1、试绘出金属波导管与光纤波导横截面示意图,比较其结构 异同点,从物理上描述电磁波在横截面不同处的工作特征。
图3 波导横截面示意图
图4 光纤波导横截面示意图
第六章 波导 习题课
6.1 试说明为什么规则金属波导内不能传播TEM模。 • TEM波是指电场和磁场分量均在传输线横截面内的一种波, 即TEM波沿波的传播方向没有电场和磁场分量。 • 假若波导管内可存在TEM波,则闭合的磁力线应完全在横 截面内。由麦克斯韦方程组知道,轴向有电流。而在空 心波导中无内导体,因而无轴向传导电流,只可能存在 有位移电流。 • 轴向位移电流的存在表明沿轴向应有交变电场存在,而 这与TEM波的定义相矛盾。故波导管中不可能存在TEM波。
合工大电磁场与电磁波习题答案

(2) ∇ ⋅ A = 4 − 2x + 2z , ∇ ⋅ A M (1,1,3) = 8 ;
( ) (3) A = xyzr = xyz xex + yey + zez = x2 yzex + xy2 zey + xyz2ez
= f ' (r) r ×r
r =0
(3) ∇ × ⎡⎣ f (r )C ⎤⎦ = ∇f (r )× C
= f ' (r )∇r ×C = f ' (r) r×C
r
(4) ∇i⎡⎣r × f (r )C ⎤⎦ = f (r )C ⋅[∇ × r] − ri⎡⎣∇ ×( f (r )C )⎤⎦
=
−r − sinθ cosϕey − cosθ ez
∂ = −e∂ r
( ) ∂ er =
ϕ
∂
ϕ
sinθ cosϕex + sinθ sin ϕey + cosθ ez
= − sinθ sinϕex + sinθ cosϕey
( ) = sinθ − sinϕex + cosϕey
f
(r)
=
C r3
( ) 1-13 求 矢 量 场 A = xyz ex + ey + ez 在 点 M (1, 3, 2) 的 旋 度 以 及 在 这 点 沿 方 向
n = ex + 2ey + 2ez 的环量面密度。
e∂x e∂y e∂z
解: ∇ × A M = ∂ x
∂ y
∂ z
合工大电磁场与电磁波第6章答案

第6章习题答案6-1在r 1、 r 4、0的媒质中,有一个均匀平面波,电场强度是E(z,t) E m sin( t kz —)3若已知f 150 MHz ,波在任意点的平均功率流密度为0.265卩w/m 2,试求:(1) 该电磁波的波数 k ?相速V p ?波长?波阻抗 ?(2)t 0, z 0的电场 E(0,0)?(3) 时间经过0.1 之后电场E(0,0)值在什么地方?(4) 时间在t 0时刻之前0.1 口 s ,电场E(0,0)值在什么地方?—2 f —解:(1) k .——.r 2 (rad/m) cv p c/. r 1.5 108(m/s)k 1(m)(4)在O 点左边15 m 处6-2 一个在自由空间传播的均匀平面波,电场强度的复振幅是—4 j 20 z— 4 j(520 z)八、,、[/ E 10 e je x 10 ee y 伏 / 米试求:(1)电磁波的传播方向?(2) 电磁波的相速V p ?波长 ?频率f ? (3) 磁场强度H ?(4) 沿传播方向单位面积流过的平均功率是多少?=12060 (Q )(2): S a vE m0 60.265 10E m 1.00 10■. 0 r2(V/m)E(0,0)(3)往右移E m sin 8.66 103z v p t 15 m3(V/m )解:(1)电磁波沿z方向传播。
(2)自由空间电磁波的相速v p c 3 108 m/s••• k —20c20 c f —10c3 109Hz217j(20 z )z(3) H ^e z E 26510 7(e 2 e x e j20 z e y )(A/m)*(4)S av ^Re(EH *)^-^e z2.65 10 11e z (W/m 2)226-3证明在均匀线性无界无源的理想介质中,不可能存在 磁波。
证•/ EjkE °e jkz 0,即不满足Maxwell 方程不可能存在E E °e jkz e z 的均匀平面电磁波。
合肥工业大学电磁场与电磁波(孙玉发版)第5章答案
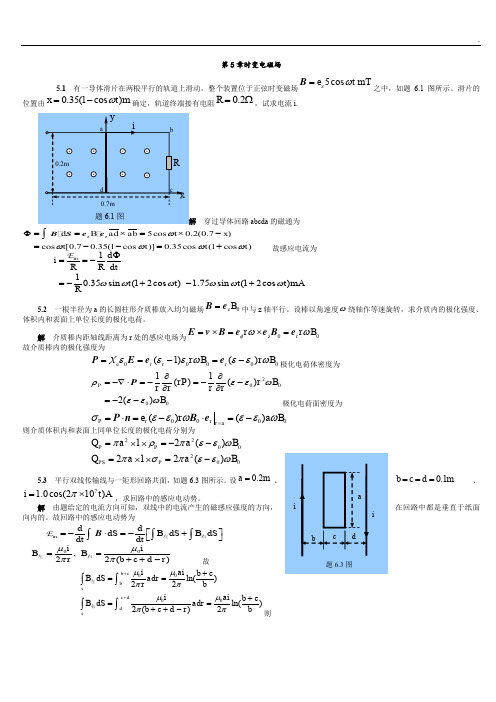
第5章时变电磁场5.1 有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场5cos mTz e t ω=B 之中,如题6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定,轨道终端接有电阻0.2R =Ω,试求电流i.穿过导体回路abcda 的磁通为)cos [0.70.35(1cos )]0.35cos (1cos )z z x t t t t ωωωωΦ-=--=+ 故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E5.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X 极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P 极化电荷面密度为0000()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-5.3 平行双线传输线与一矩形回路共面,如题6.3图所示。
设0.2a m =、0.1mb c d ===、71.0cos(210)A i t π=⨯,求回路中的感应电动势。
解 由题给定的电流方向可知,双线中的电流产生的磁感应强度的方向,在回路中都是垂直于纸面向内的。
合肥工业大学电磁场与电磁波孙玉发版答案
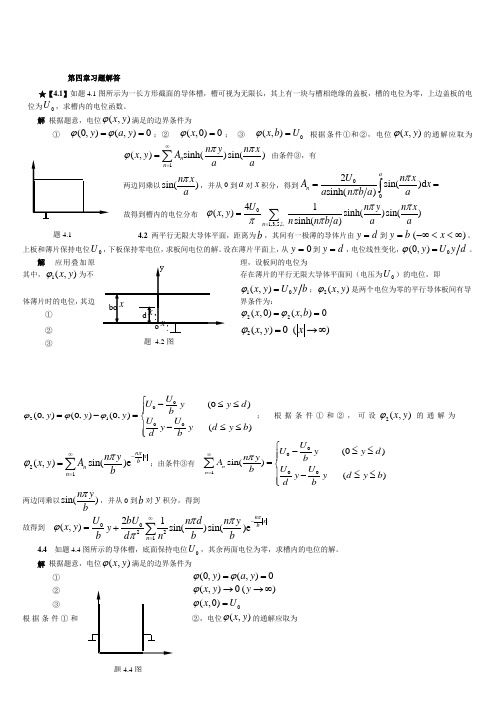
第四章习题解答★【4.1】如题4.1图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为0U ,求槽内的电位函数。
解 根据题意,电位(,)x y ϕ满足的边界条件为①(0,)(,)0y a y ϕϕ==;② (,0)0x ϕ=; ③ 0(,)x b U ϕ= 根据条件①和②,电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a aππϕ∞==∑ 由条件③,有两边同乘以sin()n xa π,并从0到a 对x 积分,得到002sin()d sinh()an U n x A x a n b a a ππ==⎰ 故得到槽内的电位分布 01,3,5,41(,)sinh()sin()sinh()n U n y n xx y n n b a a aππϕππ==∑L 4.2 两平行无限大导体平面,距离为b ,其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位0U ,下板保持零电位,求板间电位的解。
设在薄片平面上,从0=y 到d y =,电位线性变化,0(0,)y U y d ϕ=。
解 应用叠加原理,设板间的电位为其中,1(,)x y ϕ为不存在薄片的平行无限大导体平面间(电压为0U )的电位,即10(,)x y U y b ϕ=;2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:22(,0)(,)0x x b ϕϕ==① 2(,)0()x y x ϕ=→∞② ③002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b db ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩; 根据条件①和②,可设2(,)x y ϕ的通解为21(,)sin()en x bn n n yx y A b ππϕ∞-==∑;由条件③有 00100(0)sin()()n n U U y y d n y b A U U b y yd y b db π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑两边同乘以sin()n ybπ,并从0到b 对y 积分,得到 故得到 (,)x y ϕ=0022121sin()sin()e n x b n U bU n d n y y b d n b bππππ∞-=+∑ 4.4 如题4.4图所示的导体槽,底面保持电位0U ,其余两面电位为零,求槽内的电位的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
度为
Sav
Ee2 0
1 377
2.65 103 W/m2
可见,该微波炉的泄漏电场对人体的健康是安全的。 6-5 在自由空间中,有一波长为 12cm 的均匀平面波,当该波进入到某无损耗媒质时,
其波长变为 8cm,且此时 E 31.41V / m , H 0.125A / m 。求平面波的频率以及无损
10 4 e j20z e x
10
4
e
j(
2
20z
)
e
y
∥ /∥
试求: (1)电磁波的传播方向?
(2)电磁波的相速 v p ? 波长 ? 频率 f ?
(3)磁场强度 H ?
(4)沿传播方向单位面积流过的平均功率是多少?
解:(1) 电磁波沿 z 方向传播。
(2)自由空间电磁波的相速 vp c 3 108 m/s
10-2 的非磁性媒质中,沿正 e x 方向传播。
(1)求波的振幅衰减一半时,传播的距离;
(2)求媒质的波阻抗,波的相速和波长;
(3)设在
x
0 处的
E
50 sin 6
109 t
3
e
y
,写出
H (x,t)
的表示式。
解:(1) tan 102 ,这是一个低损耗媒质,平面波的传播特性,除了有微弱的
波长 v / f 0.0632(m) 6.32(cm)
(3)
6 109 3 108
2.5 99.3
H
(x,t)
50
e 0.5 x
sin(6
109 t
x
3
)ez
0.21e 0.5 x
sin(6
109 t
99.3x
3
)ez
(A/m)
6-8 微波炉利用磁控管输出的 2.45GHz 频率的微波加热食品,在该频率上,牛排的等效
6-9 已 知 海 水 的 4S/m∥ r 81, r 1 , 在 其 中 分 别 传 播 f 100MHz 或
损耗引起的衰减之外,和理想介质的相同。其衰减常数为
2
102 2
102 2 3 109 2
2.5 3 108
0.497
因为 ei 1/ 2 ,所以 l ln 2 1.40 m
(2)对低损耗媒质, / 120 / 2.5 238.4 Ω
相速 v 1 3108 1.90108 m/s 2.5
(3)时间经过 0.1μs 之后电场 E(0,0) 值在什么地方?
(4)时间在 t 0 时刻之前 0.1μs ,电场 E(0,0) 值在什么地方?
解:(1) k 2f c
r 2 (rad/m)
v p c / r 1.5 108 (m/s) 2 1 (m)
k
∥ 120 r 60 (Ω) r
复介电常数 ~r 40(1 0.3j) 。求:
(1)微波传入牛排的穿透深度 ,在牛排内 8mm 处的微波场强是表面处的百分之几? ( 2) 微 波 炉 中 盛 牛 排 的 盘 子 是 发 泡 聚 苯 乙 烯 制 成 的 , 其 等 效 复 介 电 常 数 ~r
1.03(1 j0.3 104 ) 。说明为何用微波加热时,牛排被烧熟而盘子并没有被毁。
解:(1)
1
1
2
1
2
1 2
1
0.0208m
20.8mm
E e z / e 8 / 20.8 68% E0
(2)发泡聚苯乙烯的穿透深度
12
2
1
2 3 108
2 2.45 109 0.3104
1.28 103(m) 1.03
可见其穿透深度很大,意味着微波在其中传播的热损耗极小,所以不会被烧毁。
2 k
2 20
0.1(m)
∵ k 20 c
∴ 20 c
∴ f 10c 3109 Hz 2
(3) H
1
e
z
E
2.65
10
7
(e
j(
20z
2
)e
x
e e j20z y )(A/m)
(4) S av
1 2
Re(E
H
*
)
E E*e 2 z
2.65 1011e z (W/m2 )
6-3
证明在均匀线性无界无源的理想介质中,不可能存在 E
E
0e
e jkz z
的均匀平面电
磁波。
证 ∵ Ε jkE0e jkz 0 ,即不满足 Maxwell 方程
∴ 不可能存在 E E 0e jkz ez 的均匀平面电磁波。
6-4 在微波炉外面附近的自由空间某点测得泄漏电场有效值为 1V/m,试问该点的平均 电磁功率密度是多少?该电磁辐射对于一个站在此处的人的健康有危险吗?(根据美国国 家标准,人暴露在微波下的限制量为 10-2W/m2 不超过 6 分钟,我国的暂行标准规定每 8 小时连续照射,不超过 3.8×10-2W/m2。) 解:把微波炉泄漏的电磁辐射近似看作是正弦均匀平面电磁波,它携带的平均电磁功率密
解:设 v 沿 z 轴方向,均匀平面波电场为 E ,则磁场为
H
1 0
ez
E
电荷受到的电场力为
F e
qE
其中 q 为点电荷电量,受到的磁场力为
Fm=qv B
q0ve z H
q0v E 0
qv
0 0 E
qv E c
故电荷所受磁场力与电场力比值为
Fm v Fe c
6-7 一个频率为 f 3GHz , e y 方向极化的均匀平面波在 r 2.5 ,损耗角正切值为
耗媒质的 r 和 r 。
解:因为 0 / r r ,所以 r r (12 / 8)2 9 / 4
又因为 E 120 H
r r
,所以 r r
E 120H
2
0.4443
r 1, r 2.25
6-6 若有一个点电荷在自由空间以远小于光速的速度 v 运动,同时一个均匀平面波也
沿 v 的方向传播。试求该电荷所受的磁场力与电场力的比值。
(2)∵
Sav
1 2
Em2
2
1 0
Em2 0.265 106
0 r
∴ Em 1.00 102 (V/m)
E(0,0)
Em
sin
3
8.66 103 (V/m)
(3) 往右移 z v p t 15 m
(4) 在 O 点左边15 m 处
6-2 一个在自由空间传播的均匀平面波,电场强度的复振幅是
E
第 6 章习题答案
6-1 在 r 1、 r 4 、 0 的媒质中,有一个均匀平面波,电场强度是
E(z,t)
Em
sin(t
kz
3
)
若已知 f 150MHz ,波在任意点的平均功率流密度为 0.265μw/m2 ,试求:
(1)该电磁波的波数 k ? 相速 v p ? 波长 ? 波阻抗 ? (2) t 0 , z 0 的电场 E(0,0) ?
