初三数学总复习函数基础练习含答案
初中函数测试题及答案

初中函数测试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项不是函数的定义?A. 函数是数集到数集的映射B. 函数是一种特殊的关系C. 函数是一种运算D. 函数是数集到数集的对应关系答案:C2. 如果一个函数的自变量x的取值范围是x>0,那么下列哪个选项是正确的?A. 函数的定义域为所有实数B. 函数的定义域为非负实数C. 函数的定义域为正实数D. 函数的定义域为负实数答案:C3. 函数y=2x^2+3x+1的图像是:A. 抛物线B. 直线C. 双曲线D. 圆答案:A4. 下列哪个函数是奇函数?A. y=x^2B. y=x^3C. y=x^4D. y=x答案:D5. 函数y=1/x的图像在第一象限内:A. 向右上方倾斜B. 向左上方倾斜C. 向右下方倾斜D. 向左下方倾斜答案:B6. 如果函数f(x)=x^2-4x+3,那么f(1)的值是多少?A. -2B. 0C. 2D. 4答案:A7. 函数y=3x-2的图像与y轴的交点坐标是:A. (0, -2)B. (0, 3)C. (2, 0)D. (-2, 0)答案:A8. 函数y=1/x的图像经过第几象限?A. 第一象限和第三象限B. 第二象限和第四象限C. 第一象限和第二象限D. 第三象限和第四象限答案:A9. 函数y=x+1与y=x-1的图像之间的距离是:A. 1B. 2C. 3D. 4答案:B10. 函数y=x^2的图像在x=0处的切线斜率是:A. 0B. 1C. 2D. -1答案:A二、填空题(每题4分,共20分)1. 函数y=2x+3的图像在x=2时的y值是_________。
答案:72. 如果函数f(x)=x^2-6x+8,那么f(3)的值是_________。
答案:13. 函数y=1/x的图像在x=-1处的切线斜率是_________。
答案:-14. 函数y=x^3-3x^2+2的图像在x=1处的切线斜率是_________。
中考数学《函数基础知识》专项练习题(带答案)
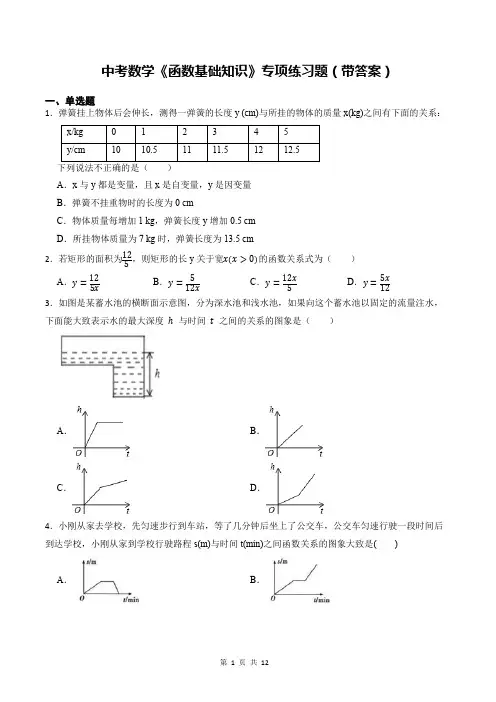
中考数学《函数基础知识》专项练习题(带答案)一、单选题1.弹簧挂上物体后会伸长,测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系:x/kg 0 1 2 3 4 5 y/cm1010.51111.51212.5A .x 与y 都是变量,且x 是自变量,y 是因变量B .弹簧不挂重物时的长度为0 cmC .物体质量每增加1 kg ,弹簧长度y 增加0.5 cmD .所挂物体质量为7 kg 时,弹簧长度为13.5 cm2.若矩形的面积为125,则矩形的长y 关于宽x(x >0)的函数关系式为( )A .y =125xB .y =512xC .y =12x 5D .y =5x 123.如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果向这个蓄水池以固定的流量注水,下面能大致表示水的最大深度 ℎ 与时间 t 之间的关系的图象是( )A .B .C .D .4.小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时间后到达学校,小刚从家到学校行驶路程s(m)与时间t(min)之间函数关系的图象大致是( )A .B .C.D.5.若代数式√x−1x−2有意义,则x的取值范围是()A.x>1且x≠2B.x≥1C.x≠2D.x≥1且x≠26.等腰三角形ABC中,AB=CB=5,AC=8,P为AC边上一动点,PQ⊥AC,PQ与△ABC的腰交于点Q,连结CQ,设AP为x,△CPQ的面积为y,则y关于x的函数关系的图象大致是()A.B.C.D.7.若直线y=kx上每一点都能在直线y=−6x上找到关于x轴对称的点,则它的解析式是()A.y=6x B.y=16x C.y=−6x D.y=−1 6x8.如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD﹣DC﹣CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2).运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是()A.B.C.D.9.函数y=√2−x+1x+1中,自变量x的取值范围是()A.x⩽2B.x⩽2且x≠−1 C.x⩾2D.x⩾2且x≠−110.在下列四个图形中,能作为y是x的函数的图象的是()A.B.C.D.11.如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是()A.15分钟B.20分钟C.25分钟D.30分钟12.下列图象中,y是x的函数的是()A.B.C.D.二、填空题13.如图1,在平面直角坐标系中,将▱ABCD(AB>AD)放置在第一象限,且AB∥x轴,直线y=−x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,则平行四边形ABCD的面积为.14.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地. 如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B−C−D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.下几种说法:①货车的速度为60千米/小时;②轿车与货车相遇时,货车恰好从甲地出发了3. 9小时;③若轿车到达乙地后,马上沿原路以CD段速度返回,则轿车从乙地出发317小时再次与货车相遇;其中正确的个数是. (填写序号)15.某商城为促进同一款衣服的销量,当同一个人购买件数达到一定数目的时候,超过的件数,每件打8折,现任意挑选5个顾客的消费情况制定表格,其中x表示购买件数,y表示消费金额,根据表格数据请写出一个y关于x的函数解析式是:.x(件)23456y(元)10015020024028016.函数y=2√x−1的自变量x的取值范围是.17.甲、乙两个车间接到加工一批零件的任务,从开始加工到完成这项任务共用了9天.其间,乙车间在加工2天后停止加工,引入新设备后继续加工,直到与甲车间同时完成这项任务为止,设甲、乙两个车间各自加工零件总数y(单位:件)与加时间x(单位:天)的对应关系如图1所示,由工厂统计数据可知,甲车间与乙车间加工零件总数之差z(单位:件)与加时间x(单位:天)的对应关系如图2所示,请根据图象提供的信息回答:(1)图中m的值是;(2)第天时,甲、乙两个车间加工零件总数相同.18.如图,△O的半径为5,点P在△O上,点A在△O内,且PA=3,过点A作AP的垂线交△O于点B,C.设PB= x ,PC=y,则y与x之间的函数解析式为三、综合题19.某旅客携带xkg的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李重量xkg的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李重量xkg的对应关系.行李的重量xkg快递费不超过1kg10元超过1kg但不超过5kg的部分3元/kg超过5kg但不超过15kg的部分5元/kg(1)如果旅客选择单托运,求可携带的免费行李的最大重量为多少kg?(2)如果旅客选择快递,当1<x≤15时,直接写出快递费y2(元)与行李的重量xkg之间的函数关系式;(3)某旅客携带25kg的行李,设托运mkg行李(10≤m<24,m为正整数),剩下的行李选择快递,当m为何值时,总费用y的值最小?并求出其最小值是多少元?20.小明一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶,若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系,如图所示,根据图象回答下列问题;(1)小汽车行驶小时后加油,中途加油升;(2)求加油前邮箱余油量Q与行驶时间t的函数关系式;(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点300km,车速为80km/h,要到达目的地,油箱中的油是否够用请说明理由.21.一农民带了若干千克自产的萝卜进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出萝卜千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)降价前他每千克萝卜出售的价格是多少?(2)降价后他按每千克0.4元将剩余萝卜售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克萝卜?22.某景区今年对门票价格进行动态管理.节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打折;非节假日期间全部打折.设游客为x人,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.(1)求不打折的门票价格;(2)求y1、y2与x之间的函数关系式;(3)导游小王5月2日(五一假日)带A旅游团,5月8日(非节假日)带B旅游团到该景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?(温馨提示:节假日的折扣与非节假日的折扣不同)23.在“世界读书日”这周的周末,小张同学上午8时从家里出发,步行到公园锻炼了一段时间后以相同的速度步行到图书馆看书,看完书后直接回到了家里,如图是他离家的距离s(米)与时间t(时)的函数关系,根据图象回答下列问题:(1)小张同学家离公园的距离是多少米?锻炼身体用了多少分钟?在图书馆看了多少分钟的书?从图书馆回到家里用了多少分钟?(2)图书馆离小张同学的家多少米?(3)小张同学从图书馆回到家里的速度是多少千米/时?24.甲、乙两车早上从A城车站出发匀速前往B城车站,在整个行程中,两车离开A城的距离s与时间t的对应关系如图所示.(1)A,B两城之间距离是多少?(2)求甲、乙两车的速度分别是多少?(3)乙车出发多长时间追上甲车?(4)从乙车出发后到甲车到达B城车站这一时间段,在何时间点两车相距40km?参考答案1.【答案】B 2.【答案】A 3.【答案】C 4.【答案】B 5.【答案】D 6.【答案】D 7.【答案】A 8.【答案】B 9.【答案】B 10.【答案】B 11.【答案】B 12.【答案】B 13.【答案】8 14.【答案】①②③15.【答案】{y =50x(0≤x ≤4)y =40x +40(x >4)16.【答案】x >1 17.【答案】(1)770(2)818.【答案】y =30x19.【答案】(1)解:设托运费y 1(元)与行李重量xkg 的函数关系式为y 1=kx+b将(30,300)、(50,900)代入y 1=kx+b , {30k +b =30050k +b =900 ,解得: {k =30b =−600 ∴托运费y 1(元)与行李质量xkg 的函数关系式为y 1=30x ﹣600. 当y 1=30x ﹣600=0时,x =20.答:可携带的免费行李的最大重量为20kg . (2)解:根据题意得:当0<x≤1时,y 2=10; 当1<x≤5时,y 2=10+3(x ﹣1)=3x+7;当5<x≤15时,y 2=10+3×(5﹣1)+5(x ﹣5)=5x ﹣3.综上所述:快递费y 2(元)与行李重量xkg 的函数关系式为y 2= {10(0<x ≤1)3x +7(1<x ≤5)5x −3(5<x ≤15) .(3)解:当10≤m <20时,5<25﹣m≤15∴y =y 1+y 2=0+5×(25﹣m)﹣3=﹣5m+122. ∵10≤m <20 ∴22<y≤72;当20≤m <24时,1<25﹣m≤5∴y =y 1+y 2=30m ﹣600+3×(25﹣m)+7=27m ﹣518. ∵20≤m <24 ∴22≤y <130.综上可知:当m =20时,总费用y 的值最小,最小值为22.答:当托运20kg 、快递5kg 行李时,总费用最少,最少费用为22元.20.【答案】(1)3;24(2)解:设直线解析式为Q=kt+b ,把(0,36)和(3,6)代入得: {3k +b =6b =36解得 {k =−10b =36 ∴Q=-10t+36,(0≤t≤3);(3)解:根据题意,每小时耗油量为10升 ∵加油站到景点用时间为:300÷80=3.75(小时) ∴需要的油量为:3.75×10=37.5升>30升 故不够用.21.【答案】(1)解:设降价前每千克萝卜价格为k 元则农民手中钱y 与所售萝卜千克数x 之间的函数关系式为:y=kx+5 ∵当x=30时,y=20 ∴20=30k+5 解得k=0.5.答:降价前每千克萝卜价格为0.5元. (2)解:(26-20)÷0.4=15 15+30=45kg.所以一共带了45kg 萝卜.22.【答案】(1)解: 800÷10=80 (元 / 人)答:不打折的门票价格是80元 / 人; (2)解:设 y 1=10k 解得: k =48 ∴y 1=48x当0⩽x⩽10时,设y2=80x 当x>10时,设y2=mx+b则{10m+b=80020m+b=1440解得:m=64∴y2=64x+160∴y2={80x(0⩽x⩽10)64x+160(x>10);(3)解:设A旅游团x人,则B旅游团(50−x)人若0⩽x⩽10,则80x+48(50−x)=3040解得:x=20,与x⩽10不相符若x>10,则64x+160+48(50−x)=3040解得:x=30,与x>10相符,50−30=20(人)答:A旅游团30人,B旅游团20人.23.【答案】(1)解:观察图象得:小张同学8时离开家,8:10到达公园,小张同学家离公园的距离是500米∵小张同学8:10到达公园,9:10离开公园∴小张同学锻炼身体用了60分钟∵小张同学9:30到达图书馆,11:40离开图书馆∴小张同学在图书馆看了130分钟的书∵小张同学11:40离开图书馆,12时回到家∴小张同学从图书馆回到家里用了20分钟∴小张同学家离公园的距离是500米,锻炼身体用了60分钟,在图书馆看了130分钟的书,从图书馆回到家里用了20分钟;(2)解:∵小张同学8时离开家,8:10到达公园,距离500米,用时10分钟∴小张同学从家到公园的速度为500÷10=50(米/分)∵步行到公园锻炼了一段时间后以相同的速度步行到图书馆着书∴小张同学从公园到图书馆的速度为50米/分∵小张同学9:10离开公园,9:30到达图书馆∴公园离图书馆的距离为:50×20=1000(米)∴图书馆离小张同学的家的距离为:1000+500=1500(米)∴图书馆离小张同学的家1500米;(3)解:∵小张同学从图书馆到家的距离为1500米,即1.5千米,从图书馆回到家里用了20分钟,即时13小时 ∴小张同学从图书馆回到家里的速度是:1.5÷13=4.5千米/时 ∴小张同学从图书馆回到家里的速度是4.5千米/时.24.【答案】(1)解:由图象可知A 、B 两城之间距离是300千米;(2)解:由图象可知,甲的速度= 3005=60(千米/小时) 乙的速度= 3003=100(千米/小时) ∴甲、乙两车的速度分别是60千米/小时和100千米/小时;(3)解:设乙车出发x 小时追上甲车由题意:60(x+1)=100x解得:x =1.5∴乙车出发1.5小时追上甲车;(4)解:设乙车出发后到甲车到达B 城车站这一段时间内,甲车与乙车相距40千米时甲车行驶了m 小时①当甲车在乙车前时得:60m ﹣100(m ﹣1)=40解得:m =1.5此时是上午6:30;②当甲车在乙车后面时100(m ﹣1)﹣60m =40解得:m =3.5此时是上午8:30;③当乙车到达B 城后300﹣60m =40解得:m = 133此时是上午9:20.∴分别在上午6:30,8:30,9:20这三个时间点两车相距40千米.。
初中函数练习题及答案

初中函数练习题及答案1. 函数的概念和性质函数是数学中非常重要且基础的概念。
下面是几个函数的定义和性质的练习题:练习题1:判断下列关系是否是函数,并说明理由。
a) {(1, 2), (2, 4), (3, 6), (4, 8)}b) {(1, 2), (2, 3), (2, 4), (3, 6)}c) {(1, 2), (2, 2), (3, 2), (4, 2)}练习题答案1:a) 是函数,因为每个x对应唯一的y值。
b) 不是函数,因为元素(2, 4)和(2, 3)违背了x对应唯一的y值的原则。
c) 是函数,因为每个x对应同样的y值2。
2. 函数的图象和性质函数的图象是函数概念的重要表现形式之一。
下面是几个与函数图象相关的练习题:练习题2:绘制函数y = 2x + 1的图象,并说明其性质。
练习题答案2:函数y = 2x + 1的图象是一条直线,斜率为2,经过点(0, 1)。
根据该函数的特点,我们可以得出以下性质:- 当x增加1个单位时,y增加2个单位。
- 当x减少1个单位时,y减少2个单位。
- 图象关于直线y = x对称。
3. 函数的实际应用函数在生活和实际问题中的应用非常广泛。
下面是一个与函数实际应用相关的练习题:练习题3:小明骑自行车从家里出发,他的速度与时间的关系可以用函数v(t) = 2t表示,其中t表示时间(分钟),v表示速度(m/s)。
已知小明骑行30分钟能骑行的路程为15km,求小明的平均速度。
练习题答案3:已知小明骑行30分钟能骑行的路程为15km,要计算平均速度,我们可以使用以下公式:平均速度 = 总路程 / 总时间平均速度 = 15km / 30分钟 = 0.5 km/min4. 函数的复合和反函数函数的复合和反函数是函数概念的深入扩展。
下面是一个与函数复合和反函数相关的练习题:练习题4:已知函数f(x) = 2x + 1和g(x) = x^2,求复合函数f(g(x))。
练习题答案4:将函数g(x)代入函数f(x)中,得到f(g(x)) = 2(x^2) + 1。
中考函数复习题及答案

中考函数复习题及答案一、选择题1. 函数y = 2x + 3的斜率是()A. 2B. 3C. -2D. -32. 下列哪个是一次函数的图象?A. 直线B. 曲线C. 抛物线D. 双曲线3. 函数f(x) = x^2 - 4x + 4的顶点坐标是()A. (2, 0)B. (-2, 0)C. (0, 4)D. (2, 4)4. 函数y = 1/x的图象不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限5. 函数y = |x|的图象是()A. 直线B. V形C. U形D. 抛物线答案:1. A 2. A 3. A 4. D 5. B二、填空题6. 函数y = 3x - 2的截距是______。
7. 如果一个函数的图象与x轴交于点(1,0),则该函数可以表示为y = ______。
8. 函数y = x^2 + 2x + 1可以化简为y = (x + ______)^2。
9. 函数y = 1/x的图象在x轴的正半轴上,y的值随着x的增大而______。
10. 函数y = kx + b,当k > 0时,图象从左向右上升;当k < 0时,图象从左向右______。
答案:6. -2 7. x - 1 8. 1 9. 减小 10. 下降三、解答题11. 已知函数f(x) = 2x - 5,求f(3)的值。
12. 已知二次函数y = ax^2 + bx + c的顶点坐标为(-1, -4),求a的值。
13. 函数y = 3x + 7与x轴的交点坐标是什么?14. 函数y = x^2 - 6x + 9的最大值是多少?15. 已知函数y = |x - 2| + 3,求x = 2时的函数值。
答案:11. f(3) = 2 * 3 - 5 = 6 - 5 = 112. 顶点坐标(-1, -4),根据顶点公式,-b/2a = -1,b = 2a,又因为顶点的y坐标是-4,所以有a(-1)^2 + b(-1) + c = -4,代入b =2a,解得a = -4。
初中函数专题试题及答案

初中函数专题试题及答案一、选择题(每题3分,共30分)1. 下列函数中,哪一个是一次函数?A. \( y = x^2 \)B. \( y = 2x + 3 \)C. \( y = \frac{1}{x} \)D. \( y = x^3 - 2x \)答案:B2. 函数 \( y = 3x - 5 \) 的图象与x轴的交点坐标是:A. \( (0, -5) \)B. \( (5, 0) \)C. \( (-5, 0) \)D. \( (0, 5) \)答案:C3. 如果函数 \( y = 2x + 1 \) 在 \( x = 2 \) 时的值为5,那么\( x = 1 \) 时的值是:A. 3B. 4C. 2D. 1答案:A4. 函数 \( y = -\frac{1}{2}x + 3 \) 的斜率是:A. \( \frac{1}{2} \)B. \( -\frac{1}{2} \)C. \( \frac{3}{2} \)D. \( -3 \)答案:B5. 函数 \( y = 4x^2 \) 的顶点坐标是:A. \( (0, 0) \)B. \( (0, 4) \)C. \( (2, 0) \)D. \( (0, -4) \)答案:A6. 函数 \( y = x^2 - 6x + 9 \) 可以写成完全平方的形式:A. \( (x - 3)^2 \)B. \( (x + 3)^2 \)C. \( (x - 3)^2 + 3 \)D. \( (x + 3)^2 - 3 \)答案:A7. 函数 \( y = 2x^2 - 8x + 7 \) 的最小值是:A. 1B. 3C. 7D. 无法确定答案:A8. 函数 \( y = \frac{1}{x} \) 的图象是:A. 一条直线B. 两条直线C. 一个双曲线D. 一个抛物线答案:C9. 函数 \( y = 3x^2 + 2x - 5 \) 的对称轴是:A. \( x = -\frac{2}{3} \)B. \( x = \frac{2}{3} \)C. \( x = -1 \)D. \( x = 1 \)答案:B10. 函数 \( y = 2x + 3 \) 和 \( y = -x + 1 \) 的交点坐标是:A. \( (-2, -1) \)B. \( (2, 5) \)C. \( (-1, 1) \)D. \( (1, 3) \)答案:C二、填空题(每题4分,共20分)11. 函数 \( y = 2x + 1 \) 在 \( x = -1 \) 时的值为 _______。
初三函数练习题及答案

初三函数练习题及答案函数是数学中一个重要的概念,也是初中数学学习的重点内容之一。
通过解决函数练习题,可以帮助学生更好地理解和掌握函数的概念和性质。
下面是一些初三函数练习题及答案,供同学们参考。
练习一:函数的定义与判断1. 函数的定义是什么?函数是两个集合之间的一种特殊对应关系。
对于定义域内的每一个元素,都有唯一对应的值域元素与之对应。
2. 下列哪些对应关系是函数?(1) (1, 2), (2, 3), (3, 4), (1, 5)(2) (1, 2), (2, 3), (1, 4), (2, 5)(3) (1, 2), (2, 3), (3, 4), (4, 2)(4) (1, 2), (2, 3), (3, 2), (4, 1)答案:(1) 是函数。
(2) 不是函数。
(3) 不是函数。
(4) 是函数。
练习二:函数的图像与性质3. 画出函数 y = 2x + 1 的图像,并描述其特点。
答案:函数 y = 2x + 1 的图像为一条直线,通过点 (0, 1)。
斜率为 2,表示函数图像上任意两点的纵坐标之差与横坐标之差的比例为 2:1。
函数图像是上升的,斜率大于 0,表示随着自变量的增大,因变量也增大。
练习三:函数的性质应用4. 已知函数 f(x) 的定义域为实数集 R,值域为区间 [-1, 3]。
若函数g(x) = f(2x),求函数 g(x) 的定义域和值域。
答案:因为 f(x) 的定义域为实数集 R,所以 g(x) 的定义域为实数集 R。
对于任意的 x,有 2x 在 R 上取值。
因此,g(x) 的定义域也为实数集 R。
对于任意的 x,2x 都在定义域内,根据 f(x) 的值域为 [-1, 3],得出f(2x) 的值域也为 [-1, 3]。
因此,函数 g(x) 的值域为 [-1, 3]。
练习四:函数关系的综合应用5. 已知函数 h(x) = |x - 2| + |3 - x|,求使 h(x) 最小的 x 的值,及最小值是多少。
初三数学函数基础知识试题答案及解析
初三数学函数基础知识试题答案及解析1.函数中自变量x的取值范围是【答案】x>2.【解析】根据被开方数大于等于0,分母不等于0列式计算即可得解.试题解析:由题意得,x-2>0,解得x>2.【考点】函数自变量的取值范围.2.函数y=中,自变量x的取值范围是【答案】x≠2.【解析】求函数自变量的取值范围,就是求函数解析式有意义的条件,分式有意义的条件是:分母不为0.试题解析:要使分式有意义,即:x-2≠0,解得:x≠2.【考点】1.函数自变量的取值范围;2.分式有意义的条件.3.函数y=的自变量x的取值范围为.【答案】x≥﹣1【解析】由题意得,x+1≥0,解得x≥﹣1.故答案为:x≥﹣1.【考点】函数自变量的取值范围4.函数的自变量x的取值范围是.【答案】x≥6.【解析】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数的条件,要使在实数范围内有意义,必须.【考点】1.函数自变量的取值范围;2.二次根式有意义的条件.5. 2014年5月10日上午,小华同学接到通知,她的作文通过了《我的中国梦》征文选拔,需尽快上交该作文的电子文稿.接到通知后,小华立即在电脑上打字录入这篇文章,录入一段时间后因事暂停,过了一会儿,小华继续录入并加快了录入速度,直至录入完成.设从录入文稿开始所经过的时间为x,录入字数为y,下面能反映y与x的函数关系的大致图象是()A. B. C.【答案】C.【解析】根据题目中叙述的过程,知整个过程包括3段:①接到通知后,小华立即在电脑上打字录入这篇文章,此时录入字数y随时间x的增加逐渐增加;②录入一段时间后因事暂停,此时录入字数y随时间x的增加不变;③过了一会儿,小华继续录入并加快了录入速度,直至录入完成,随后将两个出水管关闭,并同时打开两个进水管将水蓄满,此时录入字数y随时间x的增加逐渐增加,且比①的趋势要陡.故选C.【考点】函数图象的分析.6.函数中自变量的取值范围是().A.B.C.D.【答案】C.【解析】根据题意得:x+3>0解得x>-3故选C.【考点】1.函数自变量的取值范围;2.分式有意义的条件;3.二次根式有意义的条件.7.在函数y=中,自变量x的取值范围是.【答案】x<【解析】要使函数有意义,则,所以x<.8.函数的自变量的取值范围是.【答案】x≥-1且x≠0.【解析】试题解析:由题意得:x+1≥0且x≠0,解得x≥-1且x≠0.考点: 函数自变量的取值范围.9.函数y=+3中自变量x的取值范围是()A.x>1B.x≥1C.x≤1D.x≠1【答案】B.【解析】根据被开方数大于等于0列式计算即可得解.根据题意得,x﹣1≥0,解得x≥1.故选B.考点: 函数自变量的取值范围.10.函数中自变量x的取值范围是A.x≤2且x≠3B.x≤2C.x<2且x≠3D.x=3【答案】B.【解析】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和分式分母不为0的条件,要使在实数范围内有意义,必须.故选B.【考点】1.函数自变量的取值范围;2.二次根式和分式有意义的条件.11.函数y=中,自变量x的取值范围是【答案】x≠1.【解析】根据分式有意义的条件是分母不为0;分析原函数式可得关系式x-1≠0,解可得答案.试题解析:根据题意可得x-1≠0;解得x≠1;故答案为:x≠1.考点: 函数自变量的取值范围;分式有意义的条件.12.函数:中,自变量x的取值范围是.【答案】。
初三数学函数基础知识试题答案及解析
初三数学函数基础知识试题答案及解析1.函数y=中,自变量x的取值范围是【答案】x≠2.【解析】求函数自变量的取值范围,就是求函数解析式有意义的条件,分式有意义的条件是:分母不为0.试题解析:要使分式有意义,即:x-2≠0,解得:x≠2.【考点】1.函数自变量的取值范围;2.分式有意义的条件.2.函数中自变量x的取值范围是()A.x>2B.x≥2C.x≤2D.x≠2【答案】C.【解析】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和的条件,要使在实数范围内有意义,必须.故选C.【考点】1.函数自变量的取值范围;2.二次根式有意义的条件.3.函数y=的自变量x的取值范围为.【答案】x≥﹣1【解析】由题意得,x+1≥0,解得x≥﹣1.故答案为:x≥﹣1.【考点】函数自变量的取值范围4.如图1,在平面直角坐标系中,将□ABCD放置在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么ABCD面积为()A.4B.4C.8D.8【答案】C.【解析】根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是8时经过B,则AB=8-4=4,当直线经过D点,设交AB与N,则DN=2,作DM⊥AB于点M.∵y=-x与x轴形成的角是45°,又∵AB∥x轴,∴∠DNM=45°,∴DM=DN•sin45°=2×=2,则平行四边形的面积是:AB•DM=4×2=8.故选C.【考点】动点问题的函数图象.5.如图,在平面直角坐标系中,以点A(2,3)为顶点任作一直角∠PAQ,使其两边分别与x轴、y轴的正半轴交于点P、Q,连接PQ,过点A作AH⊥PQ于点H,设点P的横坐标为x,AH的长为y,则下列图象中,能表示y与x的函数关系的图象大致是()A.B.C.D.【答案】D.【解析】应用特殊元素法和排他法求解:如图1,当点P与点O重合时,x=0,y=2.故可排除选项C;如图2,当点Q与点O重合时, y=3.故可排除选项A;如图3,当x=2时,∵AH⊥PQ,∴,即,故可排除选项B.故选D.【考点】1.动态问题的函数图象分析;2.勾股定理;3.相似三角形的判定和性质;户4.特殊元素法和排他法的应用.6.函数y=+3中自变量x的取值范围是()A.x>1B.x≥1C.x≤1D.x≠1【答案】B.【解析】根据题意知:x-1≥0解得:x≥1.故选B.【考点】1.自变量的取值范围;2.二次根式有意义的条件.7.函数中,自变量x的取值范围是_________【答案】.【解析】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和的条件,要使在实数范围内有意义,必须.【考点】1.函数自变量的取值范围;2.二次根式有意义的条件.8.如图1,AB是半圆O的直径,正方形OPNM的对角线ON与AB垂直且相等,Q是OP的中点.一只机器甲虫从点A出发匀速爬行,它先沿直径爬到点B,再沿半圆爬回到点A,一台微型记录仪记录了甲虫的爬行过程.设甲虫爬行的时间为t,甲虫与微型记录仪之间的距离为y,表示y 与t的函数关系的图象如图2所示,那么微型记录仪可能位于图1中的()A.点M B.点N C.点P D.点Q【解析】D.应用排他法分析求解:若微型记录仪位于图1中的点M,AM最小,与图2不符,可排除A.若微型记录仪位于图1中的点N,由于AN=BM,即甲虫从A到B时是对称的,与图2不符,可排除B.若微型记录仪位于图1中的点P,由于甲虫从A到OP与圆弧的交点时甲虫与微型记录仪之间的距离y逐渐减小;甲虫从OP与圆弧的交点到A时甲虫与微型记录仪之间的距离y逐渐增大,即y与t的函数关系的图象只有两个趋势,与图2不符,可排除C.故选D.【考点】1.动点问题的函数图象分析;2.排他法的应用.9.如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是()A.B.C.当0<t≤10时,D.当时,△PBQ是等腰三角形【答案】D【解析】(1)结论A正确,理由如下:分析函数图象可知,BC=10cm,ED=4cm,故AE=AD﹣ED=BC﹣ED=10﹣4=6cm.(2)结论B正确,理由如下:如图,连接EC,过点E作EF⊥BC于点F,由函数图象可知,BC=BE=10cm,,∴EF=8。
初三数学函数练习题及答案
初三数学函数练习题及答案1. 已知函数 y = 2x + 3,求当 x 为 4 时的函数值。
解答:将 x = 4 代入函数中,得到 y = 2(4) + 3 = 11,所以当 x 为 4 时,函数值为 11。
2. 求函数 y = 3x - 1 的解析式。
解答:已知函数的解析式为 y = 3x - 1,其中 3 是函数的斜率,-1 是y 轴的截距。
所以函数的解析式为 y = 3x - 1。
3. 已知函数 y = 4x + 2,求当 y = 14 时的 x 的值。
解答:将 y = 14 代入函数中,得到 14 = 4x + 2,然后移项得到 4x = 14 - 2,即 4x = 12。
最后除以 4 得到 x = 3,所以当 y = 14 时,x 的值为3。
4. 求函数 y = 2x^2 - 3x + 1 的最大值或最小值,并说明是最大值还是最小值。
解答:首先,可以通过计算函数的导数来确定最大值或最小值。
对函数 y = 2x^2 - 3x + 1 求导得到 y' = 4x - 3。
令 y' = 0,解得 x = 3/4。
将x = 3/4 代入原函数,得到 y = 2(3/4)^2 - 3(3/4) + 1 = 7/8。
所以函数的最大值或最小值为 7/8,由于函数的二次项系数为正数,所以该值为最小值。
5. 求函数 y = x^3 - 2x^2 + 3x 的零点。
解答:函数的零点即为使 y = 0 的 x 值。
将 y = 0 代入函数中,得到x^3 - 2x^2 + 3x = 0。
通过因式分解,可得到 x(x - 1)(x - 3) = 0。
因此,函数的零点为 x = 0, x = 1, x = 3。
6. 求函数 y = log2(x) 的定义域和值域。
解答:对于函数 y = log2(x),由于对数函数的定义需满足 x > 0,所以该函数的定义域为 x > 0。
而对数函数的值域为实数集,所以函数 y= log2(x) 的值域为实数集。
初三数学函数精选练习题及答案一
初三数学函数精选练习题及答案一
1. 函数定义和性质
题目
1. 函数f(x)在定义域[1, 4]上的最大值是多少?
2. 已知函数f(x)的定义域为[-2, 5],值域为[0, 3],则这个函数的性质是什么?
答案
1. 函数f(x)在定义域[1, 4]上的最大值可以通过求导数来确定。
首先,计算f'(x)的值,然后令f'(x)等于零,解得x的值为2。
再计算f(2)的值即可得到函数f(x)在定义域[1, 4]上的最大值。
2. 由于函数f(x)的定义域为[-2, 5],值域为[0, 3],则函数f(x)是有界函数且为增函数。
有界函数表示函数在特定区间内取值有上、下界;增函数表示当自变量增大时,函数值也随之增大。
2. 函数图像和性质
题目
1. 函数f(x)=x^2的图像是什么样的?
2. 函数f(x)=3^x的图像是什么样的?
答案
1. 函数f(x)=x^2的图像是一个开口向上的抛物线。
2. 函数f(x)=3^x的图像是逐渐上升的曲线,呈现指数增长的趋势。
3. 函数相关计算
题目
1. 已知函数f(x)=2x+5,求f(3)的值。
2. 已知函数f(x)=x^2-3x+2,求f(2)和f(0)的值。
答案
1. 将x=3代入函数f(x)=2x+5中,可以求得f(3)的值为
2×3+5=11。
2. 将x=2和x=0分别代入函数f(x)=x^2-3x+2中,可以求得f(2)的值为2^2-3×2+2=2,f(0)的值为0^2-3×0+2=2。
以上为初三数学函数精选练习题及答案一,请根据需要进行练习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.姓名函数练习基础型一、选择题(本大题共35小题,共105.0分)的横坐标是P+1.如图所示,已知二次函数≠0)=(+的图象的顶点mmx) 4,那么2acaxbxyAB,0)和点B,且的长是(,图象交4>轴于点A(mmmm D.8-2-8 B. C.2A.4+)-2)作如下平移(+3的图象,将抛物线 2.要得到=-5=-5( 3个单位A.向右平移2 22xyxy个单位,再向上平移 3个单位B.向右平移2个单位,再向下平移 3个单位C.向左平移2个单位,再向上平移 3个单位D.向左平移2个单位,再向下平移2aaxyaxay≠0)与)=≠0)在同一平面直角坐标系中的图象可能是( 3.函数(=-2(D.B. C.A.则+≠0)的图象如图所示对称轴为+=-14.已知二次函数(=cbabaabc)(4<+20>0 2xabxcyax(2)2++4=0(3下列式子正确的个数是(1))2acb0 -4<)( D.4个C.3个 B.2个 A.1个2xyx -4)5.二次函数+7=的最小值为( D.-3C.3 A.2 B.-2 )1个单位,再向上平移36.将抛物线个单位,得到的抛物线是(=4 向右平移22xxyy+3 2xy-1=4() A.B.=4(+3 +1)-1) D.C.-3=4(=4+1)(-322xyxy)+2抛物线的顶点是(=( -1) 7. )-1,-22) D.() B.(1,2) C.(-1,1A.(,2xy-2的大小、(2,上,则)在抛物线、=(+-1)8.已知点A(-1-,)、B(-1,)、C311223)2yyycyyyyx关系是(yyyyyyyyyyyy D. C.A.>>>>>> B.>>1213331212322yaxyabaxb在同一坐标系中的图象大致为(和)=9.若0<,则函数 =+A. B. C. D.;②方+>10.如图为二次函数的图象,给出下列说法:①=0+22bbmaaxbxcxbcamax,2abccaxbxy且>的根为=-1,=3;③6--+<0;④-程++=021m)1≠0,其中正确的说法有( - D. C.①②④B.②③④ A.①②③②④1 / 26.的圆心坐,2),⊙C2,0)、(011.如图,已知A、B两点的坐标分别为(y轴交DA与),半径为1.若D是⊙O上的一个动点,线段0标为(-1,)于点E,则△ABE面积的最大值为(D.2 C.1 A.2+ B.2+axyax,则不等式)-1>12.如图,函数2=的解集是(-1的图象过点(1,2)xxxx>2 B.D.>1 C.2A.<<1xyaxybx的值是轴上相交于同一点,则13.已知一次函数-2=+4与的图象在= ()B.-2 D.-C. A.4naaalm)也是直(Q-1,2(-3)都在直线,14.无论上.若点取什么实数,点P nlm的值等于(线上的点,则2)-+3 D.-6 B.-4 C.6 A.4yxkxyb取不同值时,已知一次函数= +对应的值列表如下:中,15.2 -1 …2 3 x… -m2 +1 0y -1……n)为常数)的解集为(k,b,m,n则不等式kx+b>0(其中A.x>2 B.x>3 C.x <2 D.无法确定yx+4的图象与两坐标轴所围成的三角形的面积为( 16.一次函数)=-A.2B.4C.6D.8;(4);(3)17.下列函数关系式:(1)=-,其中一次函数;(2)=2=+11的个数2xxyyyx是()A.1B.2C.3D.418.小阳在如图①所示的扇形舞台上沿O-M-N匀速行走,他从点O出发,沿箭头所示的方向经过点M再走到点N,共用时70秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走tyyt的函数关系的图象大致,他与摄像机的距离为与(单位:米),表示路的时间为(单位:秒)如图②,则这个固定位置可能是图①中的()A.点QB.点PC.点MD.点N19.6月24日,重庆南开(融侨)中学进行了全校师生地震逃生演练,警报拉响后同学们匀速跑步y与时到操场,在操场指定位置清点人数后,再沿原路匀速步行回教室,同学们离开教学楼的距离x的关系的大致图象是间()A. B. C. D.2 / 26.cmcm,,中,AD∥BC,∠C=90°,CD=6AD=220.如图,在直角梯形ABCDQ停止,点运动到点C,AD,DCP、Q同时从点B出发,点P沿BA动点scm到达P点停止,两点运动时的速度都是1,而当点/沿BC运动到C st的面积点运动的时间为)(,△BPQ时,点点AQ正好到达点C.设P2tcmyy 的函数关系的大致图).为下图中能正确表示整个运动中(关于)象是(D.C. A. B.某班学生在参加做豆花的实践活动中,计划磨完一定量的黄豆,在磨了一部分黄豆后,大家中21.t,设从开始磨黄豆所经过的时间为途休息并交流磨黄豆的体会,之后加快速度磨完了剩下的黄豆,tss)剩下的黄豆量为之间的函数关系的大致图象是(,下面能反映与A. B. D.C.上,E在射线ACAB=3,点D在线段BC上,点22.如图,等边△ABC中,边长方向沿ACE点以每秒1个单位的速度向终点C运动,点点D沿BC方向从B点也停止运动,设运动点停止时EA点以每秒2个单位的速度运动,当D从tyyt的图象来表示,则三点围成的图形的面积用与时间为D秒,若、E、C )是(C. A.D.B.xy)的取值范围是(23.函数 =中自变量xxxxx D.≥1且≠2≠2B.≥1 >2 C.A.2bcmcmacm,宽是),下列判断错误的是(24.一个长方形的面积是10 ,其长是ab D.C.是变量是变量是变量 B.10A.10是常量出发沿图中某一个扇形顺时针匀速运从点OBC,是⊙O的两条互相垂直的直径,点P125.如图,AD xyy(单位:秒)的函数关系的图象大致如图与点P动,设∠APB=运动的时间(单位:度),如果()的运动路线可能为那么点2所示,P C.O→C→D→OB.O→A→C→OA.O→B→A→O D.O →B→D→O3 / 26.在运动过程中速.点P出发,沿线段AB运动至点B26.如图,动点P从点A的运与点P为圆心,线段AP长为半径的圆的面积S度大小不变.则以点A t动时间)之间的函数图象大致是(D.C.A. B.千米的早餐店吃早餐,用了一刻钟吃完早餐后,按原路返回到离小明从家中出发,到离家1.227. )1千米的学校上课,在下列图象中,能反映这一过程的大致图象是(家C. A. B.D.yx轴的交点,分别是某函数图象与轴、0),点A、B28.如图,已知点F的坐标为(3,xxdd之间满足关,,且PF的长为点P是此图象上的一动点,设点P的横坐标为与xxd,则结论:①AF=2;②BF=5;③OA=5;④OB=3,正确结论的=5-≤5)(0≤系:)序号是(D.③④ C.①②④ A.①②③ B.①③的路线O-C-D-O从圆心O出发,沿PB、C、D为⊙O上的四等分点,动点、29.如图:点Attyy之间函数秒,∠APB的度数为做匀速运动.设运动的时间为与.则下列图象中表示)关系最恰当的是(B. D.C. A.y(单位:升)随行驶里30.一辆汽车的油箱中现有汽油60升,如果不再加油,那么油箱中的油量xyx函数关系用图象表与/千米,则程(单位:千米)的增加而减少,若这辆汽车平均耗油0.2升示大致是()A. B. D.C.w),下列关此函数图象描述正的是(关的函数:已知31. 该函数图象与坐标轴有两个交点 B.该函数图象经过第一象限A. D.该函数图象在第四象限 C.该函数图象关于原点中心对称注满烧杯后继续注水,32.如图,向放在水槽底部的烧杯注水(注水速度不变),xy之间的函数关系,大致直至水槽注满.水槽中水面升上的高度与注水时间是下列图中的()4 / 26.A. B.D.C.的路点出发,沿0CDO、BC是⊙O的两条互相垂直的直径,点P从O33.如图,AD yx,那么表线匀速运动,设点P运动的时间为(单位:度)(单位:秒),∠APB=xy示)与之间关系的图象是(C. B. A.D.分BC=6.点A、D34.如图,点E、F是以线段BC为公共弦的两条圆弧的中点,22yx,下列图象中,AB-AD、BC上的动点.连接AB、AD,设BD==,别为线段EF xy)能表示与的函数关系的图象是(A. B. D.C.cmcm A→B→C的速度,沿A出发,以每秒135.如图,正△ABC的边长为3P,动点从点2xyyx的函数的图,则的方向运动,到达点C时停止,设运动时间为关于(秒),=PC )象大致为(A. B. D.C.分二、填空题(本大题共11小题,共33.0)xy ______ 时,<0.抛物线的部分图象如图所示,则当36.的取值范围是2cyaxbx37.某同学用描点法=的图象时,列出了表:+ + 2 1 …x0 … -2 -1-5-2y……-11-21______ yy由于粗心,他算错了其中一个值,则这个错误的值是.5 / 26.yxyyxyx′=,,′))和Q38.在直角坐标系(O,给出如下定义:若中,对于点P(,则称点Q 为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2),点(-1,3)的“可控变点”为点(-1,-3).若′是7,则“可控变点”Q的横坐标是+16的图象上,其“可控变点”Q的纵坐标点P在函数2yxy=-______ .的大小关系,则)两点,若(1,<)、B(39.二次函数与=,<-2A的图象上有2xxyxyyxxxyy______ .21122121是40.已知一个口袋中装有六个完全相同的小球,小球上分别标有0,3,6,9,12,a,则使得一次函数15六个数,搅匀后一次从中摸出一个小球,将小球上的数记为xxaya的解为整+)的分式方程=(5-经过一、二、四象限且关于.数的概率是 ______ yykxxy轴左侧作等边OB为边在A=,+4与B,两点,以轴分别交于41.如图,直线y上,则C′恰好落在直线的对应点沿AB轴翻折后,点C三角形OBC,将△OBCB k ______ .的值为.将△AOBAB,0),连接0,4),B(-342.如图,在平面直角坐标系中,已知点A(yx轴正半轴上的点落在A′处,折痕所在的直线交沿过点B的直线折叠,使点A .C的坐标为 ______ 轴于点C,则点bkykxb(填>,<,,的图象如图所示,则 ______ 0 ______ 43.一次函数0=+ 符号)=2mmxmy)= ______ +.44.一次函数-4=(过原点,则+2yyyxyy =-3,+2上,-345.已知点(,,(1,都在直线)则)的大小关系是 ______ .1212cmy)米,若平均每年都长高5厘米.请写出树苗的高度(46.一棵新栽的树苗高1x与时间.(年)之间的函数关系式: ______小题,共30.0分)三、计算题(本大题共52cxbxyyx在B+两点,且点+47.已知一次函数A=的图象和二次函数+1的图象都经过=A、y 5.轴上,B点的纵坐标为 1)求这个二次函数的解析式;(,求△ABP的面积;(2)将此二次函数图象的顶点记作点P在这个FE、,点在射线、DAB上,且D点的横坐标比C点的横坐标大2)已知点(3C y CDF、与点坐标.轴平行,当CF∥ED时,求二次函数图象上,且CE元,为了扩大销售减少库存,商场销售一批衬衫,每天可售出48.20件,每件盈利40 件.每天可多售出21决定采取适当的降价措施,经调查发现,如果一件衬衫每降价元,xyyx之间的函数关系式.元,每天盈利元,列出与①设每件降价元,每件衬衫降价多少元?②若商场每天要盈利1200 ③每件降价多少元时,商场每天的盈利达到最大?盈利最大是多少元?6 / 26.轴交)三点,且与,3)、N(2-1,0)、49.如图,已知二次函数B=(3+,+0的象经过2bxcaxyyA(于点C.(1)求这个二次函数的解析式,并写出顶点M及点C的坐标;ykxdx轴交于点D,试证明四边形CDANM两点,且与=是平行四边形.+ 经过C、2()若直线yx BA轴、、50.轴分别交于如图,在平面直角坐标系中,直线+2与x轴,垂足为DE⊥ABCD,过点D作两点,以AB为边在第二象限内作正方形 E. AB的长;、B的坐标,并求边(1)求点A D的坐标;(2)求点x点的周长最小?如果能,请求出M轴上找一点M(3)你能否在,使△MDB 的坐标;如果不能,说明理由.均在边长为1的正方形网格格点上.51.如图,在平面直角坐标系中,A、B )求线段AB所在直线的函数解析式;(1.若直BC,指定位置画出线段BCAB绕点B逆时针旋转90°,得到线段(2)将线段xbyykx(填“增大”或“减小”)随.线BC的函数解析式为=的增大而+ ______ ,则分)本大题共16小题,共128.0四、解答题(两点,与轴交于-A+2(、52.如图,二次函数=≠0)的图象与B .,0)轴交于点C,2yxxaaxy已知点A(-4 的函数解析式;1)求抛物线与直线AC(nm OCDA,(2)若点D()是抛物线在第二象限的部分上的一动点,四边形m的函数关系;关于的面积为S,求S x F、、A、C为抛物线上任意一点,点(3)若点EF为E轴上任意一点,当以的坐标.为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E,C轴交于点(0=(+1)+B 与轴交于A、两点,与如图,抛物线53.2ykxyx).-3k(1)求抛物线的对称轴及的值;的坐的值最小,使得P)(2抛物线的对称轴上存在一点,PA+PC求此时点P 标;7 / 26.(3)点M是抛物线上一动点,且在第三象限.①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标;x轴交线段AC于点PPM⊥,求出线段PM长度的最大值.②过点M作+6.54.已知二次函数+4=-22yxx(1)求该函数图象的顶点坐标.x轴的交点坐标. 2)求此抛物线与(绕2)两点,将△OABB(0,,经过A55.如图,抛物线(-1=-0)+,+ 落到点A′的位置.B 2cxybx逆时针旋转90°后得到△O′A′B′,点A点 1)求抛物线对应的函数关系式;(y′,求平移后所得抛物线对应的函数关系轴平移后经过点(2)将抛物线沿A 式;y在平移后的抛物,若点P轴的交点为C(3)设(2)中平移后所得抛物线与 P的坐标;面积的2倍,求点线上,且满足△OCP的面积是△O′A′P xy MD,与,点)设(2)中平移后所得抛物线与轴的交点为轴的交点为C(4x为边的CD,N为顶点的四边形是以在平移后所得抛物线上,直接写出以点C,D,在M轴上,点N 的坐标.平行四边形时点Nx A两点(点、),与B轴交于A4(1,),且经过点N(2,356.如图,已知抛物线的顶点坐标为My C左侧),与.轴交于点在点B 1)求抛物线的解析式;(xtykx CDAN试证明四边形轴交于点D+,经过C、M)(2若直线两点,=且与是平行四边形;xx轴上方是否存在这=1上运动,请探索:在(3)点P在抛物线的对称轴相切?若存B两点,并且与直线CDP样的点,使以P为圆心的圆经过A、在,请求出点P的坐标;若不存在,请说明理由.yyx,可得=-=0+1,令57.我们把使得函数值为零的自变量的值称为函数的零点.例如,对于函数2mxmmxyxxxy为常数)(-2.,我们就说=1+2=1是函数=-的零点.己知函数+1)=(-2(+1)m =-1(1)当时,求该函数的零点;m(2)证明:无论取何值,该函数总有两个零点;nxx,+2,求此时的函数解析式,并判断点(=-)设函数的两个零点分别为(3和,且+212n -10)是否在此函数的图象上.8 / 26.B,的右侧)且A两点,(点B=在点+A-4与B轴交于A58.抛物线,y为一BCBC,与,以2xbxyax轴交于点C,连接-2,0)、(8,0)两点的坐标分别为(x的坐标P轴上的一个动点,设点BDEC,点P是为对称中心作菱形边,点O lxm.于点M交抛物线于点Q,0),过点P作,交轴的垂线为(BD )求抛物线的解析式;(1m是平行四四边形上运动时,试探究CQMD为何值时,(2)当点P在线段OB 边形?,使三角Q)2)的结论下,试问抛物线上是否存在点N(不同于点(3)在( N的坐标;若不存在,请说明理由.BCN的面积等于三角形BCQ的面积?若存在,请求出点形),(50-1,=-0)+,+的顶点为Q,抛物线与B轴交于A如图,抛物线59.(y轴交于2xxcbxy点C两点,与.)求抛物线的解析式及其顶点Q的坐标;(1 ,求出点P的坐标:)在该抛物线上求一点P,使得S=S2(△ABC△PAB x.有轴,垂足为是第一象限抛物线上的一个动点,过点DD作DE⊥E(3)若点x轴相距最与一个同学说:“在第一象限抛物线上的所有点中,抛物线的顶点Q 的长度最长.”这个同学的说法正确时,折线D-E-O远,所以当点D运动至点Q 吗?请说明理由.元,经过记录某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件4060.y(件)与销售40元和90元)时,每月的销售量90分析发现,当销售单价在40元至元之间(含x单价(元)之间的关系可近似地看作一次函数,其图象如图所示.xy与)求的函数关系式.(1x P与之间的函数关系式;(2)设商场老板每月获得的利润为P(元),求2400元的利润,那么销售单价应定为多少元?3()如果想要每月获得2xyayaxaxc 轴交已知,如图,抛物线61.轴交于点=)与+3C+(,与>0.))、C(0,-30BAA于、B两点,点在点B左侧,点的坐标为(1,)求抛物线的解析式.(1面积的最D是线段AC下方抛物线上的动点,求四边形ABCD2()若点大值.x为顶C、EP、、在抛物线上,是否存在以在)若点(3E轴上,点PA的坐标;若不存在,PAC点且以为一边的平行四边形?如存在,求点请说明理由.9 / 26.2xylylykxxbl交于的直线+=-:与抛物线+=+3与,过点,已知抛物线62.如图1轴交于点:AA121x=2的距离相等.B到直线另一点B,点A,l的表达式;(1)求直线2lllx=2判断直线),C将直线,D向下平移个单位,平移后的直线(如图与抛物线2交于点(2)132是否平分线段CD,并说明理由;2bxcabcyxmyax有两个交点M,(=3,N3()已知抛物线,=+为常数)和直线+,对于任意满足条+mxhhab之间的数量关系.平分,请直接写出,件的与,线段MN都能被直线=cbxxyy的图象经过点63.如图,在平面直角坐标系=-O+中,二次函数+xxyx与二时所对应的函数值相等.一次函数),且当+3=0和=-=5A(1,0cbxy B在第一象限.,+C+两点,点次函数的图象分别交于B=-ybxc=-1+)求二次函数的表达式;(+ 的长;AB,求AB(2)连接,连N旋转180°得到点绕点是线段AC的中点,将点BM(3)连接AC,M 的形状,并证明你的结论.,判断四边形ABCN 接AN,CNyx中,如果一条抛物线平移后得到的抛物线经过原抛O64.我们给出如下定义:在平面直角坐标系的过顶FF都是抛物线物线的顶点,那么这条抛物线叫做原抛物线的过顶抛物线.如图,抛物线12 BD的对称点是点A关于直线、、F于点DB,点C的对称轴分别交抛物线,设F的顶点为A,FF212122bxyaxxy,那么,0)(1)如图1,如果抛物线=,C的过顶抛物线为(=2+ba.①= ______ = ______ , ______ABCD为C、、D四点,那么四边形②如果顺次连接A、B D 正方形 B 矩形 C 菱形平行四边形AABCD)2B,22()如图,抛物线=+的过顶抛物线为F(,-1.求四边形的面积.210 / 26 2cyaxc.y2的面积为,请直接写出F3()如果抛物线,四边形ABCD=的过顶抛物线是2的坐标.点B|+OC的长满足:|OA-2、如图,矩形OABC在平面直角坐标系中,并且OA65.2).=0(OC-6 三点的坐标.B、C(1)求A、x BB,求直线轴交于点处,落在点BAB与D(2)把△ABC沿AC对折,点B111的解析式.的P+PD的值最小?若存在,请找出点上是否存在点P使PBAC(3)在直线1的最小值;若不存在,请说明理由.PB+PD位置,并求出1的的值最大?若存在,请找出点P上是否存在点P使|PD-PB|(4)在直线AC |PD-PB|最大值.位置,并求出yyxx两点,且A+3的图象分别交、轴、B66.如图:已知一次函数轴于=xymx D)在一次函数的图象上,CD⊥=+3.4点C(,轴于点m B两点的坐标;的值及A、)求(1点的坐标;=,求(2)如果点E在线段ACE上,且x相似时,求点P)如果点3P在的坐标.轴上,那么当△APC与△ABD(移动的路线A→B→C→D的路线移动,设点P出发沿,点中,67.如图,长方形ABCDAB=6,BC=8P 从Ayx,△PAD.的面积为为xy(1与)写出之间的函数关系式,并在坐标系中画出这个函数的图象.11 / 26.xx=18时的函数值.和(2)求当 =4xy=20,并说明此时点P3)当在长方形的哪条边上.取何值时,(函数练习基础答案和解析1.C2.A3.A4.B5.C6.B7.B8.A9.B 10.B 11.B 12.B 13.D 14.A 15.A 16.D 17.B 18.B 19.C 20.B 21.D 22.C 23.C 24.B 25.C 26.C 27.B 28.A 29.B 30.D 31.D 32.B33.B 34.C 35.Cyyxx.-4140 ..-或3 39. 36.<>3或<-1 37.-5 3821yyyx+100=5 46<;>44.2 45..42.(0>,)43.212xyx+1. .47解:(1)∴二次函数解析式为-3=,)(,G抛物线对称轴与直线AB的交点记作点G)(2P,则点点坐标为(,),∴PG=,∴.a,,设C点横坐标为(3)如图2aaaa+3),D点坐标为( +2则C点坐标为(,,,+1)22aaaaaa-1),,-3 +1),F点坐标为(E点坐标为(+,+222aaa-4,+4 ,由题意,得 CE=-DF=y 轴平行,与 CE、DF∵且∴CE∥DF,又∵CF∥ED,∴四边形CEDF是平行四边形,∴CE=DF,-4,=∴- +422aaa(舍),解得,,,).∴C 点坐标为(22aaa+4,+4 ,当CE=-DF=-y轴平行,与CE、DF∵且∴CE∥DF,又∵CF∥ED,∴四边形CEDF是平行四边形,∴CE=DF,+4+4,=-∴-22aaaa=1,解得:故C点坐标为:(1,2)当C点坐标为(1,2)时CF不∥ED,舍去.12 / 26.)综上所述:C.点坐标为(,yxx)(=(40-20+248.解:①)2xx+800=-2+602xxxyy+800之间的函数关系式为;=-2所以+60与y=1200,②令2xx+800=1200,∴-2+602xxxx=20,,解得(舍去)整理得=10-30,+200=021所以商场每天要盈利1200元,每件衬衫降价20元;2xyx+800=-2③+602x-15)+1250=-2(,a=-2<0∵,xy有最大值,其最大值为1250,=15时,∴当所以每件降价15元时,商场每天的盈利达到最大,盈利最大是1250元.2yaxbxc 的图象经过点A(-1,0)、B(3,+0)、N(2,3149.()解:∵二次函数)=,+∴,解得:,2xxy+3∴这个二次函数的解析式为:,=-+2∴顶点M(1,4),点C(0,3).ykxd经过C、+M两点,(2)证明:∵直线 =∴,kd=3,即 =1,yx+3.∴直线解析式为 =yx=-3, =0,得令∴D(-3,0),AN=3,AD=2,CN=2∴CD=3,,∴CD=AN,AD=CN,∴四边形CDAN是平行四边形.)+2,(.解:1 50yx =2时,当,=0xy =-4当,=0时,由勾股定理得:,AB==22的长为,边AB2B0)、的坐标为(0,),;的坐标为(∴点A-4(2)证明:∵正方形ABCD,X 轴⊥Y轴,∴∠DAB=∠AOB=90°,AD=AB,13 / 26.∴∠DAE+∠BAO=90°∠BAO+∠ABO=90°,,在△DEA与△AOB中,,∴△DEA≌△AOB(AAS),∴OA=DE=4,AE=OB=2 ∴OE=6,;-6,4)所以点D的坐标为(x符合要求,M M,F,连接BF交则轴于3()能,过D关于X轴的对称点x轴的对称点F坐标为(-6,-4,4)关于),∵点D(-6bkxy,B F=点的坐标代入得:+ ,把设直线BF的解析式为:解得:,yx+2,= ∴直线BF的解析式为yx=-2,时,当 =0∴M的坐标是(-2,0),答案是:当点M(-2,0)时,使MD+MB的值最小.51.增大≠0)的图象上, -4,0)在二次函数+2=(-52.解:(1)∵A(a,∴0=16+6+22xayaxa,解得=-=-∴抛物线的函数解析式为-;+22yxx∴点C的坐标为(0,2),bkxy,=,则+AC设直线的解析式为解得,的函数解析式为:;∴直线ACnm,)是抛物线在第二象限的部分上的一动点,)∵点(2D()-∴D(,,-+22mmmDH=-,则H轴于点,,-+2AH=+4HO=-, DH⊥作D过点14 / 26 2xmmmm.∵四边形OCDA的面积=△ADH的面积+四边形OCDH的面积,),--)×(-- +2)-+(∴S=(+2+2+4)×(2mmm<0);-4 +4(-4化简,得S=-<22mmmmmm(3)①若AC为平行四边形的一边,则C、E到AF的距离相等,yy|=2,|=| ∴|CE y=±2.∴E+2=2时,解方程得,--当 =2E xx =-3=0,,21;∴点E的坐标为(-3,2)2xyx-=-2时,解方程得,-当+2=-2E2xyxxx =,=,21的坐标为(E ∴点)或(,-2),-2;②若AC为平行四边形的一条对角线,则CE∥AF,yy=2,∴=CE∴点E的坐标为(-3,2).(,-2、).)、(,-2)E综上所述,满足条件的点的坐标为(-3,22yxkxy轴交于点C(0,-3、B两点,与)∵抛物线)=()+1+,与轴交于A(53.解:12k,) +∴-3=(0+1k=-4,解得:+1)-4,∴抛物线的解析式为: =(x=-1;故对称轴为:直线(2)存2yx在.y,则当=0P,此时PA+PC的值最小,如图,连接AC,交对称轴于点2x,(-4+1)0=xx =-3解得:=1,,21由题意可得:△ANP∽△AOC,=则,,故= PN=2,解得:;,-1-2)则点P的坐标为:(是抛物线上的一动点,且在第三象限,3)点M(x;<0故-3<2xx,),(-4]+1①如图,设点M的坐标为:[ ∵AB=4,)+1×4×|(+1),-4|=2|(-4|∴S=△AMB在第三象限,∵点M2x)∴S=8-2(,+1△AMB x;22xx的面积最大,最大值为8)时,△AMB的坐标为(∴当=-1时,即点M-1,-42xx)[M②设点的坐标为:,(+1-4],15 / 26.yaxd,= 设直线AC的解析式为:+,)代入得:,),(0-3将(-3,0.解得:yx-3,=-故直线AC:xx-3),的坐标为:(,-设点P222xxxxx+,+4=- +-3)=-故PM=-(-3-( +1)x最大,最大值为=-时,当PM.22xxyx+8,)∵(=-2 -1+4)+6=-254.解:(1∴顶点坐标为(1,8);2yxx+6=0,-2 (2)令+4=0,则xx=3. =-1,解得x轴的交点坐标为(-1,0),(3,0).所以抛物线与,,0))如图1,把A(-155.解:(12cxybx ++=-B(0,2)两点坐标代入得:,解得:,∴抛物线对应的函数关系式:+2+=-;2xxy,2),0,∵A(-1,),B(0(2)如图2 ∴OA=1,OB=2,由旋转得:O′B=OB=2,O′A′=OA=1,且旋转角∠OBO′=90°, 1),2,2),A′(2,∴O′( A′可知,抛物线向下平移1个单位,所以由原抛物线从O′平移到+1=-∴平移后所得抛物线对应的函数关系式:+;2xyx-++1)3()设P(,,2aaa,=-++1yx =1当,=0时,2xxy∴OC=A′O′=1,(A2,2)可分三种情况:根据点a,时,如图3①当>2 ,=2S∵S△O′A′P△OCPaa,×1×∴×1×(=2×-2)a =4,16 / 26.-=-, ++×4+1=则+1=-×422aay-4,,∴P()a<2时,如图<4,②当0∵S=2S,△O′A′P△OCPaa), =2×∴×1××1×(2-a,=则×+,=-+1=-+×+1=22yaa∴P(,),a,0时,如图③当5<aa,+2)=2××(-)同理得:×1×(-a,=4(不符合题意,舍))-)或(;4综上所述,点P的坐标为(,,+1-)N(4)设(,,+x ENE⊥,轴于N如图6,过作 CMND是平行四边形,∵四边形2mmm,∴CD∥MN,CD=MN ∴∠CDO=∠MEN,∵∠COD=∠MEN=90°,∴△COD≌△NEM,∴EN=CO,-1=1∴,-m -1解得:,=3或ym =-1=3时,,当ym =-1时,,当=-1 -1,),∴N(3,2mm-1)或(-1)时,所成的平行四边-1(7就是点N-1,如图形; 8如图和如图9,∵四边形CDMN是平行四边形,∴CN∥DM,是对称点,C∴点与点Nx 10∵C(,)=-,对称轴是=1,17 / 26.∴N(2,1),的坐标为综上所述,点N)或,-1,-1)或(-1(3 ).(2,1)解:由抛物线的(156. ,)(1,4顶点是M2xya+4-1设解析式为(=)a,<0)(,2又∵抛物线经过点N(,3)2a,解得(2-1)∴3=+4a.=-122xxxy -1)+2+4=-;故所求抛物线的解析式为+3=-(:,(2)证明:如图1tykx,(1,4=)两点,+M经过C(0,3)直线、tk =1,,=3即xy +3=,直线CD的解析式为xy,0)当;=0时,D=-3,即(-32xxyx,0,解得)=-1,即A当(=0时,--1,+2+3=0 ∴AD=2. 3)3),N(2,∵C(0,∴CN=2=AD,且CN∥AD是平行四边形.∴四边形CDAN,(3)解:如图2:ux)(设P1,、点,使以P为圆心的圆经过AB两点,并且与直线CD相切,假设在轴上方存在这样的P u其中,>0222u则PA是圆的半径且PA=+2,相切.PPQ=PA时以为圆心的圆与直线CDQP过做直线CD的垂线,垂足为,则为等腰直角三角形,故△PQM2)小题易得:△MDE也是等腰直角三角形,由第(uuu,PE=1P由(,)得,PM=|4-|PQ=PM.18 / 26.,= (4-+2由PQ)=PA 得方程:22222uuuu=(不符合题意,舍),解得. =,).存在,其坐标为(1 所以,满足题意的点P22xymxmyxm-2))当1)为=-1时,-2=(=-2(+2+157.解:(2xy-2=0时,,当 =0x=±解得,+2)的零点;-2=-1时,((=是函数+1=)当-22mxxmy+2)=0))证明:当,=0时,2mxyxmxm-2(-2( +12(abmcm+2),),∵ =1,=-2=-2((+122mmacbm-4)-2 -4+1=4()-+2∴△=4×(2mmm+16=4+8+4+82mm+4()+4 +4=42m+4≥4,)=4( +22mxmx+2)=0-2(-2(有两个不等实数根,+1)∴m取何值,该函数总有两个零点;即无论xx,和3)函数的两个零点分别为(21mxxxmx=-, =(++1),? =-2(=+2)+=22112m解得,=12xmyx时,函数解析式为;=-6当-4=122nnxnyn,+2)=(+2)-6=-4(当=-10+2时,2nn +2,-10)在此函数的图象上.点(,0)代入抛物线+=-4得:,.58解:(1)将A(-20),B(82bxyax,解得:,-4=∴抛物线的解析式:-;yx =-4=0时,,)当(2 ,0,-4)∴C(∴OC=4,是菱2xyx形,∵四边形DECB ∴OD=OC=4, 4),0∴D(,bykx BD=的解析式为:,+设)代入得:4D0)、(0,,,(把B8,解得:xy∴BD=-的解析式为:+4,19 / 26.lx轴,⊥∵2mmmmm-4,)-,+4)、Q(∴M(-,如图1,∵MQ∥CD,∴当MQ=DC时,四边形CQMD是平行四边形,2mmm-4)=4-()--4(),∴(--+42mm=0化简得:, -4mm=4, =0(不合题意舍去),解得21m =4时,四边形CQMD∴当是平行四边形;点到的面积,NBCN的面积等于三角形BCQ,要使三角形(3)如图2 BC的距离相等;的距离与Q到BC bykx =,设直线BC的解析式为:+-4,)代入得:C0)、(0,把B(8,,解得:xy =∴直线BC的解析式为:,-4 为平行四边形,0)时,四边形DCQM)知:当P(4,由(2 ,∴BM∥QC,BM=QC 得△MFB≌△QFC,ll、Q作BC的平行线,分别过M、21直线与抛物线的交点即为所求,点的斜率为的所以过M或Qmym当时,=4+4=-×4+4=2,=- )2,∴M(4,-4=-6,-4=×16当-=4时,-=×4 ,-6),4Q2mmmy(bxyl +的解析式为:,=①设直线1l过∵直线Q点时,1bb =-8,∴-6=×4+,yxl=的解析式为:∴直线,-8 1x,, -8=则xx,(与Q重合,舍去)解得==421l M点,②∵直线过2xly同理求得直线=的解析式为:,220 / 26.x,=则,2xx -16=0-,xx =4+4,解得=4-4,21xy =代入,,,得),,2+2),N(则N(2-24+4,4-421),.),N(故符合条件的N的坐标为N(2-24+4,4-42+2212xxcbxy)两点,5,0,0)+,+B 与(轴交于A(解:59.(1)∵抛物线-1=-2xxxxy +4-5)=-∴(=-,+1)(+52xxy +4∴抛物线的解析为;=-+522xxyx,)+5=-(+9∵-2=-+4 ;9)∴顶点Q的坐标为(2,2yxxxy,+5中,当(2)在=5=-=0+4时,,5)的坐标为:(0,∴点C a的纵坐标为,设点P a,|=5S=S,则|若△ABC△PAB a =±5.解得2pxxaxx);的坐标为(,解得4=0(舍去)或,当=4=5时,-,此时点+45+5=52pxxax );2-的坐标为(时,=-5-,2++4,+5=-5,解得-5)或(=2±,此时点-5当p);2-综上,点,的坐标为(4,5)或()或(2+,-5-5 3)这个同学的说法不正确(2ttt,D-E-O理由:设D(,-的长度为+4L+5),折线)-.+5++=-则L=-(+4a∵,<022ttttt =时,∴当L.=最大值<L=9+2=11D与点, Q重合时,而当点∴该同学的说法不正确.kkxbyxy(的函数关系式为:,=+)设60.解:(1≠0)与,由题意得.解得xxy;故=-4≤90)+360(40≤xp与(2)由题意得,的函数关系式为:2xxpxx,-4)(+520+360)=-4-14400=(-40 时,3)当P=2400(2xx -4,-14400=2400+520xx,=60,=70解得:21元.元或70故销售单价应定为60CB1解:61.()将点、的坐标代入抛物线的解析式得:,21 / 26.ca=-3. =,解得:=+∴抛物线的解析式为-32yxx=-42xxxxy,则=1-3=0,解得)令(2+=0,21∴A(-4,0)、B(1,0)xy=-3 令,则=0∴C(0,-3)×5×3=∴S =△ABC,D(-3) +设2mmmymxym=-的解析式为于E.直线D过点-3,则E(,作- -3)DE∥AC轴交AC+322mmmm)=-+(DE=--3-3-)(+2m=-2时,DE有最大值为3 当有最大值为×DE×4=2DE=6 此时,S △ACD6+ABCD的面积的最大值为=.∴四边形3)如图所示:(xx轴于点E,此时四边形ACPEE,过点P作P∥AC交为平行四CP①过点C作∥轴交抛物线于点P1*******边形,∵C(0,-3)x,-3() P∴设1-3=-32xx+∴xx=-3,解得=02122 / 26.∴P(-3,-3);1xx轴上方的抛物线于点P,当AC=PE时,四边形E,交ACEP为平行四边形,②平移直线AC交轴于点∵C(0,-3)x,3),∴设P(-3=3∴,+2xxxx= 解得=,或(3)或P∴P(),3,23()或P(-3,-3,3)或P综上所述存在(,3个点符合题意,坐标分别是P2133).xy=3,)当 =0时,62.解:(1∴A(0,3),x=2的距离为2到直线,∴A x=2的距离相等,,B到直线∵点A x=2的距离为2到直线,∴B∴B的横坐标为4,,当=-=4时,×4+4+3=-1∴B(4,-1),2yxbkxy中得:)代入,= +BA(0,3)和(4,-1把,解得:lyx+3;∴直线=-的表达式为:2x=2平分线段CD,理由是:(2)直线xyxl+0.5,直线+3-表达式为:=-=-3yx, =-2+0.5=-1.5当,=2时,或,解得:∴C(-1,1.5)、D(5,-4.5),yx==-1.5=2=,,∴线段CD的中点坐标为:x =2平分线段CD则直线;,)(32bxcaxm=0,(--3) ++xx是此方程的两个根,、则21xx=-,+ 21xh平分,=都能被直线∵线段MNh,的横坐标为,则的中点为设线段MNPP23 / 26.h=-. =根据中点坐标公式得:xycc).,即(=0时,0=,(63.解:1)当xxc).5,=0和 =5时所对应的函数值相等,得(由当c,0)代入函数解析式,得,)(1,将(5解得.2xxy -2=-;+ 故抛物线的解析式为,)联立抛物线与直线,得(2,,解得即B(2,1),C(5,-2).由勾股定理,得=; AB=,(3)如图:四边形ABCN是平行四边形,证明:∵M是AC的中点,∴AM=CM.∵点B绕点M旋转180°得到点N,∴BM=MN,∴四边形ABCN是平行四边形.64.1;-2;D2=0.(-2|+OC-6.65解:(1)∵|OA)∴OA=2,OC=6,2),C(6,,0),∴A(0∵四边形OABC为矩形,∴BC=OA=2,2);6,∴B(ykxb,的解析式为AC =+)设直线(2坐标代入可得,、把AC24 / 26.,解得xy ,的解析式为=-+2∴直线AC ,由折叠的性质可知AC ⊥BB 1yxm =的解析式为, ∴可设直线BB+1m +2,=6把B 点坐标代入可得m ,解得=-4yx 的解析式为∴直线BB=;-41AC 对称,B 和B 关于直线(3)由(2)可知1AC 于点P ,如图1,连接BD 交 PB=PB ,则1=BD ,∴PD+PB=PD+PB 1PD+PB 最小,∴此时1,∠AOD=∠CBBD=90°,C=BC=OA=2由折叠的性质可知11在△AOD 和△CBD 中,, 1,(AAS )∴△AOD ≌△CBD 1,∴AD=DC ,OD=DB 1xx ,且设OD=,,则DC=AD=6-OA=2222222xtxx =2,即()2+,解得=(6-,)在R 中,由勾股定理可得△AODAO+OD=AD ,-2=4∴CD=AD=6t =2=△BCD中,由勾股定理可得BD=,在R2PB+PD的最小值为;综上可知存在使PB+PD的值最小的点P,11,BD、PD、(4)如图2,连接PB p,根据三角形|B1对称,|PD-PB|=|PD-PBA时|PD-PB|最大,B当与在点1.的最大值等于DB小于或等于DB,故|PD-PB|三边关系|PD-PB|1111 =AB=6,∵AB1=4,AD= =2,∴DB1的值最大,最大值为:2.∴在直线AC上,存在点P使|PD-PB|x 1=0)把,代入一次函数的解析式中,.66解:(y =3,可得:)的坐标是(B0,3;所以点y =0代入一次函数的解析式中,把x =-4可得:,25 / 26.所以点A的坐标是(-4,0),x=4代入一次函数的解析式中,把y=6,可得:m的值是6;所以xx轴,如图1,点作CD⊥EF垂直轴与F点,过C点作(2)过E∴△AEF∽△ACD,∵,,∴CD=6,∵根据题意得:EF∥CD,且AD=8,。
