一道初中数学古诗趣题的多种解法
一题多解之五种方法解一道经典数学题
O BCD①A 一题多解之五种方法解一道经典数学题江苏海安紫石中学 黄本华一题多解是我们学习数学的特好方法!通过一题多解,我们可以多角度、多方位地去思考解题的方案,这样不仅能加强知识间的联系,同时也增添新颖性和趣味性,优化我们的思维结构,提升我们的思维能力。
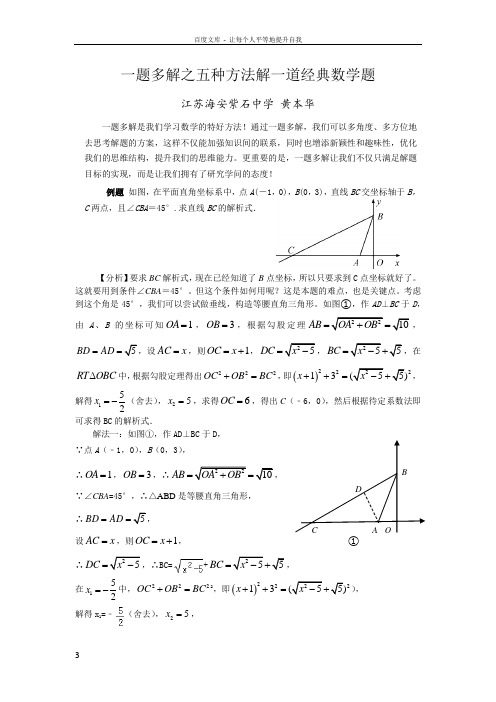
更重要的是,一题多解让我们不仅只满足解题目标的实现,而是让我们拥有了研究学问的态度!例题 如图,在平面直角坐标系中,点A (-1,0),B (0,3),直线BC 交坐标轴于B ,C 两点,且∠CBA =45°.求直线BC 的解析式.【分析】要求BC 解析式,现在已经知道了B 点坐标,所以只要求到C 点坐标就好了。
这就要用到条件∠CBA =45°。
但这个条件如何用呢?这是本题的难点,也是关键点。
考虑到这个角是45°,我们可以尝试做垂线,构造等腰直角三角形。
如图①,作AD ⊥BC 于D ,由A 、B 的坐标可知1OA =,3OB =,根据勾股定理2210AB OA OB =+=,5BD AD ==AC x =,则1OC x =+,25DC x =-255BC x =-,在RT OBC ∆中,根据勾股定理得出222OC OB BC +=,即()222213(55)x x ++=-,解得152x =-(舍去),25x =,求得6OC =,得出C (﹣6,0),然后根据待定系数法即可求得BC 的解析式.解法一:如图①,作AD ⊥BC 于D , ∵点A (﹣1,0),B (0,3),∴1OA =,3OB =,∴2210AB OA OB =+=, ∵∠CBA =45°,∴△ABD 是等腰直角三角形, ∴5BD AD ==设AC x =,则1OC x =+, ∴25DC x =-,∴BC=+255BC x =-+,在152x =-中,222OC OB BC +=2,即()222213(55)x x ++=-), 解得x 1=﹣(舍去),25x =,②③∴5AC =,6OC =,∴C (﹣6,0), 设直线BC 的解析式为3y kx =+, 解得12k =,∴直线BC 的解析式为132y x =+. 【点评】虽然这种解法思路比较清晰,但是用勾股定理得出的方程比较复杂,解方程很繁,很费时,很累。
一道题的多种解法

一
+ ・+ -
・+ “+ “+ ・
・+ 一+ ・
・+ ・+ ・ ・
”+ ”+
一+
一
+
“ +
+
一+ ・ + ”+ ・
・ ・ +
・— 一— ”+ ”+ - +-
・+ ・+ ・ ・
“ +
・
1 — 3 1一 t t 0 t 2,l
0,2 t
‘ .
又。 ቤተ መጻሕፍቲ ባይዱ . )=n+b 2 ‘ 且
6 4
1 4 即 2≤ 口+ ) ,
①
又 ‘ 1 =口+b 一1 =0—6 . ) ‘ √ ) ,
.
.
I 一2 厂 ( )=- 1 一1 , 厂 )+ ( ) 由 一1 I 一1 2 2 - 1 4, 厂 ( ) , 厂 ) ( 根据不 等式 性质 得
y+x =80 求 +Y y 8, 的值. 美 国第 九届 竞赛 (
题) 简 析 : x +Y :7 、2 让 y+ 1xy+x =8 0中的 y 8
、
) 1一Y ( )和 的结 构 . ( )隐含条 件 : 2 注意 到 、 “ 位 ”是 “ 等 ” Y的 地 对
的, 不妨 设 ≤ Y 因 ( 一 +( Y ≥ 0 于是 ( , 1 ) 1一 ) , 1
3 2
中学 数 学 研 究
2 1 年 第 2期 01
一
道 题 的 多种 解 法
贵州省沿河县宫舟 中学 ( 6 3 1 杨 昌辉 551 )
解题 方法 就 是 一 个不 断 运 用 所 学 的 知识 把 未 知转 为 已知再 创造得 到结果 的过 程. 题多解 , 一 就是 开拓学 生 的视 野 , 强 学 生 理 解 能力 , 富解 题 策 增 丰 略, 突破 思维定 势 , 发学 生 的兴 趣 , 合 运 用所 学 激 综 知识用 多种 不 同 的方 案 来 解 决 需 要 解 决 的实 际 问 题 , 面就一 道题 的多种解 法提供 我们 学 习和参考. 下 例 设 函数 )=。 。 , 一1 + 且 一1 ) 2 2≤ 1 , )≤4, _ 一2 求厂 ( )的取 值范 围. 解 法一 : 用解 方法组 的思想 利
初中数学二元一次方程组的应用题型分类汇编——古代算术问题3(附答案)

30.古代算筹图用图
1
表示方程组:
4x 6x
7 3
y y
72 4
,请写出图
2
所表示的二元一次方
程组______.
图1
图2
31.《孙子算经》是中国古代重要的数学著作,现在的传本共三卷,卷上叙述算筹记数
的纵横相间制度和筹算乘除法;卷中举例说明筹算分数算法和筹算开平方法;卷下记录
算题,不但提供了答案,而且还给出了解法,其中记载:“今有木、不知长短,引绳度
19.今有鸡兔同笼,上有二十八头,下有七十八足.问鸡兔各几何?试用列方程(组) 解应用题的方法求出问题的解. 20.《孙子算经》中有一道题目:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量 之,不足一尺,木长几何?”题大意为:“现在有一根长木,不知道它的长度.用绳子去量 这根长木,绳子还剩余 4.5 尺,将绳子对折后再量这根长木,长木还剩下 1 尺,问长木 长多少尺?”请你用所学知识,求出长木长多少尺? 21.列方程或方程组解应用题: 《九章算术》中有一个有趣的方程问题:“五只雀、六只燕,共重 1 斤(等于 16 两), 雀重燕轻.互换其中一只,恰好一样重,问:每只雀、燕的重量各为多少?”意思是: 一群雀有五只和一群燕有六只,两群合起来一共重 1 斤(等于 16 两),如果把雀群中的 一只和燕群中的一只交换后,两群的重量一样,问:每一只雀和每一只燕各有多重? 22.《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道 题:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?”译文:“几 个人一起去购买物品,如果每人出 8 钱,则多了 3 钱;如果每人出 7 钱,则少了 4 钱, 求有多少人,物品的价格是多少”. 23.鸡兔同笼,鸡和兔一共有 42 条腿,如果把鸡和兔的数量互换,一共有 36 条腿,那 么原来有几只鸡,几只兔呢? 24.我国明代数学家程大位的名著《算法统宗》里有一道著名算题,原文如下:“一百 馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”. 译文为:“有 100
一道课后练习题的多种解法

球”为事件 B “ ,取到的 4 个球 中只有 1 个红
球 ” 为事 件 ,取 到 的 4个 球 全 是 白球 ” “ 为 事件 B . 2 由题 意得 :
P 音=, ( 肚1 }
‘
警 未+。 C’ 善孥 :C CC : : + : +
八 “
分析
() 1事件“ 乙两树至少有一树 甲、
函数值 , 下面用三种 三角 函数 求
值.
的
设 D = ,B y Q xP = ,
则 AQ= ,口= 一 I 尸 1 )尸 = 一AP AQ) , 口 2 ( + = ,
x y +. 图2
角坐标系 , D , 设 Q
,
因△A 口是直角三角形 , 尸
因 <孚,a 故 < 一子, 0 ‘o< 0 ‘ <4, 4 4所
以= 一 子
=
因 < 手所 . 0 < ,以仁孚
方 法 2 o(+ =o  ̄ cs -iai cs cs +o sn s f l f n l
、丁 赤丁 者 × / 、 一 一 / 、 赤 / 、 /
新课标 ( 人教 A版 )数学④》 必修 ) 《 ( 第
10页 B组第 7题 : 6
如 图 1 正 方 形 ,
A C 的边 长 为 1 BD ,
P Q分 别 为 边 A , , B D 上 的 点 ,当 A
△A Q 的 周 长 为 2 P 时 ,求 LP Q 的 大 C
小.
先求 出 a B的大小 , + 可转 化 为 求 的三 角
因< 手所 } 0 < ,以 ・
从上面求解过程可以看出,利用正切函 数求解最为简单. 解法 3 可用 向量方法来解决本 问题 , /P Q可看作 与 的夹角 ,则 只需求 _C /P Q的余弦值. _C _
一题多解之五种方法解一道经典数学题

B一题多解之五种方法解一道经典数学题一题多解是我们学习数学的特好方法!通过一题多解,我们可以多角度、多方位地去思考解题的方案,这样不仅能加强知识间的联系,同时也增添新颖性和趣味性,优化我们的思维结构,提升我们的思维能力。
更重要的是,一题多解让我们不仅只满足解题目标的实现,而是让我们拥有了研究学问的态度!例题 如图,在平面直角坐标系中,点A (-1,0),B (0,3),直线BC 交坐标轴于B ,C 两点,且∠CBA =45°.求直线BC 的解析式.【分析】要求BC 解析式,现在已经知道了B 点坐标,所以只要求到C 点坐标就好了。
这就要用到条件∠CBA =45°。
但这个条件如何用呢?这是本题的难点,也是关键点。
考虑到这个角是45°,我们可以尝试做垂线,构造等腰直角三角形。
如图①,作AD ⊥BC 于D ,由A 、B 的坐标可知1OA =,3OB =,根据勾股定理2210AB OA OB =+=,5BD AD ==AC x =,则1OC x =+,25DC x =-255BC x =-,在RT OBC ∆中,根据勾股定理得出222OC OB BC +=,即()222213(55)x x ++=-,解得152x =-(舍去),25x =,求得6OC =,得出C (﹣6,0),然后根据待定系数法即可求得BC 的解析式.解法一:如图①,作AD ⊥BC 于D ,②∵点A (﹣1,0),B (0,3),∴1OA =,3OB =,∴AB =, ∵∠CBA =45°,∴△ABD 是等腰直角三角形,∴BD AD == 设AC x =,则1OC x =+, ∴25DC x =-,∴BC=+255BC x =-+,在152x =-中,222OC OB BC +=2,即()22213x ++=), 解得x 1=﹣(舍去),25x =,∴5AC =,6OC =,∴C (﹣6,0), 设直线BC 的解析式为3y kx =+,解得12k =,∴直线BC 的解析式为132y x =+. 【点评】虽然这种解法思路比较清晰,但是用勾股定理得出的方程比较复杂,解方程很繁,很费时,很累。
例析一道中考数学题的多种解法

/ GEF=9 0。,
・ . .
在 R aE G中 ,由直角三 角形斜 边上 t F
的中线等于斜边 的一半 , 可得 E = G . 日 F
G
. .
G _ EH = . 12 3
点评 :在梯 形 中 , 两腰 的中点 , 构造 取 可
“ E
梯形 的 中位线 . 中位线 与上 、 下底 既有 位置 关 系“ 梯形 的中位线平行于两底 ”又有数量关 系 。 “ 梯形 的中位线 等于 上 、 底 和 的一 半 ” 过 下 . 通 添加中位线 , 可将 比较分散的 已知条件 聚集 在
翡
f A= HB E.
【=、 G AB EE
:
。
. . .
E日.
△AG △B . E E
BH-AG=I。 GE= HE , F H=FB +BH +1 3. = L GEF=9 , 0。
.
‘ .
‘
.
.
F _ E. G HE. EjG 又 E=
・ . .
例, 可得 = , 而可求得 4 从 E 、 . :/
在 R AA G中 , t E 可求得 G = / , R AB F E 、了 在 t E
中, 可求得 剧1、百 , R AE G中, _/ 在 t F 可求得
G 3 .
分析 :由方法 三 可知 A = 、 B 2 /2, 而直 从
求得 E 的长. H
求出线段 H F即可. 解 : 图 4延 长 G , F 如 . E 与 B的延 长线 相交
于点 日.
解 :如 图 3 取 G 。 F的中点 日, 连接 E H.
图3
・ . 。
四边形 A C B D为正方形 .
李白打油诗数学题
李白打油诗数学题
李白打油诗数学题是一首非常有趣的数学问题,它以打油诗的形式描述了一个关于李白买酒和喝酒的场景,并给出了一个数学问题。
具体来说,这首诗描述了李白在街上走,遇到了花和店各三次,且花、店交替遇到。
每次遇到店,他的酒都会加倍;每次遇到花,他都会喝掉一斗酒。
最后,他的酒喝光了。
问题是:他原来有多少酒?
为了解决这个问题,我们可以按照题目中的描述,逐步模拟李白遇到花和店的过程,最终找出他原来有多少酒。
假设李白原来有 x 斗酒
第一次遇到店,他的酒加倍,变成 2x 斗;然后遇到花,喝掉一斗,剩下 2x - 1 斗。
第二次遇到店,酒再次加倍,变成 2(2x - 1) 斗;然后遇到花,喝掉一斗,剩下 2(2x - 1) - 1 斗。
第三次遇到店,酒再次加倍,变成 2[2(2x - 1) - 1] 斗;然后遇到花,喝掉一斗,剩下 2[2(2x - 1) - 1] - 1 斗。
由于第三次遇到花后,李白的酒喝光了,所以我们有方程:2[2(2x - 1) - 1] - 1 = 0
解这个方程,我们得到:
x = 7/8
所以,李白原来有 7/8 斗酒。
一道中考题的多种解法赏析
一6 + , .一 n 6 一 1 ,
十 +
. +
.
②
① 一② , 得
1s
=
2 +
+
+
所 一 ∑( 一k=1 ∑嘉一 以 6 + b =+ )=
…
十
掣.
2一 ≥ 2. )
k l
= 1
所以 s 一 2+ 1十 + … +
HCG 一
-二
{O 一 ( , C
所以 AO OE A C D. O
因 此 , 四 形 S 边 (
S△ H 一 1 .
一 S (, S f 一 S f 一 △,D— △ , ( △
D. 此 因
“ 积割 补法 ”是解决 几何 问 题 的 常用 方 法. 面
G 一
I G, △ HC △( 2 所 以 S 边 【B X' 故 E X D, 形zD
Sl ( H : 1 .
—
实现 问题 的解 决 ; 形 法 是 将 不 规 则 的几 何 体 补 补 形成 常规 的 、 熟悉 的 图形 , 体现 了局 部 到整体 的转
到 △ A1 B . 知 A( , ) B( , ) 0 已 4 2 , 3 0.
( ) A B 的 面 积 是 1△ O ; A.点 的 坐
的旋转 过程 中, 玲 和 小 惠发 现 旋 转 中的 三 角形 小
与 △ A B 重叠 部分 的面积 不断 变小 , O 旋转 到 9 。 0
D 一 E CG , 即 ECH
如果 图形 不规 划 , 条件 不便 使用 , 通过 “ 可 割补 法 ”
把 图形 转 化 为 熟 悉 、 单 的 图 形 , 而 使 问 题 获 简 从 解. 割 补 法 ”有 分 割 和 补形 两种 . 割 法 是 将 不 “ 分 规则 的几 何体 运 用切 割技 术手 法 , 整体 为部 分 , 化
两道趣题的多种解法及推广
两道趣题的多种解法及推广四川省邻水县九龙中学 任贤德例1:传说很久很久以前,有位智慧老人,在他临死之前立下遗嘱,将他唯一的家产17头牛分给三个儿子,长子分21,次子分31,老三分91,不能杀牛分肉,也不能伤害兄弟情谊。
若无法分,就去找他老朋友黄老头。
三兄弟无法分,只好去请教黄老头,老人略一思索,就把自己的一头牛让他们牵走,参与分配,结果长子分得了9头牛(18×21=9),次子分得了6头牛(18×31=6),老三分得了6头牛(18×1=2)。
他们刚好把17头牛分完,剩下的一头还给黄老头,三兄弟既高兴又满意。
这就是有名的黄老头分牛问题,它采用了一种奇特的技巧借一法,巧妙地解决了这一数学问题,令人回味无穷。
我们再看下面的例子。
例2:有一家商店出售啤酒,它有一个规定,即三个啤酒瓶兑换一瓶啤酒。
一位顾客从此店买了12瓶啤酒招待客人,问此人最多可从这家商店得到多少瓶啤酒喝?此题的一般解题思路是:喝完12瓶啤酒后,用12个空瓶又可兑换4瓶啤酒,喝完后,再用其中3个瓶子兑换一瓶啤酒,最后只剩下2个空瓶,即最多只能喝12+4+1=17瓶啤酒,并且剩下2个瓶子。
似乎本题的求解到此结束,但是巧妙的方法是再借1个啤酒瓶,合起来共3个啤酒瓶,可兑换一瓶啤酒,喝完后,归还一个啤酒瓶,即最多可得到12+4+1+1=18瓶啤酒喝,本题也巧妙地采用了借一法的解题方法。
事实上,以上两个例子的求解可归结为无穷递缩等比数列求极限的问题,它们都属于无限可分的问题。
其解答如下: 解法二(例1)的解答:第一次分配长子分17×21头,次子分17×31头,老三分17×91头而(1―1―31―1)=1;也就是说还剩下总数的1没参与分配,即还剩下17头第二次分配长子分1817×21头,次子分1817×31头,老三分1817×91头同样剩下参与本次分配数目17的1,本次分配结束就剩下 18172头……这个过程可一直延续下去,直至无穷,这样,每一次分配结束后,都余下上次分牛剩余数目的181没参与分配。
一道课本例题的多种解法及引申
的多种解法
及引申
云 南 杨 天 勇
所 以 a+6 f ≤ 活 应 用 知 是
识 的体现 , 开 阔了思路 , 通 了知识 间 的 内在联 系 , 它 沟
培 养 了求 异 思 维 和 应 用 知 识 解 决 问 题 的 能 力 .
B 一 1; 一 2;
则 ac 的最小值 是 ( bd
n— r o , 一 , i , 一 , o d r i 。 a + b c s 6 n a C . sp. sn p 则 c d一 a s c  ̄O ' S口 ・r O _ r i 口・r i — r C S — ) r , C C Sp } sn 一 sn p 。O ( ≤ 所
D
最 大 值 1 最 小值 { 和
解 因 为 ? y! 1 故 可 设 . C Sd, + 一 . r— O Y— sn a, i 则 有 (1一 .y) r (卜{ 一 )一 (1一 C sn a ・ OS a i )
下 面仅给 出几种 具有代表性 的解 法) .
:
。 2 z、 例 Y∈ R, + Y 一 1 则 且 ,
) .
目的 .下 面 以 一 道 课 本 例 题 为 例 说 明 .
(1 xy)(1+ .y) ( ~ r 有
A
一.
最 小 值 , 无 最 大 值 ; o 而
j
例 1 ( 中《 等 式 人教 版 ) 2 高 不 第 9页 ) 已知
璺 斗 一+ c c  ̄ F
—— —一 一
—
b d
“f…
—— 一 ‘
b 一 d —
—
—— — ~— — … i
:≥ 0 一≥ .
.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设甜果数为 x 个,苦果数为 y 个,根据题意列方程组为
x y 1000,
11 9
x
4 7
yy
6573 343
则买甜果需要的钱数为 657×11 =803(文);
9
买苦果需要的钱数为 999-803=196(文). 小结 神韵的 数学诗题,绝妙的构思,丰富的 想象,巧妙的叙述,就能用涛中珍藏的 数量关系,借助神通广大的数学方法算出甜果和苦果需要的钱数和个数.我体会到:古代 中国数学的伟大,启发我们更加热爱数学,激发运用数学解决实际问题的 积极性.
一道初中数学古诗趣题的多种解法
“两果问价”问题出自我国古代算书《四元玉鉴》(朱世杰编著).华师大版七年级《数
学》上册已入选其中,原题如下:
九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果
几个?又问各该几个钱?
将题目泽成白话文,内容如下:九百九十九文钱买了厂甜果和苦果共一千 个,已知十
9
7
总共花费为 11 ×1000 文,大于 999 文.根据题意可知,用一个甜果换一个苦果的差价为 9
( 11 - 4 )文,因此我们可以将部分甜果换成苦果,使总花费减少到 999 文, 97
111000 666
则苦果数为 9 11 4
=343(个),
97
甜果数为 1000-343=657(个).
则苦果数为 1000-657=343(个).
买甜果需要的钱数为 [来源:学|科|网]
657×11 =803(文); 9
买苦果需要的钱数为
999-803=196(文).[来源:Z&xx&] 点 评 同理,也可将买甜果需要的钱数、买苦果需要的钱数或苦果数设为未知量,分
别列方程求解.
三、用二元一次方程组求解
买苦果需要的钱数为 [来源:Z。xx 。 ]
343×4 =196(文); 7
买甜果需要的钱数为
999-196=803(文).
二、用一元一次方程求解 [来源:学科网]
设甜果数为 x 个,则苦果数为(1000-x)个,根据题意列方程为 11 x+ 4 (1000-x)=999, 97 解得 x=657 个,即甜果数为 657 个,
一文钱可买九 个甜果,四文钱可买七个苦果,那么甜果、苦果各买了多 少个?买甜果和苦
果各需要多少文钱?
本题需求四个未知数,如果列四元一次方程组求解,比较繁琐,下面介绍三种比较 简
便的解法. [来源:Zxx k. Com]
一、用算术方法求解(假设法)
因为每个甜果的 价钱为 11 文,每个苦果的价钱为 4 文,假设买的全都是甜果, 那么
