第6章 连续系统的离散化方法及近似解
合集下载
连续属性离散化
根据学习环境选择离散化方法
虽然已有很多离散化方法，但是没有一种离散 化方法对任何数据集以及任何算法都是有效的，也 没有一种离散化方法一定比其他方法产生更好的离 散化结果。因为离散化本身就是一个NP-hard 问题， 所以在使用时一定要根据数据集的特点和学习环境 以及使用者个人的偏好理解等选择合适的离散化方 法，以取得尽可能好的离散化效果。如决策树学习 容易受到碎片问题（碎片是指一个给定分枝中的样 本数太小，没有统计意义）的影响，所以离散化时 更偏好得到较少的离散化区间；决策规则希望离散 化得到的区间中的实例的类标号是唯一的；关联规 则重视特征间的相关性，所以在离散化时不能对各 个特征进行单一的离散化。
离散化结果的评价
• 完全离散化:指算法要能够完成数据集的多个 连续属性的离散化处理。因为我们不太可能只 需要对数据集的某一个连续属性进行离散化处 理，除非数据集只包含一个连续属性。 • 具有最简单的离散化结果:如果离散化处理完 成后，属性空间的规模越小，由这些离散化处 理所产生出来的数据所生成的规则越简单。因 此，由这样的属性所获得的知识就更是通用。
• 基于熵的离散化方法：该方法使用类信息计算 和确定分割点，是一种有监督的、自顶向下的 分裂技术。首先，将初始值切分成两部分，让 两个结果区间产生最小熵；然后，取一个区间， 通常选取具有最大熵的区间，重复此分割过程， 直到区间的个数达到用户指定的个数，或满足 终止条件（当得到的每个区间中的类标号都是 一样时，即停止离散化过程）。 最常用的基于熵的离散化方法是：基于最 短描述长度原则（MDLP）方法。
连续属性离散化方法
1.连续属性离散化的定义？ 2.为什么要对连续属性离散化？
3.连续属性离散化方法有哪些？
定义
连续属性离散化就是采取各种方法将 连续的区间划分为小的区间，并将这连续 的小区间与离散的值关联起来。
连续系统模型的离散化处理方法
只要T不变，三个系数均不变，可以在仿真前预先计算好，这样就减少了以后的计算工作量。 加入一个理想滤波器,保留输入信号主频段,滤掉附加的频谱分量,不失真
在离散化后，模型精度变差，可能不稳定。
S域到Z域的最基本映射关系是：Z=e （T— TS 数值积分法：将微分方程转换成差分方程，这中间是一步步离散，每一步离散都用到连续系统的原模型，这样的速度就慢了。
TeAT
m T
T eATA Bd
0
xKTTTxKTmTUKT
x(k1) TxkmTUk
B 当输入函数u（KT）在两采样 点间线性变化时（一阶保持）
uuKTukT
p
T
TeATABd
0
xkTTTxkTmTUkTpTUkT
xk1TxkmTUkpTUk
当连续系统状态方程系数A、B已知时，
可求出……
此法相比于数值积分法；只要T不变，三个系 数均不变，可以在仿真前预先计算好，这样 就减少了以后的计算工作量。
2 典型环节的离散状态方程
A 积分环节：G（S）=K/S f1=x2 ; f2=x3 ;
依据各环节的连接关系及外部作用函数 稳定性不及双线性替换法，Ts或信号重构器选择不当，离散模型的稳定性变差
二、Z域离散相似方法
1 基本方法
G z
y z u z
z G h s G s
1
z
s a
z exp( aT )
e TS 1 z
1 z
s
z 1
1
Tz
s* s
( z 1 )( z 1 )
Gz
yz uz
zGh
sGs
Gs k
sa
Gh
s
1
在离散化后，模型精度变差，可能不稳定。
S域到Z域的最基本映射关系是：Z=e （T— TS 数值积分法：将微分方程转换成差分方程，这中间是一步步离散，每一步离散都用到连续系统的原模型，这样的速度就慢了。
TeAT
m T
T eATA Bd
0
xKTTTxKTmTUKT
x(k1) TxkmTUk
B 当输入函数u（KT）在两采样 点间线性变化时（一阶保持）
uuKTukT
p
T
TeATABd
0
xkTTTxkTmTUkTpTUkT
xk1TxkmTUkpTUk
当连续系统状态方程系数A、B已知时，
可求出……
此法相比于数值积分法；只要T不变，三个系 数均不变，可以在仿真前预先计算好，这样 就减少了以后的计算工作量。
2 典型环节的离散状态方程
A 积分环节：G（S）=K/S f1=x2 ; f2=x3 ;
依据各环节的连接关系及外部作用函数 稳定性不及双线性替换法，Ts或信号重构器选择不当，离散模型的稳定性变差
二、Z域离散相似方法
1 基本方法
G z
y z u z
z G h s G s
1
z
s a
z exp( aT )
e TS 1 z
1 z
s
z 1
1
Tz
s* s
( z 1 )( z 1 )
Gz
yz uz
zGh
sGs
Gs k
sa
Gh
s
1
第6章连续系统的离散化方法及近似解
第6章连续系统的离散化方法及近似解在连续系统中，我们经常需要将其离散化为离散系统以便于分析和求解。
离散化方法能够将连续系统的微分方程转化为差分方程，从而得到近似解。
本章将介绍连续系统的离散化方法及近似解的计算。
连续系统的离散化方法有许多种，常见的有Euler方法、Runge-Kutta方法和有限差分方法等。
其中，Euler方法是最简单和最基础的离散化方法，其基本思想是将连续时间轴划分为若干个小时间间隔，并用差分逼近连续系统的导数。
具体地，对于一阶常微分方程：\[\frac{{dy}}{{dt}} = f(y, t)\]可以使用Euler方法将其离散化为：\[y_{n+1} = y_n + h \cdot f(y_n, t_n)\]其中，\(y_n\)是时间点\(t_n\)的近似解，\(h\)是时间步长。
Runge-Kutta方法是一种更精确的离散化方法，其基本思想是利用多个中间步骤来更准确地逼近连续系统的导数。
常见的是四阶Runge-Kutta 方法，其公式为：\[y_{n+1} = y_n + \frac{h}{6} \cdot (k_1 + 2k_2 + 2k_3 +k_4)\]其中\[k_1=f(y_n,t_n)\]\[k_2 = f(y_n + \frac{h}{2}k_1, t_n + \frac{h}{2})\]\[k_3 = f(y_n + \frac{h}{2}k_2, t_n + \frac{h}{2})\]\[k_4 = f(y_n + hk_3, t_n + h)\]这样可以得到更准确的近似解。
有限差分方法是一种常用的离散化方法，其基本思想是将连续的导数用差分逼近。
以二阶偏微分方程为例，该方程的一般形式为：\[\frac{{\partial^2u}}{{\partial x^2}} +\frac{{\partial^2u}}{{\partial y^2}} = f(x, y)\]可以使用中心差分公式将其离散化为：\[\frac{{u_{i+1,j} - 2u_{i,j} + u_{i-1,j}}}{{\Delta x^2}} + \frac{{u_{i,j+1} - 2u_{i,j} + u_{i,j-1}}}{{\Delta y^2}} =f_{i,j}\]其中，\(u_{i,j}\) 是近似解在网格点 \((i, j)\) 处的值，\(\Delta x\) 和 \(\Delta y\) 分别是网格在 \(x\) 和 \(y\) 方向的步长，\(f_{i,j}\) 是离散化后的右侧函数。
连续传递函数离散化的方法与原理
连续传递函数离散化的方法与原理连续传递函数离散化是将连续时间域中的传递函数转换为离散时间域中的传递函数的过程。
在控制系统设计中，离散化是非常重要的一步，因为大多数数字控制器本质上只能处理离散的输入和输出信号。
离散化方法的选择对系统的稳定性、性能和可实现性都有很大的影响。
离散化方法分为两大类：时域方法和频域方法。
时域方法根据传递函数的时间响应，或者根据传递函数的微分方程进行转换。
频域方法通过拉普拉斯变换和z变换之间的等价关系进行转换。
时域离散化方法：1. 脉冲响应不变法（Impulse Invariance Method）：这是最常用的离散化方法之一、它通过将连续时间系统的脉冲响应对应到离散时间系统的单位冲激响应上来实现离散化。
该方法的原理是保持连续系统和离散系统的单位冲激响应相同，从而尽可能保持系统的动态特性。
2. 零阶保持法（Zero Order Hold Method）：这个方法假设连续时间系统在每个采样周期内是恒定的，即将采样周期内的连续时间系统输出等效为一个恒定值。
这个方法的原理是根据离散系统的输出间隔和连续时间系统的采样间隔，使用插值方法得到离散系统的输出值。
3. 一阶保持法（First Order Hold Method）：这个方法在零阶保持法的基础上改进，考虑了连续时间系统在每个采样周期内的变化趋势。
它假设连续时间系统在每个采样周期内是线性变化的。
通过插值方法得到离散系统的输出值。
4. 向后微分法（Backward Difference Method）：这个方法根据连续时间系统微分方程中的向后差分近似来实现离散化。
它假设离散时间系统输出的变化率等于连续时间系统输出的变化率。
频域离散化方法：1. 频率响应匹配法（Frequency Response Matching Method）：这个方法将连续时间系统和离散时间系统的频率响应函数进行匹配，使它们在一定频率范围内的增益和相位相近。
通过频率响应函数的等价性，可以使用拉普拉斯变换和z变换之间的关系得到离散时间系统的传递函数。
连续系统离散化方法
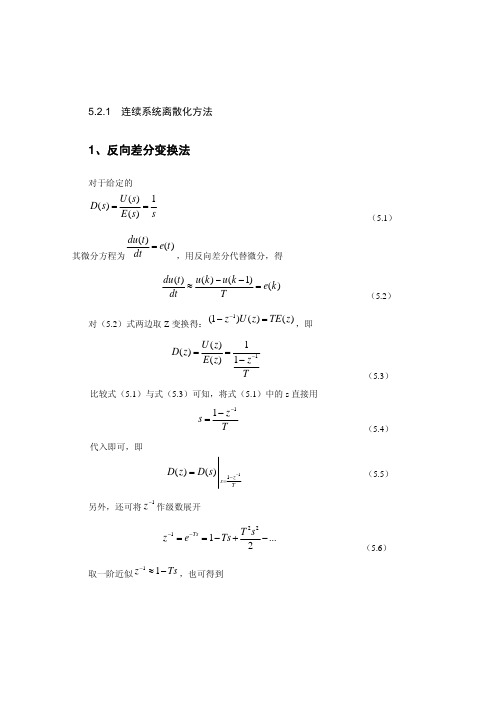
其中 y ( kT ) 为到 kT 时刻的阴影总面积。对式（5.15）进行 Z 变换，并整理得到
Y ( z ) T 1 + z −1 = X ( z ) 2 1 − z −1
（5.16）
图 5-5 梯形面积近似积分
D( z ) = D( s )
由式 （5.16） ， 也可得双线性变换：
s=
2 1− z −1 T 1+ z −1
3、双线性变换法
双线性变换法又称突斯汀（Tustin）法，是一种基于梯形积分规则的数字积分变换方法。 由 Z 变换定义 z = e ，将 e 改写为如下形式：
Ts Ts
第 2 章 计算机控制系统的信号转换
Ts
21
eTs =
e2 e
− Ts 2
（5.12）
然后将分子和分母同时展成泰勒级数，取前两项，得：
Ts 2 z= Ts 1− 2 1+
由上式计算出 s ，得双线性变换公式。
（5.13）
s=
2 1 − z −1 T 1 + z −1
T [ x[(k − 1)T ] + x( kT )] 2
（5.14）
另外，由图 5-5 所示的梯形面积近似积分可得
y (kT ) = y[(k − 1)T ] +
（5.15）
s=Biblioteka z −1 T(5.11）
另外还可将 z 级数展开 ：
z = eTs = 1 + Ts +
T 2s2 + ... 2
20
第 2 章 计算机控制系统的信号转换
取一阶近似 z ≈ 1 + Ts ，也可得到：
s=
z −1 T
连续系统的离散化方法课件
离散化方法的意义
精确性
离散化方法可以提供对连续系统的精 确近似，特别是在计算机仿真和数字 控制系统中。
可计算性
离散化方法可以将不可计算的分析转 化为可计算的形式，便于进行数值计 算和控制器设计。
离散化方法的应用场景
01
02
03
数字控制
在数字控制系统中，连续 系统的离散化是必要的步 骤，以便在数字计算机上 进行数值计算和控制。
小波基选择
常用的小波基包括Haar小波、Daubechies小波、Morlet 小波等。
误差分析
小波变换法的误差主要来自于变换误差和离散化误差。
05
离散化方法的评估与优化
评估离散化方法优劣的标准
01
02
03
04
精度
离散化方法是否能准确代表原 连续系统。
稳定性
离散化方法在一定参数变化范 围内是否能保持稳定。
状态空间模型
用状态变量和输入、输出变量描述连续系统的动态特性。
状态空间模型通常形式为：`x'(t) = Ax(t) + Bu(t)` 和 `y(t) = Cx(t) + Du(t)`，其中 `x(t)` 表 示系统状态，`u(t)` 表示系统输入，`y(t)` 表示系统输出，`A`, `B`, `C`, `D` 是系数矩阵。
化率。
通过求解 ODE，可以得到系统 在任意时刻的状态。
传递函数
表示连续系统在输入和输出之间的传递 特性。
传递函数通常形式为：`G(s) = Y(s) / U(s)`，其中 `Y(s)` 和 `U(s)` 分别是输 出和输入的拉普拉斯变换，`s` 是复变
量。
通过分析传递函数的零点、极点和增益 ，可以得到系统的稳定性和性能特性。
2.6 连续时间系统状态方程的离散化
0 0 1 1 0 1 1 0 0 0 1 0 0.63 1 1 0.37 0 1.37 0.37 0 0 0.63 1 0.63 0.865 1.37 1 0.135 0 2.05 0.135 0.63 0 0.865 1 0.95
1 (3)H(T) 0 0
T
T 1 1 / 2(1 e2 t ) 0 dt 0 2 t e 1 0
x 1[(k 1)T] x 1 (kT) (4) G(T) H(kT) U(kT) x 2 [(k 1)T] x 2 (kT)
1
解：
例2.5已知控制对象满足 0 1 0 x x u，求其离散化方程 2 0 1
2 t 1 1 / 2 ( 1 e ) 1 1 （ 1 ）( t ) L [SI A] 2 t e 0 1 1 / 2(1 e 2 t ) (2)G (T) ( t ) t T 2 t e 0
1 2T 2 t ( 2 T e 1 ) 1 / 2(1 e ) 4 dt 1 2 t 2 T e (1 e ) 2
说明：（1）当T选定后（如T＝0.5秒）G(t)和
H(t)都是确定的系数矩阵
(2)离散化后得状态方程，可按递推法或
At 1 1
（2）由u(kT)=r(kT)-y(kT)=r(kT)-x1 (kT),代入，得系统的离散化 状态方程。
x1[(k 1)] 1 1 e T x1 (kT ) T e T 1 u (kT ) x [(k 1)] T T e x2 (kT ) 1 e 2 0 2 T e T 1 e T x1 (kT ) T e T 1 T r (kT ) T T e x2 (kT ) 1 e e 1
计算机控制原理第6章2
7
数字PID 数字PID 控制器的另一个参数对系统 性能的影响
(4) 采样周期T的选择原则 采样周期T
从信号不失真要求上，必须满足采样定理的要求。 从控制系统的随动和抗干扰的性能来看，则T小些好。 根据执行机构的类型，当执行机构动作惯性大时，T应取大些。否则执行 机构来不及反应控制器输出值的变化。 从计算机的工作量及每个调节回路的计算成本来看，T应选大些。T大对 每个控制回路的计算控制工作量相对减小，可以增加控制的回路数。 从计算机能精确执行控制算式来看，T应选大些。因为计算机字长有限， T过小，偏差值e(k)可能很小，甚至为0，调节作用减弱,各微分、积分作用 不明显。
• 将连续系统的时间离散化：
t = KT ,
• 积分用累加求和近似：
t K
( K = 0, 1, L , n)
K
∫ e(t )dt = ∑ e( j )T = T ∑
0 j =0 j =0
e( j )
• 微分用一阶后向差分近似：
de(t ) e(k ) − e(k − 1) ≈ dt T
12
TD u (k ) = K p {e(k ) + ∑ e( j ) + [e(k ) − e(k − 1)]} TI j =0 T
TD u (k − 1) = K p {e(k − 1) + ∑ e( j ) + [e(k − 1) − e(k − 2)] TI j =0 T T
6
PID 控制器参数对系统性能的影响
(3) 微分时间常数TD对系统性能的影响 微分时间常数T 微分控制可以改善动态特性，如超调量减小，调节时间缩短 ，允许加大比例控制，使稳态误差减小，提高控制精度。 当TD偏大时，超调量较大，调节时间较长; 当TD偏小时，超调量也较大，调节时间也较长; 只有TD合适时，可以得到比较满意的过渡过程。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
计算轴的动能和势能 1 l T I P ( x) 2dx 2 0 l n n I P ( x) i ( x)qi (t ) j ( x)q j (t ) dx
2 0 i 1 n n 1 mij qi (t )q j (t ) 2 i 1 j 1 j 1
0
l
设梁上分别受到分布力f(x,t)和 x xd 处的集中力F(x,t)
当梁上有虚位移
l 0
w( x, t ) i qi 外力虚功为
i 1
n
ቤተ መጻሕፍቲ ባይዱ
W f ( x, t ) F (t ) ( x xd ) w( x, t )dx
l f ( x, t )i ( x)dx F (t )i ( xd ) qi 0 i 1 n
T
0.5199 2 0 Al 0.7746
T
求梁的响应时，将位移写作假设模态的线性组合
i x w( x, t ) i ( x)qi (t ) qi (t )sin l i 1 i 1
1 l n n EI ( x) i( x)qi (t ) j ( x) q j (t ) dx 0 2 i 1 j 1
1 n n k1 i( xb )qi (t ) j ( xb ) q j (t ) 2 i 1 j 1
得到原来问题的模态向量
3 x ( x) sin 0.0681sin 2l 2l
(1)
x
(2) ( x) 0.1955sin
x
2l
sin
3 x 2l
例：等截面简支梁中部有集中质量，并受有集中力 设集中质量 M a 等于梁的质量
集中力的变化的频率
50 EI / Al 4
M AT dx
0
0 l
广义质量系数
广义质量矩阵
若梁上还有集中质量，如右图
则梁的动能为
1 l 1 2 T Aw dx mw2 ( xa ) 2 0 2 n 1 l n A( x ) i ( x )qi (t ) j ( x)q j (t ) dx 2 0 i 1 j 1 n n 1 m i ( xa )qi (t ) j ( xa )q j (t ) 2 i 1 j 1 n n 1 mij qi (t )q j (t ) 1 qT Mq 2 i 1 j 1 2 l 则质量系数为 mij A( x)i ( x) j ( x)dx mi ( xa ) j ( xa )
第六章 连续系统的离散化方法及近似解
连续系统的精确解只适用于简单构件形状和边界条件，关 于这些精确解的讨论和分析有助于理解连续体振动的基本 特征，也有助于构造近似解和检验近似方法的误差。 当构件形状复杂或边界条件复杂时，只能求近似解 各种近似方法的共同点是：将无限自由度系统离散为有限 自由度系统。离散的自由度数由取决于所要求的计算精度。 常用的近似解法大致分为两大类：物理离散法和函数展开法 物理离散法： 集中质量法 传递矩阵法 假设模态法 加权残数法
1 l T A( x )w2 dx 2 0
mij A( x)i ( x) j ( x)dx
l
1 l n n A( x ) i ( x )qi (t ) j ( x)q j (t ) dx 2 0 i 1 j 1 1 n n 1 mij qi (t )q j (t ) qT Mq 2 i 1 j 1 2
0
梁的弯曲势能
1 l V EI ( x )w2 dx 2 0 1 l n n EI ( x ) i( x)qi (t ) ( x)q j (t ) dx j 2 0 i 1 j 1
1 n n kij qi (t )q j (t ) 2 i 1 j 1
i ( x) 应该是实际的模态函数，但实际计算时，常无法得到，
所以通常以假设模态代替
i 1
假设模态一般为满足全部或部分边界条件（至少应满足位移 边界条件），但不一定满足动力平衡方程的试函数族
用假设模态法可以建立有限个广义坐标表示的动力学方程， 也可以直接利用能量法，即Rayleigh和Ritz法计算固有频率 。
W qT Q
(i 1, 2, n)
L T V
Lagrange函数
得到有限个广义坐标表示的动力学方程
(m q
j 1 ij
n
j
kij q j ) Qi
(i 1, 2,
n)
矩阵形式为
Mq Kq Q
连续系统的问题转化成了有限自由度问题 以上讨论是针对梁的弯曲振动，但该方法同样也适用于如 轴的扭转振动等其它形式的振动。以例说明
i 1
n
其中
mij m ji I P ( x)i ( x) j ( x)dx
0
l
1 l V GI P ( x)[ (x, t )]2dx 2 0
1 l n n GI P ( x) i ( x)qi (t ) j ( x)q j (t ) dx 2 0 i 1 j 1 n n 1 kij qi (t )q j (t ) 2 i 1 j 1
16l 3 22 768 EI
11l 12 21 23 32 768EI
3
768 EI
7
11
9
如此，可计算系统的固有频率 也可将梁简化成两个自由度或单自由度系统
在求得相应的质量矩阵和 柔度矩阵后，便可计算系 统的固有频率 计算结果可见下表
连续系统
自由度越多，计算精度越高；基频的精度要高于高频的精度； 频率的阶次越高，误差越大。 注：集中质量法的计算精度与梁的边界条件有关
例：设图示变截面轴一端固定，另一端自由 距固定端x处截面的二次极矩为
x I P ( x) I 0 1 2l
O
x
l
x
I 0 为固定端处截面的二次极矩
求：该轴扭转振动的前二阶固有频率
解：将轴的扭转振动写作假设模态的线性组合
( x, t ) i ( x)qi (t )
1 n n k2 i ( xc )qi (t ) j ( xc )q j (t ) 2 i 1 j 1
1 n n 1 kij qi (t )q j (t ) qT Kq 2 i 1 j 1 2
其中，刚度系数为
Kij EI ( x)i( x) j ( x)dx k1i ( xb ) j ( xb ) k2i ( xc ) j ( xc )
m1 m2 m3 m / 4
1 0 0 m M 0 1 0 4 0 0 1
各质点间有相同的弹性性质，可利用材料力学或结构力学知 识计算各点的柔度影响系数并由此得到柔度矩阵。 7l 3 9l 3 9 11 7 13 31 3 11 33 l 11 16 11 768 EI 768 EI
K - 2M 0
EI 2 39.4784 Al 4
解得
EI 3 68.9944 Al 4
正则特征向量
a (1) 0.5742 2 0 Al 0.0048
T
a (2)
0 2 (3) 1 a Al 0
0
l
k11 GI P ( x)[1( x)]2 dx 1.0503GI 0 / l
0
l
因此有
k11 G 1 1.7996 m11 l 2
若欲求前二阶频率，可取n=2，计算得到
0.3243 0.0380 M I 0l 0.0380 0.3806
函数展开法
有限元法
里茨法
兼有上面这两类方法的特点
§6.1 集中质量法
以等截面简支梁为例 设梁的长度为l 密度为 弯曲刚度为EI 截面积为A 则梁的质量为 m Al 将梁分为四段，再将每小段的质量平均分到该段的两端 支点处的质量不影响梁的弯曲振动 连续梁可用三个集中质量代替 得到图示的三自由度系统 系统的质量矩阵为
GI 0 K l
代入本征方程
K - 2M 0
1.0503 0.375 0.375 8.4525
G G 1 1.7723 2 4.7795 解得 2 l l 2 T (1) T (2) a 1 0.0681 并有特征向量 a 0.1955 1
1 T q Kq 2
Kij EI ( x)i ( x) j ( x )dx K EI T dx
0 l 0
l
广义刚度系数 广义刚度矩阵
显然M和K都是对称矩阵 若梁上还有弹簧支承，如下图
则梁的势能为
1 l 1 1 2 2 V EI ( x) w dx k1w ( xb ) k2 w2 ( xc ) 2 0 2 2
Qi qi qT Q
Qi f ( x, t )i ( x)dx F (t )i ( xd )
Q Q1 Q2
0 l
n
i 1
广义力
Qn
T
广义力列阵
系统的动能、势能及外力虚功为
1 T T q Mq 2
由Lagrange方程
1 T V q Kq 2 d L L Qi dt qi qi
其中
kij k ji GI P ( x)i( x) j ( x)dx
0
l
取一端固定另一端自由的等截面轴的模态函数为试函数
2i 1 x i ( x) sin 2 l
2 0 i 1 n n 1 mij qi (t )q j (t ) 2 i 1 j 1 j 1
0
l
设梁上分别受到分布力f(x,t)和 x xd 处的集中力F(x,t)
当梁上有虚位移
l 0
w( x, t ) i qi 外力虚功为
i 1
n
ቤተ መጻሕፍቲ ባይዱ
W f ( x, t ) F (t ) ( x xd ) w( x, t )dx
l f ( x, t )i ( x)dx F (t )i ( xd ) qi 0 i 1 n
T
0.5199 2 0 Al 0.7746
T
求梁的响应时，将位移写作假设模态的线性组合
i x w( x, t ) i ( x)qi (t ) qi (t )sin l i 1 i 1
1 l n n EI ( x) i( x)qi (t ) j ( x) q j (t ) dx 0 2 i 1 j 1
1 n n k1 i( xb )qi (t ) j ( xb ) q j (t ) 2 i 1 j 1
得到原来问题的模态向量
3 x ( x) sin 0.0681sin 2l 2l
(1)
x
(2) ( x) 0.1955sin
x
2l
sin
3 x 2l
例：等截面简支梁中部有集中质量，并受有集中力 设集中质量 M a 等于梁的质量
集中力的变化的频率
50 EI / Al 4
M AT dx
0
0 l
广义质量系数
广义质量矩阵
若梁上还有集中质量，如右图
则梁的动能为
1 l 1 2 T Aw dx mw2 ( xa ) 2 0 2 n 1 l n A( x ) i ( x )qi (t ) j ( x)q j (t ) dx 2 0 i 1 j 1 n n 1 m i ( xa )qi (t ) j ( xa )q j (t ) 2 i 1 j 1 n n 1 mij qi (t )q j (t ) 1 qT Mq 2 i 1 j 1 2 l 则质量系数为 mij A( x)i ( x) j ( x)dx mi ( xa ) j ( xa )
第六章 连续系统的离散化方法及近似解
连续系统的精确解只适用于简单构件形状和边界条件，关 于这些精确解的讨论和分析有助于理解连续体振动的基本 特征，也有助于构造近似解和检验近似方法的误差。 当构件形状复杂或边界条件复杂时，只能求近似解 各种近似方法的共同点是：将无限自由度系统离散为有限 自由度系统。离散的自由度数由取决于所要求的计算精度。 常用的近似解法大致分为两大类：物理离散法和函数展开法 物理离散法： 集中质量法 传递矩阵法 假设模态法 加权残数法
1 l T A( x )w2 dx 2 0
mij A( x)i ( x) j ( x)dx
l
1 l n n A( x ) i ( x )qi (t ) j ( x)q j (t ) dx 2 0 i 1 j 1 1 n n 1 mij qi (t )q j (t ) qT Mq 2 i 1 j 1 2
0
梁的弯曲势能
1 l V EI ( x )w2 dx 2 0 1 l n n EI ( x ) i( x)qi (t ) ( x)q j (t ) dx j 2 0 i 1 j 1
1 n n kij qi (t )q j (t ) 2 i 1 j 1
i ( x) 应该是实际的模态函数，但实际计算时，常无法得到，
所以通常以假设模态代替
i 1
假设模态一般为满足全部或部分边界条件（至少应满足位移 边界条件），但不一定满足动力平衡方程的试函数族
用假设模态法可以建立有限个广义坐标表示的动力学方程， 也可以直接利用能量法，即Rayleigh和Ritz法计算固有频率 。
W qT Q
(i 1, 2, n)
L T V
Lagrange函数
得到有限个广义坐标表示的动力学方程
(m q
j 1 ij
n
j
kij q j ) Qi
(i 1, 2,
n)
矩阵形式为
Mq Kq Q
连续系统的问题转化成了有限自由度问题 以上讨论是针对梁的弯曲振动，但该方法同样也适用于如 轴的扭转振动等其它形式的振动。以例说明
i 1
n
其中
mij m ji I P ( x)i ( x) j ( x)dx
0
l
1 l V GI P ( x)[ (x, t )]2dx 2 0
1 l n n GI P ( x) i ( x)qi (t ) j ( x)q j (t ) dx 2 0 i 1 j 1 n n 1 kij qi (t )q j (t ) 2 i 1 j 1
16l 3 22 768 EI
11l 12 21 23 32 768EI
3
768 EI
7
11
9
如此，可计算系统的固有频率 也可将梁简化成两个自由度或单自由度系统
在求得相应的质量矩阵和 柔度矩阵后，便可计算系 统的固有频率 计算结果可见下表
连续系统
自由度越多，计算精度越高；基频的精度要高于高频的精度； 频率的阶次越高，误差越大。 注：集中质量法的计算精度与梁的边界条件有关
例：设图示变截面轴一端固定，另一端自由 距固定端x处截面的二次极矩为
x I P ( x) I 0 1 2l
O
x
l
x
I 0 为固定端处截面的二次极矩
求：该轴扭转振动的前二阶固有频率
解：将轴的扭转振动写作假设模态的线性组合
( x, t ) i ( x)qi (t )
1 n n k2 i ( xc )qi (t ) j ( xc )q j (t ) 2 i 1 j 1
1 n n 1 kij qi (t )q j (t ) qT Kq 2 i 1 j 1 2
其中，刚度系数为
Kij EI ( x)i( x) j ( x)dx k1i ( xb ) j ( xb ) k2i ( xc ) j ( xc )
m1 m2 m3 m / 4
1 0 0 m M 0 1 0 4 0 0 1
各质点间有相同的弹性性质，可利用材料力学或结构力学知 识计算各点的柔度影响系数并由此得到柔度矩阵。 7l 3 9l 3 9 11 7 13 31 3 11 33 l 11 16 11 768 EI 768 EI
K - 2M 0
EI 2 39.4784 Al 4
解得
EI 3 68.9944 Al 4
正则特征向量
a (1) 0.5742 2 0 Al 0.0048
T
a (2)
0 2 (3) 1 a Al 0
0
l
k11 GI P ( x)[1( x)]2 dx 1.0503GI 0 / l
0
l
因此有
k11 G 1 1.7996 m11 l 2
若欲求前二阶频率，可取n=2，计算得到
0.3243 0.0380 M I 0l 0.0380 0.3806
函数展开法
有限元法
里茨法
兼有上面这两类方法的特点
§6.1 集中质量法
以等截面简支梁为例 设梁的长度为l 密度为 弯曲刚度为EI 截面积为A 则梁的质量为 m Al 将梁分为四段，再将每小段的质量平均分到该段的两端 支点处的质量不影响梁的弯曲振动 连续梁可用三个集中质量代替 得到图示的三自由度系统 系统的质量矩阵为
GI 0 K l
代入本征方程
K - 2M 0
1.0503 0.375 0.375 8.4525
G G 1 1.7723 2 4.7795 解得 2 l l 2 T (1) T (2) a 1 0.0681 并有特征向量 a 0.1955 1
1 T q Kq 2
Kij EI ( x)i ( x) j ( x )dx K EI T dx
0 l 0
l
广义刚度系数 广义刚度矩阵
显然M和K都是对称矩阵 若梁上还有弹簧支承，如下图
则梁的势能为
1 l 1 1 2 2 V EI ( x) w dx k1w ( xb ) k2 w2 ( xc ) 2 0 2 2
Qi qi qT Q
Qi f ( x, t )i ( x)dx F (t )i ( xd )
Q Q1 Q2
0 l
n
i 1
广义力
Qn
T
广义力列阵
系统的动能、势能及外力虚功为
1 T T q Mq 2
由Lagrange方程
1 T V q Kq 2 d L L Qi dt qi qi
其中
kij k ji GI P ( x)i( x) j ( x)dx
0
l
取一端固定另一端自由的等截面轴的模态函数为试函数
2i 1 x i ( x) sin 2 l